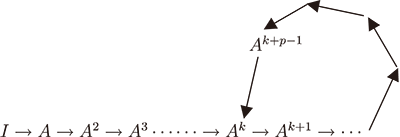| 發刊日期 |
2008年9月
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 標題 | 尋尋冪冪……—非負矩陣冪序列初探 |
|||||||||
| 作者 | ||||||||||
| 關鍵字 | ||||||||||
| 檔案下載 | ||||||||||
| 全文 |
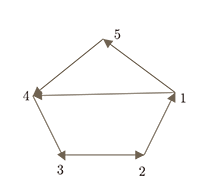
數與形的聯繫和轉化, 是數學永恆的主題。 自從電子計算機誕生以來, 資料的處理、運算成了電腦的拿手好戲, 而為了把形的研究放到電腦中進行, 數學家的看家本領是實現形和數的一一對應。 把空間中形的定性關係轉化為數之間的定量關係, 把曲線、曲面, 轉化成方程, 從而實現空間(包括平面)圖形的電腦處理。 而對於只考慮點與線連接的拓樸圖形, 則借助於矩陣把它對應成數表。 現在, 讓我們看看它是如何「變臉」的。 一.把圖存到電腦中一個網路可以看作是一個有向圖。 它的邊是按箭頭方向連通的, 稱為弧。以圖1的一個網路 $D1$ (有向圖)為例, 點 $i$ 到點 $j$ 的弧記為 $\overrightarrow{ij}$, 它稱為 $i$ 的出弧或 $j$ 的入弧, 每個點的出弧(入弧)數稱為該點的出度(入度)。
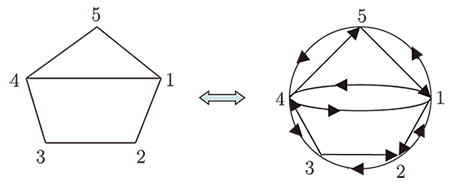
要把這個圖「數位化」, 我們把它「變臉」成一個矩陣, $n$ 階圖($n$ 個頂點)對應於一個 $n\times n$ 方陣(或稱 $n$ 階方陣)。 第 $i$ 個點對應於方陣中的第 $i$ 列(row), 第 $i$ 行(column), 而點 $i$ 到點 $j$ 有弧, 對應於矩陣中第 $i$ 列第 $j$ 行的位置有1, 否則, 在矩陣中第 $i$ 列第 $j$ 行中位置為0, 於是 $D_{1}$, 就成下面的一個5階方陣(或記作 $A(D_{1})$)。 $$ A_{1}= \begin{array}{cc} & \begin{array}{ccccc} \hbox{(1) } & \hbox{(2) } & \hbox{(3) } & \hbox{(4) } & \hbox{(5) } \end{array} \\ \begin{array}{c} (1) \\ (2) \\ (3) \\ (4) \\ (5) \end{array} & \left [ \begin{array}{ccccc} ~0~ & ~0~ & ~0~ & ~1~ & ~1~\\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{array} \right ] \end{array} $$ 顯然, 這種對應是一一的, 於是, 圖 $D_{1}$, 可以通過數(矩陣 $A_{1}$)存儲到電腦中, 或者參與 $(0, 1)$ 矩陣規定的各種運算和交換, 從而導出 $D_{1}$ 的各種性質。 $A_{1}$ 稱為 $D_{1}$ 的鄰接矩陣(adjacency matrix), 而 $D_{1}$ 稱為 $A_1$ 的伴隨有向圖(associated digragh)也可記作 $D(A_{1})$。 如果我們把 $D_{1}$ 中各弧的方向去掉, 可以變成圖2左邊的無向圖 $D_{2}$; 進而把 $D_{2}$ 的每一邊劃成來回的兩條弧, 則我們可把 $D_{2}$ 看作是有向圖 $D_{2}^{\prime}$。
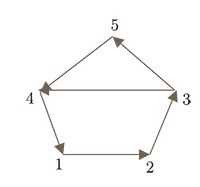
於是 $D_{2}$ 的鄰接矩陣 $$ A_{2}= \left [ \begin{array}{ccccc} ~0~ & ~1~ & 0~ & ~1~ & ~1~ \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \end{array} \right ] $$ $A_{2}$ 體現出來的特徵是: 所有的 0, 1以主對角線(位置 $(1, 1)(2, 2)\cdots(5, 5)$)為對稱。 這樣的 $A_{2}$ 矩陣稱為對稱陣(symmetric matrix), 如果把 $A$ 的轉置矩陣記作 $A^{T}$, 若 $A=A^{T}$, $A$ 稱為對稱陣。 $D_{3}$ 是 $D_{1}$ 中把頂點1和3的標號互換的結果。這反映到鄰接矩陣上,
把 $A_{1}$ 中的第一列(row)與第3列, 第一行(column)與第3行互換, 就能得到 $D_{3}$ 的鄰接矩陣 $A_{3}$。這一變換, 在矩陣論中, 即把 $A_{1}$ 左乘一個置換矩陣 $P_{1}$ (第一列與第3列互換)和右乘一個置換矩陣 $P_{1}^{T}$。 $$ P_{1} = \left [ \begin{array}{ccccc} ~0~ & ~0~ & 1~ & ~0~ & ~0~ \\ 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array} \right ] $$ 所謂置換矩陣, 就是每行每列恰有一個1的 $(0, 1)$ 方陣。 一個最簡單的置換矩陣, 就是僅僅主對角線為1的 $n$ 階方陣, 簡稱為恒等陣, 記作 $I_{n}$ 。 易見, $P_{1}$ 只不過把 $I_{5}$ 中 $(1, 1)$ 位置的1移到 $(1, 3)$ 位置上, $(3, 3)$ 位置的1移到 $(3, 1)$ 位置上。 $P_{1}A_{1}$ 就實現了把 $A_{1}$ 的第1列與第3列對調。 於是, $A_{3}=A(D_{3})=P_{1}A_{1}P_{1}^{T}$, 我們稱 $A_{1}$ 與 $A_{3}$ 是置換相似。 若 $A$ 與 $B$ 置換相似, 則它們的伴隨有向圖是同構的, 簡言之, 若把它們的頂點標號抹去, 兩個圖沒有什麼不同。 從上所述, 置換矩陣就是《線性代數》中置換的矩陣刻畫。 $1, 2, \ldots, n$ 的排列數, 就是不同 $n$ 階置換陣的個數, 即 $n!$ 個。 翻開高等代數或線性代數教材, 有一條用代數方法不容易證明的定理: 任何一個置換均可分解為互相獨立的輪換的乘積。 用上述 $(0, 1)$ 矩陣的圖論描述可以簡明地如下證出來。 證明: 任一個置換對應於一個置換陣 $A$, $A$ 的每行每列恰有一個1, 即它的伴隨有向圖每一點的出度為1, 入度也為1。即 $D(A)$ 必是由若干個有向圈組成的圖。 每個有向圈對應於一個獨立的輪換。定理得證。 二.「前度劉郎今又來」0和1是最簡單的整數, 如果我們不從數量的大小去比較它, 而賦於它「無」與「有」的意義。 則 $(0, 1)$ 矩陣可以定性地刻劃圖的組合性質。以兩個頂點的所謂可達性為例。 設有向圖 $D=(V, X)$, 其中 $V$ 是頂點集, $X$ 是弧集。 一個有向圖的一條(有向)途徑(walk)是頂點與弧的一個交替序列, $v_{0}$, $x_{1}$, $v_{1}$, $\ldots$, $x_{k}$, $v_{k}$, 其中 $v_{i}\in V$, $x_{i}\in X$, $i=1,2\cdots k$, 且 $x_{i}=\overrightarrow{v_{i-1}v_{i}}$, 這樣一條途徑的長是 $k$, 即其中出現弧的數目為 $k$ 。 一條閉途徑的起點和終點是同一個點。所有點不同的途徑稱為路(path), 僅起點終點相同的路稱為圈。 若有一條路從頂點 $u$ 到頂點 $v$, 則 $v$ 稱為是從 $u$ 可達的。 若一個圖的任何兩個頂點都可達, 則這個圖稱為強連通圖。 如果我們用1和0分別表示 $u$ 到 $v$ 的可達與不可達, 而加法「$+$」表示「並」的意義, 容易理解 $0+0=0$, $1+0=0+1=1$, $1+1=1$, 它們可解析為: 若沒有從 $u$ 到 $v$ 的任何路, 則從 $u$ 不可達 $v$, 若有路從 $u$ 到 $v$,不管是一條路還是兩條路, 都從 $u$ 可達 $v$。 把此加法運算定義列成表。
僅僅 $1+1=1$ 與我們通常的運算不同。若0, 1的乘法保持我們慣用的法則, 則這樣的 $(0, 1)$ 矩陣稱為布爾矩陣(Boolean matrix), 上述運算稱為布爾運算。 (試設想, 如果我們把1和0分別表示數的奇, 偶性, 那麼上述加法表中, 應該改動為 $1+1=0$。 又, 如果我們把上述加法表中改為 $1+1=2$, 則加法可解析為「從 $u$ 到達 $v$ 的路的條數」, 而不僅僅是可達性。) 現在, 我們考察布爾矩陣的冪。 試看 $A_{1}$ $$ A_{1}^{2} = \left [ \begin{array}{ccccc} ~0~ & ~0~ & ~1~ & ~1~ & ~0~ \\ 0 & 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{array} \right ], \qquad\qquad A_{1}^{3} = \left [ \begin{array}{ccccc} ~0~ & ~1~ & ~1~ & ~0~ & ~0~ \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \end{array}\right] $$ 按照上述布爾矩陣的組合意義, $A_{1}^{2}$ 正說明網路 $D_{1}$ 中, 每一個點 $i$ 到另一個點 $j$, 是否有長為2的途徑。 例如, $A_{1}^{2}$ 表明從點1到點3、點4都有長為2的途徑, 而到其他點沒有此類途徑(見圖1)。 類似, $A_{1}^{3}$ 表明 $D_{1}$ 中從點3可以用長為3的途徑到達點4和點5, 但卻不能到達點1, 2, 3。 當然, 從圖 $D_{1}$ 中, 我們亦不難得出結論, 但在一個密如蛛網的道路系統中, 用布爾矩陣的冪運算遠比直觀搜索容易和準確得多。 一般地, 我們有下列結論。 性質1: 設 $n$ 階布爾矩陣 $A=(a_{ij})$, 記 $A^{k}=(a_{ij}^{(k)})$。 則 $a_{ij}^{(k)}=1$ 當且僅當 $D(A)$ 中存在一條從點 $i$ 到點 $j$ 的長為 $k$ 的途徑。 證明: 由矩陣乘法法則, \begin{equation} %(1) a_{ij}^{(k)} = \sum_{1\le i_{1}, i_{2}, \ldots, i_{k-1}\le n} a_{ii_{1}} a_{i_{1}i_{2}} \cdots a_{i_{i_{k-1}}j} \end{equation} 因 $A$ 是布爾矩陣, 故 $a_{ij}^{(k)}=1$ 當且僅當式(1)右邊的和式中至少有一項不等於零, 當且僅當存在 $1\le i_{1},i_{2},\ldots,i_{k-1}\le n$ 使得 $a_{ii_{1}}\not =0$, $a_{i_{1}i_{2}}\not =0$, $\ldots a_{i_{k-1}j}\not =0$。 由伴隨有向圖的定義, 這一結論成立當且僅當 $D(A)$ 中存在一條從點 $i$ 到點 $j$ 的長為 $k$ 的途徑。 證畢。 在談到 $A$ 的冪時, 事實上, 我們涉及到布爾矩陣 $A$ 的乘法。 容易知道, $n$ 階布爾矩陣一共有 $2^{n^{2}}$ 個。 因此, 它組成一個有限集 $B_{n}$。 對於矩陣的乘法「$\bullet$」, 它是封閉的, 有恆等元 $I_{n}$, 且滿足結合律。 因此 $(B_{n}, \bullet)$ 就構成了一個有限半群。 對於 $A$ 的冪, 理論上, 我們可以從 $I$ 開始不斷地, 乘 $A$, 就得到 $I$, $A$, $A^{2}$, $A^{3}$,$\ldots\ldots$ 形成一個冪序列。 但由於 $(B_{n}, \bullet)$ 的有限性, 卻使這個冪序列不能含無限多個不同的矩陣, 無窮序列中的有限個元素, 便產生了如下的一種必然出現的迴圈模式($\rightarrow$ 表示乘 $A$)。
於是, 必出現 $A^{k+p}=A^{k}$, $k$ 是非負整數, $p$ 是正整數, 即序列 $\{A^{j}\}$, $j=0, 1, 2, \ldots\ldots$ 從第 $k+1$ 項 $A^{k}$ 起, 作週期性變化, 「前度劉郎今又來」, 準確地說 $\{I, A, \ldots\ldots A^{k+p-1}\}$ 對乘法成一個 $k+p$ 階半群。 我們稱 $p=p(A)$ 為 $A$ 的冪振動週期, 簡稱週期(period)。 $k=k(A)$ 是 $A$ 的收斂指數, 簡稱指數(index)。用數學語言來說, $k(A)$ 是使 $A^{k}=A^{k+1}t$ 是某個正整數, 成立的最小非負整數, 而 $p(A)$ 是使 $A^{k}=A^{k+p}$ 成立的最小整數。 於是冪序列 $\{A^{j}\}$ 的變化狀態被 $p(A)$ 和 $k(A)$ 所決定。 特別地, 存在正整數 $k$, 使 $A^{k}=J$ 的矩陣 $A$ 稱為本原矩陣, 而使 $A^{k}=J$ 成立的最小正整數 $k$, 稱為 $A$ 的本原指數(exponent)。 顯然, 本原矩陣 $A$ 有 $A^{k}=A^{k+1}=A^{k+2}=\cdots\cdots=J$, 因此, 它的週期 $p(A)=1$。 如果 $A$ 是本原陣, 由上述論述可知, 它的伴隨有向圖 $D(A)$ 具有一個有趣的性質: 存在一個正整數 $k$, 使 $D(A)$ 中的每一點到圖中的每一個頂點(包括自身)都有長為 $m$ 的途徑, 這裏 $m$ 是不小於 $k$ 的任一個整數。
我們把所有 $n$ 階本原矩陣的集合記為 $P_{n}$ 。顯見, $P_{n}\subset B_{n}$ 。
不要以為 $P_{n}$ 只是 $B_{n}$ 中的一類非常特殊的矩陣, Moon和Moser (1966 記 $|M|$ 是集合 $M$ 的基數(即有限集的元數), 則 $$ \lim_{n\rightarrow\infty} \frac{|P_{n}|}{|B_{n}|} = \lim_{n\rightarrow\infty} \frac{|P_{n}|}{2^{n^{2}}} = 1. $$
這就是說: 幾乎所有 $n$ 階 $(0, 1)$ 矩陣都是本原陣。
在 三.與狼共舞讓我們用布爾矩陣解決一個「與狼共舞」的問題。 兩名獵人帶著兩隻惡狼過河, 現只有一隻小船, 每次最多能乘兩個人, 或兩隻狼, 或一人一狼, 為避免惡狼傷人, 人和狼同時在場時, 人數不能少於狼數, 船過河一次要花10分鐘, 問最短幾分鐘能使獵人和狼都能過河? 這是一個常見的智力問題, 靠靈機一動或靈機幾動, 當然可以把答案湊出來, 但是, 要程式化地, 把解做出來, 還得靠數學。 正如著名數學家和數學教育家波利亞 (G. Polya) 所說的「能用一次的想法只不過是一個竅門, 能用一次以上的想法就成為一種方法了」。 我們用布爾矩陣的方法探索這個問題。 不妨設渡河從左岸到右岸。用 $(m, n, l)$ 表示左岸有 $m$ 個人, $n$ 只狼, 用 $(m, n, r)$ 表示右岸有 $m$ 個人, $n$ 只狼。於是, 從左岸到右岸全部可能的狀態為: $$ \begin{array}{lccl} v_{1} = (2, 2, l) \qquad\qquad & \qquad & \qquad & \qquad\qquad v_{7} = (2,2,r) \\ v_{2} = (2, 1, l) \qquad\qquad & \qquad & \qquad & \qquad\qquad v_{8} = (2,1,r) \\ v_{3} = (1, 1, l) \qquad\qquad & \qquad & \qquad & \qquad\qquad v_{9} = (1,1,r) \\ v_{4} = (2, 0, l) \qquad\qquad & \qquad & \qquad & \qquad\qquad v_{10} = (2,0,r) \\ v_{5} = (0, 2, l) \qquad\qquad & \qquad & \qquad & \qquad\qquad v_{11} = (0,2,r) \\ v_{6} = (0, 1, l) \qquad\qquad & \qquad & \qquad & \qquad\qquad v_{12} = (0,1,r) \end{array} $$ 我們把上述12個點畫成一個圖。若從一個點的狀態可以轉移成另一個點的狀態, 則兩個點之間連一條邊。 於是, 我們便可得到一個圖 $G$ (圖5)。
渡河, 便是從圖中尋找一條從 $v_{1}$ 到達 $v_{7}$ 的途徑, 而最短的途徑便是花最小時間的渡河方案。 我們把眼花繚亂的圖, 轉化為易於處理和識別的數位, 即借助於布爾矩陣。 圖 $G$ 的鄰接矩陣為 $$ A(G)= \left [ \begin{array}{cc} 0 & A_{1} \\ A_{1} & 0 \end{array} \right ]_{12\times 12} $$ 其中 $$ A_{1} = \left [ \begin{array}{cccccc} ~0~ & ~0~ & 1~ & ~1~ & ~1~ & ~1~ \\ 0 & 1 & 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \end{array} \right ] $$ 我們只須找出使 $A^{k}=(a_{ij}^{(k)})$ 中 $a_{17}^{(k)}=1$ 的最小的正整數 $k$。 由簡單的計算, 得 $$ A^{k} = \left \{ \begin{array}{ccc} \left [ \begin{array}{cc} A_{1}^{k} & 0 \\ 0 & A_{1}^{k} \end{array} \right ], & & k\hbox{為偶數,} \\ \left [ \begin{array}{cc} 0 & A_{1}^{k} \\ A_{1}^{k} & 0 \end{array} \right ], & & k\hbox{為奇數.} \end{array} \right. $$ 經計算可得 $a_{17}^{(1)}=a_{17}^{(2)}=a_{17}^{(3)}=a_{17}^{(4)}=0$, 但 $a_{17}^{(5)}=1$, 故小船至少5次過河才能安全地把兩個獵人和兩隻狼從左岸運到右岸, 這場「與狼共舞」的歷程至少需要50分鐘。 如果我們把布爾運算改為普通運算, 即 $1+1=2$, 所用的矩陣稱為 $(0, 1)$ 矩陣。 按上述方法, 可得 $a_{17}^{(1)}=a_{17}^{(2)}=a_{17}^{(3)}=a_{17}^{(4)}=0$, 但 $a_{17}^{(5)}=4$, 這說明有4種不同的安全而最快的過河方案。 讀者從圖5中, 可找出4條不同的從 $v_{1}$ 到達 $v_{7}$ 的長為5的途徑來。 按照這途徑便明確指示出渡河的方法。 事實上, 我們所用的布爾矩陣模型, 同樣適用於描述非負矩陣(即矩陣的每個元是非負數)的組合性質, 把正數看作是1,則兩個非負矩陣相乘時, 正數 $\times$ 正數=正數, 正數 $+$ 正數=正數, 正是 $1\times 1=1$, $1+1=1$ 的定性描述。 相應地, 我們也可以把一個本原的非負矩陣 $A$ 描述成存在某一個 $k$, 使 $A^{k}\gt0$ 的矩陣。 如果我們把 $n$ 階布爾陣 $A$ 看作是 $N=\{1, 2, \ldots, n\}$ 上的映射, 則圖4可看作是由 $A$ 經迭代而生成的離散拓樸半動力系統, 而在符號動力系統中, 非負方陣作為轉移方陣可描述有限子轉移的動力性狀。 特別地, 2階有限型子轉移就是拓撲馬爾可夫鏈, 在馬爾可夫鏈的研究中, 布爾陣的本原性正是轉移矩陣遍曆性質的反映。 四.老調新曲在數學史上, 著名的「兔子繁殖」問題產生了眾所周知的菲波那契(Fibonacci)數列, 其遞迴關係為 \begin{equation} %(1) f_{k+2} = f_{k+1} + f_{k}, \quad k = 0, 1, 2, \ldots \end{equation} \begin{equation} %(2) f_{0} = 0, ~~f_{1} = 1 \end{equation} 易知, 用組合方法或特徵方程方法可解得 $f_{k}$ 的運算式。 不怕老調重彈, 我們用 $(0, 1)$ 矩陣的冪, 試譜一闋求解遞迴關係的新曲。 我們用矩陣描述遞迴關係(1), 由(1)得 \begin{equation} %(3) \left \{ \begin{array}{ccc} f_{k+2} & = & f_{k+1} + f_{k} \\ f_{k+1} & = & f_{k+1} \end{array} \right. \quad k = 0, 1, 2, \ldots \end{equation} $$ \hbox{設 } \quad \alpha={{f_{k+1}}\choose {f_{x}}}, \qquad \alpha_{0}={{f_{1}}\choose {f_{0}}}={{1}\choose {0}} \hskip 7.8cm $$ $$ A= \left ( \begin{array}{ccc} 1 & 1 \\ 1 & 0 \end{array} \right ) \hskip 11cm $$ 由(2)和(3)得 $$ \alpha_{k+1} = A\alpha_{k}, \quad k=0, 1, 2 $$ 即 \begin{equation} %(4) \alpha_{k} = A^{k}\alpha_{0}, \quad k=1, 2, \ldots \end{equation} 於是, 求得 $A^{k}$, 便可由上式得到 $\alpha_{k}$, 從而得 $f_{k}$。 如何求 $(0, 1)$ 矩陣的 $k$ 次冪 $A^{k}$。 除了用並不容易的直接計算外, 我們運用一點線性代數的技巧: 若 $A$ 可對角化, 即存在可逆矩陣 $P$, 使得 $P^{-1}AP=\Lambda$, 其中 $\Lambda$ 為對角陣, 就得 \begin{equation} %(5) A^{k} = P\Lambda^{k} P^{-1} \end{equation} 而求對角陣 $A$ 的冪是輕而易舉的。 由線性代數可知 $\Lambda = \left ( \begin{array}{ccc} \lambda_{1} & \quad & 0 \\ 0 & \quad & \lambda_{2} \end{array} \right )$, 其中 $\lambda_{1}$, $\lambda_{2}$ 便是 $A$ 的特徵值。即 $|\lambda I-A|=\left | \begin{array}{cc} \lambda-1 & \quad -1 \\ -1 & \quad \lambda \end{array} \right| =\lambda^{2}-\lambda-1=0$ 的解, 於是得 \begin{equation}%(6) \lambda_{1} = \frac{1+{\sqrt{5}}}{2}, \quad \lambda_{2} = \frac{1-{\sqrt{5}}}{2} \end{equation} 相應 $\lambda_{1}$, $\lambda_{2}$ 的特徵向量分別是 $x_{1}=\left ( \begin{array}{c} \lambda_{1} \\ {1} \end{array} \right )$, $x_{1}=\left ( \begin{array}{c} \lambda_{2} \\ {1} \end{array}\right)$, 取 $P=(x_{1},x_{2})=\left ( \begin{array}{ccc} \lambda_{1} & \quad & \lambda_{2} \\ 1 & \quad & 1 \end{array} \right )$, 則 $P^{-1}=\frac{1}{\lambda_{1}-\lambda_{2}} \left ( \begin{array}{ccc} 1 & \quad & \lambda_{2} \\ -1 & \quad & \lambda_{1} \end{array} \right )$ 由式(5)有 $$ A^{k} = P \left ( \begin{array}{ccc} \lambda_{1}^{k} & \quad & 0 \\ 0 & \quad & \lambda_{2}^{k} \end{array} \right ) P^{-1} = \frac{1}{\lambda_{1}-\lambda_{2}} \left ( \begin{array}{ccc} \lambda_{1}^{k+1} - \lambda_{2}^{k+1} & \quad & \quad \lambda_{1}\lambda_{2}^{k+1} - \lambda_{2}\lambda_{1}^{k+1} \\ \lambda_{1}^{k} - \lambda_{2}^{k} & \quad & \quad \lambda_{1}\lambda_{2}^{k} - \lambda_{2}\lambda_{1}^{k} \end{array} \right ) $$ 由(4)得 $$ \left ( \begin{array}{c} f_{k+1} \\ f_{k} \end{array} \right ) = \alpha_{k} = A^{k}\alpha_{0} = A^{k} \left ( \begin{array}{c} 1 \\ 0 \end{array} \right ) =\frac{1}{\lambda_{1}-\lambda_{2}} \left ( \begin{array}{c} \lambda_{1}^{k+1} - \lambda_{2}^{k+1} \\ \lambda_{1}^{k} - \lambda_{2}^{k} \end{array} \right ) $$ 把結果(6)代入上式, 便得 $$ f_{k} = \frac{1}{\sqrt{5}} \Bigg (\Big [\frac{1+\sqrt{5}}{2}\Big ]^{k} - \Big [\frac{1-\sqrt{5}}{2}\Big ]^{k}\Bigg ). $$ 在拙作《從樓梯模型談起》(見數學傳播, 第二十五卷, 第一期), 我們曾用一個組合模型, 得出了帶係數齊次差分方程的一般解, 現在, 我們用矩陣冪的方法, 更簡明地處理這一問題。
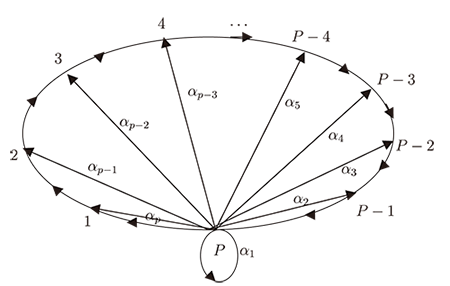
我們仍沿用文 $f(0)=c_{0}$, $f(1)=c_{1}$, $\ldots$, $f(p-1)=c_{p-1}$, $\alpha_{i}(i=1, 2, \ldots, p)$ 及 $c_{i}(i=0, 1, \ldots, p-1)$ 均是常數 眾所周知, 要解上述方程, 須解一個特徵方程 \begin{equation} %(8) \lambda^{p} - \alpha_{1}\lambda^{p-1} - \alpha_{2}\lambda^{p-2} - \cdots - \alpha_{p} = 0 \end{equation} 當 $p\ge 3$ 時, 它的解並不能手到擒來。 我們的思路是: 構造一個矩陣 $A$, 使(8)是 $A$ 的特徵方程, 從而, 用冪 $A^{m}$ 導出(7)的一般解。 構作 $p$ 階方陣 $A$ $$ A = \left [ \begin{array}{ccccc} ~0~ & ~1~ & ~0~ & ~\cdots~ & ~0~ \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & \cdots & \cdots & 1 \\ \alpha_{p} & ~\alpha_{p-1}~ & \alpha_{p} & \cdots & \alpha_{1} \end{array} \right ] $$ 則 $A$ 的特徵方程便是(8)。由線性代數的Hamilton-Cayley定理 \begin{equation} %(9) A^{p} - \alpha_{1}A^{p-1} - \alpha_{2}A^{p-2} - \cdots - \alpha_{p}I = 0 \end{equation} 考慮 $p\times 1$ 矩陣(向量) $$ C = (c_{0}, c_{1}, \ldots, c_{p-1})^{T} $$ 記 $A^{m}C=(a^{(m)},\ldots\ldots)^{T}$, 則(7)的解 $f(n)=a^{(n)}$, 要確認這一點, 我們只須證明 $f(n)=a^{(n)}$ 滿足差分方程(7)。 由方程(9) $$ A^{n}C = \sum_{i=1}^{p} \alpha_{i}A^{n-i}C $$ 因而 $(a^{(n)}, \ldots)^{T}=A^{n}C=\sum\limits_{i=1}^{p} \alpha_{i}A^{n-i}C$。 儘管式子似乎很複雜, 但我們僅著眼於第1列(row)。因 $A^{i}=\left ( \begin{array}{ccccccc} ~ & ~ & ~ & ~(i+1)~ & ~ & ~ & ~ \\ 0 & \cdots & o & 1 & 0 & \cdots & 0 \\ \\ \\ \end{array} \right )_{p\times p}$, $i=0, 1, 2, \ldots, p-1$ 故 $(a^{(n)}, \ldots\ldots)^{T}=\alpha_{1}(a^{(n-1)}, \ldots)^{T} +\alpha_{2}(a^{(n-2)}, \ldots)^{T}+\ldots\alpha_{p}(a^{(n-p)}, \ldots)^{T}$。 於是 $a^{(n)}=\alpha_{1}a^{(n-1)}+\alpha_{2}a^{(n-2)}+\cdots+\alpha_{p}a^{(n-p)}$, 因此 $a^{(n)}$ 滿足(7)的遞迴關係。又 $$(a^{(n)}, \ldots\ldots)^{T}=A^{i}C=(C_{i}, \ldots)^{T},\ i=0, 1, \ldots p-1$$ 即 $a^{(i)}=c_{i}$, $i=0, 1, \ldots p-1$, $a^{(n)}$ 滿足(7)的初值條件。 故(7)的解 $f(n)=a^{(n)}$。 剩下的工作是求 $a^{(n)}$, 即求 $A^{(n)}C$(一個 $p\times 1$ 矩陣)的第一行。 若設 $A^{m}=(a_{ij}^{(m)})$, 則 \begin{equation} %(10) a^{(n)} = c_{0}a_{11}^{(n)} + c_{1}a_{12}^{(n)} + \cdots + c_{p-1}{a_{1p}}^{(n)}, \end{equation} (10)中的 ${a_{1j}}^{(n)}$ 就是 $A$ 所表示的帶權有向圖中, 從1到 $j$ 的長為 $n$ 的所有途徑的權之和。 由矩陣 $A$, 容易畫出它對應的伴隨有向圖 $D$(圖7), 它的弧分別帶權 $\alpha_{1}, \alpha_{2}, \ldots \alpha_{p}$ 或1(無標記的弧表示權為1)。 由 $D$, 不難證明: ${a_{1j}}^{(n)}=a_{jj}^{(n+1-j)}$ 故由(10)式 $$ a^{(n)} = \sum_{j=1}^{p} c_{j-1} {a_{1}}_{j}^{(n)} = \sum_{j=1}^{p} c_{j-1} {a_{1}}_{j}^{(n+1-j)} $$
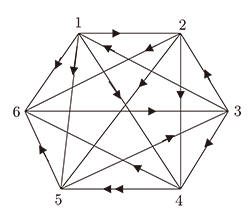
直接從圖 $D$, 用組合方法(參見文 五.排名須分先後會議的來賓, 排名可以不分先後, (也可按姓氏筆劃排列), 以示公允。 然而, 競技比賽中的金牌之爭, 事關實力、名譽的大事, 萬萬不可敷衍了事。 一場迴圈賽過後, 如何令人口服心服地排出名次, 是對舉辦者的一次挑戰。 我們考察一場由6名選手參加的不允許有平局的循環賽(例如乒乓球賽), 每兩個選手僅賽一場。 設參賽選手分別表示為頂點1, 2, 3, 4, 5, 6。 若選手 $i$ 勝選手 $j$, 則連一條, 由 $i$ 到 $j$ 箭頭指向 $j$ 的弧, 便得到一個6階共有 $3\times 5=15$條弧的有向圖(圖8)。 這種以循環賽為背景的 $n$ 階有 $\frac {1}{2}n(n-1)$ 條弧的有向圖稱為競賽圖, 記為 $T_{n}$, 它是循環賽果的數學描述, $T_{n}$ 的包含經過每個頂點恰一次的有向路稱為Hamilton路。 圖論中, 已經證明了 $T_{n}$ 的很多有趣的性質。例如
這裏 $S$ 是 $A$ 對應於 $r$ 的正特徵向量。(見
我們回到圖8中 $T_{6}$ 表示的一場6人循環賽的競賽結果。在圖中可以反映競賽中每個選手的勝負, 例如: 選手1打敗選手2, 4, 5和6, 但卻輸給了選手3。 要排出各選手的最後名次, 一個直觀而普遍傾向的辦法是找一條有向的 Hamilton 路。 (由上述的性質($t_{1}$), 這樣的路是存在的), 然後, 按參加者在路中的位置排列名次, 例如, 我們找到有向 Hamilton 路 (3, 1, 2, 4, 5, 6)。 如果由此, 舉辦者簡單地宣佈選手3是冠軍, 選手1是亞軍 $\ldots$, 那就會引進掀然大波。 因為如果某個反駁者站出來 , 從圖中舉出另一條有向 Hamilton 路 (1, 2, 4, 5, 6, 3) 或 (1, 4, 6, 3, 2, 5) 的話, 那麼局面將難以收拾。 定性的方法難以奏效, 看來, 我們應求助於定量的方法。 先計算每個選手的得分(每個點的出度), 並比較它們, 由 $T_{6}$, 我們得到一個由選手1, 2, 3, 4, 5, 6的得分構成的「得分向量」 $$ S_{1} = (4, 3, 3, 2, 2, 1). $$ 由於 $S_{1}$ 中有相同的得分 (例如選手2和3, 例如選手4和5), 我們仍不能排得一個令人服氣的次序, 那麼, 我們再看它們手下敗將的得分之和(即每個點用長為2的途徑所到達的點的個數), 得到所謂「二級得分向量」 $$ S_{2} = (8, 5, 9, 3, 4, 3). $$ 由 $S_{2}$ 觀察: 選手3名列第一, 繼續這個程式, 得到更「高級」的得分向量 \begin{eqnarray*} S_{3} &=& (15, 10, 16, 7, 12, 9), \\ S_{4} &=& (38, 28, 32, 21, 25, 16), \\ S_{5} &=& (90, 62, 87, 41, 48, 32) , \\ S_{6} &=& (183, 121, 193, 80, 119, 87) , \\ && \hskip -.8cm \ldots\ldots. \end{eqnarray*} 設 $A= A(T_{6})$, 依賴矩陣的冪, 可得第 $i$ 級的得分向量為 $S_{i}=A^{i}J$。 隨著得分向量的升級, 選手的排列名次有所波動(可觀察選手1和選手3的得分)。 可是, 令人欣慰的是, 我們可以證明 $S_{i}$ 中的各選手得分大小總是收斂於一個固定的排列。 因為, 圖8的 $T_{6}$ 是強連通的, 由性質($t_{2}$), $A$ 是一個本原矩陣, 因此, 它的最大絕對值的特徵值是正實數 $r$, $r$ 對應的正特徵向量是 $S$, 由性質($t_{3}$), 有 $$ \lim_{i\to\infty} \Big (\frac{A}{r}\Big )^{i}J = S. $$ $S$ 便可以反映了當 $i\to\infty$ 時, 各個選手的名次排列, 為了更清晰地比較, 可以把 $S$ 正規化(即使各分量之和為1), 得正規化向量。 對於圖8的 $A$, 可得 $$ R = 2.232 \hbox{ 和 } \bar S = (0.238, 0.164, 0.231, 0.113, 0.150, 0.104). $$ 於是, 可得這一循環賽各選手的排列次序為1, 3, 2, 5, 4, 6。 數學勝於雄辯, 矩陣方法, 應該給出一個大家都能接受的結果。 從眉飛色舞地談論數學, 再回到現實中來, 確實, 沒有哪一個賽事求助於如此深入的數學。 當然, 主辦方可以賽前訂出排名的依據: 先看 $S_{1}$ 的排名位, 有同分者再用 $S_{2}$ 分出高低, 如此繼續, 事實上, 這個規則正是體現了上述「收斂於一個固定排列」的數學思想。 北宋詞人李清照在那首膾炙人口的《聲聲慢》中, 開始於「尋尋覓覓」。 我們在這裏, 對矩陣做了一番「尋尋冪冪」, 以期在非負矩陣的冪序列中, 尋出對數學的領悟和樂趣。 參考文獻---本文作者任教中國廣州華南師範大學數學系--- |
2008年9月 32卷3期
尋尋冪冪……—非負矩陣冪序列初探