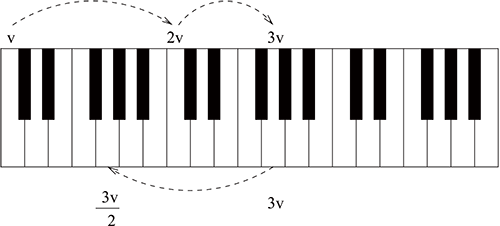| 發刊日期 |
2009年3月
|
||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 標題 | 二○○七年全國高中數學能力競賽專題演講-從鋼琴調音談數學與音樂 |
||||||||||||||||||||||||||||
| 作者 | |||||||||||||||||||||||||||||
| 關鍵字 | |||||||||||||||||||||||||||||
| 檔案下載 | |||||||||||||||||||||||||||||
| 全文 |
閏餘成歲, 律呂調陽。 --- $\langle$千字文$\rangle$。 音樂和數學, 兩者都博大精深, 卻又非常抽象。可以說, 音樂和數學是人類所創造的最了不起的文化。 這個演講裡, 我們來談一談音樂與數學的奇妙聯繫。 1. 大自然的規律大自然運行的規律告訴我們, 一個物體以頻率 $v$ 震動時, 也會同時以頻率 $2v, 3v, \dots$ 震動。 因此若此物體震動發出了頻率為 $v$ 的音高, 它也同時發出頻率為 $2v, 3v, \dots$ 的音高。 這些音叫做 泛音。 在音樂上, 從 $v$ 發出的音高到 $2v$ 發出的音高稱為一個 八度 (聽起來就是低音 Do 到 高音 Do 的感覺)。 從 $2v$ 發出的音高到 $3v$ 發出的音高稱為一個 完全五度 (聽起來就是 Do 到 Sol 的感覺)。 泛音聽得到嗎? 可以。古典吉他的演奏中就有 `泛音' 的技巧。 比如, 輕觸弦的第十二格位置, 然後撥弦的同時把手指放開, 則同學會聽到高八度的泛音。底下我們聽聽吉他的泛音 (示範)。 為什麼? 因為古典吉他第十二格的位置剛好是弦的一半長, 撥弦的同時把手指放開, 相當於用手指抵銷頻率 $v$ 的震動, 凸顯頻率為 $2v$ 的震動, 這就是第一泛音。 人也是震動聲帶才能發出聲音。所以, 理論上人的聲音也有泛音。 有沒有可能唱出泛音, 或是同時唱兩個音? 可以。 西伯利亞的圖瓦族 (Tuva) 有一種稱為 "泛音唱法" (overtone singing) 的傳統歌唱方式, 可以同時唱出兩個音。 聽聽這個例子 (播放音樂)。 即使發出相同的音高, 我們仍然能分辨不同樂器的音色 (timbre), 因為音色就是不同泛音疊合之後的結果 --- 也許長笛的第四泛音比單簧管的第四泛音大, 諸如此類。 有程式設計經驗的同學可以試著寫個簡單的程式讓電腦發出單一頻率, 沒有泛音的震動非常乾澀, 毫無美感可言。 2. 畢達哥拉斯的音階傳說中畢達哥拉斯 (Pythagoras (579-520 B.C.)) 路過一家鐵匠店發現四個鐵匠打鐵的聲音 異常悅耳 而開始研究聲音。 他用以下的兩個規則試圖建立起西洋音樂的音階。
現行的西方音樂是 $12$ 音階, 即一個八度共有 $12$ 個半音。 我們按照畢達哥拉斯的兩個規則可幫樂器調音: 以中央 $C$ 為基準。 設這個音的頻率是 $v$, 則高八度的 $C$ 頻率是 $2v$, 高八度 $G$ 的頻率是 $3v$。 因此 $G$ 的頻率是 $\frac{3}{2}v$。因此我們得到 $G$ 的頻率了。
同理, 下一個得到的音是 $D$, 頻率為 $\frac{9}{8}v$. 再下一個得到的音是 $A$, 頻率為 $\frac{27}{16}v$。 在此我們要強調, 這個調音方法是合理的, 是符合大自然的規律的。 按此我們可得到調音的順序: $$ C(=v) \to G \Big (=\frac{3}{2}v\Big ) \to D\Big(=\frac{9}{8}v\Big ) \to \cdots $$ 注意到每下一個音是完全五度 ($7$ 個半音), 但因為一個八度有 $12$ 個半音, 而 $$ \gcd(7, 12) = 1, $$ 因此會繞回來。 這樣繞一圈回來所出現的音的順序, 稱為一個五度圈。 五度圈是古典音樂中所有轉調與和聲的基礎。
我們按五度圈一直調音下去: $C\to G\to D\to A\to \cdots \to \cdots F$。 此時 $F$ 的頻率為 $\frac{177147}{131072}v$。 按照五度圈, 再下一個要變成高音 $C$, 頻率為 $\frac{177147}{131072}\times \frac{3}{2}=\frac{531441}{262144}v$。 但是不要忘了原來起始的 $C$ 頻率為 $v$, 因此這個高音 $C$ 的頻率是 $2v$。 我們得到一個非常難堪的結果: $$ \frac{531441}{262144} \sim 2.02728653 \ne 2 $$ 同學知道這有多糟糕吧, 這告訴我們, 按照大自然的規則調音, 調出來的音階是走音的。 而且還往上走音。 3. 永遠調不準問題出在哪裡? 問題在於按照五度圈調音的過程中, 每往上五度都是頻率由 $v\to \frac{3}{2}v$, 每降八度都是把頻率除以 $2$。 上式就是 $\frac{3^{12}}{2^{18}}\ne 2$, 換句話就是 $$ \Big (\frac{3}{2}\Big )^{12}\ne 2^7, $$ 即把從 $C$ 開始每個音都走一次 (五度往上 $12$ 次) 到很高音的 $C$ (離基準的 $C$ 有 $7$ 個八度), 不會等於從 $C$ 開始直接頻率兩倍兩倍兩倍 $\cdots$ 七次後走到的 $C$。 追根究底, 就是一開始打定一個八度有 12 個半音, 這是 錯誤的抉擇。 那放開這個假設, 假設一個八度有若干個半音, 那按照大自然的規律, 這個若干要是多少? 這相當於要求 $(\frac{3}{2})^{a}=2^b$ 的正整數解。 就是要求 $$ 2^x = 3^y $$ 的正整數解。 很不幸, 根據算術基本定理, 這是不可能的。 因此, 調音永遠調不準, 不管一個八度有多少半音都一樣, 反正就是想按照大自然的規律調音, 一定調不準。 這是非常令人驚嚇的哲學性問題。 音樂不過就是空氣的震動, 所有理論的發展都應該依循著大自然的規律。 但是我們用數學 證明 了, 整個音樂系統有 根本的缺陷。 調律因此變成西方音樂發展中非常重要的問題。 許多音樂家和理論家都試圖解決這樣的困境。 歷史發展的過程中出現了許多調律的方法。 因為一定調不準, 所以不管怎麼調, 就是會有一些音不對, 一些調子比較不諧和。 巴哈寫名為 "十二平均律" 的鋼琴曲, 其中的一個意圖就是為了證明所謂 "十二平均律" 的調律是可行 (人耳可以接受)的。 十二平均律是一個複雜的調律方法, 在此不擬討論。 我們已經證明了調律這個問題無解。 那怎麼辦呢? 人們早已妥協了, 我們決定讓 每個音都不對。 現在絕大多數的樂器調律採取等律 (equal temperament)。 這是非常暴力數學的調律 --- 把 $v\to 2v$ 的八度按等比分成 $12$ 個半音, 所以每一格為 $\sqrt[12]{2}$。 (註: 十二平均律不是等律, 這是長久以來的誤解。) 現代的等律調音, 多以 $A=440$ mHz 為基準, 往上往下一直乘 $\sqrt[12]{2}$ 而得到下一個音:
標準音高 $440$ mHz 到底聽起來多高? 隨便拿一支電話起來聽。 話筒中長長的 "嘟---" 聲, 音高就是 $440$ mHz。 有些音樂家喜歡把樂器音高調高一點, 聽起來會比較亮。 事實上, 標準音 $A$ 的頻率要調多高, 在音樂史上一直變來變去。 三十年前, $A=440$ mHz 是標準的, 但是現在調 $A=442$ mHz 似乎快要凌駕 $A=440$ mHz, 變成主流了。 現在不少演出場地在出租鋼琴時, 都會順便詢問演奏者要把基準的 $A$ 調成 $440$mHz 還是 $442$mHz。 每個人的習慣不同, 那合奏時怎麼辦呢? 所以演出前一定要調音。 下次聽管弦樂音樂會時可以注意節目一開始樂團的調音 --- 雙簧管首席會吹一個 $A$, 整個樂團的其他樂器就必須以這個 $A$ 為基準, 不管這個音是 $A=440$ 還是 $A=442$。 用等律調音, 兩個音之間的比例是固定的。 由 $C$ 到 $G$ 的完全五度 (有 $7$ 個半音) 頻率比是 $(\sqrt[12]{2})^7=1.498307077$ 倍。 但回憶大自然的規律, 完全五度應是 $\frac{3}{2}=1.5$ 倍。 因此等律調音中, 完全五度是往下走音的。 同理, $C$ 到 $D$ 的全音(兩個半音) 是 $(\sqrt[12]{2})^2=1.122462048$ 倍; 但按照五度圈調音, 應該是 $\frac{9}{8}=1.125$ 倍。 這樣的小差距, 有些敏感的耳朵是可以聽得出差別的。 在這些特殊的耳朵聽起來, 鋼琴的每個音都走音。 有些音樂家的耳朵已經到了匪夷所思的地步, 這就是所謂的 "絕對音感"。 由上面的討論知道, "絕對音感" 是存在的 (對於音的比例特別敏銳), 這和 "絕對音高" 完全不同 --- "絕對音高" 是一個空泛的概念, 不過就是把音背起來而已。 我們回到數學。 上述音階和調律的討論基於 $2^{19}\sim 3^{12}$, 就是說 $(x, y)=(19, 12)$ 是 $2^x=3^y$ 的一個 `差不多的解'。 還有沒有其他 $(x, y)$ 也是差不多的解? 有沒有方法找? 有的, 用連分數。 觀察 $\sqrt{2}=1+(\sqrt{2}-1)=1+\frac{1}{1+\sqrt{2}}=1+\frac{1}{2+(\sqrt{2}-1)}$, 因此迭代下去得到 $$ \sqrt{2} = 1 + \frac{1}{2+\displaystyle\frac{1}{2+\displaystyle\frac{1}{2+\displaystyle\frac{1}{2+\cdots}}}}, $$ 這就是 $\sqrt{2}$ 的連分數展開式。 為節省篇幅, 記為 $$ \sqrt{2} = [1, 2, 2, 2, 2, \dots] $$ 仔細想想是有點不可思議的, $\sqrt{2}$ 是無理數, 但是寫成連分數後居然有這麼漂亮的表示。 最簡潔的連分數是黃金分割: $$ \frac{1+\sqrt{5}}{2} = [1, 1, 1, 1, 1, \dots] $$ 圓周率呢? 很不幸, $\pi$ 寫成連分數後還是沒什麼規律 $$ \pi = [3, 7, 15, 1, 292, 1, 1, 1, 2, \dots] $$ 但神奇的是 $e$, 它的連分數表示有神奇的規律: $$ e = [2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, \dots] $$ 連分數有什麼用? 想法很簡單: 既然無限多層後是原來的數, 所以只取有限多層, 就是此數的近似值。 比如 $\sqrt{2}=[1, 2, 2, \dots]$, 取 $[1], [1, 2], [1, 2, 2], [1, 2, 2, 2], [1, 2, 2, 2, 2], \dots$ 展開後為 $$ 1, \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \frac{41}{29}, \dots, $$ 這些分數就可以當作 $\sqrt{2}$ 的近似值。 黃金比例 $\phi=\frac{1+\sqrt{5}}{2}$ 的漸近分數是什麼? $$ 1, \frac{2}{1}, \frac{3}{2}, \frac{5}{3}, \frac{8}{5}, \frac{13}{8}, \frac{21}{13}, \frac{34}{21}, \dots $$ 就是相鄰兩項費波那契數的比例! 直覺上取愈多層, 這個近似值會愈好。 對。 而且不只如此, 連分數還是最好的! 看底下這個神奇的結果: Theorem 5.1. 對於無理數 $x=[a_0, a_1, \dots]$, 假設 $\frac{p_n}{q_n}:=[a_0, a_1, \dots a_n]$ 為 $x$ 的第 $n$ 個漸近分數。 則對於任意整數 $0\lt q \le q_n$, 都有 $$ \Big |x - \frac{p_n}{q_n}\Big | \lt \Big |x - \frac{p}{q}\Big | $$ 即, 在所有分母小於 $q_n$ 的整數中, $\frac{p_n}{q_n}$ 是 $x$ 的最佳近似值。 來看看 $\pi$ 的近似值。 取連分數, 得到漸近分數 $$ 3, \frac{22}{7}, \frac{333}{106}, \frac{355}{113}, \frac{103993}{33102}, \dots $$ 非常令人吃驚的是, $\frac{22}{7}$ 和 $\frac{355}{113}$ 就是祖沖之算出來的疏率和密率。 所以祖沖之不止得出 $\frac{355}{113}$ 這個分數, 這個分數還是所有分母不超過 $113$ 的分數之中, $\pi$ 的最佳近似值! 祖沖之的神奇密率領先了西方整整一千年, 這真是不簡單。 他怎麼弄出來的? 沒人知道。 祖沖之難道不會繼續往下找下一個分數嗎? 我猜他會。 但數學告訴我們, 下一個更好的逼近是 $\frac{103993}{33102}$, 差太遠了。 以人力可以達的範圍內, 祖沖之的密率已經做到頂了。 因此華羅庚猜測祖沖之已經有連分數的概念, 是合理的猜測。 用漸近分數來當近似值, 夠不夠好? 誤差有多大? 也有一個簡潔的結果: Theorem 5.2. 用 $\frac{p_n}{q_n}$ 來當作 $x$ 的近似值, 誤差可由下式估計: $$ \Big |x - \frac{p_n}{q_n}\Big | \lt \frac{1}{q_nq_{n+1}} \lt \frac{1}{q_n^2} $$ 因此用 $\frac{355}{113}$ 當作 $\pi$, 誤差已經小於 $\frac{1}{113\cdot 33102}= 0.00000026 \dots$ 了。 6. 回到調音回到我們的音階問題。 要找 $2^x=3^y$ 的 "差不多的解", 兩邊取對數, 得 $\frac{x}{y}=\log _2 3$。 所以相當於要找 $\log_2 3$ 的近似值。 把 $\log_2 3$ 寫成連分數得到 $$ \log_2 3 = [1, 1, 1, 2, 2, 3, 1, 5, 2, 23, 2, 2, 1, \dots], $$ 漸近分數為 $$ 1, 2, \frac{3}{2}, \frac{8}{5}, \frac{19}{12}, \frac{65}{41}, \frac{84}{53}, \frac{485}{306}, \dots $$ 另一個神奇的事發生了。 若取 $\frac{19}{12}$ 當作近似值, 就是原來的 "差不多的解" --- 這表示一個八度分成十二個半音。 這個 "$12$ 音階" 的解是大自然與西方音樂家們共同努力很久的結果, 現在我們用數學找到了。 附帶一提的是, 中國有五聲音階, 和 $\frac{8}{5}$ 的分母恰好一致。 但奇怪的是, 在音樂史發展的軌跡中, 出現過 $19$ 音階, $22$ 音階, $24$ 音階, $31$ 音階, $34$ 音階, $53$ 音階, $72$ 音階, $88$ 音階, 但是沒有 $41$ 音階。 數學告訴我們, $41$ 音階才是合理的選擇。 7. 閏年
只要遇到要取近似值的問題, 用連分數都管用。
地球繞太陽一週稱為一年, 一年其實是 $365.24219878 \cdots$ 天。 因此每隔幾年就會多出完整的一天。
怎麼閏年? 取 $0.24219878$ 連分數, 然後取漸近分數, 得到
$$
\frac{1}{4}, \frac{7}{29}, \frac{8}{33}, \frac{31}{128}, \frac{163}{673}, \frac{1009}{4166}, \dots
$$
因此每四年閏一天, 但每二十九年閏七天, 但每三十三年閏八天, $\ldots$
現行的每四年閏年一次, 但是每一百年不閏, 四百又閏, 其實就是要湊到剛好。
更詳細的討論可參考 8. 結語
數學無處不在, 這篇文章算是一個小小的例子。
文中的題材大部分取自 如內文, 如果堅持連分數中每個分子都是 $1$, 那 $\pi$ 的確不好看。 但是如果沒有這個堅持, 連 $\pi$ 都有很漂亮的展開式, 比如 $$ \pi = 3 + \frac{1}{6+\displaystyle\frac{9}{6+\displaystyle\frac{25}{6+\displaystyle\frac{49}{6+\dots}}}}. $$ 連分數在數學發展中有一定的地位, 但是在現代數學中沒有受到很大的重視, 也許未來會有復興的時候。
調律在音樂史理論中是非常複雜的, 歷史上至少出現過有幾十種不同的調律方法, 材料足以寫一本專書。
有興趣的同學可參考 回到畢達哥拉斯的四個鐵匠, 傳說他們用的鐵錘分別重 $12:9:8:6$。 因為 $12:9=8:6=$ 完全四度, $12:8 = 9:6 =$ 完全五度, $12:6=$ 八度, $9:8=$大二度, 因此畢達哥拉斯聽到的打鐵聲就是 $Do$, $Fa$, $Sol$, 高音 $Do$ 這四個音, 難怪會 異常悅耳。 不過真正的情形已經不可考, 就當作浪漫的故事吧 --- 就像 "閏餘成歲, 律呂調陽", 就是這麼巧, 都和連分數有關! 最後謝謝彰化師範大學數學系的演講邀約, 以及審稿學者細心的修正。 參考文獻---本文作者任教於高雄大學應用數學系--- |
2009年3月 33卷1期
二○○七年全國高中數學能力競賽專題演講-從鋼琴調音談數學與音樂