I. 前言

一般形平面凸五邊形、凸六邊形面積公式的探討頗耐人尋味, 其公式的結構是否能具有如 Heron 或 Bretschneider 公式那樣的類似形態, 但卻不能像那樣的簡潔完美? 在觀察、比對三角形面積的Heron公式與四邊形面積的Bretschneider公式之證明過程時, 發現兩者皆可用同一種方法推證而得！ 此方法為先將圖形分割成兩部份較少邊數面積, 次以餘弦公式及面積表示式聯繫這兩部份, 最後再以聯立式, 演算推證而成。這使我聯想到要應用這種思索方式, 來研究處理更複雜的凸五邊形及凸六邊形面積問題, 想像起來真令人期待又好奇！

經分析研判後, 確認凸五邊形圖形分割的要領是; 將第一及第三頂點連成對角線, 把圖形分割成一個三角形與一個四邊形, 也可選取第二及第四頂點連成對角線。 而凸六邊形則被一條對角線分割成兩個四邊形。在列出相對應圖形之數學關係式時, 需以選定的對角線來聯繫被分割出的兩圖形之餘弦關係式及面積組合的表示式。 三角形面積容易表示, 而四邊形面積的表示式則需配合四邊形餘弦公式的每一餘弦項, 所以四邊形面積不是任意表示的。 也因為發現到這需配合的特定四邊形面積表示式, 使得凸五邊形及凸六邊形面積的研究獲得突破性進展！利用四邊形餘弦公式及相對應的四邊形面積表示式, 再加上細心、毅力的演繹、推導、驗證, 使得在尋覓凸五邊形、凸六邊形等面積公式的推理過程中, 得以克服途中所遭遇到的思考瓶頸及繁雜計算情形, 終能將研究心得統合整理, 並據實以條理分明、巨細靡遺的呈現出論述結果！詳情請看以下完整的解析研究過程。

II. 本文

A. 平面凸多邊形的向量性質

任給一個平面凸 $n$ 邊形, 其各頂點依序為 $A_1$, $A_2$, $A_3$, $\ldots$, $A_{n-2}$, $A_{n-1}$, $A_n$ 並令一邊 $A_1A_2$ 的向量為 $\longvec{V_1}$, $\stackrel{-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_2A_3}\vphantom{i}\,}=\longvec{V_2}$, $\stackrel{-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_3A_4}\vphantom{i}\,}=\longvec{V_3}$, $\ldots$, $\stackrel{-\!\!-\!\!-\!\!-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_mA_{m+1}}\vphantom{i}\,}=\longvec{V_m}$, $\ldots$, $\stackrel{-\!\!-\!\!-\!\!-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_{n-1}A_{n}}\vphantom{i}\,}= \stackrel{-\!\!-\!\!-\!\!\longrightarrow}{\smash{V_{n-1}}\vphantom{i}\,}$, $\stackrel{-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_nA_{1}}\vphantom{i}\,}=\longvec{V_n}$, 則此平面凸 $n$ 邊形即為 $\longvec{V_1}$, $\longvec{V_2}$, $\longvec{V_3}$, $\ldots$, $\longvec{V_n}$, 等 $n$ 個向量按序箭頭接箭尾相加而成的封閉凸 $n$ 邊形。 依向量加法性質知; $\sum_{m=1}^n \longvec{V_m}=0=\sum_{m=1}^n (V_m\cos \theta_m)\vec i+\sum_{m=1}^n(V_m\sin \theta_m)\vec j$, $\theta_m$ 為 $V_m$ 在直角座標平面上的方位角。 $\vec i$ 為正 $X$ 軸方向的單位向量, $\vec j$ 為正 $Y$ 軸方向的單位向量, 再由平面正交座標系性質知; $\sum_{m=1}^n(V_m\cos \theta_m)=0$ 且 $\sum_{m=1}^n(V_m\sin \theta_m)=0$。

性質1. 任給一個平面凸 $n$ 邊形 $A_1A_2A_3\cdots A_n$ 令 $\stackrel{-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_1A_2}\vphantom{i}\,}=\longvec{V_1}$, $\stackrel{-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_2A_3}\vphantom{i}\,}=\longvec{V_2}$, $\stackrel{-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_3A_4}\vphantom{i}\,}=\longvec{V_3}$, $\ldots$, $\stackrel{-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_{n-1}A_n}\vphantom{i}\,}=\longvec{V_{n-1}}$, $\stackrel{-\!\!-\!\!-\!\!\longrightarrow}{\smash{A_{n}A_1}\vphantom{i}\,}=\longvec{V_{n}}$。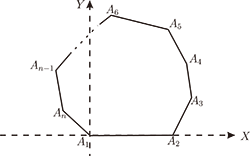 將頂點 $A_1$ 置於直角座標平面上的原點 $O$, 使 $\overline{A_1A_2}$ 邊完全重疊並貼置於 $X$ 軸, 以使此 $n$ 邊形完全落在第 1 及第 2 象限區域內 (含 $X$ 軸), 如下圖 (1), 則

$$V_1+\sum_{m=2}^n V_m\cos\Big((m-1)\pi-\sum_{k=2}^m A_k\Big)=0 \qquad \hbox{且}\qquad \sum_{m=2}^n V_m\sin\Big((m-1)\pi-\sum_{k=2}^m A_k\Big)=0$$

證明： 由圖 1 知凸 $n$ 邊形的內角依次為 $A_1$, $A_2$, $A_3$, $\ldots$, $A_n$, 故 $V_1$ 的方位角 $\theta_1$ 為零, $V_2$ 的方位角 $\theta_2$ 為 $\pi-A_2$, $V_3$ 的方位角 $\theta_3$ 為 $\pi-A_2+\pi-A_3$, $V_4$ 的方位角 $\theta_4$ 為 $\pi-A_2+\pi-A_3+\pi-A_4,\ldots$, $V_n$ 的方位角 $\theta_n$ 為 $(n-1)\pi-(A_2+A_3+A_4+\cdots+A_n)$。 將這 $n$ 個方位角全部代入以下方程式中： $$\sum_{m=1}^n(V_m\cos\theta_m)=0\qquad \hbox{且}\qquad \sum_{m=1}^n(V_m\sin \theta_m)=0$$ 則 \begin{eqnarray*} &&\hskip-10pt \sum_{m=1}^n(V_m\cos\theta_m)\\ &=&V_1+V_2\cos(\pi-A_2)+V_3\cos(2\pi-A_2-A_3)+\cdots+V_n\cos\Big((n-1)\pi-\sum_{k=2}^n A_k\Big)=0 \end{eqnarray*} 將上列等式改寫成下式; 得 \begin{equation} V_1+\sum_{m=2}^n V_m\cos\Big((m-1)\pi-\sum_{k=2}^m A_k\Big)=0\label{1} \end{equation} 另 $$\sum_{m=1}^n(V_m\sin\theta_m)\!=\!V_2\sin(\pi\!-\!A_2)\!+\!V_3\sin(2\pi\!-\!A_2\!-\!A_3)\!+\!\cdots\!+\!V_n\sin\Big((n\!-\!1)\pi\!-\!\sum_{k=2}^m A_k\Big)=0$$ 再將上列等式改寫成下式; 得 \begin{equation} \sum_{m=2}^n V_m\sin\Big((m-1)\pi-\sum_{k=2}^m A_k\Big)=0\label{2} \end{equation} 證明完成。 $\Box$

性質2. 平面凸 $n$ 邊形 $A_1A_2A_3\cdots A_n$, 其所有內角的總和恰為 $(n-2)\pi$; 證明 (略)。

接著要利用上述性質 1 的 \eqref{1} 式與 \eqref{2} 式及性質 2 來尋找、 證明平面凸 $n$ 邊形的餘弦公式、正弦公式及面積表示式。而餘弦公式、正弦公式則有邊長型及面積型的兩型態。

B. 平面凸四邊形的餘弦公式、正弦公式及面積表示式

1. 證明平面凸四邊形的邊長型餘弦公式、正弦公式：

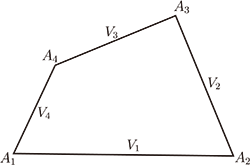
• (a) 求證邊長型餘弦公式： 取 $n= 4$ 代入性質 1 的方程式 \eqref{1}, 得第一式如下; $$V_1+V_2\cos(\pi-A_2)+V_3\cos(2\pi-A_2-A_3)+V_4\cos(3\pi-A_2-A_3-A_4)=0$$ 經化簡, 代換角度後, 得 \begin{eqnarray} V_1-V_2\cos A_2+V_3\cos(A_2+A_3)-V_4\cos A_1&=&0\\ {\hbox{依次又可得}} V_2-V_3\cos A_3+V_4\cos(A_3+A_4)-V_1\cos A_2&=&0\\ V_3-V_4\cos A_4+V_1\cos(A_4+A_1)-V_2\cos A_3&=&0\\ V_4-V_1\cos A_1+V_2\cos(A_1+A_2)-V_3\cos A_4&=&0 \end{eqnarray} 見下圖 2
  

  

  
  此上述四式即為平面凸四邊形的邊長型餘弦公式。
• (b) 求證邊長型正弦公式：以 $n = 4$ 代入性質 1 的方程式 \eqref{2}, 得第一式如下; $$V_2\sin(\pi-A_2)+V_3\sin(2\pi-A_2-A_3)+V_4\sin(3\pi-A_2-A_3-A_4)=0$$ 經化簡, 代換角度後, 得 \begin{eqnarray} V_2\sin A_2-V_3\sin(A_2+A_3)-V_4\sin A_1&=&0\\ {\hbox{依次又可得}} V_3\sin A_3-V_4\sin(A_3+A_4)-V_1\sin A_2&=&0\\ V_4\sin A_4-V_1\sin(A_4+A_1)-V_2\sin A_3&=&0\\ V_1\sin A_1-V_2\sin(A_1+A_2)-V_3\sin A_4&=&0 \end{eqnarray} 此上述四式即為平面凸四邊形的邊長型正弦公式。見上圖 2。

2. 證明平面凸四邊形的面積型餘弦公式：

將 (4c-1)式移項, 得 \begin{equation} V_3\cos(A_2+A_3)=V_4\cos A_1+V_2\cos A_2-V_1\label{3} \end{equation} 將 (4s-1)式移項, 得 \begin{equation} V_3\sin(A_2+A_3)=V_2\sin A_2-V_4\sin A_1\label{4} \end{equation} 將 \eqref{3} 式的平方加 \eqref{4} 式的平方, 經化簡, 得 $$V_3^2=V_4^2+V_1^2+V_2^2-2V_4V_1\cos A_1-2V_1V_2\cos A_2+2V_4V_2\cos(A_1+A_2){\hbox{(4c-a-1)}}$$ 此 (4c-a-1)式 即為平面凸四邊形的面積型餘弦公式。 因為此式各項的量綱都是長度的平方, 故稱為面積型餘弦公式; 同理, 依次可得另外三式。見上圖 2。

3. 證明平面凸四邊形的面積表示式：

令平面凸四邊形的面積為 $S(4)$, 則 \begin{equation} 2S(4)=V_4V_1\sin A_1+V_2V_3\sin A_3\label{5} \end{equation} 將 (4s-2)式乘以 $V_2$, 移項, 得 \begin{equation} V_2V_3\sin A_3=V_1V_2\sin A_2+V_4V_2\sin (A_3+A_4)\label{6} \end{equation} 以 $\sin(A_3+A_4)=-\sin (A_1+A_2)$ 及 \eqref{6} 式代入 \eqref{5} 式, 得 $$2S(4)=V_4V_1\sin A_1+V_1V_2\sin A_2-V_4V_2\sin(A_1+A_2){(4s-a-1)}$$ 此 (4s-a-1) 式即為平面凸四邊形的面積表示式。見上圖 2。

比較 (4c-a-1) 式及 (4s-a-1) 式, 可發現兩表示式中的文字項 $\sin$ 項及 $\cos$ 項完全相似！ 這就是關鍵的、相配合的兩對應式。

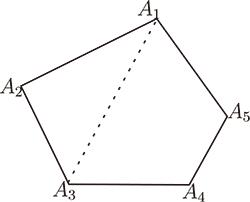
C. 平面凸五邊形的面積

在平面上給定一個凸五邊形 $A_1A_2A_3A_4A_5$, 令 $\overline{A_1A_2}=V_1$, $\overline{A_2A_3}=V_2$, $\overline{A_3A_4}=V_3$, $\overline{A_4A_5}=V_4$, $\overline{A_5A_1}=V_5$, 並且連接一對角線, 如圖 3, 將圖形分割成三角形 $A_1A_2A_3$ 與一個四邊形 $A_1A_3A_4A_5$, 這兩圖形共同擁有邊長 $A_1A_3$, 則由面積型餘弦公式可得 $$V_1^2+V_2^2-2V_1V_2\cos A_2=V_3^2+V_4^2+V_5^2-2V_3V_4\cos A_4-2V_4V_5\cos A_5+2V_3V_5\cos(A_4+A_5)$$ 移項並整理成下式 \begin{equation} (V_3^2+V_4^2+V_5^2-V_1^2-V_2^2)/2=V_3V_4\cos A_4+V_4V_5\cos A_5-V_3V_5\cos (A_4+A_5)-V_1V_2\cos A_2\label{7} \end{equation} 再由凸五邊形面積 $S(5)$ 等於四邊形與三角形面積之和, 倣照 (4s-a-1) 式, 得 \begin{equation} 2S(5)=V_3V_4\sin A_4+V_4V_5\sin A_5-V_3V_5\sin (A_4+A_5)+V_1V_2\sin A_2\label{8} \end{equation} 請看 \eqref{7} 式 和 \eqref{8} 式 兩式中的 $\sin$ 項及 $\cos$ 項完全相似！ 這就是本文最關鍵的搭配！ 聯立解 \eqref{7}、 \eqref{8} 兩關係式如下; 先將 \eqref{7} 式的平方加 \eqref{8} 式的平方, 經化簡, 得 \begin{eqnarray*} &&\hskip -25pt 4[S(5)]^2+(V_3^2+V_4^2+V_5^2-V_1^2-V_2^2)^2/4\\[5pt] &=&V_1^2V_2^2+V_3^2V_4^2+V_4^2V_5^2+V_3^2V_5^2-2V_1V_2V_3V_4\cos(A_2+A_4)\\[5pt] &&-2V_1V_2V_4V_5\cos(A_2+A_5)+2V_1V_2V_3V_5\cos(A_2+A_4+A_5)\\[5pt] &&-2V_3V_4V_5^2\cos A_4-2V_3^2V_4V_5\cos A_5+2V_3V_4^2V_5\cos(A_4-A_5)\\[5pt] &=&(V_1V_2+V_3V_4+V_4V_5+V_3V_5)^2-2V_1V_2V_3V_4(\cos(A_2+A_4)+1)\\[5pt] &&-2V_1V_2V_4V_5(\cos(A_2+A_5)+1)+2V_1V_2V_3V_4(\cos(A_2+A_4+A_5)-1)\\[5pt] &&-2V_3V_4V_5^2(\cos A_4+1)-2V_3^2V_4V_5(\cos A_5+1)+2V_3V_4^2V_5(\cos(A_4-A_5)-1)\\[5pt] &=&(V_1V_2+V_3V_4+V_4V_5+V_3V_5)^2-4V_1V_2V_3V_5\sin^2\Big(\frac{A_2+A_4+A_5}2\Big)\\[5pt] &&-4V_1V_2V_3V_4\cos^2\Big(\frac{A_2+A_4}2\Big)-4V_1V_2V_4V_5\cos^2\Big(\frac{A_2+A_5}2\Big)\\[5pt] &&-4V_3V_4V_5^2\Big(\cos^2\frac{A_4}2\Big)-4V_3^2V_4V_5\Big(\cos^2\frac{A_5}2\Big)-4V_3V_4^2V_5\sin^2\Big(\frac{A_4-A_5}2\Big) \end{eqnarray*} 再移項並整理, 得五邊形面積的平方 \begin{eqnarray} [S(5)]^2&=&\Big(\frac{V_1V_2+V_3V_4+V_4V_5+V_3V_5}{2}\Big)^2-\Big(\frac{V_3^2+V_4^2+V_5^2-V_1^2-V_2^2}{2}\Big)^2\nonumber\\[5pt] &&-V_1V_2V_3V_5\sin^2\Big(\frac{A_2+A_4+A_5}2\Big)-V_1V_2V_3V_4\cos^2\Big(\frac{A_2+A_4}2\Big)\nonumber\\[5pt] &&-V_1V_2V_4V_5\cos^2\Big(\frac{A_2+A_5}2\Big)-V_3V_4V_5^2\Big(\cos^2\frac{A_4}2\Big)\nonumber\\[5pt] &&-V_3^2V_4V_5\Big(\cos^2\frac{A_5}2\Big)-V_3V_4^2V_5\sin^2\Big(\frac{A_4-A_5}2\Big)\label{9} \end{eqnarray} 先將上列 \eqref{9} 式等式右側的前兩個平方式項作整理, 則 \begin{eqnarray} &&\hskip -25pt \Big(\frac{V_1V_2+V_3V_4+V_4V_5+V_3V_5}{2}\Big)^2-\Big(\frac{V_3^2+V_4^2+V_5^2-V_1^2-V_2^2}{2}\Big)^2\nonumber\\ &=&\Big[\frac{V_3^2+V_4^2+V_5^2+2V_3V_4+2V_4V_5+2V_3V_5-(V_1-V_2)^2}4\Big]\nonumber\\ &&\times \Big[\frac{(V_1+V_2)^2+2V_3V_4+2V_4V_5+2V_3V_5-V_3^2-V_4^2-V_5^2}4\Big]\nonumber\\ &=&\frac{(V_3+V_4+V_5)^2-(V_1-V_2)^2}4\nonumber\\ &&\times \Big[\frac{V_3^2+V_4^2+V_5^2+2V_3V_4+2V_4V_5+2V_3V_5+(V_1+V_2)^2-2V_3^2-2V_4^2-2V_5^2}4\Big]\nonumber\\ &=&\Big[\frac{V_3+V_4+V_5+V_1-V_2}4\Big]\Big[\frac{V_2+V_3+V_4+V_5-V_1}4\Big]\nonumber\\ &&\times[(V_1+V_2)^2-(V_3-V_4)^2-(V_3-V_5)^2-(V_4-V_5)^2+V_3^2+V_4^2+V_5^2]\label{10} \end{eqnarray} 將此 \eqref{10} 式代入 \eqref{9} 式中, 則可完整的描述出平面凸五邊形面積的平方為 \begin{eqnarray} [S(5)]^2&=&\frac1{16}(V_2+V_3+V_4+V_5-V_1)(V_3+V_4+V_5+V_1-V_2)\nonumber\\ &&\times[(V_1+V_2)^2-(V_3-V_4)^2-(V_3-V_5)^2-(V_4-V_5)^2+V_3^2+V_4^2+V_5^2]\nonumber\\ &&-V_1V_2V_3V_5\sin^2\Big(\frac{A_2+A_4+A_5}2\Big)-V_1V_2V_3V_4\cos^2\Big(\frac{A_2+A_4}2\Big)\nonumber\\ &&-V_1V_2V_4V_5\cos^2\Big(\frac{A_2+A_5}2\Big)-V_3V_4V_5^2\Big(\cos^2\frac{A_4}2\Big)-V_3^2V_4V_5\Big(\cos^2\frac{A_5}2\Big)\nonumber\\ &&-V_3V_4^2V_5\sin^2\Big(\frac{A_4-A_5}2\Big) \label{11} \end{eqnarray} 由此觀察到; \eqref{11} 式雖然繁瑣, 但是它涵蓋下面三個特例 :

• (1) 將頂點 $A_5$ 趨近於頂點 $A_1$, 使 $V_5 = 0$, 則凸五邊形退化成凸四邊形, \eqref{11} 式蛻變成下式; 如此可得, \begin{eqnarray*} [S(4)]^2&=&\frac1{16}(V_2+V_3+V_4-V_1)(V_3+V_4+V_1-V_2)[(V_1+V_2)^2-(V_3-V_4)^2]\\ &&-V_1V_2V_3V_4\cos^2\Big(\frac{A_2+A_4}2\Big) \end{eqnarray*} 因此, \begin{eqnarray} [S(4)]^2&=&\frac1{16}(V_2\!+\!V_3\!+\!V_4\!-\!V_1)(V_3\!+\!V_4\!+\!V_1\!-\!V_2)(V_4\!+\!V_1\!+\!V_2\!-\!V_3)(V_1\!+\!V_2\!+\!V_3\!-\!V_4)\nonumber\\ &&-V_1V_2V_3V_4\cos^2\Big(\frac{A_2+A_4}2\Big)\label{12} \end{eqnarray} 此 \eqref{12} 式 明顯表示出平面凸四邊形的 Bretschneider 面積平方式！
• (2) 若再令 $V_5 =V_4 = 0$, 則凸五邊形退化成三角形, \eqref{11}式又蛻變成下式; 得, \begin{equation} [S(3)]^2=\frac1{16}(V_1+V_2-V_3)(V_1+V_2+V_3)(V_3+V_1-V_2)(V_3-V_1+V_2) \label{13} \end{equation} 此 \eqref{13} 式 明顯表示出三角形的 Heron 面積平方式！
• (3) 已知單邊長 $d$ 的正凸五邊形面積平方為 $[S(5)]^2=\dfrac1{16}(25+10\sqrt{5})d^4$ 現在將 \eqref{11} 式的每一邊長全換成 $d$, 每一內角都等於 $108^\circ$, 再利用三角函數值代入 \eqref{11} 式, 經詳盡正確的計算, 即可得到前述已知的正凸五邊形面積平方值。

由以上的推證與檢驗, 可知 \eqref{11} 式即為平面凸五邊形面積的平方式, 因此歸納出下述定理;

定理1. 平面凸五邊形面積的平方式為 \begin{eqnarray} [S(5)]^2&=&\frac1{16}(V_2+V_3+V_4+V_5-V_1)(V_3+V_4+V_5+V_1-V_2)\nonumber\\ &&\times[(V_1+V_2)^2-(V_3-V_4)^2-(V_3-V_5)^2-(V_4-V_5)^2+V_3^2+V_4^2+V_5^2]\nonumber\\ &&-V_1V_2V_3V_5\sin^2\Big(\frac{A_2+A_4+A_5}2\Big)-V_1V_2V_3V_4\cos^2\Big(\frac{A_2+A_4}2\Big)\nonumber\\ &&-V_1V_2V_4V_5\cos^2\Big(\frac{A_2+A_5}2\Big)-V_3V_4V_5^2\Big(\cos^2\frac{A_4}2\Big)-V_3^2V_4V_5\Big(\cos^2\frac{A_5}2\Big)\nonumber\\ &&-V_3V_4^2V_5\sin^2\Big(\frac{A_4-A_5}2\Big) \end{eqnarray} 因為公式很長, 用面積的平方式來表示較為方便, 以上就是平面凸五邊形面積平方式的證明。

D. 平面凸六邊形的面積

在平面上給定一個凸六邊形 $A_1A_2A_3A_4A_5A_6$ 令 $\overline{A_1A_2}=V_1$, $\overline{A_2A_3}=V_2$, $\overline{A_3A_4}=V_3$, $\overline{A_4A_5}=V_4$, $\overline{A_5A_6}=V_5$, $\overline{A_6A_1}=V_6$, 並且連接一對角線, 如圖 4, 將圖形分割成兩個四邊形 $A_1A_2A_3A_4$ 與 $A_1A_4A_5A_6$, 這兩圖形共同擁有邊長 $A_1A_4$, 則由面積型餘弦公式可得 \begin{eqnarray*} &&\hskip -25pt V_1^2+V_2^2+V_3^2-2V_1V_2\cos A_2-2V_2V_3\cos A_3+2V_1V_3\cos(A_2+A_3)\\ &=&V_4^2+V_5^2+V_6^2-2V_4V_5\cos A_5-2V_5V_6\cos A_6+2V_4V_6\cos(A_5+A_6) \end{eqnarray*} 移項後, 得 \begin{eqnarray} &&\hskip -25pt V_1^2+V_2^2+V_3^3-V_4^2-V_5^2-V_6^2\nonumber\\ &=& 2V_1V_2\cos A_2+2V_2V_3\cos A_3-2V_1V_3\cos(A_2+A_3)-2V_4V_5\cos A_5\nonumber\\ &&-2V_5V_6\cos A_6+2V_4V_6\cos(A_5+A_6)\label{14} \end{eqnarray} 再由凸六邊形面積 $S(6)$ 等於兩個四邊形面積之和, 倣照 (4s-a-1) 式, 得 \begin{eqnarray} 2S(6)&=&V_1V_2\sin A_2+V_2V_3\sin A_3-V_1V_3\sin(A_2+A_3)+V_4V_5\sin A_5\nonumber\\ &&+V_5V_6\sin A_6-V_4V_6\sin(A_5+A_6)\label{15} \end{eqnarray} 再一次看到 \eqref{14} 式和 \eqref{15} 式兩式中的 $\sin$ 項及 $\cos$ 項完全相似！ 這就是思考的關鍵點！

聯立解 \eqref{14}、\eqref{15} 兩關係式, 倣效平面凸五邊形面積平方式的證明; 先將 \eqref{14} 式的平方 加上 \eqref{15} 式的平方, 經多次複雜的化簡及移項, 此次工程非常巨大, 不再贅述過程, 最後得 \begin{eqnarray} [S(6)]^2&=&\frac1{16}[(V_1+V_2+V_3)^2-(V_4-V_5)^2-(V_4-V_6)^2-(V_5-V_6)^2+V_4^2+V_5^2+V_6^2]\nonumber\\ &&\times [(V_4+V_5+V_6)^2-(V_1-V_2)^2-(V_1-V_3)^2-(V_2-V_3)^2+V_1^2+V_2^2+V_3^2]\nonumber\\ &&-V_1V_3V_4V_6\cos^2\Big(\frac{A_2+A_3+A_5+A_6}2\Big)-V_1V_2V_4V_6\sin^2\Big(\frac{A_2+A_5+A_6}2\Big)\nonumber\\ &&-V_2V_3V_4V_6\sin^2\Big(\frac{A_3+A_5+A_6}2\Big)-V_1V_3V_4V_5\sin^2\Big(\frac{A_2+A_3+A_5}2\Big)\nonumber\\ &&-V_1V_3V_5V_6\sin^2\Big(\frac{A_2+A_3+A_6}2\Big)-V_1V_2V_4V_5\cos^2\Big(\frac{A_2+A_5}2\Big)\nonumber\\ &&-V_1V_2V_5V_6\cos^2\Big(\frac{A_2+A_6}2\Big)-V_2V_3V_4V_5\cos^2\Big(\frac{A_3+A_5}2\Big)\nonumber\\ &&-V_2V_3V_5V_6\cos^2\Big(\frac{A_3+A_6}2\Big)-V_1V_2V_3^2\cos^2\frac{A_2}2-V_1^2V_2V_3\cos^2\frac{A_3}2\nonumber\\ &&-V_4V_5V_6^2\cos^2\frac{A_5}2-V_4^2V_5V_6\cos^2\frac{A_6}2-V_1V_2^2V_3\sin^2\Big(\frac{A_2-A_3}2\Big)\nonumber\\ &&-V_4V_5^2V_6\sin^2\Big(\frac{A_5-A_6}2\Big)\label{16} \end{eqnarray} 由以上的推證, 可知 \eqref{16} 式即為平面凸六邊形面積的平方式, 因此歸納出下述定理;

定理2. 平面凸六邊形面積的平方式為上述 \eqref{16} 式的公式內容。

同樣地, 此定理2公式 \eqref{16} 式的美妙處是, 涵納先前所有的特例; 謹敘述於下;

• (1) 使 $V_3 = 0$, 則凸六邊形退化成凸五邊形, \eqref{16} 式 蛻變成型態完全類似的 \eqref{11} 式。
• (2) 再令 $V_3 =V_4 = 0$, 則凸六邊形退化成凸四邊形, \eqref{16} 式又蛻變成型態類似的 \eqref{12} 式。
• (3) 再令 $V_3=V_4 =V_5 = 0$, 則凸六邊形退化成三角形, \eqref{16} 式蛻變成型態類似的 \eqref{13} 式。
• (4) 已知單邊長 $d$ 的正凸六邊形面積平方為 $[S(6)]^2 =\dfrac{27}4 d^4$ 現在將 \eqref{16} 式的每一邊長全換成 $d$, 每一內角都等於 $120^\circ$, 經詳盡正確的計算, 即可得到此數值。

以上就是本文完整的解析論證過程。 正文中省略了許多計算流程, 讀者可自行實際運算查證, 以 確實體驗研究過程所遭遇的障礙與轉折, 及筆者費神思考以尋獲關鍵對應式的心得！

III. 結論

• (a) 已知三角形面積的Heron公式內容只含邊長; 凸四邊形面積的Bretschneider公式含有四邊長及兩個對角; 現在作者所研究發現到的凸五邊形面積公式裡含有五邊長及三個內對角; 而凸六邊形面積公式裡含有六邊長及四個內對角; 這樣連續歸納起來誠屬合理, 因此可知凸七邊形面積公式裡必有七個邊長及五個內對角; 以此類推, 可「猜測」凸 $n$ 邊形面積公式裡必有 $n$ 個邊長及 $n-2$ 個內對角！ 由於三角形的三頂點必共圓, 其面積公式裡不會有內角。頂點共圓必可簡化公式內容！
• (b) 利用性質 1 與 2, 可先找出任一凸多邊形的邊長型正餘弦公式, 進而求出面積型正餘弦公式, 因而能再發現出更多平面凸多邊形面積的平方式！但顯然, 這些凸多邊形面積公式內容的表示式已是非常冗長複雜了！
• (c) 本文提出的主要目的, 是提供一個發現平面凸多邊形面積平方式的思考歷程方法, 其中計算的癥結是大量使用三角恆等式; 尤其是三角畢氏恆等式最有效！ 演算中在配成完全平方式時, 需以餘弦項的正負係數作參考, 使完全平方式內各項的係數都取正號, 才能證得出型態完全相同的公式！雖然在推導證明方程式的過程中, 遇到相當多的繁瑣計算, 但那些都只是技術層次的問題, 可以克服; 最重要的是要有策略方法, 要能掌握思考研究的要領, 才能導引出正確的方向！
• (d) 凸多邊形的邊長型正餘弦公式, 可以非常有效地應用在處理幾何圖形的問題上; 尤其是求解四邊形及五邊形的邊長與內角題型更有利！

參考文獻

---本文作者任教嘉義縣同濟中學---