| 發刊日期 |
2014年3月
|
|---|---|
| 標題 | 注重問題引申推廣培養學生數學探究能力 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
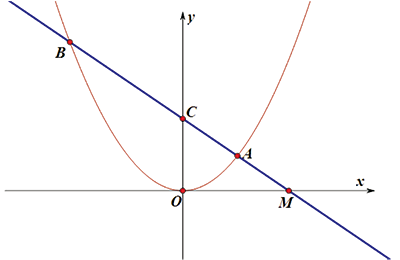
在中學數學教學中, 如何運用引申和推廣的方法來培養學生探究問題的能力, 這是廣大數學教育者值得重視的問題, 知識的難易性不是決定性因素。 我們可以根據學生的實際水平選擇不同層次的命題作為教學材料, 使不同水平的學生可以作不同的推廣, 不必強求, 力求所獲。 引申和推廣中運用最多的是從特.殊到一般化的推理, 是合情推理, 是提出猜想的最常見方式。 在教學中我們經常可以這樣問學生, 這個數學命題能否一般化, 或去掉某些約束條件, 獲得普遍結論。 下面通過一個習題的推廣具體說明之。 我在高三的一節複習課中遇到這樣一題: 如圖1: 已知拋物線 $x^2=4y$ 過點 $M(2,0)$ 的直線 $l$ 與拋物線交於 $A,B$ 兩點, 且直線 $l$ 與 $y$ 軸交於點 $C$。 (1) 求證: $|MA|$, $|MC|$, $|MB|$ 成等比數列;
(2) 設 $\overrightarrow{MA}=\alpha\overrightarrow{AC}$, $\overrightarrow{MB}=\beta\overrightarrow{BC}$, 則 $\alpha+\beta=-1$。
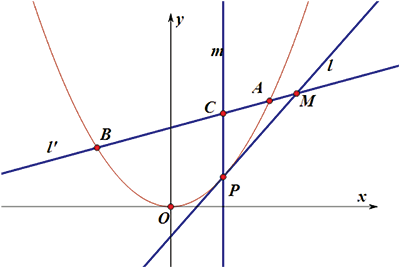
講完這題後, 我問學生: 如果將拋物線方程改為 $x^2=2py$ $(p\gt 0)$, 點 $M$ 改為 $x$ 軸上任意一點, 上述結論是否成立? 學生非常感興趣, 有的動筆算起來, 我說別忙, 先用《幾何畫板》軟體驗證一下。 經實驗發現是正確的。 但不能代替理論證明, 於是師生共同證明。 證明: (1) 由題設知直線 $l$ 的斜率存在, 可設 $M(a,0)$ 直線 $l$ 的方程為: $$y=k(x-a), \ (k\not=0),\ \hbox{聯立}\left\{\begin{array}{l} y=k(x-a)\\ x^2=2py\end{array} \right. ,\hbox{消去 $y$ 並化簡得:}$$ $x^2\!-\!2pkx\!+\!2pka\!=\!0$, 設 $A(x_1,y_1)$, $B(x_2,y_2)$, $C(0,-ka)$, 則 $x_1\!+\!x_2\!=\!2pk$, $x_1x_2\!=\!2pka$。 因為 \begin{eqnarray*} |MA|\cdot |MB|&=&\sqrt{1+k^2}|x_1-a|\cdot \sqrt{1+k^2}|x_2-a|=(1+k^2)|x_1x_2-a(x_1+x_2)+a^2|\\ &=&(1+k^2)|2pka-2pka+a^2|=a^2(1+k^2),\\ |MC|^2&=&(a-0)^2+(0+ka)^2=a^2(1+k^2), \end{eqnarray*} 所以 $|MC|^2=|MA|\cdot |MB|$ 即 $|MA|$, $|MC|$, $|MB|$ 成等比數列。 (2) 由 $\overrightarrow{MA}=\alpha\overrightarrow{AC}$, $\overrightarrow{MB}=\beta\overrightarrow{BC}$ 得, $(x_1-a,y_1)=\alpha(-x_1,-ka-y_1)$, $(x_2-a,y_2)=\beta(-x_2,-ka-y_2)$, 即得: $\alpha=\dfrac{a-x_1}{x_1}$, $\beta=\dfrac{a-x_2}{x_2}$, 於是 $$\alpha+\beta=\frac{(a-x_1)x_2+(a-x_2)x_1}{x_1x_2}=\frac{a(x_1+x_2)-2x_1x_2}{x_1x_2}=\frac{2pka-4pka}{2pka}=-1.$$ 從以上證明說明猜想是成立的, 我繼續追問: 還能推廣嗎? 注意到 $x$ 軸是拋物線的切線, $M$ 點是切線上一點, 如果換成拋物線的任意一條切線, 結論成立嗎? 於是有 猜想: 如圖2:已知拋物線 $x^2=2py$, $(p\gt 0)$, 點 $P$ 是拋物線上任一點, 直線 $l$ 是過點 $P$ 的拋物線的切線, 在直線 $l$ 上任取一點 $M$ 過點 $M$ 的直線 $l'$ 與拋物線交於 $A,B$ 兩點, 且直線 $l'$ 與過 $P$ 點且平行 $y$ 軸的直線 $m$ 交於點 $C$。 (1) 求證: $|MA|$, $|MC|$, $|MB|$ 成等比數列;
(2) 設 $\overrightarrow{MA}=\alpha\overrightarrow{AC}$, $\overrightarrow{MB}=\beta\overrightarrow{BC}$ 則 $\alpha+\beta=-1$。
用《幾何畫板》軟體驗證發現結論是成立的。下面給出證明。 證明: (1) 設 $P\Big(t,\dfrac{t^2}{2p}\Big)$, 直線 $l$ 的方程為: $y=\dfrac tp x-\dfrac{t^2}{2p}$, 設 $M\Big(a,\dfrac{ta}{p}-\dfrac{t^2}{2p}\Big)$, 由題意直線 $l'$ 的斜率存在, 設為 $k$, 直線 $l'$ 方程: $y=k(x-a)+\dfrac {ta}p-\dfrac{t^2}{2p}$, $(k\not=0)$, 聯立 $x^2=2py$ 消去 $y$ 並化簡得: $x^2-2pkx+2pka-2ta+t^2=0$, 設 $A(x_1,y_1)$, $B(x_2,y_2)$, $C\Big(t,k(t-a)+\dfrac {ta}p-\dfrac{t^2}{2p}\Big)$, 則 $x_1+x_2=2pk$, $x_1x_2=2pka-2ta+t^2$。 因為 \begin{eqnarray*} |MA|\cdot |MB|&=&\sqrt{1+k^2}|x_1-a|\cdot \sqrt{1+k^2}|x_2-a|=(1+k^2)|x_1x_2-a(x_1+x_2)+a^2|\\ &=&(1+k^2)|2pka-2ta+t^2-2pka+a^2|=(1+k^2)(t-a)^2.\\ |MC|^2&=&(t-a)^2+\Big(k(t-a)+\frac{ta}p-\frac{t^2}{2p}-\frac{ta}p+\frac{t^2}{2p}\Big)^2=(1+k^2)(t-a)^2. \end{eqnarray*} 所以 $|MC|^2=|MA|\cdot |MB|$ 即 $|MA|$, $|MC|$, $|MB|$ 成等比數列。 (2)由 $\overrightarrow{MA}=\alpha\overrightarrow{AC}$, $\overrightarrow{MB}=\beta\overrightarrow{BC}$, 得: $\alpha=\dfrac{x_1-a}{t-x_1}$, $\beta=\dfrac{x_2-a}{t-x_2}$, 於是 $$\alpha+\beta=\frac{(x_1-a)(t-x_2)+(x_2-a)(t-x_1)}{(t-x_1)(t-x_2)}=\frac{t(x_1+x_2)+a(x_1+x_2)-2x_1x_2-2at} {t^2-t(x_1+x_2)+x_1x_2}.$$ 將 $x_1+x_2=2pk$, $x_1x_2=2pka-2ta+t^2$ 代入化簡得: $\alpha+\beta=-1$。 確定無疑, 本結論成立。 我們以上的推廣似乎很玄妙, 如果從仿射幾何的角度來看則比較明顯, 考慮在仿射變換 $\left\{\begin{array}{l} x'=ax+c\\ y'=2acqx+a^2y+c^2q \end{array}\right.$ 下, 拋物線 $y=qx^2$ 變為 $y'=q{x'}^2$, 形狀沒有改變, 但拋物線 $y=qx^2$ 上原點變為拋物線 $y'=q{x'}^2$ 上另一點 $(c,c^2q)$ 拋物線 $y=qx^2$ 原點處的切線方程 $y=0$ 變為拋物線 $y'=q{x'}^2$ 的點 $(c,c^2q)$ 處切線方程 $y'=2cq x'-c^2q$, 而直線 $x=0$ 變為直線 $x'=c$ 依然平行 $y'$ 軸,而仿射變換保持簡比不變, 故顯然成立。 本節課從一個普通的問題出發, 引導學生進行探究, 將問題大大推廣, 獲得了新的結論, 平時教學中我們經常進行這樣的訓練, 對學生的探究能力的培養是非常有益的。 ---本文作者任教安徽省旌德中學--- |
2014年3月 38卷1期
注重問題引申推廣培養學生數學探究能力