| 發刊日期 |
2015年12月
|
|---|---|
| 標題 | 2015 年第56 屆國際數學奧林匹亞競賽試題解答 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
2015 年第 56 屆國際數學奧林匹亞競賽 (International Mathematical Olympiad, 簡稱 IMO) 在泰國清邁 (Chiang Mai, Thailand) 舉行。本屆共 有 104 個國家 (含 3 個觀察國) 與會、合計 577 位學生 (含 52 位女學生) 代 表參賽。競賽活動是由各國領隊組成的評審會議 (Jury Meeting) 揭開序幕。除 了確認各項議題外, 評審會議的主要工作是挑選本屆的競賽試題。國際數學奧林 匹亞競賽試題是先由各參賽國 (主辦國除外) 於規定時間內提交數道試題, 再由 主辦國的試題委員會 (Problem Selection Committee) 研究選出 20 至 30 道預 選試題, 分屬代數、組合、幾何、數論等不同領域和不同難度的試題;最後再經 由評審會議票選暨修訂出最後 6 道 IMO 試題, 依主題內容及難易層次分配成兩 份試題, 分別在連續的兩天舉行競試, 每天 3 道試題, 考試時間都是 4 小時 又 30 分鐘。 本屆試題經由主辦國的試題委員會選出他們認為較適當的試題, 再由各國領隊組 成的評審會議經過四天的討論票選出 6 道正式試題, 其中第一題的領域為組合、 第二題為數論、第三, 四題為幾何, 第五題為代數, 第六題為組合。對此次我國 代表團所翻譯成正體中文版的 6 道 IMO 試題提供參考解答, 以供國內相關學者 研究、應用與參考。
(a) 證明:對所有的整數 $n \geqslant 3$, 皆存在 $n$ 個點的平衡點集。 (b) 找出所有的整數 $n \geqslant 3$, 使得 $n$ 個點的平衡且無中心的點集是存在的。 試題委員會公布的參考答案:(b) 小題的答案: 所有的奇數 $n \geqslant 3$。 以下的證明過程中, 均假設 $n$ 是大於或等於 $3$ 的整數。 (a) 小題的證明. 當 $n$ 是奇數時, 考慮正 $n$ 邊形, 其頂點依 逆時針方向標記為 $A_1, A_2, \dots, A_n$, 並令 $\mathcal S = \{ A_1, \dots, A_n \}$。 以下檢查 $\mathcal S$ 是平衡的。 對任意兩相異頂點 $A_i$, $A_j$, 令 $k \in \{ 1, 2, \dots, n \}$ 為同餘方程 $2 k \equiv i + j \pmod{n}$ 的解。由於 $k - i \equiv j - k \pmod{n}$, 知 $A_i A_k = A_k A_j$, 符合題意。 現在開始假設 $n$ 是偶數。 考慮一個正 $(3n-6)$ 邊形, 令 $O$ 為其外心。同 樣地我們依逆時針方向將其頂點標記為 $A_1, \dots, A_{3n-6}$, 並 令 $\mathcal S = \{ O, A_1, A_2, \dots, A_{n-1} \}$。 以下檢 查 $\mathcal S$ 是平衡的。 對任意兩相異頂點 $A_i$, $A_j$, 總有 $OA_i = O A_j$。再來考慮 $O$ 與其中一頂點 $A_i$。首先, 對於所有的 $i \leqslant \frac{n}{2}$ 時, $O A_i A_{i'}$ 形成正三角形, 其中 $i' = \frac{n}{2} - 1 + i$;所以 當 $i \leqslant \frac{n}{2}$ 時, 均有 $OA_{i'} = A_i A_{i'}$。反之, 若 $i \gt \frac{n}{2}$, 就有 $O A_{i''} = A_i A_{i''}$, 其中 $i'' = i - \frac{n}{2} + 1$。本小題得證。 註. 本小題還有其他的建構方式, 有興趣的讀者可以自行 嘗試。 (b) 小題的證明. 由 (a) 小題的建構知:當 $n$ 為大 於或等於 $3$ 的奇數時, 正 $n$ 邊形的所有頂點形成的集合為平衡且無中心的; 它是無中心的理由為:對任意三個相異頂點 $A$, $B$, $C \in \mathcal S$, 其外心就是這個正 $n$ 邊形的中心, 但它不在此點集中。 現在假設 $n$ 為大於 $3$ 的偶數, 而 $\mathcal S$ 為 $n$ 個點的平衡且無中 心的點集;以下將得出矛盾。 對於兩個相異點 $A$, $B \in \mathcal S$, 我 們將集合 $\{ A, B \}$ 對應到滿足 $AC = BC$ 的點 $C \in \mathcal S$。 因為 $\mathcal S$ 可形成 $\frac{n(n-1)}{2}$ 對的點, 由鴿籠原理知有 一點 $P \in \mathcal S$ 與至少 $\bigl\lceil \frac{ n(n-1) }{2} / n \bigr\rceil = \frac{n}{2}$ 對點對應。注意到這 $\frac{n}{2}$ 對點都不包 含 $P$, 所以它們的聯集最多包含 $n-1$ 個點;亦即有兩對點同時包含某一個 點。令這兩對點為 $\{ A, B \}$ 與 $\{ B, C \}$, 由定義知 $PA = PB = PC$, 此與無中心的假設矛盾。證畢。 $\Box$ 評註: 本題為考慮幾何配置的簡易組合題, 係考慮平面上有 限點集的特殊性質, 只要能連結到正多邊形、或是圓上適當配置的點加上圓心, 就能得到第一部分的證明。而第二部分對於排除偶數點集的方法, 可以利用鴿籠 原理、或是利用二分圖 (bipartite graph) 的概念討論即可。
($2$ 的乘冪指的是形如 $2^n$ 的整數, 其中 $n$ 為非負整數。) 試題委員會公布的參考答案:本題共有 16 組解: $(2, 2, 2)$、 $(2, 2, 3)$ 的 3 個排列、以及 $(2, 6, 11)$ 與 $(3, 5, 7)$ 的各 6 個排列。 易知以上的 16 個三元組符合題意。以下說明滿足題意的三元組 $(a, b, c)$ 必為上述各組之一。 如果 $a = 1$, 則 $c - b$ 與 $b - c$ 都是 $2$ 的乘冪; 但此不能發生, 因為 $(b - c) + (c - b) = 0$, 而 $2$ 的乘冪必為正數。由 對稱性, 知 $a, b, c \geqslant 2$。 第 1 種情形. $a, b, c$ 中至少有兩數相等。 不失一般性, 設 $a = b$。 於是 $a^2 - c$ 與 $a (c - 1)$ 都是 $2$ 的乘冪。 由後者可得 $a$ 與 $c - 1$ 皆為 $2$ 的乘冪, 故可設 $a = 2^\alpha$、 $c = 2^\gamma + 1$, 其中 $\alpha, \gamma$ 是非負整數。因為 $a^2 - c = 2^{2\alpha} - 2^\gamma - 1$ 也是 $2$ 的乘冪, 此數模 $4$ 的餘數必不為 $-1$, 由此得 $\gamma \leqslant 1$。而 $2^{2\alpha} - 2$ (當 $\gamma = 0$) 與 $2^{2\alpha} - 3$ (當 $\gamma = 1$) 兩數都只能在 $\alpha = 1$ 的情 形下成為 $2$ 的乘冪。故三元組 $(a, b, c)$ 必為 $(2, 2, 2)$ 或 $(2, 2, 3)$ (以及它的排列)。 第 2 種情形. $a, b, c$ 兩兩互異。 由對稱性, 可設 \begin{equation} \label{eq:2-1} 2 \leqslant a \lt b \lt c. \end{equation} 以下證明 $(a, b, c) = (2, 6, 11)$ 或 $(a, b, c) = (3, 5, 7)$。 由題設, \begin{gather} bc - a = 2^\alpha, \label{eq:2-2} \\ ca - b = 2^\beta, \label{eq:2-3} \\ ab - c = 2^\gamma, \label{eq:2-4} \end{gather} 其中 \begin{equation} \label{eq:2-5} \alpha \gt \beta \gt \gamma \end{equation} 為三個非負整數。 根據 $a$ 的大小, 以下我們再分兩種子情形。 情形 2-1. $a=2$。 我們先來證明 $\gamma = 0$。 假設不然 (即 $\gamma \gt 0$), 由 (\ref{eq:2-4}) 可知 $c$ 是偶數, 同樣由 (\ref{eq:2-3}) 及 (\ref{eq:2-5}) 式知 $b$ 也是偶數。於是 (\ref{eq:2-2}) 式的左邊模 $4$ 的餘數等於 $2$, 而此情形只有在 $bc = 4$ 的時候才能成立。此與 (\ref{eq:2-1}) 式矛盾, 故 $\gamma$ 必為 $0$, 而由此知 $c = 2b - 1$。 現在由 (\ref{eq:2-3}) 式得 $3b - 2 = 2^\beta$。因為 $b \gt 2$, 所以 $\beta \geqslant 4$。如果 $\beta = 4$, 就得 $b = 6$、 $c = 2b - 1 = 11$, 此為一解。 如果 $\beta \geqslant 5$, 由 (\ref{eq:2-2}) 式可得 \begin{equation*} 9 \cdot 2^\alpha = 9b (2b-1) - 18 = (3b - 2)(6b + 1) - 16 = 2^\beta (2^{\beta+1} + 5) - 16, \end{equation*} 但在 $\beta \geqslant 5$ 時, 上式的右邊不被 $32$ 所整除。所以 $\alpha \leqslant 4$, 而與 (\ref{eq:2-5}) 式矛盾。 情形 2-2. $a \geqslant 3$。 自 $\{ -1, +1 \}$ 中選出一個整數 $\vartheta$ 使得 $c - \vartheta$ 不被 $4$ 整除。由於 \begin{equation*} 2^\alpha + \vartheta \cdot 2^\beta = (bc - a \vartheta^2) + \vartheta (ca - b) = (b + a\vartheta)(c - \vartheta) \end{equation*} 可被 $2^\beta$ 整除, 所以 $b + a\vartheta$ 可被 $2^{\beta-1}$ 整除。另 一方面, 由 $2^\beta = ca - b \gt (a - 1) c \geqslant 2 c$ 可得 $a$ 與 $b$ 皆小於 $2^{\beta-1}$。這些條件只能在 $\vartheta = 1$ 且 $a + b = 2^{\beta - 1}$ 時成立。由 (\ref{eq:2-3}) 式知 \begin{equation} \label{eq:2-6} ca - b = 2 (a+b), \end{equation} 於是 $4b \gt a + 3b = a(c-1) \geqslant ab$, 故得 $a = 3$。 現在代回 (\ref{eq:2-6}) 式可得 $c = b + 2$, 而 (\ref{eq:2-2}) 式告訴我 們 $b (b+2) - 3 = (b-1)(b+3)$ 是 $2$ 的乘冪, 由此知 $b-1$ 和 $b+3$ 也 都是 $2$ 的乘冪。因為這兩個數的差是 $4$, 所以唯一的答案是 $b = 5$, 而 $c = b + 2 = 7$。 本題至此全部分析完畢。 $\Box$ 評註: 本題的敘述連國中程度的學生都能看懂, 但其實是中 間偏難的數論題。除了要掌握 $2$ 的乘冪數的性質以外, 對於各情形的分類討 論, 是需要小心處理的。分類原則除了按照官方解答之外, 另可依照 $a, b, c$ 三數的奇偶性來分析。
證明: 三角形 $KQH$ 的外接圓與三角形 $FKM$ 的外接圓相切。 試題委員會公布的參考答案: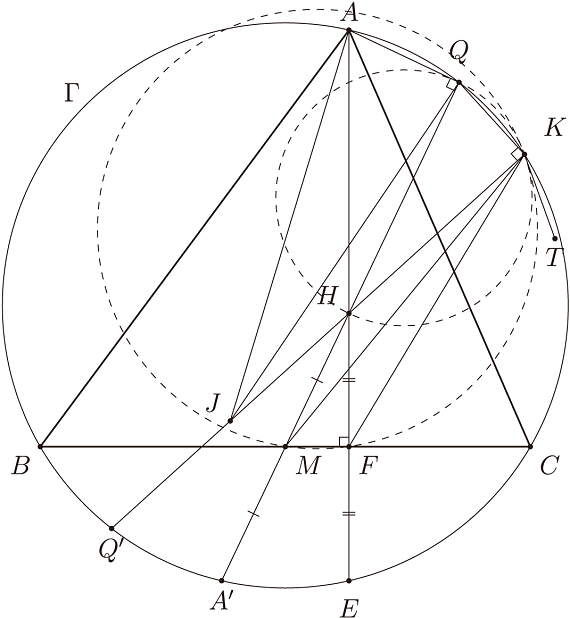
令點 $A'$ 為 $A$ 在 $\Gamma$ 上的對徑點。 因 $\angle AQA' = 90^\circ$ 及 $\angle AQH = 90^\circ$, 故 $Q, H, A'$ 三點共線。 一樣地, 若令 $Q'$ 為 $Q$ 在 $\Gamma$ 上的對徑點, 同樣會有 $K, H, Q'$ 三點共線。 令直線 $AHF$ 與 $\Gamma$ 的另一個交點為 $E$。 熟知 $M$ 是 $HA'$ 線段的中點, 且 $F$ 為 $HE$ 線段的中點。 令點 $J$ 為線段 $HQ'$ 的中點。 考慮平面上一點 $T$ 滿足: $TK$ 與 $KQH$ 外接圓切於 $K$ 點, 且 $Q, T$ 位於直線 $KH$ 的兩側 (如圖 1)。 則有 $\angle HKT = \angle HQK$, 而我們需證明的是 $\angle MKT = \angle CFK$。 所以我們只要再證明 $\angle HQK = \angle CFK + \angle HKM$ 即可。 因為 $\angle HQK = 90^\circ - \angle Q'HA'$ 以及 $\angle CFK = 90^\circ - \angle KFA$, 上式等價於 $\angle Q'HA' = \angle KFA - \angle HKM$。 現在, 由於 $\triangle KHE$ 相似於 $\triangle AHQ'$, 且 $F, J$ 為分別對應邊的中點, 得 $\angle KFA = \angle HJA$; 一樣可推得 $\angle HKM = \angle JQH$。至此, 我們只需要證出 \begin{equation*} \angle Q'HA' = \angle HJA - \angle JQH \end{equation*} 即可。 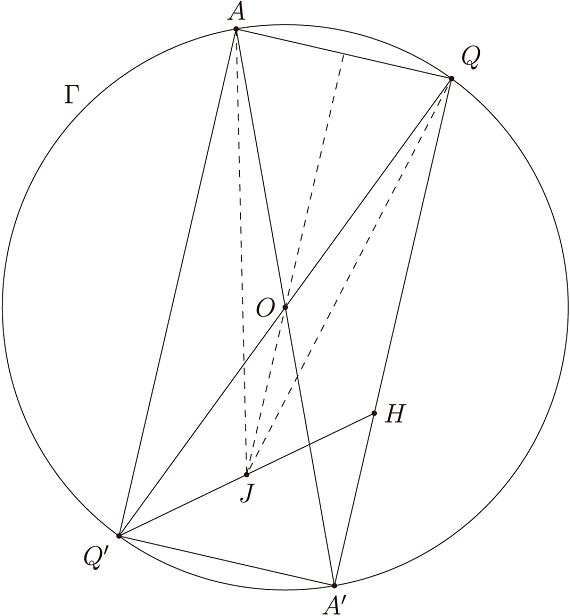
參考圖 2。 因為 $\angle Q'HA' = \angle JQH + \angle HJQ$ 以及 $\angle HJA = \angle QJA + \angle HJQ$, 我們可將欲證之式子化簡為 $2 \angle JQH = \angle QJA$。但 $AQA'Q'$ 為矩形, 而 $J$ 是 $HQ'$ 的中點, $J$ 必然落在 $AQ$ 與 $A'Q'$ 兩邊中點的連線上, 從而得證。 $\Box$ 評註: 本題是偏難的幾何題。為了證明兩圓內切, 官方解答 的過程是考慮其中一圓的切線, 會造成對另一圓的弦切角性質;經過相似三角形 與共圓的轉換之後, 得到一個不明顯的中間性質 ($\angle Q'HA' = \angle HJA - \angle JQH$)。本道試題大會另外提供了其他作法, 每一種作法都有一個重大 的中間步驟。選手們在時間壓力要找到可行的解題路徑, 實屬不易。本題另有一 個相當漂亮的證明, 係採取對垂心 $H$ 作反演變換, 讀者可以嘗試看看。
設直線 $FK$ 與直線 $GL$ 相異, 且兩線交於點 $X$。 證明: $X$ 落在直線 $AO$ 上。 試題委員會公布的參考答案:本題只需證明直線 $FK$ 與 $GL$ 對稱於 $AO$ 即可。 首先, 線段 $AF$ 與 $AG$ 是圓 $\Omega$ 上等長的弦, 故對稱於 $AO$。 下證 \begin{equation} \label{eq:4-1} \angle AFK = \angle LGA. \end{equation} 將三角形 $BDF$ 與 $CGE$ 的外接圓分別記為 $\omega_B$ 與 $\omega_C$。 我們從下式出發: \begin{equation*} \angle AFK = \angle GFD + \angle AFG - \angle KFD. \end{equation*} 由 $\omega_B$, $\Gamma$, $\Omega$ 三個圓來看, 上式可改寫為 \begin{equation*} \angle AFK = \angle GEC + \angle ABG - \angle KBD = \angle GEC - \angle GBC. \end{equation*} 再來看 $\omega_C$ 與 $\Omega$ 兩個圓, 可得 $\angle AFK = \angle GLC - \angle GAC = \angle LGA$。本題得證。 $\Box$ 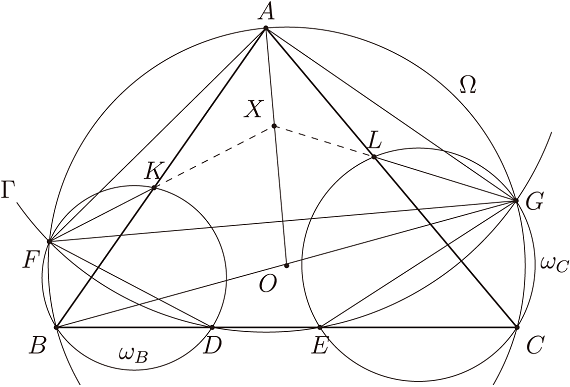
評註: 本題是較簡單的幾何題, 利用角度計算、數點共圓與 對稱性等性質即可得證。
令 $\mathbb R$ 代表所有實數所成的集合。找出所有函數 $f: \mathbb R \to \mathbb R$, 使得對任意實數 $x$ 與$y$, \begin{equation} \label{eq:5-1} f \bigl( x + f(x+y) \bigr) + f(xy) = x + f(x+y) + y \, f(x) \end{equation} 均成立。 試題委員會公布的參考答案:本題有兩解, 分別是: (a) 恆等函數 $f(x) = x$;或是 (b) $f(x) = 2 - x$。 代入易知此二函數為解。以下論證此問題只有這兩個解。 設 $f$ 為滿足 (\ref{eq:5-1}) 式的函數。 (\ref{eq:5-1}) 式中代入 $y=1$ 得 \begin{equation} \label{eq:5-2} f \bigl( x + f(x+1) \bigr) = x + f(x+1); \end{equation} 換句話說, 對所有 $x \in \mathbb R$, $x + f(x+1)$ 必為 $f$ 的不動點。 以下我們用 $f(0)$ 之值分成兩種情形討論: 第 1 種情形. $f(0) \neq 0$. (\ref{eq:5-1}) 式中代入 $x=0$, 可得 \begin{equation*} f \bigl( f(y) \bigr) + f(0) = f(y) + y f(0). \end{equation*} 所以如果 $y_0$ 是 $f$ 的不動點, 在上式中代入 $y = y_0$ 可解得 $y_0 = 1$。 因此, 由 (\ref{eq:5-2}) 式可知:對所有 $x \in \mathbb R$, $x + f(x+1) = 1$ 恆成立。故得一解 $f(x) = 2 - x$ ($\forall\, x \in \mathbb R$)。 第 2 種情形. $f(0) = 0$. (\ref{eq:5-1}) 式中代入 $(x, y) = (x+1, 0)$, 得 \begin{equation} \label{eq:5-3} f \bigl( x + f(x+1) + 1 \bigr) = x + f(x+1) + 1. \end{equation} 並於 (\ref{eq:5-1}) 式中代入 $x=1$ 得 \begin{equation} \label{eq:5-4} f \bigl( 1 + f(y+1) \bigr) + f(y) = 1 + f(y+1) + y f(1). \end{equation} 在 (\ref{eq:5-2}) 式中代入 $x = -1$, 得 $f(-1) = -1$。 再於 (\ref{eq:5-4}) 式中代入 $y=-1$ 得到 $f(1) = 1$。 於是 (\ref{eq:5-4}) 式成為 \begin{equation} \label{eq:5-5} f \bigl( 1 + f(y+1) \bigr) + f(y) = 1 + f(y+1) + y. \end{equation} 由上可知:如果 $y_0$ 與 $y_0 + 1$ 都是 $f$ 的不動點的話, 那麼 $y_0 + 2$ 也是。於是由 (\ref{eq:5-2})、(\ref{eq:5-3}) 兩式知: 對所有的 $x \in \mathbb R$, $x + f(x+1) + 2$ 亦為 $f$ 的不動點, 即: \begin{equation*} f \bigl( x + f(x+1) + 2 \bigr) = x + f(x+1) + 2. \end{equation*} 上式中 $x$ 以 $x-2$ 代入化簡得 \begin{equation*} f \bigl( x + f(x-1) \bigr) = x + f(x-1). \end{equation*} 另一方面, (\ref{eq:5-1}) 式中代入 $y=-1$ 得 \begin{equation*} f \bigl( x + f(x-1) \bigr) = x + f(x-1) - f(x) - f(-x). \end{equation*} 所以對所有的 $x \in \mathbb R$, 都有 $f(-x) = - f(x)$, 即 $f$ 為奇函數。 最後, 在 (\ref{eq:5-1}) 式中 $(x, y)$ 以 $(-1, -y)$ 代入, 並利用 $f(-1) = -1$, 得 \begin{equation*} f \bigl( -1 + f(-y-1) \bigr) + f(y) = -1 + f(-y-1) + y. \end{equation*} 由於 $f$ 是奇函數, 上式成為 \begin{equation*} - f \big( 1 + f(y+1) \bigr) + f(y) = -1 - f(y+1) + y. \end{equation*} 將此式與 (\ref{eq:5-5}) 式相加, 即得 $f(y) = y$ ($\forall\, y \in \mathbb R$)。 證畢。 $\Box$ 評註: 函數方程的問題是 IMO 歷史上一類特殊的代數問題。 通常的解題過程, 係將變數代入一些特殊數字後, 觀察、歸納滿足函數方程的解 所需的必要條件, 從而論證這些必要條件所找到的函數確為其解。如本題中, 先 觀察其解函數 $f$ 的不動點的行為, 然後 (在其中一個情形下) 得出 $f$ 為奇 函數的推論, 最後得到 $f$ 的完整形式。 函數方程求解的問題, 在高等數學中常常出現, 例如微分方程、遞迴關係求解等 問題, 都在這個脈絡底下。因為 IMO 的命題範圍只到高中數學, 所以函數方程的 問題大多以類似本題的形式出現, 是比較特異的。但這樣的訓練與想法, 還是可 以運用在高等數學的研究當中, 也是值得學習的。
(i) 對所有的 $j \geqslant 1$,均滿足 $1 \leqslant a_j \leqslant 2015$; (ii) 對所有的 $1 \leqslant k \lt \ell$,都有 $k + a_k \neq \ell + a_\ell$。 證明:存在兩個正整數 $b$ 與 $N$,使得對所有滿足 $n \gt m \geqslant N$ 的整數 $m$ 與 $n$, \begin{equation*} \left| \sum_{j=m+1}^n ( a_j - b ) \right| \leqslant 1007^2 \end{equation*} 均成立。 試題委員會公布的參考答案:對所有正整數 $n$, 令 $s_n = n + a_n$。由題設知:對所有的 $n \in \mathbb Z_{\gt 0}$, \begin{equation*} n + 1 \leqslant s_n \leqslant n + 2015 \end{equation*} 恆成立。 數列 $s_1, s_2, \dots$ 中的任意兩項均不相同。考慮集合 \begin{equation*} M = \mathbb Z_{\gt 0} \setminus \{ s_1, s_2, \dots \}. \end{equation*} 性質. $M$ 最多只有 $2015$ 個元素。 證. 假設不然。令 $m_1 \lt m_2 \lt \cdots \lt m_{2016}$ 為 $M$ 中的 $2016$ 個相異元素。 令 $n = m_{2016}$, 有 \begin{equation*} \{ s_1, \dots, s_n \} \cup \{ m_1, \dots, m_{2016} \} \subseteq \{ 1, 2, \dots, n + 2015 \}. \end{equation*} 上式的左邊為 $n + 2016$ 個相異元素形成的聯集, 但右邊只有 $n + 2015$ 個 元素, 此為不可能。故性質成立。 $\heartsuit$ 令 $b = |M|$ (即 $M$ 的元素個數), $N = \max(M)$。以下證明 $b$, $N$ 滿 足題設。上段已經證出 $b \leqslant 2015$。 考慮任何一個滿足 $r \geqslant N$ 的整數 $r$。如同上面性質的論證, 集合 \begin{equation} \label{eq:6-1} B_r = M \cup \{ s_1, \dots, s_r \} \end{equation} 為 $[1, r+2015] \cap \mathbb Z$ 的子集合, 並且恰有 $b + r$ 個元素。 由 $M$ 與 $N$ 的定義, 可知 $[ 1, r + 1 ] \cap \mathbb Z \subseteq B_r$。因此可定義一集合 $C_r \subseteq \{ 1, 2, \dots, 2014 \}$ 使得 $|C_r| = b-1$ 且滿足 \begin{equation} \label{eq:6-2} B_r = \bigl( [1, r+1] \cap \mathbb Z \bigr) \cap \{ r + 1 + x \mid x \in C_r \}. \end{equation} 以下用 $\sum J$ 代表有限整數集合 $J$ 的元素總和。 現在 (\ref{eq:6-1})、 (\ref{eq:6-2}) 兩式給出兩種計算 $\sum B_r$ 的方法, 知 \begin{equation*} \sum M + \sum_{j=1}^r s_j = \sum_{j=1}^r j + b (r+1) + \sum C_r, \end{equation*} 移項整理得 \begin{equation} \label{eq:6-3} \sum M + \sum_{j=1}^r (a_j - b) = b + \sum C_r. \end{equation} 經過以上的整理工作後, 現在考慮滿足 $n \gt m \geqslant N$ 的兩整數 $m$, $n$。 (\ref{eq:6-3}) 式中 $r$ 分別以 $n$ 與 $m$ 代入, 兩式相減可得 \begin{equation*} \sum_{j=m+1}^n ( a_i - b ) = \sum C_n - \sum C_m. \end{equation*} 由於 $C_n$ 與 $C_m$ 都是 $\{ 1, 2, \dots, 2014 \}$ 的子集合, 且 $|C_n| = |C_m| = b-1$, 易知絕對值 $\sum C_n - \sum C_m$ 的最大可能值發生在 $C_m = \{ 1, 2, \dots, b-1 \}$, $C_n = \{ 2016 - b, \dots, 2014 \}$ 或 者兩者角色互換。此時有 \begin{equation*} \left| \sum C_n - \sum C_m \right| = (b-1)(2015-b), \end{equation*} 故得一般情形有 \begin{equation*} \left| \sum_{j=m+1}^n (a_j - b) \right| \leqslant (b-1)(2015-b) \leqslant \Bigl( \frac{ (b-1) + (2015-b) }{2} \Bigr)^2 = 1007^2, \end{equation*} 即為所求。證畢。 $\Box$ 評註: 本題是難度較高的組合題, 原本是數線上的正整數點 的有限差距的有向連通集問題。本題的自然解題過程, 是先將題目中的 2015 換 成較小的正整數 (如 $2, 3, 4$ 等), 猜測欲解之 $b$, $N$ 兩數該有的性質。 於是知道:先論證入度 (in-degree) 為 $0$ 的點 (即集合 $M$) 的個數不超 過 $2015$, 再利用組合中計算兩次的方法得到 $b, N$ 兩數, 最後利用算幾不等 式得出欲證之上界, 是一條需要高度想像力才能完整作答的題目。 ---本工作小組係由教育部委託國立中央大學, 於「中華民國參加 2015 年亞太數學暨國際數學奧林匹亞競賽計畫」下成立。本文的主要作者為林延輯助理教授, 任教國立台灣師範大學數學系--- |
2015年12月 39卷4期
2015 年第56 屆國際數學奧林匹亞競賽試題解答

