| 發刊日期 |
2015年12月
|
|---|---|
| 標題 | 善待學生的提問 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
數學課堂上, 孩子提問是再正常不過的現象。 然而課堂上也會出現個別學生提出一些在常人看來比較怪異甚至超常的問題。 作為教師不能忽視這些學生的提問, 更不能譏諷甚至鄙視學生, 因為這樣做會傷害孩子的自尊心, 更為重要的是容易扼殺學生的好奇心, 挫傷學生的求知慾。 只要是學生真實的想法, 教師都應該給予學生肯定和鼓勵。 作為教師要善待學生的提問。 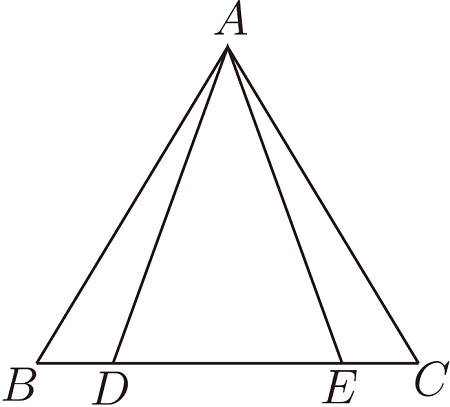
在復習「等腰三角形」的課堂上, 我給學生佈置一組與之有關的練習題, 其中一道題目如下: 如圖1, 點 $D$、$E$ 在 $\triangle ABC$ 的邊 $BC$ 上, $AB=AC$, $AD=AE$。 求證: $BD=CE$, $\angle BAD= \angle CAE$。 本題難度不大, 利用等腰三角形的性質和三角形全等的判定 不難證明, 大部分學生很快證畢。 正當我繼續往下進行時, 突然一 位學生提出這樣一個問題: 如圖 1, 點 $D$、$E$ 在 $\triangle ABC$ 的邊 $BC$ 上, $BD=CE$, $\angle BAD= \angle CAE$。 那麼 $\triangle ABD$ 與 $\triangle ACE$ 是否全等? 提出這個問題的學生數學成績平平, 不知道他為什麼會提出這個問題。 我對這個問題進行了短暫的思考, 由於事先沒有準備, 一時竟無法答覆這個學生。 不過我並不認為學生是在故意刁難而責罰學生。 學生能夠主動提出問題說明他用心學習, 積極思考, 因為我曾經遇到過類似的情形: 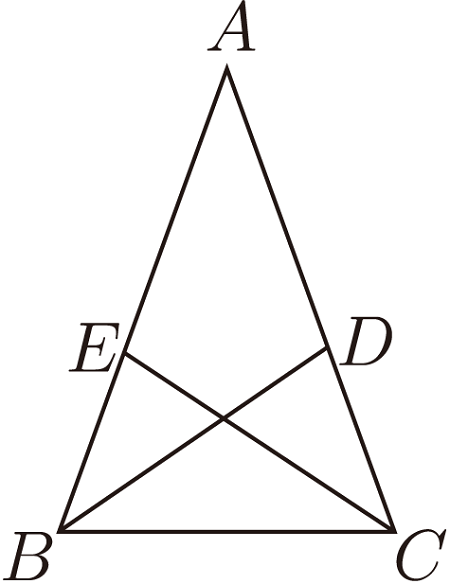
記得以前在學習 「等腰三角形」時, 教材中有這樣一道幾何題: 如圖2, $\triangle ABC$ 中, $AB=AC$, $BD$、$CE$ 是 $\triangle ABC$ 的兩內角平分線。 求證: $BD=CE$。 這道幾何題當然容易證明。誰知課堂上一位學生卻向我提出了一道 與之相反的問題: 如圖 2, $BD$、$CE$ 是 $\triangle ABC$ 的兩內角平分線, 且 $BD=CE$, 那麼 $\triangle ABC$ 是否是等腰三角形? 由於這道題的難度非常大, 我無法當場回答學生的提問。 課後我查閱相關資料才知道, 原來這個學生所提的問題, 正是德國數學家萊默斯在 1840 年給法國數學家斯圖姆的一封信中提到的問題, 也就是證明兩內角平分線相等的三角形是等腰三角形。首先解決這個問題的是瑞士幾何學家斯坦納, 因而這一定理被人們稱為斯坦納 --- 萊默斯定理, 這道幾何題也由此聞名於世。沒想到一個學生提出的問題竟是一道世界有名的幾何題! 通過這個學生提出的問題, 不僅使我增長了數學知識, 開闊了數學視野, 而且讓我深刻認識到慎重對待學生提問的重要性。 不端正對待學生提問的態度, 不僅會使自己停滯不前甚至倒退, 可能還會抹煞一位數學天才。 考慮到上課時間比較緊張, 加上一時半會我也無法解決這個問題, 但我必須對這個學生的提問進行評價, 給這個學生一個交待。 於是我親切地問那個學生是怎樣想到這個問題的。 他回答說要證的結論正好是根據 $\triangle ABD \simeq \triangle ACE$ 推出的, 反過來能不能根據要證的結論來推斷 $\triangle ABD$ 與 $\triangle ACE$ 是否全等? 看來學生提出的問題自然、合理, 並不是信口開河。 我對學生這種積極思考、 能從正反兩個方面考慮問題的精神給予了充分肯定和鼓勵。 然後我坦誠地告訴那個學生:「你提的問題很有價值, 請容我再想一想, 以後答覆你。」 課後我對這個問題進行了深入的思考和研究。 通過運用幾何畫板軟體作圖, 我發現 $\triangle ABD$ 與 $\triangle ACE$ 確實全等。 不過到底怎樣證明這兩個三角形全等, 我一時不知從何下手。 因為證明兩個三角形全等一般需要三個條件, 而這個問題卻只給出兩個條件: 一邊相等和一角相等。 只有從已知條件中再挖掘出一個條件 (一邊相等或一角相等) 才能證明兩個三角形全等。 到底如何挖掘呢? 當我注意到 $\triangle ABD$ 與 $\triangle ACE$ 這兩個三角形的底邊相等, 高相同時, 想到從面積入手, 證明過程如下: $\because\ BD=CE$, 且 $\triangle ABD$ 與 $\triangle ACE$ 同高, $\therefore \ S_{\triangle ABD}=S_{\triangle ACE}$。 而 $S_{\triangle ABD}\!=\! \frac 12AB\cdot AD\cdot\sin \angle BAD$, $S_{\triangle ACE}\!=\! \frac 12AC\cdot AE\cdot\sin \angle CAE$, 且 $\angle BAD\!=\! \angle CAE$, $\therefore \frac 12 AB\cdot AD\cdot\sin \angle BAD= \frac 12 AC\cdot AE\cdot\sin \angle CAE$。 即 $AB\cdot AD=AC\cdot AE$. (1) $\because \angle BAD= \angle CAE$, $\therefore \angle BAD+ \angle DAE= \angle CAE+ \angle DAE$, 即 $\angle BAE= \angle CAD$. $\because S_{\triangle ABD}=S_{\triangle ACE}$, $\therefore S_{\triangle ABD}+S_{\triangle ADE}=S_{\triangle ACE} +S_{\triangle ADE}$, 即 $S_{\triangle ABE}=S_{\triangle ACD}$. 而 $S_{\triangle ABE}= \frac 12 AB\cdot AE\cdot\sin \angle BAE$, $S_{\triangle ACD}=\frac 12 AC\cdot AD\cdot\sin \angle CAD$, $\therefore \frac 12 AB\cdot AE\cdot\sin \angle BAE= \frac 12 AC\cdot AD\cdot\sin \angle CAD$, 即 $AB\cdot AE=AC\cdot AD$ (2) (1)$\times$(2), 得 $AB^2\cdot AD\cdot AE=AC^2\cdot AD\cdot AE$, 即 $AB^2=AC^2$。 而 $AB$、$AC$ 表示線段的長, 都是正數, $\therefore\ AB=AC$。 下面再證明 $\triangle ABD\simeq\triangle ACE$ 就是一件簡單的事了! 這種方法主要是從面積入手。 接下來我又注意到 $\angle BAD$ 與 $\angle CAE$ 分別是 $BD$、$CE$ 的對角, 於是又想到嘗試運用正弦定理進行分析和研究, 也證出了 $\triangle ABD$ 與 $\triangle ACE$ 全等, 證明過程如下: 設 $\angle BAD= \angle CAE=\alpha $, 則 $\angle ADE= \angle B+\alpha$, $\angle AED=\angle C+\alpha$。 在 $\triangle ABD$ 中, 由正弦定理, 得 $\dfrac{BD}{\sin\alpha}=\dfrac{AD}{\sin B}$, 在 $\triangle ACE$ 中, 由正弦定理, 得 $\dfrac{CE}{\sin\alpha}=\dfrac{AE}{\sin C}$。 $\because\ BD=CE$, $\therefore\ \dfrac{AD}{\sin B}=\dfrac{AE}{\sin C}$。 即 $\dfrac{AD}{AE}=\dfrac{\sin B}{\sin C}$。 在 $\triangle ADE$ 中, 由正弦定理, 得 $\dfrac{AD}{\sin(C+\alpha)}=\dfrac{AE}{\sin (B+\alpha)}$。 即 $\dfrac{AD}{AE}=\dfrac{\sin (C+\alpha)}{\sin (B+\alpha)}$。 $\therefore \ \dfrac{\sin B}{\sin C}=\dfrac{\sin (C+\alpha)}{\sin (B+\alpha)}$。 即 $\sin B \sin(B+\alpha )=\sin C \sin(C+\alpha )$。 即 $2\sin B\sin(B+\alpha)=2\sin C \sin(C+\alpha)$, $\cos(2B+\alpha)-\cos\alpha=\cos(2C+\alpha)-\cos\alpha$。 $\therefore$ $\cos(2B+\alpha)=\cos(2C+\alpha)$。 顯然 $\angle B$、 $\angle C$ 和 $\alpha$ 都是銳角, $\therefore\ 0^\circ \lt 2B+\alpha\lt 270^\circ$, $0^\circ \lt 2C+\alpha\lt 270^\circ$。 $\therefore\ 0^\circ \lt (2B+\alpha)+(2C+\alpha)\lt 540^\circ$。 $\therefore\ (2B+\alpha)+(2C+\alpha)=360^\circ$ 或 $2B+\alpha=2C+\alpha$。 當 $(2B+\alpha)+(2C+\alpha)=360^\circ$ 時, $B+C+\alpha=180^\circ$。 觀察圖 1 可知 $B+C+\alpha\lt 180^\circ$, 因此 $B+C+\alpha=180^\circ$ 不合題意, 捨去。 $\therefore\ 2B+\alpha =2C+\alpha$。 $\therefore\ B=C$, 即 $\angle B= \angle C$。 由 「角角邊」 得 $\triangle ABD\simeq \triangle ACE$。 證明完畢之後, 我在思考像 $\triangle ABD$ 與 $\triangle ACE$ 這類表面上只有兩個全等條件的三角形為什麼能夠全等呢? 這類三角形到底有什麼特點呢? 通過觀察圖形, 我發現 $\triangle ABD$ 與 $\triangle ACE$ 這兩個三角形有三個特點: (1) 有一個公共頂點; (2) 公共頂點所對的邊相等且在一條直線上; (3) 以公共頂點為頂點的角相等。 由此得到判定三角形全等的一個定理: 定理1: 如果兩個三角形有一個公共頂點, 以這個公共頂點為頂點的一對角相等, 這對角所對的邊也相等且在一條直線上, 那麼這兩個三角形全等。 可以看出, 能用上面的定理判定全等的兩個三角形位置非常特殊, 不僅要求有公共頂點, 而且公共頂點所對的邊還必須在一條直線上。 接著我想如果兩個三角形有一角對應相等, 該角所對的邊也相等且在同一條直線上, 如果這兩個三角形沒有公共頂點, 還能使這兩個三角形仍然全等嗎? 我通過平移三角形的辦法很快得出答案。 將圖 1 中的 $\triangle ACE$ 向右平移得到圖 3, 顯然 $\triangle A_1BD$ 與 $\triangle A_2CE$ 就是滿足條件的全等三角形。 $\triangle A_1BD$ 與 $\triangle A_2CE$ 只有一邊和一角對應相等, 可為什麼這兩個三角形會全等呢? 我反覆思考, 突然頓悟: 在平移的過程中, 點 $A$ 到直線 l 的距離不變, 因此 $\triangle A_1BD$ 的邊 $BD$ 上的高與 $\triangle A_2CE$ 的邊 $CE$上的高相等, 這樣 $\triangle A_1BD$ 與 $\triangle A_2CE$ 就會有三個元素對應相等(雖然不直接滿足三角形全等的一般條件)。 或許正是這個條件導致 $\triangle A_1BD$ 與 $\triangle A_2CE$ 全等, 奧秘或許就在此。 於是我大膽猜想: 有一邊及其對角以及該邊上的高分別對應相等的兩個三角形全等。 我利用餘弦定理和三角形的面積公式 $S=\frac 12 ab\sin C$ 順利證明這個猜想, 過程如下: 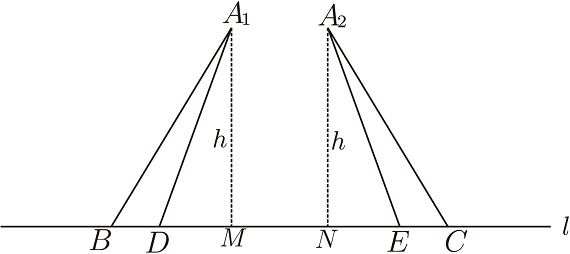
設兩個三角形相等的邊為 $m$, $m$ 的對角為 $\alpha$。 其中一個三角形的另外兩邊為 $a, b$, 另一個三角形的另外兩邊為 $c, d$。 由餘弦定理, 得 $m^2=a^2+b^2-2ab\cos\alpha$, $m^2=c^2+d^2-2cd\cos\alpha$。 $\therefore\ a^2+b^2-2ab\cos\alpha =c^2+d^2-2cd\cos\alpha$。 由題意知兩個三角形的面積相等, $\therefore\ \frac 12 ab\sin\alpha = \frac 12 cd\sin\alpha$。 即 $ab=cd$。 $\therefore\ a^2+b^2=c^2+d^2$。 由 $\left\{\begin{array}{l} ab=cd\\ a^2+b^2=c^2+d^2 \end{array}\right.$ 容易推出 $\left\{\begin{array}{l} a=c\\ b=d \end{array}\right.$ 或 $\left\{\begin{array}{l} a=d\\ b=c \end{array}\right.$。 根據「邊邊邊」 易知兩個三角形全等。由此又得到判定三角形全等的一個定理: 定理2: 有一邊及其對角以及該邊上的高分別對應相等的兩個三角形全等。 可以看出, 定理 2 包含定理 1, 定理 1 是定理 2 的一個特例。 因此表面上看定理 1 和定理 2 是兩個定理, 本質上是一個定理, 也就是定理 2。 由於定理 2 包含三角形的邊、 角和高這些元素, 因此不妨稱這個定理叫做 「邊角高」 定理。 發現 「邊角高」 定理抑制不住內心的喜悅, 不過我想如果能用所學的知識對這個定理進行解釋才會使這個定理更加完美。 通過嘗試、 作圖, 終於成功解釋 「邊角高」 定理: 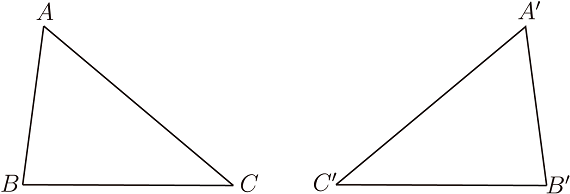
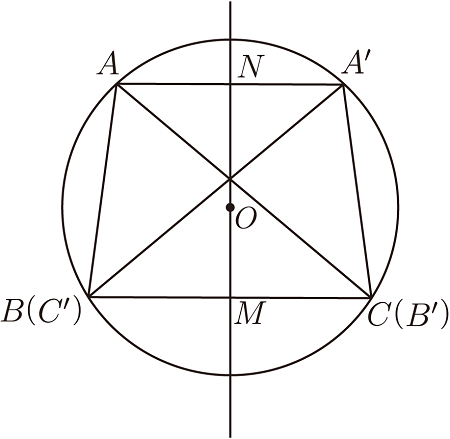
如圖4, 在 $\triangle ABC $ 和 $\triangle A'B'C'$ 中, $BC=B'C'$, $\angle A= \angle A'$, $BC$ 邊上的高與 $B'C'$ 邊上的高相等。 由於 $BC=B'C'$, 將 $\triangle ABC$ 和 $\triangle A'B'C'$ 按圖 5 的方式放置, 使線段 $BC$ 與線段 $B'C'$ 重合(其中點 $B$ 與點 $C'$、 點 $C$ 與點 $B'$ 分別重合), 作 $\triangle ABC$ 的外接圓$\odot\,O$。 由 $\angle A= \angle A'$ 知點 $A'$ 也在 $\odot\,O$ 上。 連結 $AA'$。 因為 $BC$ 邊上的高與 $B'C'$ 邊上的高相等, 因此必有 $AA'\| BC$。 過點 $O$ 作線段 $BC$ 的垂線 $MN$ 分別交 $BC$、 $AA'$ 於點 $M$、 $N$, 則 $MN$ 必然垂直 $AA'$。 由垂徑定理知點 $B$、 $C$ 和 $A$、 $A'$ 都關於直線 $MN$ 對稱。 所以 $\triangle ABC$ 與 $\triangle A'B'C'$ 關於直線 $MN$ 對稱, $\triangle ABC$ 與 $\triangle A'B'C'$ 當然全等。 也就是說, 對於滿足 「邊角高」 的兩個三角形, 總可以通過擺放使這兩個三角形關於相等邊的垂直平分線對稱。 (圖 5 實際上提供了一種證明「邊角高」定理的幾何方法, 也間接給出了等腰梯形判定的一個定理: 以梯形的兩腰和兩條對角線以及其中一條底邊為邊的兩個三角形, 如果以底邊為邊的對角相等, 那麼這個梯形是等腰梯形。) 對 「邊角高」 定理解釋完畢, 我意猶未盡, 再次對這個定理進行深思。 我們知道三角形都有六個元素 (三個內角和三條邊)。 如果從尺規作圖的角度來看, 三角形全等的本質是以滿足三角形全等的三個元素進行尺規作圖, 總可以作出符合條件的三角形 (至少可以作出一個三角形。 如果可以作出兩個或兩個以上的三角形, 那麼這些三角形一定全等)。 因此我想如果以滿足「邊角高」 的條件進行尺規作圖, 也一定能做出符合條件的三角形。 通過反覆思考、嘗試, 終於如願以償。 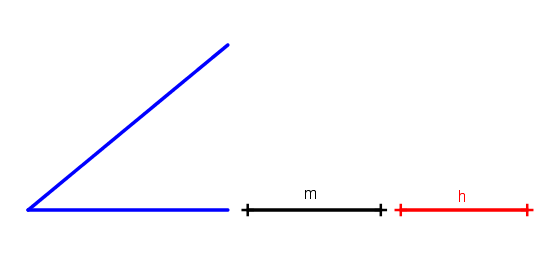
如圖6, 已知 $\angle \alpha $, 線段 $m$ 和線段 $h$。 求作一個三角形, 使這個三角形的一邊為 $m$, 該邊的對角為 $\angle \alpha $, 該邊上的高為 $h$。 作法: (一) 作 $\triangle ABC$, 使 $\angle A=\angle \alpha $, $CB=m$; (二) 作 $\triangle ABC$ 的外接圓 $O$; (三) 作弦 $C'B'$ 平行 $CB$, 且使 $C'B'$ 與 $CB$ 的距離為 $h$; (四) $\triangle CC'B$ 和 $\triangle BB'C$ 均為所求, 且這兩個三角形關於 $CB$ 的垂直平分線對稱, 如圖 7 所示。 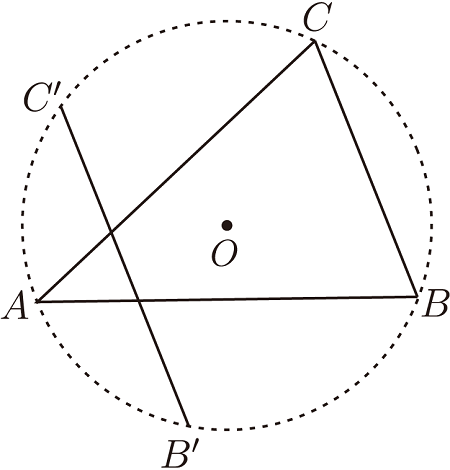
這樣我們又從尺規作圖的角度對 「邊角高」 定理的本質進行了揭示。 至此, 我感覺對這個問題的研究總算可以暫告一段落了。 感悟: 今天收穫真大, 因為我發現了判定三角形全等的一個重要定理 --- 「邊角高」 定理。 同時這也讓我再次感悟到善待學生提問的重要性。 是學生的提問提供了我這麼好的研究素材, 才讓我有機會發現這個定理, 否則我很難甚至不可能發現這個定理。 在教學過程中, 學生的疑與思伴隨相生, 學生主動向教師提問, 體現了學生學習的主動性, 同時有利於促進教師的教學水準和知識水準。 教師要尊重學生, 鼓勵和引導學生提問, 形成教師與學生 「雙向交流」 的氛圍, 相得益彰。 最後借用網路上的一句話 「善待別人就是善待自己」, 我要說: 「善待學生的提問, 就是善待教師的教學。」 ---本文作者任教湖北省襄陽市襄州區黃集鎮初級中學--- |
2015年12月 39卷4期
善待學生的提問

