| 發刊日期 |
2020年3月
|
|---|---|
| 標題 | 一類最小值問題的通法通解 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
胡不歸問題是一個古老的問題, 近年各地頻繁出現以胡不歸問題為原型的中考題, 學生普遍感到問題陌生, 無從下手。 筆者查閱了部分文獻和資料, 也有提及這類中考題的文獻, 多數是在討論問題的答案, 沒有說明這類問題的通法通解, 本文以 2017 廣州中考數學 24 題為例, 通過分析解題思路, 歸納總結出這類問題的通法通解, 整理成短文, 供參考。 為使讀者清楚問題的背景, 先簡要說明古老的胡不歸問題。
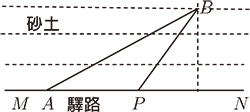
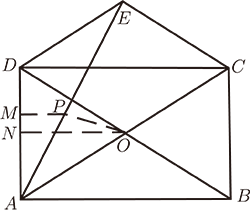
如圖 1, $A$ 是出發點, $B$ 是目的地, $MN$ 是一條驛路, 在目的地 $B$ 一側全是砂土地帶。 在驛路 $MN$ 上的速度為 $v_1$, 在砂土地上的速度為 $v_2$。 $AP$ 在確定的直線 $MN$ 上, $BP$ 是位置不確定的線段。 為使得從 $A$ 經過 $P$ 到 $B$ 的時間最少, $P$ 點選在什麼位置? 一、問題(2017 廣州 24 題) 如圖 2, 矩形 $ABCD$ 的對角線 $AC$、 $BD$ 交於點 $O$, $\triangle COD$ 關於 $CD$ 的對稱圖形為 $\triangle CED$。
思路分析
現在問題轉化為求 $OP+\dfrac 23 PA$ 的最小值問題。 兩條線段的倍數都為 1 的 $a+b$ 類型的最小值問題, 是大家熟悉的問題, 考慮將 $\dfrac 23PA$ 經過變換, 變換成另外一條倍數是1線段, 就轉化成了 $a+b$ 類型的最小值問題。 有如下思考: (1) 代替 $\dfrac 23PA$ 的線段與線段 $OP$ 有公共端點 $P$, 以便運用「兩點之間線段最短」來解決; (2) 過點 $A$ 作一個銳角, 且其正弦值是 $\dfrac 23$, 再過點 $P$ 作垂線。 由 1, $\sin \angle EAD=\dfrac 23$, $\angle EAD$ 恰好就是要作的銳角。 過點 $P$ 作 $PM \bot AD$, 此時 $PA$ 是直角三角形 $\triangle PAM$ 的斜邊。 因為 $\sin \angle PAM=\dfrac {PM}{PA}=\dfrac 23$, 得到 $PM=\dfrac 23 PA$。 此時有 $t=OP+\dfrac 23 PA=OP+PM$。 求 $t$ 的最小值也就是求 $OP+PM$ 的最小值, 當 $O$、 $P$、 $M$ 在同一條直線上時, $OP+PM$ 取最小值。 如圖 2, 過點 $O$ 作 $ON\bot AD$, 交 $AE$ 於點 $P$, 交 $AD$ 於點 $N$, 圖 2 中的 $OP+PM$ 的最小值就是圖 2 中 $ON$ 的長。 在直角三角形 $\triangle DAB$ 中, $ON$ 是直角三角形 $\triangle DAB$ 的中位線, 所以 $ON=\dfrac 12AB=3$。 說明: 上述問題中, $OP$ 是位置不確定的動線段, $PA$ 在定線段 $AE$ 上, 線段 $PA$ 上有一個動點 $P$ 和一個定點 $A$。 以定線段 $AE$ 上的 $PA$ 為斜邊作直角三角形, 根據 1 中的 $\sin\angle EAD=\dfrac 23$, 將 $\dfrac 23PA$ 轉化為 $PM$。 當原題中沒有 $\sin\angle EAD=\dfrac 23$ 這個條件時, 也應作一個以 $A$ 為頂點、 正弦值等於 $\dfrac 23$ 銳角, 再過點 $P$ 作垂線。
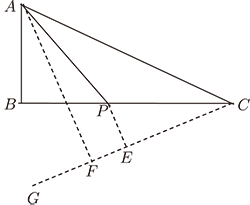
二、通法通解如圖 3, $P$ 是線段 $BC$上一個動點, 求 $AP+k\cdot PC$ $(0\lt k\lt 1)$ 的最小值。 此問題中, 動點 $P$ 在直線上運動, $AP$ 是位置不確定的動線段, 倍數不為 1 的線段 $PC$ 在定線段 $BC$ 上, 線段 $PC$ 上有一個動點 $P$ 和一個定點 $C$。 通常思路: 動點 $P$ 在直線上運動時, 倍數不為 1 線段 $PC$ 上的定點 $C$ 作一個角 $\angle BCG$, 使得 $\sin\angle BCG=k$, $\angle BCG$ 與動線段 $AP$ 分別在確定線段 $BC$ 的兩側; 再過倍數不為 1 的線段 $PC$ 上的動點 $P$ 作 $PE\bot CG$。 在直角三角形 $\triangle PCE$ 中, $\sin\angle BCG=\dfrac{PE}{PC}=k$, 即 $PE=k\cdot PC$。 至此, $AP+k\cdot PC$ 的最小值轉化為 $AP+PE$ 的最小值, 當 $A$、 $P$、 $E$ 在同一直線上時, $AP+PE$ 的值最小。 過點 $A$ 作 $AF\bot CG$, 線段 $AF$ 的長就是 $AP+PE$ 的最小值, 也就是所求的 $AP+k\cdot PC$ 最小值。 上述通法可以簡述為:動點在直線上運動時, 過倍數不為 1 的線段上定點作銳角, 使銳角的正弦值等於 $k$, 再過倍數不為 1 的線段上動點作垂線。
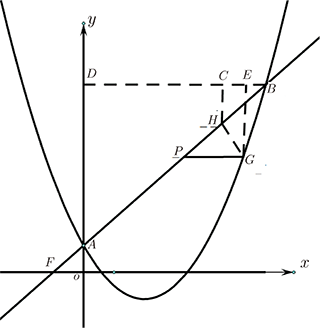
三、通法應用例1: (2016 重慶 B 卷壓軸題改編) 如圖 4, 二次函數 $y=\dfrac 12x^2-2x+1$ 的圖像與一次函數 $y=x+1$ 的圖像交於 $A$、 $B$ 兩點, 點 $P$在 $AB$ 線段上。 其橫坐標是 $\dfrac 52$, 過點 $P$作 $PG// x$ 軸, 交拋物線於點 $G$, 線段 $AB$ 上找一點 $H$ (不與 $A$、 $B$ 重合), 使 $GH+\dfrac{\sqrt{2}}{2} BH$ 的值最小, 求 $GH+\dfrac{\sqrt{2}}{2} BH$ 的最小值。 思路分析$BH$ 在定線段 $AB$ 上, $H$ 是動點, $B$是定點。 過定點 $B$ 作 $\angle ABD=45^\circ$, $\angle ABD$ 在直線 $y=x+1$ 上方, 過動點 $H$ 作 $HC\bot BD$。 在直角三角形 $\triangle HBC$ 中, $\sin\angle ABD=\dfrac{CH}{BH}=\dfrac{\sqrt 2}{2}$, 所以 $CH=\dfrac{\sqrt 2}{2}BH$。 $GH+\dfrac{\sqrt 2}{2}BH$ 的最小值轉化為 $GH+CH$ 的最小值。 當 $G$、 $H$、 $C$ 在同一直線上的時候, $GH+CH$ 最小。 過點 $G$ 作 $GE\bot BD$, 線段 $GE$ 的長度就是 $GH+CH$ 的最小值。 下面求線段 $GE$ 的長。 由一次函數的解析式為 $y\!=\!x\!+\!1$ 可以計算出 $\angle AFO\!=\!45^\circ$, 又 $\angle ABD\!=\!45^\circ$, 所以 $BD//x$ 軸, 所以 $BD\bot y$軸。 只需用點 $E$ 的縱坐標減去點 $G$ 的縱坐標就可以計算出線段 $GE$ 的長。 $P$ 在 $AB$ 上, 可以計算出 $P\Big(\dfrac 52,\dfrac 72\Big)$。 因為 $PG//x$ 軸, 所以 $G$ 的縱坐標為 $\dfrac 72$. 由拋物線和直線的解析式列方程組, 求出點 $B$ 的縱坐標為 7, 所以, $GE$ 的長為 $\dfrac 72$。 即 $GH+\dfrac{\sqrt 2}{2}BH$ 的最小值為 $\dfrac 72$。
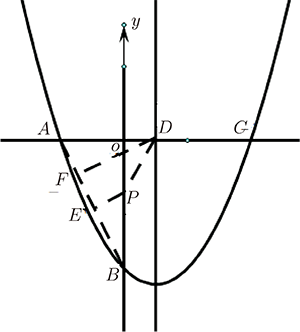
例2: (2016 徐州壓軸題) 如圖 5, 在平面直角坐標系中, 二次函數 $y=ax^2+bx+c$ 的圖像經過點 $A(-1, 0)$, $B(0, -\sqrt 3)$、 $C(2, 0)$, 其中對稱軸與 $x$ 軸交於點 $D$。
思路分析
過定點 $B$ 在 $y$ 軸左側作一個銳角, 使得正弦值等於 $\dfrac 12$。 分析題目的條件發現, $A(-1, 0)$, $B(0, -\sqrt 3)$, 有 $\sin\angle PBA=\dfrac 12$; 再過點 $P$ 作 $PE\bot AB$, 在直角三角形 $\triangle PBE$ 中, $PE=\dfrac 12PB$。 所以, $PD+\dfrac 12 PB$ 的最小值轉化為 $PD+PE$ 的最小值, 當 $D$、 $P$、 $E$ 三個點在同一直線上時, $PD+PE$ 最短。 過點 $D$ 作 $DF\bot AB$, 線段 $DF$ 的長是 $PD+PE$ 的最小值, 也就是 $PD+\dfrac 12PB$ 的最小值。 在直角三角形 $\triangle DAF$ 中, 由 $AD=\dfrac 32$, $\angle DAB=60^\circ$, 可以計算出 $DF=\dfrac{3\sqrt 3}{4}$。 即 $PD+\dfrac 12PB$ 的最小值為 $\dfrac{3\sqrt 3}{4}$。 四、思考圖 3 中, 求 $AP+k\cdot PC$ $(0\lt k\lt 1)$ 的最小值, 問題中有顯著特徵: $0\lt k\lt 1$、 倍數不為 1 的線段 PC 在固定線段上、 動點 $P$ 在直線上運動。
參考文獻---本文作者任教中國山東高青縣實驗中學--- |
2020年3月 44卷1期
一類最小值問題的通法通解