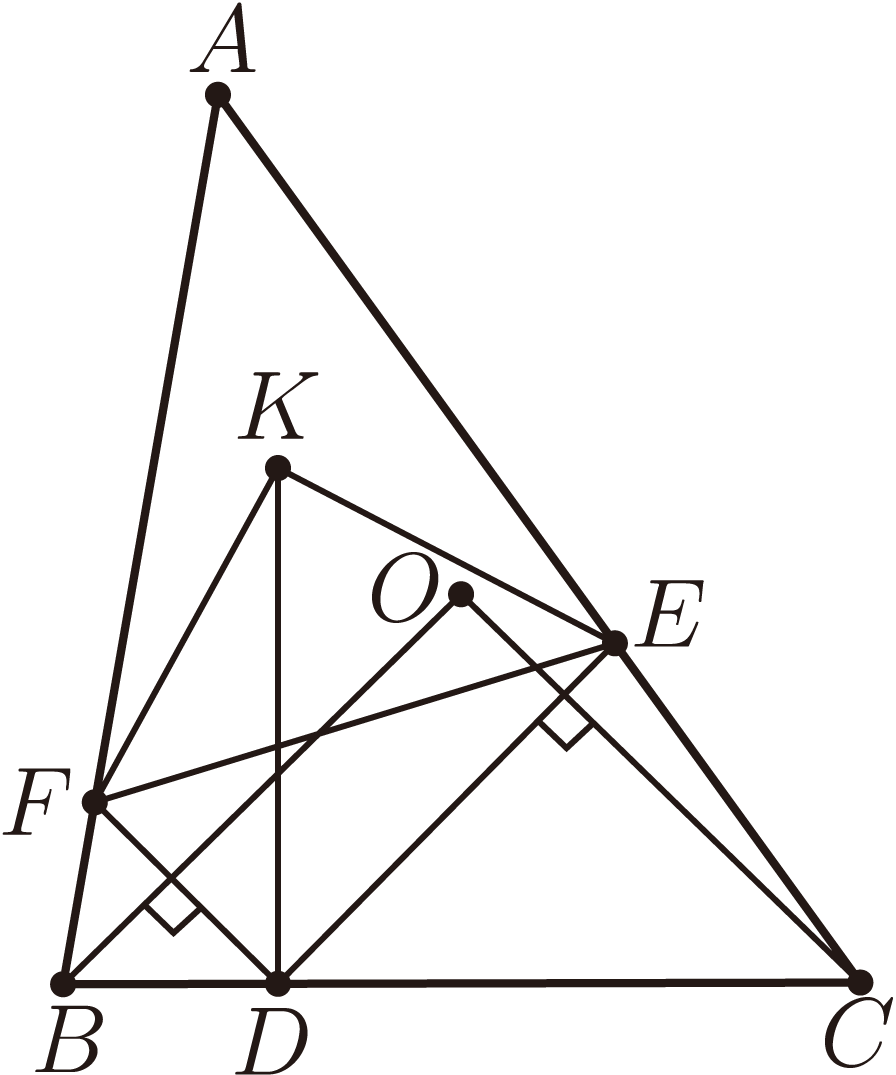| 發刊日期 |
2021年3月
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 標題 | 向量恆等式證明幾何題 |
||||||||||||
| 作者 | |||||||||||||
| 關鍵字 | |||||||||||||
| 檔案下載 | |||||||||||||
| 全文 |
平面幾何是數學中歷史悠久的一個學科分支。 有許多趣味問題, 引人思考, 讓人著迷。 同時歐氏幾何要求論證嚴謹, 讓一些學習者望而卻步。 解析幾何的出現, 使得千變萬化的幾何題有了統一的證明思路。 本文則將介紹一種新的幾何證明方法, 這種方法基於向量恆等式, 不但可以一個式子證明幾何命題, 而且還能發現新的幾何性質。
例1:
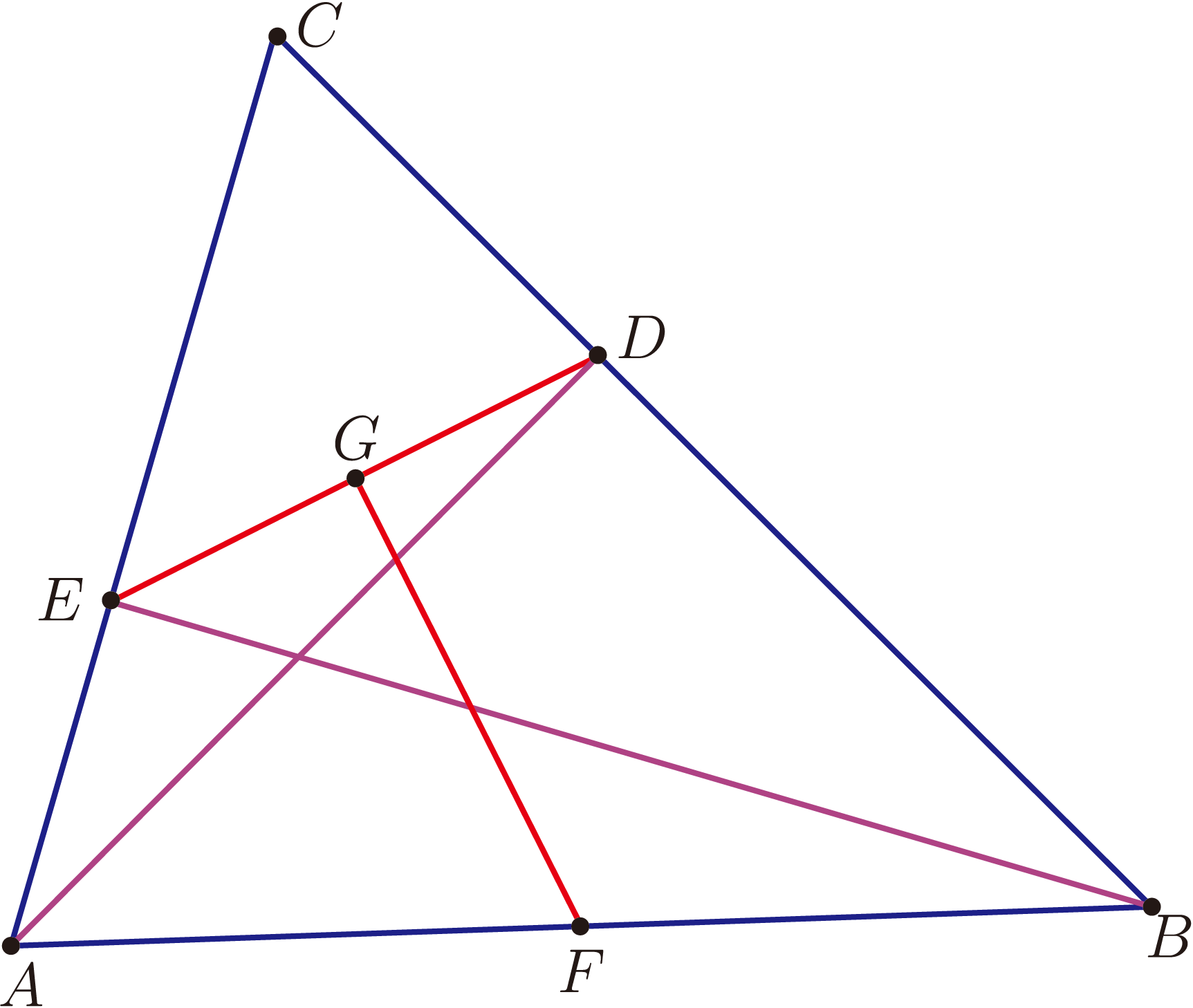
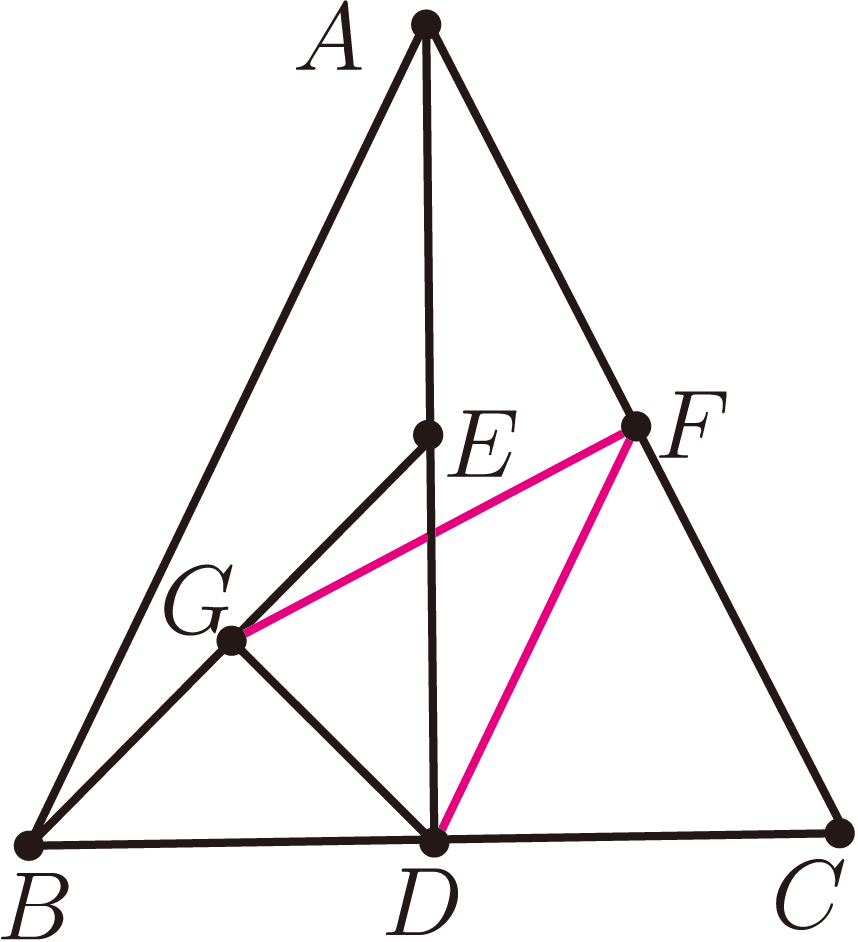
如圖1, $\triangle ABC$ 中, $AD$、$BE$ 是高, $F$、$G$ 是 $AB$、 $DE$ 的中點, 求證: $FG\perp ED$。
$$\left. \begin{array}{r} \left. \begin{array}{r} \left. \begin{array}{l} AD \perp BC\Rightarrow Rt\triangle ADB \\ F\ \hbox{是}\ AB\ \hbox{中點} \end{array} \right\}\Rightarrow AF=DF\\[20pt] \left. \begin{array}{l} EB \perp AC\Rightarrow Rt\triangle AEB \\ F\ \hbox{是}\ AB\ \hbox{中點} \end{array} \right\}\Rightarrow AF=EF \end{array} \right\}\Rightarrow EF=DF\\ G\ \hbox{是}\ DE\ \hbox{中點}\end{array} \right\}\Rightarrow ED \perp FG. $$ 傳統解法有幾個難點。 一是輔助線難以想到, 例 1 中的 $EF$ ($DF$ 類似) 既是直角 $\triangle EAB$ 斜邊上的中線, 又是等腰 $\triangle FDE$ 的腰, 起到很重要的橋樑作用; 二是已知條件如何應用, 包括什麼時候用, 如何結合其他條件以及允許使用的推理規則, 變化繁多, 例 1 中的 $F$ 和 $G$ 雖都是中點, 但應用規則卻不同。 傳統推理採用層層遞進、 環環相扣的演繹推理模式, 中間環節只要一步沒有理順, 則整個推理失敗。 輔助線的添加雖有一定規律, 但多數情況下還是需要人的靈機一動, 因此我們希望提出一種新的證明模式, 能避開輔助線的添加; 同時希望能縮短推理過程, 採用計算來代替邏輯演繹。
本文首先假定, 若設 $O$ 為原點 (簡記為 $O=0$), 將 $\overrightarrow{OX}$ 簡記為 $X$,
將 $\overrightarrow{XY}=\overrightarrow{OY}-\overrightarrow{OX}$ 簡記為 $Y-X$, $\overrightarrow{OX}\cdot \overrightarrow{OY}$ 簡記為
$X\cdot Y$ 或 $XY$ (根據上下文理解, 莫與線段 $XY$ 混淆) ;這樣的簡記看似只是形式上的改變, 但簡單的符號表示豐富的含義, 使得發明創新成為可能。
其中, 關於向量的一些基本知識和運算可參看筆者的著作 簡記之後, 例 1 則變成如何用條件多項式 $(A-E)(B-E)=0$, $(A-D)(B-D)=0$ 來推出結論多項式 $\Big(\dfrac{A\!+\!B}2\!-\!\dfrac{D\!+\!E}{2}\Big)(D\!-\!E)=0$, 其中 $F=\dfrac{A\!+\!B}2$, $G=\dfrac{D\!+\!E}2$; 不妨設 $$\Big(\dfrac{A+B}2-\dfrac{D+E}{2}\Big)(D-E)+k_1(A-E)(B-E)+k_2(A-D)(B-D)=0,$$ 以 $A,B,D,E$ 為變數展開: \begin{eqnarray*} &&\hskip -20pt\Big(\frac 12+k_1\Big)E^2+\Big(-\frac 12-k_1\Big)BE+\Big(\frac 12-k_2\Big)BD+\Big(-\frac 12+k_2\Big)D^2+\Big(-\frac 12-k_1\Big)AE\\ &&+\Big(\frac 12-k_2\Big)AD+(k_1+k_2)AB=0; \end{eqnarray*} 解係數方程組 $$\frac 12+k_1=-\frac 12-k_1=\frac 12-k_2=-\frac 12+k_2=-\frac 12-k_1=\frac 12-k_2=k_1+k_2=0$$ 得 $k_1=-\dfrac 12$, $k_2=\dfrac 12$, 得到恆等式 $$\Big(\dfrac{A\!+\!B}2\!-\!\dfrac{D\!+\!E}{2}\Big)(D\!-\!E)-\frac 12(A-E)(B-E)+\frac 12(A-D)(B-D)=0.$$ 由恆等式以及 $(A-E)(B-E)=0$ 和 $(A-D)(B-D)=0$, 可得 $$\Big(\dfrac{A\!+\!B}2\!-\!\dfrac{D\!+\!E}{2}\Big)(D\!-\!E)=0,$$ 即 $FG\perp ED$。 從恆等式發現, 對於結論的成立, 點 $C$ 並未起到任何作用, 純屬多餘, 而 $A, B, D, E$ 四點也未必共面。這樣的發現, 讓我們對問題認識更加深刻, 突出了的本質, 並推廣到高維。 $n$ 個多項式相加等於 0, 其中 $n-1$ 個都為 0, 剩餘那一個自然為 0。 這看似平凡的道理, 卻有妙用。 可以將例 1 由一變成五 (這裡需要用到同一法的思想)。
例2: 如圖 2, $\triangle ABC$ 中, 設 $BC$ 為最大邊, 在 $BC$ 上取點 $P$、 $Q$, 滿足 $BA=BQ$, $CA=CP$, 求證: $PQ^2=2BP\cdot QC\Leftrightarrow AB \perp AC$。 證法1: 設 $a=BC$, $b=CA=CP$, $c=BA=BQ$, $BP=a-b$, $PQ=-a+b+c$, $QC=a-c$, 根據恆等式 $(-a+b+c)^2-2(a-b)(a-c)=b^2+c^2-a^2$, 命題得證。 證法2: 設 $A=0$, $$[(P-Q)^2-2(B-P)(Q-C)]-2BC+[C^2-(C-P)^2]+[B^2-(B-Q)^2]=0.$$ 在傳統幾何研究中, 構造一個有幾何意義的恆等式不太容易, 譬如例 2 的證法 1。 但如果挖掘向量恆等式這一寶庫, 則很容易構造有幾何意義的恆等式。 這一發現, 在數與形之間搭建了一座橋樑, 數與形進一步融合, 人們對於代數恆等式可以找到幾何意義, 而從幾何問題則又可反推構造代數恆等式。 事實上, 向量恆等式在中學數學裡早有出現, 只是沒有被重視。 經典案例有 : $\triangle ABC$ 中的餘弦定理: $(C\!-\!A)^2\!-\!(A\!-\!B)^2\!-\!(B\!-\!C)^2+2(B\!-\!A)(B\!-\!C)\!=\!0$, 其特例是是畢氏定理, $BA\perp BC\Leftrightarrow b^2=c^2+a^2$。 若將恆等式 $(a+b)^2-(a-b)^2=4ab$ 中的 $a, b$ 看作是向量, 設 $a=\overrightarrow{OA}$, $b=\overrightarrow{OB}$, 則 $(\overrightarrow{OA}+\overrightarrow{OB})^2-(\overrightarrow{OA}-\overrightarrow{OB})^2=4\overrightarrow{OA}\cdot \overrightarrow{OB}$ 則有幾何意義: 平行四邊形中, 若一個角是直角, 則對角線相等;反之也成立。 類似地, 平方差公式 $A^2-B^2=(A+B)(A-B)$ 也有幾何意義: 平行四邊形中, 鄰邊相等的充要條件是對角線垂直。 恆等式 $(P-A)(P-B)=\Big(P-\dfrac{A+B}2\Big)^2-\Big(\dfrac{A-B}2\Big)^2$ 則表示泰勒%斯 定理: 若點 $P$ 滿足 $\Big(P-\dfrac{A+B}2\Big)^2=\Big(\dfrac{A-B}2\Big)^2$, 則 $\angle APB$ 為直角, 反之也成立。 經過幾年的研究, 筆者已經構造出數以千計的向量恆等式。限於篇幅, 僅舉例如下。 例3: 如圖 3, $\triangle ABC$ 中, $D$ 是 $BC$ 上的點, 若 $AB\perp AC$, $AD\perp BC$, 求證 $AB^2=BC\cdot BD$, $AD^2=BD\cdot DC$。 (直角三角形射影定理) 證明: $(A-B)^2-(B-C)(B-D)=(A-B)(A-C)-(B-C)(A-D)$。 這其實證明了, $\triangle ABC$ 中, $D$ 是 $BC$ 上的點, 若已知三個條件 $AB\perp AC$, $AD\perp BC$, $AB^2=BC\cdot BD$ 中的任意兩個, 可推得第三個。也就是一個恆等式一舉證明了三個命題。 這一點在下文中不再一一指出。 $$(A-D)^2-(B-D)(D-C)=(A-B)(A-C)+(D-A)(D-C)+(D-A)(D-B).$$
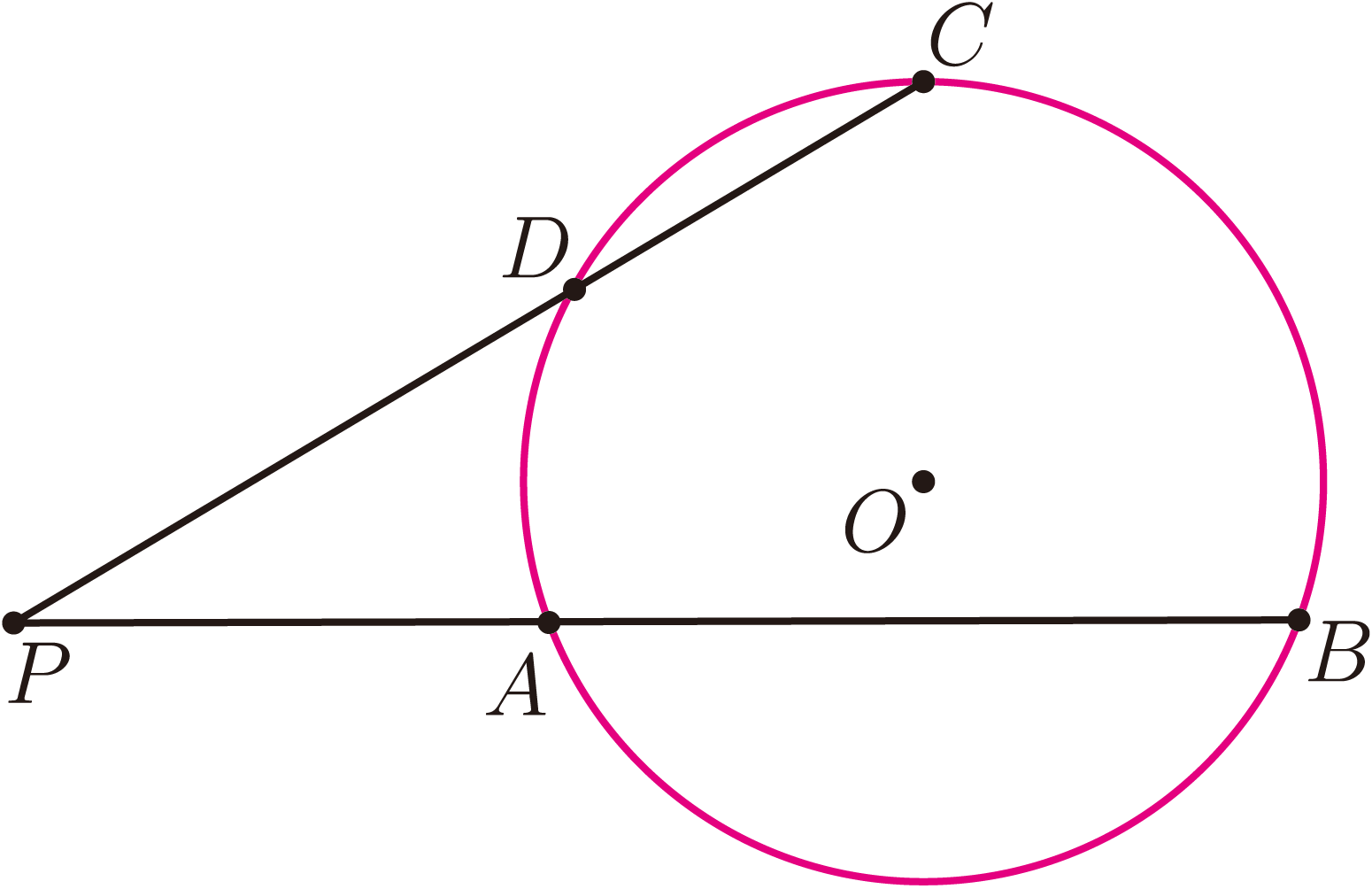
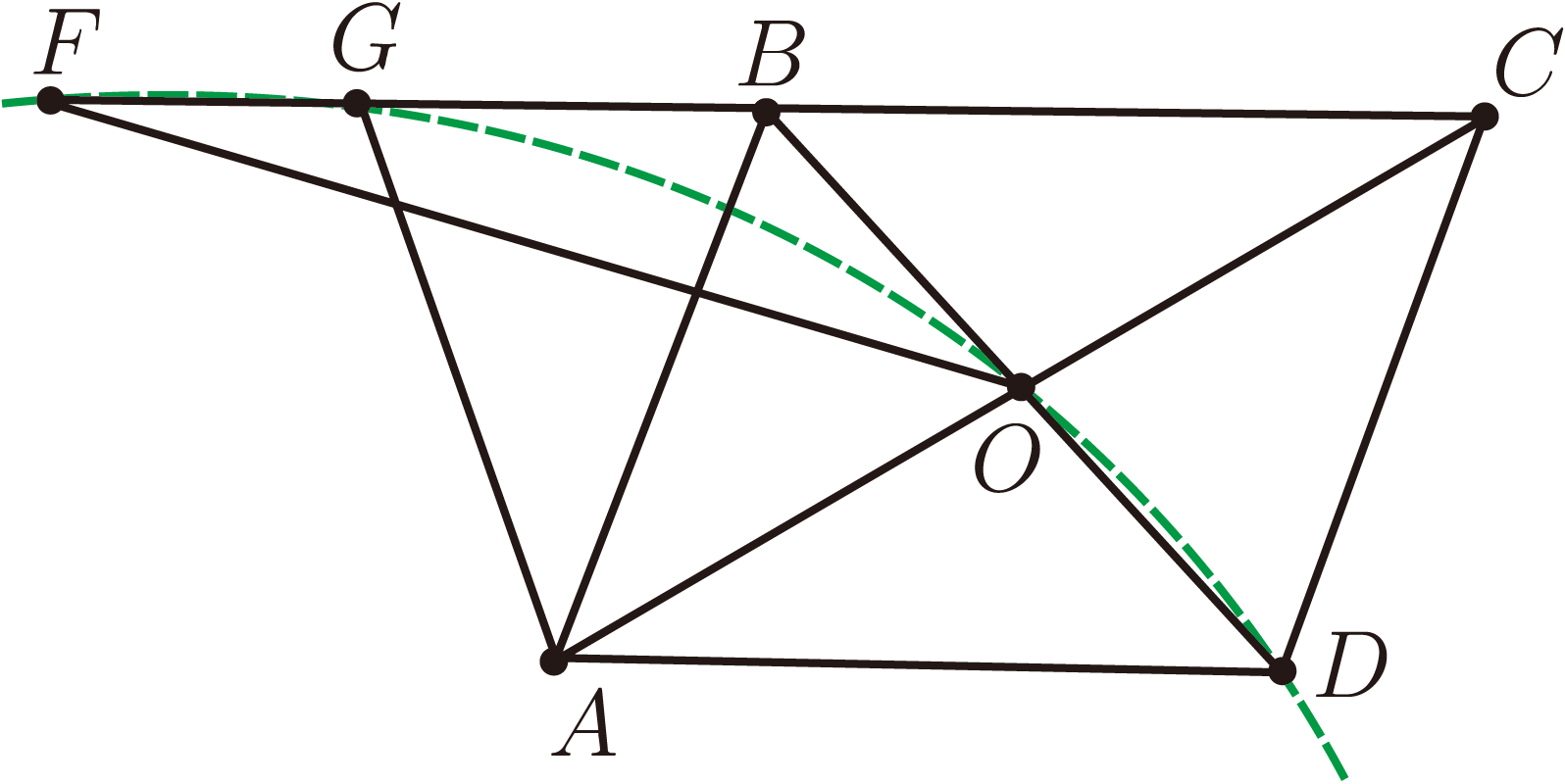
例4: 如圖 4, 四邊形 $ABCD$ 內接於圓 $O$, 直線 $AB$ 交 $CD$ 於 $P$, 則 $PA\cdot PB=PC\cdot PD$ (圓冪定理) 。 證明: 設 $O=0$, $$[(P\!-\!A)(P\!-\!B)\!-\!(P\!-\!C)(P\!-\!D)]\!-\!2\frac{A+B}{2}(B\!-\!P)+2\frac{C+D}2(D-P)\!-\!2\frac{B+D}2(D\!-\!B)=0.$$
例5:
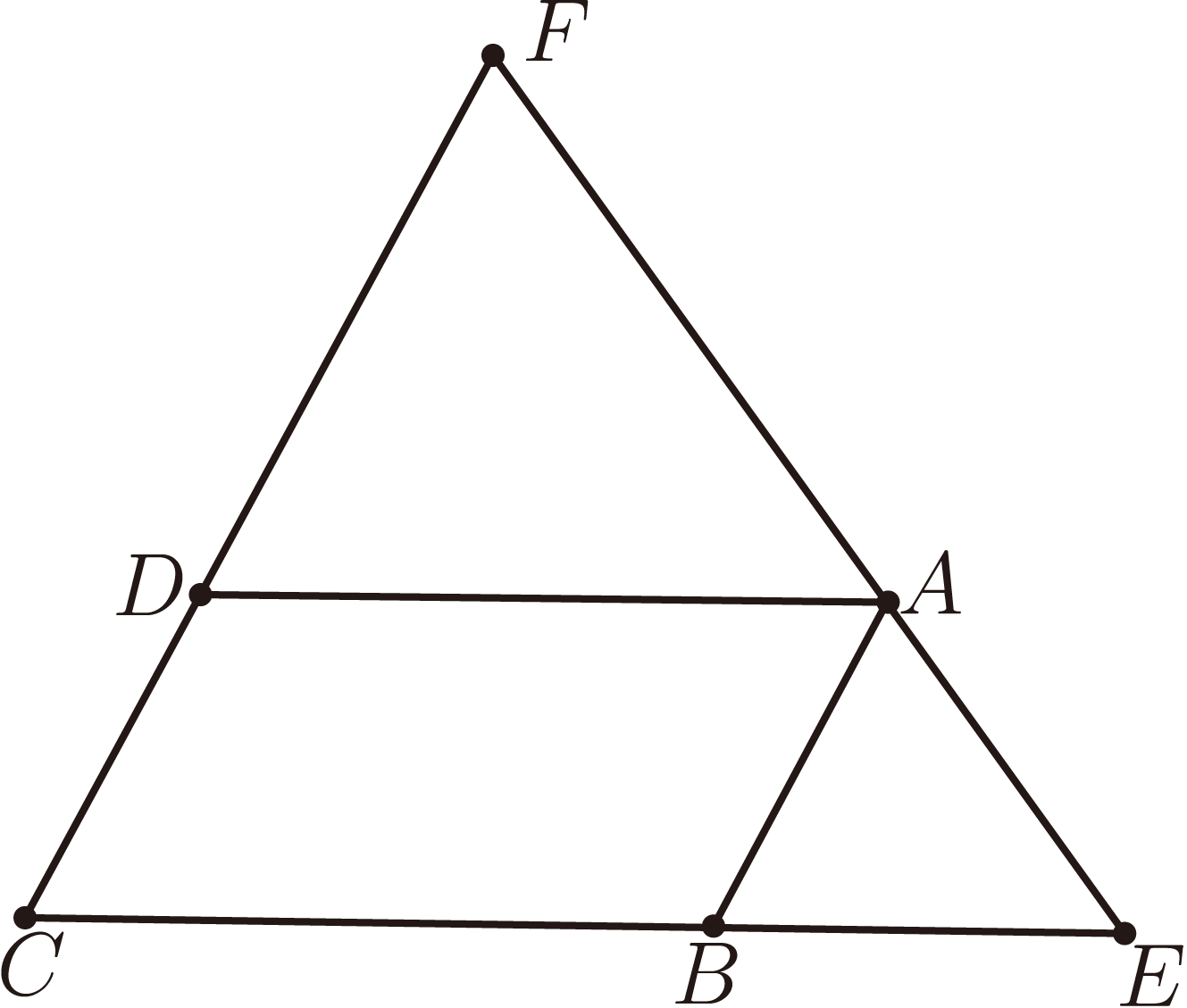
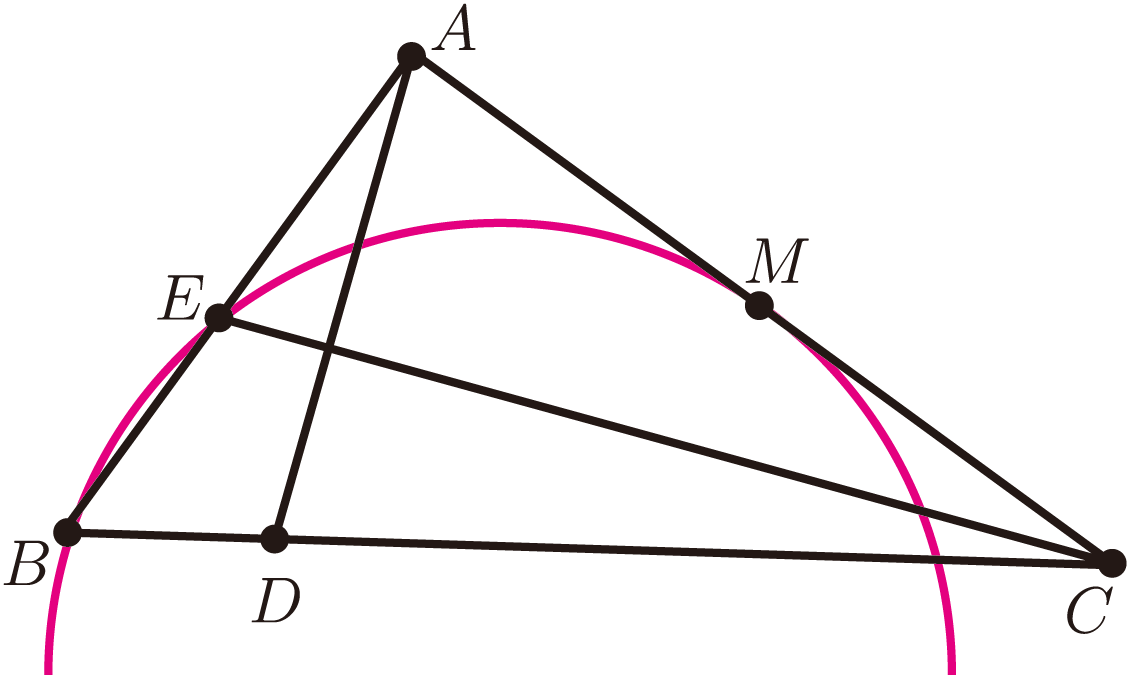
如圖 5, 平行四邊形 $ABCD$, 過 $A$ 作直線交 $CB$ 於 $E$, 交 $CD$ 於 $F$, 證明: 設 $C=0$, $A=B+D$, $[BE+DF-(B+D)^2+(B+D-E)(B+D-F)]+[(F-D)(F-E)-(F-(B+D))F]=0$。 說明: $(F-D)(F-E)-(F-(B+D))F=0$ 用到了三角形相似, 即 $\dfrac{|FD|}{|FC|}=\dfrac{|FA|}{|FE|}$。 例6: 如圖6, $\triangle ABC$ 中, $\angle BAC=90^\circ$, $M$ 為 $AC$ 中點。 在 $BC$ 上取點 $D$, 使得 $4BD=CD$。 過 $B$、 $M$ 作圓使得該圓與 $AC$ 相切於 $M$。 記 $AB$ 與圓交於點 $E$。 求證: $AD\perp CE$。 證明: 設 $A=0$, $5\dfrac{4B+C}{5}(C-E)-4BC+EC+4\Big[BE-\Big(\dfrac C2\Big)^2\Big]=0$。
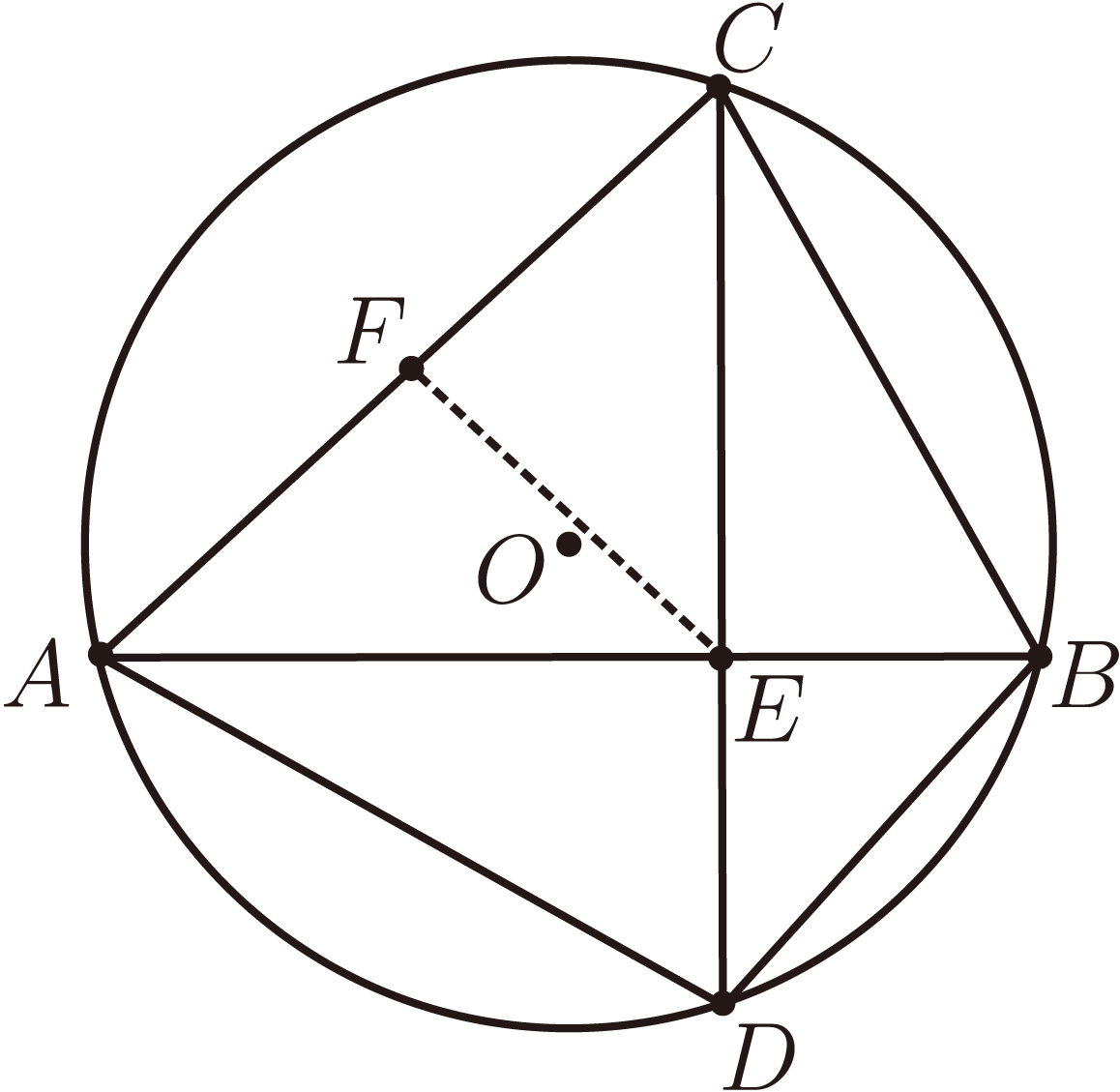
例7: 如圖 7, 對角線互相垂直的圓內接四邊形 $ACBD$, $E$ 是對角線 $AB$、 $CD$ 的交點, $F$ 是 $AC$ 的中點, 則 $EF\perp BD$。 證明: 設圓心 $O=0$, $E=\dfrac{A+B}{2}+\dfrac{C+D}{2}=\dfrac{A+B+C+D}{2}$, $F=\dfrac{A+C}{2}$, $2\Big(\dfrac{A+B+C+D}{2}-\dfrac{A+C}{2}\Big)(B-D)+(D^2-B^2)=0$。
例8: 如圖 8, 圓內接四邊形 $ABCD$, 圓心為 $P$, 對角線互相垂直交於點 $Q$, $E$、$F$ 分別是 $BC$、$AD$ 的中點, 求證: $QE=PF$。 證明: 設圓心 $P=0$, $Q=M+N=\dfrac{A+B+C+D}{2}$, $\Big(\dfrac{A+B+C+D}{2}-\dfrac{B+C}{2}\Big)-\dfrac{A+D}{2}=0$, 說明 $QE$ 與 $FP$ 平行且相等。 例9: 如圖 9, 已知 $BC$ 是圓上的定弦, 而動點 $A$ 在圓上運動, $M$ 是 $AC$ 中點, 作 $MP\perp AB$ 於 $P$。 求 $P$ 點的軌跡。 證明: 設圓心 $O$ 為原點, 則 $\Big(P-\dfrac{-C+B}{2}\Big)(P-C)-\dfrac{B+C}{2}(B-C)-\dfrac{A+B}{2}(P-B)+(P-B)\Big(\dfrac{A+C}{2}-P\Big)=0$, $\Big(P-\dfrac{-C+B}{2}\Big)(P-C)=0$ 說明點 $P$ 的軌跡是圓。 注意 $-C$ 的幾何意義是 $C$ 關於 $O$ 的對徑點。
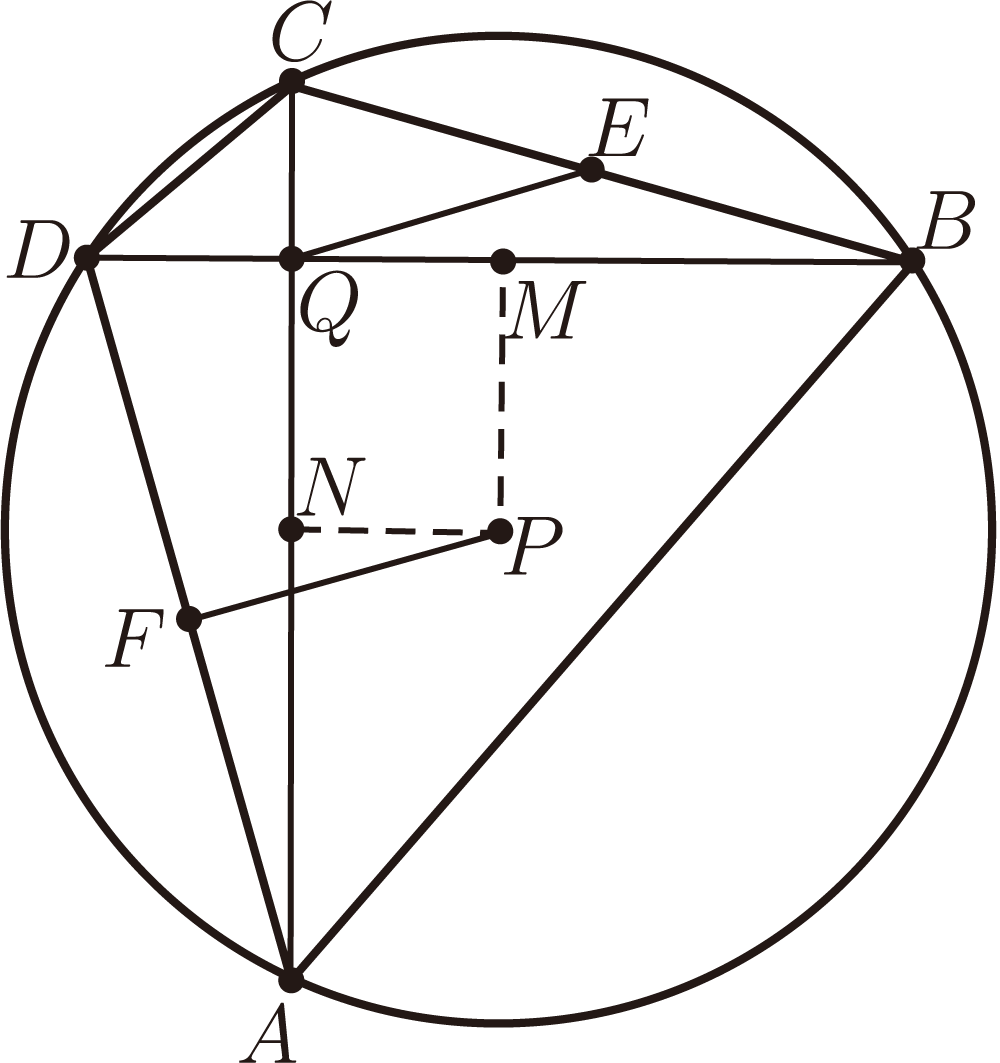
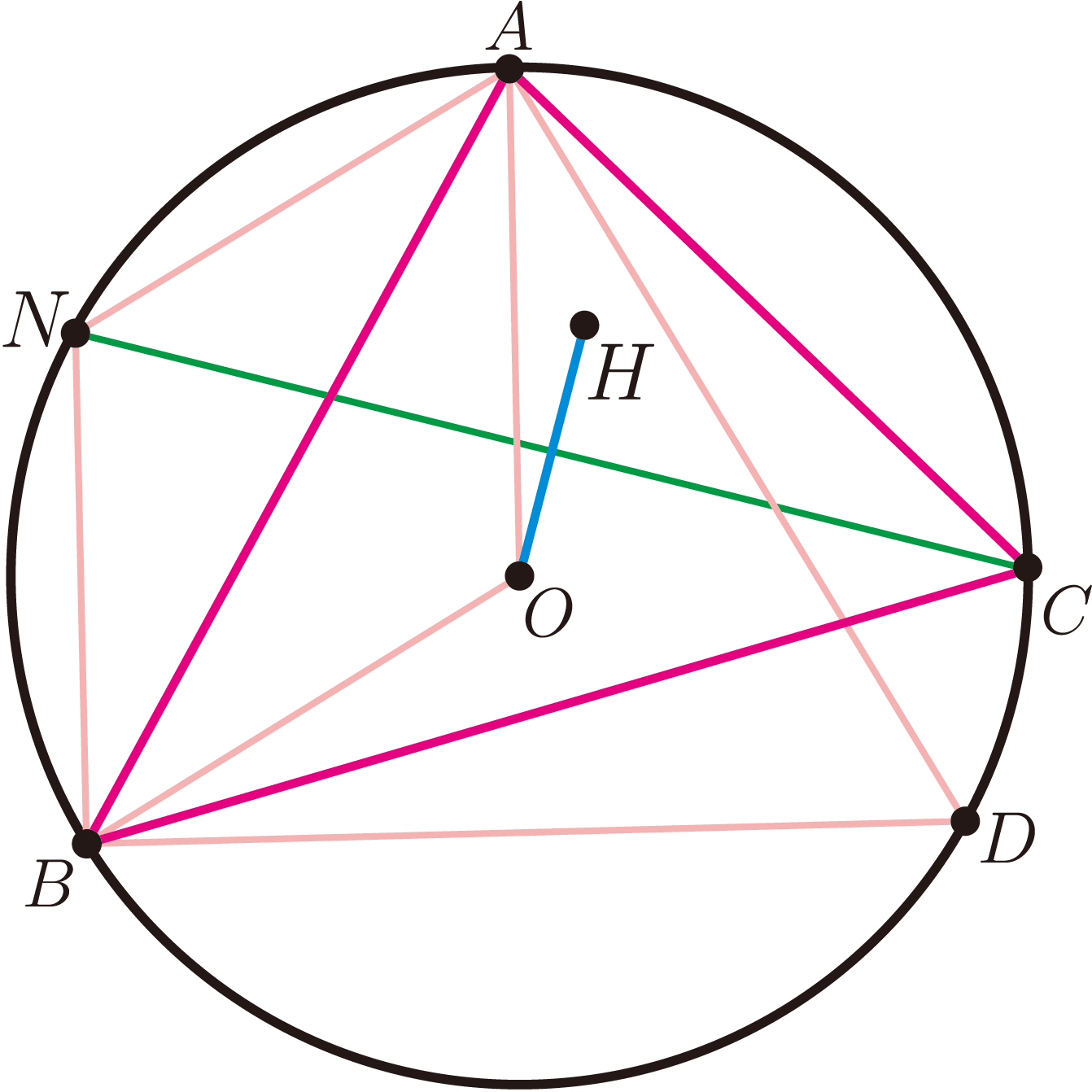
例10: 如圖 10, 圓上的弦 $AC$ 和 $BD$ 交於點 $P$, 在點 $C$ 和 $D$ 處分別對 $AC$ 和 $BD$ 所作的垂線交於點 $Q$, 求證: 直線 $AB\perp PQ$。 (第一屆沙雷金幾何競賽) 證明: 設 $P=0$, $Q(A-B)-(AC-BD)+A(C-Q)-B(D-Q)=0$。 例11: 如圖 11, $\triangle ABC$, $O$ 是外心, $H$ 是垂心, $\angle C=60^\circ$, $N$ 是 $\triangle ABC$ 外接圓劣弧 $AB$ 的中點, 求證 $CN\perp OH$。 (1994年保加利亞競賽試題) 證明: 作正 $\triangle ABD$, 且 $C$ 和 $D$ 在 $AB$ 的同側, 設 $O=0$, $H=A+B+C$, $N=A+B$, $D=-A-B$, $(A+B-C)(A+B+C)+[C^2-(A+B)^2]=0$。
例12: 如圖 12, $\triangle ABC$ 中, $AB=AC$, 點 $D$ 為 $BC$ 的中點, 連接 $AD$, 點 $E$ 為 $AD$ 的中點, 作 $DG\perp BE$ 於點 $G$, 點 $F$ 為 $AC$ 的中點, 連接 $FG,FD$, 求證: $GF=DF$。 證明: $\Big[\Big(G\!-\!\dfrac{A\!+\!C}{2}\Big)^2\!-\!\Big(\dfrac{B\!+\!C}{2}\!-\!\dfrac{A\!+\!C}{2}\Big)^2\Big] \!+\!2\Big(G\!-\!\dfrac{B\!+\!C}{2}\Big)\Big(\dfrac{\dfrac{B\!+\!C}{2}\!+\!A}{2}\!-\!\dfrac{B\!+\!G}{2}\Big)\!=\!0$。 容易發現 $GF=DF$ 並不依賴於 $AB=AC$。 傳統解法則會不自覺地使用這一條件。 而恆等式方法有發現多餘條件的功能, 即使用上了這一條件, 在最後係數求解的時候, 也會求出其係數為 0。 例13: 如圖 13, 平行四邊形 $ABCD$ 對角線交於點 $O$, 過 $O$ 作 $\triangle BOC$ 的外接圓的切線交 $CB$ 於點 $F$, 直線 $BC$ 與 $\triangle FOD$ 的外接圓不同於 $F$ 的交點為 $G$。 證明: $AG=AB$。 證明: $2\Big(A-\dfrac{G+B}{2}\Big)(F-B)+2\Big[\Big(F\!-\!\dfrac{A+C}{2}\Big)^2\!-\!(F-B)(F-C)\Big] +\Big[(B-G)(B-F)-\Big(B-\dfrac{A+C}{2}\Big)(B-(A+C-B))\Big]\!=\!0$。
例14: 如圖 14, $\triangle ABC$ 中, $O$ 是外心, $D$、 $E$、 $F$ 分別在 $BC$、 $CA$、 $AB$ 上, $DE\perp CO$, $DF\perp BO$, 設 $K$ 是 $\triangle AFE$ 的外心, 求證: $DK\perp BC$。 (2012 年歐洲女子奧林匹克競賽 ) 證明: 設 $O=0$, $(K-D)(B-C)-(F-D)B+(E-D)C-\dfrac{B+A}{2}(A-F)-\dfrac{C+A}{2}(E-A)+\Big(K-\dfrac{F+A}{2}\Big)(A-B)-\Big(K-\dfrac{E+A}{2}\Big)(A-C)=0$。 $(B\!-\!D)(B\!-\!C)\!-\!(B\!-\!F)(B\!-\!A)\!-\!2(F\!-\!D)B+2\dfrac{B+C}{2}(B\!-\!D)\!-\!2\dfrac{B+A}{2}(B\!-\!F)=0$,
額外發現 $D$、$C$、$F$、$A$ 四點共圓。
根據對稱可知 $B$、 $D$、 $E$、 $A$ 四點共圓。
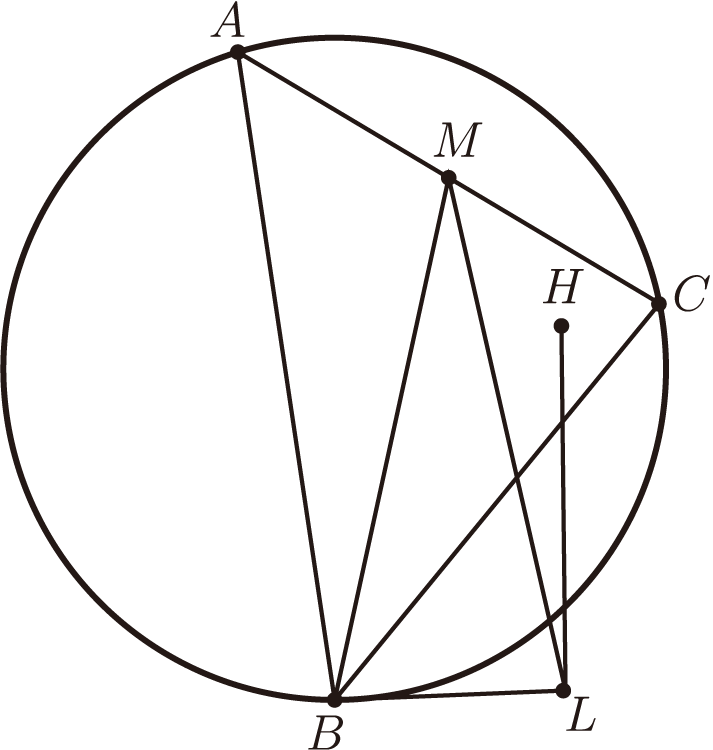
例15: 如圖 15, 設 $H$ 為 $\triangle ABC$ 的垂心, $M$ 為 $CA$ 的中點, 過點 $B$ 作 $\triangle ABC$ 的外接圓的切線 $BL$, $HL\perp BL$, 求證: $\triangle MBL$ 是等腰三角形。 (俄羅斯聖彼德堡數學奧林匹克, 2000)
證明:
設 $\triangle ABC$ 外心為原點, $M=\dfrac{A+C}2$, $H=A+B+C$, 參考文獻---本文作者任教中國武漢市華中師範大學國家數字化學習工程技術研究中心 |
2021年3月 45卷1期
向量恆等式證明幾何題