| 發刊日期 |
2023年3月
|
|---|---|
| 標題 | 構造妙解 感覺何來 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
1. 寫在前面一些富有挑戰性的最值試題, 其呈現的「構造」技巧, 確實讓人讚歎「構造」奇妙, 解法的感覺何來? 這些試題的切入點在那裡? 解法很精彩, 解答的感覺從哪裡來更重要, 作為教師如何讓學生找到感覺, 開啟思考的路徑, 變得尤為重要。 2. 構造妙解案例1: 在 $\triangle ABC$ 中, $\angle ABC=60^\circ $, $BC=8$, $AC=10$, 點 $D$、 $E$ 分別在 $AB$、 $AC$ 上, 且 $AD=CE$, 則 $CD+BE$ 的最小值為 $\_\_\_\_\_\_\_\_\_\_$ 。

解析: 我們從求 $CD+BE$ 的最小值的形式, 這兩條線段不在一個三角形中, 我們研究最小值根本上就是利用了「兩點之間線段最短」、「垂線段最短」, 從圖形特徵考慮是下面兩個模型: (1) 如圖 2, 已知線段 $AB=m$, 點 $P$ 為任意一點, 則 $PA+PB$ 的最小值為 $m$; (2) 如圖 3, 點 $P$ 為定點, $PA\bot MN$ 於 $A$, $PA=m$, 點 $B$ 是動點, $BC\bot MN$ 於 $C$, 則 $PB+BC$ 的最小值為 $m$。 (1) 用「兩點之間線段最短」、 (2) 用「垂線段最短」, 雖然兩個最小值的依據不同, 但是它們這兩條線段的和在圖形中都有一個共同端點, 我們考慮能不能把線段 $CD$、 $BE$ 改造到有一個共同頂點; 這個題目中有 $AD=CE$, 這是一個非常好的條件, 我們可以考慮把 $\triangle ADC$ 拼到使得 $AD$、 $CE$ 重合, 如圖 4, 過 $C$ 作 $CA'//AB$, 使得 $CA'=AC$, 連接 $A'E$、 $A'B$,
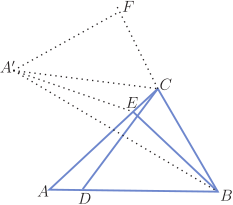
作 $A'F\bot BC$ 於 $F$, 從 $CA'//AB$, 得到 $\angle A'CE= \angle A$, $\angle A'CF= \angle ABC=60^\circ $; 因為 $A'C=AC$, $\angle A'CE= \angle A$, $CE=AD$, 所以 $\triangle A'CE\cong\triangle CAD$, 所以 $A'E=CD$, 所以 $CD+BE=A'E+BE$, 在 $\triangle A'CF$ 中, $A'C=10$, 得到 $CF=5$, $A'F=5\sqrt 3$, $BF=5+8=13$, 在 $\triangle BA'F$ 中, $A'B=\sqrt{(5\sqrt 3)^2+13^2}=\sqrt{244}=2\sqrt{61}$, 考慮 $\triangle A'BE$, 得到 $A'E+BE\ge A'B$ 所以 $CD+BE$ 的最小值為 $2\sqrt{61}$。 點評: 這個題目構造的關鍵是通過作出平行線來完成圖形的拼接, 作出 $A'F$ 是為了構造特殊的直角三角形, 把問題轉化為模型 (1)。 變式1: 如圖 5, 在 $\triangle ABC$ 中, $\angle BAC=60^\circ $, $AC=8$, $AB=10$, 點 $D$、 $E$ 分別在 $AC$、 $AB$ 上, 且 $AD=AE$, 則 $CE+BD$ 的最小值為 $\_\_\_\_\_\_\_\_\_\_$ 。
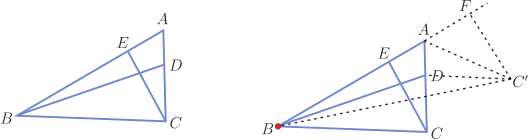
分析: 把 $\triangle AEC$ 繞點 $A$ 逆時針旋轉 $60^\circ$ 到 $\triangle ADC'$, 連接 $DC'$、 $BC'$, 作 $C'F\bot AB$ 於 $F$, 得到 $\angle DAC'= \angle BAC=60^\circ $, 所以 $\angle FAC'=60^\circ $, 所以 $AF=4$, $C'F=4\sqrt 3$, $BF=10+4=14$, $BC'=\sqrt{14^2+(4\sqrt 3)^2}=2\sqrt{61}$, 因為 $DC'=CE$, 所以 $CE+BD=BD+DC'\ge BC'=2\sqrt{61}$, 所以, $CE+BD$ 的最小值為 $2\sqrt{61}$。 點評: 這個變式 1 是我們熟悉的旋轉變換, 案例 1 反而是變式 1 的推廣。 案例2: 如圖 7, 在直角坐標系中, 點 $A$ 的坐標為 $(3,2\sqrt{10})$, 以原點 $O$ 為圓心, 以 13 為半徑作 $\odot O$, 點 $B$、 $C$ 在 $\odot O$ 上, 且 $\angle BAC=90^\circ $, 連接 $BC$, 則線段 $BC$ 長的最小值是 $\_\_\_\_\_\_\_\_\_\_$ 。
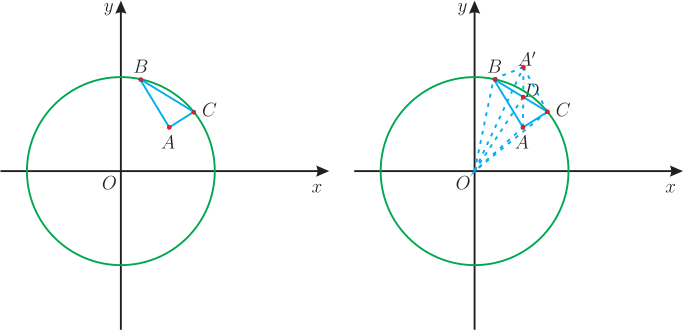
解析: 如圖 8, 取 $BC$ 的中點 $D$, 連接 $OA$、 $AD$、 $OD$, 因為 $\angle BAC=90^\circ $, $D$ 是 $BC$ 的中點, 所以 $AD=\dfrac 12BC$, 只要研究 $AD$ 的最小值; 容易得到 $$OA=\sqrt{3^2+(2\sqrt{10})^2}=7.$$ 考慮 $\triangle ADO$, $AD$ 和 $OD$ 都是未知的, 案例 1 的方法無法解決, 怎麼辦? 我們作出矩形 $ABA'C$, 連接 $AA'$ 交 $BC$ 於 $D$, 得到 $BC=AA'$, 只要研究 $AA'$ 的最小值, 連接 $OA$、 $OA'$、 $OB$、 $OC$, 得到 \begin{eqnarray*} &&\hskip -20pt OA^2+{OA'}^2=OB^2+OC^2,\ OB=OC=13,\ OA=7,\\ &&\hskip -20pt {OA'}^2=338-49=289,\ OA'=17\\ &&\hskip -20pt AA'\ge OA'-OA=17-7=10 \end{eqnarray*} 所以線段 $BC$ 長的最小值是 10。 點評: 這裡關鍵是把問題轉化為求 $AA'$ 的最小值問題, 事實上我們希望 $OA$ 和 $BC$ 要整合到有公共端點, 由於這裡有直角三角形的條件, 構造出矩形就有矩形的對角線相等, 餘下就是要得到 $OA'$ 是已知的; 事實上, 這裡利用了平行四邊形中一個特徵, 平行四邊形的四條邊的平方和等於對角線的平方和。 延長 $OD$ 到 $O'$,使得 $DO'=OD$, 連接 $BO'$、 $CO'$、 $AO'$、 $A'O'$, 構造出平行四邊形 $OBO'C$、 $OAO'A'$, 這兩個四邊形對角線交點就是 $D$, 得到 $$2OB^2+2OC^2=BC^2+{OO'},\ 2OA^2+2{OA'}^2=AA'^2+{OO'}^2,$$ $BC=AA'$, 得到 $OA^2+OA'^2=OB^2+OC^2$, 這樣把問題轉為我們能夠思考的問題。 變式1: 如圖 3 在直角坐標系中, 點 $A$ 的坐標為 $(3,2\sqrt{10})$, 以原點 $O$ 為圓心, 以 13 為半徑作 $\odot O$, 點 $B$、 $C$ 在 $\odot O$ 上, 且 $\angle BAC=90^\circ $, 連接 $BC$, 則線段 $BC$ 長的最大值是 $\_\_\_\_\_\_\_\_\_\_$ 。
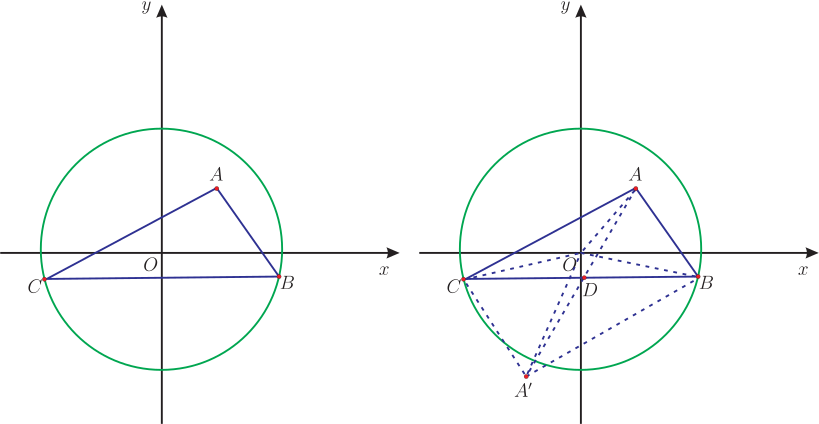
解析: 作矩形 $ABA'C$ 連接 $OA$、 $AA'$、 $OA'$, 同理得到 $OA=7$, $OA'=17$, 考慮 $\triangle OAA'$, 得到 $$AA'\le OA+OA'=7+17=24$$ 所以線段 $BC$ 長的最大值是 24。 點評: 變式的方法與案例 2 方法類似, 可以作為對於這個構造技巧的強化訓練。 案例3: 如圖 11, 在 $\triangle ABC$ 中, $AC=BC=10$, $\angle B=30^\circ $, 點 $D$ 為 $AB$ 上一個點, 且 $AD=4BD$, $E$ 為射線 $AC$ 上一動點, $F$ 為射線 $CB$ 上一動點, 且 $\angle EDF=60^\circ $, 求 $EF$ 的最小值 $\_\_\_\_\_\_\_\_\_\_$ 。
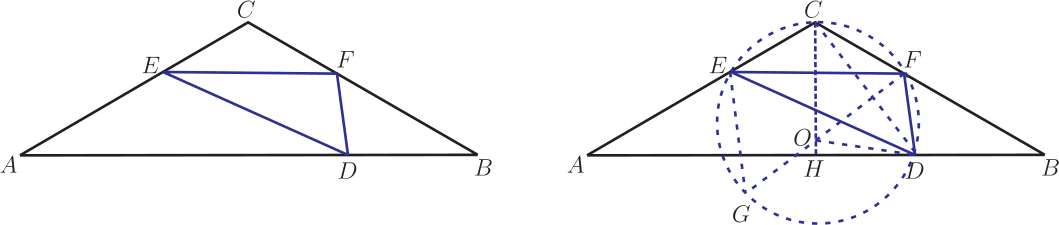
解析: 如圖 12, 我們從條件想到 $\angle C+ \angle EDF=180^\circ $, 得到四邊形 $CEDF$ 有外接圓 $\odot O$, 作出直徑 $FG$, 連接 $EG$, 得到 $\angle GEF=90^\circ $, $\angle EGF= \angle EDF=60^\circ $, 得到 $EF=FG\sin60^\circ =\dfrac{\sqrt 3}{2}FG$, 於是問題轉化為研究 $FG$ 的最小值, 連接 $OC$、 $OD$、 $CD$, 得到 $OC+OD\ge CD$, $FG\ge CD$; 只要求出 $CD$, 作 $CH\bot AB$ 於 $H$, 從 $AC=CB=10$, 得到 $AH=HB$, 從 $AD=4DB$, 得到 $AB=5DB$, $HB=\dfrac 52DB$, $\angle B=30^\circ$, $CH=5$, $BH=5\sqrt 3$, $\dfrac 52DB=5\sqrt 3$, $DB=2\sqrt 3$, $$HD=5\sqrt 3-2\sqrt 3=3\sqrt 3,\ CD=\sqrt{5^2+(3\sqrt 3)^2}=2\sqrt{13}$$ $EF\ge \dfrac{\sqrt 3}{2}CD=\sqrt {39}$, $EF$ 的最小值為 $\sqrt{39}$。 思考: $EF$ 取得最小值的位置是怎麼樣呢? 這時 $CD$ 為以 $O$ 為圓心的圓 $\odot O$ 的直徑, 得到 $\angle CED= \angle CFD=90^\circ $, 如圖 13
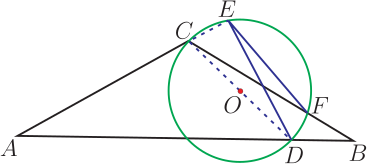
這時, $AD=8\sqrt 3$, $BD=2\sqrt 3$, $\angle A=\angle B=30^\circ$, 得到 $DE=4\sqrt 3$, $DF=\sqrt 3$, $EF=\sqrt{39}$, $\triangle DEF$ 的周長為 $5\sqrt 3+\sqrt{39}$, 面積為 $\dfrac 12DE\cdot DF\sin 60^\circ=3\sqrt 3$。 下面要說明圖 13 的位置就是周長和面積最小值位置。 變式1: 如圖 11, 在 $\triangle ABC$ 中, $AC=BC=10$, $\angle B=30^\circ $, 點 $D$ 為 $AB$ 上一個點, 且 $AD=4BD$, $E$ 為射線 $AC$ 上一動點, $F$ 為射線 $CB$ 上一動點, 且 $\angle EDF=60^\circ $, 求 $\triangle DEF$ 的周長最小值 $\_\_\_\_\_\_\_\_\_\_$ 。 分析: 如圖 12, 我們從條件想到 $\angle C+ \angle EDF=180^\circ $, 得到四邊形 $CEDF$ 有外接圓 $\odot O$, 得到 $\angle FED= \angle BCD$, $\angle ACD= \angle EFD$, 因為點 $D$ 是定點, 所以 $\angle BCD$, $\angle ACD$ 保持不變, 這樣 $\triangle DEF$ 的形狀保持不變。 研究 $\triangle DEF$ 的周長最小值的位置就是 $EF$ 最小值的位置, 於是 $\triangle DEF$ 的周長最小值為 $5\sqrt 3+\sqrt{39}$。 變式2: 如圖 12, 在 $\triangle ABC$ 中, $AC=BC=10$, $\angle B=30^\circ $, 點 $D$ 為 $AB$ 上一個點, 且 $AD=4BD$, $E$ 為射線 $AC$ 上一動點, $F$ 為射線 $CB$ 上一動點, 且 $\angle EDF=60^\circ $, 求 $\triangle DEF$ 的面積最小值 $\_\_\_\_\_\_\_\_\_\_$ 。 解析: 從上面知道 $\triangle DEF$ 的形狀不變, 研究 $\triangle DEF$ 的面積最小值的位置就是 $EF$ 最小值的位置, 於是 $\triangle DEF$ 的面積最小值為 $3\sqrt 3$。 點評: 在研究過程中, 我們發現研究 $\triangle DEF$ 的周長和面積的最小值更加耐人尋味。 3. 結束語我們在文 參考文獻本文作者鄒黎明任教中國江蘇省無錫市碩放中學, 浦敘德任職中國江蘇省無錫市新吳區教師發展中心 |
2023年3月 47卷1期
構造妙解 感覺何來

