| 發刊日期 |
2023年9月
|
|---|---|
| 標題 | 人算不如機算──電腦輔助數學探索兩例 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
人類解決問題, 憑藉的是以往經驗, 加上臨時的靈光閃現。 有些問題相當複雜, 超過人腦能處理的範疇, 雖說人算不如天算, 可惜天意從來高難問, 還是借助電腦這個工具比較靠譜。 君子生非異也,善假於物也。電腦的優勢是不知疲憊, 計算速度快, 對於能夠演算法化、 遍歷窮舉的問題, 能較好地解決。 本文將分享兩則基於數學軟體 Mathematica 輔助探索的案例, 希望這兩則案例探索所得結論或是探索使用的方法, 能給讀者朋友帶來啟發。 正文中會大致介紹解決問題的思路, 相關的 Mathematica 代碼見本文附錄。 案例1: 探索關聯正多邊形的面積相等問題。 如圖 1, 分別以 $\triangle ABC$ 的 $AB$、 $AC$ 邊向外作正方形 $BADE$、 $ACGF$, 則 $S_{\triangle ABC}=S_{\triangle AFD}$。 這個幾何性質常見, 也顯然。 如果將這一問題進行擴展, 探索圖 1 中 7 點所構成的三角形面積相等關係, 就未必容易。
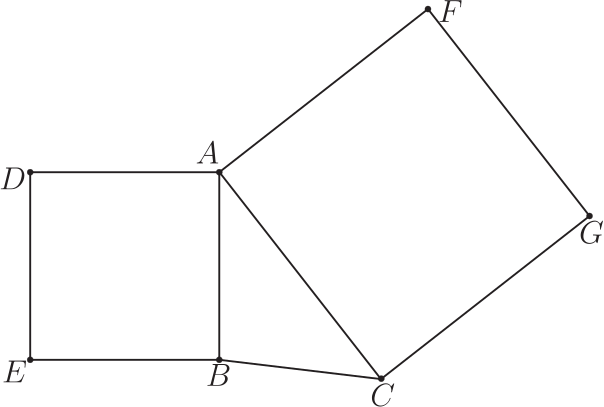
初步分析: 第1類:類似 $S_{\triangle ABE}=S_{\triangle ADE}$, 結論極其顯然, 小學生都能輕鬆看出。 第2類:類似 $S_{\triangle ABC}=S_{\triangle AFD}$ 或 $S_{\triangle ADC}=S_{\triangle ABF}$, 是中學數學中的常見結論。 第3類:類似 $S_{\triangle ADG}=S_{\triangle AEF}$ 或 $S_{\triangle AEC}=S_{\triangle ABG}$, 可看作是第2類結論的進一步加深。 是否還存在另外形式? 難找到, 並不意味著就不存在。 7 個點選 3 個, 可構成 $C^7_3=35$ 個三角形。 35 個三角形面積兩兩比較, 有 $C^{35}_2= 595$ 種可能。 只有遍歷所有情況, 才能得到確切的結論。 而這對於人工演算, 工作量很大。 基於座標, 使用行列式計算三角形面積是比較方便的。 因此不妨設 $A=(0,0)$, $B=(1,0)$, $C=(xc,yc)$, $D=(0,-1)$, $E=(1,-1)$, $F(-yc,xc)$, $G=(xc-yc,xc+yc)$。 計算點的座標, 用向量和複數的性質比較簡單。 如設 $D=(xd,yd)$, 則根據 $\overrightarrow{AD} i=\overrightarrow{AB}$, 即 $[(xd+ydi)-(0+0i)]i=(1+0i)-(0+0i)$, 解得 $xd=0$, $yd=-1$。 其餘點的座標都可照此方法計算。 從點座標集合 $\{A,B,C,D,E,F,G\}$ 中任取 3 個, 然後利用三角形面積公式 $S_{\triangle ABC}=\dfrac 12\left\| \begin{array}{ccccc} x_A&&y_A&&1\\ x_B&&y_B&&1\\ x_C&&y_C&&1 \end{array} \right\|$ , 公式裡面的兩分隔號表示行列式, 外面的兩分隔號表示絕對值。 計算 35 個三角形面積, 電腦只需花費幾秒。 除去上文討論過的類型, 電腦還發現以下三個結論 (形式對稱的只算一種)。 為方便這些結論在教學、 測試或競賽中使用, 我們另外給出證明。 結論1: 如圖 2, 以 $(xc,yc),(0,-1),(1,-1)$ 和 $(1,0),(1,-1),(-yc,xc)$ 為頂點的三角形面積都為 $\dfrac{|1+yc|}2$, 即 $S_{\triangle DEC}=S_{\triangle FEB}$。
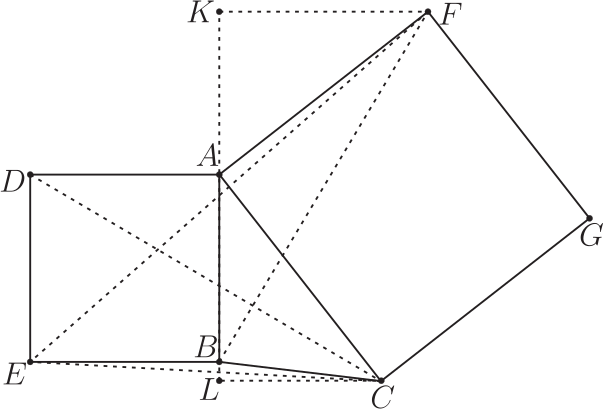
證明: 過 $F$ 作 $FK\bot AB$ 於 $K$, 過 $C$ 作 $CL\bot AB$ 於 $L$。 $\triangle DEC$ 中 $DE$ 所對的高為 $EB+LC=EB+AC\sin \angle BAC$; $\triangle FEB$ 中 $EB$ 所對的高為 $BA+AK=EB+AF\sin \angle BAC$; 所以 $\triangle DEC$ 和 $\triangle FEB$ 等底等高, $S_{\triangle DEC}=S_{\triangle FEB}$。 結論2: 如圖 3, 以 $(0,-1),(1,-1),(xc-yc,xc+yc)$ 和 $(0,-1),(1,0),(-yc,xc)$ 為頂點的三角形面積都為 $\dfrac{|1+xc+yc|}2$, 即 $S_{\triangle GDE}=S_{\triangle DBF}$。
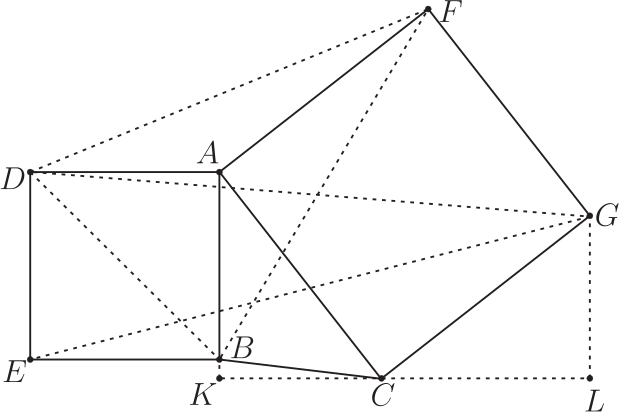
證明: 過 $C$ 作 $CK\bot AB$ 於 $K$, 過 $G$ 作 $GL\bot CK$ 於 $L$。 \begin{align*} 2S_{\triangle GDE}=&DE\cdot (EB+KC+CL)=DE^2+DE\cdot KC+DE\cdot AC\cdot\cos\angle BAC\\ =&2S_{\triangle ADB}+2S_{\triangle ABC}+DE\cdot AC\cdot\sin(\angle BAC+90^\circ)\\ &\hskip 20pt =2S_{\triangle ADB}+2S_{\triangle AFD}+2S_{\triangle ABF}=2S_{\triangle DBF}. \end{align*} 結論3: 如圖 4, 以 $(1,-1),(1,0),(xc-yc,xc+yc)$ 和 $(0,-1),(1,0),(xc,yc)$ 為頂點的三角形面積都為 $\dfrac{|1-xc+yc|}2$, 即 $S_{\triangle GEB}=S_{\triangle DBC}$。
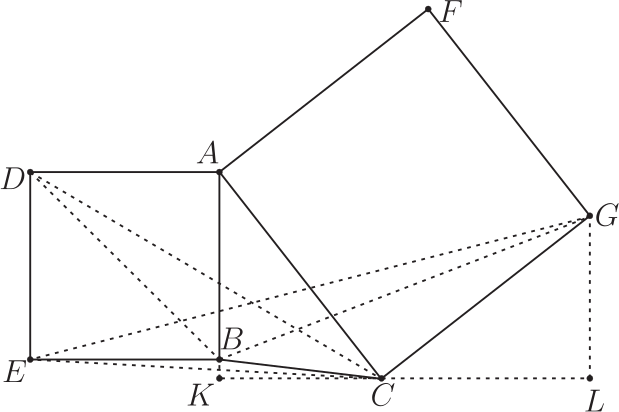
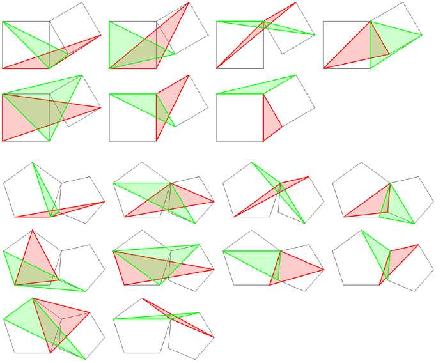
證明: 過 $C$ 作 $CK\bot AB$ 於 $K$, 過 $G$ 作 $GL\bot CK$ 於 $L$。 連接 $CE$。 \begin{align*} &\hskip 15pt 2 S_{\triangle GEB}=EB\cdot (GL-BK)=EB\cdot (AC\cdot\sin\angle BAC+BC\cdot\cos\angle ABC),\\ &\hskip -20pt 2S_{\triangle DBC}=2S_{\triangle DEC}-2S_{\triangle DEB}-2S_{\triangle EBC}\\ &\hskip 20pt =DE\cdot(EB+KC)-DE^2-EB\cdot BC\cdot\sin\angle EBC\\ &\hskip 20pt =DE\cdot AC\cdot\sin\angle BAC+EB\cdot BC\cdot\cos\angle ABC,\ \hbox{所以}\ S_{\triangle GEB}=S_{\triangle DBC}. \end{align*} 以上三個結論, 證明並不是太困難, 但希望憑藉人的觀察就能發現, 頗為不易。 我們將上述問題擴展, 即分別以 $\triangle ABC$ 的 $AB$、 $AC$ 邊向外作正 $n$ 邊形, 這些頂點構成的三角形, 面積關係如何? 事實上, 基於上文方法發現相等面積的三角形後, 還可進一步將圖形構造出來, 這樣就更直觀一些。 圖 5 是基於 Mathematica 發現的結論, 其中 $n=4,5$, 供有興趣的讀者進一步探索。
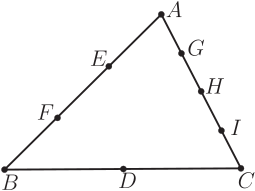
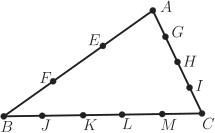
案例2: 探索三角形各邊等分點連線的三線共點問題。 一本科普資料上記載這樣一道趣題。 如圖6, $\triangle ABC$ 中, 將 $BC$ 二等分, $BA$ 三等分, $AC$ 四等分, 嘗試連接這些等分點, 盡可能多地找到哪些三點共線的情況。 類似 $BA$、 $DA$、 $CA$ 三線共點的平凡情況忽略。
此題如何解, 又如何推廣? 用座標容易表示等分點。 設 $C$ 是 $AB$ 中點, 則 $x_C\!=\!\dfrac{x_A\!+\!x_B}{2}$、 $y_C\!=\!\dfrac{y_A\!+\!x_B}{2}$, 橫縱坐標兩個式子形式上完全一樣, 使用向量表示 $\overrightarrow {OC}\!=\!\dfrac{\overrightarrow {OA}\!+\!\overrightarrow {OB}}{2}$ 可做到二合一。 如果嫌向量符號麻煩, 可把向量看作是終點和起點之差, 則 $\overrightarrow {AC}=\overrightarrow {CB}$ 轉化為 $C-A=B-C$ 或 $C=\dfrac{A+B}{2}$, 可看成是 $\overrightarrow {OC}\!=\!\dfrac{\overrightarrow {OA}\!+\!\overrightarrow {OB}}{2}$ 或 $x_C\!=\!\dfrac{x_A\!+\!x_B}{2}$、 $y_C\!=\!\dfrac{y_A\!+\!x_B}{2}$ 的濃縮版。 這裡的字母 $X$ 看作 $\overrightarrow {OX}$ 的省寫, 任意點 $O$ 為原點。 類似定義直線 $AB$ 上的點 $C=tA+(1-t)B$。 當 $t=\dfrac 12$ 時, 即為中點。 擴展開去, $\triangle ABC$ 平面上任意點定義為 $P=xA+yB+(1-x-y)C$。 這樣定義的好處是使用少量符號描繪幾何事實, 簡明而幾何意義豐富。
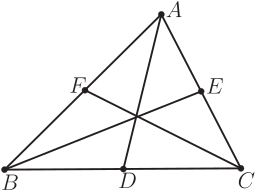
如著名的重心定理即可用恒等式表示: $\dfrac{A+B+C}{3}=\dfrac 23\,\dfrac{A+B}{2}+\dfrac 13 C=\dfrac 23\,\dfrac{A+C}{2}+\dfrac 13 B=\dfrac 23\,\dfrac{B+C}{2}+\dfrac 13 A.$ 幾何意義是存在點 $\dfrac{A+B+C}{3}$ 在 $AD$ 上, 因為 $\dfrac{A+B+C}{3}=\dfrac 23\,\dfrac{B+C}{2}+\dfrac 13 A$, 此處 $D=\dfrac{B+C}{2}$, 還說明點 $\dfrac{A+B+C}{3}$ 是 $AD$ 的三等分點。 同理點 $\dfrac{A+B+C}{3}$ 在 $BE$、 $CF$ 上。 恒等式表示幾何定理, 既包括定理的敘述, 同時也是定理的證明。 回到原問題, 經過嘗試, 我們得到兩組解, 所對應圖形 (圖 8) 和恒等式如下:
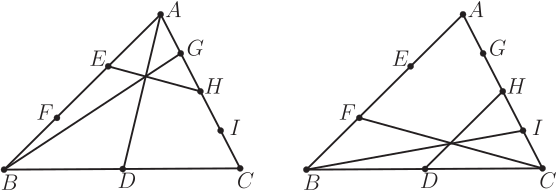
$\dfrac{3A\!+\!B\!+\!C}{5}\!=\!\dfrac 25\,\dfrac{B\!+\!C}{2}\!+\!\Big(1\!-\!\dfrac 25\Big)A\!=\!\dfrac 45\,\dfrac{3A\!+\!C}{4}\!+\!\Big(1\!-\!\dfrac 45\Big)B\!=\!\dfrac 25\,\dfrac{A\!+\!C}{2}\!+\!\Big(1\!-\!\dfrac 25\Big) \dfrac{2A\!+\!B}{3}$, $\dfrac{A\!+\!2B\!+\!3C}{6}\!=\!\dfrac 23\,\dfrac{A\!+\!3C}{4}\!+\!\Big(1\!-\!\dfrac 23\Big)B\!=\!\dfrac 23\,\dfrac{B\!+\!C}{2}\!+\!\Big(1\!-\!\dfrac 23\Big) \dfrac{A\!+\!C}{2}\!=\!\dfrac 12C\!+\!\Big(1\!-\!\dfrac 12\Big)\dfrac{A\!+\!2B}{3}$. 是否還存在其他情形? 雖人工試驗多次, 但未必沒有漏網之魚。 為了一網打盡, 還得借助電腦進行遍歷搜索。 思路: 每次從點集合 $P:\Big\{A,B,C,\dfrac{A+2B}{3},\dfrac{2A+B}{3},\dfrac{B+C}{2},\dfrac{A+3C}{4},\dfrac{A+C}{2},\dfrac{3A+C}{4}\Big\}$, 中選取 6 個為一組 $\{P_1,P_2,P_3,P_4,P_5,P_6\}$, $P_i\in P$ 表示三條直線 $P_1P_2$、 $P_3P_4$、 $P_5P_6$, 若方程組 $xP_1+(1-x)P_2=yP_3+(1-y)P_4=zP_3+(1-z)P_6$ 存在解, 則符合要求。遍歷所有情況, 發現確實只有上面兩組解。
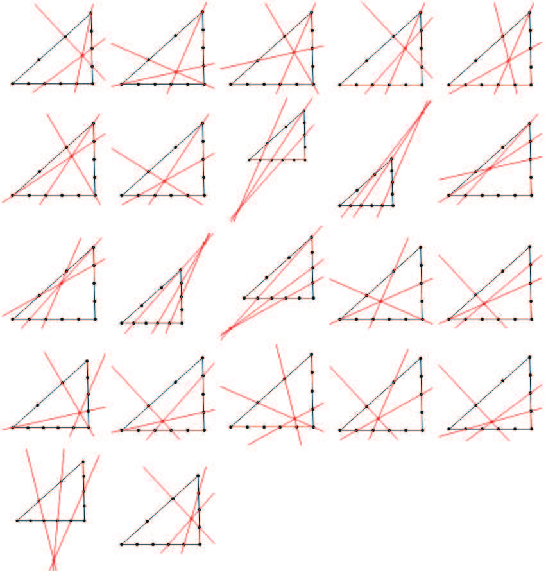
下面我們將上述問題進行擴展。 探索 $\triangle ABC$ 中 (圖9), 將 $BC$ 五等分, $BA$ 三等分, $AC$ 四等分, 嘗試連接這些等分點, 能找到哪些三點共線的情況。 經電腦搜索, 共 22 種可能, 如圖 10 所示。 圖 10 中前 3 個圖形所對應恒等式如下: \begin{align*} \frac{10A\!+\!3B\!+\!12C}{25}\!=&\frac 35\,\frac{B\!+\!4C}{5}\!+\!\Big(1\!-\!\frac 35\Big)A \!=\!\frac {16}{25}\,\frac{A\!+\!3C}{4}\!+\!\Big(1\!-\!\frac {16}{25}\Big)\frac{2A\!+\!B}{3}\\ \!=&\frac 15\,\frac{3B\!+\!2C}{5}\!+\!\Big(1\!-\!\frac 15\Big)\frac{A\!+\!C}{2},\\ \frac{A\!+\!2B\!+\!3C}{6}\!=&\frac 56\,\frac{2B\!+\!3C}{5}\!+\!\Big(1\!-\!\frac 56\Big)A \!=\!\frac 23\,\frac{A\!+\!3C}{4}\!+\!\Big(1\!-\!\frac 23\Big)B\\ \!=&\frac C2\!+\!\Big(1\!-\!\frac 12\Big)\frac{A\!+\!2B}{3},\\ \frac{4A\!+\!2B\!+\!3C}{9}\!=&\frac 59\,\frac{2B\!+\!3C}{5}\!+\!\Big(1\!-\!\frac 59\Big)A \!=\!\frac 23\,\frac{A\!+\!C}{2}\!+\!\Big(1\!-\!\frac 23\Big)\frac{A\!+\!2B}{3}\\ \!=&\frac C3\!+\!\Big(1\!-\!\frac 13\Big)\frac{2A\!+\!B}{3}, \end{align*} 其餘以此類推。
目前初等數學的研究, 多數時候還是紙筆手算, 也有數學老師使用數學軟體幾何畫板或 GeoGebra 等。 這兩個軟體作幾何圖形方便, 且具備測量多邊形面積等功能, 還能通過拖動點的方式來動態觀察圖形中蘊含的性質, 為研究案例 1 這樣的問題, 提供了便利。 假設你猜想哪兩個三角形的面積相等, 就可以通過測量的方式來驗證。 但問題是, 有時根本提不出猜想, 那就難辦了。 但這種情況下, 窮舉是笨方法, 也是好方法。 而案例 1 涉及 35 個三角形, 如果基於幾何畫板或 GeoGebra, 靠手工一個個去測量, 需要花費較多時間, 且容易遺漏。 案例 2 也是如此, 不斷地在圖形中畫三條直線, 看是否交於一點, 這樣的操作提供給小學生練習觀察力, 讓他們享受發現的樂趣, 是可以的。 但如果拿給中學生, 特別是成年人來做, 就有點浪費時間。我們應該把精力留給做更有創造力的事情, 譬如設計思路和演算法, 具體地``畫線和計算''留給 Mathematica 這種具有強大程式設計功能的軟體來完成。 正如數學大師萊布尼茲所言, 一個出色的人像奴隸一樣把時間浪費在計算的勞動上是很不值得的, 有了機器, 這種工作可以放心地交給任何人。 在電腦高速發展的今天, 萊布尼茲的建議格外值得體味。 同時也要注意, 目前的電腦雖然已經能自動推理一些數學問題, 但離人的高級智慧還有距離。 在案例 1 中, 如果希望電腦生成本文作者給出的證明, 進而找到面積相等的三角形, 恐怕難度較大。 而基於座標計算, 正是電腦所擅長。 所以我們要取長補短, 人機協同, 共同解決一些難題。 附錄 (本文實驗 mathematica 代碼)案例1: 下面代碼能找出 7 個點構成的 35 個三角形中, 哪些面積相等。 由於 C, D, E 在 mathematica 中被保留為常數、 求導、 歐拉常數, 因此涉及點的標籤用 C1, D1, E1 表示。
Clear["`*"];
A = {0, 0}; B={1,0};C1 = {xc, yc}; E1 = {1, -1};
D1 = {0, -1}; F = {-yc, xc}; G = C1 + F;
(*寫出所有點的座標*)
Subsets[{A, B, C1, D1, E1, F, G}, {3}](*每次取三個點的座標*)
Area@Polygon[#] & /@ Subsets[{A, B, C1, D1, E1, F, G}, {3}]
(*測量所取三個點構成的三角形面積*)
SortBy[Thread[%% -> %], Last];(*根據三角形面積進行排序*)
Framed /@ GatherBy[%,Last] /. {(k_ -> v_) :> (k -> Style[v, Red])} // Column
(*將面積相等的三角形收集在一起*)
下面代碼能自動生成圖 5, 可嘗試將 $n$ 改成其他大於 4 的整數。
n = 4;
pts = Table[(-1)^((2 i - 3)/n - 1/2), {i, n}];(*生成第一個正n邊形的頂點*)
pt = pts[[3]];
pts2 = pt + (pts - pt) RandomReal[{0.8, 0.82}]
E^(I RandomReal[{120, 123} Pi/180]);
(*生成第二個正n邊形的頂點*)
pair = Cases[GatherBy[Flatten[Table[{pts[[i]], pts[[j]],k},{i,n},{j,i+1,n},
{k, Select[pts2, Abs[# - pt] > 10^-8 &]}], 2],
Round[Abs@Im[Conjugate[#]. RotateLeft[#]], 10.^-8] &], {_, _}];
(*將所有面積相等的三角形收集在一起*)
Graphics[{RegionBoundary /@ Polygon /@ ReIm@{pts, pts2}, {Opacity[0.2],
Flatten@Riffle[{EdgeForm[{#,Thick}],#} &/@{Red,Green},Polygon/@ ReIm@#]}},
BaseStyle -> 14, ImageSize -> 250] & /@ pair //
Partition[#, 2, 2, 1, {}] & // Grid (*繪製圖形, 使之視覺化*)
案例2: 下面代碼能自動生成圖 10。
Clear["`*"];
eps = 10^-8.;
sameLine[{{x1_, y1_}, {x2_, y2_}}]
:=Round[#/Total@# &@{y1-y2, x2-x1, x1 y2-x2 y1}, eps];
lineConcurrent[{{{x1_,y1_},{x2_,y2_}},{{x3_,y3_},{x4_, y4_}},
{{x5_, y5_},{x6_, y6_}}}] := Abs[Det[{{y1-y2, x2-x1, x1 y2-x2 y1},
{y3-y4, x4-x3, x3 y4-x4 y3}, {y5-y6, x6-x5, x5 y6-x6 y5}}]] < eps;
(*判斷三條線是否共點*)
{A1, B1, C1} = {RandomReal[{0.3, 1}, 2], {0, 0}, {1, 0}} // N;
{X1, X2} = ({{1, 2}, {2, 1}}/3) . {A1, B1};
{Y1, Y2, Y3} = ({{1, 3}, {2, 2}, {3, 1}}/4) . {C1, A1};
{Z1,Z2,Z3,Z4} = ({{1, 4},{2, 3},{3, 2},{4, 1}}/5) . {B1, C1};
(*生成基本圖形*)
Dimensions[
ans = Select[Select[Subsets[DeleteDuplicatesBy[Subsets[{A1,
B1, C1, X1, X2, Y1, Y2, Y3, Z1, Z2, Z3, Z4}, {2}], sameLine], {3}],
DuplicateFreeQ@*Catenate], lineConcurrent]];
Length /@ (gb =GatherBy[ans, Equal @@
Round[Mod[ArcTan @@@ Subtract @@@ #, Pi], eps] &]);
Graphics[{Line[{A1, B1, C1, A1}], PointSize[0.03],
Point[{A1, B1, C1, X1, X2, Y1, Y2, Y3, Z1, Z2, Z3, Z4}],
{Red, InfiniteLine /@ #,
RegionIntersection[InfiniteLine /@ #[[1 ;; 2]]]}},
PlotRangePadding -> Scaled[.1]] & /@ gb[[1]] //
Partition[#,5,5,1, {}] & // Grid(*遍歷查找三線共點的情況, 作圖輸出*)
下面代碼能自動生成 22 個恒等式。
Clear["`*"];
(*定義三點共線的函數sdgxQ*)
sdgxQ[{P1_, P2_, P3_, P4_, P5_, P6_}] := Module[{ },
sol = {Solve[
Coefficient[t1 P1 + (1 - t1) P2 - P3 , {A, B, C}] == 0, {t1,
t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t2 P1 + (1 - t2) P2 - P4 , {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t3 P1 + (1 - t3) P2 - P5 , {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t4 P1 + (1 - t4) P2 - P6, {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t5 P3 + (1 - t5) P4 - P1 , {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t6 P3 + (1 - t6) P4 - P2 , {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t7 P3 + (1 - t7) P4 - P5 , {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t8 P3 + (1 - t8) P4 - P6 , {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t9 P5 + (1 - t9) P6 - P1 , {A, B, C}] == 0, {t1,
t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t10 P5 + (1 - t10) P6 - P2 , {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t11 P5 + (1 - t11) P6 - P3 , {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }],
Solve[Coefficient[t12 P5 + (1 - t12) P6 - P4 , {A, B, C}] ==
0, {t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12 }]}// Flatten;
If[sol =!={}, False, True ]]
(*求出三線共點的交點*)
f[{P1_, P2_, P3_, P4_, P5_, P6_}] := Module[{ },
sol = Solve[Coefficient[k1 P1+(1-k1)P2-(k2 P3+(1-k2) P4), {A,B,C}]==0
&& Coefficient[k1 P1+(1-k1) P2-(k3 P5+(1-k3) P6), {A,B,C}]==0 && k1!=0
&& k1!=1 && k2!=0 && k2!=1 && k3!=0 && k3!=1, {k1,k2,k3}] // Factor;
If[sol=!={},{k1 P1 + (1 - k1) P2 /. sol[[1]] //
Factor, HoldForm[k1 P1 +(1-k1)P2==k2 P3+(1-k2)P4
==k3 P5+(1-k3)P6] /. sol[[1]]}, Nothing]]
pailie6[{P1_,P2_,P3_,P4_,P5_,P6_}] := Module[{ },{{P6, P1, P5, P2, P4, P3},
{P6, P1, P5, P3, P4, P2},{P6, P1, P5, P4, P3, P2},{P6, P2, P5, P1, P4, P3},
{P6, P2, P5, P3, P4,P1},{P6, P2, P5, P4, P3, P1},{P6, P3, P5, P1, P4, P2},
{P6, P3,P5, P2, P4, P1},{P6, P3, P5, P4, P2, P1},{P6, P4, P5, P1, P3, P2},
{P6, P4, P5, P2, P3, P1},{P6, P4, P5, P3, P2, P1},{P6, P5,P4, P1, P3, P2},
{P6, P5, P4, P2, P3, P1},{P6, P5, P4, P3, P2,P1}}]
(*pailie6是對六點進行排列。*)
V5 = {A, B, (A + 2 B)/3, (2 A + B)/3, (4 B + C)/5, (2 B + 3 C)/5,
(3B+2C)/5,(B+4 C)/5,(4B+C)/5,(A+3C)/4, (3A+C)/4, (A+C)/2,C} // Union;
SS1 = Flatten[pailie6 /@ Union@Subsets[V5, {6}], 1] ;
SS5 = Select[SS1, sdgxQ ];
f /@ SS5 //. {{A, _} -> 0, {B, _} -> 0, {C, _} -> 0}
本文作者彭翕成任教中國華中師範大學人工智能教育學部, 曹洪洋任職中國常州九章教育科技有限公司 |
2023年9月 47卷3期
人算不如機算──電腦輔助數學探索兩例

