| 發刊日期 |
2023年12月
|
|---|---|
| 標題 | 廣義的幾何分佈之期望值探討及一些結果 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
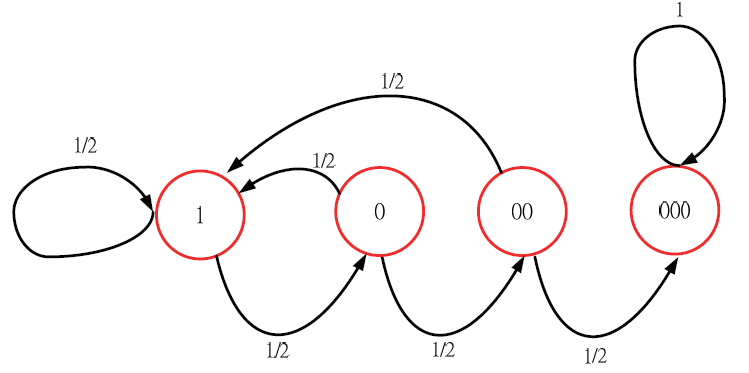
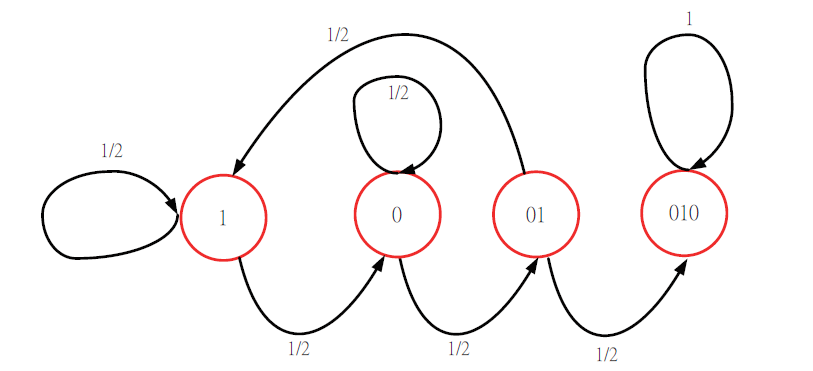
作者老家位在台南鹿耳門天后宮的後面, 國小的操場是借用天后宮的廟埕, 小時候有個疑問, 媽祖的信徒擲筊過程預期幾次才會出現連續 3 個聖杯 (以 '000' 表示)? 長大後, 從教科書 \begin{align} E[Y]=\,&E[E(Y\mid Z)]=E[Y\mid Z=1]\cdot P(Z=1)+E[Y\mid Z=2]\cdot P(Z=2) +E[Y\mid Z=3]\cdot P(Z=3)+E(Y\mid Z\ge 4]\cdot P(Z\ge 4)\nonumber\\ =\,&\frac 12(1+E(Y])+\frac 14(2+E[Y])+\frac 18(3+E[Y])+3\cdot (1-\frac 12-\frac 14-\frac 18)\label{1} \end{align} 整理得 $E[Y]=E[\hbox{'000'}]=14$, 也就是說擲筊過程預期平均 14 次才會出現連續 3 個聖杯。 利用相同的技巧並定義 $Y_n$ 表示連續出現 $N$ 次 '0' 所需的次數, \eqref{2} 式列出不同次數的期望值的結果: \begin{align} E[Y_N]=\,&2^N\cdot \!\sum_{k=1}^N\! k\cdot(\frac 12)^k\!\!+\!\!N=2^{N+1}\!-\!2\nonumber\\ =\,&[2\ 6\ 14\ 30\ 62\ 126\ 254\ 510\ 1022\ 2046\ \cdots],\label{2} \end{align} 其中第 3 項為 14, 表示連續出現 3 個聖杯的期望值, 或者也可以寫成遞迴關係如下: \begin{align} E[Y_0]=0,\ E[Y_N]\!=\!2E[Y_{N-1}]\!+\!2\!=\![2\ 6\ 14\ 30\ 62\ 126\ 254\ 510\ 1022\ 2046\ \cdots].\label{3} \end{align} 延續這樣的討論, 本文想把這個問題一般化。 假設硬幣出現人頭(正面)用 0 表示, 反面用 1 表示, 題目敘述如下: 「擲一公正硬幣預期幾次才會出現特定的樣式(pattern)?」。 例如: 預期幾次才會出現樣式 '010101'? 前面 '000' 的例子由於只要出現 '1' 就會從頭來, 所以做法相對簡單, 狀態圖如圖 1, 其中每一個箭頭代表一次的投擲。 如果要求的樣式為 '010', 圖 2 是出現 '010' 就停止的狀態圖, 會發現每一次的錯誤並不是簡單的從頭來, 因此無法直接利用 \eqref{1} 式的作法。
本文研究的結論是''每一種樣式對應到一個樣式矩陣, 透過反矩陣運算 (或解聯立方程式或高斯消去法)可以得到答案'', 這樣的問題我們稱作: 「廣義的幾何分佈之期望值」。 先從最簡單的例子說起, 擲一公正硬幣預期幾次才會出現 1 個人頭, 這是最簡單的幾何分佈的例子, 根據幾何分佈的公式答案是 $E[Y_1]=E[\hbox{'0'}]=\dfrac 1p=\dfrac{1}{1/2}=2$ 次, 或者簡單計算過程如下: \begin{align} E[\hbox{'0'}]=1\times \frac 12+2\times \frac 14+3\times \frac 18+\cdots +n\times \frac 1{2^n}+\cdots=\sum_{k=1}^\infty k\times \frac 1{2^k}=2.\label{4} \end{align} 接著我們討論 $Y_2$ 的情況, 先來個素養題。 小明去逛夜市, 看到一個攤位在玩賭博遊戲。 規則很簡單, 有 4 個樣式可以選擇, 包括 $\{00, 01, 10, 11\}$, '00' 表示連續 2 次人頭朝上。 玩 1 次要 5 元, 小明先選其中 1 個樣式, 例如 '00', 假設連續丟擲一枚公正的硬幣, 出現 '010110101100', 當 '00' 出現遊戲就停止, 小明丟了 12 次才停止, 老闆必須付 12 元給小明。 本題目敘述如下: (a) 請問小明選擇哪個樣式贏錢的機會較大? (b) 假設玩家隨機選擇 4 個樣式的其中 1 個, 請問當莊家的老闆平均來說是輸是贏? 還是說這個賭博遊戲是公平的? 由於 $E[\hbox{'01'}]$ 及 $E[\hbox{'10'}]$ 的答案要到本文中段才會提出簡潔的做法, 這裡我們先採用大學才會學到的馬可夫鏈來求出 $E[\hbox{'01'}]$。 參考教科書

由於狀態 $S_2=\hbox{'00'}$ 與 $S_4=\hbox{'11'}$ 有相同的結構, 由 \eqref{2} 式知 $E[\hbox{'00'}]=E[\hbox{'11'}]=6$, 又狀態 $S_1=\hbox{'01'}$ 與 $S_3=\hbox{'10'}$ 有相同的結構, 由上面討論知 $E[\hbox{'01'}]=E[\hbox{'10'}]=4$, 四種狀態之期望值的平均值為 $${\rm mean}(S)=\frac 14(E[\hbox{'00'}]+E[\hbox{'11'}]+E[\hbox{'00'}]+E[\hbox{'11'}])=\frac 14\times (6+6+4+4)=5,$$ 因此我們得知這題素養題的答案是(a) 選擇 '00' 或 '11' 贏錢的機會較大, (b)這個賭博遊戲是公平的。 也可以說選擇 '00' 或 '11' 平均一次可以賺 1 元, 選擇 '01' 或 '10' 平均一次虧 1 元, 這樣的結果有些顛覆大家平常的認知。 簡單的解釋如下: 以選擇 '00' 為例, 出現 '01' 時就得從頭來, 以選擇 '01' 為例, 出現 '00' 時第 2 個 '0' 可以留下當 '01' 的第 1 個 '0' 來用, 所以 $E[\hbox{'01'}]=4$ 會比 $E[\hbox{'00'}]=6$ 小。 為了降低讀者的疑慮, 我們採用蒙地卡羅模擬來驗證。 蒙地卡羅模擬是一種機率統計採用的技術, 可預測不確定事件的可能結果。 電腦程式語言使用 Matlab, 此程式模擬小明選擇 '01' 並且玩了 100 萬次, 期望值是 4.0019, 與 $E[\hbox{'01'}]=4$ 相比, 誤差很小, 程式寫法如圖 4 所示。

在研究這個題目時我們發現一個可用的公式, mean$(S)=2^N+N-1$。 由於缺乏證明, 先稱之為第一個猜想, 陳述如下: 已知樣式長度為 $N$, 則 $2^N$ 種樣式之期望值的平均值 mean$(S)=2^N+N-1$, 以 $N=2$ 為例, 也就是說當不考慮何種樣式, 擲一公正硬幣 $2^2+2-1=5$ 次可以期望看到 4 個樣式各出現一次, 包括 $\{00, 01, 10, 11\}$。 我們試著說明第一個猜想成立的理由: 由於每一種樣式都是等機率的, 且每一種樣式誰先誰後都有可能, 因此平均 4 種樣式的每一種會出現 1 次。 程式統計結果發現這個猜想在 $N\le 6$ 都是對的, 由於沒有找到相關的文章敘述, 有興趣的讀者也許可以提出方法來證明這個猜想。 行文至此我們換另一個角度來計算 $E[\hbox{'01'}]$。 想像連續丟擲一枚公正的硬幣 5 次, 根據猜想, $\{00, 01, 10, 11\}$ 平均各別出現 1 次, 所以不考慮單一樣式的情況下, 其期望值的平均值是 $E[\hbox{'XX'}]=\dfrac 14(E[\hbox{'00'}]+E[\hbox{'01'}]+E[\hbox{'10'}]+E[\hbox{'11'}])=2^2+2-1=5$, 玩 1 次要 5 元, 因此這個賭博遊戲是公平的。 由 \eqref{2} 式知 $E[\hbox{'00'}]=E[\hbox{'11'}]=6$, 所以 $E[\hbox{'01'}]=E[\hbox{'10'}]=2\times E[\hbox{'XX'}]-6=2\times 5-6=4$, 與前面採用馬可夫鏈來求出 $E[\hbox{'01'}]=4$ 是相符的。 為了處理任意的「廣義的幾何分佈之期望值」的計算, 底下我們將提出一種簡潔且通用的解題技巧。 先定義 $f(m,P)$, 其中 $P$ 表示某個樣式, 長度為 $N$。 函數 $f(m,P)$ 表示樣式 $P$ 中已出現前 $m$ 個單元, 剩餘的樣式平均還需要幾次才能結束。 例如: $f(0,\hbox{'00'})=6$, $f(1,\hbox{'00'})=4$。 $f(0,\hbox{'00'})=6$ 表示目標是 '00', 如果第 1 個 '0' 還未出現, 平均需要 6 次才會看到 '00', $f(1,\hbox{'00'})=4$ 表示目標是 '00', 如果第 1 個 '0' 已經出現, 平均需要 4 次才會看到 '00'。 再來定義 $g(P_n)$, $n=1,2,\ldots,N$, 假設樣式 $P$ 的前面 $n$ 個單元為 $P_n$, $P_n$ 的最後一次出錯, 仍可當作 $P$ 的前面部分樣式的長度(個數)稱作 $g(P_n)$。 舉例說明, $g(P_n)=0$ 表示最後一次出錯無法取代 $P$ 的前面部分樣式。 例如: $g(\hbox{'00'})=0$ 表示若第 2 個 0 錯成 1, 那就前功盡棄得重新來, $g(\hbox{'01'})=1$ 表示若第 2 個位置的 1 錯成 0, 這個錯掉的 0 可以取代 '01' 的第 1 個位置的 0, 所以 $g(\hbox{'01'})=1$, $g(\hbox{'00101'})=2$ 表示若第 5 個位置的 1 錯成 0, 後面 2 個 0 可以取代 '00101' 最前面的 2 個 0, 所以 $g(\hbox{'00101'})=2$。 我們的問題簡化成給定樣式 $P$, 求出 $f(0,P)$ 的值即是期望值。 以 $g(\hbox{'01100'})$ 為例, 先列出 $g(P_n)$ 函數如下: $g(\hbox{'0'})=0$, $g(\hbox{'01'})=1$, $g(\hbox{'011'})=1$, $g(\hbox{'0110'})=0$, $g(\hbox{'01100'})=2$。 求解樣式 $P(\hbox{'01100'})$ 的狀態圖如圖 5 所示, 可提供列式時的參考比較。
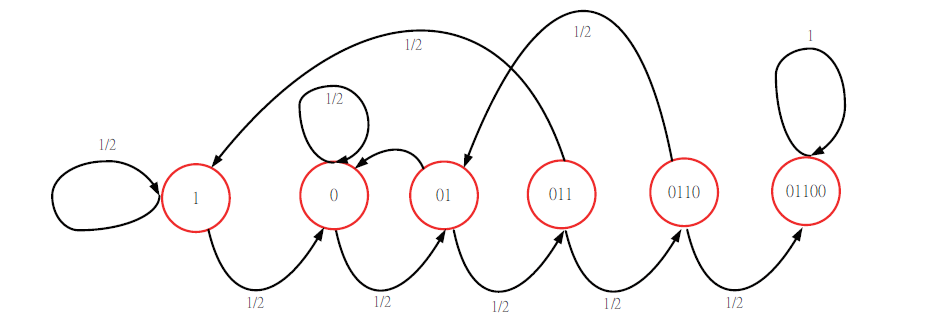
解法如下: \begin{align} \begin{array}{rccccccccccc} f(0,\!P)\!=\!\!&\frac 12[1\!\!+\!\!f(0,\!P)]&\!\!+\!\!&\frac 12[1\!\!+\!\!f(1,\!P)],&&\\[7pt] f(1,\!P)\!=\!\!&&&\frac 12[1\!\!+\!\!f(1,\!P)]&\!\!+\!\!&\frac 12[1\!\!+\!\!f(2,\!P)],&&&&\\[7pt] f(2,\!P)\!=\!\!&&&\frac 12[1\!\!+\!\!f(1,\!P)]&&&\!\!+\!\!&\frac 12[1\!\!+\!\!f(3,\!P)],&&&&\\[7pt] f(3,\!P)\!=\!\!&\frac 12[1\!\!+\!\!f(0,\!P)]&&&&&&&\!\!+\!\!&\frac 12[1\!\!+\!\!f(4,\!P)],&&\\[7pt] f(4,\!P)\!=\!\!&&&&&\frac 12[1\!\!+\!\!f(2,\!P)]&&&&&\!\!+\frac 12\!\!\times\!\! 1, \end{array}\label{5} \end{align} 整理後以矩陣表示如下: \begin{align} \left(\left[\begin{array}{ccccc} ~2~&-1&0&0&0\\ 0&2&-1&0&0\\ 0&0&2&-1&0\\ 0&0&0&2&-1\\ 0&0&0&0&2\end{array}\right]- \left[\begin{array}{ccccc} ~1~&~0~&~0~&~0~&~0~\\ 0&1&0&0&0\\ 0&1&0&0&0\\ 1&0&0&0&0\\ 0&0&1&0&0 \end{array}\right]\right)\times \left[\begin{array}{c} f(0,P)\\ f(1,P)\\ f(2,P)\\ f(3,P)\\ f(4,P)\end{array}\right]= \left[\begin{array}{c} 2\\ 2\\ 2\\ 2\\ 2\end{array}\right].\label{6}\end{align} 左邊第 1 個矩陣與樣式 $P$ 無關, 稱作 $A$ 矩陣, 第 2 個矩陣與樣式 $P$ 有關, 稱作 $B(P)$ 矩陣, 兩者相減稱為 $C$ 矩陣, $C=A-BP$。 經由反矩陣運算後得 \begin{align} \left[\begin{array}{c} f(0,P)\\ f(1,P)\\ f(2,P)\\ f(3,P)\\ f(4,P)\end{array}\right]= [A-B(P)]^{-1}\times \left[\begin{array}{c} 2\\ 2\\ 2\\ 2\\ 2\end{array}\right]= \left[\begin{array}{c} 34\\ 32\\ 30\\ 26\\ 16\end{array}\right] \Rightarrow f(0,\hbox{'01100'})=34.\label{7}\end{align} 因此我們得到樣式 $P(\hbox{'01100'})$ 的期望值為 34。 由上述例子可知 $B(P)$ 的每一個列 (row) 只會出現一個 '1', 第 $n$ 個列的 '1' 出現在第 $g(P_n)+1$ 個位置。 例如 $g(\hbox{'01100'})=2$ 表示第 5 個列的 '1' 出現在第 $g(P_5)+1=2+1=3$ 的位置上。 為了加深讀者對函數 $f(m,P)$ 的理解, 我們再一次補充說明, \eqref{7} 式中的 $f(1,P)=32$ 表示 $P(\hbox{'01100'})$ 的第一個 '0' 出現, 平均還需要投擲 32 次才能完成任務, \eqref{7} 式中的 $f(4,P)=16$ 表示 $P(\hbox{'01100'})$ 的前四個結果 '0110' 已經出現, 平均還需要投擲 16 次才能完成任務。 介紹了這個技巧後我們再回到前面提到的素養題, 已知 $P=(\hbox{'01'})$, $g(\hbox{'0'})=0$, $g(\hbox{'01'})$ $=1$, 採用本文提出的方法: \begin{align} A=\left[\begin{array}{cc} ~2~&-1\\ 0 &2 \end{array}\right]\!,\quad B(\hbox{'01'})=\left[\begin{array}{cc} ~1~&~0~\\ 0 &1 \end{array}\right]\!,\quad b=\left[\begin{array}{c} 2\\ 2 \end{array}\right].\label{8}\\ [A-B(P)]^{-1}\times b=\left[\begin{array}{c} 4\\ 2 \end{array}\right] \Rightarrow f(0,P)=4.\qquad~\label{9} \end{align} 結果得 $E[\hbox{'01'}]=4$, 跟前面的討論是一樣的, 從這個例子可以知道此方法是簡潔有效的。 討論到此, 我們針對樣式長度 $N=6$ 的情形做更詳細的研究。 先舉一個 $P(\hbox{'000000'})$ 的例子, 其中 $B(\hbox{'000000'})$ 矩陣的 1 只會出現在每一列的第一行, 因為 $g(\hbox{'0'})=g(\hbox{'00'})=g(\hbox{'000'})=g(\hbox{'0000'})=g(\hbox{'00000'})=g(\hbox{'000000'})=0$, 只要錯 1 個就得重新來過。 其矩陣寫法如下: \begin{align} A=\left[\begin{array}{ccccc} ~2~&-1&0&0&0\\ 0&2&-1&0&0\\ 0&0&2&-1&0\\ 0&0&0&2&-1\\ 0&0&0&0&2\end{array}\right]\!,\ B(\hbox{'000000'})= \left[\begin{array}{ccccc} ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~ \end{array}\right]\!,\ b=\left[\begin{array}{c} 2\\ 2\\ 2\\ 2\\ 2\\ 2\end{array}\right],\label{10}\\[6pt] [A-B(P)]^{-1}\times b= \left[\begin{array}{c} 126\\ 124\\ 120\\ 112\\ 96\\ 64\end{array}\right]\Rightarrow f(0,P)=126.\qquad\quad~\label{11} \end{align} $E[\hbox{'000000'}]=126$ 與 \eqref{2} 式的第 6 項結果相符, 我們也觀察到 $B$ 矩陣的元素 1 只出現在第一行, 此時對應到各種樣式期望值的最大值。 再舉一個 $P=(\hbox{'001100'})$ 的例子 $g(\hbox{'0'})=g(\hbox{'00'})=0$, $g(\hbox{'001'})=2$, $g(\hbox{'0011'})=1$, $g(\hbox{'000110'})=g(\hbox{'001100'})=0$, 矩陣寫法如下: \begin{align} A=\!\left[\begin{array}{ccccc} ~2~&-1&0&0&0\\ 0&2&-1&0&0\\ 0&0&2&-1&0\\ 0&0&0&2&-1\\ 0&0&0&0&2\end{array}\right]\!,\ B(\hbox{'001100'})\!=\! \left[\begin{array}{ccccc} ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~0~&~0~&~1~&~0~&~0~\\ ~0~&~1~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~ \end{array}\right]\!,\ b\!=\! \left[\begin{array}{c} 2\\ 2\\ 2\\ 2\\ 2\\ 2\end{array}\right],\qquad\ ~\label{12}\\[6pt] C\!=\!A\!-\!B(P) \!=\!\left[\begin{array}{cccccc} 1&-1&0&0&0&0\\ -1&2&-1&0&0&0\\ 0&0&1&-1&0&0\\ 0&-1&0&2&-1&0\\ -1&0&0&0&2&-1\\ -1&0&0&0&0&2\end{array}\right]\!,\ P\!=\!C^{-1}b\!=\!\! \left[\begin{array}{c} 70\\ 68\\ 64\\ 62\\ 54\\ 36\end{array}\right]\Rightarrow f(0,P)\!=\!70.\label{13} \end{align} 其中的 $f(1)=f(0,P)=70$ 即表示 $E[\hbox{'001100'}]=70$。 也可以解聯立方程式如下: \begin{align} \left[\begin{array}{cccccc} ~1~&-1&~0~&~0~&~0~&~0~\\ -1&~2~&-1&0&0&0\\ 0&0&1&-1&0&0\\ 0&-1&0&2&-1&0\\ -1&0&0&0&2&-1\\ -1&0&0&0&0&2\end{array}\right]\times \left[\begin{array}{c} x\\ y\\ z\\ u\\ v\\ w\end{array}\right]=\left[\begin{array}{c} 2\\ 2\\ 2\\ 2\\ 2\\ 2\end{array}\right]\!,\ \hbox{得}\ x=70.\label{14} \end{align} 比較 $P=(\hbox{'000000'})$ 與 $P=(\hbox{'001100'})$ 的結果知 $E=(\hbox{'000000'})=126$ 大於 $E=(\hbox{'001100'})=70$, 可以發覺樣式 $B$ 矩陣的結構似乎與期望值大小有關聯性。 透過程式的幫忙, 以 $N=6$ 為例, 整理一些結果如下: (1) $N=6$ 共有 $2^N=64$ 種樣式, 以 2 進位對應到非負整數 0$\sim$63, 前面 32 個與後面有互補型態, 因此期望值相同, 式 \eqref{15} 列出前面 32 個的結果, 第 1 列表示 0 到 9, 第 2 列表示 10 到 19, 依此類推。 例如 ('000000') 表示 10 進位整數的 0, $E(\hbox{'000000'})=126$; 001100 表示 10 進位自然數的 12, $E(\hbox{'001100'})=70$。 圖 6 則是以圖形將結果展示出來。 \begin{align} S=\left[\begin{array}{cccccccccc} ~126~&~64~&~66~&~64~&~70~&~64~&~66~&~64~&~70~&~72\\ 66&64&70&64&66&64&66&68&74&64\\ 66&84&66&64&66&68&66&72&66&68\\ 66&64&&&&&&&& \end{array}\right]. \label{15} \end{align}
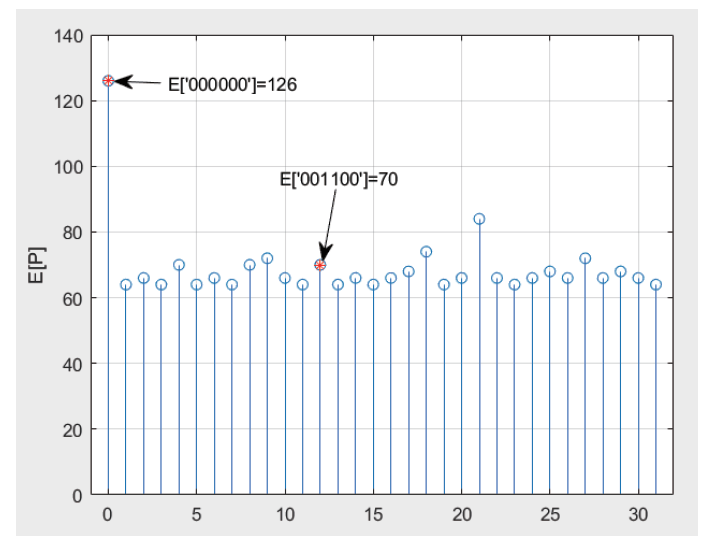
(2) 64 種期望值的平均值 mean$(S)=E[\hbox{'XXXXXX'}]=2^N+N-1=69$, 也就是說當不考慮樣式, 擲一公正硬幣 69 次, 平均 64 種樣式的每一種會出現 1 次, 利用程式統計得到 64 種期望值的平均值確實是 69, 與本文前面提到的第一個猜想相符。 (3) 透過程式幫忙, 我們得到第二組公式, $S_{\rm max}=2^{N+1}-2$, $S_{\rm min}=2^N$, 以 $N=6$ 為例, 64 種期望值的最大值 $S_{\rm max}=2^{N+1}-2=126$, 最小值 $S_{\rm min}=2^{N}=64$, 與 \eqref{15} 式或圖 6 看到的結果相符。 最大值 $S_{\rm max}=2^{N+1}-2$ 出現在狀態內元素皆相同時, 例如 $E(\hbox{'000000'})=E(\hbox{'111111'})=126$, 這是顯而易見, 因為元素皆相同時, 不管對了幾個, 只要一錯就前功盡棄從頭來過, 所以期望值最大, 最大值如式 \eqref{2} 所示。 (4) 觀察式 \eqref{15} 知最小值出現在 10 進位表示法的 $\{1, 3, 5, 7,11,13,19, 23, 31\}$, 以 1 與 13 為例, $E(\hbox{'000001'})=E(\hbox{'001101'})=64$ 皆是最小值, 其 $B$ 矩陣如式 \eqref{16} 所示, 可以看出 $B$ 矩陣中的元素 1 出現的位置座標似乎與期望值有關, 不考慮 $B$ 矩陣的第 1 行, 剩下的元素 1 之行座標總和計算結果是 $D(0)=0+0+0+0+0+6=6$ 及 $D(13)=0+0+2+1+0+3=6$, 同時比較前面提到的 $E(\hbox{'000000'})=126$, 它的 $D(0)=0+0+0+0+0+0=0$, 以及 $E(\hbox{'001100'})=70$, 它的 $D(12)=0+0+3+2+0+0=5$, 我們觀察到當行座標總和越大, 對應的樣式之期望值越小, 似乎可以感覺到 $B$ 矩陣藏著期望值的資訊。 有興趣的讀者或是想做數學科展的同學可以把最小值的公式 $S_{\rm min}=2^N$ 看成第二個猜想, 繼續研究為什麼或試著給出嚴格的證明。 \begin{align} B(\hbox{'000001'})=\left[\begin{array}{cccccc} ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~0~&~0~&~0~&~0~&~1~ \end{array}\right]\!,\ B(\hbox{'001101'})=\left[\begin{array}{cccccc} ~1~&~0~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~0~&~0~&~1~&~0~&~0~\\ ~0~&~1~&~0~&~0~&~0~\\ ~1~&~0~&~0~&~0~&~0~\\ ~0~&~1~&~0~&~0~&~1~ \end{array}\right]. \label{16} \end{align} 最後我們把相同的技巧推廣到丟擲公正的 6 面骰子, 題目敘述如下: 「擲一公正的骰子預期幾次才會出現特定的樣式?」。 例如 '123', 經由擴展上述技巧知 \begin{align} &\hskip 2cm A=\left[\begin{array}{ccc} ~6~&-1&~0~\\ 0 &6&-1\\ 0&0&6 \end{array}\right]\!,\quad B(\hbox{'123'})=\left[\begin{array}{ccc} ~5~&~0~&~0~\\ 4 &1&0\\ 4 &1&0 \end{array}\right]\!,\quad b=\left[\begin{array}{c} 6\\ 6\\ 6 \end{array}\right],\label{17}\\ C=&A-B(\hbox{'123'})=\left[\begin{array}{ccc} ~1~&-1&0\\ -4&5&-1\\ -4&-1&6 \end{array}\right]\!,\ P=C^{-1}b=\left[\begin{array}{c} 216\\ 210\\ 186\end{array}\right]\!,\Rightarrow \ f(0,P)=216.\label{18} \end{align} 因此我們得到結果是擲一公正的骰子預期 216 次才會出現特定的樣式 ('123'), 或者說期望值 $E(\hbox{'123'})=216$。 再次採用蒙地卡羅模擬來驗證。 考慮運算時間, 此程式只試驗 10 萬次, 期望值是 217.0986, 與 $E(\hbox{'123'})=216$ 相比, 誤差約 1.1 次, 誤差比是 $0.51\%$, 應該算合理範圍, 程式寫法如圖 7 所示。

年輕人喜歡用數字的組合來表示特殊的句子, 因此我們最後再練習一題, 擲一公正的骰子預期幾次才會出現特定的樣式 ('1314521'), 它代表 ('一生一世我愛伊'), 經由類似計算過程得知 \begin{align} &\hskip -50pt A\!\!=\!\left[\!\begin{array}{ccccccc} ~6~&~1~&~0~&~0~&~0~&~0~&~0~\\[-2pt] ~0~&~6~&~1~&~0~&~0~&~0~&~0~\\[-2pt] ~0~&~0~&~6~&~1~&~0~&~0~&~0~\\[-2pt] ~0~&~0~&~0~&~6~&~1~&~0~&~0~\\[-2pt] ~0~&~0~&~0~&~0~&~6~&~1~&~0~\\[-2pt] ~0~&~0~&~0~&~0~&~0~&~6~&~1~\\[-2pt] ~0~&~0~&~0~&~0~&~0~&~0~&~6~ \end{array}\!\right]\!, B(\hbox{'1314521'})\!\!=\!\left[\!\begin{array}{ccccccc} ~5~&~0~&~0~&~0~&~0~&~0~&~0~\\[-2pt] ~4~&~1~&~0~&~0~&~0~&~0~&~0~\\[-2pt] ~5~&~0~&~0~&~0~&~0~&~0~&~0~\\[-2pt] ~3~&~1~&~1~&~0~&~0~&~0~&~0~\\[-2pt] ~4~&~1~&~0~&~0~&~0~&~0~&~0~\\[-2pt] ~4~&~1~&~0~&~0~&~0~&~0~&~0~\\[-2pt] ~5~&~0~&~0~&~0~&~0~&~0~&~0~ \end{array}\!\right]\!, b\!\!=\!\left[\!\begin{array}{c} 6\\[-2pt] 6\\[-2pt] 6\\[-2pt] 6\\[-2pt] 6\\[-2pt] 6\\[-2pt] 6 \end{array}\!\right],\!\label{19}\\[12pt] C&=A-B(\hbox{'1314521'})=\!\!\left[\!\begin{array}{ccccccc} ~1~&-1&~0~&~0~&~0~&~0~&~0~\\[-2pt] -4&5&-1&~0~&~0~&~0~&~0~\\[-2pt] -5&~0~&~6~&-1&~0~&~0~&~0~\\[-2pt] -3&-1&-1&~6~&-1&~0~&~0~\\[-2pt] -4&-1&0&0&~6~&-1&~0~\\[-2pt] -4&-1&0&0&0&~6~&-1\\[-2pt] -5&~0~&~0~&~0~&~0~&~0~&~6~ \end{array}\!\right]\!,\nonumber\\[-2pt] P\!=\!C^{-1}b &\!=\!\!\left[\!\begin{array}{c} 279942\\[-2pt] 279936\\[-2pt] 279906\\[-2pt] 279720\\[-2pt] 278646\\[-2pt] 272166\\[-2pt] 233286 \end{array}\!\right]\, \Rightarrow \, f(0,P)\!=\!279942. \label{20} \end{align} 因此我們得到結果為丟擲一枚公正的骰子, 預期 279942 次才會出現特定的式樣 $(\hbox{'1314521'})$, 或者說期望值 $E(\hbox{'1314521'})=279942$, 這表示需要花很長的時間。 計算的程式如圖 8 所示。

最後感謝臉書社團「高中數學討論區」的組員(沈愈騰沈)的發文, 他在群組裡提出這樣的問題, 引發作者做出這一篇的研究及相關結果。 參考文獻本文作者林福林任教南台科技大學電子工程學系, 林子喬為聯發科技技術副理 |
2023年12月 47卷4期
廣義的幾何分佈之期望值探討及一些結果

