| 發刊日期 |
2023年12月
|
|---|---|
| 標題 | 不同構毛毛蟲圖的數量與組合性質 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
壹、前言一個連通圖若沒有包含任何的圈, 則稱為『樹狀圖 (tree)』。 若樹狀圖中頂點 $v$ 僅與一條邊相連, 則稱此點 $v$ 為樹狀圖的一個『葉子點 (leaf)』。 一個樹狀圖中, 若移去所有的葉子點後, 剩下的圖為一個路徑圖, 則特別將此樹狀圖稱為『毛毛蟲圖 (caterpillar)』。 毛毛蟲圖中可取最長的一段路徑稱之為『主幹』。 在 1973 年『The number of caterpillars』一文中(參考資料 當毛毛蟲圖的頂點數量為$n$, 葉子點數量為$k$時, 將所有不同構毛毛蟲圖所形成的集合記為『$\pmb{F(n,k)}$』, 元素數量記為『$\pmb{f(n,k)}$』, 以下將$f(n,k)$的值排成類巴斯卡三角形以方便觀察。

透過將 $f(n,k)$ 排列成類巴斯卡三角形後, 可觀察到的幾個特殊現象, 四點性質條列如下: (1) 每一列的最左邊與最右邊的值皆恆為 1。 意即對任意 $n\ge 3$, $f(n,2)=f(n,n-1)=1$; (2) 每一列的數值皆為左右對稱。 意即 $n\ge 3$, $2\le k\le n-1$, $f(n,k)=f(n,n-k+1)$ 恆成立; (3) 考慮 $n\ge 5$, 當 $nk$ 為偶數時, $f(n,k)$ 的值皆等於上方相鄰兩項的總和。 意即 $f(n,k)=f(n-1,k-1)+f(n-1,k)$, 在上方圖形以藍色標示的數字皆屬於此類; (4) 考慮 $n\ge 5$, 當 $nk$ 為奇數時, $f(n,k)$ 的值皆小於上方相鄰兩項的總和。 意即 $f(n,k) \lt f(n-1,k-1)+f(n-1,k)$, 在上方圖形以紅色標示的數字皆屬於此類。 針對性質 1 的觀察, 當 $k=2$ 時, 不難得知 $n$ 個頂點皆是主幹上的點, 即為筆直的路徑圖 (path), 故 $f(n,2)=1$, 如下圖 $f(6,2)$ 及 $f(7,2)$ 為例;當 $k=n-1$ 時, 可確定主幹的頂點數量必為 3, 即為星狀圖 (star), 故 $f(n,n-1)=1$, 如下圖 $f(6,5)$ 及 $f(7,6)$ 為例。 依此類推, 我們可以得知對於 $n\ge 3$ 的毛毛蟲圖, $f(n,2)=f(n,n-1)=1$ 恆成立。
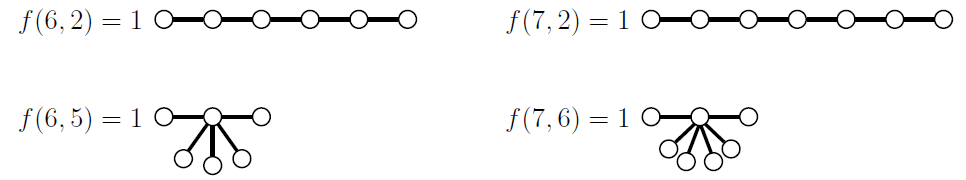
而其中最特別的是性質 4, 為了深入分析, 我們令 $f(n,k)$ 上方相鄰兩項之和與 $f(n,k)$ 的差為 $\Delta f(n,k)$, 將 $\Delta f(n,k)$ 的值排成另一個陣列, 以紫色數字表示, 如下圖, 可以發現這個陣列中的每項數字都恰好與巴斯卡三角形相同, 因此我們猜測當 $n$ 與 $k$ 兩者皆為奇數時, $f(n,k)$ 為上方相鄰兩項的總和減去特定的組合數。 以下本文將依序證明為何後續三個性質皆會成立。

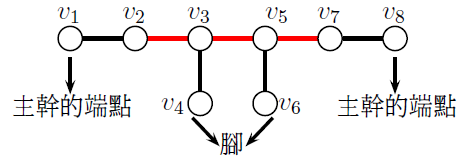
貳、基本知識在一個毛毛蟲圖中, 若頂點位於主幹上且不為主幹的兩端點, 我們將其稱為『內部點』; 內部點之間所連的邊稱作『內部邊』; 由於主幹上的兩端點必為葉子點, 特別將非主幹上的葉子點稱為毛毛蟲圖的『腳』。如下圖所示, $v_1,v_8$ 為主幹的端點, $v_2,v_3,v_5,v_7$ 為內部點, 以紅色標示的邊皆為內部邊, 意即 $\{v_2v_3,v_3v_5,v_5v_7\}$ 為內部邊的集合, $\{v_4,v_6\}$ 為腳形成的集合。
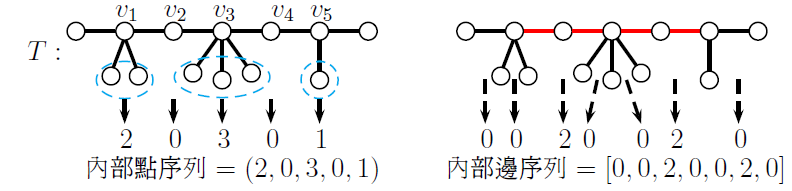
將各個內部點連接的腳數量依據由左至右的順序紀錄, 此特殊序列稱作『內部點序列』, 並將此序列的左右兩側用小括號表示, 不難得知, 內部點序列中各項總和即為腳的總量。此外, 我們針對主幹上每一個被腳分隔出來的區段, 計算在此區段內的內部邊總數, 將各個數字由左至右紀錄形成一個序列, 將其稱作『內部邊序列』, 並將此序列的左右兩側用中括號表示, 可知內部邊序列中各項總和即為內部邊的總量。 如下圖 $T$ 所示, 紅色標示的邊為內部邊, 可看出圖 $T$ 的內部點序列為 $(2,0,3,0,1)$, 內部邊序列為 $[0,0,2,0,0,2,0]$。 事實上, 這兩個序列都可以唯一決定毛毛蟲圖的結構。
參、 ${F(n,k)}$ 與 ${F(n,n-k+1)}$ 的對偶關係對於上述性質 2 的觀察, 每一列的數值皆呈現左右對稱, 事實上兩集合內的圖形結構有著對應的關係。 我們發現將 ${F(n,k)}$ 中每個圖形的內部邊與腳的角色互換後即可轉換成\\ ${F(n,n-k+1)}$ 中的所有圖形。 若 $G\in{F(n,k)}$, 將 $G$ 的內部邊序列 $[a_1,a_2,\ldots,a_{k-1}]$ 轉換成內部點序列 $(a_1,a_2,\ldots,a_{k-1})$, 令此內部點序列所唯一決定的毛毛蟲圖為 $G'$, 則稱 $G'$ 為 $G$ 的對偶圖, 其中 $G'\in F(n,n-k+1)$, 簡單來說, 對偶圖的概念就是將圖 $G$ 中主幹上每個區段內的內部邊數量, 轉換成另一個圖形 $G'$ 中內部點所連接的腳數量。 由此對應過程中不難得知, $G$ 亦為 $G'$ 的對偶圖。 轉換過程如下圖所示, 即可建立 $F(n,k)$ 與 ${F(n,n-k+1)}$ 圖形之間的一一對應關係, 進而推論出 $f(n,k)={f(n,n-k+1)}$。

肆、不同構毛毛蟲圖的數量刻劃考慮 $n$ 個點, $k$ 個葉子點的毛毛蟲圖, $F(n,k)$ 為不同構圖形所形成的集合, 隨著 $n$ 的數值增加, $F(n,k)$ 的圖形數量也隨之增加, 利用重複組合的概念, 可以具體地使用組合數刻劃 $f(n,k)$ 的值, 並從中思考圖形結構與數值之間的相關變化。 引理1 ($f(n,k)$ 的刻劃): 考慮 $n\ge 5$ 個點, $k$ 個葉子點的毛毛蟲圖, 則 $f(n,k)=\dfrac 12\big(C_{k-2}^{n-3}$ $+s(n,k)\big)$, 其中 $s(n,k)$ 為 $n$ 個點, $k$ 個葉子點具有對稱結構的毛毛蟲圖總數量。 證明: 令 $T\in F(n,k)$, 其中 $n\ge 5$, 可知內部點數量為 $n-k$ 個, 腳數量為 $k-2$ 個, 假設其內部點序列為 $(a_1,a_2,\ldots,a_{n-k})$, 已知毛毛蟲圖的內部點序列各項加總即為腳數量, 所以 $F(n,k)$ 集合內圖形皆符合 $a_1+a_2+\cdots+a_{n-k}=k-2$, 又以重複組合計算 $a_1+a_2+\cdots+a_{n-k}=k-2$ 的所有非負整數解的個數為 $H_{k-2}^{n-k}=C_{k-2}^{n-3}$, 該組合數代表所有以 $n$ 個點、 $k$ 個葉子點構成之毛毛蟲圖的內部點序列總數量。 根據圖形的對稱與否, 考慮圖 $T$ 的兩種可能結構, 若 $T$ 為不對稱圖形, $T$ 的內部點序列總共有兩種表示方法 $(a_1,a_2,\ldots,a_{n-k})$ 及 $(a_{n-k},\ldots,a_2,a_1)$, 這兩個序列皆會被計算於重複組合數中, 所以在該組合數 $C_{k-2}^{n-3}$ 中同一個不對稱圖形將被重複計算到兩次; 然而若圖 $T$ 為對稱圖形, 可知其內部點序列及其倒序後為相同序列, 所以同一個對稱圖形只會被計算到一次, 故 $C_{k-2}^{n-3}$ 的值為兩次重覆計算的不對稱圖形加上一次對稱圖形的總數量。 因此 $f(n,k)=\dfrac 12\big(C_{k-2}^{n-3}+s(n,k)\big)$。 ${\Box}$ 由上述證明可看出, 若想得知 $f(n,k)$ 的確切值, 我們必須回過頭來探討 $F(n,k)$ 中對稱圖形的總數量。 令具有 $n$ 個點、 $k$ 個葉子點的對稱毛毛蟲圖所形成的集合為『$S(n,k)$ 』, 元素數量以『$s(n,k)$』表示, 將 $n$ 與 $k$ 的奇偶性分成四大類討論, 運用重複組合的概念即可用組合數來刻劃 $s(n,k)$, 則有以下引理: 引理2 (對稱毛毛蟲圖的數量 $s(n,k)$): 考慮 $n$ 個點, $k$ 個葉子點的毛毛蟲圖, 令結構具有左右對稱的毛毛蟲圖數量為 $s(n,k)$, 則 $$s(n,k)=\left\{\begin{array}{cl} C_{\frac{k-2}{2}}^{\frac{n-4}{2}},&\hbox{當 $n$ 為偶數, $k$ 為偶數}\\[6pt] C_{\frac{k-3}{2}}^{\frac{n-4}{2}},&\hbox{當 $n$ 為偶數, $k$ 為奇數} \end{array}\right.\quad s(n,k)=\left\{\begin{array}{cl} C_{\frac{k-2}{2}}^{\frac{n-3}{2}},&\hbox{當 $n$ 為奇數, $k$ 為偶數}\\[6pt] 0,&\hbox{當 $n$ 為奇數, $k$ 為奇數} \end{array}\right.\hbox{。}$$ 證明: 對於 $n$ 個點與 $k$ 個葉子點且結構為左右對稱的毛毛蟲圖, 只要知道主幹的左半邊中, 考慮腳在內部點上的分布狀態, 即可得知整體圖形結構。 配合 $n$ 與 $k$ 的奇偶性, 透過下列的圖示, 即可得到 $s(n,k)$ 的公式。 (1) 當 $n$ 為偶數, $k$ 為偶數。 將 $\dfrac{k-2}{2}$個腳分配給左半部 $\dfrac{n-k}{2}$個內部點, 共有 $H_{\frac{k-2}{2}}^{\frac{n-k}{2}}$ 種情形。
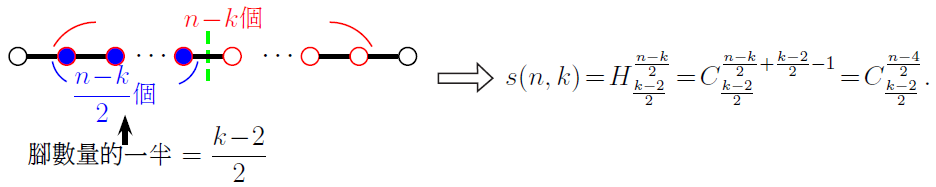
(2) 當 $n$ 為偶數, $k$ 為奇數。 先固定1個腳在中心點上, 將 $\dfrac{k\!-\!3}{2}$ 個腳分配給左半部 $\dfrac{n\!-\!k\!+\!1}{2}$個內部點, 共有 $H_{\frac{k-3}{2}}^{\frac{n - k + 1}{2}}$種情形。
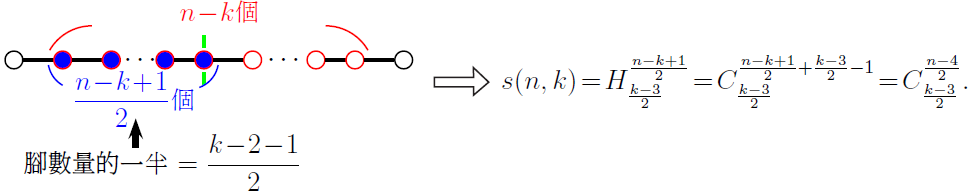
(3) 當 $n$為奇數, $k$為偶數。 將 $\dfrac{k\!-\!2}{2}$個腳分配給左半部 $\dfrac{n\!-\!k\!+\!1}{2}$個內部點, 共有$H_{\frac{k-2}{2}}^{\frac{n - k + 1}{2}}$種情形。
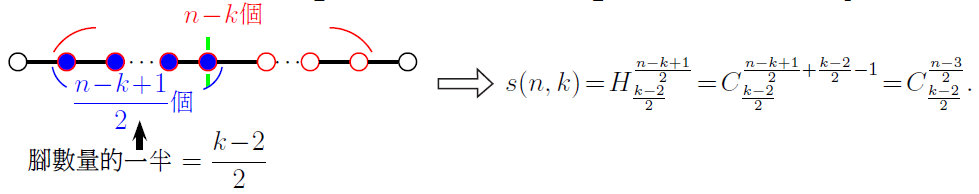
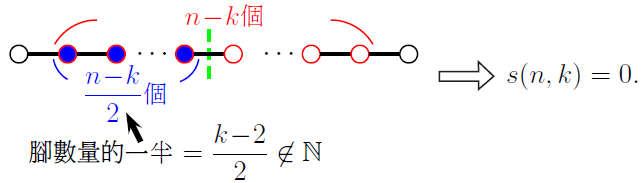
(4) 當 $n$ 為奇數, $k$ 為奇數。 因為腳的數量 $k\!-\!2$ 為奇數, 所以不存在對稱圖形。
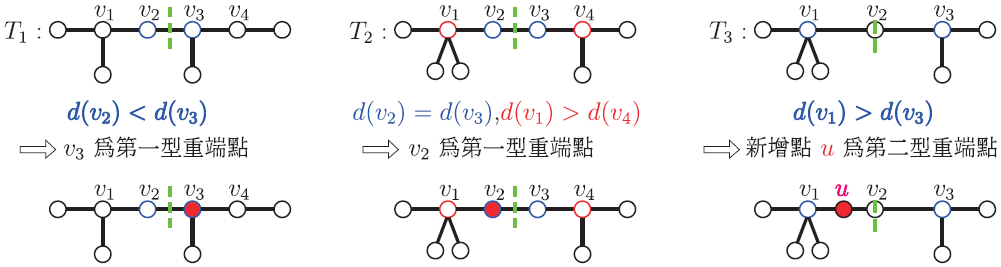
由引理 1 和引理 2 可知 $f(n,k)$ 的確切值, 而對於類巴斯卡三角形的性質 3 和 4, 我們必須將上層相鄰兩項數字加總再和 $f(n,k)$ 的值比較, 找出其中關連性。 透過巴斯卡定理即可證明出數量上的遞迴關係, 則有以下定理。 定理1 ($f(n,k)$ 的遞迴關係): 考慮 $n\ge 5$ 個點, $k$ 個葉子點的毛毛蟲圖: (1) 當 $n$ 與 $k$ 其中一個不是奇數時, 則 $f(n,k)=f(n-1,k-1)+f(n-1,k)$; (2) 當 $n$ 與 $k$ 兩者皆為奇數時, 則 $f(n,k)=f(n-1,k-1)+f(n-1,k)-s(n-1,k-1)$。 證明: (1) 考慮 $n$ 與 $k$ 其中一個不是奇數時, 由引理 1 可知 $f(n\!-\!1,k\!-\!1)\!=\!\dfrac 12\big(C_{k-3}^{n-4}+s(n\!-\!1,k\!-\!1)\big)$ 且 $f(n\!-\!1,k)=\dfrac 12\big(C_{k-2}^{n-4}+s(n-1,k)\big)$。 利用引理 2 可知 $s(n-1,k-1)+s(n-1,k)=s(n,k)$, 根據巴斯卡定理可知 $C_{k-3}^{n-4}+C_{k-2}^{n-4}=C_{k-2}^{n-3}$。 考慮 $f(n-1,k-1)$ 與 $f(n-1,k)$ 的總和, 可推得 $f(n\!-\!1,k\!-\!1)\!+\!f(n\!-\!1,k)\!=\!\dfrac 12\big(C_{k-3}^{n-4}\!+\!s(n-1,k-1)\big)\!+\! \dfrac 12\big(C_{k-2}^{n-4}\!+\!s(n\!-\!1,k)\big)\!=\!\dfrac 12\big(C_{k-2}^{n-3}\!+\!s(n,k)\big)\!=\!f(n,k)$。 可知當 $n$ 與 $k$ 其中一個不是奇數時, $f(n,k)=f(n-1,k-1)+f(n-1,k)$ 恆成立。 (2) 考慮 $n$ 與 $k$ 兩者皆為奇數時, 由引理 1 與引理 2 可知 $f(n,k)=\dfrac 12C_{k-2}^{n-3}$, $f(n\!-\!1,k\!-\!1)$ $=\dfrac 12\big(C_{k-3}^{n-4}+s(n-1,k-1)\big)$ 與 $f(n-1,k)=\dfrac 12\big(C_{k-2}^{n-4}+s(n-1,k)\big)$。 根據巴斯卡定理可知 $f(n-1,k-1)+f(n-1,k)=\dfrac 12\big(C_{k-2}^{n-3}+s(n-1,k-1)+s(n-1,k)\big)$。 利用引理 2 可知 $s(n-1,k-1)=s(n-1,k)=C_{\frac{k-3}{2}}^{\frac{n-5}{2}}$, 由此可得當 $n$ 與 $k$ 兩者皆為奇數時, 可推得 $f(n,k)=f(n-1,k-1)+f(n-1,k)-s(n-1,k-1)$。 由此定理可得知, 當 $nk$ 為偶數時, $f(n,k)$ 確實為上方相鄰兩項的總和; 當 $nk$ 為奇數時, 可以確定 $f(n,k)$ 與上方相鄰兩項總和的差, 其數量為左上方集合中的對稱圖形總數, 亦印證了我們當初猜測數值的差為一個組合數, 而該組合數即為 $s(n\!-\!1,k\!-\!1)=C_{\frac{k-3}{2}}^{\frac{n-5}{2}}$。 根據引理 1 及引理 2, 亦可得知類巴斯卡三角形的同一列數值加總後, 即為 $n$ 個頂點的毛毛蟲圖總數量。 推論1 ($n$ 個頂點的毛毛蟲圖總數量): $n$ 個點的不同構毛毛蟲圖數量為 $2^{n-4}+2^{\lfloor \frac{n-4}{2}\rfloor}$。 證明: 根據引理 1 可知 $n$ 個點、 $k$ 個葉子點的不同構毛毛蟲圖總數為 $f(n,k)=\dfrac 12\big(C_{k-2}^{n-3}+s(n,k)\big)$, 而由引理 2 可知 $$s(n,k)=\left\{\begin{array}{cl} C_{\frac{k-2}{2}}^{\frac{n-4}{2}},&\hbox{當 $n$ 為偶數, $k$ 為偶數}\\[6pt] C_{\frac{k-3}{2}}^{\frac{n-4}{2}},&\hbox{當 $n$ 為偶數, $k$ 為奇數} \end{array}\right.\quad s(n,k)=\left\{\begin{array}{cl} C_{\frac{k-2}{2}}^{\frac{n-3}{2}},&\hbox{當 $n$ 為奇數, $k$ 為偶數}\\[6pt] 0,&\hbox{當 $n$ 為奇數, $k$ 為奇數} \end{array}\right.\hbox{。}$$ 以下計算 $\{f(n,k):k=2,3,\ldots,n-1\}$ 的總和。 考慮 \begin{align*} \sum_{k=2}^{n-1} \!f(n,k)=\,&f(n,2)+f(n,3)+f(n,4)+\cdots+f(n,n-1)\\ =\,&\frac 12\big(C_0^{n-3}+s(n,2)\big)+\frac 12\big(C_1^{n-3}+s(n,3)\big) +\cdots+\frac 12\big(C_{n-3}^{n-3}+s(n,n-1)\big)\\ =\,&\frac 12\big(C_0^{n-3}+C_1^{n-3}%+C_2^{n-3} +\cdots+C_{n-3}^{n-3})+\frac 12\big(s(n,2)+s(n,3)+\cdots+s(n,n-1)\big)\\ =\,&\frac 12\sum_{i=0}^{n-3}C_i^{n-3}+\frac 12\big(s(n,2)+s(n,3)%+s(n,4) +\cdots+s(n,n-1)\big)\\ =\,&\frac 12\times 2^{n-3}+\frac 12\big(s(n,2)+s(n,3)%+s(n,4) +\cdots+s(n,n-1)\big)\ \hbox{(根據二項式定理)}\\ =\,&2^{n-4}+\frac 12\big(s(n,2)+s(n,3)%+s(n,4) +\cdots+s(n,n-1)\big). \end{align*} 接下來依照 $n$ 的奇偶性整合 $\big(s(n,2)+s(n,3)+s(n,4)+\cdots+s(n,n-1)\big)$ 的值。 當 $n$ 是偶數時, \begin{align*} \sum_{k=2}^{n-1} \!f(n,k)=\,&2^{n-4}+\frac 12\big(s(n,2)+s(n,3)%+s(n,4) +\cdots+s(n,n-1)\big)\\ =\,&2^{n-4}+\frac 12\Big(C_0^{\frac{n-4}{2}}+C_0^{\frac{n-4}{2}}+C_1^{\frac{n-4}{2}}+C_1^{\frac{n-4}{2}} +\cdots +C_{\frac{n-4}{2}}^{\frac{n-4}{2}}+C_{\frac{n-4}{2}}^{\frac{n-4}{2}}\Big)\\ =\,&2^{n-4}+\frac 12\Bigg(2\sum_{i=0}^{\frac{n-4}{2}}C_i^{\frac{n-4}{2}}\Bigg) =2^{n-4}+\sum_{i=0}^{\frac{n-4}{2}}C_i^{\frac{n-4}{2}}=2^{n-4}+2^{\frac{n-4}{2}}. \end{align*} 當 $n$ 是奇數時, \begin{align*} \sum_{k=2}^{n-1} \!f(n,k)=\,&2^{n-4}+\frac 12\big(s(n,2)+s(n,3)%+s(n,4) +\cdots+s(n,n-1)\big)\\ =\,&2^{n-4}+\frac 12\Big(C_0^{\frac{n-3}{2}}+0+C_1^{\frac{n-3}{2}}+0+C_2^{\frac{n-3}{2}}+0 +\cdots+0 +C_{\frac{n-3}{2}}^{\frac{n-3}{2}}\Big)\\ =\,&2^{n-4}+\frac 12\sum_{i=0}^{\frac{n-3}{2}}C_i^{\frac{n-3}{2}} =2^{n-4}+\frac 12 \times 2^{\frac{n-3}{2}}=2^{n-4}+2^{\frac{n-5}{2}}. \end{align*} 由上述證明可知, 不論 $n$ 為奇數或是偶數, 我們皆可以將 $\{f(n,k):k=2,3,\ldots,n-1\}$ 的加總數值利用高斯符號將兩式概括, 即可記為 $2^{n-4}+2^{\lfloor\frac{n-4}{2}\rfloor}$, 也就是說, 由 $n$ 個點所構成的不同構毛毛蟲圖總數量為 $2^{n-4}+2^{\lfloor\frac{n-4}{2}\rfloor}$。 ${\Box}$ 伍、毛毛蟲圖的圖形結構對應關係在引理 1 中已經刻劃了 $f(n,k)$ 的計算方法, 並於定理 1 中說明 $f(n,k)$ 具有遞迴關係, 於是我們開始思索這樣的遞迴關係是否能在毛毛蟲圖的結構上找出圖形對應的模式, 能夠建立 $F(n-1,k-1)$、 $F(n-1,k)$ 與 $F(n,k)$ 不僅限於數量上的相關性, 還能更進一步描述集合中圖形結構的變化過程。 令 $d(v)$ 為圖形上的點 $v$ 所連接的邊數量, 稱為 $v$ 的度數。 為了清楚說明圖形的變化方式, 對於非對稱的毛毛蟲圖, 透過比較度數的大小關係, 我們提出了『重端點』的概念, 依照毛毛蟲圖內部點數量的奇偶性, 重端點的概念共有兩種類型, 其定義如下: 考慮毛毛蟲圖$G\!\in\! F(n,k)$, 令主幹上的內部點依序為$v_1,v_2,\ldots,v_{n-k}$, 重端點有以下兩種類型: 第一型: 當內部點數量 $n-k$ 為偶數, 令 $v_iv_{i+1}\in E(G)$ 為主幹的中心邊。 第二型: 當內部點數量 $n-k$ 為奇數, 令 $v_i\in V(G)$ 為主幹的中心點。
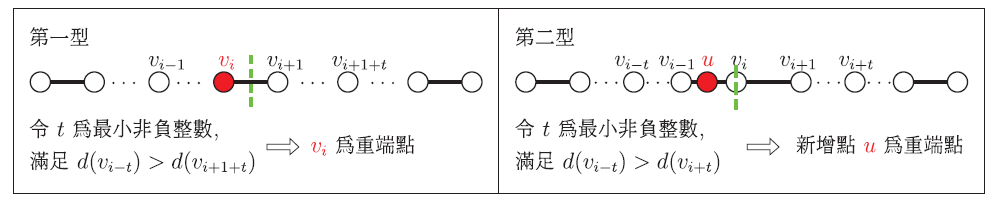
由上方示意圖可知, 第一型重端點屬於原本圖形結構中的一個頂點, 但這裡要特別提醒讀者的是, 第二型重端點並不存在於原本的圖形上, 而是另外新增的一個點, 在後續說明對應規則時, 此類型的重端點將成為一個重要的對應機制。 下方以圖形為例, 主幹的對稱軸以綠色虛線表示。 $T_1$ 主幹上的點 $v_3$ 為第一型重端點; $T_2$ 主幹上的點 $v_2$ 為第一型重端點; $T_3$ 主幹上新增的點 $u$ 為第二型重端點。
對於有 $n$ 個點、 $k$ 個葉子點的毛毛蟲圖, 該圖形結構可能是來自於『集合 $F(n-1,k-1)$ 中的圖再新增一個腳』所得到; 也可能是來自於『集合 $F(n-1,k)$ 中的圖再新增一個內部點』所形成。 接下來我們將根據 $n$ 與 $k$ 的奇偶性, 區分為三個類別說明圖形結構是如何變化。
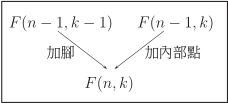
當 $n$ 與 $k$ 為相異奇偶性(1) 若圖 $G\in F(n-1,k-1)$, 則 $G$ 主幹上有中心點, 在 $G$ 的中心點新增一隻腳, 所得的圖形 $G_1\in F(n,k)$。 如下圖 $T_1$ 變換至 $T_2$; $T_3$ 變換至 $T_4$。

(2) 若圖 $G\in F(n-1,k)$, 則 $G$ 主幹上有中心邊, 在 $G$ 的中心邊新增一個頂點, 所得的圖形 $G_1\in F(n,k)$。 如下圖 $T_5$ 變換至 $T_6$; 變換至 $T_7$ 變換至 $T_8$。

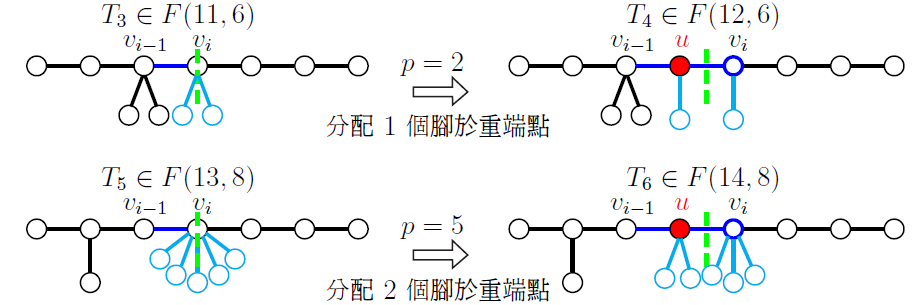
當 $n$ 與 $k$ 皆為偶數(1) 若圖 $G\in F(n-1,k-1)$, 則 $G$ 主幹上有中心邊。 因為 $S(n-1,k-1)=\varnothing$, 所以 $G$ 必為不對稱圖形。 因為 $G$ 的內部點數量等於 $n-k$ 為偶數, 可知 $G$ 有第一型的重端點 $v$, 則在重端點 $v$ 上新增一個腳, 所得的圖形 $G_1\in F(n,k)$。 如下圖 $T_1$ 變換至 $T_2$。

(2) 若圖 $G\in F(n-1,k)\backslash S(n-1,k)$ 為不對稱圖形, 則 $G$ 主幹上有中心點 $v_i$。 因為 $G$ 的內部點數量等於 $n-k-1$ 為奇數, 可知 $G$ 有第二型的重端點 $u$, 則在 $G$ 的主幹上新增第二型重端點 $u$, 可得圖形 $G_1$。 新增重端點後雖然已使圖 $G_1$ 有 $n$ 個點、 $k$ 個葉子點, 但是依據中心點所連接的腳數量, 進一步還需做出相應的調整。 若 $G$ 中心點 $v_i$ 所連接的腳數量為 $p$, 則在 $G_1$ 中將 $\Big\lfloor \dfrac p2\Big\rfloor$ 個腳由點 $v_i$ 轉移至重端點 $u$, 所得的圖形 $G_2\in F(n,k)$。 如下圖 $T_3$ 變換至 $T_4$; $T_5$ 變換至 $T_6$。
(3) 特別的, 當圖 $G\in S(n-1,k)$ 為對稱圖形時, 則 $G$ 主幹上有中心點 $v_i$, 因為圖 $G$ 為對稱圖形, 由正中央向左右兩側對應之內部點皆具有相同點度數, 所以沒有重端點, 對此需特別建立一種對應規則。 在圖 $G$ 對稱軸左側的內部邊上 $v_{i-1}v_i$ 新增一點 $u$, 可得圖形 $G_1$ , 若圖 $G$ 中心點 $v_i$ 所連接的腳有 $p$ 個, 則將 $G_1$ 中 $\Big\lfloor \dfrac p2\Big\rfloor$ 個腳由點 $v_i$ 轉移至新增的內部點 $u$, 令所得的圖形為 $G_2$。 因為圖 $G$ 為對稱圖形且腳數量為偶數個, 所以中心點連接的腳數量 $p$ 必為偶數, 不難得知, 在圖 $G_1$ 中由 $v_i$ 轉移至點 $u$ 的腳數量必恰好為 $\dfrac p2$ 個, 因此所得的圖 $G_2$ 必為對稱結構, 屬於 $S(n,k)$。 如下圖 $T_7$ 變換至 $T_8$。

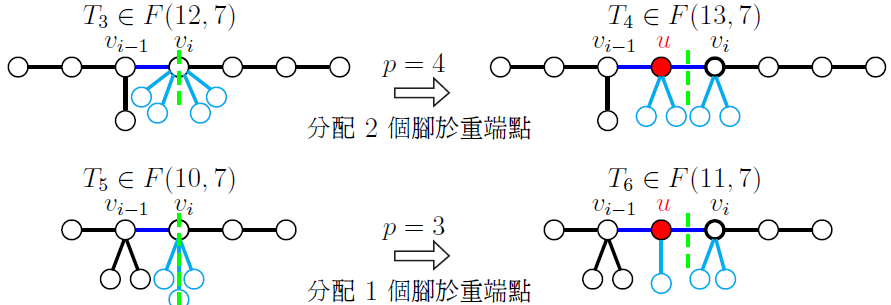
當 $n$ 與 $k$ 皆為奇數此類型情況較為複雜, 必須視毛毛蟲圖是否為對稱圖形, 再進一步區分圖形變換的方式。 (1) 若圖 $G\in F(n-1,k-1)\backslash S(n-1,k)$ 為不對稱圖形, 則 $G$ 主幹上有中心邊。 因為 $G$ 的內部點數量等於 $n-k$ 為偶數, 可知 $G$ 有第一型的重端點 $v$, 則在重端點 $v$ 上新增一隻腳, 所得的圖形 $G_1\in F(n,k)$。 如下圖 $T_1$ 至 $T_2$ 之對應。

(2) 若圖 $G\in F(n-1,k)\backslash S(n-1,k)$ 為不對稱圖形, 則 $G$ 主幹上有中心點 $v_i$。 因為 $G$ 的內部點數量等於 $n-k-1$ 為奇數, 可知 $G$ 有第二型的重端點 $u$, 則在 $G$ 的主幹上新增第二型重端點 $u$, 可得圖形 $G_1$。 進一步對於點 $v_i$ 上的腳還需做出相應的調整, 若 $G$ 中心點 $v_i$ 所連接的腳數量為 $p$, 則在 $G_1$ 中將 $\Big\lfloor \dfrac p2\Big\rfloor$ 個腳由點 $v_i$ 轉移至重端點 $u$, 所得的圖形 $G_2\in F(n,k)$。 如下圖 $T_3$ 變換至 $T_4$; $T_5$ 變換至 $T_6$。
(3) 特別的, 當圖 $G\in S(n-1,k-1)\cup S(n-1,k)$ 為對稱圖形時, 不論主幹上的正中央是內部邊或是內部點, 由正中央向左右兩側對應的內部點皆具有相同的點度數, 所以這樣的對稱圖 $G$ 沒有重端點。 當 $n$ 與 $k$ 皆為奇數時, 因為 $S(n,k)=\varnothing$, 所以這種對稱毛毛蟲圖 $G$, 將會被對應至 $F(n,k)$ 中的不對稱圖形, 我們為這類對稱圖形建立另一種對應方式。 ① 若 $G\in S(n-1,k-1)$ 的對稱圖形, 則 $G$ 主幹上有中心邊 $v_iv_{i+1}$。 在 $v_{i+1}$ 上新增一個腳, 即可得圖形 $G_1\in F(n,k)$; ② 若 $G\in S(n-1,k)$ 的對稱圖形, 則 $G$ 主幹上有中心點 $v_i$。 在對稱軸左側的內部邊 $v_{i-1}v_i$ 上新增一個內部點 $u$, 即可得圖形 $G_1$。 若 $G$ 中心點 $v_i$ 所連接的腳數量為 $p$, 則在 $G_1$ 中將 $\Big\lfloor \dfrac p2\Big\rfloor$ 個腳由點 $v_i$ 轉移至新增的內部點 $u$, 所得圖形 $G_2\in F(n,k)$。 透過上述 ① 與 ② 的對應方式, 可發現 $S(n-1,k-1)$ 與 $S(n-1,k)$ 將會變換成同構的毛毛蟲圖。 如下圖 $S(8,4)$ 與 $S(8,5)$ 變換成 $F(9,5)$ 中為同構的圖形。
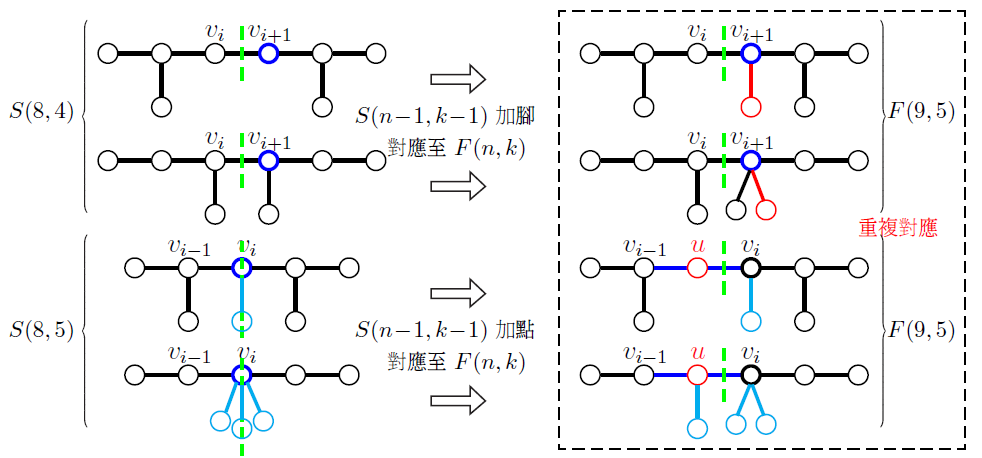
由上述說明可知, 當 $n$ 與 $k$ 其中一個不為奇數時, $ F(n\!-\!1,k\!-\!1)$ 與 $ F(n\!-\!1,k)$ 中的圖形, 經過對應規則後即可變換至 $ F(n,k)$ 中的不同構圖形, 故滿足 $f(n,k)\!=\!f(n\!-\!1,k\!-\!1)+f(n\!-\!1,k)$, 這個結果也同時呼應著定理 1 的結論 (1); 此外, 當 $n$ 與 $k$ 皆為奇數時, 除了 $F(n\!-\!1,k\!-\!1)$ 與 $ F(n\!-\!1,k)$ 中不對稱圖形將變換至 $F(n,k)$ 中的部分圖形外, 對於 $S(n\!-\!1,k\!-\!1)$ 與 $S(n\!-\!1,k)$ 中的圖形, 經過對應後將會變換至 $ F(n,k)$ 的同構圖形, 這即呼應著定理 1 的結論 (2), 在數量上滿足的關係式為 $f(n,k)\!=\!f(n\!-\!1,k\!-\!1)+f(n\!-\!1,k)\!-\!s(n\!-\!1,k\!-\!1)$。 因為 $n$ 與 $k$ 皆為奇數時, 對稱圖形在結構上的變化會有重複對應的現象, 所以在計算數值 $f(n,k)$ 時需要扣掉同構的圖形。 上述的圖形對應關係, 不僅可確認 $f(n,k)$ 在數量上的遞迴關係, 更可由圖形結構上的變化瞭解 $F(n,k)$ 的對應過程。 陸、結語本文從計算不同構的毛毛蟲圖數量開始著手, 延伸至各個集合間的遞迴關係, 進而探索出圖形結構的對應規則, 此外, 本文中所使用的證明方法如: 巴斯卡定理、重複組合、組合數的計算等, 都是高中生所擁有的背景知識, 相較於論文中使用 Polya 計數原理, 我們所使用的方式更為淺白通俗, 對於圖形結構的解析也幫助我們越來越接近事物的本質, 希望透過這個機會可以將此數學研究推廣給大眾閱讀, 增進更多年齡層對於數學領域的探索興趣。另外, 毛毛蟲圖也不僅侷限於數學範疇, 透過特殊的轉換模式可以將 $n$ 個頂點毛毛蟲圖對應至有機化學中 $n$ 個碳所組成的 $C_nH_{n+2}$ 分子結構, 由此可知, 數學知識不但可以應用在生活中, 更是研究自然科學領域的重要工具。 參考資料本文作者游雁婷投稿時為臺北市立第一女子高級中學高三學生, 楊宗穎任教於臺北市立第一女子高級中學 |
2023年12月 47卷4期
不同構毛毛蟲圖的數量與組合性質

