| 發刊日期 |
2023年12月
|
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 標題 | 初等的問題宜用初等的辦法 |
||||||||||||||||||||||||
| 作者 | |||||||||||||||||||||||||
| 關鍵字 | |||||||||||||||||||||||||
| 檔案下載 | |||||||||||||||||||||||||
| 全文 |
緣起與大綱在數學傳播 187 期的 簡單地說: 于文等於「一個公式 $+ 6$ 個例證」。 這個公式是座標平面上的「三點會共線的充分必要條件」, 但卻不是用通常的縱橫坐標, 而是用極座標表達。 那 6 個例子, 我們現在馬上重述 1 1 我們保持于文中的順序, 由 1 到 6。 但是在數碼之後, 我們另外加綴了一個天干, 這個由易到難的標籤(從甲到己)是我們逐例討論時的順序。 為下列的命題。
本文的動機于文合適的對象主要是中學老師以及較高階的中學生。 這樣子才可以談使用極座標法。 但是, 在中學數學課程中, 極座標法絕對是相當「後程的」。 事實上, 在科學中, 極座標法常常是配合了微積分法, 才變成是「非常有用」,乃至於「不得不用」的工具。 換句話說: 要處理初等幾何的題材, 極座標法無法與縱橫的笛卡爾座標法競爭。 「三點共線的充要條件」雖然也可以說「並不算太難」, 可是要用極座標來表達, 然後用 Sarrus 的定準(determinant $=$ 行列式)來驗算, 計算量與難度也比笛卡爾座標法更大更高。 我們看到: 于文的這些例子全都是(我們從來理解為)初中平面幾何的題材, 也就是只涉及直線形(尤其三角形)以及圓, 但沒有錐線。 所以我們這裡, 將把這些題目, 全部用初學者可以理解的, 綜合幾何的方式來解。 換句話說, (幾乎) 連笛卡爾座標法也用不到! 各節工作述要•§1 處理 例 1 甲, 例 6 乙。 它們的圖形是確定不移的, 而且所需要知道的幾何算術知識, 也最少 2 2 就分別只是: 「正三角形的高長是邊長的 $\frac{\sqrt{3}}{2}$ 倍」, 與 「正四角形的對角線長是邊長的 $\sqrt{2}$ 倍」。 , 因此它們是最最容易的幾何計算題。 它們題目中原有的圓, 只有一點點功能 3 3 「圓心到切點的半徑, 垂直於切線」。 , 可以刪掉。 •§2 處理 例 3 丙, 例 2 丁, 例 5 戊。 它們的圖形中含有可動的自由度, 比上一組難一些。 因為我們是用綜合幾何的方式來解, 命題之間的蘊含關係就很重要了。 我們此地就是由例 3 丙出發而推導出例 2 丁與例 5 戊。 •§3 處理例 4 己, 這是軌跡題, 應該算是最難的。 但是我們仍然用綜合幾何的方式 4 4 對於一個優秀的初中生, 這一題真正的難處是軌跡的概念。 來解, 不用到 sin, cos. 小小的結論越是簡單淺顯的題目, 越是值得我們思考: 怎麼用簡單初等的方法來解它。 1. 兩題簡單的幾何計算對於前述的例 1 甲, 其實只用到正三角形的性質而已, 圓的性質只用到一點點, 所以現在擦拭掉圖中的圓, 同時把原先的命題, 改述成如下等價的
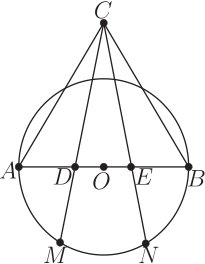
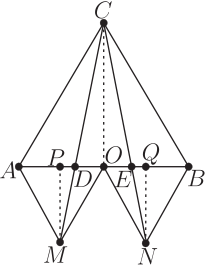
證明: 設: $\overline{OA}$ 的中點為 $P$, $\overline{OB}$ 的中點為 $Q$; 而: $\overline{CM}$ 與 $\overline{AB}$ 的交點為 $D$, $\overline{CN}$ 與 $\overline{AB}$ 的交點為 $E$。 所以 $\overline{MP}$, $\overline{NQ}$, 與 $\overline{CO}$ 分別是正三角形 $\triangle AMO,\triangle BNO, $ 與 $\triangle ACB$ 的高線。 這三個正三角形當然相似, $$ \triangle AMO \sim \triangle BNO \sim \triangle ACB; $$ 相似比是 $$ \overline{AO}:\overline{AB}:\overline{BO}= 1:2:1; $$ 所以: $$ \overline{MP}:\overline{CO}:\overline{NQ}= 1:2:1; $$ 現在考慮兩個直角三角形 $\triangle MPD $ 與 $\triangle COD$ 是否相似。 我們也就同時考慮兩個直角三角形 $\triangle NQE $ 與 $\triangle COE$ 是否相似。 因為: $$ \overline{MP} \parallel \overline{CO};\hspace{8mm} \overline{NQ} \parallel \overline{CO}; $$ 所以: 內錯角相等: $$ \angle PMD=\angle OCD; \hspace{8mm} \angle QNE=\angle OCE; $$ 於是這兩組直角三角形相似: $$ \triangle MPD \sim \triangle COD; \hspace{8mm} \triangle NQE \sim \triangle COE; $$ 兩組對應邊的相似比都是: $$ \overline{PD}:\overline{OD}=\overline{MP}:\overline{CO}=1:2; \hspace{8mm} \overline{QE}:\overline{EO}=\overline{NQ}:\overline{CO}=1:2. $$ 把 $AB$ 直線上的這些線段的長度都用基本線段長度 $\overline{AB}$ 表達出來: \begin{align*} \overline{AO}=\overline{BO}& =\frac{1}{2}\times\overline{AB}; \\ \overline{AP}=\overline{PO}=\overline{OQ}=\overline{QB}& =\frac{1}{4}\times\overline{AB}; \\ \overline{PD}=\overline{QE}& = \Big(\frac{1}{4}\times\frac{1}{3}\Big)\times\overline{AB}; \\ \overline{DO}=\overline{EO}& =\Big(\frac{1}{4}\times\frac{2}{3}\Big)\times\overline{AB}; \end{align*} 於是, 用簡單的加法就可以算出來: $$ \overline{AD}=\overline{DE}=\overline{EB}= \frac{1}{3}\times\overline{AB}. $$ 推廣: 上述命題中'正'三角形的'正', 可以改為'等腰'。
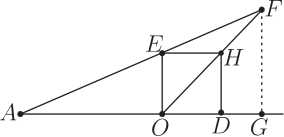
證明: 上述的證明原封不動! 對於前述的例乙 6,其實只用到正方形的性質而已, 圓的性質只用到一點點, 所以現在擦拭掉圖中的圓, 同時把原先的命題, 改述成如下等價的。
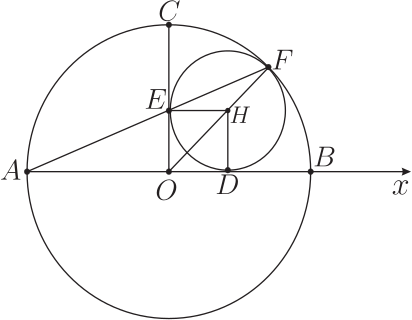
證明: 記正方形 $ODHE$ 的邊長為 $\rho = \overline{OD}=\overline{OE}=\overline{HD};$ 於是 $\overline{OH}=\sqrt{2}\times\rho$。 依照題意 $\overline{HF}=\rho$; 因此 $\overline{OA}=\overline{OF}= \overline{OH}+\overline{HF}=(\sqrt{2}+1)\times\rho$。 若從 $F$ 做垂線 $\overline{FG}$ 到直線 $\overline{AD}$, 則得: 相似直角三角形 $\triangle OGF \sim \triangle ODH$; (因 $O,H,F$ 三點共線;) 由等腰直角三角形 $\triangle OGF$ 的斜邊長 $\overline{OF}$, 算出兩腰之長 \begin{align*} \overline{OG}=\,&\overline{GF}=\frac{\overline{OF}}{\sqrt{2}}= \frac{\sqrt{2}+1}{\sqrt{2}}\times\rho;\\ {\hbox{於是 }} \overline{AG}=\,&\overline{AO}+\overline{OG}=\frac{(\sqrt{2}+1)^2}{\sqrt{2}}\times \rho. \end{align*} 注意到三點 $E,H,F$ 都在直線 $\overline{AODG}$ 的同側, 我們比較兩個直角三角形 $ \triangle AOE$ 與 $ \triangle AGF$, 是否相似? 計算對應的腰長之比例: \begin{align*} \overline{AO}:\overline{AG}&=(\sqrt{2}+1)\times\rho:\frac{(\sqrt{2}+1)^2}{\sqrt{2}}\times\rho&= \sqrt{2}:(\sqrt{2}+1);\\ \overline{OE}:\overline{GF}&=\rho: \frac{\sqrt{2}+1}{\sqrt{2}}\times\rho&=\sqrt{2}:(\sqrt{2}+1); \end{align*} 這就證明了兩個直角三角形相似: $ \hspace{5mm} \triangle AOE \sim \triangle AGF$。 於是: 角度一致: $\angle OAE=\angle GAF$. 因為 $E,F$ 都在直線 $\overline{AG}$ 的同側, 而且一邊 $\overline{AO}$ 與 $\overline{GF}$ 重合, 所以另一邊 $\overline{AE}$ 與 $\overline{AF}$ 也重合: $A,E,F,$ 三點共線。 2. 邏輯上的關聯要對付例 3 丙、 例 2 丁與例 5 戊這幾個題目, 我們將利用如下的。 基本定理: 如果兩個三角形 $\triangle A_1U_1V_1$ 與 $\triangle A_2U_2V_2$ 有一個角度相等: $\angle U_1A_1V_1=\angle U_2A_2V_2$, 則它們面積的比, 就等於夾這個角度的兩個鄰邊長度相乘積的比: $$ |\triangle A_1U_1V_1| : |\triangle A_2U_2V_2|= \overline{A_1U_1}\times \overline{A_1V_1}: \overline{A_2U_2}\times \overline{A_2V_2}. $$ 定理的特例: 如果兩個三角形 $\triangle A_1U_1V_1$ 與 $\triangle A_2U_2V_2$ 不但有一個角度相同, 而且這角度的一個鄰邊也重合為一, 則兩者面積的比就等於另外的那一鄰邊長度的比: $$ |\triangle A_1U_1V| : |\triangle A_2U_2V|= \overline{A_1U_1}: \overline{A_2U_2}. $$
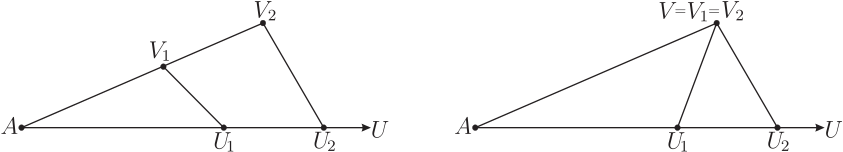
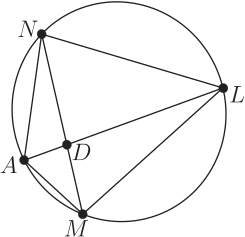
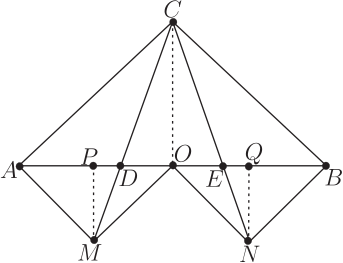
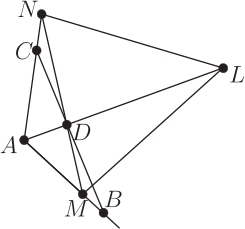
例 3 丙的證明: (請參看其處的圖) 考慮頂角(與一鄰邊!) 相同的 $\triangle AND$ 與 $\triangle ACD$, 故: $$ \frac{ \triangle AND}{\triangle ACD}= \frac{\overline{AN}}{\overline{AC}}. $$ 同樣考慮頂角(與一鄰邊!)相同的 $\triangle AMD$ 與 $\triangle ABD$, 故: $$ \frac{ \triangle AMD}{\triangle ABD}= \frac{\overline{AM}}{\overline{AB}}.$$ 這兩式相加, 注意到分母 $$ \triangle ACD= \triangle ABD;\;\;\; \hspace{8mm} \overline{AC}=\overline{AB}.$$ 因此: $$ \frac{ \triangle AND+\triangle AMD}{\triangle ACD}= \frac{\overline{AN}+\overline{AM}}{\overline{AC}}.$$ 即: $$ \frac{ \triangle ANM}{\triangle ACD}= \frac{\overline{AN}+\overline{AM}}{\overline{AC}}.$$ 或即: $$ \frac{\overline{AN}+\overline{AM}}{\triangle ANM}=\frac{\overline{AC}}{\triangle ACD} =\frac{2\times\overline{AC}}{2\times\triangle ACD}= \frac{2\times\overline{AC}}{\triangle ABC}. $$ 但是分母之比, 依照基本定理, $$ \triangle ANM: \triangle ABC=(\overline{AN}\times\overline{AM}):(\overline{AB}\times\overline{AC}). $$ 那麼: $$ \frac{\overline{AN}+\overline{AM}}{\overline{AN}\times\overline{AM}}=\frac{2\times\overline{AC}}{\overline{AB}\times\overline{AC}} =\frac{2}{\overline{AB}}. $$ 這就是待證式。 例 2 丁的證明: (請先參看其處的圖) 我們把那個外接圓刪掉, 就變成下圖。 但是先要注意有五個 $60^{\circ}$ 的角度, 於是原命題可以改為如下等價的。
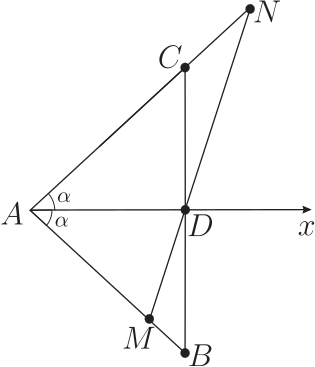
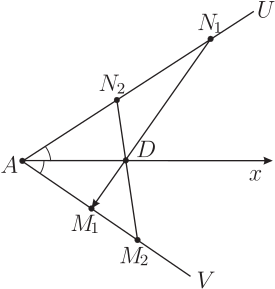
證明: 過 $D$ 做 $\overline{AD}$ 的垂線, 交 $\overrightarrow{AN}$ 於 $C$ 點, 交 $\overrightarrow{AM}$ 於 $B$ 點 (如上圖)。 注意到 $\angle DAN=\angle DAM=60^{\circ}$, 而且此地有特別角 $\angle ABD=\angle ACD=30^{\circ}$, 因而: $\overline{AB}=2\times\overline{AD}$。 整個狀況就適用命題(例) 3丙 ! 例 $5$ 戊的證明: 過 $D$ 做 $\overline{AD}$ 的垂線,交 $\overrightarrow{AU}$ 於 $C$ 點, 交 $\overrightarrow{AV}$ 於 $B$ 點。 整個狀況就適用命題(例) 3丙, 只是現在要施用兩次, 因為有兩組線段 $\overline{M_1DN_1}$ 與 $\overline{M_2DN_2}$。 我們設: \begin{align*} \overline{AN_1}\gt\overline{AB}&\gt\overline{AM_1},\;\;\;\hspace{8mm} \overline{AM_2}\gt\overline{AB}\gt\overline{AN_2}.\\ {\hbox{現在有兩組調和數列:}} \hbox{(i:)}&\ \frac{1}{\overline{AM_1}}-\frac{1}{\overline{AB}} = \frac{1}{\overline{AB}}-\frac{1}{\overline{AN_1}};\\ \hbox{(ii:)}&\ \frac{1}{\overline{AM_2}}-\frac{1}{\overline{AB}}= \frac{1}{\overline{AB}}-\frac{1}{\overline{AN_2}}.\\ {\hbox{兩式相減:}} &\frac{1}{\overline{AM_1}}-\frac{1}{\overline{AM_2}}= \frac{1}{\overline{AN_2}}-\frac{1}{\overline{AN_1}};\\ {\hbox{通分成:}} &\frac{\overline{AM_2}-\overline{AM_1}}{ \overline{AM_2}\times\overline{AM_1}} = \frac{\overline{AN_1}-\overline{AN_2}}{\overline{AN_1}\times\overline{AN_2}}.\\ {\hbox{也就是:}} &\frac{\overline{M_1M_2}}{ \overline{AM_2}\times\overline{AM_1}} = \frac{\overline{N_1N_2}}{\overline{AN_1}\times\overline{AN_2}}. \end{align*} 3. 軌跡問題
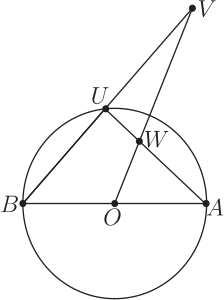
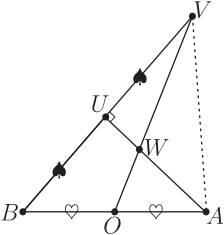
最重要的是: 因為(♡:) $\overline{BO}=\overline{OA}$, 所以 $\overline{VO}$, $\overline{AU}$ 是 $\triangle ABV$ 的兩條中線, 這就讓我們可以運用如下(週知)的重心定理。
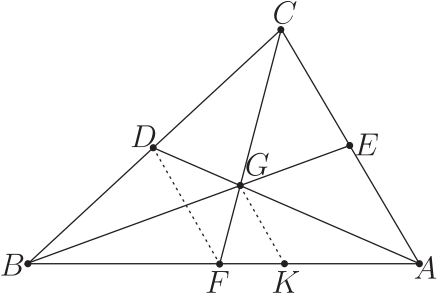
注意到: 要運用重心定理時, 必須把 圖 $4''$ 己中的那些點重新標誌, 對照到圖 $4''$ 己 中的對應點: $$V=C; U=D; O=F; W=G;$$ 而且這裡的圖 $4''$ 己, 非常一般, 沒要求等腰, 即允許 $\overline{AB} \neq \overline{AC}$。 而在 $4'$ 己圖中, 其實有 $\overline{AB}=\overline{AV}$。 回到例 $4$ 己。 根據這個重心定理, 如果: 固定線段 $AB$, 因而固定了其中點 $F=O$, 以及 三分點 $K$, 但是: 讓點 $D=U$ 在以 $\overline{AB}$ 為直徑的定圓上變動, 那麼: 點 $C=V$ 就跟著變動, $\triangle ABC$ 的重心 $G=W$ 也跟著變動! 雖然 $G=W$ 是動點, 但是: $\overline{KG}=\dfrac{1}{3}\times\overline{AB}$ 是固定的: 這裡的 $\overline{AC}$ 是例 4 中的 $\overline{AV}=\overline{AB}$。 而 $K$ 點也是固定的, 所以得到原軌跡問題的解答: 動點 $W$ 的軌跡是一圓, 圓心 $K$ 是從 $A$ 到 $B$ 的三分點,半徑是 $\dfrac{1}{3}\times\overline{AB}$。 參考文獻本文作者為台北市退休數學教師 |
2023年12月 47卷4期
初等的問題宜用初等的辦法