| 發刊日期 |
2024年3月
|
|---|---|
| 標題 | Stokes轉換與Cesaro和在Fourier級數逐項微分不合法時的應用 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
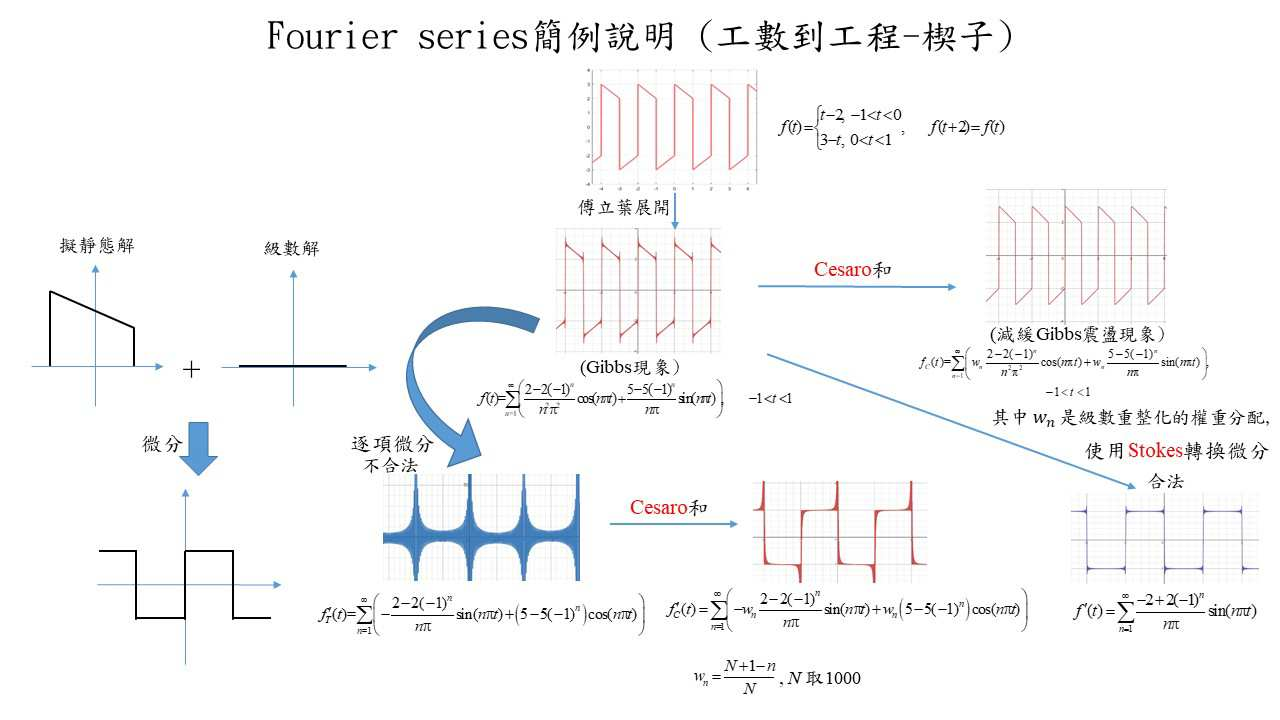
謹以此文緬懷葉超雄與汪定順兩位教授 摘要: 本文使用Stokes轉換進行Fourier級數的微分(不能逐項微分), 也引入 Cesaro 和 (Cesaro Sum) 技巧, 針對級數發散也可以求和的神奇功效進行探討。 Fourier 級數不僅在數學分析有著不可抹滅的角色, 更是工程應用不可或缺的工具, 其應用可謂無遠弗屆。 本文就 Fourier 級數呈現週期函數或訊號時, 是否可以逐項微分做探討。 當 Fourier 級數逐項微分不合法時, 本文提出兩種解決方案 : 一為 Stokes 轉換, 此方法治本也治標; 另一個方法為 Cesaro 和, 此法係將死馬當活馬救, 在進行逐項微分的動作後, 力求補救挽回。 本文將說明 Stokes 轉換與 Cesaro 和的技巧, 並舉一實例做說明以饗讀者。 這些方法已成功應用至地震工程、 振動問題、 挫曲與複合材料力學方面, 詳見相關文獻。 引言學過微積分或工程數學的人, 都知道有所謂的 Leibniz 公式 \begin{align} \frac{d}{dx}\int_{a(x)}^{b(x)}f(x,s)ds= \int_{a(x)}^{b(x)}\frac{\partial f(x,s)}{\partial x}ds +f(x,b(x))b'(x)-f(x,a(x))a'(x).\label{1} \end{align} 此公式告訴我們, 如果積分上下限是變數 $x$ 的函數, 如式 \eqref{1} 之 $a(x)$ 與 $b(x)$, 則微分與積分的順序是不可以隨意交換的。 若隨意交換, 將漏掉式 \eqref{1} 中的邊界項 $f(x,b(x))b'(x)-f(x,a(x))a'(x)$。 另外學過勢能理論 (potential theory) 的人都會面對 Hadamard 主值 \begin{align} H.P.V.\int_{-1}^1 \frac{f(s)}{(s-x)^2}ds= \frac{d}{dx}\Big(C.P.V. \int_{-1}^1 \frac{f(s)}{(s-x)}ds\Big),\label{2} \end{align} 其中 $H.P.V.$ 表示阿達瑪主值 (Hadamard principal value), 而 $C.P.V.$ 為柯西主值 (Cauchy principal value)。 直接將 Cauchy 主值微分, 利用 Leibniz 公式 (式 \eqref{1}), 可得下式 \begin{align} \frac{d}{dx}\Big\{C.P.V.\int_{-1}^1 \frac{f(s)}{(s-x)}ds\Big\}=\lim_{\varepsilon\to 0} \Big[\Big(\int_{-1}^{x-\varepsilon}+\int_{x+\varepsilon}^1\Big) \frac{f(s)}{(s-x)^2}ds-\frac{2f(x)}{\varepsilon}\Big]. \label{3} \end{align} 若沒有用到 Leibniz 公式 (式 \eqref{1}) 的觀念, 直接交換微分與積分操作元, 會得到 \begin{align} \lim_{\varepsilon\to 0} \Big[\Big(\int_{-1}^{x-\varepsilon}+\int_{x+\varepsilon}^1\Big) \frac{\partial}{\partial x} \frac{f(s)}{(s-x)}ds\Big] =\lim_{\varepsilon\to 0} \Big[\Big(\int_{-1}^{x-\varepsilon}+\int_{x+\varepsilon}^1\Big) \frac{f(s)}{(s-x)^2}ds\Big]. \label{4} \end{align} 觀察式 \eqref{3} 與式 \eqref{4}, 可知若隨意交換微分與積分操作元, 會漏掉 $\lim\limits_{\varepsilon\to 0} \dfrac{-2f(x)}{\varepsilon}$。 從積分值無窮的結果取出 Hadamard 有限值, 這就是所謂 Hadamard 有限部分 (Hadamard Finite Part) 的由來。 1822 年出版的『熱的解析理論』 於 1882 年, Fourier 終於出版了『熱的解析理論』一書。 Fourier 在最後一章也討論了 Fourier 級數的收斂性證明的綱要。 後來, Dirichlet (1805$\sim$1859) 給了 Fourier 級數收斂的充分條件, 並給出第一個嚴謹的證明。 之後, Riemann, Fejér, Cantor 等人都對這個問題做出了具體貢獻。 這中間出現一個著名的 Dirichlet 函數: \begin{align} f(t)=\left\{\begin{array}{lcl} 1,&~\quad &x\in[0,1]-{\Bbb Q}\\[5pt] 0,&&x\in[0,1]\cap{\Bbb Q} \end{array}\right., \label{5} \end{align} 這個函數按 Riemann 積分的定義是不可積的, 為了克服這個難題, 必須將 Riemann 積分推廣, 這正是法國數學家 Lebesgue 的工作, 如今被稱為 Lebesgue 積分, 是整個實變函數論的重心。 Fourier 級數的收斂性問題一直到 1966 年 Lennart Carleson 證明了一個平方可積函數 ($L^2$) 的 Fourier 級數幾乎是逐點收斂才算告一段落。 在這漫長的發展歷程中, 解決這問題所延伸出來的學問幾乎是數學分析的核心。 我們更可以大膽地說 Fourier 分析佔了數學大部分的重要地位。 (詳細請參考 另外在工程上, Fourier 級數也被廣泛地應用
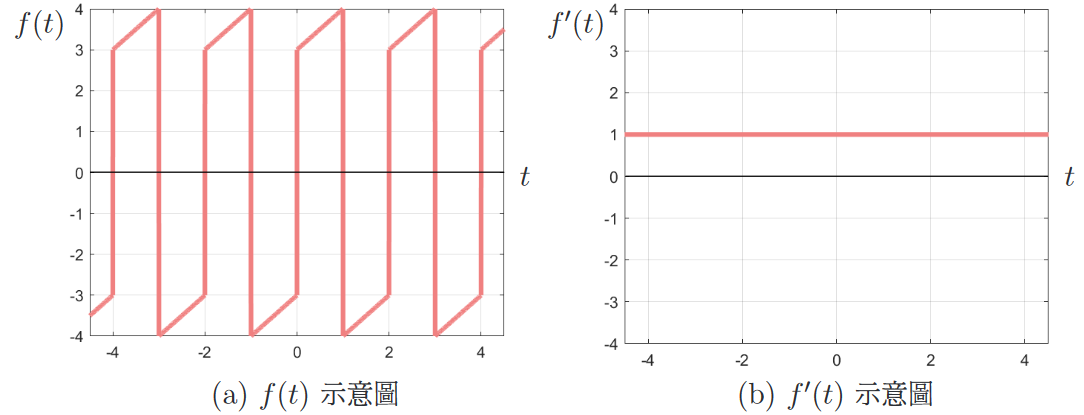
實例例一: 此節將舉一實例來說明 Fourier 級數表示函數時, 其函數微分不可透過 Fourier 級數逐項微分。給一不連續的週期函數如圖二 (a) 所示: \begin{align} f(t)=\left\{\begin{array}{lcl} t-2,&~\quad &-1\lt t\lt 0\\[5pt] 3-t,&&0\lt t\lt 1 \end{array}\right.,\qquad f(t+2)=f(t). \label{6} \end{align} 由式 \eqref{6}, 可知此函數 $f(t)$ 的導函數如圖二 (b) 為 \begin{align} f(t)=\left\{\begin{array}{lcl} 1,&~\quad &-1\lt t\lt 0\\[5pt] -1,&&0\lt t\lt 1 \end{array}\right.,\qquad f'(t+2)=f'(t). \label{7} \end{align}
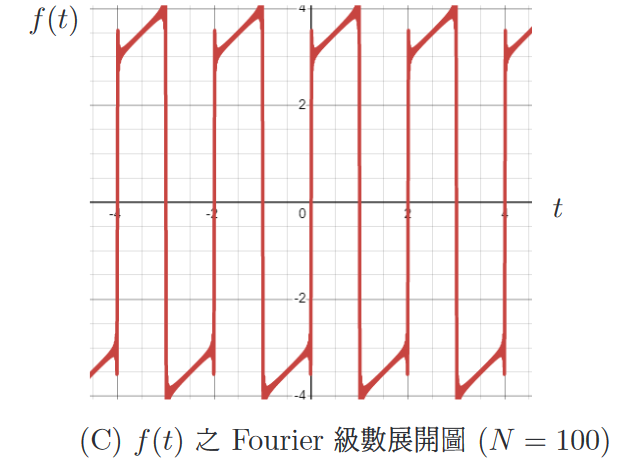
註: $\sum\limits_{n=1}^\infty\! \Big(\frac{-2(-1)^n}{(n\pi)^2}\Big)=\dfrac 16=\dfrac 12 \displaystyle\int_{-1}^1 \dfrac 12 t^2dt$. 將 $f(t)$ 做 Fourier 展開後, 可寫成: \begin{align} f(t)=\frac{a_0}2+\sum_{n=1}^\infty a_n\cos(n\pi t)+b_n\sin(n\pi t),\label{8} \end{align} 其中 Fourier 係數可求得如下: \begin{align} \frac{a_0}2=\,&\frac 12\int_{-1}^1 f(t)dt=0,\nonumber\\ a_n=\,&\int_{-1}^1 f(t)\cos(n\pi t)dt=\frac{2-2(-1)^n}{n^2\pi^2},\label{9}\\ b_n=\,&\int_{-1}^1 f(t)\sin(n\pi t)dt=\frac{5-5(-1)^n}{n\pi}.\nonumber \end{align} 故 $f(t)$ 之 Fourier 級數形式為 \begin{align} f(t)=\sum_{n=1}^\infty \Big(\frac{2-2(-1)^n}{n^2\pi^2}\cos(n\pi t)+\frac{5-5(-1)^n}{n\pi}\sin(n\pi t)\Big),\qquad -1\lt t\lt 1,\label{10} \end{align} 其函數圖形如圖二 (c) 所示:
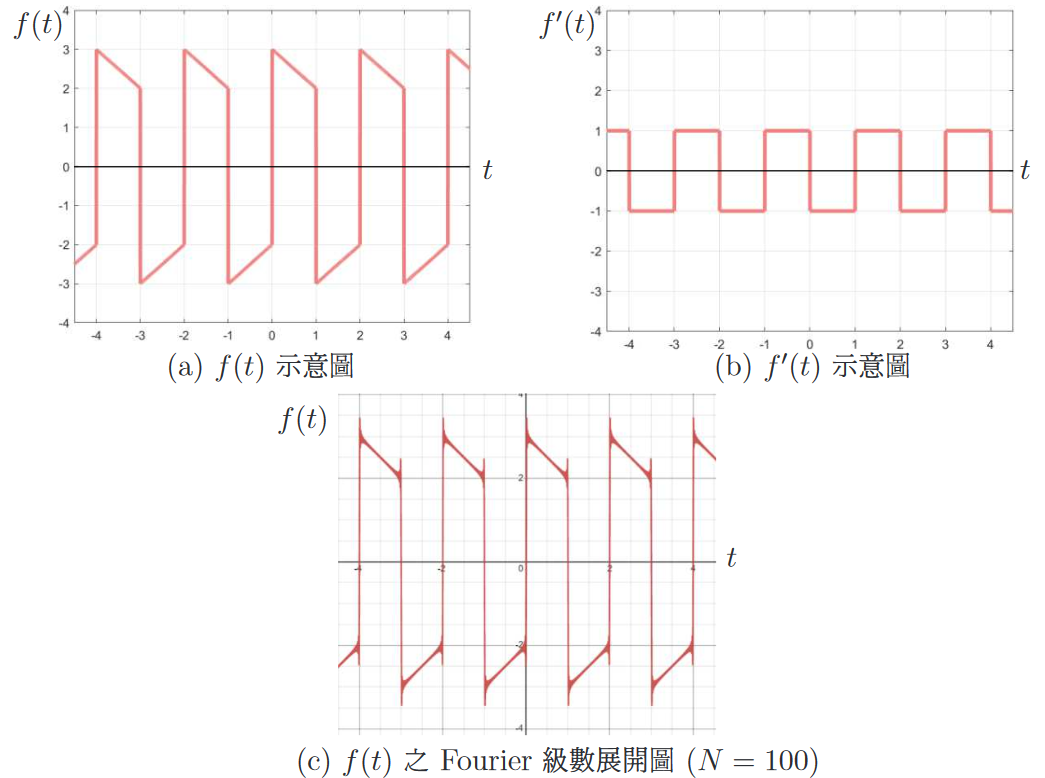
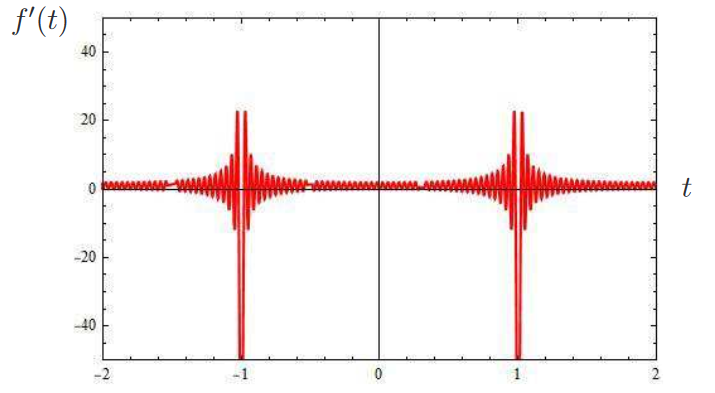
這邊從圖二(c)可以看到當函數不連續且跳躍時, 使用 Fourier 級數展開之函數圖形會有 Gibbs phenomenon。 接著我們將 $f$ 的 Fourier 級數 (式 \eqref{10}) 直接逐項微分(termwise differentiation)(即微分操作與 $\sum$ 交換), 可得 $f'_T(t)$ 的 Fourier 級數 \begin{align} f'_T(t)=\sum_{n=1}^\infty \Big(-\frac{2-2(-1)^n}{n\pi}\sin(n\pi t)+({5-5(-1)^n})\cos(n\pi t)\Big),\label{11} \end{align} 其中下標 $T$ 表示逐項微分 (termwise)。 式 \eqref{11} 中 $f'_T(t)$ 圖形如圖三所示:
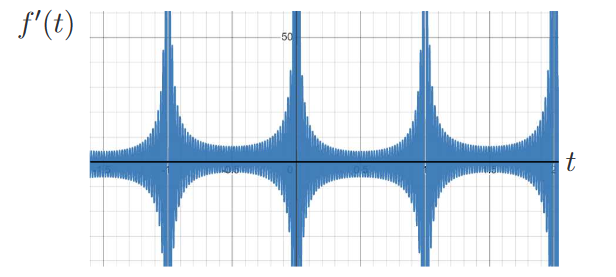
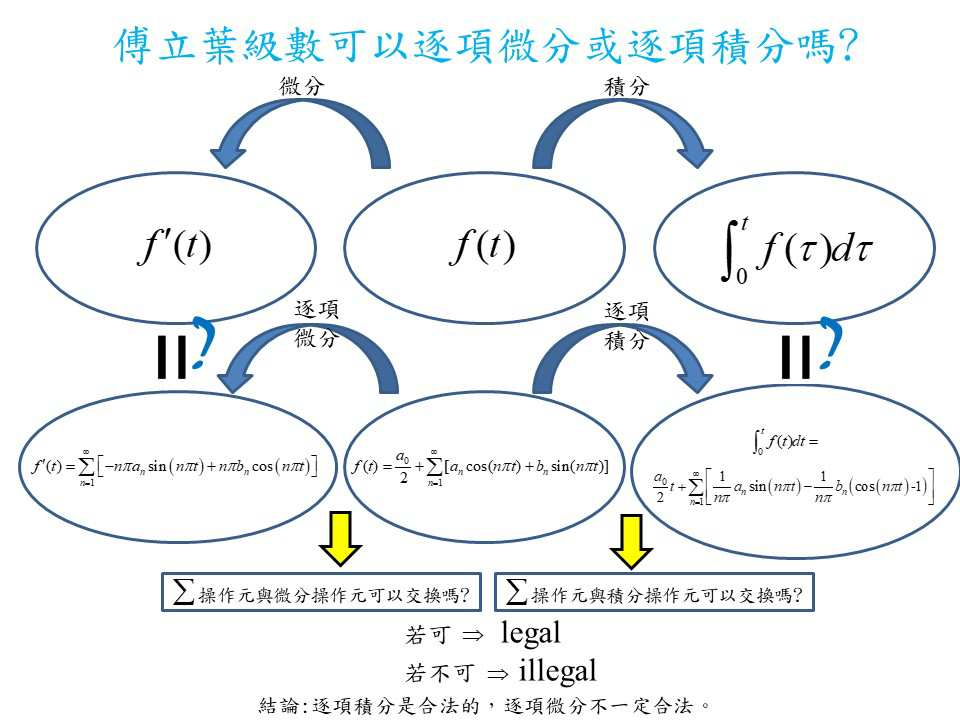
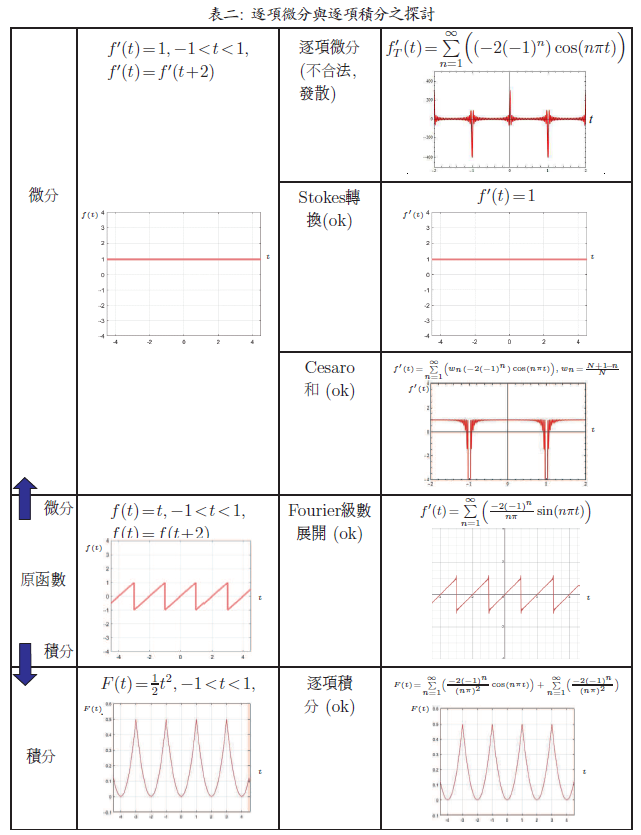
觀察圖三可知, 直接對 $f(t)$ 的 Fourier 級數逐項微分, 其微分後的函數 $f'_T(t)$ 隨著項數增加而發散。 從此可知對不連續函數的 Fourier 級數逐項微分是不合法的。 如圖四所示, 函數做 Fourier 級數展開並將其直接逐項微分得到 $f'_T(t)$ 後, 常數基底將會消失, 然而我們將 $f'(t)$ 做 Fourier 級數展開後, 是否存在常數基底, 需要做計算後才能確認。 但若直接逐項微分, 常數基底內涵一定不存在, 這與 $f'(t)$ 做 Fourier 級數展開可能會有常數基底的成份是互相違背的。 因此我們可以知道直接逐項微分是不合法的。 接下來介紹處理函數 Fourier 級數微分的兩個技巧, Stokes 轉換與 Cesaro 和。
方法一: Stokes轉換Stokes 轉換的精神是按部就班地對函數微分後將其以 Fourier 級數表示, 亦即先將函數微分後假設成 Fourier 級數求係數後再進行加總。 以下將示範先對 $f(t)$ 微分後再作 Fourier 展開的過程: 首先將微分過後的函數 $f'(t)$, 先以 Fourier 級數做展開, 可寫成下式: \begin{align} f'(t)=\frac{a'_0}{2}+\sum_{n=1}^\infty a'_n\cos(n\pi t) +b'_n\sin(n\pi t),\label{12} \end{align} 其中 $a'_0$, $a'_n$ 與 $b'_n$ 為導函數 $f'(t)$ 的Fourier係數。 接著根據 Fourier 級數之定義, 可得 $f'(t)$ 的 Fourier 係數 \begin{align} \frac{a'_0}2=\,&\frac 12\int_{-1}^1 f'(t)dt=\underline{\frac 12 f(t)\cdot 1\Big|_{0}^1+\frac 12 f(t)\cdot 1\Big|_{-1}^0}-\int_{-1}^1f(t)\cdot 0dt=0,\nonumber\\ a'_n=\,&\int_{-1}^1 f'(t)\cos(n\pi t)dt\nonumber\\ =\,&\underline{\Big(f(t)\cos(n\pi t)\Big|_{0}^1+ f(t) \cos(n\pi t)\Big|_{-1}^0\Big)}+\Big(n\pi\int_{-1}^1 f(t)\sin(n\pi t)dt \Big)=0,\label{13}\\ b'_n=\,&\int_{-1}^1 f'(t)\sin(n\pi t)dt\nonumber\\ =\,&\underline{\Big(f(t)\sin(n\pi t)\Big|_{0}^1+ f(t) \sin(n\pi t)\Big|_{-1}^0\Big)}+\Big(-n\pi\int_{-1}^1 f(t)\cos(n\pi t)dt \Big)\nonumber\\ =\,&\frac{-2+2(-1)^n}{n\pi}.\nonumber \end{align} 上述過程中, 透過分部積分公式, 將函數 $f(t)$ 的邊界資訊引入, 使其在運算過程中取得了逐項微分的漏項。 式 \eqref{13} 中畫底線的項為直接微分方法之漏項部分, 其為邊界資訊。 由於此例為不連續函數, 因此使用分部積分公式做積分時需分段做處理。 可看此例題中直接逐項微分法在 $a'_0$ 項所漏項部分為 0, 在 $a'_n$ 項所漏項為 $\big(-5+5(-1)^n\big)$, 和 $n\pi b_n$ 相加之後的 $a'_n$ 為 0, 在 $b_n$ 項所漏項部分為 $\sin(n\pi)$, $n\in N$, 其值為 0。 如無使用分部積分公式, 利用圖二(b)及式 \eqref{7} 的 $f'(t)$ 函數, 直接代入圖二(b) $f'(t)$ 求 Fourier 級數之係數則為 \begin{align} \frac{a'_0}2=\,&\frac 12\int_{-1}^1 f'(t)dt=0,\nonumber\\ a'_n=\,&\int_{-1}^1 f'(t)\cos(n\pi t)dt=0,\label{14}\\ b'_n=\,&\int_{-1}^1 f'(t)\sin(n\pi t)dt=\frac{-2+2(-1)^n}{n\pi}.\nonumber \end{align} 可以看到式 \eqref{14} 與式 \eqref{13} 相同。 但在實際工程問題中求解偏微分方程數學模型時, 均會先將解寫成 Fourier 級數表示, 此時的係數是未知的。 $f(t)$ 是假設成未知 Fourier 係數的 Fourier 展開式, 其導函數 $f'(t)$ 的表示式或圖形是不能預先知道的。 因此在實際工程應用方面, 還是需使用分部積分公式來求解函數微分之 Fourier 級數之係數。 經過式\eqref{13}的計算後, 可得$f'(t)$為 \begin{align} f'(t)=\sum_{n=1}^\infty \frac{-2+2(-1)^n}{n\pi}\sin(n\pi t).\label{15} \end{align} $f'(t)$ 的圖形如圖五所示, 可得到 $+1$ 與 $-1$ 的值。
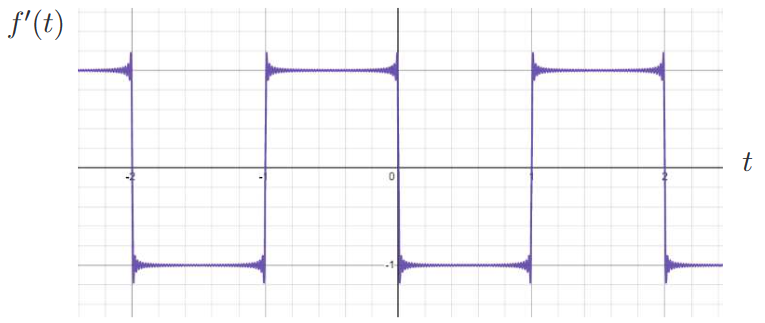
由式 \eqref{11} (逐項微分) 與式 \eqref{15} 比較得知 Stokes 轉換可得真正的函數微分。 我們知道 Fourier 級數呈現一個函數時, 他是由一系列完備基底, 包括常數基底以及低頻至高頻的基底, 加上各自對應的權重 (Fourier 常數) 疊加而成。 然而將函數之 Fourier 級數直接逐項微分, 此常數基底必然不見了。 那麼如果有一函數, 其導函數之 Fourier 級數仍有常數基底的成分, 那麼用 Fourier 級數表示原函數, 又將此 Fourier 級數直接強行逐項微分, 那這必然無常數項, 這中間顯然是矛盾的。 在上述案例一中, 微分後之 Fourier 級數無常數項基底, 與將原函數之 Fourier 級數直接逐項微分一致, 但在 $a'_n$ 項卻仍有漏項, 因此逐項微分還是不合法, 但在常數基底我們看不出差別, 因此以下將舉兩個反應常數基底較明顯的例子說明。 例二: 給一不連續的週期函數如圖六 (a) 所示: \begin{align} f(t)=t, \qquad -1\lt t\lt 1,\qquad f(t+2)=f(t).\label{16} \end{align} 由式 \eqref{16}, 可知此函數的微分如圖六 (b) 為 \begin{align} f'(t)=1, \qquad -1\lt t\lt 1,\qquad f'(t+2)=f'(t).\label{17} \end{align} 將 $f(t)$ 做 Fourier 展開後, 可寫成: \begin{align} f(t)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos(n\pi t) +b_n\sin(n\pi t),\label{18} \end{align} 其 Fourier 係數可求得如下: \begin{align} \frac{a_0}2=\,&\frac 12\int_{-1}^1 f(t)dt=0,\nonumber\\ a_n=\,&\int_{-1}^1 f(t)\cos(n\pi t)dt=0,\label{19}\\ b_n=\,&\int_{-1}^1 f(t)\sin(n\pi t)dt=\frac{-2(-1)^n}{n\pi}.\nonumber \end{align} 故 $f(t)$ 之 Fourier 級數形式為 \begin{align} f(t)=\sum_{n=1}^\infty \Big(\frac{-2(-1)^n}{n\pi}\sin(n\pi t)\Big),\label{20} \end{align} 其函數圖形如圖六(c)所示:
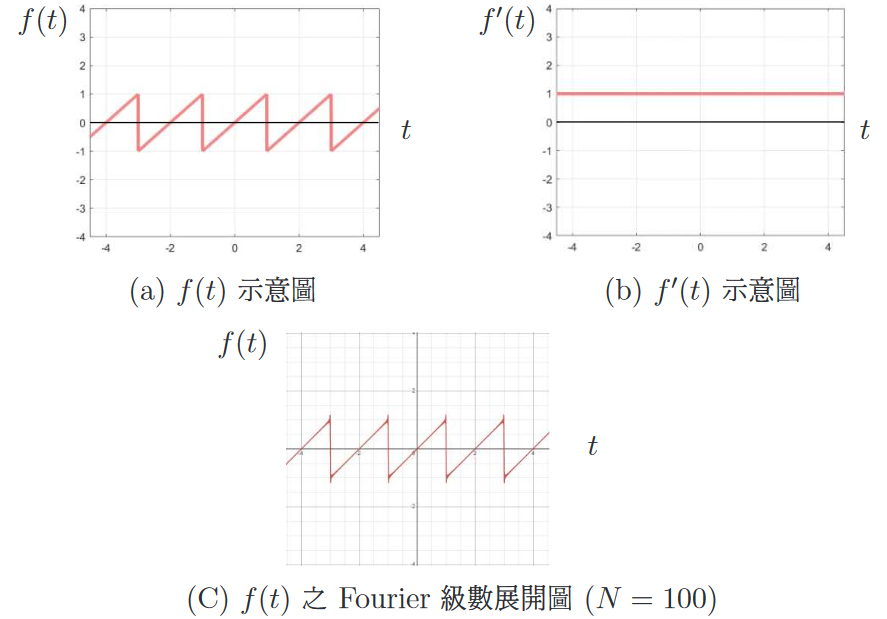
接著我們將 $f(t)$ 的 Fourier 級數直接逐項微分 (termwise differentiation) (微分操作與 $\sum$ 交換), 可得 $f'_T(t)$ 為 \begin{align} f'_T(t)=\sum_{n=1}^\infty \Big((-2(-1)^n)\cos(n\pi t)\Big).\label{21} \end{align} 式 \eqref{21} 中 $f'_T(t)$ 會發散, 如圖七所示:
將微分過後的函數 $f'(t)$, 以 Fourier 級數做展開, 可寫成下式: \begin{align} f'(t)=\frac{a'_0}2+\sum_{n=1}^\infty a'_n\cos(n\pi t)+b'_n\sin(n\pi t),\label{22} \end{align} 其中 $a'_0$, $a'_n$ 與 $b'_n$ 為 $f'(t)$ 之 Fourier 係數。 接著根據 Fourier 級數之定義, 可得 $f'(t)$ 的 Fourier 係數如下: \begin{align} \frac{a'_0}2=\,&\frac 12\int_{-1}^1 f'(t)dt=\underline{1},\nonumber\\ a'_n=\,&\int_{-1}^1 f'(t)\cos(n\pi t)dt=0,\label{23}\\ b'_n=\,&\int_{-1}^1 f'(t)\sin(n\pi t)dt=0.\nonumber \end{align} 如上個例題, 透過分部積分公式, 將邊界資訊(畫底線的項)引入, 使其在運算過程中取得了逐項微分的漏項。 經過式 \eqref{23} 的計算後, 可得 $f'(t)$ 為 \begin{align} f'(t)=1,\quad f'(t+2)=f'(t).\label{24} \end{align} 在這個案例中, 我們可以看到將原函數之 Fourier 級數直接逐項微分, 無常數基底, 但如果將 $f'(t)$ 做 Fourier 級數展開後, 存在常數基底 $(a'_0=1$), 故明顯看到逐項微分不合法, 因為永遠無法呈現存在的常數基底的貢獻。 這邊我們再舉一例子 : 例三: 給一不連續的週期函數如圖八(a)所示: \begin{align} f(t)=\left\{\begin{array}{lcl} t+3,&~\quad &0\lt t\lt 1\\[5pt] t-3,&&-1\lt t\lt 0 \end{array}\right., \qquad f(t+2)=f(t).\label{25} \end{align} 由式 \eqref{25}, 可知此函數的微分如圖八(b)為 \begin{align} f'(t)=\left\{\begin{array}{lcl} 1,&~\quad &0\lt t\lt 1\\[5pt] 1,&&-1\lt t\lt 0 \end{array}\right., \qquad f'(t+2)=f'(t).\label{26} \end{align} 將 $f(t)$ 做 Fourier 展開後, 可寫成: \begin{align} f(t)=\frac{a_0}2+\sum_{n=1}^\infty a_n\cos(n\pi t)+b_n\sin(n\pi t),\qquad -1\lt t\lt 1,\label{27} \end{align} 其 Fourier 係數可求得如下: \begin{align} \frac{a_0}2=\,&\frac 12\int_{-1}^1 f(t)dt=0,\nonumber\\ a_n=\,&\int_{-1}^1 f(t)\cos(n\pi t)dt=0,\label{28}\\ b_n=\,&\int_{-1}^1 f(t)\sin(n\pi t)dt=\frac{6-8(-1)^n}{n\pi}.\nonumber \end{align} 故 $f(t)$ 之 Fourier 級數形式為 \begin{align} f(t)=\sum_{n=1}^\infty\Big(\frac{6-8(-1)^n}{n\pi}\sin(n\pi t)\Big),\label{29} \end{align} 其函數圖形如圖八(c)所示:
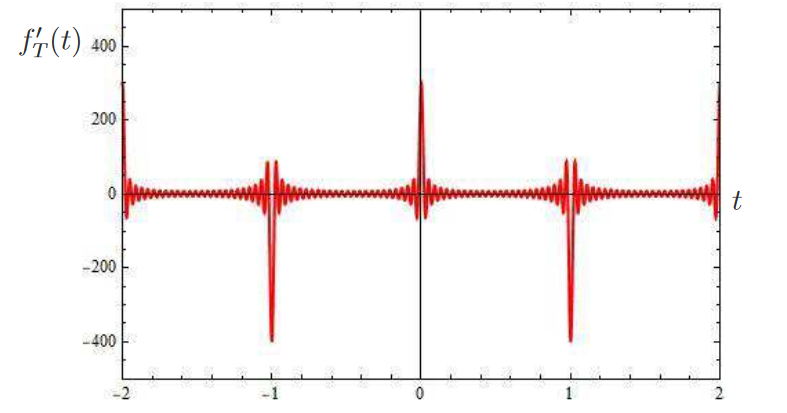
接著我們將 $f(t)$ 的 Fourier 級數直接逐項微分 (termwise differentiation) (微分操作與 $\sum$ 交換), 可得 $f'_T$ 為 \begin{align} f'_T(t)=\sum_{n=1}^\infty \Big((6-8(-1)^n)\cos(n\pi t)\Big).\label{30} \end{align} 式 \eqref{30} 中 $f'_T$ 發散如圖九所示:
將微分過後的函數 $f'(t)$, 先以 Fourier 級數做展開, 可寫成下式: \begin{align} f'(t)=\frac{a'_0}2+\sum_{n=1}^\infty a'_n\cos(n\pi t)+b'_n\sin(n\pi t),\label{31} \end{align} 其中 $a'_0$, $a'_n$ 與 $b'_n$ 為 $f'(t)$ 之 Fourier 係數。 接著根據 Fourier 級數之定義, 可得 $f'(t)$ 的 Fourier 係數 \begin{align} \frac{a'_0}2=\,&\frac 12\int_{-1}^1 f'(t)dt=\underline{1},\nonumber\\ a'_n=\,&\int_{-1}^1 f'(t)\cos(n\pi t)dt=0,\label{32}\\ b'_n=\,&\int_{-1}^1 f'(t)\sin(n\pi t)dt=0.\nonumber \end{align} 如例一, 透過分部積分公式, 將邊界資訊(畫底線的項)引入, 使其在運算過程中取得了逐項微分的漏項。 經過式 \eqref{32} 的計算後, 可得 $f'(t)$ 為 \begin{align} f'(t)=1,\quad f'(t+2)=f'(t).\label{33} \end{align} 在這個案例中, 我們可以看到將原函數之 Fourier 級數直接逐項微分, 無常數基底, 但如果將 $f'(t)$ 做 Fourier 級數展開後, 存在常數基底, 故明顯看到逐項微分不合法。 在三個案例中, 函數逐項微分是否有常數基底以及是否漏項, 都需要透過 Stokes 轉換精神找到函數微分的 Fourier 級數, 無法將原函數之 Fourier 級數直接逐項微分求得。 方法二: Cesaro和Cesaro 和是將直接逐項微分的級數和結果進行加權, 將高頻導致的發散做有效壓制, 進行模態重整化。 接著我們來看 Cesaro 和的實際應用。 我們根據例一進行示範, 將已逐項微分函數式 \eqref{11} 引入權重 $w_n$ 修正如下表示: \begin{align} f'_C(t)=\sum_{n=1}^\infty \Big(-w_n\frac{2-2(-1)^n}{n\pi}\sin(n\pi t)+w_n({5-5(-1)^n})\cos(n\pi t)\Big),\label{34} \end{align} 此時 $w_n$ 為權重函數, 如下式 \begin{align} w_n=\frac{(N+1-n)}{N}.\label{35} \end{align} 將式 \eqref{35} 代入式 \eqref{34}, $N$ 取 1000 項, 可得 $f'_C(t)$ 如下: \begin{align} f'_C(t)=\sum_{n=1}^{1000} &\Big(-\frac{(1000+1-n)}{1000}\,\frac{2-2(-1)^n}{n\pi}\sin(n\pi t)\nonumber\\ &+\frac{(1000+1-n)}{1000}({5-5(-1)^n})\cos(n\pi t)\Big),\label{36} \end{align} 其重整化結果如圖十所示:
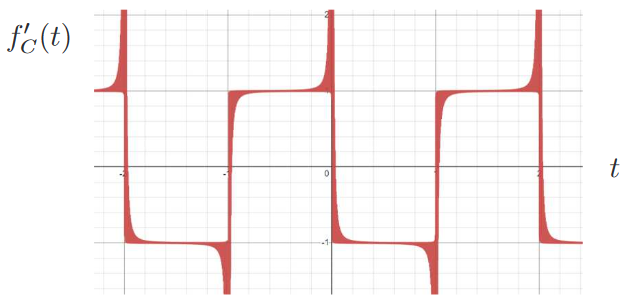
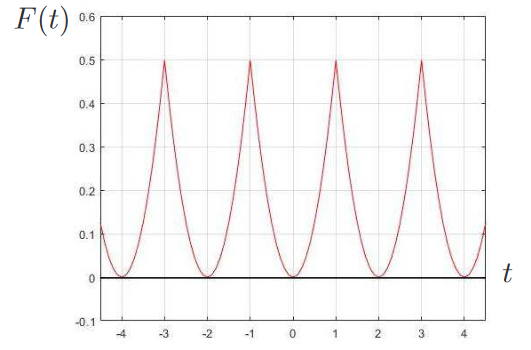
觀察圖十, 可發現式 \eqref{11} 經重整化之後, 其圖形已接近圖二(b), 可萃取出 $+1$ 與 $-1$ 的值。 透過權重分配將高頻的汙染壓制下來, 正是 Cesaro 和的精神, 可去蕪存菁, 亡羊補牢, 得到想要的正確結果 ($+1$ 與 $-1$)。 Fourier 級數逐項積分的探討上述我們已針對 Fourier 級數逐項微分合不合法作探討, 並也給出了解決方案。 那 Fourier 級數的逐項積分合法嗎? 以下我們將用式 \eqref{16} 的函數做舉例。 以例二為例, 將式 \eqref{16} 做積分可得 \begin{align} F(t)=\frac 12 t^2+C, \quad -1\lt t\lt 1,\quad F(t+2)=F(t).\label{37} \end{align} 令 $F(0)=0$, 亦即積分 $F(t)=\int_0^t f(\tau)d\tau$ (調整積分後的函數過原點) 求不定積分常數 $C$, 可得 $C=0$。 故式 \eqref{37} 可整理為, \begin{align} F(t)=\frac 12 t^2, \quad -1\lt t\lt 1,\quad F(t+2)=F(t).\label{38} \end{align} 式 \eqref{38} 中 $F(t)$ 圖形如圖十一所示。
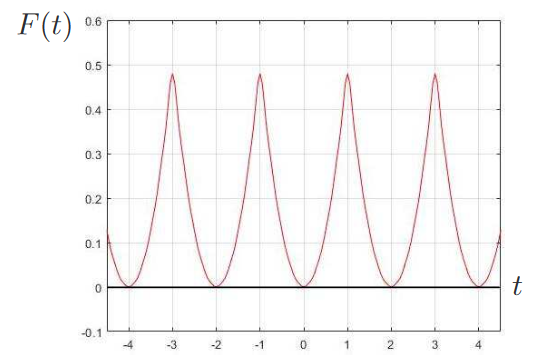
接著我們將式 \eqref{16} 之 Fourier 級數展開式 \eqref{20} 直接逐項積分可得 \begin{align} F(t)=\sum_{n=1}^\infty \Big(\frac{2(-1)^n}{(n\pi)^2}\cos(n\pi t)\Big)+C_T,\label{39} \end{align} 其中 $C_T$ 為不定積分常數。 因 $F(0)=0$, 可得 $C_T=\sum\limits_{n=1}^\infty \Big(\frac{-2(-1)^n}{(n\pi)^2}\Big)$。 故式 \eqref{39} 可整理為 \begin{align} F(t)=\sum_{n=1}^\infty \Big(\frac{2(-1)^n}{(n\pi)^2}\cos(n\pi t)\Big)+\sum\limits_{n=1}^\infty \Big(\frac{-2(-1)^n}{(n\pi)^2}\Big),\label{40} \end{align} 其中可由恆等式 $\sum\limits_{n=1}^\infty \Big(\frac{-2(-1)^n}{(n\pi)^2}\Big)=\dfrac 16$ 知此值為式 \eqref{38} 之 Fourier 級數之常數項, $\dfrac 12\displaystyle \int_{-1}^1 \dfrac 12 t^2dt$。 式 \eqref{40} 中 Fourier 級數展開圖形如圖十二所示:
經過比對可看到 Fourier 級數做逐項積分的圖形與直接對原函數積分的圖形比對一致。 因此逐項積分是合法的。 積分後的 Fourier 級數常數項是和不定積分有關, 因此和積分下限需配合。 雖然逐項微分可能會漏掉常數項, 但是逐項積分後, 原來頻率內含基底, 和逐項微分一樣也都保有, 但是常數項 $a_0$ 積分變成 $a_0t$, 再展開Fourier級數而常數項則由積分代下限求得, 所以說逐項積分是合法的!值得一提的是在逐項積分時, 不定積分中有未定下限。 因此, 逐項積分將取同一下限(此例取0)。 最後以兩個圖表綜整說明, 詳見圖十三與圖十四。 結論本文透過 Leibniz 公式, Hadamard 主值與 Stokes 轉換說明微分與積分(或 summation)運算元不可輕易交換。 交換後可能導入邊界項的缺損, 綜整詳見表三。 文中透過三實例(不連續函數)說明 Fourier 級數不能逐項微分, 並以 Stokes 轉換與 Cesaro 和予以克服。 雖然, 本文僅示範圖三發散級數的 Cesaro 和, 讀者可自行體驗圖七與圖九, 另對函數逐項積分合法也做了討論。 期望可以縮小數學與工程的距離, 對讀者有所幫助。

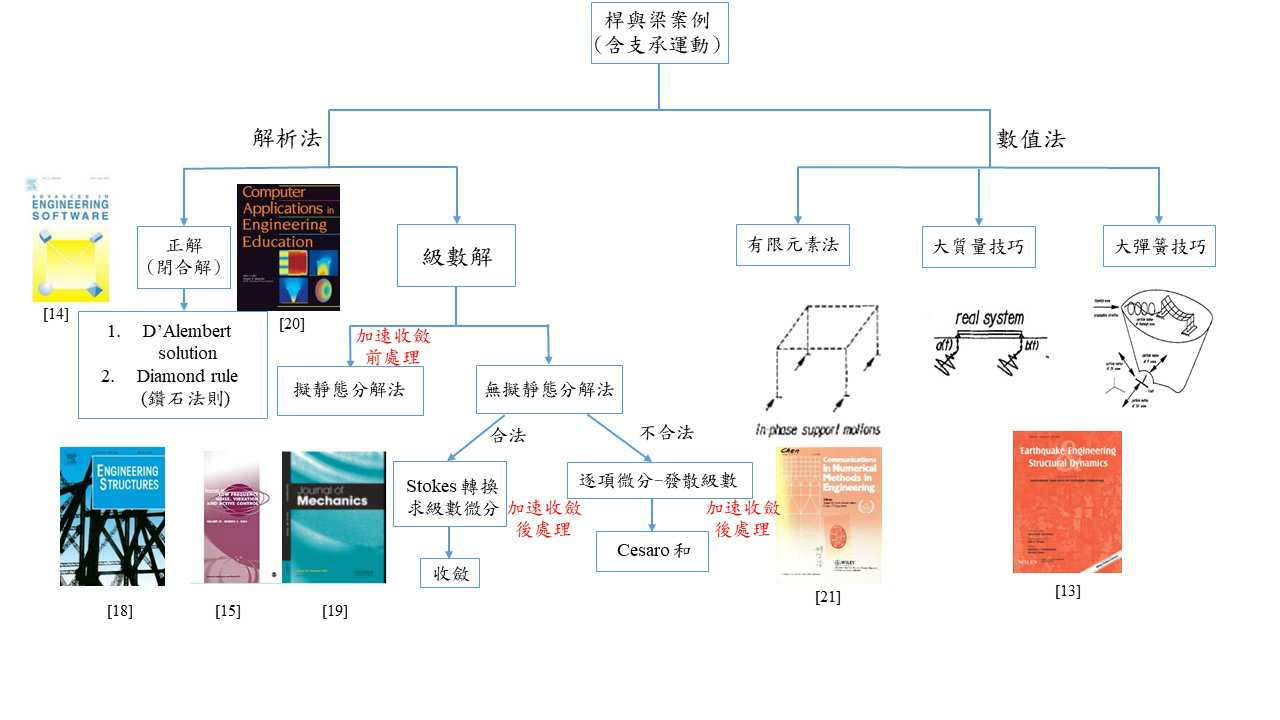
致謝: 感謝國立臺灣海洋大學河海工程學系的大二 2B 班工數修課學生 (2023.03$\sim$2023.06), 楊佳穎同學提供本文例一所使用之圖形。 更感謝汪定順老師1990年代的台大土木演講 Stokes 轉換的啟發與第一屆國家地震工程研究中心主任葉超雄老師在地震工程應用的指導。 在此以本文緬懷兩位學者, 哲人日已遠, 典型在夙昔。 也感謝教育部與國科會的對NTOU/MSV持續經費支持與鼓勵, 方有此成果分享。 後記: 本研究係地震工程所面對的支承運動問題, 對應數學模式為時間相關邊界條件的偏微分方程以模態疊加法均須面對 Fourier 級數微分的問題。 參考文獻本文作者陳正宗特聘講座教授任教國立臺灣海洋大學河海工程學系,於 2022.08$\sim$2023.07期間在台大土木系擔任客座教授。 戴暐宸就讀國立臺灣海洋大學河海工程學系碩士班。高浩真就讀國立臺灣海洋大學河海工程學系碩士班。高聖凱為國立臺灣海洋大學河海工程學系 NTOU/MSV 國科會計畫專任助理 |
2024年3月 48卷1期
Stokes轉換與Cesaro和在Fourier級數逐項微分不合法時的應用

