| 發刊日期 |
2024年3月
|
|---|---|
| 標題 | 平面凸四邊形分式型連續等式方程式 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
壹、前言三角形正弦定理的特徵是其擁有 1 組 (3 個同形分式型) 連續等式, 而其中每一個分式型都是形如 (邊長)/$(\sin A)$ 的形式。 同樣作類比出圓的內接四邊形則有 1 組 (4 個同形分式型) 連續等式, 再找到圓的內接五邊形則有 2 組 (5 個同形分式型)連續等式; 以此類推至六邊形、 $\cdots$ 等可持續作到圓的內接 $n$ 邊形。 謹此透過圓的內接四邊形、 五邊形同形分式型連續等式的啟發, 分析思考, 期望在平面凸四邊形、 五邊形中能找到另類的分式型連續等式; 仔細推演的結果得知: 平面凸四邊形至少有 16 組相異的 (4 個分式型) 連續等式, 而凸五邊形至少有 20 組相異的 (5 個分式型)連續等式。 造成有這麼多組等式全因各頂點不共圓。 主文中將詳盡敘述平面凸四邊形各組等式演繹運算過程, 同時也要加入一些應用理論藉以適時強化主題論述內涵正確推演驗證的實質功能。 貳、本文在正文的敘述推論驗證過程中, 需要應用到下列 8 個數學性質 --- 引理; 一、數學基本性質 --- 引理引理1: 三角形正弦定理: 請見下圖 1, 半徑 $R$ 圓的內接三角形 $A_1 A_2 A_3$, 令邊長線段 $\overline{A_1A_2}=V_1 $, $\overline{A_2A_3}=V_2 $, $\overline{A_3A_1}=V_3 $, 則精簡、 對稱的正弦定理公式為: $$\frac{V_1}{\sin A_3}=\frac{V_2}{\sin A_1}=\frac{V_3}{\sin A_2}=2R .$$
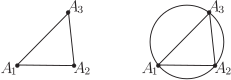
證明: 略。 引理2: 三角形餘弦定理: 請見圖 1, 則有餘弦定理公式之一為: $$V_1^2=V_2^2+V_3^2\!-\!2V_2 V_3 \cos A_3.$$ 證明: 略。 引理3: 三角函數角度的和差轉換公式 \begin{align*} \sin(\alpha \pm \beta )=\,&\sin \alpha \cos \beta \pm \cos \alpha \sin \beta ,\\ \cos(\alpha \pm \beta )=\,&\cos \alpha \cos \beta \mp \sin \alpha \sin \beta . \end{align*} 證明: 略。 引理4: 任給一個平面凸 $n$ 邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n$, 則此多邊形的頂角組合; $$A_1\!+\!A_2\!+\!A_3+\cdots+A_{n-1}+A_n=(n-2)\pi.$$ 證明: 略。 引理5: 任給一個圓的內接 $n$ 邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n $, 其中 $n$ 為偶數, $n=2k+2$, $k$ 為正整數, 則此多邊形的頂角組合; $$A_1\!+\!A_3+A_5+\cdots+A_{n-3}+A_{n-1}=A_2\!+\!A_4+A_6+\cdots+A_{n-2}+A_n=\frac 12 (n-2)\pi .$$ 證明: 略。 引理6: 平面凸 $n$ 邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n$ 的向量性質: 設定邊長向量為 $\overrightarrow{A_1A_2}=\overrightarrow{V_1}$, $\overrightarrow{A_2A_3}=\overrightarrow{V_2}$, $\overrightarrow{A_3A_4}=\overrightarrow{V_3}$, $\ldots$ , $\overrightarrow{A_{n-2}A_{n-1}}=\overrightarrow{V_{n-2}}$, $\overrightarrow{A_{n-1}A_n}=\overrightarrow{V_{n-1}}$, $\overrightarrow{A_nA_1}=\overrightarrow{V_n}$, $1\le i\le n$, $i$ 與 $n$ 皆為正整數。 則因 $n$ 邊形圖形的封閉性質, 使得 $\overrightarrow{V_1}+\overrightarrow{V_2}+\overrightarrow{V_3}+\overrightarrow{V_4}+\cdots+ \overrightarrow{V_i}+\cdots+\overrightarrow{V_{n-2}}+\overrightarrow{V_{n-1}}+\overrightarrow{V_n}=0$ 證明: 略。
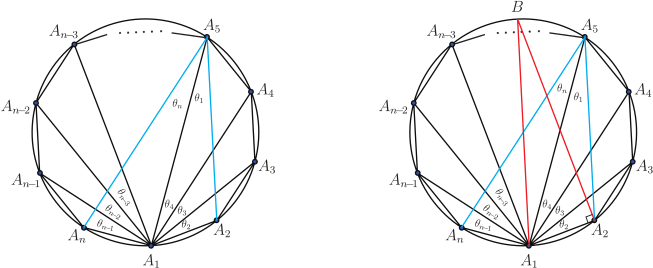
引理7: (圓的內接多邊形各圓周角與其對應弦長度組合的正弦定理) 圖2, 半徑為 $R$, 圓的內接 $n$ 邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n$, 令邊長線段 $\overline{A_1A_2}=V_1$, $\overline{A_2A_3}=V_2$, $\overline{A_3A_4}=V_3$, $\ldots$ , $\overline{A_{n-2}A_{n-1}}=V_{n-2}$, $\overline{A_{n-1}A_n}=V_{n-1}$, $\overline{A_nA_1}=V_n$, 而邊長 $V_1$ 所對應的圓周角為 $\theta_1$, $V_2$ 所對應的圓周角為 $\theta_2$, $V_3$ 所對應的圓周角為 $\theta_3$, $\ldots $, $V_{n-2}$ 所對應的圓周角為 $\theta_{n-2}$, $V_{n-1}$ 所對應的圓周角為 $\theta_{n-1}$, $V_n$ 所對應的圓周角為 $\theta_n$, 則此多邊形各邊長所對應的圓周角的正弦定理方程為下列 \eqref{1} 式: \begin{align} \frac{V_1}{\sin\theta_1}=\frac{V_2}{\sin\theta_2}=\frac{V_3}{\sin\theta_3}=\cdots=\frac{V_{n-2}}{\sin\theta_{n-2}}=\frac{V_{n-1}} {\sin\theta_{n-1}}=\frac{V_{n}}{\sin\theta_{n}}=2R.\label{1} \end{align} 證明: 應用輔助線幾何圖形作圖法來達成推理實證, 過程如下; 見圖3, 自頂點 $A_1$ 作一直線通過圓心並與圓周相交於 $B$ 點, 線段長 $\overline{A_1B}$ 恰相等於此圓的直徑長 $2R$, 再連接線段長 $\overline{A_2B}$, 得 $\triangle A_1 A_2 B$ 為直角三角形, 邊長 $V_1$ 所對應的圓周角 $\theta_1=\angle A_1 BA_2$, 所以 $V_1= 2R \sin\theta_1$。 仿此過程並引申推廣成 : 弦 $V_1, V_2, \ldots , V_n$ 對應的圓周角大小分別為 $\theta_1, \theta_2, \ldots , \theta_n $, 根據三角函數正弦定理及外接圓半徑 $R$ 的關係而有 \eqref{1} 式。 引理8: 向量內積運算: 在歐幾里得空間中 2 個向量的內積可以直觀地定義為 $$\overrightarrow{A}\cdot\overrightarrow{B}=|\overrightarrow{A} ||\overrightarrow{B} |\cos\theta$$ 其中 $|\vec x |$ 表示 $\vec x$ 的模(長度), $\theta$ 表示兩個向量之間的夾角角度。 二、 輔助定理:三角形與平面凸四邊形的 SASAS 定理在平面凸多邊形中任意相鄰三段邊長與居間的兩頂角組合結構恰好形成以邊長-頂角-邊長 -頂角-邊長 SASAS 分佈排列出 \_/ 圖樣的幾何形狀, 而此三段邊長與居間兩頂角的正弦值與餘弦值也都能分別構建成各自一組互對應的兩相關方程式, 即稱為平面凸多邊形中任意相鄰三段邊長與居間頂角的 SASAS 方程式。 [A]、 三角形 SASAS 定理: 圖 1 的任意三角形 $\triangle A_1 A_2 A_3 $, 則其 SASAS 定理的第 1 組正弦型方程式為 \begin{align} \left\{\begin{array}{c} V_1\sin(A_1\!-\!A_2)= V_2\sin A_1\!-\!V_3\sin A_2,\\ \dfrac{\sin(A_1\!-\!A_2 )}{V_3 V_2}=\dfrac{\sin A_1}{V_3 V_1}-\dfrac{\sin A_2}{V_1 V_2}. \end{array}\right. \label{2a} \end{align} 第 1 組餘弦型方程式為 \begin{align} \left\{\begin{array}{c} V_1\cos(A_1\!-\!A_2 )=V_2\cos A_1+V_3\cos A_2,\\ \dfrac{\cos(A_1\!-\!A_2 )}{V_3 V_2}=\dfrac{\cos A_1}{V_3 V_1}+\dfrac{\cos A_2}{V_1 V_2}.\end{array}\right.\label{3a} \end{align} 證明: (i) 依據引理 6 的向量性質知: $\triangle A_1 A_2 A_3$ 的 3 邊長向量 $\overrightarrow{V_1}$、 $\overrightarrow{V_2}$、 $\overrightarrow{V_3}$ 有 $\overrightarrow{V_1}+\overrightarrow{V_2} +\overrightarrow{V_3}=0$ 關係, 則對此關係式作向量內積運算, 可形成下列運算式: $$ (\overrightarrow{V_1}+\overrightarrow{V_2}+\overrightarrow{V_3})\cdot(\overrightarrow{V_1}+\overrightarrow{V_2}+\overrightarrow{V_3})=0=(\overrightarrow{V_3}+\overrightarrow{V_1}+\overrightarrow{V_2})\cdot(\overrightarrow{V_3}+\overrightarrow{V_1}+\overrightarrow{V_2}),$$ 展開後可得 $$\begin{aligned} &\hskip -20pt {V_3}^2\!+\!{V_1}^2\!+\!{V_2}^2+2V_3V_1\cos(\pi-A_1)+2V_1V_2\cos(\pi-A_2)+2V_3V_2\cos(\pi-A_3)\\ =\,&{V_3}^2\!+\!{V_1}^2\!+\!{V_2}^2\!-\!2V_3V_1\cos A_1-2V_1V_2\cos A_2-2V_3V_2\cos A_3=0. \end{aligned}{\hbox{(a1)}} $$ (ii) 接著將 (a1) 式中的各項角度作適當的轉換, 使得 $A_1=A_2\!+\!(A_1\!-\!A_2 )$, $A_2=A_1\!-\!(A_1\!-\!A_2 ) $, $A_3=\pi \!-\!(A_1\!+\!A_2 ) $, 則 (a1) 式轉換成下式: \begin{align*} {V_3}^2\!+\!{V_1}^2\!+\!{V_2}^2\!-\!2V_3V_1\cos [A_2\!+\!(A_1\!-\!A_2)]-2V_1V_2\cos [A_1\!-\!(A_1\!-\!A_2)]\qquad~\\ -2V_3V_2\cos [\pi\!-\!(A_1\!+\!A_2)]=0. \end{align*} 詳細展開演算後, 可得下式: $$\begin{aligned} &\hskip -15pt {V_3}^2\!+\!{V_1}^2\!+\!{V_2}^2\!-\!2V_3V_1\cos A_2\cos(A_1\!-\!A_2)+2V_3V_1\sin A_2\sin(A_1\!-\!A_2)\\ &-2V_1V_2\cos A_1\cos(A_1\!-\!A_2)-2V_1V_2\sin A_1\sin(A_1\!-\!A_2)+2V_3V_2\cos A_1\cos A_2\\ &-2V_3V_2\sin A_1\sin A_2=0. \end{aligned} $$ 仔細比對上式各項乘積關係後, 再將其擴充成下式: $$\begin{aligned} &\hskip -15pt [{V_3}^2 \cos^2 A_2\!+\!{V_3}^2\sin^2 A_2 ]+[{V_1}^2 \cos^2 (A_1\!-\!A_2 )+{V_1}^2\sin^2 (A_1\!-\!A_2 )]\\ &+[{V_2}^2 \cos^2 A_1+{V_2}^2\sin^2 A_1 ]-2V_3 V_1\cos A_2\cos(A_1\!-\!A_2 ) \\ &+2V_3 V_1 \sin A_2\sin(A_1\!-\!A_2 )-2V_1 V_2\cos A_1\cos(A_1\!-\!A_2 )\\ &-2V_1 V_2 \sin A_1\sin(A_1\!-\!A_2 )+2V_3 V_2\cos A_1\cos A_2-2V_3 V_2 \sin A_1 \sin A_2=0 . \end{aligned}{\hbox{(a2)}} $$ (iii) 特意整理 (a2) 式, 使得其中的 $\cos$ 項與 $\sin$ 項分開各成一組表示式, 得 $$\begin{aligned} &\hskip -15pt [{V_3}^2 \cos^2 A_2\!+\!{V_1}^2 \cos^2 (A_1\!-\!A_2 )+{V_2}^2 \cos^2 A_1-2V_3 V_1\cos A_2\cos(A_1\!-\!A_2 )\\ &-2V_1 V_2\cos A_1\cos(A_1\!-\!A_2 )+2V_3 V_2\cos A_1\cos A_2 ]+[{V_3}^2\sin^2 A_2\\ &+{V_1}^2\sin^2 (A_1\!-\!A_2 )+{V_2}^2\sin^2 A_1+2V_3 V_1 \sin A_2\sin(A_1\!-\!A_2 )\\ &-2V_1 V_2 \sin A_1\sin(A_1\!-\!A_2 )-2V_3 V_2 \sin A_1 \sin A_2 ]=0. \end{aligned} $$ 檢視整理後的結果, 發現兩者各為完全平方式, 於是得 $$[V_3 \sin A_2\!+\!V_1\sin(A_1\!-\!A_2 )\!-\!V_2 \sin A_1 ]^2+[V_3\cos A_2-V_1\cos(A_1\!-\!A_2 )\!+\!V_2\cos A_1 ]^2=0 .$$ 得: \begin{align*} &V_3 \sin A_2\!+\!V_1\sin(A_1\!-\!A_2 )\!-\!V_2 \sin A_1=0 .\\ {\hbox{及}} &V_3\cos A_2-V_1\cos(A_1\!-\!A_2 )\!+\!V_2\cos A_1=0 . \end{align*} 從而有: \begin{align} V_1\sin(A_1\!-\!A_2 )=\,&V_2 \sin A_1\!-\!V_3 \sin A_2 ,\label{2-1}\\ {\hbox{及}} V_1\cos(A_1\!-\!A_2 )=\,&V_2\cos A_1+V_3\cos A_2 .\label{3-1} \end{align} (iv) 這樣的推演即得到第1組正弦型、餘弦型方程式於下: \begin{align} \hbox{正弦型方程式為}\ &\left\{\begin{array}{c} V_1\sin(A_1\!-\!A_2)= V_2\sin A_1\!-\!V_3\sin A_2,\\ \dfrac{\sin(A_1\!-\!A_2 )}{V_3 V_2}=\dfrac{\sin A_1}{V_3 V_1}-\dfrac{\sin A_2}{V_1 V_2}. \end{array}\right.\hskip 2cm\qquad \label{2} \\ \hbox{餘弦型方程式為}\ & \left\{\begin{array}{c} V_1\cos(A_1\!-\!A_2 )=V_2\cos A_1+V_3\cos A_2,\\ \dfrac{\cos(A_1\!-\!A_2 )}{V_3 V_2}=\dfrac{\cos A_1}{V_3 V_1}+\dfrac{\cos A_2}{V_1 V_2}.\end{array}\right.\hskip 2cm\qquad \label{3} \end{align} (v) 若再將 (a1) 式中的各項角度作另一型的轉換, 使得 $$A_2=A_3\!+\!(A_2\!-\!A_3) ,\quad A_3=A_2\!-\!(A_2\!-\!A_3 ) ,\quad A_1=\pi \!-\!(A_2\!+\!A_3 ) ,$$ 則 (a1) 式轉換成下式: \begin{align*} {V_1}^2\!+\!{V_2}^2\!+\!{V_3}^2\!-\!2V_3 V_1\cos [\pi \!-\!(A_2\!+\!A_3 )]-2V_1 V_2\cos [A_3\!+\!(A_2\!-\!A_3 )]\qquad~\\ -2V_3 V_2\cos [A_2\!-\!(A_2\!-\!A_3 )]=0 . \end{align*} 同理, 再詳細展開演算後, 整理可得下式: \begin{align*} &\hskip -25pt [V_1 \sin A_3\!+\!V_2\sin(A_2\!+\!A_3 )\!-\!V_3 \sin A_2 ]^2\\ &+[V_1\cos A_3-V_2\cos(A_2\!+\!A_3 )\!+\!V_3\cos A_2 ]^2=0 .\hskip 3cm~\\ \hbox{得出}\hskip 2cm &V_1 \sin A_3\!+\!V_2\sin(A_2\!+\!A_3 )\!-\!V_3 \sin A_2=0 .\\ \hbox{及}\hskip 2.3cm &V_1\cos A_3-V_2\cos(A_2\!+\!A_3 )\!+\!V_3\cos A_2=0 . \end{align*} 從而再得到第 2 組正弦型、 餘弦型方程式於下: \begin{align} \hbox{正弦型方程式為 }\hskip .6cm& \left\{\begin{array}{c} V_2\sin(A_2\!-\!A_3 )=V_3 \sin A_2-V_1 \sin A_3 .\\[6pt] \dfrac{\sin(A_2\!-\!A_3 )}{V_1 V_3}=\dfrac{\sin A_2}{V_1 V_2}-\dfrac{\sin A_3}{V_2 V_3}.\end{array}\right.\label{2-2}\\[8pt] \hbox{餘弦型方程式為 }\hskip .6cm& \left\{\begin{array}{c} V_2\cos(A_2\!-\!A_3 )=V_3\cos A_2\!+\!V_1\cos A_3 .\\[6pt] \dfrac{\cos(A_2\!-\!A_3 )}{V_1 V_3}=\dfrac{\cos A_2}{V_1 V_2}+\dfrac{\cos A_3}{V_2 V_3}.\end{array}\right.\hskip 2cm~\label{3-2} \end{align} (vi) 同樣再作角度的第 3 型轉換, 使得 $A_3=A_1+(A_3-A_1 )$, $ A_1=A_3\!-\!(A_3-A_1 ) $, $A_2=\pi \!-\!(A_3\!+\!A_1 ) $, 則再仿效前述的所有推演運算可得到第3組正弦型、餘弦型方程式於下: \begin{align} \hbox{正弦型方程式為}\hskip .6cm& \left\{\begin{array}{c} V_3\sin(A_3-A_1 )=V_1\sin A_3\!-\!V_2\sin A_1.\\[6pt] \dfrac{\sin(A_3-A_1 )}{V_2 V_1}=\dfrac{\sin A_3}{V_2 V_3}-\dfrac{\sin A_1}{V_3 V_1}.\end{array}\right.\label{2-3}\\[8pt] \hbox{餘弦型方程式為}\hskip .6cm& \left\{\begin{array}{c} V_3\cos(A_3-A_1 )=V_1\cos A_3\!+\!V_2\cos A_1 .\\[6pt] \dfrac{\cos(A_3-A_1 )}{V_2 V_1}=\dfrac{\cos A_3}{V_2 V_3}+\dfrac{\cos A_1}{V_3 V_1}.\end{array}\right.\hskip 2cm~\label{3-3} \end{align} 綜合以上的所有推演運算, 使三角形 SASAS 定理得以證明完成。 [B]、 平面凸四邊形 SASAS 定理: 圖 5 的平面凸四邊形 $A_1 A_2 A_3 A_4$, 則由各邊長 $V_i$ 與各頂角 $A_i$ 組合成的第 1 組 SASAS 方程式為: $$V_4 \sin A_2\!+\!V_1\sin(A_1\!-\!A_2 )\!-\!V_2 \sin A_1= -V_3\sin(A_1\!+\!A_3 ). (4s)$$ 與 $$ V_4\cos A_2-V_1\cos(A_1\!-\!A_2 )\!+\!V_2\cos A_1= V_3\cos(A_1\!+\!A_3 ) . (4c)$$ 還有同類型的另外 3 組 SASAS 方程式。
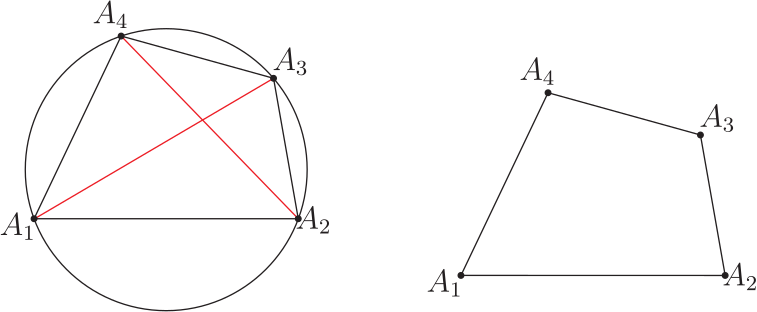
證明: (i) 依據引理 6 的向量性質知: 圖 5 的 4 段邊長向量 $\overrightarrow{V_1}$、 $\overrightarrow{V_2}$、 $\overrightarrow{V_3}$、 $\overrightarrow{V_4}$ 有 $\overrightarrow{V_1}+\overrightarrow{V_2}+\overrightarrow{V_3}+\overrightarrow{V_4}=0$ 關係, 則對此關係式作向量內積運算, 可形成下式: $$(\overrightarrow{V_1}+\overrightarrow{V_2}+\overrightarrow{V_3}+\overrightarrow{V_4})\!\cdot\! (\overrightarrow{V_1}+\overrightarrow{V_2}+\overrightarrow{V_3}+\overrightarrow{V_4})=0,$$ 展開內積運算後可得 \begin{align} &\hskip -10pt {V_1}^2\!+\!{V_2}^2\!+\!{V_3}^2\!+\!{V_4}^2\!+\!2V_1V_2\cos(\pi\!-\!A_2)\!+\!2V_1 V_3\cos(2\pi \!-\!A_2\!-\!A_3 )\!+\!2V_1 V_4\cos(\pi \!-\!A_1 )\nonumber\\ &\hskip 20pt +2V_2 V_3\cos(\pi\!-\!A_3 )+2V_2 V_4\cos(2\pi\!-\!A_3\!-\!A_4 )+2V_3 V_4\cos(\pi\!-\!A_4 )=0.\nonumber\\ \Rightarrow\ & {V_1}^2\!+\!{V_2}^2\!+\!{V_3}^2\!+\!{V_4}^2\!-\!2V_1 V_2\cos A_2\!+\!2V_1 V_3\cos(A_2\!+\!A_3)\!-\!2V_1 V_4\cos A_1\nonumber\\ &\hskip 20pt -2V_2 V_3\cos A_3+2V_2 V_4\cos(A_1\!+\!A_2 )-2V_3 V_4\cos(A_1\!+\!A_2\!+\!A_3 )=0 .\label{b1} \end{align} (ii) 接著將 (b1) 式中的各項角度作適當的轉換, 使得 $A_2=A_1\!-\!(A_1\!-\!A_2 ) $, $ A_2\!+\!A_3=(A_1\!+\!A_3 )\!-\!(A_1\!-\!A_2 ) $, $A_1=(A_1\!-\!A_2 )+A_2 $, $A_3=(A_1\!+\!A_3 )\!-\!A_1 $, $A_1\!+\!A_2\!+\!A_3=A_2\!+\!(A_1\!+\!A_3 ) $, 則 (b1) 式轉換成下式: \begin{align*} {V_1}^2\!+\!{V_2}^2\!+\!{V_3}^2\!+\!{V_4}^2\!-\!2V_1V_2\cos [A_1\!-\!(A_1\!-\!A_2 )]+2V_1 V_3\cos [(A_1\!+\!A_3 )\!-\!(A_1\!-\!A_2 )]\\ -2V_1 V_4\cos [(A_1\!-\!A_2 )+A_2 ]-2V_2 V_3\cos [(A_1\!+\!A_3 )\!-\!A_1 ]+2V_2 V_4\cos(A_1\!+\!A_2 )\\ -2V_3 V_4\cos [A_2\!+\!(A_1\!+\!A_3 )]=0 . \end{align*} 再將含有 cos 的部份各項式詳細展開演算後, 可得下式: \begin{align} &{V_1}^2\!+\!{V_2}^2\!+\!{V_3}^2\!+\!{V_4}^2\!-\!2V_1 V_2\cos A_1\cos(A_1\!-\!A_2 )\!-\!2V_1 V_2 \sin A_1\sin(A_1\!-\!A_2 )\nonumber\\ &\hskip 10pt \!+\!2V_1 V_3\cos(A_1\!+\!A_3 )\cos (A_1\!-\!A_2 )\!+\!2V_1 V_3\sin(A_1\!+\!A_3 )\sin (A_1\!-\!A_2 )\nonumber\\ &\hskip 10pt \!-\!2V_1 V_4\cos(A_1\!-\!A_2 )\cos A_2\!+\!2V_1 V_4\sin(A_1\!-\!A_2 )\sin A_2\!-\!2V_2 V_3\cos(A_1\!+\!A_3 )\cos A_1\nonumber\\ &\hskip 10pt \!-\!2V_2 V_3\sin(A_1\!+\!A_3 )\sin A_1\!+\!2V_2 V_4\cos A_1\cos A_2\!-\!2V_2 V_4 \sin A_1 \sin A_2\nonumber\\ &\hskip 10pt \!-\!2V_3 V_4\cos A_2\cos(A_1\!+\!A_3 )\!+\!2V_3 V_4 \sin A_2\sin(A_1\!+\!A_3 )=0 .\label{b2} \end{align} (iii) 特意整理擴充 (b2) 式, 使得其中的 $\cos$ 項與 $\sin$ 項分開各成一組表示式, 得 \begin{align} &[{V_1}^2\sin^2 (A_1\!\!-\!\!A_2 )\!+\!{V_2}^2\sin^2 A_1\!+\!{V_3}^2\sin^2 (A_1\!\!+\!\!A_3 )\!+\!V_4^2\sin^2 A_2\!-\!2V_1 V_2\sin(A_1\!\!-\!\!A_2 )\sin A_1\nonumber\\ &\hskip 10pt \!+\!2V_1 V_3\sin(A_1\!\!+\!\!A_3 )\sin (A_1\!\!-\!\!A_2 )\!+\!2V_1 V_4\sin(A_1\!\!-\!\!A_2 )\sin A_2\!-\!2V_2 V_3\sin(A_1\!\!+\!\!A_3 )\sin A_1\nonumber\\ &\hskip 10pt \!-\!2V_2 V_4 \sin A_1 \sin A_2\!+\!2V_3 V_4 \sin A_2\sin(A_1\!+\!A_3 ) ] \!+\! [ {V_1}^2 \cos^2 (A_1\!-\!A_2 )\!+\!{V_2}^2 \cos^2 A_1\nonumber\\ &\hskip 10pt \!+\!{V_3}^2 \cos^2 (A_1\!\!+\!\!A_3 )\!+\!V_4^2 \cos^2 A_2\!-\!2V_1 V_2\cos A_1\cos(A_1\!\!-\!\!A_2 ) \nonumber\\ &\hskip 10pt \!+\!2V_1 V_3\cos(A_1\!\!+\!\!A_3 )\cos (A_1\!\!-\!\!A_2 )\!\!-\!\!2V_1 V_4\cos(A_1\!\!-\!\!A_2 )\cos A_2\!\!-\!\!2V_2 V_3\cos(A_1\!\!+\!\!A_3 )\cos A_1\nonumber\\ &\hskip 10pt \!+\!2V_2 V_4\cos A_1\cos A_2 \!-\!2V_3 V_4\cos A_2\cos(A_1\!+\!A_3 ) ]=0 .\label{b3} \end{align} 檢視(b3)式整理後的結果, 發現兩者各為完全平方式, 於是得 \begin{align*} [V_1\sin(A_1\!-\!A_2 )\!-\!V_2 \sin A_1+V_3\sin(A_1\!+\!A_3 )\!+\!V_4 \sin A_2 ]^2\qquad\qquad~\\ +[V_1\cos(A_1\!-\!A_2 )\!-\!V_2\cos A_1+V_3\cos(A_1\!+\!A_3 )\!-\!V_4\cos A_2 ]^2=0 . \end{align*} 從而有: $$V_4 \sin A_2\!+\!V_1\sin(A_1\!-\!A_2 )\!-\!V_2 \sin A_1=-V_3\sin(A_1\!+\!A_3 ) . (4s)$$ 及 $$V_4\cos A_2-V_1\cos(A_1\!-\!A_2 )\!+\!V_2\cos A_1=V_3\cos(A_1\!+\!A_3 ) . (4c)$$ 這就是平面凸四邊形 $A_1 A_2 A_3 A_4$ 的第 1 組正弦型、 餘弦型 SASAS 方程式。 (iv) 同理, 再應用 $V_i$ 與 $A_i$ 下標序號的循環對稱性可得另 3 組 SASAS 方程式: 第2組: $$V_1 \sin A_3\!+\!V_2\sin(A_2\!-\!A_3 )\!-\!V_3 \sin A_2=-V_4\sin(A_2\!+\!A_4 ) . (4s.2)$$ $$V_1\cos A_3-V_2\cos(A_2\!-\!A_3 )\!+\!V_3\cos A_2=V_4\cos(A_2\!+\!A_4 ) . (4c.2)$$ 第3組: $$V_2 \sin A_4\!+\!V_3\sin(A_3\!-\!A_4 )\!-\!V_4 \sin A_3=-V_1\sin(A_3+A_1 ) . (4s.3)$$ $$V_2\cos A_4-V_3\cos(A_3\!-\!A_4 )\!+\!V_4\cos A_3=V_1\cos(A_3+A_1 ) . (4c.3)$$ 第4組: $$V_3 \sin A_1\!+\!V_4\sin(A_4\!-\!A_1 )\!-\!V_1 \sin A_4=-V_2\sin(A_4+A_2 ) . (4s.4)$$ $$V_3\cos A_1\!-\!V_4\cos(A_4\!-\!A_1 )\!+\!V_1\cos A_4=V_2\cos(A_4+A_2 ) . (4c.4)$$ 這樣就證明了平面凸四邊形 SASAS 定理的 4 組方程式。 推論1: 若此四邊形 $A_1 A_2 A_3 A_4$ 內接於半徑 $R$ 的一圓, 則其 SASAS 方程式第 1 組變換為 $$V_4 \sin A_2\!+\!V_1\sin(A_1\!-\!A_2 )\!-\!V_2 \sin A_1=0, (4s-1)$$ 及 $$V_4\cos A_2-V_1\cos(A_1\!-\!A_2 )\!+\!V_2\cos A_1=-V_3 . (4c-1)$$ 另外可再得第 2、 3、 4 組為 第2組: $$V_1 \sin A_3\!+\!V_2\sin(A_2\!-\!A_3 )\!-\!V_3 \sin A_2=0 . (4s.2-1)$$ $$V_1\cos A_3-V_2\cos(A_2\!-\!A_3 )\!+\!V_3\cos A_2=-V_4 . (4c.2-1)$$ 第3組: $$V_2 \sin A_4\!+\!V_3\sin(A_3\!-\!A_4 )\!-\!V_4 \sin A_3=0 . (4s.3-1)$$ $$V_2\cos A_4-V_3\cos(A_3\!-\!A_4 )\!+\!V_4\cos A_3=-V_1 . (4c.3-1)$$ 第4組: $$V_3 \sin A_1\!+\!V_4\sin(A_4\!-\!A_1 )\!-\!V_1 \sin A_4=0 . (4s.4-1)$$ $$V_3\cos A_1\!-\!V_4\cos(A_4\!-\!A_1 )\!+\!V_1\cos A_4=-V_2 . (4c.4-1)$$ 證明: 圓的內接四邊形其對角 $A_1\!+\!A_3=A_2\!+\!A_4=\pi$, 可證出 4 組方程式。 三、平面凸四邊形分式型連續等式方程式依據引理 7 知 : 圓的內接四邊形 $A_1 A_2 A_3 A_4$ 其正弦定理方程式應為下列的 (4 個同形分式型) 連續等式: $$\dfrac{V_1}{\sin\theta_1}=\dfrac{V_2}{\sin\theta_2}=\dfrac{V_3}{\sin\theta_3}=\dfrac{V_4}{\sin\theta_4}=2R_4.$$ 見下圖 6,
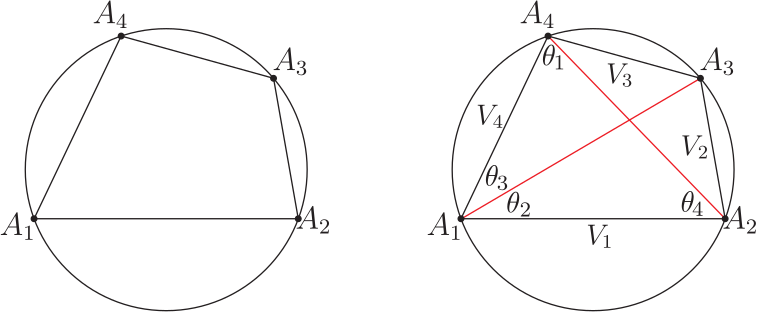
圖中四邊形 $A_1 A_2 A_3 A_4$ 的外接圓其圓周半徑為 $R_4 $。 由於任意平面凸四邊形的 4 頂點不一定共圓, 所以不存在有(4 個同形分式型) 連續等式。 對求解歐幾里得平面幾何命題而言, 需要作出一個最貼近凸四邊形的輔助圓, 並應用輔助圓的內接新四邊形 (4 個同形分式型) 等式來引導推演運算, 以求證出平面凸四邊形相對應的 (4 項式分式型) 連續等式; [C1]、 取平面凸四邊形 $A_1 A_2 A_3 A_4$ 的 3 頂點 $A_1, A_2, A_3$ 共圓情形; 下圖 7,

(I) 首先延長線段 $\overline{A_4A_1}=V_4$ 至與圓周相交於 $B$ 點, 再連接 $B$ 點與 $A_3$ 點, 以形成圓的新內接四邊形 $A_1 A_2 A_3 B $, 見圖 7 的第 3、 第 4 位置圖形。 (i) 在圓的新內接四邊形 $A_1 A_2 A_3 B$ 中標註出邊長的對應圓周角 $\theta_1, \theta_2, \theta_3$, 而 $\angle BA_3 A_1=\theta_4 $, 因此, 對圓的新內接四邊形 $A_1 A_2 A_3 B$ 言, 有等式關係: \begin{align} \frac{V_1}{\sin\theta_1} =\frac{V_2}{\sin\theta_2}= \frac{\overline{A_3B}}{\sin\theta_3}=\frac{\overline{BA_1}}{\sin(\angle BA_3A_1)}.\label{c1} \end{align} (ii) 對 $\triangle A_1 A_3 A_4$ 言, $\overline{A_1A_3}=d_{13}$ 且有 $\dfrac{V_3}{\sin \theta_3}=\dfrac{d_{13}}{\sin A_4}$, 得 $\sin\theta_3=\dfrac{V_3\sin A_4}{d_{13}}$, $$d_{13}=({V_3}^2\!+\!{V_4}^2\!-\!2V_3 V_4 \cos A_4)^{1/2}=[(V_3\!+\!V_4)^2\!-\!2V_3 V_4\cdot (1\!+\!\cos A_4)]^{1/2} ,$$ 得 $$\sin\theta_3 \!=\!\frac{V_3\sin A_4}{({V_3}^2\!+\!{V_4}^2\!-\!2V_3 V_4 \cos A_4 )^{1/2}}\!=\! \frac{V_3\sin A_4}{(V_3\!+\!V_4 )\!\cdot\! \Big[1 \!-\! \dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big) \Big)\Big]^{1/2}}.$$ 應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 2 組方程式為 \begin{align*} \,&V_1\sin(\angle A_2 A_3 B)\!+\!V_2\sin(A_2\!-\!(\angle A_2 A_3 B))\!-\!\overline{A_3B}\!\cdot\!\sin A_2=0 .\hskip 2cm~\\ \Rightarrow\qquad\,&V_1\sin(\pi\!-\!A_1)\!+\!V_2\sin(A_2\!-\!(\pi\!-\!A_1))\!-\!\overline{A_3B}\!\cdot\!\sin A_2=0 .\\ \Rightarrow\qquad\,&V_1 \sin A_1\!-\!V_2\sin(A_1\!+\!A_2 )\!-\!\overline{A_3B}\!\cdot\!\sin A_2=0 .\\ \Rightarrow\qquad\,&\overline{A_3B}=\dfrac{V_1 \sin A_1\!-\!V_2\sin(A_1\!+\!A_2 )}{\sin A_2}. \end{align*} 得 \begin{align} \frac{\overline{A_3B}}{\sin \theta_3 }=\,&\dfrac{V_1 \sin A_1\!-\!V_2\sin(A_1\!+\!A_2 )}{V_3\sin A_4 \cdot\sin A_2}\!\cdot\!({V_3}^2\!+\!{V_4}^2\!-\!2V_3 V_4 \cos A_4)^{1/2}\nonumber\\ =\,&\frac{V_1 \sin A_1\!-\!V_2\sin(A_1\!+\!A_2 )}{V_3\sin A_4 \cdot\sin A_2}\!\cdot\!(V_3\!+\!V_4 ) %\nonumber\\& \!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\Big(1\!-\!\sin^2\Big(\frac{A_4}2\Big)\Big)\Big]^{1/2}\nonumber\\ \Rightarrow\ \frac{\overline{A_3B}}{\sin \theta_3}=\,&\frac{V_1 \sin A_1\!-\!V_2\sin(A_1\!+\!A_2 )}{\sin A_4\cdot\sin A_2} \!\cdot\!\Big(1\!+\!\dfrac{V_4}{V_3}\Big) %\nonumber\\&\quad \!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\Big(1\!-\!\sin^2\Big(\frac{A_4}{2}\Big)\Big)\Big]^{1/2}.\label{c2} \end{align} (iii) 由於 $A_2=\theta_3\!+\!\theta_4 $, 得 $\theta_4=\angle BA_3 A_1=A_2\!-\!\theta_3 $, 且還有 $$\theta_3=\sin^{-1} \left\{\frac{V_3\sin A_4}{(V_3\!+\!V_4 ) \!\cdot\! \Big[1 - \dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_4}2\Big) \Big)\Big]^{1/2}}\right\} ,$$ 再應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 1 組方程式為 \begin{align*} \,&\overline{BA_1}\!\cdot\!\sin A_2\!+\!V_1\sin(A_1\!-\!A_2 )\!-\!V_2 \sin A_1=0 .\qquad\qquad ~\\ \Rightarrow\qquad\,&\overline{BA_1}\!\cdot\!\sin A_2=V_2 \sin A_1\!-\!V_1\sin(A_1\!-\!A_2 ) .\\ \Rightarrow\qquad\,&\overline{BA_1}=\frac{V_2 \sin A_1\!-\!V_1\sin(A_1\!-\!A_2 )}{\sin A_2}, \end{align*} 得 \begin{align} \frac{\overline{BA_1}}{\sin(\angle BA_3 A_1)}=\frac{V_2 \sin A_1\!-\!V_1\sin(A_1\!-\!A_2 )}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_3 )}.\label{c3} \end{align} (iv) 對 $\triangle A_1 A_2 A_3$ 言, $\theta_1=\pi\!-\!A_2-\theta_2=\pi\!-\!A_2-A_1\!+\!\theta_3=A_3\!+\!A_4\!+\!\theta_3\!-\!\pi $, 得 $\sin\theta_1 =-\sin (A_3\!+\!A_4\!+\!\theta_3 ) $, 因此有 \begin{align} \dfrac{V_1}{\sin \theta_1}=- \frac{V_1}{\sin (A_3\!+\!A_4\!+\!\theta_3 )}.\label{c4} \end{align} (v) 由 $A_1=\theta_2\!+\!\theta_3 $, 得 $\theta_2=A_1\!-\!\theta_3 $, 因此有 \begin{align} \dfrac{V_2}{\sin \theta_2}=\frac{V_2}{\sin (A_1\!-\!\theta_3 )}.\label{c5} \end{align} (vi) 綜合上述等式 \eqref{c1}、 \eqref{c2}、 \eqref{c3}、 \eqref{c4}、 \eqref{c5}, 可得到 \begin{align} &\hskip -25pt \frac{V_1}{-\sin (A_3\!+\!A_4\!+\!\theta_3 )}=\frac{V_2}{\sin (A_1\!-\!\theta_3 )}\nonumber\\ =\,&\frac{V_1 \sin A_1\!-\!V_2\sin(A_1\!+\!A_2 )}{\sin A_4 \!\cdot\!\sin A_2}\!\cdot\! \Big(1+\frac{V_4}{V_3}\Big)\!\cdot\! \Big[1-\Big(\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\Big(1\!-\!\sin^2\Big(\frac {A_4}2\Big)\Big)\Big]^{1/2}\nonumber\\ =\,&\frac{V_2 \sin A_1\!-\!V_1\sin(A_1\!-\!A_2 )}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_3 )}.\label{5} \end{align} 這第 \eqref{5} 式等式方程其中的 $$\theta_3=\sin^{-1} \left\{\frac{V_3\sin A_4}{(V_3\!+\!V_4 )\!\cdot\! \Big[1 \!-\! \dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_4}{2}\Big)\Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{5} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_2, A_3$ 共圓情形時的第 1 組 (4 項不同形式分式型) 連續等式。 (II) 其次延長線段 $\overline{A_3A_4}=V_3$ 至與圓周相交於 $B_2$ 點, 再連接 $B_2$ 點與 $A_1$ 點, 以形成圓的新內接四邊形 $A_1 A_2 A_3 B_2 $, 見圖 8 的第 3、 第 4 位置圖形。

(i) 在圓的新內接四邊形 $A_1 A_2 A_3 B_2$ 中標註出邊長的對應圓周角 $\theta_1, \theta_2, \theta_4$, 而 $\angle B_2 A_1 A_3=\theta_3 $, 因此, 對圓的新內接四邊形 $A_1 A_2 A_3 B_2$ 言, 有等式關係: \begin{align} \frac{V_1}{\sin \theta_1}=\frac{V_2}{\sin \theta_2} =\frac{\overline{A_3B_2}}{\sin (\angle B_2 A_1 A_3 )} =\frac{\overline{B_2A_1}}{\sin \theta_4 }. \label{c6} \end{align} (ii) 對 $\triangle A_1 A_3 A_4$ 言, $\overline{A_1A_3}=d_{13}$ 且有 $\dfrac{V_4}{\sin \theta_4}=\dfrac{d_{13}}{\sin A_4}$, 得 $\sin\theta_4 =\dfrac{V_4\sin A_4}{d_{13}}$, $$d_{13}=({V_3}^2\!+\!{V_4}^2\!-\!2V_3 V_4 \cos A_4)^{1/2}=[(V_3\!+\!V_4 )^2\!-\!2V_3 V_4\!\cdot\! (1\!+\!\cos A_4)]^{1/2} ,$$ 得 $$\sin\theta_4=\frac{V_4\sin A_4}{({V_3}^2\!+\!{V_4}^2\!-\!2V_3 V_4 \cos A_4)^{1/2}} =\frac{V_4\sin A_4}{(V_3\!+\!V_4 )\!\cdot\!\Big[1 \!-\! \dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big)\Big)\Big]^{1/2}}.$$ 應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 1 組方程式為 \begin{align*} \,&\overline{B_2A_1}\!\cdot\! \sin A_2\!+\!V_1\sin((\angle B_2 A_1 A_2)\!-\!A_2 )\!-\!V_2\sin(\angle B_2 A_1 A_2)=0 .\hskip 2cm~\\ \Rightarrow\qquad\,&\overline{B_2A_1}\!\cdot\! \sin A_2\!+\!V_1\sin((\pi\!-\!A_3)\!-\!A_2 )\!-\!V_2\sin(\pi\!-\!A_3)=0 .\\ \Rightarrow\qquad\,&\overline{B_2A_1}=\frac{V_2 \sin A_3\!-\!V_1\sin(A_2\!+\!A_3 )}{\sin A_2}, \end{align*} 得 \begin{align} \frac{\overline{B_2A_1}}{\sin \theta_4 }=\,&\frac{V_2 \sin A_3\!-\!V_1\sin(A_2\!+\!A_3 )}{V_4\sin A_4 \!\cdot\!\sin A_2}\!\cdot\! (V_3\!+\!V_4 )%\nonumber\\&\quad \!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\Big(1\!-\!\sin^2\Big(\frac{A_4}2\Big)\Big)\Big]^{1/2}\nonumber\\ \Rightarrow\ \frac{\overline{B_2A_1}}{\sin \theta_4 }=\,&\frac{V_2 \sin A_3\!-\!V_1\sin(A_2\!+\!A_3 )}{\sin A_4 \!\cdot\!\sin A_2}\!\cdot\! \Big(1\!+\!\frac{V_3}{V_4}\Big) %\nonumber\\&\quad \!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\Big(1\!-\!\sin^2\Big(\frac{A_4}{2}\Big)\Big)\Big]^{1/2}.\label{c7} \end{align} (iii) 由於 $A_2=\theta_3\!+\!\theta_4 $, 得 $\theta_3=\angle B_2 A_1 A_3=A_2\!-\!\theta_4 $, 且還有 $$\theta_4=\sin^{-1} \left\{\frac{V_4\sin A_4}{(V_3\!+\!V_4 )\!\cdot\! \Big[1 \!-\! \dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_4}{2}\Big)\Big)\Big]^{1/2}}\right\},$$ 再應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 2 組方程式為 \begin{align} &~\hskip 2.5cm V_1 \sin A_3\!+\!V_2\sin(A_2\!-\!A_3 )\!-\!\overline{A_3B_2}\!\cdot\! \sin A_2=0 .\nonumber\\ \Rightarrow\ &\overline{A_3B_2}\!=\!\frac{V_1 \sin A_3\!+\!V_2\sin(A_2\!-\!A_3 )}{\sin A_2},\ \hbox{得}\ \frac{\overline{A_3B_2}}{\sin(\angle B_2 A_1 A_3 )} \!=\!\frac{V_1 \sin A_3\!+\!V_2\sin(A_2\!-\!A_3 )}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_4 )}.\label{c8} \end{align} (iv) 對 $\triangle A_1 A_2 A_3$ 言, $\theta_2=\pi\!-\!A_2-\theta_1=\pi\!-\!A_2\!+\!A_3\!+\!\theta_4=A_1\!+\!A_4\!+\!\theta_4-\pi $, 得 $\sin\theta_2 =-\sin (A_1\!+\!A_4\!+\!\theta_4 ) $, 因此有 \begin{align} \frac{V_2}{\sin \theta_2}=- \frac{V_2}{\sin(A_1\!+\!A_4\!+\!\theta_4 )}.\label{c9} \end{align} (v) 由 $A_3=\theta_1\!+\!\theta_4 $, 得 $\theta_1=A_3\!-\!\theta_4 $, 因此有 \begin{align} \frac{V_1}{\sin \theta_1}=\frac{V_1}{\sin(A_3\!-\!\theta_4)}.\label{c10} \end{align} (vi) 綜合上述等式 \eqref{c6}、 \eqref{c7}、 \eqref{c8}、 \eqref{c9}、 \eqref{c10}, 可得到 \begin{align} &\hskip -20pt \frac{V_1}{\sin (A_3\!-\!\theta_4 )} = \frac{V_2}{-\sin (A_1\!+\!A_4\!+\!\theta_4 )}=\frac{V_1 \sin A_3\!+\!V_2\sin(A_2\!-\!A_3 )}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_4 )}\nonumber\\ =\,&\frac{V_2 \sin A_3\!-\!V_1\sin(A_2\!+\!A_3 )}{\sin A_4 \!\cdot\!\sin A_2}\!\cdot\! \Big(1+\frac{V_3}{V_4}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_4}2\Big)\Big)\Big]^{1/2}.\label{6} \end{align} 這第 \eqref{6} 式等式方程其中的 $$\theta_4=\sin^{-1} \left\{\frac{V_4\sin A_4}{(V_3\!+\!V_4 )\!\cdot\! \Big[1 \!-\! \dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_4}{2}\Big)\Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{6} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_2, A_3$ 共圓情形時的第 2 組 (4 項不同形式分式型) 連續等式。 [C2]、 取平面凸四邊形 $A_1 A_2 A_3 A_4$ 的 3 頂點 $A_1, A_2, A_4$ 共圓情形; 下圖 9, (I) 首先設定線段 $\overline{A_2A_3}=V_2$ 與圓周相交於C點, 再連接C點與 $A_4$ 點, 以形成圓的新內接四邊形 $A_1 A_2 CA_4 $, 見圖 9 的第3、 第 4 位置圖形。
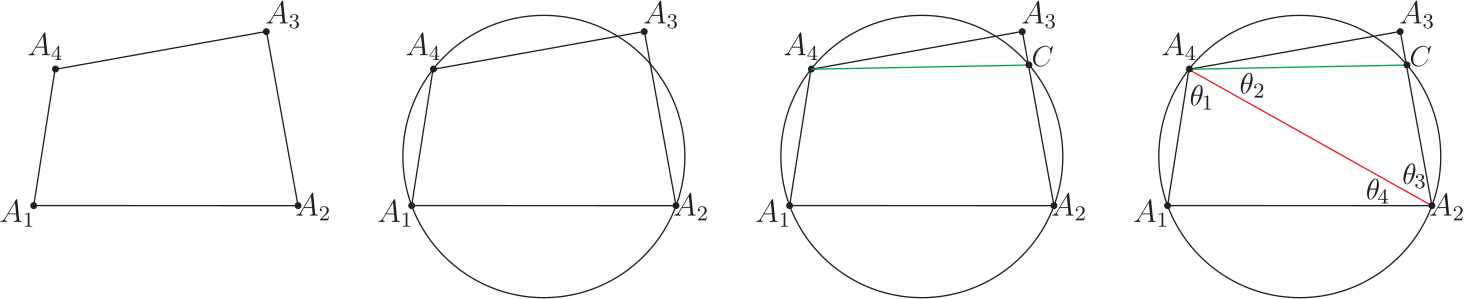
(i) 在圓的新內接四邊形 $A_1 A_2 C A_4$ 中標註出邊長的對應圓周角 $\theta_1, \theta_3, \theta_4$, 而 $ \angle CA_4 A_2=\theta_2 $, 因此, 對圓的新內接四邊形 $A_1 A_2 CA_4$ 言, 有等式關係: \begin{align} \frac{V_1}{\sin \theta_1}=\frac{\overline{A_2C}}{\sin (\angle CA_4 A_2 )} =\frac{\overline{CA_4}}{\sin \theta_3}=\frac{V_4}{\sin \theta_4}.\label{c21} \end{align} (ii) 對 $\triangle A_2 A_3 A_4$ 言, $\overline{A_2A_4}=d_{24}$ 且有 $\dfrac{V_3}{\sin \theta_3}=\dfrac{d_{24}}{\sin A_3}$, 得 $\sin\theta_3=\dfrac{V_3\sin A_3}{d_{24}}$, $$ d_{24}=({V_2}^2\!+\!{V_3}^2\!-\!2V_2 V_3 \cos A_3)^{1/2}=[(V_2\!+\!V_3)^2\!-\!2V_2 V_3\cdot (1\!+\!\cos A_3)]^{1/2} ,$$ 得 $$\sin\theta_3 \!=\!\frac{V_3\sin A_3}{({V_2}^2\!+\!{V_3}^2\!-\!2V_2 V_3 \cos A_3)^{1/2}}\!=\! \frac{V_3\sin A_3}{(V_2\!+\!V_3 )\!\cdot\! \Big[1 \!-\! \dfrac{4V_2 V_3}{(V_2\!+\!V_2 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_3}2\Big) \Big)\Big]^{1/2}}.$$ 應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 4 組方程式為 \begin{align*} \,&\overline{CA_4}\!\cdot\!\sin A_1\!+\!V_4\sin\big((\angle CA_4A_1)\!-\!A_1\big)\!-\!V_1\sin (\angle CA_4A_1)=0 .\hskip 2cm~\\ \Rightarrow\qquad\,&\overline{CA_4}\!\cdot\!\sin A_1\!+\!V_4\sin\big((\pi\!-\!A_2 )\!-\!A_1\big)\!-\!V_1\sin (\pi\!-\!A_2)=0 .\\ \Rightarrow\qquad\,&\overline{CA_4}\!\cdot\!\sin A_1\!+\!V_4\sin(A_1\!+\!A_2 )\!-\!V_1\!\cdot\! \sin A_2=0 .\\ \Rightarrow\qquad\,&\overline{CA_4}=\frac{V_1\sin A_2 \!-\!V_4 \sin(A_1\!+\!A_2 )}{\sin A_1}. \end{align*} 得 \begin{align} \frac{\overline{CA_4}}{\sin \theta_3}=\frac{V_1\sin A_2\!-\!V_4 \sin(A_1\!+\!A_2 )}{\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\frac{V_2}{V_3} \Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_3}2\Big) \Big)\Big]^{1/2}.\label{c22} \end{align} (iii) 在 $\triangle A_2 CA_4$, $\angle CA_4 A_2=\theta_2=\pi \!-\!(\angle A_2 CA_4 )\!-\!\theta_3=\pi \!-\!(\pi\!-\!A_1 )\!-\!\theta_3=A_1\!-\!\theta_3 $, 且還有 $$\theta_3=\sin^{-1} \left\{\frac{V_3\sin A_3}{(V_2\!+\!V_3 )\!\cdot\! \Big[1 \!-\! \dfrac{4V_2 V_3}{(V_2\!+\!V_3)^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_3}{2}\Big)\Big)\Big]^{1/2}}\right\},$$ 再應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 1 組方程式為 \begin{align} &V_4 \sin A_2\!+\!V_1\sin(A_1\!-\!A_2 )\!-\!\overline{A_2C}\!\cdot\! \sin A_1=0 .\hskip 4cm~\nonumber\\ \Rightarrow\qquad &\overline{A_2C}=\frac{V_4\sin A_2 \!+\!V_1 \sin(A_1\!-\!A_2 )}{\sin A_1}.\nonumber\\ \hbox{得}\qquad&\frac{\overline{A_2C}}{\sin (\angle CA_4 A_2 )} =\frac{V_4\sin A_2 \!+\!V_1 \sin(A_1\!-\!A_2 )}{\sin(A_1\!-\!\theta_3) \!\cdot\!\sin A_1}.\label{c23} \end{align} (iv) 由 $A_2=\theta_3\!+\!\theta_4 $, 得 $\theta_4=A_2\!-\!\theta_3 $, 因此有 \begin{align} \frac{V_4}{\sin \theta_4 }=\frac{V_4}{\sin (A_2\!-\!\theta_3 )}.\label{c24} \end{align} (v) 對 $\triangle A_1 A_2 A_4$ 言, $\theta_1=\pi\!-\!A_1\!-\!\theta_4=\pi\!-\!A_1\!-\!A_2\!-\!\theta_3=A_3\!+\!A_4\!+\!\theta_2\!-\!\pi $, 得 $\sin\theta_1 =-\sin (A_3\!+\!A_4\!+\!\theta_3 ) $, 因此有 \begin{align} \frac{V_1}{\sin \theta_1}=\frac{V_1}{-\sin (A_3\!+\!A_4\!+\!\theta_3 )}.\label{c25} \end{align} (vi) 綜合上述等式 \eqref{c21}、 \eqref{c22}、 \eqref{c23}、 \eqref{c24}、 \eqref{c25}, 可得到 \begin{align} &\hskip -20pt \frac{V_1}{-\sin (A_3\!+\!A_4\!+\!\theta_3)}=\frac{V_4\sin A_2 +V_1 \sin(A_1\!-\!A_2 )}{\sin(A_1\!-\!\theta_3 ) \!\cdot\!\sin A_1}\nonumber\\ =\,&\frac{V_1\sin A_2 \!-\!V_4 \sin(A_1\!+\!A_2 )}{\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\frac{V_2}{V_3}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2} \Big(1\!-\!\sin^2\Big(\frac{A_3}2\Big)\Big)\Big]^{1/2}\nonumber\\ =\,&\frac{V_4}{\sin(A_2\!-\!\theta_3 )}\label{7} \end{align} 這第 \eqref{7} 式等式方程其中的 $$\theta_3=\sin^{-1} \left\{\frac{V_3\sin A_3}{(V_2\!+\!V_3 ) \!\cdot\! \Big[1 \!-\! \dfrac{4V_2 V_3}{(V_2\!+\!V_3)^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_3}2\Big) \Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{7} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_2, A_4$ 共圓情形時的第 1 組 (4 項不同形式分式型)連續等式。 (II) 其次設定線段 $\overline{A_3A_4}=V_3$ 與圓周相交於 $C_2$ 點, 再連接 $C_2$ 點與 $A_2$ 點, 以形成圓的新內接四邊形 $A_1 A_2 C_2 A_4 $, 見圖 10 的第 2、 第 3 位置圖形。
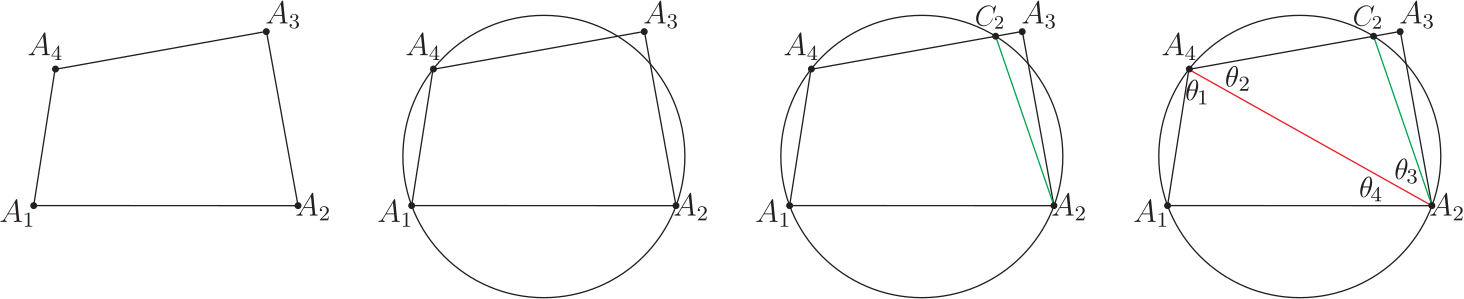
(i) 在圓的新內接四邊形 $A_1 A_2 C_2 A_4$ 中標註出邊長的對應圓周角 $\theta_1, \theta_2, \theta_4$, 而 $\angle A_4 A_2 C_2=\theta_3 $, 因此, 對圓的新內接四邊形 $A_1 A_2 C_2 A_4$ 言, 有等式關係: \begin{align} \frac{V_1}{\sin \theta_1 }=\frac{\overline{A_2C_2}}{\sin\theta_2}=\frac{\overline{C_2A_4}}{\sin (\angle A_4 A_2 C_2 )} =\frac{V_4}{\sin \theta_4}.\label{c26} \end{align} (ii) 對 $\triangle A_2 A_3 A_4$ 言, $\overline{A_2A_4}=d_{24}$ 且有 $\dfrac{V_2}{\sin \theta_2}=\dfrac{d_{24}}{\sin A_3}$, 得 $\sin\theta_2 =\dfrac{V_2\sin A_3}{d_{24}}$, $$ d_{24}=({V_2}^2\!+\!{V_3}^2\!-\!2V_2 V_3 \cos A_3)^{1/2}=[(V_2\!+\!V_3)^2\!-\!2V_2 V_3\cdot (1\!+\!\cos A_3)]^{1/2} ,$$ 得 $$\sin\theta_2=\frac{V_2\sin A_3}{({V_2}^2\!+\!{V_3}^2\!-\!2V_2 V_3 \cos A_3)^{1/2}} =\frac{V_2\sin A_3}{(V_2\!+\!V_3 )\!\cdot\!\Big[1 \!-\! \dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_3}2\Big)\Big)\Big]^{1/2}}.$$ 應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 1 組方程式為 \begin{align*} \,&V_4\sin(\angle A_1 A_2 C_2 )\!+\!V_1\sin(A_1\!-\!(\angle A_1 A_2 C_2 ))-\overline{A_2C_2}\!\cdot\! \sin A_1=0 .\hskip 2cm~\\ \Rightarrow\qquad\,&V_4\sin(\pi\!-\!A_4 )\!+\!V_1\sin(A_1\!-\!(\pi\!-\!A_4 ))-\overline{A_2C_2}\!\cdot\! \sin A_1=0 .\\ \Rightarrow\qquad\,&V_4 \sin A_4\!-\!V_1\sin(A_4\!+\!A_1 )-\overline{A_2C_2}\!\cdot\! \sin A_1=0 .\\ \Rightarrow\qquad\,&\overline{A_2C_2}=\frac{V_4\sin A_4 \!-\!V_1 \sin(A_4\!+\!A_1 )}{\sin A_1}. \end{align*} 得 \begin{align} \frac{\overline{A_2C_2}}{\sin \theta_2}=\frac{V_4\sin A_4\!-\!V_1 \sin(A_4\!+\!A_1)}{\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\frac{V_3}{V_2} \Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2}\Big(1\!-\!\sin^2\Big(\dfrac{A_3}2\Big) \Big)\Big]^{1/2}.\label{c27} \end{align} (iii) 因 $A_1=\theta_2\!+\!\theta_3 $, 得 $\theta_3=A_1\!-\!\theta_2 $, 且還有 $$\theta_2=\sin^{-1} \left\{\frac{V_2\sin A_3}{(V_2\!+\!V_3 )\!\cdot\! \Big[1 \!-\! \dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_4}{2}\Big)\Big)\Big]^{1/2}}\right\}.$$ 應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 4 組方程式為 \begin{align} &\overline{C_2A_4}\!\cdot\! \sin A_1\!+\!V_4\sin(A_4\!-\!A_1 )\!-\!V_1 \sin A_4=0\hskip 4cm~\nonumber\\ \Rightarrow\qquad &\overline{C_2A_4}=\frac{V_1\sin A_4 \!-\!V_4 \sin(A_4\!-\!A_1 )}{\sin A_1}.\nonumber\\ \hbox{得}\qquad&\frac{\overline{C_2A_4}}{\sin (\angle A_4 A_2C_2 )}=\frac{\overline{C_2A_4}}{\sin\theta_3} =\frac{V_1\sin A_4 \!-\!V_4 \sin(A_4\!-\!A_1)}{\sin(A_1\!-\!\theta_2)\cdot\sin A_1 }.\label{c28} \end{align} (iv) 由 $A_4=\theta_1\!+\!\theta_2 $, 得 $\theta_1=A_4\!-\!\theta_2 $, 因此有 \begin{align} \frac{V_1}{\sin \theta_1 }=\frac{V_1}{\sin (A_4\!-\!\theta_2 )}.\label{c29} \end{align} (v) 對 $\triangle A_1 A_2 A_4$ 言, $\theta_4=\pi\!-\!A_1\!-\!\theta_1=\pi\!-\!A_1-A_4\!+\!\theta_2=A_2\!+\!A_3\!+\!\theta_2-\pi $, 得 $\sin\theta_4 =-\sin (A_2\!+\!A_3\!+\!\theta_2 )$, 因此有 \begin{align} \frac{V_4}{\sin \theta_4 }=-\frac{V_4}{\sin (A_2\!+\!A_3\!+\!\theta_2 )}.\label{c30} \end{align} (vi) 綜合上述等式 \eqref{c26}、 \eqref{c27}、 \eqref{c28}、 \eqref{c29}、 \eqref{c30}, 可得到 \begin{align} \frac{V_1}{\sin (A_4\!-\!\theta_2 )} \!=\,&\frac{V_4\sin A_4\!-\!V_2 \sin(A_4\!+\!A_1 )}{\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\frac{V_3}{V_2}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2} \Big(1\!-\!\sin^2\Big(\frac{A_3}2\Big) \Big)\Big]^{1/2}\nonumber\\ =\,&\frac{V_1\sin A_4\!-\!V_4 \sin(A_4\!-\!A_1 )}{\sin(A_1\!-\!\theta_2 ) \!\cdot\!\sin A_1} =\frac{V_4}{-\sin (A_2\!+\!A_3\!+\!\theta_2 )}.\label{8} \end{align} 這第 \eqref{8} 式等式方程其中的 $$\theta_2=\sin^{-1} \left\{\frac{V_2\sin A_3 }{(V_2\!+\!V_3 ) \!\cdot\! [1 \!-\! \dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_3}2\Big) \Big)\Big]^{1/2}} \right\}.$$ 第 \eqref{8} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_2, A_4$ 共圓情形時的第 2 組 (4 項不同形式分式型)連續等式。 [C3]、 取平面凸四邊形 $A_1 A_2 A_3 A_4$ 的 3 頂點 $A_1, A_3, A_4$ 共圓情形;下圖 11,
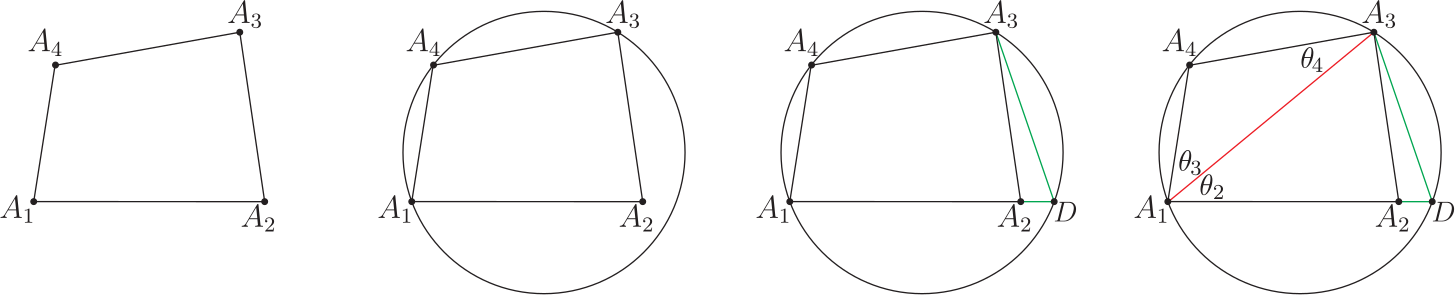
(I) 首先延長線段 $\overline{A_1A_2}=V_1$ 至與圓周相交於 $D$ 點, 再連接 $D$ 點與 $A_3$ 點, 以形成圓的新內接四邊形 $A_1 DA_3 A_4 $, 見圖 11 的第 3、 第 4 位置圖形。 (i) 在圓的新內接四邊形 $A_1 DA_3 A_4$ 中標註出邊長的對應圓周角 $\theta_2, \theta_3, \theta_4$, 而 $\angle DA_3 A_1=\theta_1 $, 因此, 對圓的新內接四邊形 $A_1 DA_3 A_4$ 言, 有等式關係: \begin{align} \frac{\overline{A_1D}}{\sin (\angle DA_3 A_1 )} =\frac{\overline{DA_3}}{\sin \theta_2}=\frac{V_3}{\sin \theta_3}=\frac{V_4}{\sin \theta_4 }.\label{c31} \end{align} (ii) 對 $\triangle A_1 A_2 A_3$ 言, $\overline{A_1A_3}=d_{13}$ 且有 $\dfrac{V_2}{\sin \theta_2}=\dfrac{d_{13}}{\sin A_2}$, 得 $\sin\theta_2=\dfrac{V_2\sin A_2}{d_{13}}$, $$d_{13}=({V_1}^2\!+\!{V_2}^2\!-\!2V_1 V_2 \cos A_2)^{1/2}=[(V_1\!+\!V_2 )^2\!-\!2V_1 V_2\cdot (1\!+\!\cos A_2 )]^{1/2} ,$$ 得 $$\sin\theta_2 \!=\!\frac{V_2\sin A_2}{({V_1}^2\!+\!{V_2}^2\!-\!2V_1 V_2 \cos A_2)^{1/2}}\!=\!\frac{V_2\sin A_2}{ (V_1\!+\!V_2 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2 } \!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_2}2\Big)\Big)\Big]^{1/2}}.$$ 應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 3 組方程式為 \begin{align*} \,&\overline{DA_3}\!\cdot\! \sin A_4\!+\!V_3\sin((\angle DA_3 A_4)\!-\!A_4 )\!-\!V_4\sin(\angle DA_3 A_4)=0 .\hskip 2cm~\\ \Rightarrow\qquad\,&\overline{DA_3}\!\cdot\! \sin A_4\!+\!V_3\sin((\pi\!-\!A_1)\!-\!A_4 )\!-\!V_4\sin(\pi\!-\!A_1)=0 .\\ \Rightarrow\qquad\,&\overline{DA_3}\!\cdot\! \sin A_4\!+\!V_3\sin(A_4\!+\!A_1 )\!-\!V_4 \sin A_1=0 .\\ \Rightarrow\qquad\,&\overline{DA_3}=\frac{V_4 \sin A_1\!-\!V_3\sin(A_4\!+\!A_1 )}{\sin A_4}. \end{align*} 得 \begin{align} \frac{\overline{DA_3}}{\sin \theta_2}= \frac{V_4 \sin A_1\!-\!V_3\sin(A_4\!+\!A_1 )}{\sin A_2 \!\cdot\!\sin A_4}\!\cdot\! \Big(1\!+\!\frac{V_3}{V_2} \Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2)^2}\Big(1\!-\!\sin^2\Big(\dfrac{A_2}2\Big)\Big)\Big]^{1/2}.\label{c32} \end{align} (iii) 由於 $A_4=\theta_1\!+\!\theta_2 $, 得 $\theta_1=\angle DA_3 A_1=A_4\!-\!\theta_2 $, 且還有 $$\theta_2=\sin^{-1} \left\{\frac{V_2\sin A_2}{(V_1\!+\!V_2 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_2}2\Big)\Big)\Big]^{1/2}}\right\} ,$$ 再應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 4 組方程式為 \begin{align} &V_3 \sin A_1\!+\!V_4\sin(A_4\!-\!A_1 )\!-\!\overline{A_1D}\!\cdot\! \sin A_4=0 .\hskip 4cm~\nonumber\\ \Rightarrow\qquad &\overline{A_1D}=\frac{V_3 \sin A_1\!+\!V_4\sin(A_4\!-\!A_1 )}{\sin A_4} ,\nonumber\\ \hbox{得}\qquad&\frac{\overline{A_1D}}{\sin (\angle DA_3 A_1 )} =\frac{V_3 \sin A_1\!+\!V_4\sin(A_4\!-\!A_1 )}{\sin A_4 \!\cdot\! \sin(A_4\!-\!\theta_2 )}.\label{c33} \end{align} (iv) 由 $A_1=\theta_2\!+\!\theta_3 $, 得 $\theta_3=A_1\!-\!\theta_2 $, 因此有 \begin{align} \frac{V_3}{\sin \theta_3}=\frac{V_3}{\sin (A_1\!-\!\theta_2 )}.\label{c34} \end{align} (v) 對 $\triangle A_1 A_3 A_4$ 言, $\theta_4=\pi\!-\!A_4\!-\!\theta_3=\pi\!-\!A_4\!-\!A_1\!+\!\theta_2=A_2\!+\!A_3\!+\!\theta_2-\pi $, 得 $\sin\theta_4=-\sin (A_2\!+\!A_3\!+\!\theta_2 ) $, 因此有 \begin{align} \frac{V_4}{\sin \theta_4}=\frac{V_4}{-\sin (A_2\!+\!A_3\!+\!\theta_2)}.\label{c35} \end{align} (vi) 綜合上述等式 \eqref{c31}、 \eqref{c32}、 \eqref{c33}、 \eqref{c34}、 \eqref{c35}, 可得到 \begin{align} &\hskip -20pt \frac{V_3 \sin A_1\!+\!V_4\sin(A_4\!-\!A_1 )}{\sin A_4 \!\cdot\! \sin(A_4\!-\!\theta_2 )}\nonumber\\ \!=\,&\frac{V_4 \sin A_1\!-\!V_3\sin(A_4\!+\!A_1 )}{\sin A_2 \!\cdot\!\sin A_4}\!\cdot\! \Big(1\!+\!\frac{V_1}{V_2}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2} \Big(1\!-\!\sin^2\Big(\frac{A_2}2\Big)\Big)\Big]^{1/2}\nonumber\\ =\,&\frac{V_3}{\sin (A_1\!-\!\theta_2 )} =\frac{V_4}{-\sin (A_2\!+\!A_3\!+\!\theta_2 )}.\label{9} \end{align} 這第 \eqref{9} 式等式方程其中的 $$\theta_2=\sin^{-1} \left\{\frac{V_2\sin A_2}{(V_1\!+\!V_2 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_2}2\Big)\Big)\Big]^{1/2}}\right\} ,$$ 第 \eqref{9} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_3, A_4$ 共圓情形時的第 1 組 (4 項不同形式分式型) 連續等式。 (II) 其次延長線段 $\overline{A_2A_3}=V_2$ 至與圓周相交於 $D_2$ 點, 再連接 $D_2$ 點與 $A_1$ 點, 以形成圓的新內接四邊形 $A_1 D_2 A_3 A_4 $, 見圖 12 的第 2、 第 3 位置圖形。
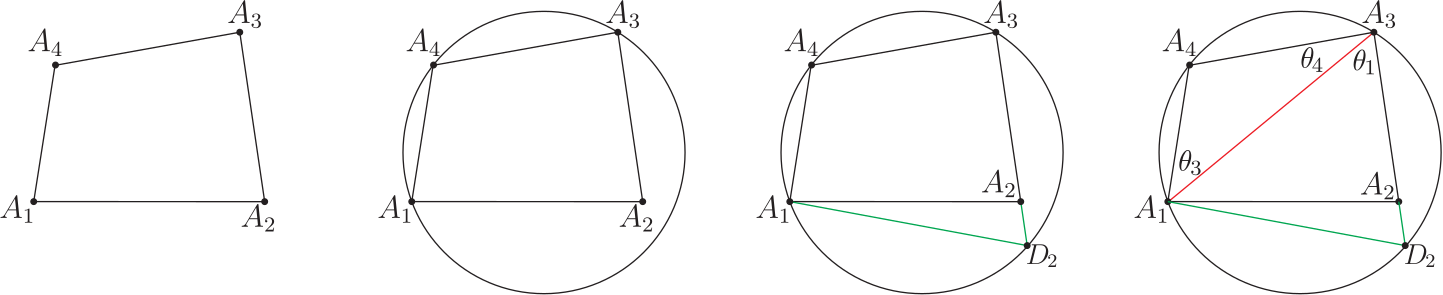
(i) 在圓的新內接四邊形 $A_1 D_2 A_3 A_4$ 中標註出邊長的對應圓周角 $\theta_1, \theta_3, \theta_4$, 而 $\angle A_3 A_1 D_2$ $=\theta_2 $, 因此, 對圓的新內接四邊形 $A_1 D_2 A_3 A_4$ 言, 有等式關係: \begin{align} \frac{\overline{A_1D_2}}{\sin \theta_1}=\frac{\overline{D_2A_3}}{\sin (\angle A_3 A_1 D_2 )} =\frac{V_3}{\sin \theta_3 }=\frac{V_4}{\sin \theta_4}.\label{c36} \end{align} (ii) 對 $\triangle A_1 A_2 A_3$ 言, $\overline{A_1A_3}=d_{13}$ 且有 $\dfrac{V_1}{\sin \theta_1 }=\dfrac{d_{13}}{\sin A_2}$, 得 $\sin\theta_1 =\dfrac{V_1\sin A_2}{d_{13}}$, $$d_{13}=({V_1}^2\!+\!{V_2}^2\!-\!2V_1 V_2 \cos A_2)^{1/2}=[(V_1\!+\!V_2 )^2\!-\!2V_1 V_2\cdot (1\!+\!\cos A_2)]^{1/2},$$ 得 $$\sin\theta_1=\frac{V_1\sin A_2}{({V_1}^2\!+\!{V_2}^2\!-\!2V_1 V_2 \cos A_2)^{1/2}}=\dfrac{V_1\sin A_2}{(V_1\!+\!V_2 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_2}2\Big)\Big)\Big]^{1/2}}.$$ 應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 4 組方程式為 \begin{align*} \,&V_3\sin(\angle A_4 A_1 D_2)\!+\!V_4\sin(A_4\!-\!(\angle A_4 A_1 D_2))\!-\!\overline{A_1D_2}\!\cdot\! \sin A_4=0 .\hskip 2cm~\\ \Rightarrow\qquad\,&V_3\sin(\pi\!-\!A_3)\!+\!V_4\sin(A_4\!-\!(\pi\!-\!A_3))\!-\!\overline{A_1D_2}\!\cdot\! \sin A_4=0 .\\ \Rightarrow\qquad\,&V_3 \sin A_3\!-\!V_4\sin(A_3\!+\!A_4 )\!-\!\overline{A_1D_2}\!\cdot\! \sin A_4=0 .\\ \Rightarrow\qquad\,&\overline{A_1D_2}=\frac{V_3 \sin A_3\!-\!V_4\sin(A_3\!+\!A_4 )}{\sin A_4}. \end{align*} 得 \begin{align} \frac{\overline{A_1D_2}}{\sin \theta_1}= \frac{V_3 \sin A_3\!-\!V_4\sin(A_3\!+\!A_4 )}{\sin A_2 \!\cdot\!\sin A_4}\!\cdot\! \Big(1\!+\!\frac{V_2}{V_1} \Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2)^2}\Big(1\!-\!\sin^2\Big(\dfrac{A_2}2\Big)\Big)\Big]^{1/2}.\label{c37} \end{align} (iii) 由於 $A_4=\theta_1\!+\!\theta_2 $, 得 $\theta_2=\angle A_3 A_1 D_2=A_4\!-\!\theta_1 $, 且還有 $$\theta_1=\sin^{-1} \left\{\dfrac{V_1\sin A_2}{(V_1\!+\!V_2 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2 } \!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_2}2\Big)\Big)\Big]^{1/2}}\right\} ,$$ 應用推論 1: 圓的內接四邊形 SASAS 方程式, 可得第 3 組方程式為 \begin{align} &\overline{D_2A_3}\!\cdot\! \sin A_4\!+\!V_3\sin(A_3\!-\!A_4 )\!-\!V_4 \sin A_3=0 .\hskip 4cm~\nonumber\\ \Rightarrow\qquad &\overline{D_2A_3}=\frac{V_4 \sin A_3\!-\!V_3\sin(A_3\!-\!A_4 )}{\sin A_4}.\nonumber\\ \hbox{得}\qquad&\frac{\overline{D_2A_3}}{\sin (\angle A_2 A_1D_2)} =\frac{\overline{D_2A_3}}{\sin\theta_2} =\frac{V_4 \sin A_3\!-\!V_3\sin(A_3\!-\!A_4 )}{\sin(A_4\!-\!\theta_1 ) \!\cdot\! \sin A_4}.\label{c38} \end{align} (iv) 由 $A_3=\theta_4\!+\!\theta_1 $, 得 $\theta_4=A_3\!-\!\theta_1 $, 因此有 \begin{align} \frac{V_4}{\sin \theta_4}=\frac{V_4}{\sin (A_3\!-\!\theta_1 )}.\label{c39} \end{align} (v) 對 $\triangle A_1 A_3 A_4$ 言, $\theta_3=\pi\!-\!A_4\!-\!\theta_4=\pi\!-\!A_4-A_3\!+\!\theta_1=A_1\!+\!A_2\!+\!\theta_1-\pi $, 得 $\sin\theta_3=-\sin (A_1\!+\!A_2\!+\!\theta_1 ) $, 因此有 \begin{align} \frac{V_3}{\sin \theta_3}=\frac{V_3}{-\sin (A_1\!+\!A_2\!+\!\theta_1)}.\label{c40} \end{align} (vi) 綜合上述等式 \eqref{c36}、 \eqref{c37}、 \eqref{c38}、 \eqref{c39}、 \eqref{c40}, 可得到 \begin{align} &\hskip -20pt \frac{V_3 \sin A_3\!-\!V_4\sin(A_3\!+\!A_4 )}{\sin A_2 \!\cdot\!\sin A_4 }\!\cdot\! \frac{V_2}{V_1}\Big)\!\cdot\! \Big[1\!-\! \dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2}\Big(1\!-\!\sin^2\Big(\frac{A_2}2\Big)\Big)\Big]^{1/2}\nonumber\\ \!=\,&\frac{V_4 \sin A_3\!-\!V_3\sin(A_3\!-\!A_4 )}{\sin(A_4\!-\!\theta_1)} =\frac{V_3}{-\sin (A_1\!+\!A_2\!+\!\theta_1 )}=\frac{V_4}{\sin (A_3\!-\!\theta_1 )}.\label{10} \end{align} 這第 \eqref{10} 式等式方程其中的 $$\theta_1=\sin^{-1} \left\{\dfrac{V_1\sin A_2}{(V_1\!+\!V_2 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_2}2\Big)\Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{10} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_3, A_4$ 共圓情形時的第 2 組 (4 項不同形式分式型) 連續等式。 [C4]、 取平面凸四邊形 $A_1 A_2 A_3 A_4$ 的 3 頂點 $A_2, A_3, A_4$ 共圓情形; 下圖 13,
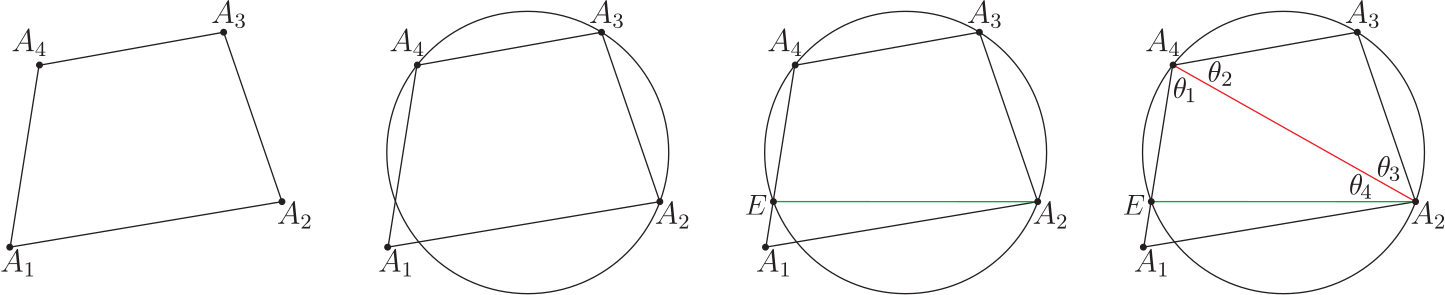
(I) 首先設定線段 $\overline{A_4A_1}=V_4$ 與圓周相交於 $E$ 點, 再連接 $E$ 點與 $A_2$ 點, 以形成圓的新內接四邊形 $EA_2 A_3 A_4 $, 見圖 13 的第 2、 第 3 位置圖形。 (i) 在圓的新內接四邊形 $EA_2 A_3 A_4$ 中標註出邊長的對應圓周角 $\theta_1, \theta_2, \theta_3$, 而 $\angle EA_2 A_4=\theta_4 $, 因此, 對圓的新內接四邊形 $EA_2 A_3 A_4$ 言, 有等式關係: $$\frac{\overline{EA_2}}{\sin \theta_1}=\frac{V_2}{\sin \theta_2}=\frac{V_3}{\sin \theta_3 }=\frac{\overline{A_4E}}{\sin(\angle EA_2 A_4 )}.$$ (ii) 仿效標題 [C1]、 [C2]、 [C3] 敘述及演算內容, 得出對應的各個分式: \begin{align*} &\frac{\overline{EA_2}}{\sin \theta_1}=\frac{V_3 \sin A_4\!-\!V_2\sin(A_3\!+\!A_4 )}{\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\frac{V_4}{V_1}\Big) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2}\Big(1\!-\!\sin^2\Big(\frac{A_1}2\Big)\Big)\Big]^{1/2}.\\ &\frac{V_2}{\sin \theta_2}=\frac{V_2}{\sin (A_4\!-\!\theta_1 )},\qquad \frac{V_3}{\sin \theta_3}=\frac{V_3}{-\sin (A_1\!+\!A_2\!+\!\theta_1 )}.\\ &\frac{\overline{A_4E}}{\sin (\angle EA_2 A_4 )} =\frac{\overline{A_4E}}{\sin (A_3\!-\!\theta_1 )} =\frac{V_2 \sin A_4\!+\!V_3\sin(A_3\!-\!A_4 )} {\sin(A_3\!-\!\theta_1 ) \!\cdot\! \sin A_3}. \end{align*} 從而得到此設定條件下的連續等式: \begin{align} &\hskip -20pt \frac{V_3 \sin A_4\!-\!V_2\sin(A_3\!+\!A_4 )}{\sin A_1 \!\cdot\!\sin A_3 }\!\cdot\! \Big(1\!+\!\frac{V_4}{V_1}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2}\Big(1\!-\!\sin^2\Big(\frac{A_2}2\Big)\Big)\Big]^{1/2}\nonumber\\ &=\frac{V_2}{\sin (A_4\!-\!\theta_1 )} =\frac{V_3}{-\sin (A_1\!+\!A_2\!+\!\theta_1 )}=\frac{V_2 \sin A_4\!+\!V_3\sin(A_3\!-\!A_4 )}{\sin(A_3\!-\!\theta_1 ) \!\cdot\! \sin A_3}. \label{11} \end{align} 這第 \eqref{11} 式等式方程其中的 $$\theta_1=\sin^{-1} \left\{\frac{V_1\sin A_1}{(V_1\!+\!V_4 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_1}2\Big)\Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{11} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_2, A_3, A_4$ 共圓情形時的第 1 組 (4 項不同形式分式型) 連續等式。 (II) 其次設定線段 $\overline{A_1A_2}=V_1$ 與圓周相交於 $E_2$ 點, 再連接 $E_2$ 點與 $A_4$ 點, 以形成圓的新內接四邊形 $E_2 A_2 A_3 A_4 $, 見圖 14 的第 2、 第 3 位置圖形。
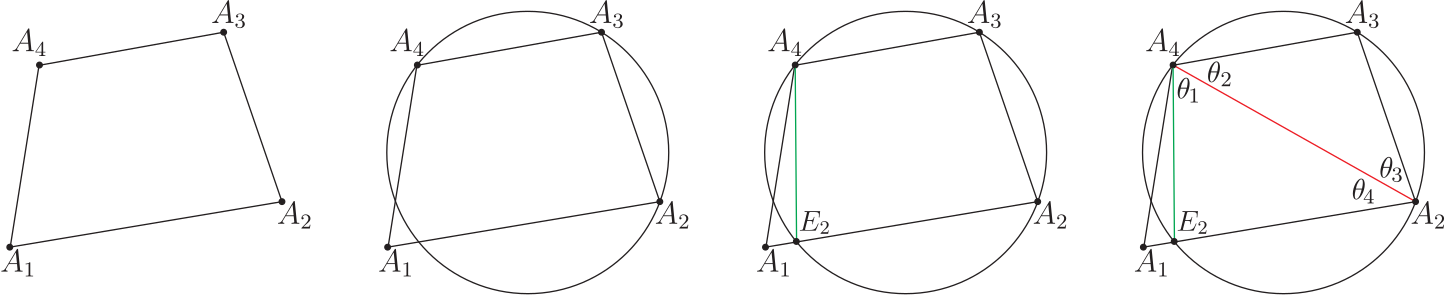
(i) 在圓的新內接四邊形 $E_2 A_2 A_3 A_4$ 中標註出邊長的對應圓周角 $\theta_2, \theta_3, \theta_4$, 而 $\angle A_2 A_4 E_2=\theta_1 $, 因此, 對圓的新內接四邊形 $E_2 A_2 A_3 A_4$ 言, 有等式關係: $$\frac{\overline{E_2A_2}}{\sin (\angle A_2 A_4 E_2 )} =\frac{V_2}{\sin \theta_2}=\frac{V_3}{\sin \theta_3}=\frac{\overline{A_4E_2}}{\sin \theta_4 }.$$ (ii) 仿效標題 [C1]、 [C2]、 [C3] 敘述及演算內容, 得出對應的各個分式: \begin{align*} &\frac{\overline{E_2A_2}}{\sin(\angle A_2 A_4 E_2 )} =\frac{\overline{E_2A_2}}{\sin \theta_1}=\frac{\overline{E_2A_2}}{\sin (A_3\!-\!\theta_4 )} =\frac{V_3 \sin A_2\!-\!V_2\sin(A_2\!-\!A_3 )}{(\sin(A_3\!-\!\theta_4 ) \!\cdot\! \sin A_3}.\\ &\frac{V_2}{\sin \theta_2}=\frac{V_2}{-\sin (A_4\!+\!A_1\!+\!\theta_4 )},\qquad \frac{V_3}{\sin \theta_3}=\frac{V_3}{\sin (A_2\!-\!\theta_4 )}.\\ &\frac{\overline{A_4E_2}}{\sin \theta_4}=\frac{V_2 \sin A_2-V_3\sin(A_2\!+\!A_3 )}{\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\dfrac{V_1}{V_4} \Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2}\Big(1\!-\!\sin^2\Big(\frac{A_1}2\Big)\Big)\Big]^{1/2}. \end{align*} 從而得到此設定條件下的連續等式: \begin{align} &\hskip -15pt \frac{V_3 \sin A_2\!-\!V_2\sin(A_2\!-\!A_3 )}{\sin(A_3\!-\!\theta_4 ) \!\cdot\! \sin A_3}=\frac{V_2}{-\sin (A_4\!+\!A_1\!+\!\theta_4 )}= \frac{V_3}{\sin (A_2\!-\!\theta_4 )}\nonumber\\ &=\frac{V_2 \sin A_2-V_3\sin(A_2\!+\!A_3 )}{\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\frac{V_1}{V_4}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \Big(1\!-\!\sin^2\Big(\frac{A_1}2\Big) \Big)\Big]^{1/2}.\label{12} \end{align} 這第 \eqref{12} 式等式方程其中的 $$\theta_4=\sin^{-1} \left\{\frac{V_4\sin A_1}{ (V_1\!+\!V_4 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_1}2\Big)\Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{12} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_2, A_3, A_4$ 共圓情形時的第 2 組 (4 項不同形式分式型)連續等式。 (III) 對本段落 (I) 而言, 還有其它解法可得另一類表示型式; 再檢視圖 13, (i) 對 $\triangle A_1 A_2 E$ 言, $$\frac{V_1}{\sin(\angle A_2 EA_1 )}=\frac{V_1}{\sin A_3}=\frac{\overline{EA_2}}{\sin A_1}=\frac{\overline{EA_1}}{\sin [A_2\!-\!(\pi\!-\!A_4 )]},$$ 得 $\overline{EA_2}=\dfrac{V_1\sin A_1}{\sin A_3}$, $\overline{EA_1}=\dfrac{-V_1\sin(A_2\!+\!A_4 )}{\sin A_3}$。 對圓的新內接四邊形 $EA_2 A_3 A_4$ 言, 有等式關係: $$\frac{\overline{EA_2}}{\sin \theta_1 }=\frac{V_2}{\sin \theta_2}=\frac{V_3}{\sin \theta_3}=\frac{V_4-\overline{EA_1}}{\sin (\angle EA_2 A_4 )}.$$ 且 $$\sin\theta_1=\frac{V_1\sin A_1}{(V_1\!+\!V_4 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_1}2\Big) \Big)\Big]^{1/2}}.$$ $\sin\theta_2=\sin(A_4\!-\!\theta_1 ) $, $\sin\theta_3=-\sin (A_1\!+\!A_2\!+\!\theta_1 ) $, $\sin(\angle EA_2 A_4 )=\sin\theta_4 =\sin(A_3\!-\!\theta_1 )$。 (ii) 因此可得 \begin{align} &\hskip -15pt \frac{V_1 \Big(1\!+\!\dfrac{V_4}{V_1}\Big) \!\cdot\! [1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_1}2\Big)\Big)\Big]^{1/2}}{\sin A_3 }=\frac{V_2}{\sin (A_4\!-\!\theta_1 )}\nonumber\\ &=\frac{V_3}{-\sin (A_1\!+\!A_2\!+\!\theta_1 )}=\frac{V_4\!\cdot\! \Big[\sin A_3 \!+\!\Big(\dfrac{V_1}{V_4}\Big)\!\cdot\! \sin(A_2\!+\!A_4 )\Big]} {\sin(A_3\!-\!\theta_1 ) \!\cdot\!\sin A_3 }. \label{13} \end{align} 這第 \eqref{13} 式等式方程其中的 $$\theta_1=\sin^{-1} \left\{\frac{V_1\sin A_1}{(V_1\!+\!V_4 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_1}2\Big)\Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{13} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_2, A_3, A_4$ 共圓情形時的第 3 組 (4 項不同形式分式型) 連續等式。 (IV) 同理, 對本段落(II)而言, 還可得另一類表示型式; 再檢視圖 14, (i) 對 $\triangle A_1 E_2 A_4$ 言, 有 $$\frac{V_4}{\sin A_3}=\frac{\overline{A_4E_2}}{\sin A_1}=\frac{\overline{A_1E_2}}{\sin [A_4\!-\!(\pi\!-\!A_2 )]} ,$$ 得 $$ \overline{A_4E_2}=\frac{V_4\sin A_1}{\sin A_3},\qquad \overline{A_1E_2}=\frac{-V_4\sin(A_2\!+\!A_4 )}{\sin A_3}.$$ 對圓的新內接四邊形 $E_2 A_2 A_3 A_4$ 言, 有等式關係: $$\frac{V_1-\overline{A_1E_2}}{\sin \theta_1}=\frac{V_2}{\sin \theta_2}=\frac{V_3}{\sin \theta_3}=\frac{\overline{A_4E_2}}{\sin \theta_4}.$$ 且 $$\sin\theta_4=\frac{V_4\sin A_1}{(V_1\!+\!V_4 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \!\cdot\! (1\!-\!\sin^2\Big(\frac{A_1}2\Big)\Big)\Big]^{1/2}},$$ $\sin\theta_2=-\sin (A_4\!+\!A_1\!+\!\theta_4 )$, $\sin\theta_1 =\sin(A_3\!-\!\theta_4 ) $, $\sin\theta_3 =\sin(A_2\!-\!\theta_4 )$。 (ii) 因此可得 \begin{align} &\hskip -15pt \frac{V_1\!\cdot\! \Big[\sin A_3\!+\!\Big(\dfrac{V_4}{V_1}\Big)\!\cdot\!\sin(A_2\!+\!A_4 )\Big]}{\sin(A_3\!-\!\theta_4 ) \!\cdot\!\sin A_3} =\frac{V_2}{-\sin (A_4\!+\!A_1\!+\!\theta_4 )}=\frac{V_3}{\sin (A_2\!-\!\theta_4 )}\nonumber\\ &=\frac{V_4 \Big(1\!+\!\dfrac{V_1}{V_4}\Big) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_1}2\Big)\Big)\Big]^{1/2}} {\sin A_3}. \label{14} \end{align} 這第 \eqref{14} 式等式方程其中的 $$\theta_4=\sin^{-1} \left\{\frac{V_4\sin A_1 }{ (V_1\!+\!V_4 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_1}2\Big)\Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{14} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_2, A_3, A_4$ 共圓情形時的第 4 組 (4 項不同形式分式型) 連續等式。 [C5]、 同樣地, 標題 [C1]、 [C2]、 [C3] 也都能各自再求解出第 3 組 (4 項不同形式分式型)與第 4 組 (4 項不同形式分式型) 連續等式。 (I) 回溯到標題 [C1], 省略演算過程而直接寫出圖形下的兩列連續等式結果; 圖7為: \begin{align} \frac{V_1}{-\sin (A_3\!+\!A_4\!+\!\theta_3 )}=\,&\frac{V_2}{\sin (A_1\!-\!\theta_3)} =\dfrac{V_3 \Big(1\!+\!\dfrac{V_4}{V_3}\Big) \!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\frac{A_4}2\Big)\Big)\Big]^{1/2}} {\sin A_2}\nonumber\\ =\,&\dfrac{V_4\!\cdot\! \Big[\sin A_2\!+\!\Big(\dfrac{V_3}{V_4}\Big)\sin (A_1\!+\!A_3)\Big]}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_3 )}. \label{15} \end{align} 這第 \eqref{15} 式等式方程其中的 $$\theta_3=\sin^{-1} \left\{\frac{V_3\sin A_4}{(V_3\!+\!V_4 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big) \Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{15} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_2, A_3$ 共圓情形時的第3組 (4 項不同形式分式型)連續等式。 圖 8 為: \begin{align} \frac{V_1}{\sin (A_3\!-\!\theta_4 )} = \,& \frac{V_2}{-\sin (A_1\!+\!A_4\!+\!\theta_4 )} =\frac{V_3\cdot \Big[\sin A_2\!+\!\Big(\dfrac{V_4}{V_3} \Big)\sin (A_1\!+\!A_3 )\Big]}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_4 )}\nonumber\\ =\,&\frac{V_4\cdot \Big(1\!+\!\dfrac{V_3}{V_4}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big) \Big)\Big]^{1/2}}{ \sin A_2}. \label{16} \end{align} 這第 \eqref{16} 式等式方程其中的 $$\theta_4=\sin^{-1} \left\{\frac{V_4\sin A_4}{(V_3\!+\!V_4 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big) \Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{16} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_2, A_3$ 共圓情形時的第 4 組 (4 項不同形式分式型)連續等式。 (II) 回溯到標題 [C2] 而直接寫出圖形下的兩列連續等式結果; 圖 9 為: \begin{align} &\hskip -20pt \frac{V_1}{-\sin (A_3\!+\!A_4\!+\!\theta_3)} = \dfrac{V_2\!\cdot\! \Big[\sin A_1\!+\!\Big(\dfrac{V_3}{V_2}\Big)\sin (A_2\!+\!A_4)\Big]} {\sin(A_1\!-\!\theta_3 ) \!\cdot\!\sin A_1}\nonumber\\ =\,&\frac{V_3\cdot \Big(1\!+\!\dfrac{V_2}{V_3}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2}\!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_3}2\Big) \Big)\Big]^{1/2}}{ \sin A_1}=\frac{V_4}{\sin (A_2\!-\!\theta_3 )}. \label{17} \end{align} 這第 \eqref{17} 式等式方程其中的 $$\theta_3=\sin^{-1} \left\{\frac{V_3\sin A_3}{(V_2\!+\!V_3 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_3}2\Big) \Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{17} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_2, A_4$ 共圓情形時的第 3 組 (4 項不同形式分式型) 連續等式。 圖10為: \begin{align} &\hskip -20pt \frac{V_1}{\sin (A_4\!-\!\theta_2)} = \dfrac{V_2\!\cdot\! \Big(1\!+\!\dfrac{V_3}{V_2}\Big) \!\cdot\! \Big[1\!-\!\dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_3}2\Big) \Big)\Big]^{1/2}}{\sin A_1}\nonumber\\ =\,&\frac{V_3\!\cdot\!\Big[\sin A_1 \!+\!\Big(\dfrac{V_2}{V_3}\Big) \sin(A_2\!+\!A_4 ) \Big]} {\sin(A_1\!-\!\theta_2 ) \!\cdot\!\sin A_1}=\frac{V_4}{-\sin (A_2\!+\!A_3\!+\!\theta_2 )}. \label{18} \end{align} 這第 \eqref{18} 式等式方程其中的 $$\theta_2=\sin^{-1} \left\{\frac{V_2\sin A_3}{(V_2\!+\!V_3 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_2 V_3}{(V_2\!+\!V_3 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_3}2\Big) \Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{18} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_2, A_4$ 共圓情形時的第 4 組 (4 項不同形式分式型) 連續等式。 (III) 回溯到標題 [C3] 而直接寫出圖形下的兩列連續等式結果; 圖 11 為: \begin{align} &\hskip -20pt \frac{V_1\!\cdot\! \Big[\sin A_4\!+\!\Big(\dfrac{V_2}{V_1}\Big)\sin (A_1\!+\!A_3 )\Big]}{\sin A_4 \!\cdot\! \sin(A_4\!-\!\theta_2 )} =\frac{V_2\!\cdot\! \Big(1\!+\!\dfrac{V_1}{V_2}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_2}2\Big) \Big)\Big]^{1/2}}{\sin A_4}\nonumber\\ =\,&\frac{V_3}{\sin (A_1\!-\!\theta_2 )} =\frac{V_4}{-\sin (A_2\!+\!A_3\!+\!\theta_2 )}. \label{19} \end{align} 這第 \eqref{19} 式等式方程其中的 $$\theta_2=\sin^{-1} \left\{\frac{V_2\sin A_2}{(V_1\!+\!V_2 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_2}2\Big) \Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{19} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_3, A_4$ 共圓情形時的第 3 組 (4 項不同形式分式型) 連續等式。 圖 12 為: \begin{align} &\hskip -20pt \frac{V_1\!\cdot\! \Big(1\!+\!\dfrac{V_1}{V_2}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_2}2\Big) \Big)\Big]^{1/2}}{\sin A_4} =\frac{V_2\!\cdot\! \Big[\sin A_4\!+\!\Big(\dfrac{V_1}{V_2}\Big)\sin (A_1\!+\!A_3 )\Big]}{ \sin(A_4\!-\!\theta_1 )\!\cdot\!\sin A_4 } \nonumber\\ =\,&\frac{V_3}{-\sin (A_1\!+\!A_2\!+\!\theta_1 )}=\frac{V_4}{\sin (A_3\!-\!\theta_1 )}. \label{20} \end{align} 這第 \eqref{20} 式等式方程其中的 $$\theta_1=\sin^{-1} \left\{\dfrac{V_1\sin A_2}{(V_1\!+\!V_2 ) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_2}{(V_1\!+\!V_2 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_2}2\Big) \Big)\Big]^{1/2}}\right\}.$$ 第 \eqref{20} 式連續等式方程式即稱為平面凸四邊形 $A_1 A_2 A_3 A_4$ 在 3 頂點 $A_1, A_3, A_4$ 共圓情形時的第 4 組 (4 項不同形式分式型) 連續等式。 綜合上述證明出連續等式的 \eqref{5} 式、 \eqref{6} 式、 \eqref{7} 式、 $\ldots$、 \eqref{20} 式合計有 16 式, 各式都能分別獨自表示出平面凸四邊形 $A_1 A_2 A_3 A_4$ 的 (4 項不同形式分式型) 連續等式。 事實上, 這平面凸四邊形還不止有此 16 式而已; 依據頂點分佈在圓周的內外側情形全部作分析探討, 還會出現其它的連續等式, 形成豐富多方樣態。 由此可知, 不同作圖法可以構造推演出不同的連續等式。 四、平面凸四邊形連續等式的檢驗若平面凸四邊形 $A_1 A_2 A_3 A_4$ 內接於一圓, 則有 $A_1=\theta_2\!+\!\theta_3 $, $A_2=\theta_3\!+\!\theta_4 $, $A_3=\theta_4\!+\!\theta_1 $, $A_4=\theta_1\!+\!\theta_2 $, 且 $\theta_1\!+\!\theta_2\!+\!\theta_3\!+\!\theta_4=\pi$ 的關係式; (I) 先以圖7的 \eqref{5} 式、\eqref{15} 式作為檢視代表。 因為平面凸四邊形內接於一圓, 則由 \eqref{5} 式中的 $$\frac{V_1}{-\sin (A_3\!+\!A_4\!+\!\theta_3 )}=\frac{V_1}{\sin\theta_1},\quad \frac{V_2}{\sin (A_1\!-\!\theta_3 )} \!=\!\frac{V_2}{\sin\theta_2},$$ 應用 SASAS 定理, 得 $$\frac{V_2 \sin A_1\!-\!V_1\sin(A_1\!-\!A_2 )}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_3 )}=\frac{V_4 \sin A_2}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_3 )} =\frac{V_4}{\sin\theta_4},$$ 應用 $A_1=\pi\!-\!A_3 $, 再應用 SASAS 定理, 使得 \begin{align*} &\frac{V_1 \sin A_1\!-\!V_2\sin(A_1\!+\!A_2 )}{\sin A_4 \!\cdot\!\sin A_2}\!\cdot\! \Big(1\!+\!\dfrac{V_4}{V_3}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big) \Big)\Big]^{1/2}\\ =\,&\frac{V_1 \sin A_3\!+\!V_2\sin(A_2\!-\!A_3 )}{\sin A_4 \!\cdot\!\sin A_2 }\!\cdot\! \Big(1\!+\!\dfrac{V_4}{V_3}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big) \Big)\Big]^{1/2}\\ =\,&\frac{V_3 \sin A_2}{\sin A_4 \!\cdot\!\sin A_2}\!\cdot\! \Big(1\!+\!\dfrac{V_4}{V_3}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big) \Big)\Big]^{1/2}\\ =\,&\frac{(V_3\!+\!V_4 )}{\sin A_4}\!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big) \Big)\Big]^{1/2} =\frac{d_{13}}{\sin A_4}=\frac{V_3}{\sin\theta_3}. \end{align*} 則原 \eqref{5} 式轉換為 $$\frac{V_1}{\sin\theta_1}=\frac{V_2}{\sin\theta_2}=\frac{V_3}{\sin\theta_3}=\frac{V_4}{\sin\theta_4}=\frac{d_{13}}{\sin A_4},$$ 完全正確。 另 \eqref{15} 式中的 $$\frac{V_1}{-\sin (A_3\!+\!A_4\!+\!\theta_3 )}=\frac{V_1}{\sin\theta_1},\qquad \frac{V_2}{\sin (A_1\!-\!\theta_3 )} = \frac{V_2}{\sin\theta_2},$$ $$\frac{V_3 \Big(1\!+\!\dfrac{V_4}{V_3}\Big) \!\cdot\! \Big[1\!-\!\dfrac{4V_3 V_4}{(V_3\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_4}2\Big) \Big)\Big]^{1/2}}{\sin A_2}=\frac{d_{13}}{\sin A_2}=\frac{V_3}{\sin\theta_3},$$ $$\frac{V_4\!\cdot\! \Big[\sin A_2\!+\!\Big(\dfrac{V_3}{V_4}\Big)\sin (A_1\!+\!A_3 )\Big]}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_3 )}= \frac{V_4\!\cdot\! \sin A_2}{\sin A_2 \!\cdot\! \sin(A_2\!-\!\theta_3 )}=\frac{V_4}{\sin\theta_4}.$$ 因 $A_1\!+\!A_3=\pi$。 使得 \eqref{15} 式轉換為 $$\frac{V_1}{\sin\theta_1}=\frac{V_2}{\sin\theta_2}=\frac{V_3}{\sin\theta_3}=\frac{V_4}{\sin\theta_4}=\frac{d_{13}}{\sin A_2}, \ \hbox{完全正確。}$$ (II) 次以圖 14 的 \eqref{12} 式、 \eqref{14} 式作為檢視代表。 因為平面凸四邊形內接於一圓, 由 \eqref{12} 式中的 \begin{align*} &\frac{V_3 \sin A_2\!-\!V_2\sin(A_2\!-\!A_3 )}{\sin(A_3\!-\!\theta_4 ) \!\cdot\! \sin A_3} =\frac{V_1 \sin A_3}{\sin(A_3\!-\!\theta_4 ) \!\cdot\! \sin A_3}=\frac{V_1}{\sin\theta_1},\\ & \frac{V_2}{-\sin (A_4\!+\!A_1\!+\!\theta_4 )}=\frac{V_2}{\sin\theta_2},\quad \frac{V_3}{\sin (A_2\!-\!\theta_4 )} =\frac{V_3}{\sin\theta_3 }, \end{align*} 再由 \begin{align*} &\frac{V_2 \sin A_2\!-\!V_3\sin(A_2\!+\!A_3 )} {\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\dfrac{V_1}{V_4}\Big)\!\cdot\! \Big[1\!-\!\frac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \Big(1\!-\!\sin^2\Big(\frac{A_1}2\Big) \Big)\Big]^{1/2}\\ =\,&\frac{V_2 \sin A_4\!+\!V_3\sin(A_3\!-\!A_4 )}{\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\dfrac{V_1}{V_4}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_1}2\Big) \Big)\Big]^{1/2}\\ =\,&\frac{V_4 \sin A_3}{\sin A_1 \!\cdot\!\sin A_3}\!\cdot\! \Big(1\!+\!\dfrac{V_1}{V_4}\Big)\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_1}2\Big) \Big)\Big]^{1/2}\\ =\,&\frac{(V_4\!+\!V_1 )}{\sin A_1}\!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \Big(1\!-\!\sin^2\Big(\dfrac{A_1}2\Big) \Big)\Big]^{1/2}=\frac{d_{24}}{\sin A_1}=\frac{V_4}{\sin\theta_4}. \end{align*} 則原 \eqref{12} 式轉換為 $$\frac{V_1}{\sin\theta_1}=\frac{V_2}{\sin\theta_2}=\frac{V_3}{\sin\theta_3}=\frac{V_4}{\sin\theta_4}=\frac{d_{24}}{\sin A_1},$$ 完全正確。 另 \eqref{14} 式中的 $$\frac{V_1\cdot \Big[\sin A_3\!+\!\Big(\dfrac{V_4}{V_1}\Big)\!\cdot\!\sin(A_2\!+\!A_4 )\Big]}{\sin(A_3\!-\!\theta_4 ) \!\cdot\!\sin A_3} =\frac{V_1 \!\cdot\!\sin A_3}{\sin(A_3\!-\!\theta_4 ) \!\cdot\!\sin A_3}=\frac{V_1}{\sin(A_3\!-\!\theta_4 )}=\frac{V_1}{\sin\theta_1},$$ $$\frac{V_2}{-\sin (A_4\!+\!A_1\!+\!\theta_4 )}=\frac{V_2}{\sin\theta_2},\qquad \frac{V_3}{\sin(A_2\!-\!\theta_4 )} =\frac{V_3}{\sin\theta_3},$$ $$\frac{V_4 \Big(1\!+\!\dfrac{V_1}{V_4}\Big) \!\cdot\! \Big[1\!-\!\dfrac{4V_1 V_4}{(V_1\!+\!V_4 )^2} \!\cdot\! \Big(1\!-\!\sin^2\Big(\dfrac{A_1}2\Big) \Big)\Big]^{1/2}}{\sin A_3}=\frac{d_{24}}{\sin A_3}=\frac{V_4}{\sin\theta_4}.$$ 使得 \eqref{14} 式轉換為 $$\frac{V_1}{\sin\theta_1}=\frac{V_2}{\sin\theta_2}=\frac{V_3}{\sin\theta_3}=\frac{V_4}{\sin\theta_4}=\frac{d_{24}}{\sin A_3},$$ 完全正確。 (III) 同理, 其餘的 12 式完全可以仿效 (I)、 (II) 的運算而得到正確的檢驗。 參、結論從應用已知的基礎理論、 輔助定理及透過圓的內接四邊形性質的引導, 我們探討了平面凸四邊形在任意3頂點共圓情形時的 4 種構圖; 每一種構圖至少可求解出 4 組 (4 項不同形式分式型)連續等式, 各等式完全依據不同的作圖法而定。 輔助作圖法是求解平面幾何問題的重要利器; 通過適切巧妙的作圖, 架構了平面凸四邊形與圓的內接四邊形兩者的連結, 而連結之間所蘊含的有效思考推演運算, 則來自於我們在平日嚴謹、 頻繁地對相關數學資訊的認知解讀。 參考文獻本文作者為嘉義市私立輔仁中學退休教師 |
2024年3月 48卷1期
平面凸四邊形分式型連續等式方程式

