| 發刊日期 |
2024年6月
|
|---|---|
| 標題 | 圓內接偶數邊數多邊形四項式正弦型方程式 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
壹、引言在研究探討平面多邊形領域裡的各支系範疇時, 能適時直覺的聯想到應用精準合宜的公式定理並整合其它數學基本性質, 以演繹推理、 分析引證出新穎創見的方程式型態理論, 有秉持這樣的探索推理觀點, 是任一位創發思考者恆常領受綿密解題薰陶與多方勤練後所必備的特徵才能, 也是在製作理論發展過程中其經常感觸領會到的一項親力體驗。 圓內接奇數邊數多邊形皆具有正弦定理的美妙對稱型態方程式。 但截至目前為止, 無論如何思考, 圓內接偶數邊數多邊形都無法尋獲如是正弦定理的那種美妙對稱型態方程式; 相對地, 由應用三角形正弦定理, 卻能在圓內接偶數邊數多邊形中導證出其獨特專屬的四項式正弦型態方程式! 研究時亦發現擁有這四項式方程式型態的最少邊數多邊形是六邊形, 然後八邊形、十邊形、$\cdots$ 等。 因四邊形無這項性質, 也暗示著不易發掘到這類四項式正弦型態方程式。 而所有圓內接奇數邊數多邊形完全不具有這類四項式正弦型態方程式。 即這兩相異類型多邊形各有所屬方程式; 其型態分明, 各擁相互支援應用效益, 互領風騷輝映! 以下正文敘述將應用三角形正弦定理專對圓內接四邊形、六邊形、八邊形、$\cdots$、等等圖形作四項式性質的比對探討, 之後再推廣到 $n=2k+4$ 偶數邊數多邊形一般化情形的一組 $n$ 個同型對稱性四項式正弦型態方程式。 並以嚴謹論述, 翔實地歸納演繹成一系列完整對照推理過程, 將全文綜合整理成清晰順暢的品讀脈絡, 詳盡地呈現出此類完善規律四項式正弦型方程式的獨特本質。 貳、本文考慮任意一個圓內接 $n$ 邊形 $A_1A_2\cdots A_n$, 令 $R$ 為此圓半徑, 並令各邊邊長為 $\overline{A_1A_2}=V_1$, $\overline{A_2A_3}=V_2$, $\overline{A_3A_4}=V_3$, $\ldots$ , $\overline{A_{i}A_{i+1}}=V_{i}$, $\ldots$ , $\overline{A_{n-3}A_{n-2}}=V_{n-3}$, $\overline{A_{n-2}A_{n-1}}=V_{n-2}$, $\overline{A_{n-1}A_n}=V_{n-1}$, $\overline{A_nA_1}=V_n$, $1\le i\le n$, $i$ 與 $n$ 皆為自然數。 而在以下內文的敘述推論驗證過程中, 所有須使用的多邊形邊長線段表示式均以上述明列的表示式為準, 且當演繹證明時需要應用到下列5個數學性質 --- 引理; 一、數學基本性質 --- 引理引理1: 三角形正弦定理 : 請見下圖 1, 半徑 $R$ 的圓內接三角形 $A_1A_2A_3$, 令邊長線段 $\overline{A_1A_2}=V_1$, $\overline{A_2A_3}=V_2$, $\overline{A_3A_1}=V_3$, 則精簡、 對稱的正弦定理公式為: $$ \frac{V_1}{\sin A_3}=\frac{V_2}{\sin A_1}=\frac{V_3}{\sin A_2}=2R. $$ (L-1) 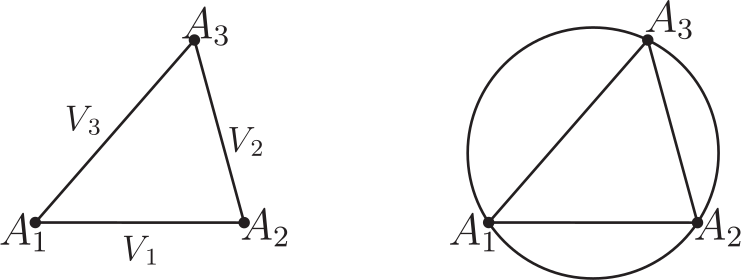 證明: 略。 引理2: 三角函數角度的和差轉換公式 \begin{eqnarray*} \sin(\alpha \pm \beta )&=&\sin \alpha \cos\beta \pm \cos \alpha \sin \beta,\\ \cos(\alpha \pm \beta )&=&\cos \alpha \cos\beta \mp \sin \alpha \sin \beta. \end{eqnarray*} 引理3: 任給一個圓內接偶數邊數 $n$ 邊形 $A_1A_2A_3A_4\cdots A_{n-1}A_n$, $n=2k+2$, $k$ 為自然數, 則此多邊形的頂角組合; $$ A_1\!+\!A_3\!+\!\cdots\!+\!A_{n-3}\!+\!A_{n-1} \!=\!A_2\!+\!A_4\!+\!\cdots\!+\!A_{n-2}\!+\!A_{n}\!=\!\frac 12(n\!-\!2)\pi. $$ (L-2) 證明: 略。 引理4: 圓內接多邊形各圓周角與對應弦長的正弦定理: 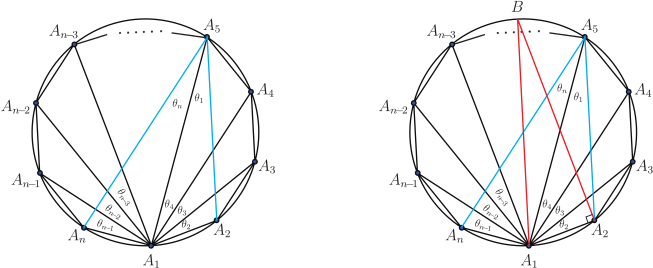 圖2, 半徑 $R$ 的圓內接 $n$ 邊形 $A_1A_2A_3A_4\cdots A_{n-2}A_{n-1}A_n$, 令邊長線段 $\overline{A_1A_2}=V_1$, $\overline{A_2A_3}=V_2$, $\overline{A_3A_4}=V_3$, $\ldots$ , $\overline{A_{n-2}A_{n-1}}=V_{n-2}$, $\overline{A_{n-1}A_n}=V_{n-1}$, $\overline{A_nA_1}=V_n$, 而邊長 $V_1$ 所對應的圓周角為 $\theta_1$, $V_2$ 所對應的圓周角為 $\theta_2$, $V_3$ 所對應的圓周角為 $\theta_3$, $\ldots$ , $V_{n-2}$ 所對應的圓周角為 $\theta_{n-2}$, $V_{n-1}$ 所對應的圓周角為 $\theta_{n-1}$, $V_n$ 所對應的圓周角為 $\theta_n$, 則此多邊形各邊長所對應的圓周角的正弦定理方程式為下列 (L-3) 式: $$ \frac{V_1}{\sin\theta_1}=\frac{V_2}{\sin\theta_2}=\frac{V_3}{\sin\theta_3}=\cdots=\frac{V_{n-2}}{\sin\theta_{n-2}}=\frac{V_{n-1}}{\sin\theta_{n-1}}=\frac{V_{n}}{\sin\theta_{n}}=2R. $$ (L-3) 證明: 參見圖 3。 引理5: 托勒密定理 (Ptolemy's Theorem) : 任給一個圓內接四邊形 $A_1A_2A_3A_4$, 令邊長線段 $\overline{A_1A_2}=V_1$, $\overline{A_2A_3}=V_2$, $\overline{A_3A_4}=V_3$, $\overline{A_4A_1}=V_4$, 對角線長 $\overline{A_1A_3}=d_{13}$, $\overline{A_2A_4}=d_{24}$, 則托勒密定理關係方程式為 $$d_{13}d_{24}=V_1V_3+V_2V_4.$$ (L-4) 證明: 略。 二、圓內接偶數邊數 $n$ 邊形四項式正弦型方程式 $n=2k+2$A. 圓內接四邊形 (A-1) 現在要應用三角形正弦定理來尋找四邊形的四項式正弦型方程式型態; 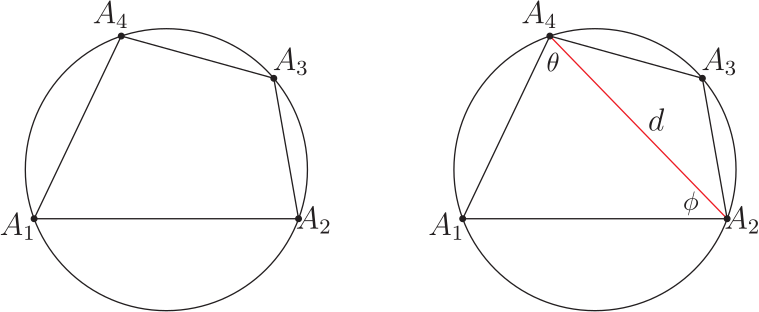 請看圖 4 的圓內接四邊形 $A_1A_2A_3A_4$, 連接兩頂點 $A_2$ 與 $A_4$ 形成直線段 $\overline{A_2A_4}=d$, 對三角形 $A_2A_3A_4$ 言, 由三角形正弦定理知 : $$\frac{d}{\sin A_3}=\frac{V_2}{\sin(A_4-\theta)}=\frac{V_3}{\sin(A_2-\phi)},$$ 且 $V_1\cos\phi+V_4\cos\theta=d$ 與 $V_1\sin\phi=V_4\sin\theta$, 以此三關係式開始推導演算, \begin{eqnarray*} \Rightarrow\ V_2\sin A_3&=&d\sin(A_4-\theta)=(V_1\cos\phi+V_4\cos\theta)(\sin A_4\cos\theta-\cos A_4\sin\theta)\\ &=&V_1\sin A_4\cos\phi\cos\theta-V_1\cos A_4\cos\phi\sin\theta\\ &&+V_4\sin A_4\cos^2\theta-V_4\cos A_4\cos\theta\sin\theta\\ &=&V_1\sin A_4\cos\phi\cos\theta-V_1\cos A_4\cos\phi\sin\theta\\ &&+V_4\sin A_4-V_4\sin A_4\sin^2\theta-V_4\cos A_4\cos\theta\sin\theta\\ &=&V_1\sin A_4\cos\phi\cos\theta-V_1\cos A_4\cos\phi\sin\theta\\ &&+V_4\sin A_4-V_1\sin A_4\sin\theta\sin\phi-V_1\cos A_4\cos\theta\sin\phi\\ &=&V_1\sin A_4\cos(\phi+\theta)-V_1\cos A_4\sin(\phi+\theta)+V_4\sin A_4\\ &=&V_1\sin A_4\cos(\pi-A_1)-V_1\cos A_4\sin(\pi-A_1)+V_4\sin A_4\\ &=&-V_1\sin A_4\cos A_1-V_1\cos A_4\sin A_1+V_4\sin A_4\\ &=&-V_1\sin (A_4+A_1)+V_4\sin A_4 \end{eqnarray*} $\Rightarrow\ V_2\sin A_3=-V_1\sin (A_4+A_1)+V_4\sin A_4$, 應用引理 3 對角互補性質, 得 \begin{eqnarray} \Rightarrow\ &&V_2\sin(\pi-A_1)=-V_1\sin(\pi-A_2+A_1)+V_4\sin(\pi-A_2)\nonumber\\ \Rightarrow\ &&V_2\sin A_1=V_1\sin (A_1-A_2)+V_4\sin A_2\nonumber\\ \Rightarrow\ &&V_1\sin (A_1-A_2)=V_2\sin A_1-V_4\sin A_2\nonumber\\ \Rightarrow\ &&\frac{\sin (A_1-A_2)}{V_4V_2}=\frac{\sin A_1}{V_4V_1}-\frac{\sin A_2}{V_1V_2}.\label{1.1} \end{eqnarray} 方程式 \eqref{1.1} 式為圓內接四邊形的第 1 個 SASAS 正弦型方程式, 也是在所有圓內接多邊形裡普遍必定存在的 SASAS 正弦型方程式, 此式只有 3 項沒有 4 項式 ! $\divideontimes$圓內接多邊形中任意三段連續相鄰邊長與居間的兩頂角恰形成以 邊長$-$頂角$-$邊長$-$頂角$-$ 邊長 SASAS 分佈排列出 \ / 或 / \ 圖樣的幾何形狀, 而此三段邊長與居間的兩頂角正弦值恰能構建成一組的兩相關方程式, 即被定義為圓內接多邊形邊長與頂角的 SASAS 正弦型方程式。 (A-2) 同理, 可再找到以 $V_3$ 領導的同類型第 3 個 SASAS 正弦型方程式, 如下式: \begin{equation} V_3\sin(A_3-A_4)=V_4\sin A_3-V_2\sin A_4\Rightarrow \frac{\sin (A_3-A_4)}{V_2V_4}=\frac{\sin A_3}{V_2V_3}-\frac{\sin A_4}{V_3V_4}.\label{1.2} \end{equation} 再應用引理 3 對角互補性質, 得 \begin{equation} \sin(A_1-A_2)=-\sin(A_3-A_4)\Rightarrow\sin(A_1-A_2)+\sin(A_3-A_4)=0\nonumber \end{equation} \begin{equation} \Rightarrow\ \frac{\sin(A_1-A_2)}{V_4V_2}+\frac{\sin(A_3-A_4)}{V_2V_4}=0\nonumber \end{equation} \begin{equation} \Rightarrow\ \frac{\sin A_1}{V_4V_1}-\frac{\sin A_2}{V_1V_2}+\frac{\sin A_3}{V_2V_3}-\frac{\sin A_4}{V_3V_4}=0\nonumber \end{equation} \begin{equation} \Rightarrow\ \frac{\sin A_1}{V_4V_1}+\frac{\sin A_3}{V_2V_3}=\frac{\sin A_2}{V_1V_2}+\frac{\sin A_4}{V_3V_4}.\label{1.3} \end{equation} 方程式 \eqref{1.3} 式為圓內接四邊形各邊長與頂角正弦值關係方程式。 等號左側是奇數標記頂角正弦值組合, 等號右側是偶數標記頂角正弦值組合, 整個方程式完全是具有規律型態的組合結構。 方程式 \eqref{1.3} 式呈現的是 4 項式! 希望此 4 項式能符合六邊形、 八邊形、 十邊形、 $\cdots$ 等等具有相同型態結構的期待! (A-3) 同理, 再應用引理 3 對角互補性質, 得 $\sin A_1=\sin A_3$ 且 $\sin A_2=\sin A_4$ \begin{equation} \Rightarrow\qquad\sin A_1+\sin A_2=\sin A_3+\sin A_4.\qquad~\label{1.4} \end{equation} 方程式 \eqref{1.4} 式是最精簡又最容易獲得的圓內接四邊形頂角正弦值關係方程式。 其與 \eqref{1.3} 式的型態結構不同, 但卻具有 4 項式的格局, 可能符合期望? 而最能顯露出四項式正弦型方程式型態結構的, 就要從下列圓內接六邊形論述起。 B. 圓內接六邊形 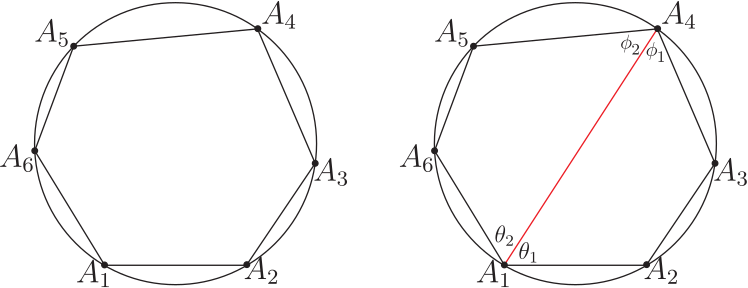 (B-1) 給定一個圓內接六邊形 $A_1A_2A_3A_4A_5A_6$, 見圖 5, 連接兩頂點 $A_1$ 與 $A_4$ 形成直線段 $\overline{A_1A_4}=d_{14}$, 將六邊形分割成四邊形 $A_1A_2A_3A_4$ 與另一個四邊形 $A_1A_4A_5A_6$。 見圖 6, 直線段又將頂角 $A_1$ 分割出 2 個分角, 使 $A_1=\theta_1+\theta_2$。 同時又將另一頂角 $A_4$ 分割出 2 個分角, 使 $A_4=\phi_1+\phi_2$。 現在要應用圓內接四邊形的 \eqref{1.3} 式關係方程式; 對圖 6 的四邊形 $A_1A_2A_3A_4$ 言, 必有下述關係式 : $$\frac{\sin \theta_1}{d_{14}V_1}+\frac{\sin A_3}{V_2V_3}=\frac{\sin A_2}{V_1V_2}+\frac{\sin\phi_1}{V_3d_{14}},$$ 同樣地對圖 6 的另一個四邊形 $A_1A_4A_5A_6$ 也必有下述關係式: $$\frac{\sin \theta_2}{d_{14}V_6}+\frac{\sin A_5}{V_4V_5}=\frac{\sin A_6}{V_5V_6}+\frac{\sin\phi_2}{V_4d_{14}},$$ 將此兩關係式相加合併, 得到下列 \eqref{2.1} 式: \begin{equation} \frac{\sin \theta_1}{d_{14}V_1}+\frac{\sin A_3}{V_2V_3}+\frac{\sin \theta_2}{d_{14}V_6}+\frac{\sin A_5}{V_4V_5} =\frac{\sin A_2}{V_1V_2}+\frac{\sin \phi_1}{V_3d_{14}}+\frac{\sin A_6}{V_5V_6}+\frac{\sin \phi_2}{V_4d_{14}}. \label{2.1} \end{equation} 接下來需應用到引理 5 托勒密定理公式, 見下圖 7; 連接直線段 $\overline{A_2A_4}=d_{24}$, 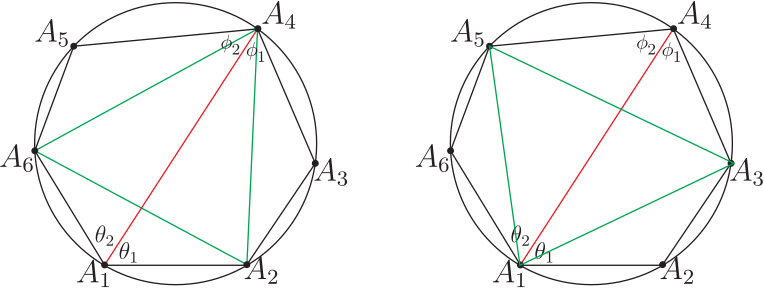 再連接直線段 $\overline{A_6A_4}=d_{64}$, 再連接直線段 $\overline{A_2A_6}=d_{26}$, 得一個新的圓內接四邊形 $A_1A_2A_4A_6$, 由托勒密定理知; $d_{14}d_{26}=V_6d_{24}+V_1d_{64}$, 再應用引理 4 圓周角的正弦定理, 得 \begin{equation} d_{14}\sin A_1=V_6\sin\theta_1+V_1\sin\theta_2\Rightarrow \frac{\sin A_1}{V_6V_1}=\frac{\sin\theta_1}{d_{14}V_1}+\frac{\sin\theta_2}{V_6d_{14}}.\label{2.2} \end{equation} 同理, 見圖 8, 再得一個新的圓內接四邊形 $A_1A_3A_4A_5$, 仿效圖 7 的做法, 再應用托勒密定理與圓周角的正弦定理, 必得 \begin{equation} \frac{\sin A_4}{V_3V_4}=\frac{\sin\phi_1}{d_{14}V_3}+\frac{\sin\phi_2}{V_4d_{14}}.\label{2.3} \end{equation} 最後, 再將 \eqref{2.2} 式與 \eqref{2.3} 式一起同步代入 \eqref{2.1} 式中, 即得美妙的下列 \eqref{2.4} 式; \begin{equation} \frac{\sin A_1}{V_6V_1}+\frac{\sin A_3}{V_2V_3}+\frac{\sin A_5}{V_4V_5}=\frac{\sin A_2}{V_1V_2}+\frac{\sin A_4}{V_3V_4}+\frac{\sin A_6}{V_5V_6}.\label{2.4} \end{equation} \eqref{2.4} 式即為圓內接六邊形各邊長與頂角正弦值關係方程式, 媲美 \eqref{1.3} 式。 (B-2) 應用三角形正弦定理與 \eqref{2.4} 式尋找圓內接六邊形四項式正弦型方程式 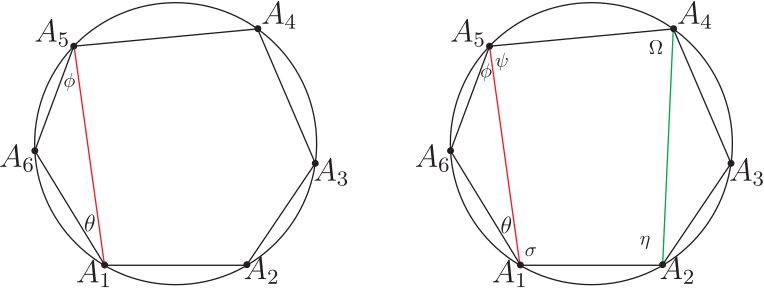 (i) 見圖 9, 連接 $A_1$ 與 $A_5$ 頂點成對角線長 $d_{15}=\overline{A_1A_5}$, 對三角形 $\triangle A_1A_5A_6$ 言, 利用其正弦定理可得下列關係式: $$\frac{d_{15}}{\sin A_6}=\frac{V_5}{\sin \theta}=\frac{V_6}{\sin\phi}=2R;$$ (2B.1) 此處 $d_{15}=V_5\cos\phi+V_6\cos\theta$ 且 $V_5\sin\phi=V_6\sin \theta$, 由 (2B.1) 式, 再應用引理 3 的 $A_1+A_3+A_5=A_2+A_4+A_6=2\pi$ 性質, 可得: $\dfrac{d_{15}}{-\sin(A_2+A_4)}=2R$. (ii) 見圖 10, 連接 $A_2$ 與 $A_4$ 頂點成對角線, 對三角形 $\triangle A_2A_3A_4$ 言, 利用其正弦定理可得下列關係式: $$\frac{V_2}{\sin (A_4-\Omega)}=\frac{V_3}{\sin (A_2-\eta)}=2R.$$ (2B.2) 又由圓內接四邊形 $A_1A_2A_4A_5$ 的 $\psi+\eta=\Omega+\sigma=\pi$ 性質, 見圖 10, 可得; $A_4-\Omega=A_4-(\pi-\sigma)=A_4-(\pi-A_1+\theta)=A_1+A_4-\theta-\pi $ 及 $A_2-\eta=A_2-(\pi-\psi)=A_2-(\pi-A_5+\phi)=A_2+A_5-\phi-\pi$, 代入(2B.2)式, 得: $$\frac{V_2}{-\sin (A_1+A_4-\theta)}=\frac{V_3}{-\sin (A_2+A_5-\phi)}=2R.$$ (iii) 綜合 (i) 與 (ii), 可對照得到下列重要關鍵的居間聯繫關係式 \eqref{2.5} 式: \begin{equation} \frac{d_{15}}{-\sin(A_2+A_4)}=\frac{V_2}{-\sin (A_1+A_4-\theta)}=\frac{V_3}{-\sin (A_2+A_5-\phi)},\label{2.5} \end{equation} 且 $d_{15}=V_5\cos\phi+V_6\cos\theta$ 及 $V_5\sin\phi=V_6\sin\theta$, 現在繼續推演運算; 由 \begin{align*} &\hskip -15pt V_2\sin(A_2+A_4)=d_{15}\sin(A_1+A_4-\theta)=(V_5\cos\phi+V_6\cos\theta)\cdot \sin(A_1+A_4-\theta)\\ &=V_5\cos\phi\cos\theta\sin(A_1+A_4)-V_5\cos\phi\sin\theta\cos(A_1+A_4)\\ &\quad +V_6\cos^2\theta\sin(A_1+A_4)-V_6\cos\theta\sin\theta\cos(A_1+A_4)\\ &=V_5\cos\phi\cos\theta\sin(A_1+A_4)+V_6(1-\sin^2\theta)\sin(A_1+A_4)\\ &\quad -V_5(\cos\phi\sin\theta+\sin\phi\cos\theta)\cos(A_1+A_4)\\ &=V_5\cos\phi\cos\theta\sin(A_1+A_4)+V_6\sin(A_1+A_4)\\ &\quad -V_6\sin^2\theta\sin(A_1+A_4)-V_5\sin(\theta+\phi)\cos(A_1+A_4)\\ &=V_5\cos\phi\cos\theta\sin(A_1+A_4)+V_6\sin(A_1+A_4)\\ &\quad -V_5\sin\theta\sin\phi\sin(A_1+A_4)-V_5\sin A_6\cos(A_1+A_4)\\ &=V_5\cos(\theta+\phi)\sin(A_1+A_4)+V_6\sin(A_1+A_4)-V_5\sin A_6\cos(A_1+A_4)\\ &=-V_5\cos A_6\sin(A_1+A_4)+V_6\sin(A_1+A_4)-V_5\sin A_6\cos(A_1+A_4)\\ &=-V_5\sin(A_1+A_4+A_6)+V_6\sin(A_1+A_4)\\ &=V_6\sin(A_1+A_4)-V_5\sin(A_1-A_2)\\ \Rightarrow\ &\qquad~\frac{\sin(A_2+A_4)}{V_5V_6}=\frac{\sin(A_1+A_4)}{V_2V_5}-\frac{\sin(A_1-A_2)}{V_6V_2}\\ \Rightarrow\ &\qquad~-\frac{\sin A_6}{V_5V_6}=\frac{\sin(A_1+A_4)}{V_2V_5}-\frac{\sin A_1}{V_6V_1}+\frac{\sin A_2}{V_1V_2}\\ \Rightarrow\ &\qquad~\frac{\sin(A_1+A_4)}{V_2V_5}-\frac{\sin A_1}{V_6V_1}+\frac{\sin A_2}{V_1V_2}+\frac{\sin A_6}{V_5V_6}=0.\tag*{(2.5-1)} \end{align*} (iv) 同理, 再由方程式 \eqref{2.5} 式, 可得下列另一組關係式; $$V_3\sin(A_2+A_4)=d_{15}\sin(A_2+A_5-\phi)=(V_5\cos\phi+V_6\cos\theta)\cdot\sin(A_2+A_5-\phi).$$ 仿照 (iii) 的推導過程, 將上式展開, 變換關係後, 再化簡, 運算, 組合, 可得 \begin{align*} V_3\sin(A_2+A_4)&=V_5\sin(A_2+A_5)-V_6\sin(A_2+A_5+A_6)\\ &=V_5\sin(A_2+A_5)+V_6\sin(A_4-A_5)\\ \Rightarrow\ \qquad~&\frac{\sin(A_2+A_5)}{V_3V_6}+\frac{\sin A_4}{V_3V_4}-\frac{\sin A_5}{V_4V_5}+\frac{\sin A_6}{V_5V_6}=0.\hskip 4cm\tag*{(2.5-2)}\\ {\hbox{引用 \eqref{2.4} 式, 可得}} &\hskip 5pt \frac{\sin A_4}{V_3V_4}-\frac{\sin A_5}{V_4V_5}+\frac{\sin A_6}{V_5V_6}=\frac{\sin A_1}{V_6V_1}+\frac{\sin A_3}{V_2V_3}-\frac{\sin A_2}{V_1V_2}.\\ {\hbox{代入 (2.5-2) 式}} \Rightarrow\ \qquad~&\frac{\sin(A_2+A_5)}{V_3V_6}+\frac{\sin A_1}{V_6V_1}+\frac{\sin A_3}{V_2V_3}-\frac{\sin A_2}{V_1V_2}=0.\tag*{(2.5-3)} \end{align*} (v) 將方程式 (2.5-1) 式與 (2.5-3) 式兩者相加, 化簡後得下式: \begin{eqnarray} &&\frac{\sin(A_1+A_4)}{V_2V_5}+\frac{\sin A_6}{V_5V_6}+\frac{\sin(A_2+A_5)}{V_3V_6}+\frac{\sin A_3}{V_2V_3}=0\nonumber\\ \Rightarrow\ \qquad~&&\frac{\sin(A_1+A_4)}{V_2V_5}+\frac{\sin(A_2+A_5)}{V_3V_6}=-\Big(\frac{\sin A_3}{V_2V_3}+\frac{\sin A_6}{V_5V_6}\Big).\hskip 1cm\qquad~\label{2.6} \end{eqnarray} 此方程式 \eqref{2.6} 式就是圓內接六邊形四項式正弦型方程式 ! 方程式 \eqref{2.6} 式的內涵包括全部六個內角及四段邊長, 這是圓內接六邊形的必然性質。 也是平面凸六邊形在六段邊長皆固定情況下, 適當調整其各內角角度而成最大面積的必然結果; 這是在應用拉格朗日乘數法 (Lagrange multiplier method) 求算出平面凸六邊形最大面積時所伴隨存在的一個相關方程式 \eqref{2.6} 式。 此外, 依圓內接六邊形圖形的一般性還可得到另外五個同類型對稱方程式如下: \begin{eqnarray} \frac{\sin(A_2+A_5)}{V_3V_6}+\frac{\sin(A_3+A_6)}{V_4V_1}&=&-\Big(\frac{\sin A_4}{V_3V_4}+\frac{\sin A_1}{V_6V_1}\Big),\hskip 1cm\qquad~\label{2.7}\\ \frac{\sin(A_3+A_6)}{V_4V_1}+\frac{\sin(A_4+A_1)}{V_5V_2}&=&-\Big(\frac{\sin A_5}{V_4V_5}+\frac{\sin A_2}{V_1V_2}\Big),\hskip 1cm\qquad~\label{2.8}\\ \frac{\sin(A_4+A_1)}{V_5V_2}+\frac{\sin(A_5+A_2)}{V_6V_3}&=&-\Big(\frac{\sin A_3}{V_2V_3}+\frac{\sin A_6}{V_5V_6}\Big),\hskip 1cm\qquad~\label{2.9}\\ \frac{\sin(A_5+A_2)}{V_6V_3}+\frac{\sin(A_6+A_3)}{V_1V_4}&=&-\Big(\frac{\sin A_4}{V_3V_4}+\frac{\sin A_1}{V_6V_1}\Big),\hskip 1cm\qquad~\label{2.10}\\ \frac{\sin(A_6+A_3)}{V_1V_4}+\frac{\sin(A_1+A_4)}{V_2V_5}&=&-\Big(\frac{\sin A_5}{V_4V_5}+\frac{\sin A_2}{V_1V_2}\Big).\hskip 1cm\qquad~\label{2.11} \end{eqnarray} 將 \eqref{2.6} 式、 \eqref{2.7} 式、 \eqref{2.8} 式與 \eqref{2.9} 式、 \eqref{2.10} 式、 \eqref{2.11} 式作比對, 兩組完全相同, 故 6 個同類型對稱方程式中有兩兩重複, 僅需 3 個方程式就能完整表述。 方程式 \eqref{2.6} 式、 \eqref{2.7} 式、 \eqref{2.8} 式就是 3 個圓內接六邊形四項式正弦型方程式! 現在將此 3 個方程式提回去對照四邊形的 \eqref{1.3} 式、 \eqref{1.4} 式, 顯然型態完全不符! 所以確認知圓內接四邊形沒有這類結構型態的四項式正弦型方程式。 C. 圓內接八邊形 (C-1) 給定一個圓內接八邊形 $A_1A_2A_3A_4A_5A_6A_7A_8$, 見下圖 11, 連接 $A_1$ 與 $A_7$ 頂點 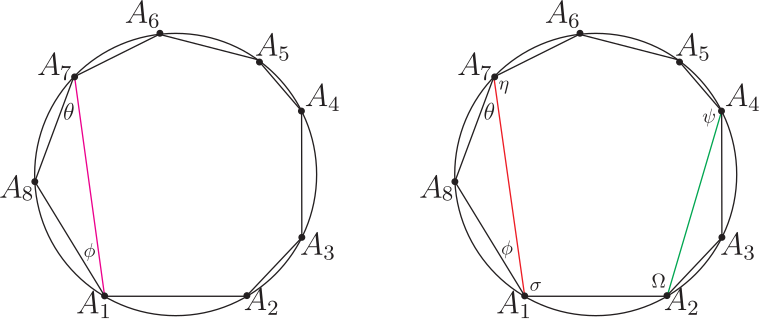 成對角線長 $d_{17}=\overline{A_1A_7}$, 對三角形 $\triangle A_1A_7A_8$ 言, 利用其正弦定理可得下列關係式: $$ \frac{d_{17}}{\sin A_8}=\frac{V_8}{\sin \theta}=\frac{V_7}{\sin \phi}=2R. $$ (3C.1) 此處配合有 $d_{17}=V_8\cos\phi+V_7\cos\theta$ 且 $V_8\sin\phi=V_7\sin\theta$ 的兩關係式, (i) 由 (3C.1) 式, 再應用引理 3 的 $A_1\!+\!A_3\!+\!A_5\!+\!A_7=A_2\!+\!A_4\!+\!A_6\!+\!A_8\!=\!3\pi$ 性質, 可得: $$\frac{d_{17}}{\sin A_8}=\frac{V_8}{\sin \theta}=\frac{V_7}{\sin \phi}=\frac{d_{17}}{\sin (A_2+A_4+A_6)}=2R.$$ (ii) 見圖 12, 連接 $A_2$ 與 $A_4$ 頂點成對角線, 對三角形 $\triangle A_2A_3A_4$ 言, 利用其正弦定理可得下列關係式: $$ \frac{V_2}{\sin (A_4-\psi)}=\frac{V_3}{\sin (A_2-\Omega)}=2R. $$ (3C.2) 又由圓內接六邊形 $A_1A_2A_4A_5A_6A_7$ 的 $\psi+A_6+\sigma=\Omega+A_5+\eta=2\pi$ 性質, 見圖 12, 可得: $A_4-\psi=A_4-(2\pi-A_6-\sigma)=A_4+A_6-(2\pi-A_1+\phi)=A_1+A_4+A_6-\phi-2\pi $ 及 $A_2-\Omega=A_2-(2\pi-A_5-\eta)=A_2+A_5-(2\pi-A_7+\theta)=A_2+A_5+A_7-\theta-2\pi$, 代入 (3C.2) 式, 得: $$\frac{V_2}{\sin (A_1+A_4+A_6-\phi)}=\frac{V_3}{\sin (A_2+A_5+A_7-\theta)}=2R.$$ (iii) 綜合 (i) 與 (ii), 可對照得到下列重要關鍵的居間聯繫關係式 \eqref{3.1} 式: \begin{equation} \frac{d_{17}}{\sin (A_2+A_4+A_6)}=\frac{V_2}{\sin (A_1+A_4+A_6-\phi)}=\frac{V_3}{\sin (A_2+A_5+A_7-\theta)}=2R.\label{3.1} \end{equation} 且 $d_{17}=V_8\cos\phi+V_7\cos\theta$ 及 $V_8\sin\phi=V_7\sin\theta$, 現在繼續推演運算: \begin{align} \Rightarrow\ &V_2\sin(A_2+A_4+A_6)=d_{17}\cdot \sin(A_1+A_4+A_6-\phi)\nonumber\\ &=(V_8\cos\phi+V_7\cos\theta)\cdot\sin(A_1+A_4+A_6-\phi)\nonumber\\ &=V_8\sin(A_1+A_4+A_6)\cos^2\phi-V_8\cos(A_1+A_4+A_6)\sin\phi\cos\phi\nonumber\\ &\quad +V_7\sin(A_1+A_4+A_6)\cos\theta\cos\phi-V_7\cos(A_1+A_4+A_6)\cos\theta\sin\phi\nonumber\\ &=V_8\sin(A_1+A_4+A_6)-V_8\sin(A_1+A_4+A_6)\sin^2\phi\nonumber\\ &\quad -V_8\cos(A_1+A_4+A_6)\sin\phi\cos\phi+V_7\sin(A_1+A_4+A_6)\cos\theta\cos\phi\nonumber\\ &\quad -V_7\cos(A_1+A_4+A_6)\cos\theta\sin\phi\nonumber\\ &=V_8\sin(A_1+A_4+A_6)-V_7\sin(A_1+A_4+A_6)\sin\theta\sin\phi\nonumber\\ &\quad -V_7\cos(A_1+A_4+A_6)\sin\theta\cos\phi+V_7\sin(A_1+A_4+A_6)\cos\theta\cos\phi\nonumber\\ &\quad -V_7\cos(A_1+A_4+A_6)\cos\theta\sin\phi\nonumber\\ &=V_8\sin(A_1+A_4+A_6)+V_7\sin(A_1+A_4+A_6)\cos(\theta+\phi)\nonumber\\ &\quad -V_7\cos(A_1+A_4+A_6)\sin(\theta+\phi)\nonumber\\ &=V_8\sin(A_1+A_4+A_6)-V_7\sin(A_1+A_4+A_6)\cos A_8\nonumber\\ &\quad -V_7\cos(A_1+A_4+A_6)\sin A_8\nonumber\\ &=V_8\sin(A_1+A_4+A_6)-V_7\sin(A_1+A_4+A_6+A_8)\nonumber\\ \Rightarrow\ & V_2\sin(A_2+A_4+A_6)=V_8\sin(A_1+A_4+A_6)-V_7\sin(A_1+A_4+A_6+A_8)\nonumber\\ \Rightarrow\ & ~\qquad\frac{\sin(A_1+A_4+A_6+A_8)}{V_2V_8}=\frac{\sin(A_1+A_4+A_6)}{V_2V_7}-\frac{\sin A_8}{V_7V_8}\nonumber\\ \Rightarrow\ & ~\qquad-\frac{\sin (A_1-A_2)}{V_2V_8}=\frac{\sin(A_1+A_4+A_6)}{V_2V_7}-\frac{\sin A_8}{V_7V_8}\nonumber\\ \Rightarrow\ & ~\qquad\frac{\sin(A_1+A_4+A_6)}{V_2V_7}+\frac{\sin A_1}{V_8V_1}-\frac{\sin A_2}{V_1V_2}-\frac{\sin A_8}{V_7V_8}=0.\label{3.2} \end{align} (C-2) 見下圖 13, 連接 $A_2$ 與 $A_8$ 頂點成對角線長 $d_{28}=\overline{A_2A_8}$, 對三角形 $\triangle A_1A_2A_8$ 言, 由正弦定理可得下列關係式: $$\frac{d_{28}}{\sin A_1}=\frac{V_8}{\sin \phi}=\frac{V_1}{\sin \theta}=2R.$$ (3C.3) 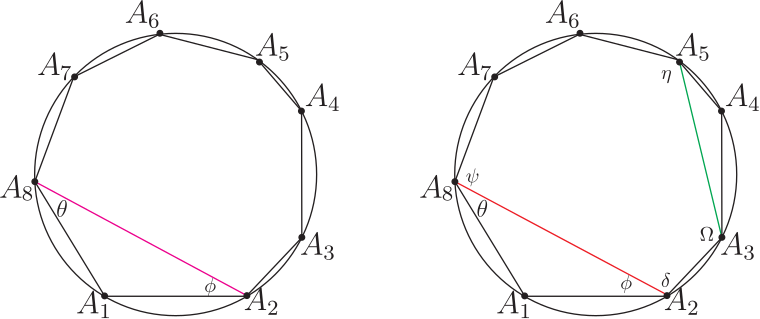 此處配合有 $d_{28}=V_1\cos\phi+V_8\cos\theta$ 且 $V_1\sin\phi=V_8\sin\theta$ 的兩關係式, (i) 由 (3C.3) 式, 再應用引理 3 的 $A_1\!+\!A_3\!+\!A_5\!+\!A_7=A_2\!+\!A_4\!+\!A_6\!+\!A_8\!=\!3\pi$ 性質, 可得; $$\frac{d_{28}}{\sin A_1}=\frac{V_8}{\sin \phi}=\frac{V_1}{\sin \theta}=\frac{d_{28}}{\sin (A_3+A_5+A_7)}=2R.$$ (ii) 見圖 14, 連接 $A_3$ 與 $A_5$ 頂點成對角線, 對三角形 $\triangle A_2A_4A_5$ 言, 利用其正弦定理可得下列關係式: $$ \frac{V_4}{\sin (A_3-\Omega)}=\frac{V_3}{\sin (A_5-\eta)}=2R, $$ (3C.4) 又由圓內接六邊形 $A_2A_3A_5A_6A_7A_8$ 的 $\psi+A_6+\Omega=\delta+A_7+\eta=2\pi$ 性質, 見圖 14, 可得: $A_5-\eta=A_5-(2\pi-A_7-\delta)=A_5+A_7-(2\pi-A_2+\phi)=A_2+A_5+A_7-\phi-2\pi $, 代入 (3C.4) 式, 得: $$\frac{V_3}{\sin (A_2+A_5+A_7-\phi)}=2R.$$ (iii) 綜合 (i) 與 (ii), 可再對照得到下列重要關鍵的居間聯繫關係式 \eqref{3.3} 式: \begin{equation} \frac{d_{28}}{\sin (A_3+A_5+A_7)}=2R=\frac{V_3}{\sin (A_2+A_5+A_7-\phi)}\label{3.3} \end{equation} 且 $d_{28}=V_1\cos\phi+V_8\cos\theta$ 及 $V_1\sin\phi=V_8\sin\theta$, 接著繼續推演運算; 由 \eqref{3.3} 式並仿效上述 (C-1)之全部計算推理過程, 可得下式: \begin{align} &\hskip -10pt V_3\sin(A_3+A_5+A_7)=d_{28}\cdot \sin(A_2+A_5+A_7-\phi)\nonumber\\ &=(V_1\cos\phi+V_8\cos\theta)\cdot\sin(A_2+A_5+A_7-\phi)\nonumber\\ \Rightarrow\ & V_3\sin(A_3+A_5+A_7)=V_1\sin(A_2+A_5+A_7)-V_8\sin(A_2+A_5+A_7+A_1)\nonumber\\ \Rightarrow\ & \frac{\sin(A_2+A_5+A_7)}{V_3V_8}-\frac{\sin(A_2+A_5+A_7+A_1)}{V_3V_1}-\frac{\sin A_1}{V_8V_1}=0\nonumber\\ \Rightarrow\ & \frac{\sin (A_2+A_5+A_7)}{V_3V_8}+\frac{\sin(A_2-A_3)}{V_3V_1}-\frac{\sin A_1}{V_8V_1}=0\nonumber\\ \Rightarrow\ & \frac{\sin(A_2+A_5+A_7)}{V_3V_8}+\frac{\sin A_2}{V_1V_2}-\frac{\sin A_3}{V_2V_3}-\frac{\sin A_1}{V_8V_1}=0.\label{3.4} \end{align} (C-3) 將方程式 \eqref{3.2} 式與 \eqref{3.4} 式兩者相加, 化簡後得下式: \begin{eqnarray} &&\frac{\sin(A_1+A_4+A_6)}{V_2V_7}-\frac{\sin A_8}{V_7V_8}+\frac{\sin(A_2+A_5+A_7)}{V_3V_6}-\frac{\sin A_3}{V_2V_3}=0\nonumber\\ \Rightarrow\ \qquad~&&\frac{\sin(A_1+A_4+A_6)}{V_2V_7}+\frac{\sin(A_2+A_5+A_7)}{V_3V_8}=\frac{\sin A_3}{V_2V_3}+\frac{\sin A_8}{V_7V_8}.\hskip 1cm\qquad~\label{3.5} \end{eqnarray} 此方程式 \eqref{3.5} 式就是圓內接八邊形四項式正弦型方程式! 方程式 \eqref{3.5} 式的內涵包括全部八個內角及四段邊長, 這是圓內接八邊形的必然性質。 此外, 依圓內接八邊形圖形的一般性還可得到另外七個同類型對稱方程式如下; \begin{align*} \frac{\sin(A_2+A_5+A_7)}{V_3V_8}+\frac{\sin(A_3+A_6+A_8)}{V_4V_1}&=\frac{\sin A_4}{V_3V_4}+\frac{\sin A_1}{V_8V_1},\hskip 1cm\qquad~\tag*{(3.5.2)}\\ \frac{\sin(A_3+A_6+A_8)}{V_4V_1}+\frac{\sin(A_4+A_7+A_1)}{V_5V_2}&=\frac{\sin A_5}{V_4V_5}+\frac{\sin A_2}{V_1V_2},\hskip 1cm\qquad~\tag*{(3.5.3)}\\ \frac{\sin(A_4+A_7+A_1)}{V_5V_2}+\frac{\sin(A_5+A_8+A_2)}{V_6V_3}&=\frac{\sin A_6}{V_5V_6}+\frac{\sin A_3}{V_2V_3},\hskip 1cm\qquad~\tag*{(3.5.4)}\\ \frac{\sin(A_5+A_8+A_2)}{V_6V_3}+\frac{\sin(A_6+A_1+A_3)}{V_7V_4}&=\frac{\sin A_7}{V_6V_7}+\frac{\sin A_4}{V_3V_4},\hskip 1cm\qquad~\tag*{(3.5.5)}\\ \frac{\sin(A_6+A_1+A_3)}{V_7V_4}+\frac{\sin(A_7+A_2+A_4)}{V_8V_5}&=\frac{\sin A_8}{V_7V_8}+\frac{\sin A_5}{V_4V_5},\hskip 1cm\qquad~\tag*{(3.5.6)}\\ \frac{\sin(A_7+A_2+A_4)}{V_8V_5}+\frac{\sin(A_8+A_3+A_5)}{V_1V_6}&=\frac{\sin A_1}{V_8V_1}+\frac{\sin A_6}{V_5V_6},\hskip 1cm\qquad~\tag*{(3.5.7)}\\ \frac{\sin(A_8+A_3+A_5)}{V_1V_6}+\frac{\sin(A_1+A_4+A_6)}{V_2V_7}&=\frac{\sin A_2}{V_1V_2}+\frac{\sin A_7}{V_6V_7}.\hskip 1cm\qquad~\tag*{(3.5.8)} \end{align*} 以上的圓內接八邊形所有四項式正弦型方程式全組 8 個方程式都被尋獲了 ! D. 接著省略繼續展示與證明 $n=10, 12, \ldots$ 等等的圓內接偶數邊數多邊形各同類方程式情形, 直到以下的一般化圓內接 $n=2k+4$ 邊形, $k$ 為自然數; E. 圓內接 $n=2k+4$ 邊形, $k$ 為所有任意自然數。 現在先來對照比較上述的方程式 \eqref{2.6} 式與 \eqref{3.5} 式四項式正弦型內容結構; 發覺到方程式等號右側兩項是由第三個頂角 $A_3$ 與最後的頂角 $A_n$ 分別形成分式型。 而等號左側兩項分別是由 $A_1+A_4+A_6+\cdots$ 與 $A_2+A_5+A_7+\cdots$ 的規律角度組合各自形成分式型。 今將此觀察分析結果, 作一個歸納類推並推廣至一般化的圓內接 $n=2k+4$ 邊形, 進而證明出其獨特的四項式正弦型方程式組。 (E-1) 給定一個圓內接 $n=2k+4$ 邊形 $A_1A_2A_3\cdots A_{n-3}A_{n-2}A_{n-1}A_n$, 由觀察分析知 (i) 先選定有頂角 $A_n$ 的三角形;見圖 15, 連接頂點 $A_1$ 與 $A_{n-1}$ 頂點形成對角線長 $d_{1(n-1)}=\overline{A_1A_{n-1}}$, 對三角形 $\triangle A_1A_{n-1}A_n$ 言, 利用其正弦定理可得下列關係式: $$\frac{d_{1(n-1)}}{\sin A_n}=\frac{V_n}{\sin \phi}=\frac{V_{n-1}}{\sin \theta}=2R,$$ (4E.1) 且配合著 $d_{1(n-1)}=V_{n-1}\cos\phi+V_n\cos\theta$ 及 $V_{n-1}\sin\phi=V_n\sin\theta$ 的兩關係式, 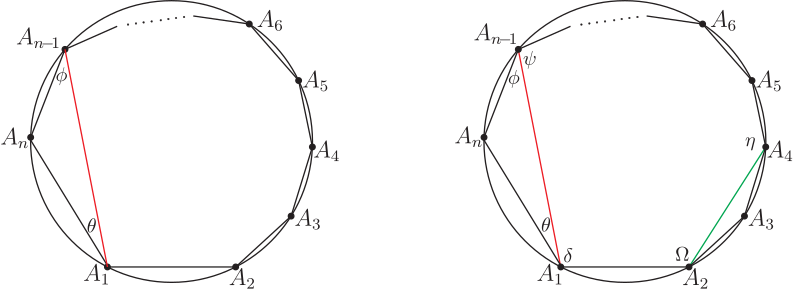 (ii) 見圖 16, 連接 $A_2$ 與 $A_4$ 頂點成對角線, 對三角形 $\triangle A_2A_3A_4$ 言, 利用其正弦定理可得下列關係式: $$\frac{V_2}{\sin (A_4-\eta)}=\frac{V_3}{\sin (A_2-\Omega)}=2R,$$ (4E.2) 又由圓內接 $n-2$ 邊形 $A_1A_2A_4A_5\cdots A_{n-2}A_{n-1}$ 的 $\eta+A_6+A_8+\cdots+A_{n-4}+A_{n-2}+\delta=\Omega+A_5+\cdots+A_{n-3}+\psi=\Big(\dfrac n2-2\Big)\pi$ 性質, 見圖 16, 可得: \begin{eqnarray*} A_4-\eta&=&A_4-\Big[\Big(\frac n2-2\Big)\pi-A_6-A_8-\cdots-A_{n-2}-\delta\Big]\\ &=&A_4+A_6+\cdots+A_{n-2}-\Big[\Big(\frac n2-2\Big)\pi-A_1+\theta\Big]\\ &=&A_1+A_4+A_6+A_8+\cdots+A_{n-4}+A_{n-2}-\theta-\Big(\frac n2-2\Big)\pi. \end{eqnarray*} 代入 (4E.2) 式, 得: \begin{align*} &\frac{V_2}{\sin(A_1+A_4+A_6+A_8+\cdots+A_{n-4}+A_{n-2}-\theta)\cdot \cos[(\frac n2-2)\pi]}=2R\\ \Rightarrow\ &\frac{V_2}{(-1)^{\frac n2}\cdot \sin(A_1+A_4+A_6+A_8+\cdots+A_{n-4}+A_{n-2}-\theta)}=2R.\tag*{(4E.3)} \end{align*} (iii) 由 (4E.1) 式與 (4E.3) 式, 可得到下列重要關鍵的居間聯繫關係式 (21) 式: \begin{equation} \Rightarrow\qquad~ \frac{d_{1(n-1)}}{\sin A_n}= \frac{V_2}{(-1)^{\frac n2}\cdot \sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-4}\!+\!A_{n-2}\!-\!\theta)}\!=\!2R,\label{4.1} \end{equation} 且配合著 $d_{1(n-1)}=V_{n-1}\cos\phi+V_n\cos\theta$ 及 $V_{n-1}\sin\phi=V_n\sin\theta$, 繼續推演運算: \begin{align*} \Rightarrow\qquad &\hskip -15pt V_2\sin A_n=d_{1(n-1)}\cdot (-1)^{\frac n2}\cdot \sin(A_1\!+\!A_4\!+\!A_6\!+\!A_8+\cdots\!+\!A_{n-4}\!+\!A_{n-2}\!-\!\theta)\\ =&(V_{n-1}\cos\phi\!+\!V_n\cos\theta)(-1)^{\frac n2}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2}\!-\!\theta)\\ =&(-1)^{\frac n2}[V_{n-1}\cos\phi\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\cos\theta\\ &\ -V_{n-1}\cos\phi\cos(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\sin\theta\\ &\ +V_{n}\cos\theta\cdot \sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\cos\theta\\ &\ -V_{n}\cos\theta\cdot \cos(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\sin\theta]\\ =&(-1)^{\frac n2}[V_{n-1}\cos\phi\!\cdot\! \sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\cos\theta\\ &\ -V_{n-1}\cos\phi\cdot \cos(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\sin\theta\\ &\ +V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\\ &\ -V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\sin^2\theta\\ &\ -V_{n-1}\cos\theta\sin\phi\cdot\cos(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})]\\ =&(-1)^{\frac n2}[V_{n-1}\cos\phi\!\cdot\! \sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\cos\theta\\ &\ -V_{n-1}\cos\phi\cdot \cos(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\sin\theta\\ &\ +V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\\ &\ -V_{n-1}\sin\phi\cdot \sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\sin\theta\\ &\ -V_{n-1}\cos\theta\sin\phi\cdot\cos(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})]\\ =&(-1)^{\frac n2}[V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\\ &\ +V_{n-1}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\cos(\theta+\phi)\\ &\ -V_{n-1}\sin(\theta+\phi)\cos(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})]\\ =&(-1)^{\frac n2}[V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\\ &\ -V_{n-1}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\cos A_n\\ &\ -V_{n-1}\sin A_n\cos(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})]\\ =&(-1)^{\frac n2}[V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\\ &\ -V_{n-1}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2}\!+\!A_n)]\\ \Rightarrow\ &V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\!-\!V_{n-1}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2}+A_n)\\ &\quad =(-1)^{\frac n2}V_2\sin A_n\\ \Rightarrow\ &V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})-\!V_{n-1}\sin[A_1+(\frac n2-1)\pi-A_2]\\ &\qquad =(-1)^{\frac n2}V_2\sin A_n\\ \Rightarrow\ &V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\!-\!V_{n-1}\sin(A_1\!-\!A_2)\cos[(\frac n2\!-\!1)\pi]\\ &\qquad =(-1)^{\frac n2}V_2\sin A_n\\ \Rightarrow\ &V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})-(-1)^{\frac n2-1}\!V_{n-1}\sin(A_1-A_2)\\ &\qquad =(-1)^{\frac n2}V_2\sin A_n\\ \Rightarrow\ &V_{n}\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})\\ &\qquad =(-1)^{\frac n2-1}V_{n-1}\sin(A_1-A_2)+(-1)^{\frac n2}V_2\sin A_n\\ \Rightarrow\ &\frac{\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})}{V_2V_{n-1}}\\ &\qquad =(-1)^{\frac n2-1}\frac{\sin(A_1-A_2)}{V_nV_2}+(-1)^{\frac n2}\frac{\sin A_n}{V_{n-1}V_n}\\ \Rightarrow\ &\frac{\sin(A_1\!+\!A_4\!+\!A_6+\cdots\!+\!A_{n-2})}{V_2V_{n-1}}\\ &\qquad =(-1)^{\frac n2}\frac{\sin A_n}{V_{n-1}V_n}\!+\!(-1)^{\frac n2-1}\frac{\sin A_1}{V_nV_1}\!-\!(-1)^{\frac n2-1}\frac{\sin A_2}{V_1V_2}.\tag*{(4.1-1)} \end{align*} (4.1-1)式等式右側出現的是以被選定頂角 $A_n$ 和其相連續的下兩個頂角 $A_1$ 與 $A_2$ 各自形成正弦值分式項的線性組合, 請參考圖 16 的此 3 個角度順序位置。 (E-2) 其次選定有頂角 $A_1$ 的三角形, 因其下有相連續的兩個所需頂角 $A_2$ 與 $A_3$;  (i) 請見圖 17, 連接頂點 $A_2$ 與 $A_n$ 形成對角線長 $d_{2n}=\overline{A_2A_n}$, 對三角形 $\triangle A_1A_2A_n$ 言, 利用其正弦定理可得下列關係式: $$\frac{d_{2n}}{\sin A_1}=\frac{V_{1}}{\sin \phi}=\frac{V_n}{\sin \theta}=2R,$$ (4E.4) 且配合著 $d_{2n}=V_{n}\cos\phi+V_1\cos\theta$ 及 $V_{n}\sin\phi=V_1\sin\theta$ 的兩關係式。 (ii) 見圖 18, 連接 $A_3$ 與 $A_5$ 頂點成對角線, 對三角形 $\triangle A_3A_4A_5$ 言, 利用其正弦定理可得下列關係式: $$\frac{V_{3}}{\sin (A_5-\Omega)}=\frac{V_4}{\sin (A_3-\psi)}=2R,$$ (4E.5) 又由圓內接 $n-2$ 邊形 $A_2A_3A_5A_6\cdots A_{n-2}A_{n-1}A_n$ 的 $\Omega+A_7+A_9+\cdots+A_{n-3}+A_{n-1}+\delta=\psi+A_6+\cdots+A_{n-2}+\eta=\Big(\dfrac n2-2\Big)\pi$ 性質, 見圖18, 可得; \begin{align*} A_5-\Omega=&A_5-\Big[\Big(\frac n2-2\Big)\pi-A_7-A_9-\cdots-A_{n-1}-\delta\Big]\\ =&A_5+A_7+\cdots+A_{n-1}-\Big[\Big(\frac n2-2\Big)\pi-A_2+\theta\Big]\\ =&A_2+A_5+A_7+A_9+\cdots+A_{n-3}+A_{n-1}-\theta-\Big(\frac n2-2\Big)\pi. \end{align*} 代入(4E.5)式, 得: \begin{align*} &\frac{V_3}{\sin(A_2+A_5+A_7+A_9+\cdots+A_{n-3}+A_{n-1}-\theta)\cos[(\frac n2-2)\pi]}=2R\\ \Rightarrow\quad\ &\frac{V_3}{(-1)^{\frac n2}\sin(A_2+A_5+A_7+A_9+\cdots+A_{n-3}+A_{n-1}-\theta)}=2R. \tag*{(4E.6)} \end{align*} (iii) 由 (4E.4) 式與 (4E.6) 式, 可得到下列重要關鍵的居間聯繫關係式 (22) 式: \begin{equation} \frac{d_{2n}}{\sin A_1}=\frac{V_3}{(-1)^{\frac n2}\sin(A_2+A_5+A_7+A_9+\cdots+A_{n-3}+A_{n-1}-\theta)}=2R, \end{equation} 且又配合著 $d_{2n}=V_{n}\cos\phi+V_1\cos\theta$ 及 $V_{n}\sin\phi=V_1\sin\theta$, 繼續推演運算; \begin{align*} \Rightarrow\ &V_3\sin A_1=d_{2n}(-1)^{\frac n2}\sin(A_2+A_5+A_7+A_9+\cdots+A_{n-3}+A_{n-1}-\theta)\\ &=(V_{n}\cos\phi\!+\!V_1\cos\theta)(-1)^{\frac n2}\sin(A_2\!+\!A_5\!+\!A_7\!+\!A_9\!+\!\cdots\!+\!A_{n-3}\!+\!A_{n-1}\!-\!\theta). \end{align*} 接著仿效上述 (E-1) 的步驟 (iii) 完整演算過程;經代換, 化簡運算後, 得下式: \begin{align*} V_3\sin A_1=& (-1)^{\frac n2}[V_1\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1})\\ &\qquad \quad -\!V_n\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1}\!+\!A_1)]\\ \Rightarrow\qquad &V_1\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1})\\ &=(-1)^{\frac n2}V_3\sin A_1+V_n\sin(A_2+A_5+A_7+\cdots+A_{n-1}+A_1)\qquad~\\ \Rightarrow\qquad &V_1\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1})\\ &=(-1)^{\frac n2}V_3\sin A_1+V_n\sin[A_2+(\frac n2-1)\pi-A_3]\\ \Rightarrow\qquad &V_1\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1})\\ &=(-1)^{\frac n2}V_3\sin A_1+V_n\sin(A_2-A_3)\cos[(\frac n2-1)\pi]\\ \Rightarrow\qquad &V_1\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1})\\ &=(-1)^{\frac n2}V_3\sin A_1+(-1)^{\frac n2-1}V_n\sin(A_2-A_3)\\ \Rightarrow\qquad &\frac{\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1})}{V_3V_n}\!=\!(-1)^{\frac n2}\frac{\sin A_1}{V_nV_1}+(-1)^{\frac n2-1} \frac{\sin (A_2\!-\!A_3)}{V_1V_3}\\ \Rightarrow\qquad &\frac{\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1})}{V_3V_n}\\ &=(-1)^{\frac n2}\frac{\sin A_1}{V_nV_1}+(-1)^{\frac n2-1}\frac{\sin A_2}{V_1V_2}-(-1)^{\frac n2-1}\frac{\sin A_3}{V_2V_3}.\tag*{(4.2-1)} \end{align*} (E-3) 將 (4.1-1) 式與 (4.2-1) 式兩者合併相加, 即得下式: \begin{align} &\frac{\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})}{V_2V_{n-1}}+\frac{\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1})}{V_3V_n}\nonumber\\ &=(-1)^{\frac n2}\frac{\sin A_n}{V_{n-1}V_n}+(-1)^{\frac n2-1}\frac{\sin A_1}{V_nV_1}-(-1)^{\frac n2-1}\frac{\sin A_2}{V_1V_2}\nonumber\\ &\quad +(-1)^{\frac n2}\frac{\sin A_1}{V_nV_1}+(-1)^{\frac n2-1}\frac{\sin A_2}{V_1V_2}-(-1)^{\frac n2-1}\frac{\sin A_3}{V_2V_3}\nonumber\\ \Rightarrow\qquad &\frac{\sin(A_1\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-2})}{V_2V_{n-1}}+\frac{\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-1})}{V_3V_n}\nonumber\\ &=(-1)^{\frac n2}\frac{\sin A_3}{V_2V_3}+(-1)^{\frac n2}\frac{\sin A_n}{V_{n-1}V_n}.\label{4.3} \end{align} 方程式 \eqref{4.3} 式即為圓內接 $n=2k+4$ 邊形的第 1 個四項式正弦型方程式。 同理, 又可獲得與 \eqref{4.3} 式同類型的下列 $n-1$ 個方程式 ; \begin{align*} &\frac{\sin(A_2\!+\!A_5\!+\!A_7\!+\!\cdots\!+\!A_{n-3}\!+\!A_{n-1})}{V_3V_n}+\frac{\sin(A_3\!+\!A_6\!+\!A_8\!+\!\cdots\!+\!A_{n-2}+A_n)}{V_4V_{1}}\\ &=(-1)^{\frac n2}\frac{\sin A_4}{V_3V_4}+(-1)^{\frac n2}\frac{\sin A_1}{V_{n}V_1},\tag*{(4.3.2)}\\ &\frac{\sin(A_3\!+\!A_6\!+\!A_8\!+\!\cdots\!+\!A_{n-2}+A_n)}{V_4V_{1}}+\frac{\sin(A_4\!+\!A_7\!+\!A_9\!+\!\cdots\!+\!A_{n-3}\!+\!A_{n-1}+A_1)}{V_5V_2}\\ &=(-1)^{\frac n2}\frac{\sin A_5}{V_4V_5}+(-1)^{\frac n2}\frac{\sin A_2}{V_{1}V_2},\tag*{(4.3.3)}\\ &\qquad \vdots\\ &\frac{\sin(A_{n-2}\!+\!A_1\!+\!A_3\!+\!\cdots\!+\!A_{n-7}+A_{n-5})}{V_{n-1}V_{n-1}}+\frac{\sin(A_{n-1}\!+\!A_2\!+\!A_4\!+\!\cdots\!+\!A_{n-6}\!+\!A_{n-4})} {V_nV_{n-3}}\\ &=(-1)^{\frac n2}\frac{\sin A_n}{V_{n-1}V_n}+(-1)^{\frac n2}\frac{\sin A_{n-3}}{V_{n-4}V_{n-3}},\tag*{(4.3.$n$-2)}\\ &\frac{\sin(A_{n-1}\!+\!A_2\!+\!A_4\!+\!\cdots\!+\!A_{n-6}+A_{n-4})}{V_{n}V_{n-3}}+\frac{\sin(A_{n}\!+\!A_3\!+\!A_5\!+\!\cdots\!+\!A_{n-5}\!+\!A_{n-3})} {V_1V_{n-2}}\\ &=(-1)^{\frac n2}\frac{\sin A_1}{V_{n}V_1}+(-1)^{\frac n2}\frac{\sin A_{n-2}}{V_{n-3}V_{n-2}},\tag*{(4.3.$n$-1)}\\ &\frac{\sin(A_{n}\!+\!A_3\!+\!A_5\!+\!\cdots\!+\!A_{n-5}+A_{n-3})}{V_{1}V_{n-2}}+\frac{\sin(A_{1}\!+\!A_4\!+\!A_6\!+\!\cdots\!+\!A_{n-4}\!+\!A_{n-2})} {V_2V_{n-1}}\\ &=(-1)^{\frac n2}\frac{\sin A_2}{V_{1}V_2}+(-1)^{\frac n2}\frac{\sin A_{n-1}}{V_{n-2}V_{n-1}},\tag*{(4.3.$n$)} \end{align*} 故知, 一組圓內接 $n=2k+4$ 邊形的四項式正弦型方程式總計有 $n$ 個方程式! 上述 $n$ 個方程式 $n\ge 6$ 已經完全涵蓋所有圓內接偶數邊數多邊形的四項式正弦型方程式, 使六邊形、 八邊形、 十邊形、 $\cdots$ 等對應方程式都成為它的特例 ! 參、結論1. 圓內接偶數邊數多邊形的四項式正弦型方程式, 也恰是在求算平面凸多邊形最大面積時所衍生得到的方程式; 是當多邊形的邊長固定而變動其各頂角所得之最大面積。 例如; 將平面凸六邊形 $A_1A_2A_3A_4A_5A_6$ 分割成兩個四邊形, 見下圖 19, 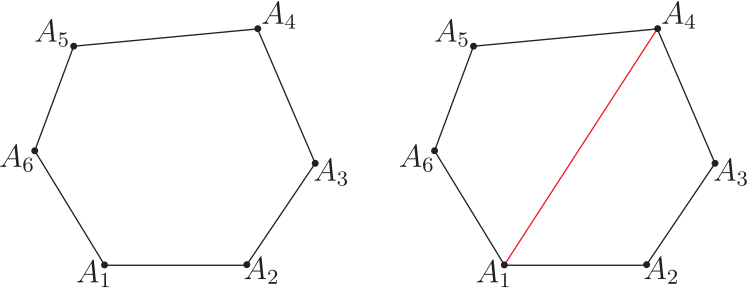 應用四邊形餘弦定理可得下列相對應組合成的餘弦關係式: \begin{align*} \frac 12(V_1^2\!+\!V_2^2\!+\!V_3^2\!-\!V_4^2\!-\!V_5^2\!-\!V_6^2) =&V_1V_2\cos A_2\!+\!V_2V_3\cos A_3\!-\!V_1V_3\cos(A_2\!+\!A_3)\\ &\!-\!V_4V_5\cos A_5\!-\!V_5V_6\cos A_6\!+\!V_4V_6\cos(A_5\!+\!A_6). \end{align*} 另由四邊形的面積公式性質, 並令六邊形的面積為 $S(6)$, 可得下列關係式: \begin{align*} 2S(6)=&V_1V_2\sin A_2+V_2V_3\sin A_3-V_1V_3\sin(A_2+A_3)\\ &+V_4V_5\sin A_5+V_5V_6\sin A_6-V_4V_6\sin(A_5+A_6). \end{align*} 此六邊形的面積是由 4 個頂角 $A_2$、 $A_3$、 $A_5$、 $A_6$ 來決定, 而 4 個頂角又被控制在餘弦關係式中, 故需應用到 Lagrange multiplier method 來求算出面積的極值: \begin{align*} \hbox{令}\quad f=&S(6)=\frac 12[V_1V_2\sin A_2+V_2V_3\sin A_3-V_1V_3\sin(A_2+A_3)\\ &\hskip 1.5cm +V_4V_5\sin A_5+V_5V_6\sin A_6-V_4V_6\sin(A_5+A_6)]\\ \hbox{且}\quad \Phi=&V_1V_2\cos A_2\!+\!V_2V_3\cos A_3\!-\!V_1V_3\cos(A_2\!+\!A_3)\!-\!V_4V_5\cos A_5\!-\!V_5V_6\cos A_6\\ &\!+\!V_4V_6\cos(A_5\!+\!A_6)\!-\!\frac 12(V_1^2\!+\!V_2^2\!+\!V_3^2\!-\!V_4^2\!-\!V_5^2\!-\!V_6^2)=0 \end{align*} 取 $F(A_2,A_3,A_5,A_6)=f+\lambda\Phi$, $\lambda$ 為不等於零的實數。 對 $F$ 作微分運算, 並使微分式為零, 推演出聯立方程式, 即可證明出衍生的四項式正弦型方程式。 2. 三角形正弦定理與 SASAS 正弦型方程式在本文內推理演繹的過程中, 所扮演的角色與任務可謂合作無間、 相輔相成; 兩者在任何圓內接多邊形領域內的應用至為普遍、 強大 ! 時時可見到它們被應用到的美妙蹤影, 而其方程式清晰簡易, 隨處都可上手引申借用。 試看以高規格的 Lagrange multiplier method 所求得的四項式正弦型方程式, 單單引用三角形正弦定理與 SASAS 正弦型方程式也可推證獲得, 兩者在應用上的效益真是細微又廣泛! 3. 回顧以上正文內精實完整的敘述證明後, 知悉: 任意圓內接多邊形無論是奇數邊數形或是偶數邊數形都能以正弦定理與SASAS方程式來推導出許多獨特一般化方程式。 觀察這些同類型的 $n$ 個方程式 \eqref{4.3} 式特徵, 發現每一個分式項結構的分母都只包含兩段邊長, 而此兩邊長與其同分式項分子的內角在次序上也具有呈現某種特殊規律分佈。 最完美的是所有同類方程式都呈現出規律對稱性! 這樣的規則化使得在證明及敘述表達這所有方程式內涵時, 即能體驗出堅定明確的紮實收穫感, 更增強了推廣思維、 努力研發的信念 ! 參考文獻本文作者為嘉義市私立輔仁中學退休教師 |
2024年6月 48卷2期
圓內接偶數邊數多邊形四項式正弦型方程式

