| 發刊日期 |
2024年6月
|
|---|---|
| 標題 | 歐拉線的一個性質及其應用 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
摘要: 歐拉 (Euler, 1707$\sim$1783) 於 1765 年提出了著名的歐拉線定理"三角形的垂心、 重心與外心在一條直線上。" 本文先介紹一種解析證法, 而後談談從證明中得到一個性質的應用。 供高中師生教與學時參考。 關鍵字: 歐拉線性質、證明、應用。  一、歐拉線定理的解析證明證明: 如圖 1, $O$、$G$、$H$ 分別為 $\triangle ABC$ 的外心、 重心和垂心, 以 $AB$ 為 $x$ 軸, $CH$ 為 $y$ 軸建立平面直角坐標系, 設 $A(a,0)$、 $B(b,0)$、 $C(0,c)$, $E$、 $F$ 分別為 $\overline{AB}$、 $\overline{BC}$ 的中點, 則 $E\Big(\dfrac{a+b}2, 0\Big)$、 $F\Big(\dfrac b2,\dfrac c2\Big)$, $CH$ 的直線方程為 $x=0$, $OE$ 的直線方程為 $x=\dfrac{a+b}2$。 連結 $AH$ 並延長交 $CB$ 於點 $D$, 則 $AD$ 的直線方程為 $y=\dfrac bc(x-a)$, $OF$ 的直線方程為 $y-\dfrac c2=\dfrac bc(x-\dfrac b2)$, 即 $2bx-2cy-b^2+c^2=0$, 從而可求得 $H$、 $O$、 $G$ 三點的坐標分別為 $H\Big(0,-\dfrac{ab}{c}\Big)$、 $O\Big(\dfrac{a+b}{2},\dfrac{ab+c^2}{2c}\Big)$、 $G\Big(\dfrac{a+b}{3},\dfrac{c}3\Big)$。 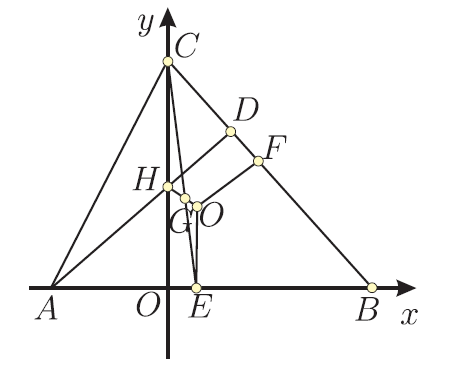 由於 $\dfrac{a+b}{3}=\dfrac 13\times 0+\dfrac 23\times \dfrac{a+b}2$ 以及 $\dfrac c3=\dfrac 13\times\Big(-\dfrac{ab}c\Big)+\dfrac 23\times \dfrac{ab+c^2}{2c}$, 所以由分點公式知道, 點 $G$ 介於點 $O$ 與點 $H$ 之間, 而且 $\overline{OG}:\overline{GH}=1:2$。 二、歐拉線定理性質的應用例: 設 $A_1A_2A_3A_4$ 為圓的內接四邊形, $H_1$、 $H_2$、 $H_3$、 $H_4$ 依次為 $\triangle A_1A_2A_3$、 $\triangle A_2A_3A_4$、 $\triangle A_3A_4A_1$、 $\triangle A_4A_1A_2$ 的垂心, 求證 $H_1$、 $H_2$、 $H_3$、 $H_4$ 四點在同一圓上, 並定出該圓的圓心位置。 (1992 年全國數學聯賽第二試第一題) 證明: 如圖 2, 不失一般性, 設 $A_1A_2A_3A_4$ 的外接圓圓心 $O$ 在座標原點, 半徑為 $r$, 設四個頂點坐標依次為 $A_i(x_i, y_i)$ $(i=1, 2, 3, 4)$, $G_i$ 分別為 $\triangle A_1A_2A_3$、 $\triangle A_2A_3A_4$、 $\triangle A_3A_4A_1$、 $\triangle A_4A_1A_2$ 的重心, 則 $G_i$ 的坐標依次為 \begin{align*} &G_1=\Big(\dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}{3}\Big),\\ &G_2=\Big(\dfrac{x_2+x_3+x_4}{3},\dfrac{y_2+y_3+y_4}{3}\Big),\\ &G_3=\Big(\dfrac{x_3+x_4+x_1}{3},\dfrac{y_3+y_4+y_1}{3}\Big),\\ &G_4=\Big(\dfrac{x_4+x_1+x_2}{3},\dfrac{y_4+y_1+y_2}{3}\Big). \end{align*} 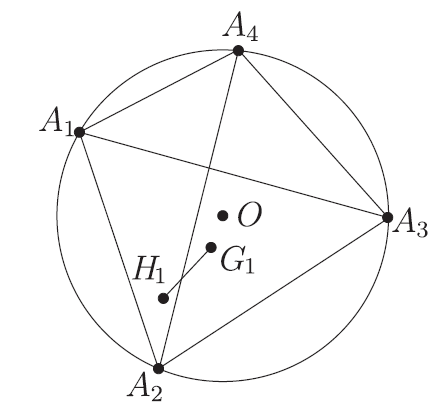 而由上述歐拉線的性質知 $\overline{OG_i}:\overline{G_iH_i}=1:2$ $(i=1, 2, 3, 4)$, $\therefore \overline{OG_i}= \dfrac 13\overline{OH_i}$, 所以由分點公式和 $\overline{OG_i}:\overline{G_iH_i}=1:2(i=1, 2, 3, 4)$ 可得垂心 $H_i$ 的坐標公式依次為: \begin{align*} &H_1(x_1+x_2+x_3, y_1+y_2+y_3),&&H_2(x_2+x_3+x_4, y_2+y_3+y_4),\\ &H_3(x_3+x_4+x_1, y_3+y_4+y_1),&&H_4(x_4+x_1+x_2, y_4+y_1+y_2). \end{align*} 考慮點 $O'(x_1+x_2+x_3+x_4, y_1+y_2+y_3+y_4)$, 容易計算 \begin{align*} O'H_1=\,&\sqrt{(x_1+x_2+x_3+x_4-x_1-x_2-x_3)^2+(y_1+y_2+y_3+y_4-y_1-y_2-y_3)^2}\\ =\,&\sqrt{x_4^2+y_4^2}=r \end{align*} 同理可計算得到 $O'H_2=\sqrt{x_1^2+y_1^2}=r$, $O'H_3=\sqrt{x_2^2+y_2^2}=r$, $O'H_4=\sqrt{x_3^2+y_3^2}=r$, 所以 $O'H_1=O'H_2=O'H_3=O'H_4=r$。 於是 $H_1$、 $H_2$、 $H_3$、 $H_4$ 四點在以 $O'$ 為圓心, 以 $r$ 為半徑的圓上, 從而命題獲證。 綜上所述可知: 在平時的教學過程中, 注意對著名定理的研究, 符合新課程標準關於"讓學生的思維活躍起來"的理念要求, 利於提高學生學習和研究專題講座的水準, 利於提高教學品質, 利於學生在總結的過程中, 開拓思路, 鞏固所學知識。 利於提高學習和解題效率, 利於培養學生的探索精神和創新意識, 利於激發學生學數學用數學的積極性。 能夠幫助學生理解課本內容, 提高分析問題和實際問題的能力, 對於啟迪學生思維, 開闊視野、 培養和發展學生的思維能力頗有益處。 故筆者認為:在今後的教學過程中, 做好引導學生進行這類專題內容的探索與研究, 很有必要。 參考資料本文作者中國江蘇省泰州中學附屬初級中學退休教師 |
2024年6月 48卷2期
歐拉線的一個性質及其應用

