| 發刊日期 |
2024年9月
|
|
|---|---|---|
| 標題 | 廣義閔可夫斯基不等式的介紹及推廣 |
|
| 作者 | ||
| 關鍵字 | ||
| 檔案下載 | ||
| 全文 |
最近在臉書社團"高中數學討論區"看到一個同學的提問, 為了方便說明, 把它簡化成如下的題目: 已知 $a,b,c,d$ 為正實數, 證明 \begin{align} {\root 4\of{a^4+b^4}} +{\root 4\of{c^4+d^4}} \ge {\root 4\of{(a+c)^4+(b+d)^4}}; \label{1} \end{align} 當 $\dfrac ab=\dfrac cd$ 時等式成立。 式 \eqref{1} 是閔可夫斯基不等式 (Minkowski inequality) 的一個簡單的例子。 閔可夫斯基不等式的簡易寫法如下: 設向量 $\vec x=(x_1,x_2,\ldots,x_n)$ 與 $\vec y=(y_1,y_2,\ldots,y_n)$ 中的元素皆為正實數且 $q \gt 1$, 則下式成立: \begin{align} \Big(\sum\limits_{i=1}^n (x_i)^q\Big)^{\frac 1q}+\Big(\sum\limits_{i=1}^n (y_i)^q\Big)^{\frac 1q}\ge \Big(\sum\limits_{i=1}^n (x_i+y_i)^q\Big)^{\frac 1q}; \label{2} \end{align} 當 $\vec y=k\vec x$ 時等式成立。 反之, 若 $q \lt 1$, 則 \eqref{2} 式的 $\ge $ 改成 $\le $ 即可。 如果 \eqref{1} 式只是要提供說明, 可以敘述如下: 設 $\vec x=(a,b)$, $\vec y=(c, d)$, $n=2$, $q=4$, 因為 $q=4 \gt 1$, 根據閔可夫斯基不等式, 證明結束。 事實上當作者第一次看到式 \eqref{1} 這個題目, 想到的是採用一個更廣義的不等式。由於這個不等式幾乎沒有人注意, 因此希望藉由本文的推廣, 讓更多人認識。 這個不等式來自於參考文獻
先說明此不等式的由來, 大約八年前, 在台大電信所讀博士班的林子喬同學, 基於研究的需求, 希望透過某個不等式來證明自己提出的研究方法理論是上是對的, 由於在文獻上沒找到可用的不等式, 所以就自己提出並完成證明。 林同學的指導教授是馮世邁老師, 借用他們名字上各一個同音字, 我們戲稱「蕎麥不等式」, 嚴格說來應該稱作廣義閔可夫斯基不等式。 設定式 \eqref{3} 中不等式之參數, $M=2$, $N=n$, $p=1$, 此時的蕎麥不等式 (廣義閔可夫斯基不等式) 就簡化成與閔可夫斯基不等式 \eqref{2} 式同義。 回到 \eqref{1} 式的問題, 看到題目, 作者想到的證明過程如下: 設正實數矩陣 $A=\left[\begin{array}{ccc} a&&b\\ c&&d\end{array}\right]$, $p=1$, $q=4$, 因為 $q=4 \gt p=1$, 根據廣義閔可夫斯基不等式, 證明結束。 $\Box$ 第二個要討論的題目是來自於作者自製的挑戰題, 第一次出現於臉書社團``高中數學討論區'' 的留言區, 題目結合不等式與機率, 應該可以歸類為高中數學競賽題, 題目敘述如下: 擲一粒公正的骰子四次, 出現的點數依序為 $a,b,c,d$, 則 \begin{align} \frac{(a+b)(b+c)(c+d)(d+a)}{(a+b+c+d)(abc+bcd+cda+dab)}\gt 1\label{4} \end{align} 的機率是多少? 題目後面提供的參考解答為 $\dfrac{605}{648}$。 要回答這個問題之前, 我們再介紹一個簡化版的廣義閔可夫斯基不等式, 當 $p=-1$, $q=1$, 此時也等效成電阻不等式 矩形電阻網路是由 $M\times N$ 個電阻組成的雙埠電路, 以 $M=N$ 為例, 圖 1 顯示了兩種結構, 左邊稱為先串(聯)後並(聯)電路, 等效電阻值表示為 $R_{SP}$, 右邊稱為先並後串電路, 等效電阻值表示為 $R_{PS}$。 通常來講, 矩形電阻網路可以矩陣的形式表示為 \begin{align} R=\left[\begin{array}{ccccc} R_{11}&R_{12}&\cdots&R_{1(N-1)}&R_{1N}\\ R_{21}&R_{22}&\cdots&R_{2(N-1)}&R_{2N}\\ \vdots&\vdots&\ddots&\vdots&\vdots\\ R_{(M-1)1}&\vdots&\ddots&\vdots&R_{(M-1)N}\\ R_{M1}&R_{M2}&\cdots&R_{M(N-1)}&R_{MN} \end{array}\right], \label{5} \end{align} 其中矩陣內所有元素的數值皆大於 0。 電阻不等式敘述如下: 兩種結構所得到的電阻值會以不等式出現, 即 $R_{SP}\ge R_{PS}$, 且當矩陣 $R$ 的秩 rank$(R)=1$ 時等式成立。 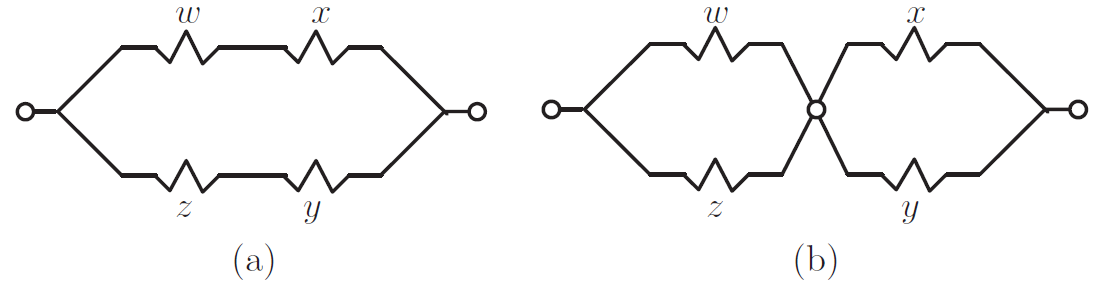 補充說明, 由 $M\times N$ 個電阻組成的矩形電阻網路, 先串後並電路, 電阻值表示為 $R_{SP}$, \begin{align} R_{SP}=\dfrac{1}{\sum\limits_{i=1}^M\dfrac{1}{\sum\limits_{j=1}^N R_{ij}}};\label{6} \end{align} 先並後串電路, 電阻值表示為 $R_{PS}$ \begin{align} R_{PS}=\sum\limits_{j=1}^N\dfrac{1}{\sum\limits_{i=1}^M R_{ij}}.\label{7} \end{align} 兩種結構所得到電阻值會以不等式出現, 即 $R_{SP}\ge R_{PS}$, \begin{align} R_{SP}=\dfrac{1}{\sum\limits_{i=1}^M\dfrac{1}{\sum\limits_{j=1}^N R_{ij}}}\ge R_{PS}=\sum\limits_{j=1}^N\dfrac{1}{\sum\limits_{i=1}^M R_{ij}}; \label{8} \end{align} 當矩陣 $R$ 的秩 rank$(R)=1$ 時等式成立。 參考文獻 再回到本文提到的第二個題目, 擲一粒公正的骰子四次, 出現的點數依序為a,b,c,d, 設電阻矩陣 , 由電阻不等式知 \begin{align} R_{SP}=&\dfrac{1}{\dfrac{1}{a+b}+\dfrac{1}{c+d}}\ge R_{PS}=\dfrac{1}{\dfrac{1}a+\dfrac{1}d}+\dfrac{1}{\dfrac{1}b+\dfrac{1}c}, \label{9}\\ {\hbox{整理得}} R_{SP}=\dfrac{(a+b)(c+d)}{a+b+c+d}&\ge R_{PS}=\dfrac{ad}{a+d}+\dfrac{bc}{b+c}=\dfrac{(adb+adc+abc+dbc)}{(a+d)(b+c)}. \label{10}\end{align} 比較 \eqref{10} 式與第二個題目的 \eqref{4} 式是相同的形式, 只是它問的是大於的機率, 因此我們要先算的是等式成立時 $\dfrac ab=\dfrac dc$ 的機率 $P_{eq}=P\Big(\dfrac ab=\dfrac dc\Big)$, 最後再用 1 減掉 $P_{eq}$ 即是所求。 符合等式的 $(a,b,c,d)$ 先分成兩類: 第一類屬於 $(a,b)=(d,c)$, 共有 $6\times 6=36$ 個; 第二類屬於 $(a,b)\not=(d,c)$, 分成 3 種, 分別是 (1) $r=\dfrac ab=3$ 或 $\dfrac 13$, 例如 $(1,1,2,2)$, 有 $6\times 5=30$ 個, (2) $r=\dfrac ab=2$ 或 $\dfrac 12$, 例如 $(1,2,4,2)$, 有 $3\times 2\times 2=12$ 個, (3) $r=\dfrac ab=3$ 或 $\dfrac 13$, 例如 $(1,3,6,2)$, 有 $2\times 2\times 2=8$ 個, 最後得到大於 1 的機率 $P=1-P_{eq}=1-\dfrac{36+30+12+8}{6^4}=\dfrac{605}{648}$, 為了檢查答案是否正確, 我們寫了 Matlab 程式將每一種可能做判斷並統計, 結果如圖 2 所示, 答案確實是 $P=\dfrac{605}{648}$。 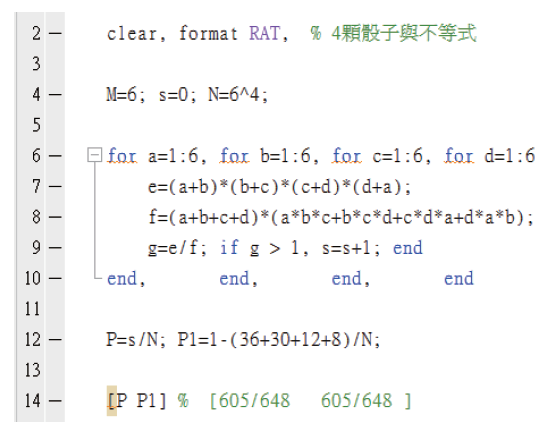 如果熟悉廣義閔可夫斯基不等式並善加利用, 應該可以產生很多新的題目, 這裡我們舉一個例子來說明新題目如何產生。 先假設正實數矩陣 $A=\left[\begin{array}{ccccc} a&&b&&c\\ 1&&2&&3 \end{array}\right]$, $q=2$, $p=-1$, 此時產生的新題目(第三題)敘述如下: 已知 $a,b,c$ 為正實數且 $a^2+b^2+c^2=1$, 證明 \begin{align} \Big(\dfrac{a}{a+1}\Big)^2+\Big(\dfrac{2b}{b+2}\Big)^2+\Big(\dfrac{3c}{c+3}\Big)^2\le\dfrac{14}{15+2\sqrt{14}}, \label{11} \end{align} 並求出等式成立時 $a$ 的值為何? 假設讀者第一次看到此題, 可以試著用你熟悉的不等式技巧試試看。 由於這是作者行文至此隨意出的題目, 因此屬意的解法如下: 考慮正實數矩陣 $A=\left[\begin{array}{ccccc} a&&b&&c\\ 1&&2&&3 \end{array}\right]$, $q=2$, $p=-1$, 根據廣義閔可夫斯基不等式, 由於 $q=2 \gt p=-1$, 因此底下不等式成立, \begin{align} \sqrt{\left(\dfrac{1}{\dfrac 1a+\dfrac 11}\right)^2+\left(\dfrac{1}{\dfrac 1b+\dfrac 12}\right)^2 +\left(\dfrac{1}{\dfrac 1c+\dfrac 13}\right)^2}\le\dfrac{1}{\dfrac{1}{\sqrt{a^2+b^2+c^2}}+\dfrac{1}{\sqrt{1^2+2^2+3^2}}}. \label{12} \end{align} 整理得到: \begin{align} \sqrt{\left(\dfrac a{a\!+\!1}\right)^2\!+\!\left(\dfrac {2b}{b\!+\!2}\right)^2\!+\!\left(\dfrac {3c}{c\!+\!3}\right)^2} \le\dfrac{\sqrt{a^2\!+\!b^2\!+\!c^2}\times\sqrt{1^2+2^2+3^2}}{\sqrt{a^2+b^2+c^2}\!+\!\sqrt{1^2\!+\!2^2\!+\!3^2}} =\dfrac{\sqrt{14}}{1\!+\!\sqrt{14}}. \label{13} \end{align} 兩邊平方, 結果如下 \begin{align} \Big(\dfrac{a}{a+1}\Big)^2+\Big(\dfrac{2b}{b+2}\Big)^2+\Big(\dfrac{3c}{c+3}\Big)^2\le\dfrac{14}{15+2\sqrt{14}}; \label{14} \end{align} 等式成立時 $a:b:c=1:2:3$, 設 $a=k$, $14k^2=1$ 知 $a=\dfrac 1{\sqrt{14}}$。 為了驗證, 設定 $a,b,c$ 為介於 0 到 1 的正實數, Matlab 程式與結果如圖 3 所示, 計算結果知最大值確實為 $\dfrac{14}{15+2\sqrt{14}}$, 答案正確。 接著我們把計算的結果以等高線畫成圖 4, 稱為等高線圖, 可以知道當 $a=\dfrac{1}{\sqrt{14}}$ 及 $b=\dfrac 2{\sqrt{14}}$ 時確實出現最大值 $\dfrac{14}{15+2\sqrt{14}}$。 圖 5 則是連續的曲面圖, 可以看到 $a,b$ 變化時目標函數值的變化。  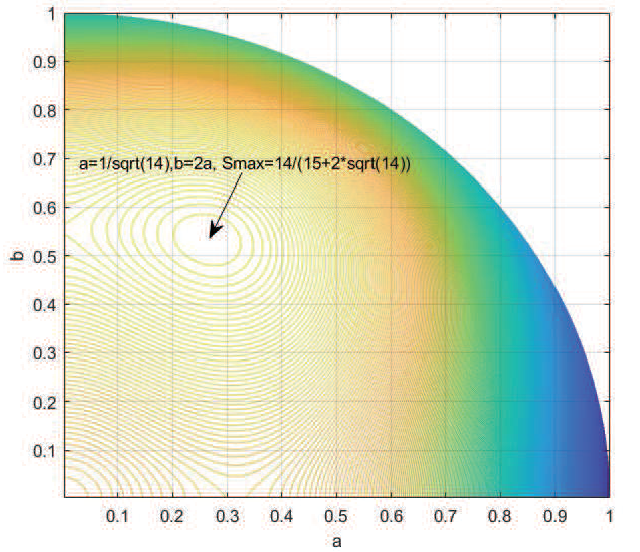 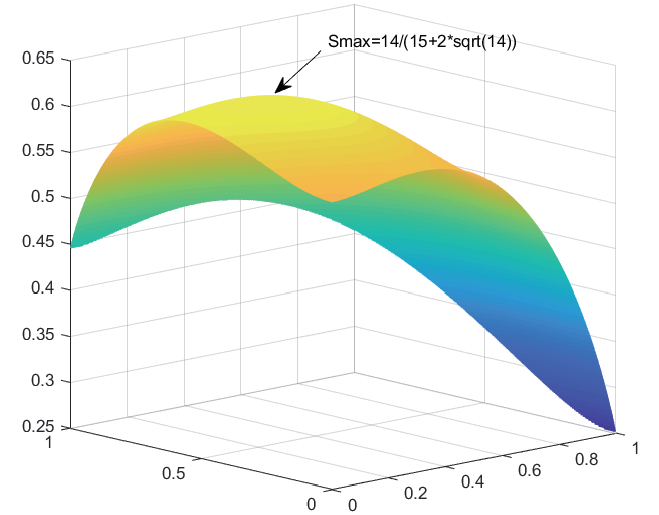 由於廣義閔可夫斯基不等式很少被人提及, 因此隨意設定參數所產生的題目對讀者來說將會很陌生, 底下我們再提出一些題目, 第四個題目敘述如下: 已知 $a,b,c$ 為正實數且 $a^3+b^3+c^3=8$, 證明 \begin{align} \Big(a^2+9\Big)^{\frac 32}+\Big(b^2+16\Big)^{\frac 32}+\Big(c^2+25\Big)^{\frac 32}\le 80\sqrt{10}. \label{15} \end{align} 我們建議的解法如下: 考慮正實數矩陣 $A=\left[\begin{array}{ccccc} a&&b&&c\\ 3&&4&&5 \end{array}\right]$, $q=2$, $p=3$, 根據廣義閔可夫斯基不等式, 由於 $q=2 \lt p=3$, 因此底下不等式成立, \begin{align} {\root {\frac 23}\of{\Big(a^2\!+\!3^2\Big)^{\frac 32}\!+\!\Big(b^2\!+\!4^2\Big)^{\frac 32}\!+\!\Big(c^2\!+\!5^2\Big)^{\frac 32}}}\le \sqrt{\Big(a^3+b^3+c^3\Big)^{\frac 23}+\Big(3^3+4^3+5^3\Big)^{\frac 23}}\!\!. \label{16} \end{align} 整理得到: \begin{align} {\root 3\of{\Big(a^2\!+\!3^2\Big)^{\frac 32}\!+\!\Big(b^2+4^2\Big)^{\frac 32}\!+\!\Big(c^2\!+\!5^2\Big)^{\frac 32}}}\le 2\sqrt{10}. \label{17} \end{align} 兩邊三次方, 結果如下 \begin{align} {\Big(a^2+3^2\Big)^{\frac 32}+\Big(b^2+4^2\Big)^{\frac 32}+\Big(c^2+5^2\Big)^{\frac 32}}\le 80\sqrt{10}. \label{18} \end{align} Matlab 程式與結果如圖 6 所示, 可以知道最大值的確是 $80\sqrt{10}$。  第五個題目敘述如下: 已知 $a,b,c$ 為正實數且 $a^2+b^2+c^2=1$, 證明 \begin{align} %\Rightarrow\ \sqrt{(\sqrt a+1)^4+(\sqrt b+\sqrt 2)^4+(\sqrt c+\sqrt 2)^4}\le 4+2\sqrt 3. \label{19} \end{align} 我們建議的解法如下: 考慮正實數矩陣 $A=\left[\begin{array}{ccccc} a&&b&&c\\ 1&&2&&2 \end{array}\right]$, $q=2$, $p=\dfrac 12$, 根據廣義閔可夫斯基不等式, 由於 $q=2 \gt p=\dfrac 12$, 因此底下不等式成立, \begin{align} \Big[(a^2\!+\!b^2\!+\!c^2)^{\frac 14}\!+\!(1^2\!+\!2^2\!+\!2^2)^{\frac 14}\Big]^2\ge \sqrt{(\sqrt a\!+\!1)^4\!+\! (\sqrt b\!+\!\sqrt 2)^4\!+\!(\sqrt c\!+\!\sqrt 2)^4}. \label{20} \end{align} 整理得到: \begin{align} (1+\sqrt{3})^2 \ge \sqrt{(\sqrt a+1)^4+(\sqrt b+\sqrt 2)^4+(\sqrt c+\sqrt 2)^4}. \label{21} \end{align} 兩邊交換得 \begin{align} \sqrt{(\sqrt a+1)^4+(\sqrt b+\sqrt 2)^4+(\sqrt c+\sqrt 2)^4}\le 4+2\sqrt 3. \label{22} \end{align} Matlab 程式與結果如圖 7 所示, 可以知道最小值的確是 $4+2\sqrt 3$。  行文至此, 我們想了解當 $q$ 為無理數, 甚至是超越數時是否真的適用? 第六個題目敘述如下: 已知 $a,b$ 為正實數且 $a^2+b^2=1$, 證明 \begin{align} \sqrt{(a^\pi+3^\pi)^{\frac 2\pi}+(b^\pi+4^\pi)^{\frac 2\pi}}\ge [1+(\sqrt 5)^\pi]^{\frac 1\pi}. \label{23} \end{align} 我們建議的解法如下: 考慮正實數矩陣 $A=\left[\begin{array}{ccc} a&&b\\ 3&&4 \end{array}\right]$, $q=\pi$, $p=2$, 根據廣義閔可夫斯基不等式, 由於 $q=\pi \gt p=2$, 因此底下不等式成立, \begin{align} \sqrt{(a^\pi+3^\pi)^{\frac 2\pi}+(b^\pi+4^\pi)^{\frac 2\pi}}\ge \Big[(a^2+b^2)^{\frac \pi 2}+(3^2+4^2)^{\frac \pi 2}\Big]^{\frac 1\pi}. \label{24} \end{align} 整理得到: \begin{align} \sqrt{(a^\pi+3^\pi)^{\frac 2\pi}+(b^\pi+4^\pi)^{\frac 2\pi}}\ge [1+5^\pi]^{\frac 1\pi}. \label{25} \end{align} Matlab 程式與結果如圖 8 所示, 可以知道最小值的確是 $[1+5^\pi]^{\frac 1\pi}$。  最後我們再加一些變化, 第七個題目敘述如下:已知 $a,b,c$ 為正實數, 證明 \begin{align} \sqrt{(a+5)^2+(b+8)^2+(c+9)^2}\le \sqrt{a^2+13}+\sqrt{b^2+40}+\sqrt{c^2+45}. \label{26} \end{align} 我們建議的解法如下:考慮正實數矩陣 $A=\left[\begin{array}{ccccc} a&&2&&3\\ 2&&b&&6\\ 3&&6&&c \end{array}\right]$, $q=2$, $p=1$, 根據廣義閔可夫斯基不等式, 由於 $q=2 \gt p=1$, 因此底下不等式成立, \begin{align} \sqrt{a^2\!+\!2^2\!+\!3^2}\!+\!\sqrt{2^2\!+\!b^2\!+\!6^2}\!+\!\sqrt{3^2\!+\!5^2\!+\!c^2}\ge \sqrt{(a\!+\!2\!+\!3)^2\!+\!(2\!+\!b\!+\!6)^2\!+\!(3\!+\!6\!+\!c)^2}\!\!. \label{27} \end{align} 整理後兩邊交換得到: \begin{align} \sqrt{(a+5)^2+(b+8)^2+(c+9)^2}\le \sqrt{a^2+13}+\sqrt{b^2+40}+\sqrt{c^2+45}. \label{28} \end{align} 證明結束。 為了驗證式 \eqref{24} 是對的, 我們任意假設 $a+b+c=14$, 計算新的目標函數值如式 \eqref{29}, 並檢查 $S\ge 0$ 是否成立, \begin{align} S=\sqrt{a^2+13}+\sqrt{b^2+40}+\sqrt{c^2+45}-\sqrt{(a+5)^2+(b+8)^2+(c+9)^2}. \label{29} \end{align} Matlab 程式與結果如圖 9 所示, 可以知道目標函數值最小值的確是 0。 我們把計算的結果以等高線畫成圖 10, 由圖 10 知當 $a:b:c=1:4:9$ 時, 不等式 \eqref{28} 中的等式成立。  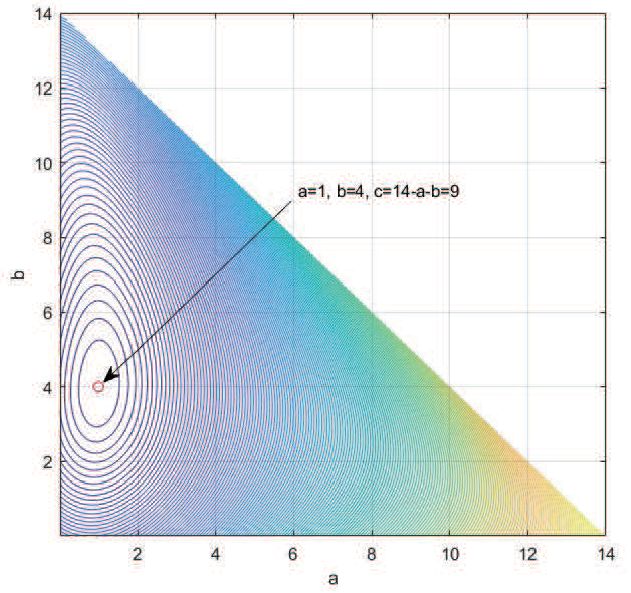 最後做個結論, 本文討論了七個與不等式相關的數學題目, 第一題來自臉書社團"高中數學討論區", 第二題作者曾經發表於 "高中數學討論區"的留言區給同學挑戰, 第三題到第七題皆是作者在寫文章的這兩天內無中生有產生出來的。 以上七個題目若熟悉廣義閔可夫斯基不等式, 皆可輕鬆解題, 若老師們想要提出新的題目, 只要設定廣義閔可夫斯基不等式之參數, 例如 $M=2$, $N=3$, $q=2$, $p=1$, 再加上一點適當的數字與未知數, 就可以源源不絕地產生很多新的不等式考題, 因此希望藉著這篇文章來推廣這個較少人知道的廣義閔可夫斯基不等式(蕎麥不等式), 也許在參加數學競賽或教甄考試時多了一個解題的方法, 也希望對做高中數學科展的同學有所幫助。 參考文獻本文作者林福林任教南台科技大學電子工程學系, 林子喬為聯發科技技術副理 |
2024年9月 48卷3期
廣義閔可夫斯基不等式的介紹及推廣

