| 發刊日期 |
2024年9月
|
||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 標題 | 用對偶觀點深入了解幾何圖形的關係 |
||||||||||||||||||||||||||||||||||||||||
| 作者 | |||||||||||||||||||||||||||||||||||||||||
| 關鍵字 | |||||||||||||||||||||||||||||||||||||||||
| 檔案下載 | |||||||||||||||||||||||||||||||||||||||||
| 全文 |
一、前言中學階段的幾何主要學習歐氏平面幾何 (Euclidean plane geometry) 的相關知識, 而且課綱集中在介紹三角形、 四邊形與圓等平面幾何圖形的性質, 尤其是三角形。 課本介紹的方式通常是透過圖形外觀及各種邊及角等元素之間的關係, 然後開始給予圖形分類、命名, 並歸納共通性質, 選擇最能代表圖形特徵的性質作為定義, 並進行幾何圖形的探究與推理。 然而, 在傳統幾何教材設計上, 三角形、 四邊形的分類仍比較鬆散, 不像代數學習有固定的方法, 學生學習幾何知識時往往比較片斷, 未能充分掌握形與形之間的關係推理。 這些圖形之間是否還有其它的關係呢? 本文旨在透過介紹用對偶的觀點來了解幾何圖形中各種四邊形之間的關係, 期望教師在幾何教學上能更豐富地介紹幾何圖形的關係, 幫助學生深入理解幾何概念, 甚至透過類比推理臆測幾何圖形的新性質。 二、傳統觀點下四邊形的圖形關係四邊形的家族樹分類有很多種, 無論是基於排他性 (exclusive)、 包含性 (inclusive) 或其它方式來表示附屬關係, 通常是藉由判斷下一層比上一層增加或減少條件的方式來進行, 使得下一層圖形都具有上一層圖形特性, 或者是下一層比上一層減少一些特徵的附屬關係, 也就是「包含關係」。 以基於包含性定義的四邊形家族樹為例 (Josefsson, 2016; Usiskin, 2008), 如圖 1, 從最上層具一般性的四邊形開始, 若增加「一組對邊平行」這一個條件, 則產生相較四邊形更為特殊的梯形; 若再增加「另一組對邊平行」或「另一組對邊相等」這第二個條件, 則分別形成更特殊的平行四邊形或等腰梯形。 此時, 對於具有「兩組對邊等長、兩組對邊平行、兩組對角相等、鄰角互補$\cdots$」等性質的平行四邊形, 我們通常選擇以 「兩組對邊平行」來作為平行四邊形的定義。 若再增加「鄰角相等」或「鄰邊相等」這第三個條件, 則會分別形成兩個獨立、 更為特殊的矩形與菱形, 且兩者又都分別具有平行四邊形的特性; 最後再分別增加「鄰邊相等」或「鄰角相等」這第四個條件, 則形成同時具有矩形與菱形特性的正方形。 如果我們利用下一層圖形都具有上一層圖形特性的包含關係, 則當我們證明有關平行四邊形的某一個命題時, 就可推論該命題對其下一層圖形矩形也必成立。 例如, 當證明了「過平行四邊形中心的一直線必平分其面積」這一個命題成立時, 只要根據「因為矩形是平形四邊形的一種」, 就可以推論「過矩形中心的一直線平分其面積」的命題也必然成立。 同樣, 換成菱形時該命題亦會成立, 我們可以運用諸如此類的思考方式, 重新檢視其它命題是否在上一層圖形與下一層圖形都成立的情況。 這種包含關係的思考, 像是一種「垂直式的思考」, 當教導平面幾何時, 我們可以利用這思考方式來引導學生進行演繹推理。 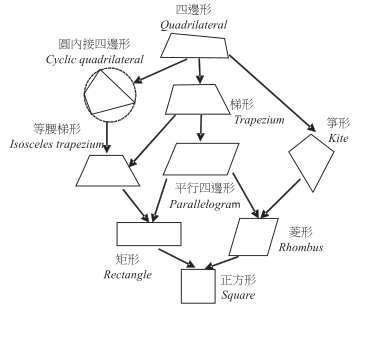 三、對偶觀點下四邊形的圖形關係除了圖 1 所展示的四邊形家族外, 我們好奇的是在這個家族中看似互不隸屬的圖形, 它們之間是否還存在其它的幾何關係呢? 以矩形為例, 除了與分屬上、 下層的平行四邊形、 正方形有包含關係之外, 矩形與其它如菱形、 梯形、 等腰梯形與箏形等圖形, 是否還存在其它幾何關係呢? 我們試著觀察不同四邊形邊與角的基本性質, 在中學階段, 我們建議進行如下探究的方法, 並以矩形為例首先進行觀察。 矩形有「四個等角、 兩組對邊等長」, 我們若在上述關於矩形的命題中將邊換成角, 並將命題中原來的角換成邊, 就會改變成為「四個等邊、 兩組對角相等」的性質, 而「四個等邊、 兩組對角相等」則是另一個圖形所屬的性質。 接下來, 我們可以逐一選取其它圖形與矩形相比較, 其中, 我們會觀察到菱形具有「四個等邊、 兩組對角相等」的性質, 而且當小心檢查其它圖形時, 矩形與它們之間的邊及角明顯沒有這一類對應關係。 亦即矩形的四個等角可以對應到菱形的四個等邊, 而矩形的兩組對邊等長則可以對應到菱形的兩組對角相等, 因此矩形經過 「邊交換成為角以及角交換成為邊」後, 矩形與菱形似乎就會出現一種對應的關係。 我們若對圖形之間小心地進行前述的交換邊與角的方法, 即可以比較系統地進行探索。 當然, 一個幾何圖形有很多性質, 考量到嚴謹性, 我們需要進一步作如下的驗證, 從中還會介紹對偶(duality)、 對偶變換和自對偶的概念。 此外, 我們會繼續介紹另外三組對偶圖形的關係。 (一) 矩形與菱形的對偶首先, 我們對前述矩形與菱形的各種性質做仔細的觀察, 如果我們小心排列, 並將對應的性質整理如表 1 所示, 我們可看到兩者之間有很多對應關係, 例如「四個等角」對應「四個等邊」、 「鄰角相等」 對應「鄰邊等長」等等, 這反映出矩形與菱形應該有更深入的關係。 表1:矩形與菱形的基本性質對應
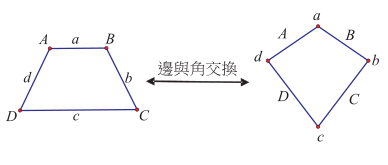
如果我們透過圖形來展現「邊與角交換」的對應關係, 參考圖 2 左, 若將矩形的四個等角 $A$、 $B$、 $C$、 $D$ 分別換成四個等邊, 而矩形的四個邊 $a$、 $b$、 $c$、 $d$ 分別換成四個角, 其中 $a$ 與 $c$ 的等邊換成一對等角, $b$ 與 $d$ 的等邊換成另外一對等角, 最後形成的四邊形即為右圖的菱形。 相反地, 若將菱形的四個等邊 $A$、 $B$、 $C$、 $D$ 分別換成四個等角, 菱形的四個角 $a$、 $b$、 $c$、 $d$ 分別換成四個邊, 其中 $a$ 與 $c$ 的等角換成一對等邊, $b$ 與 $d$ 的等角換成另外一對等邊, 最後形成的四邊形即為左圖的矩形。  在基本性質上, 我們會發現這兩種在四邊形家族中似乎不相干的圖形存在一種先前不容易察覺的關係。 我們不妨稱這兩種圖形具有「對偶關係」, 兩者彼此互為對偶圖形, 而這種「邊與角交換」的對應, 則稱為一種「對偶變換」。 但這樣的對偶關係是否只局限於用來整理已知的性質, 還是它也可以用來延伸出新的性質? 接下來, 我們進一步討論如何可以透過類比推理, 從矩形與菱形的對偶關係臆測出延伸的性質。  我們先再觀察兩組矩形與菱形的對應關係。 如圖 3, 矩形有「兩組對角等距(兩對角線等長)」, 經過「邊與角交換」之後, 會對應到菱形有「兩組對邊等距」這一個性質, 經驗證後亦成立。 又如圖 4, 矩形的「兩組對邊中點連線互相垂直平分 (中心到兩組對邊等距)」, 則可以對應到菱形有「兩組對角角平分線互相垂直平分 (中心到兩組對角等距)」 這一個性質, 經驗證後亦成立。  可是, 矩形有非常多的性質, 當我們探討一個有關矩形的幾何命題成立時, 那麼其對應有關菱形的幾何命題是否也會成立? 例如, 參考圖 5, 當我們證明了「若四邊形為矩形, 則其四邊中點連線為菱形」此一命題成立時, 我們會發現其對應的命題「若四邊形為菱形, 則其四邊中點連線為矩形」 也成立, 我們不妨稱此命題為原命題的「對偶命題」。 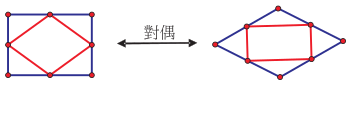 事實上, 矩形除了上述性質外, 還有很多其它性質 $P$ 存在, 我們可根據矩形和菱形的對偶關係, 運用類比推理而臆測菱形具對應的性質 $P'$, 如圖 6, 但仍需要進行證明以確立。 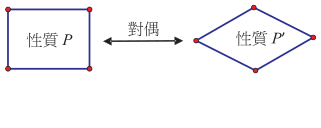 綜合上述觀察, 在四邊形的家族中, 以對偶的觀點來看矩形和菱形的關係, 似乎可以帶出新的眼光, 看出更多形與形之間的關係。 我們會發現矩形與菱形的關係不再是傳統的四邊形家族中不相干的兩個圖形, 它們彼此有對偶關係, 像是一對舞伴, 隨著舞步一前一後, 一左一右, 相互輝映。 特別說明一點, 上述「邊與角交換」的對偶觀點類似於在射影幾何中的「點與線交換」的對偶變換, 例如: 參考圖 7, 「兩直線 $m$、 $n$ 交於一點 $A$」對偶到「兩點 $m$、 $n$ 皆在同一直線 $A$」, 進而有「三條直線 $m$、 $n$、 $l$ 共交於一點 $A$」 對偶到「三點 $m$、 $n$、 $l$ 皆在一直線 $A$」。 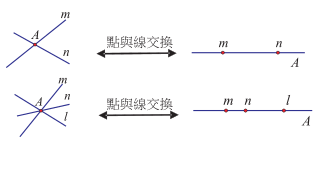 但若依射影幾何的「點與線交換」的對偶變換, 矩形的對偶圖形應該如下圖 8 所示, 有興趣的讀者可參考陳傳麟 (2011) 的說明: 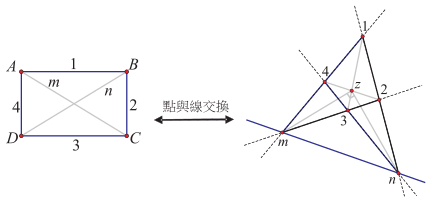 然而本文所處理的「邊與角交換」的對偶觀點是在歐氏平面上進行, 很明顯兩者是有差異的。 接下來, 我們在歐氏平面中繼續探討除了矩形與菱形具有互為對偶圖形的關係之外, 是否還有其它的圖形具有這種對偶關係? (二) 等腰梯形與箏形的對偶我們同樣以「邊與角交換」的對應來思考, 等腰梯形會與哪一個四邊形具有對偶的關係? 等腰梯形有「兩組鄰角相等、一組對邊等長」, 若要對應到其它四邊形, 可發現具有「兩組鄰邊等長、一組對角相等」的箏形與之對應。 我們列出兩者對應的基本性質, 如表 2 所示: 表2: 等腰梯形與箏形的基本性質對應
 同前述矩形與菱形的處理方式, 我們仔細列出等腰梯形與箏形對應的其它性質及圖形, 列舉如表 3, 請讀者自行驗證其性質對偶的狀況, 不再贅述。 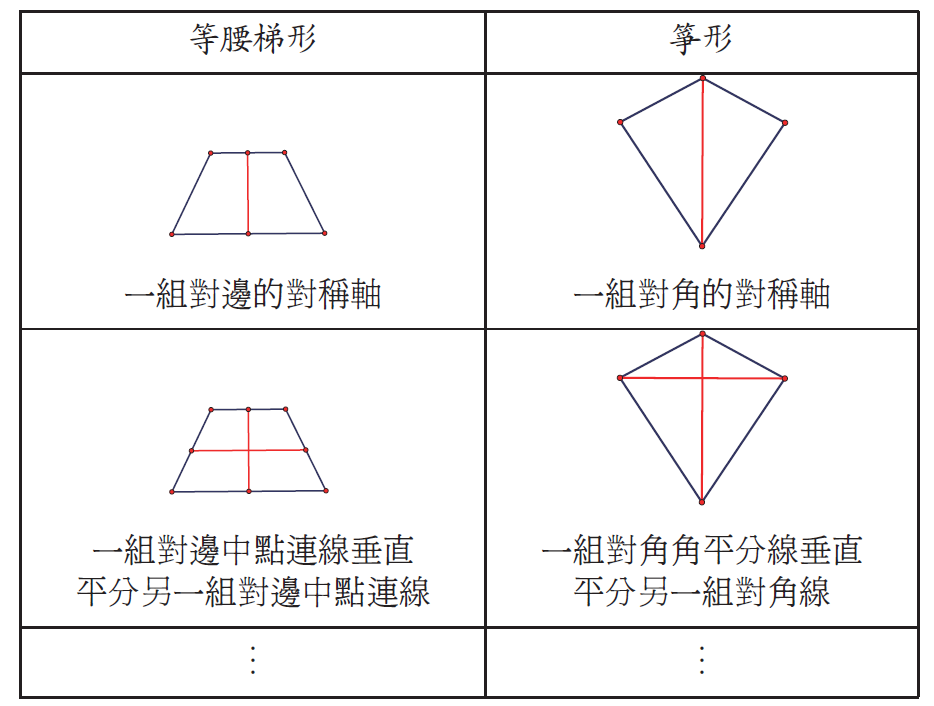 同樣地, 當我們在探討一個有關等腰梯形的幾何命題時, 相對地有關箏形的對偶命題是否也會成立呢? 例如, 參考圖 10, 我們發現「若四邊形為等腰梯形, 則其四邊中點連線為菱形」此一命題成立時, 其對偶命題「若四邊形為箏形, 則其四邊中點連線為矩形」也成立。 有興趣者可自行驗證, 並探究其它可能成立的對偶命題。 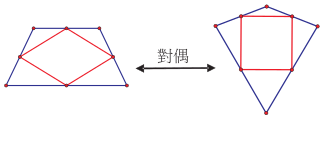 如同矩形與菱形的對偶關係, 等腰梯形與箏形具對偶關係, 彼此像是另一對舞者。 接下來, 我們來觀察一下正方形和平行四邊形的對偶性質。 (三) 正方形、 平行四邊形的自對偶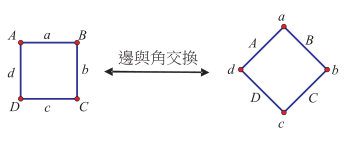 如圖 11, 首先, 我們發現「四個等邊且四個等角」的正方形, 經過「邊與角交換」後, 其對偶為「四個等角且四個等邊」的四邊形, 仍為正方形。 進一步列舉性質如表 4, 正方形基本性質仍對應到正方形自身的性質, 因此, 我們不妨稱正方形為「自對偶 (self-dual)」圖形。 表4:正方形的自相對應的性質
又如圖 12 「 兩組對角相等」的平行四邊形, 對偶到「兩組對邊等長」的圖形仍然是平行四邊形:  進一步列舉性質如表 5, 平行四邊形的基本性質對應到同為平行四邊形的性質, 所以我們會發現平行四邊形也是自對偶圖形。 表5:平形四邊形自相對應的性質
接著, 我們增加「圓內接」或「圓外切」這一個條件, 以考慮更複雜的圖形, 並觀察圓內接四邊形與圓外切四邊形的對偶性質, 進一步探討對偶關係如何應用於更複雜的圖形。 (四) 圓內接四邊形與圓外切四邊形的對偶我們從與圓內接或圓外切四邊形構圖有關的垂直平分線與角平分線開始, 從定義來看, 垂直平分線為「與一線段 (邊) 兩端點等距離的所有點所形成的軌跡」, 而角平分線是「與一個角的兩邊等距離的所有點所形成的軌跡」, 從「邊與角交換」來看, 我們會發現這兩個圖形為對偶圖形, 參考圖 13。  將上述推廣至三角形的外接圓與內切圓, 參考圖 14, 「三角形的三個邊的垂直平分線共交一點 (外心, 外接圓圓心), 且到三頂點等距離」這命題, 與「三角形的三個角的角平分線共交一點 (內心, 內切圓圓心), 且到三邊等距離」這命題為對偶命題, 這兩個圖形具有對偶關係。 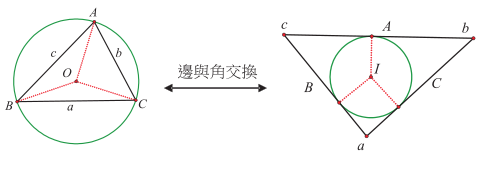 如果考慮用圓內接四邊形或圓外切四邊形來思考有關矩形與菱形或等腰梯形與箏形的命題, 我們會發現, 參考圖 15, 我們可以證明「如果四邊形 $ABCD$ 為矩形, 則其必有一個外接圓, 且四個角的頂點的切線構成一個菱形」這命題成立, 若將矩形對偶轉換到菱形, 不難證出其對偶命題「如果四邊形 $PQRS$ 為菱形, 則其必有一個內切圓, 且四個邊的切點的連線構成一個矩形」也成立。  同樣地, 對於有關圓內接等腰梯形與圓外切箏形的命題, 參考圖16左圖, 我們也會發現「如果一個內接於圓的四邊形為等腰梯形, 則其四個角的頂點的切線構成一個箏形」成立, 其對偶命題「如果一個外切於圓的四邊形為箏形, 則其四個邊的切點的連線構成一個等腰梯形」也成立, 如右圖。 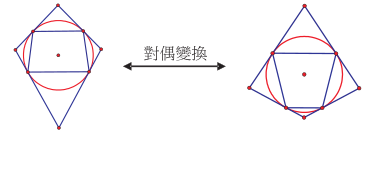  歸結上述圓內接與圓外切的特殊四邊形, 如矩形與菱形或等腰梯形與箏形均具有對偶關係, 那麼對於一般的圓內接四邊形與圓外切四邊形是否也具有對偶關係呢?  我們列舉兩者性質如表 6, 例如「兩組對角和相等」對應於「兩組對邊和相等」, 我們可以確認圓內接四邊形與圓外切四邊形也互為對偶圖形。 表6:圓內接四邊形與圓外切四邊形的性質對應
至目前為止, 我們對討論過的四邊形做一個小結, 矩形與菱形、 等腰梯形與箏形、 圓內接四邊形與圓外切四邊形互為對偶。 此外, 正方形及平行四邊形則為自對偶圖形。 四、歐氏幾何中圖形對偶的有限性通過上述各小節討論四邊形的性質來檢驗, 經執行「邊與角交換」後, 似乎即可得到對偶圖形。 但根據陳傳麟 (2011) 及De Villiers (1996, 1998) 等學者指出, 在歐氏平面上, 把「角(頂點或點)」換成「邊(線段)」 的前後圖形, 在一般情形下其對偶性是不一定會成立的。 關於這一點, 我們可以舉幾個例子說明, 例如三角形「兩邊之和大於第三邊」此一命題成立, 但其對偶命題「兩角之和大於第三角」 卻不成立。又例如四邊形內角和360度為定值, 但其對偶命題的「四邊形的四邊長度和」卻不是定值。 再者, 一個內角換成一個邊, 那若有需要將此內角的外角進行對偶轉換, 又該如何對應呢? 又或者如「對邊平行」的梯形該如何進行對偶轉換? 由此來看, 在歐氏平面上的圖形或其相關命題, 並不見得存在對偶圖形或對偶命題。 本文所討論歐氏幾何的對偶關係, 雖然類似於射影幾何中的「點和線交換」的對偶變換, 但這樣的對偶性在歐氏平面的圖形中是有限制的, 不像在射影幾何「點與線」的對偶變換具有一般性。 特別是歐氏幾何的對偶似乎並不適用於與第五公設有關的命題或定理, 也就是與「平行」有關的命題或定理 (De Villiers, 1996)。 即便如此, 在歐氏平面中, 我們仍可看到四邊形之間具有豐富的對偶關係。 在中學階段學習歐氏幾何內容中, 若加入採用對偶觀點來思考四邊形圖形中形與形的關係, 它雖然有局限, 但仍能幫助我們思考用一種新的眼光來看待圖形之間的關係。 這好比在歐氏幾何中, 雖然無法像在射影幾何中能用廣泛的對偶眼鏡來看清楚圖形關係, 但至少能像是用一副近視的眼鏡, 看到近處圖形之間隱藏的對偶關係, 這反而可以形塑出我們對平面幾何圖形之間更大的探索想像空間。 以對偶觀點來看中學幾何, 除了可以指導學生學習以垂直式的包含關係進行幾何推理之外, 若也輔以學習以水平式的對偶關係來思考形與形之間的關係, 可以幫助學生更深入了解幾何圖形的關係, 無論是探索已知或探索未知, 對偶提供了另一種思考的方式, 特別是對於從事幾何專題研究的學生是有助益的。 關於教導的方式, 我們作如下進一步的說明, 我們可以引導學生追問當一個與某圖形有關的幾何命題成立時, 其對偶命題是否也會成立呢?例如, 我們與學生討論命題「任意四邊形四個角的角平分線交會所構成的四邊形, 必有一個外接圓」成立之後, 我們可以問學生臆測其對偶命題為何? 當他們能說出對偶命題為「任意四邊形四個邊的垂直平分線交會所構成的四邊形, 必有一個內切圓」之後, 我們再追問該對偶命題是否成立?學生經構圖、測量與驗證後發現此對偶命題結果是不成立的。 於是, 我們可以建議學生增加「圓內接四邊形」這一個條件再出發, 修正的命題如下: 「任意圓內接四邊形四個角的角平分線交會所構成的四邊形, 必有一個外接圓。」 如圖18, 此命題當然仍會成立。此時, 我們請學生研究修正後的對偶命題是否會成立, 即如下命題: 「任意圓外切四邊形四個邊的垂直平分線交會所構成的四邊形, 必有一個內切圓。」 如圖 19, 經構圖、測量與驗證後, 令人意外驚喜的是該命題竟然是成立的, 而證明留給有興趣的讀者自行挑戰自己。 這是一段透過對偶觀點, 提出其對偶命題的幾何臆測, 得到新發現的有趣歷程。 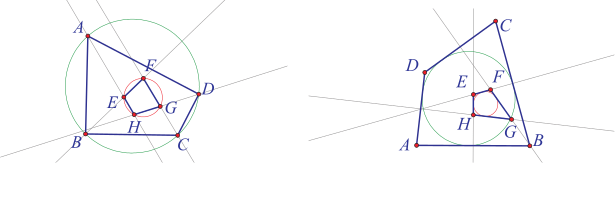 五、用新的眼光看中學幾何本文透過對偶的觀點重新探究中學幾何的圖形關係, 從過去多以垂直式的包含關係來思考四邊形, 會發現四邊形家族之間的圖形關係似乎存在一種特殊「對稱」的對偶關係。 雖然在歐氏幾何中, 圖形的對偶性是有限的, 不像在射影幾何「點與線」的對偶變換中具有一般性, 但透過類似水平式的對偶思考, 我們可以重新思考幾何圖形之間的關係, 然後進行另類的幾何探究。 至於前文提到對邊平行的梯形該如何進行對偶轉換的問題, 以及透過對偶轉換將四邊形進行分類, 其分類樹會有何新面貌? 這些問題需要更長的篇幅來說明, 我們將著手撰寫另文以作交代。 對很多學生來說, 他們會誤會幾何知識已經是前人已經探索完成的知識, 他們只能盡力學習, 既學不完, 也沒有發現新知識的機會, 無法體會新成果的樂趣, 但教師若能引入對偶的概念, 幫助學生更深入理解幾何圖形的關係, 學生就可能有領會到親身參與探索新知識的機會, 甚至於有機會經歷幾何的新發現, 而上述情況便有可能得到改善。 不過話得說回來, 對偶轉換只能視為是臆測的過程, 我們必須提醒學生要小心證明臆測的命題是否成立。 因此, 我們推薦教師在中學的幾何教學中, 能向學生介紹對偶觀點, 更全面認識與掌握中學幾何圖形的關係。 參考文獻本文作者林永發任教臺北市濯亞國際學院實驗教育機構,譚克平任教國立臺灣師範大學科學教育研究所 |
||||||||||||||||||||||||||||||||||||||||
2024年9月 48卷3期
用對偶觀點深入了解幾何圖形的關係

