| 發刊日期 |
2024年9月
|
|---|---|
| 標題 | 2024年第13屆歐洲女子數學奧林匹亞競賽試題解答 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
2024 年第 13 屆歐洲女子數學奧林匹亞競賽 (Euporean Girls' Mathematical Olympiad, 簡稱 EGMO) 在喬治亞茨卡圖博 (Tskaltubo, Georgia) 舉行。 本屆共有 54 個國家與會、 合計 212 位女學生代表參賽。 我國則是首次正式參賽, 獲得一金一銀一銅的成績, 表現優異。 競賽內容與國際數學奧林匹亞競賽 (International Mathematical Olympiad, 簡稱 IMO) 相仿, 由試題委員會在代數、 組合、 幾何、 數論等領域中挑選六道試題, 供領隊會議確認成為正式考題, 以兩天每天 3 道試題、 4 小時又 30 分鐘的形式由選手作答。 本屆的六道試題, 第一、 六道屬代數, 第二題為幾何, 第三、 五題為數論, 第四題為組合。 本文提供我國代表團所翻譯成正體中文版的 6 道 EGMO 試題以及官方釋出的參考解答, 作為國內相關學者、 數學教師等輔導數學資優生之研究、 應用與參考之用。 問題一: 黑板上寫有兩個不同的整數 $u$ 與 $v$, 我們將實施一系列的操作步驟。 在每一步驟時, 我們從下列兩種操作中擇一執行: (i) 若 $a$ 和 $b$ 是黑板上的相異數, 而且 $a+b$ 還沒出現在黑板上, 則我們可以在黑板上寫下 $a+b$ 這個數。 (ii) 若 $a, b$ 和 $c$ 是黑板上的三個相異數, 整數 $x$ 滿足 $ax^2 + bx + c = 0$ 而且 $x$ 還沒有出現在黑板上, 則我們可以在黑板上寫下 $x$ 這個數。 試找出所有的初始數對 $(u,v)$, 使得任意整數都能在有限次操作步驟後出現在黑板上。 試題委員會公布的參考答案: 滿足下列條件的數對 $(u,v)$ 皆可為初始數對: $u,v$ 中不能有 $0$, $u,v$ 中至少有一正數, 且 $\{u,v\} \ne \{1,-1\}$。 (將這些條件全部記為 (*)。) 首先注意到, 若 $v = 0$, 則黑板上永遠只有 $u, 0$ 兩個數字。 若 $u,v$ 皆為負數, 則操作 (i) 只會製造負數;而當 $a, b, c$ 皆為負整數時, 對任意正整數 $x$ 皆有 $ax^2 + bx + c \lt 0$, 故操作 (ii) 不會生出任何正整數, 與題意不合。最後當 $\{ u, v \} = \{1, -1\}$ 時, 雖然可以用 (i) 在黑板上寫出 0, 但此後 (i)(ii) 都生不出任何新的整數了。 至此, 我們知道 (*) 為必要條件。 以下證明充分性, 假設 $u, v$ 都不是 0, $u,v$ 之中至少有一正數, 且 $\{u,v\} \ne \{1,-1\}$。 不失一般性, 設 $u \gt \max \{v, 0\}$。 因為 $u,v$ 都不是 0, 所以 $u, v, u+v$ 是三個相異整數。在操作 (ii) 中代入 $(a,b,c) = (u,u+v,v)$, 知道可以寫出 $-1$ (不論它一開始在不在黑板上)。 如果 $u \gt 1$, 則反覆操作 (i) 可以得到正整數 $u, u-1, \dots, 2, 1$ (就算 $v$ 在其中也可以)。再利用 (i) 可以從 $u$ 開始一直往上加 1, 所以任意正整數都寫得出來。 有了 $1, -1$ 後利用 (i) 可以寫出 $0$。最後在操作 (ii) 中代入 $(a,b,c) = (0,1,k)$ 可以得到任意負整數 $-k$。 如果 $u = 1$, 則由 (*) 知 $v \lt -1$。從 $v$ 開始反覆利用 (i) 及 $u=1$ 可以得到 $1, 0, -1, -2, \dots, v$ 這些整數。因為有 $-1,-2,\dots, v$, 所以一直操作 (i) 一直減 1 可以得到任意負整數。 最後在操作 (ii) 中代入 $(a,b,c) = (0,1,-k)$ 可以得到任意正整數 $k$。 至此證明完畢。 $\Box$ 評註: 此題為本屆賽事最簡單的代數題, 考驗選手對於一次與二次方程式的整數根性質的掌握程度。 但其中有些小狀況是同學們容易忽略的, 造成本題獲得滿分的選手人數並未如預期的多。 同學作題的時候, 細心檢視各種情況, 還是很重要的。 問題二: 在三角形 $ABC$ 中, $\overline{AC} \gt \overline{AB}$, 將其外接圓記為 $\Omega$, 內心記為 $I$。 設其內切圓分別與 $BC, CA, AB$ 邊交於點 $D, E, F$。 令 $X, Y$ 分別是內切圓的劣弧 $DF$ 及 $DE$ 上兩點, 滿足 $\angle BXD = \angle DYC$。 設直線 $XY$ 與直線 $BC$ 交於點 $K$。 設點 $T$ 在圓 $\Omega$ 上, 滿足 $\overline{KT}$ 與圓 $\Omega$ 相切, 且 $T$, $A$ 兩點在直線 $BC$ 的同側。 證明: 直線 $TD$ 與直線 $AI$ 交在圓 $\Omega$ 上。 試題委員會公布的參考答案: 我們首先證明 $X, B, C, Y$ 四點共圓。我們有下列一串等式: \begin{align*} 180^\circ &= \angle DCY + \angle CYD + \angle YDC & & \text{(三角形內角和)} \\ &= \angle BCY + \angle DXB + \angle YXD & & \text{(題設 $\angle CYD = \angle DXB$, 弦切角)} \\ &= \angle BCY + \angle YXB. \end{align*} 至此, 四邊形 $XBCY$ 有一組對角互補, 故其四頂點共一圓。 現在考慮 $K$ 到三角形 $ABC$ 的內切圓、圓 $\Omega$ (外接圓)、與圓 $XBCY$ 的圓冪, 可知 \begin{align*} \overline{KT}^2 &= \overline{KB} \cdot \overline{KC} & & \text{(圓 $\Omega$)} \\ &= \overline{KX} \cdot \overline{KY} & & \text{(圓 $XBCY$)} \\ &= \overline{KD}^2. & & \text{($ABC$ 內切圓)} \end{align*} 故得 $\overline{KD} =\overline{KT}$。 設直線 $AI$ 與圓 $\Omega$ 再交於點 $M$;因為直線 $AI$ 是內角平分線, $M$ 為 $BC$ 弧中點。 過 $M$ 作圓 $\Omega$ 的切線, 設其與直線 $KT$ 交於點 $Q$。 因為 $M$ 是弧中點, 知 $\overline{QM}$ 與 $\overline{KD}$ 平行, 推得 $\angle TKD = \angle TQM$。 又由 $\overline{KT} = \overline{KD}$ 及 $\overline{QT} = \overline{QM}$, 所以 $\triangle TKD \sim \triangle TQM$ (SAS 相似性質)。 最後由於 $T, K, Q$ 共線, 故 $T, D, M$ 也共線。 所以直線 $TD \cap$ 直線 $AI = M$ 落在圓 $\Omega$ 上, 證明完畢。 $\Box$ 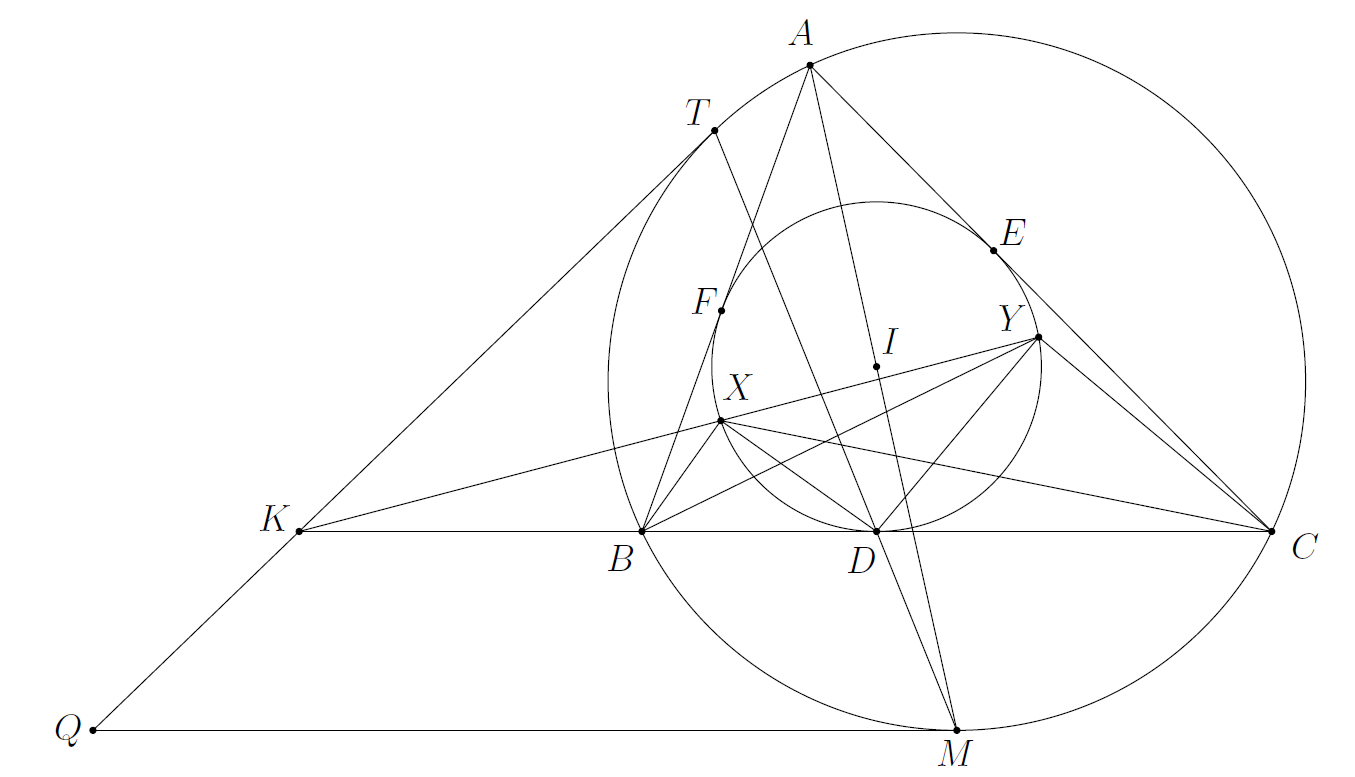 評註: 本題為中等難度的幾何題, 除了開始的追角度與四點共圓性質之外, 最後以位似變換確認直線交點的位置, 是值得學習的技巧。 問題三: 我們稱正整數 $n$ 是奇特數, 如果對 $n$ 的任意正因數 $d$, 都有整數 $d(d+1)$ 整除 $n(n+1)$。 證明:對任意四個相異的奇特正整數 $A, B, C, D$, 都有 $$ \gcd(A,B,C,D)=1. $$ 這裡 $\gcd(A,B,C,D)$ 是同時整除 $A, B, C, D$ 的最大正整數。 試題委員會公布的參考答案: 我們來分析奇特數的性質。明顯知 1 與任意質數皆是奇特數。 當奇特數 $n \gt 1$ 時, 令 $p$ 為 $n$ 的最小質因數。 考慮 $n$ 的因數 $\frac{n}{p}$, 由題設有 $\frac{n}{p} \left( \frac{n}{p} + 1 \right) \mid n (n + 1) \Rightarrow (n+p) \mid p^2 (n+1)$。 再推下去有 $$ (n+p) \mid p^2(n+1) - p^2(n+p) = p^2 - p^3. $$ 所以 $n \lt n+p \leqslant p^3 - p^2 \lt p^3$, 即 $n \lt p^3$。 由此知 $n$ 最多只有兩個質因數 (計算重數)。事實上, 若 $n = p^2$ 是奇特數的話, 會有 $p+1 \mid (p^2 - p)$, 即 $p+1 \mid 2$, 矛盾。 以下假設奇特數 $n = pq$, 其中 $p,q$ 為相異質數。 由題設, 真正重要的條件是 $p(p+1) \mid n(n+1)$ 及 $q(q+1) \mid n(n+1)$。 由 $p(p+1) \mid n(n+1) = pq (pq + 1)$ 得 $p+1 \mid q (pq+1)$, 由此推知 $p+1 \mid \left( q^2(p+1) - q(pq+1) \right) = q(q-1)$。 同理有 $q+1 \mid p(p-1)$。 由對稱性, 可設 $p \gt q$。 若 $q$ 不整除 $p+1$ 的話, 此兩數必互質, 因此 $p+1 \mid (q-1)$。 但 $p+1 \gt p \gt q \gt q-1 \gt 0$, 此為矛盾;故 $q$ 必整除 $p+1$。 另外, 由於 $p \gt q$, 知道 $p$ 不整除 $q+1$, 除非 $p = q+1$, 亦即 $p = 3$、 $q = 2$; 但此時 $p+1 = 4 \not| \,\,\, 2 = q(q-1)$。 既然 $p$ 不整除 $q+1$, 就有 $q+1$ 整除 $p-1$。 由 $q$ 整除 $p+1$, 可設 $p+1 = mq$, 其中 $m$ 為正整數。 於是 $q+1$ 整除 $p-1 = mq - 2 = m(q+1) - m - 2$, 得到 $q+1$ 整除 $m+2$。 另一方面, 由 $p+1 \mid q(q-1)$ 推得 $m$ 整除 $q-1$。 若 $\frac{q-1}{m} \gt 1$, 則 $m \leqslant \frac{q-1}{2}$; 但 $q+1$ 又整除 $m+2$, 可知 $q \leqslant m+1$。 放在一起就有 $m \leqslant \frac{q-1}{2} \leqslant \frac{m}{2}$, 此式對正整數 $m$ 矛盾。 故 $m = q - 1$, 而我們證明了以下性質:如果 $n \gt 1$ 是奇特數並為合數, 則 $n = pq$, 其中 $p \gt q$ 為兩相異質數, 且 $p = q^2 - q - 1$。 綜上所述, 質數 $p$ 只能是下列奇特數的因數: $p$; $p (p^2-p-1)$ (此時 $p^2 - p - 1$ 為質數); $pq$, 其中 $q$ 為質數且 $p = q^2 - q - 1$。 也就是說, 四個以上的奇特數的最大公因數必為 1。 (注意到的確有三個奇特數有共同的質因數。 例如 $5$; $15 = 3 \cdot 5$; $95 = 5 \cdot 19$。) 證明完畢。 $\Box$ 評註: 本題是偏難的數論題。題目中敘述不可能有四個相異的奇特數有共同的質因數, 因此解題策略上就在於尋找奇特數的質因數性質。 經由多方的討論與檢驗後, 確定任一質數最多可為三個奇特數的因數。 本題是很優質的探索題, 選手們需經各種嘗試, 才能找到正確的解題路徑。 問題四: 對一個整數數列 $a_1 \lt a_2 \lt \cdots \lt a_n$, 我們稱數對 $(a_i, a_j)$ 為有趣數對, 其中 $1 \le i \lt j \le n$, 如果存在整數數對 $(a_k, a_\ell)$ 滿足 $1 \le k \lt \ell \le n$ 且 $$ \frac{a_\ell - a_k}{a_j - a_i} = 2. $$ 對於每個 $n \ge 3$, 試決定在一個 $n$ 項數列中找到的有趣數對之最大可能數量。 試題委員會公布的參考答案: 本題的答案為 $\frac12 (n-1)(n-2) + 1 = \binom{n-1}{2} + 1$。 先討論下界。 考慮數列 $a_1, \dots, a_n$ 定義如下: $a_1 = 0$; 當 $2 \leqslant i \leqslant n$ 時, 令 $a_i = 2^i$。 選任意整數數對 $(a_i,a_j)$, 其中 $1 \leqslant i \lt j \leqslant n$。 當 $i = 1$ 時, 由於對任一 $j = 2, 3, \dots, n-1$, 有 $\dfrac{a_{j+1} - a_1}{a_j - a_1} = \dfrac{2^{j+1}}{2^j} = 2$, 所以 $(a_1,a_2)$, $(a_1,a_3)$, \dots, $(a_1,a_{n-1})$ 都是有趣數對。 當 $i \geqslant 2$ 時, 由於對任一 $j = i+1, \dots, n-1$, 有 $\dfrac{a_{j+1} - a_{i+1}}{a_j - a_i} = \dfrac{2^{j+1} - 2^{i+1}}{2^j - 2^i} = 2$, 所以這些 $(a_i,a_j)$ 也都是有趣數對。 最後, $(a_{n-1}, a_n)$ 也是有趣數對, 因為 $\dfrac{a_n-a_1}{a_n-a_{n-1}} = \dfrac{2^n}{2^n - 2^{n-1}} = 2$。 綜上, 只要數對 $(a_i,a_j)$ 滿足 $1 \leqslant i \lt j \leqslant n-1$, 或者 $(a_i,a_j) = (a_{n-1}, a_n)$, 都是此數列所得的有趣數對。 所以共有 $\binom{n-1}{2} + 1$ 個有趣數對。 接下來我們證明此數為有趣數對數量的上界。由於 $\binom{n}{2} - (\binom{n-1}{2} + 1) = n - 2$, 我們將證明至少有 $n-2$ 個數對不是有趣數對。 首先, $(a_1,a_n)$ 不可能是有趣的, 因為 $a_n - a_1$ 是所有 $a_j - a_i$ 的最大數。 並且, 當 $(a_i,a_j)$ 是有趣數對時, $a_j - a_i = \frac12 (a_\ell - a_k)$ 對某 $1 \leqslant k \lt \ell \leqslant n$ 成立, 因此 $a_j - a_i = \frac12 (a_\ell - a_k) \leqslant \frac12 (a_n - a_1)$。由於當 $2 \leqslant k \leqslant n-1$ 時, $(a_k - a_1) + (a_n - a_k) = a_n - a_1$, 這兩個數至少有一個大於或等於 $\frac12 (a_n - a_1)$;並且最多只能有一個 $k$ 在此範圍內滿足 $a_k - a_1 = a_n - a_k = \frac12 (a_n-a_1)$。所以對於此範圍中, 至少有 $(n-2) - 1 = n-3$ 個 $k$ 使得 $(a_1, a_k)$, $(a_k, a_n)$ 之中有一個不有趣數對。 再加上 $(a_1, a_n)$ 這一對, 我們證明了任一 $n$ 項數列至少有 $(n-3) + 1 = n-2$ 個不有趣數對。 證明完畢。 $\Box$ 評註: 本題看起來是數論題, 但實際上屬於組合題, 為標準的估計構造題。 由於題目給的整除條件很特殊, 一般人都會由等比數列或等差數列下手。 除了官解提供的幾乎等比數列外, 幾乎等差數列 $1, 2, \dots, n-2, n-1, 2n-3$ 也符合最多有趣數對的規則。 但本題的困難點在於論證此數量即為最大值, 所以大部分的分數都配到了估計上界這邊。 問題五: 設 $\mathbb N$ 為所有正整數所成的集合。試找出所有函數 $f: \mathbb N \to \mathbb N$, 使得對任意正整數數對 $(x,y)$, 下列敘述皆成立: (i) $x$ 和 $f(x)$ 有相同數量的正因數。 (ii) 若 $x$ 不整除 $y$ 且 $y$ 也不整除 $x$, 則 $$ \gcd\left( f(x), f(y) \right) \gt f \left( \gcd(x,y) \right). $$ 這裡 $\gcd(m,n)$ 是同時整除 $m, n$ 的最大正整數。 試題委員會公布的參考答案: 本題答案是 $f(n) = k^{d(n)-1}$, 其中 $k$ 為質數, $d(n)$ 代表 $n$ 的正因數個數。 為求簡潔, 以 $\mathbb P$ 代表質數所成的集合。 另外, 以 $P(x,y)$ 代表 (ii) 中的不等式。 由 (i) 立得 $f(1) = 1$, 且對任意質數 $p \in \mathbb{P}$, 都有 $f(p) \in \mathbb{P}$。 對兩相異質數 $p, p' \in \mathbb{P}$, 由 $P(p,p')$ 得 $$ \gcd( f(p), f(p') ) \gt f \left( \gcd(p,p') \right) = f(1) = 1, $$ 故存在一質數 $k \in \mathbb{P}$ 使得 $f(p) = k$ 對任意質數 $p$ 皆成立。 以下我們將證明 $f(n)$ 總是 $k$ 的次方, 配合 (i) 就知道 $f(n) = k^{d(n)-1}$。 Claim 1. $f(p^2) = k^2$ 對所有 $p \in \mathbb{P}$ 均成立。 Claim 1 的證明: 對於任意 $p \in \mathbb{P}$, 取另一個 $q \in \mathbb{P}$ 並代入 $P(p^2,pq)$: $$ \gcd \left( f(p^2), f(pq) \right) \gt f \left( \gcd( p^2, pq ) \right) = f(p) = k. $$ 故 $f(p^2)$ 是 $k$ 的倍數。配合 (i), $k$ 的倍數之中只有 $k^2$ 恰有 3 個因數, 所以 $f(p^2) = k^2$。 $\Diamond$ Claim 2. $f(pq) = k^3$ 對任意 $p,q\in\mathbb{P}$, $p \ne q$ 皆成立。 Claim 2 的證明: 由 Claim 1 及 $P(p^2, pq)$ 得 $$ \gcd( k^2, f(pq) ) = \gcd( f(p^2), f(pq) ) \gt f \left( \gcd( p^2, pq ) \right) = f(p) = k. $$ 所以 $f(pq)$ 必為 $k^2$ 的倍數。配合 (i), $k^2$ 的倍數之中只有 $k^3$ 恰有 4 個因數 ($d(pq) = 4$), 所以 $f(pq) = k^3$。 $\Diamond$ Claim 3. $f(p^n) = k^n$ 且 $f(p^{n-1} q) = k^{2n-1}$ 對所有 $p, q \in \mathbb{P}$, $p \ne q$ 及 $n \in \mathbb{N}$ 皆成立。 Claim 3 的證明: 對 $n$ 作數學歸納法。 初始狀況 $n=1$ 為顯然, $n=2$ 即為 Claims 1, 2。 現假設命題在正整數 $n \geqslant 2$ 時成立, 並考慮 $n+1$ 的情況。 代入 $P(p^{n+1}, p^n q)$ 可得 $$ \gcd( f(p^{n+1}), f(p^n q) ) \gt f \left( \gcd (p^{n+1}, p^n q) \right) = f(p^n) = k^n. $$ 由此, $f(p^{n+1})$ 會是 $k^n$ 的倍數。設 $f(p^{n+1}) = k^n \cdot t$, $t \gt 1$ 為正整數。 如果 $t$ 的質因數中有不是 $k$ 的質數的話, $d(k^n \cdot t) \geqslant 2(n+1) \gt n + 2 = d(p^{n+1})$, 不合。 所以 $t$ 只有 $k$ 這個質因數, 即 $f(p^{n+1})$ 為 $k$ 的次方。 $k$ 的次方中因數個數恰為 $n+2$ 的只有 $k^{n+1}$ 這個數, 所以 $f(p^{n+1}) = k^{n+1}$, 命題的第一部分成立。 再來考慮 $f(p^{n+1}),f(p^n q)$。 得到 $$ \gcd ( k^{n+1}, f(p^n q) ) = \gcd( f(p^{n+1}), f(p^n q) ) \gt f \left( \gcd (p^{n+1}, p^n q) \right) = f(p^n) = k^n. $$ 因為 $k^{n+1}$ 的因數中比 $k^n$ 大的只有 $k^{n+1}$, 所以 $\gcd ( k^{n+1}, f(p^n q) ) = k^{n+1}$, 也就是說, $f(p^n q)$ 也是 $k^{n+1}$ 的倍數。 設 $f(p^n q) = k^{n+1} \cdot t'$, $t' \gt 1$ 為正整數。 如果 $t'$ 的質因數中有不是 $k$ 的質數的話, $d(k^{n+1} \cdot t') \geqslant 2(n + 2) \gt 2(n+1) = d(p^n q)$, 不合。 所以 $t'$ 只有 $k$ 這個質因數, 即 $f(p^n q)$ 為 $k$ 的次方。 $k$ 的次方中因數個數恰為 $2(n+1)$ 的只有 $k^{2n+1}$ 這個數, 所以 $f(p^n q) = k^{2n+1} = k^{2(n+1)-1}$, 命題的第二部分也成立。 至此, Claim 3 對任意相異質數 $p, q$ 及任意正整數 $n$ 均成立, 證明完畢。 $\Diamond$ Claim 4. 對任意正整數 $n$, 都有 $f(n) = k^{d(n)-1}$。 Claim 4 的證明: 這次我們對 $n$ 的相異質因數的個數 $m$ 作數學歸納法。 Claim 3 證明了 $m=1$ 的情況 ($m=0$, 即 $n=1$ 早就成立了)。 現設此結論對於相異質因數個數不超過 $m \geqslant 1$ 的任意正整數均成立。 考慮任意一個相異質因數等於 $m$ 的正整數 $N$, 及不整除 $N$ 的任意質數 $p$。 數學歸納法步驟就是要證明, 對任意非負整數 $r$, $f(Np^r)$ 總是 $k$ 的次方; 再由因數個數即得結論。 這裡我們進一步對非負整數 $r$ 進行數學歸納法。 初始情形 $r=0$ 成立。 假設此敘述對某個整數 $r \geqslant 0$ 成立。 設 $s$ 為 $N$ 的某個質因數, 我們來看 $P(Np^{r+1}, Nsp^r)$: $$ \gcd( f(Np^{r+1}), k^{d(Nsp^r)-1} ) = \gcd ( f(Np^{r+1}), f(Nsp^r) ) \gt f(Np^r) = k^{d(Np^r)-1}. $$ 所以 $k^{d(Np^r)}$ 整除 $f(Np^{r+1})$。 如果 $f(Np^{r+1})$ 還有其他不是 $k$ 的質因數的話, $$ d(f(Np^{r+1})) \geqslant 2 ((r+1) d(N) + 1) = (2r+2) d(N) + 2 \gt (r+2) d(N) = d(Np^{r+1}), $$ 此與 (i) 不合。 故 $f(Np^{r+1})$ 是 $k$ 的次方。 Claim 4 由數學歸納法原理得證。 $\Diamond$ 最後我們來驗解。 (i) 顯然成立。 而當正整數 $x$ 與 $y$ 不互相整除的時候, $$ \gcd(f(x),f(y)) = k^{\min(d(x),d(y)) - 1} \gt k^{d(\gcd(x,y))-1} = f(\gcd(x,y)). $$ 故 (ii) 也成立。全題證明完畢。 $\Box$ 評註: 本題雖屬數論題, 但其中又有函數不等式的內涵。 由於不等式中有互質兩數的關係, 而且條件一中提到了正因數數量, 因此由正整數的質因數來破題是正規的手法。 後面的討論需要同學們耐心地處理, 不等式的成立也有不同的路徑, 還請各位讀者多方嘗試求解。 問題六: 試找出所有正整數 $d$, 滿足有一個 $d$ 次的實係數多項式 $P$, 使得 $P(0)$, $P(1)$, $P(2)$, $\dots$, $P(d^2-d)$ 中至多有 $d$ 個相異值。 試題委員會公布的參考答案: 本題答案為 $d = 1, 2, 3$。 我們首先給兩個一般性註解。 第一是: 我們總是可以在多項式上加任意常數, 不改變題目要求的多項式性質。 第二是透過伸縮與平移, 我們可以把原題化為: 能否找到 $d$ 次實係數多項式 $P$, 使得 $P$ 在連續的 $d^2-d+1$ 個整數上的取值, 只有最多 $d$ 個相異值? 在 $d = 1, 2, 3$ 時有如下的構造: \begin{align*} d &= 1: & d^2 - d &= 0, & P_1(x) &= x, & &\quad P(0) = 0; \\ d &= 2: & d^2 - d &= 2, & P_2(x) &= x(x-1), & &\begin{cases} P(0) = P(1) = 0, \\ P(2) = 2; \end{cases} \\ d &= 3: & d^2 - d &= 6, & P_3(x) &= x(x-4)(x-5), & &\begin{cases} P(0) = P(4) = P(5) = 0, \\ P(1) = P(2) = P(6) = 12, \\ P(3) = 6. \end{cases} \end{align*} 加上任意常數可以得到更多例子。 以下我們證明:當 $d \geqslant 4$ 時, 滿足題設的多項式不存在。 不失一般性, 我們作以下的假設:我們想找的多項式 $P$ 為首么多項式 (乘以適當常數即得), 且當 $i = 0, 1, \dots, d^2-d$ 時, $P(i)$ 的值都是正的 (加上夠大的常數項即得)。 以歸謬法證之。 設滿足題設的 $d \geqslant 4$ 次多項式 $P$ 滿足 $P(0)$, $P(1)$, $\dots$, $P(d^2-d)$ 的取值發生於 $p_1 \lt p_2 \lt \cdots \lt p_d$。 對於 $i = 1, \dots, d$, 令 $n_i \geqslant 0$ 代表 $p_i$ 在 $P(0), \dots, P(d^2-d)$ 之中出現的次數。 由定義知 $n_1 + \cdots + n_d = d^2 - d + 1$。由於 $P$ 為 $d$ 次多項式, $n_i \leqslant d$ 皆成立。 下面是關鍵性質。 Claim 1. 定義 $n_0 = n_{d+1} = 0$。 若對某個 $i$ 有 $n_i = d$, 則 $n_{i\pm 1} \leqslant d-2$。 Claim 1 的證明: 由於 $n_i=d$, 存在整數 $0 \leqslant a_{1,i} \lt \cdots \lt a_{d,i} \leqslant d^2 - d$ 使得 $$ P(X) = (X-a_{1,i}) \cdots (X-a_{d,i}) + p_i. $$ 由此建構, 在每一個區間 $I_j = [a_{j,i}, a_{j+1,i}]$, $1 \leqslant j \leqslant d-1$, 都包含至少一個 $P$ 的極值。 因為 $P$ 的次數是 $d$, 它最多只有 $d-1$ 個極值, 所以每一個 $I_j$ 都恰包含一個 $P$ 的極值。 假設 $i \leqslant d-1$ 且對某個 $m \in \{ 0, 1, \dots, d^2-d \}$ 有 $P(m) = p_{i+1} \gt p_i$。 因為 $P$ 的首項係數為正, 當 $d$ 為奇數時有 $$ m \in (a_{d,i},\infty) \cup (a_{d-2,i}, a_{d-1,i}) \cup \cdots \cup (a_{1,i}, a_{2,i}); $$ 而當 $d$ 為偶數時有 $$ m \in (a_{d,i},\infty) \cup (a_{d-2,i}, a_{d-1,i}) \cup \cdots \cup (a_{2,i}, a_{3,i}) \cup (-\infty, a_{1,i}). $$ 設 $a_{j,i} \lt m \lt a_{j+1,i}$ 對某個 $j \in \{1, 2, \dots, d-1\}$ 成立。 若 $a_{j,i}+1 \lt m \lt a_{j+1,i} - 1$, 則由於 $I_j$ 恰包含一個極值 (它現在必須是極大值), 有 $p_{i+1} = P(m) \gt P(a_{j,i}+1)$ 或 $p_{i+1} = P(m) \gt P(a_{j+1,1}-1)$。 再因為 $P(a_{j,i}+1) \gt P(a_{j,i}) = p_i$ 及 $P(a_{j+1,i}-1) \gt P(a_{j+1,i}) = p_i$, 此與 $P(a_{j,i}+1), P(a_{j+1,i}-1) \in \{ p_1, \dots, p_d \}$ 矛盾。 所以有 $m = a_{j,i}+1$ 或 $m = a_{j+1,i}-1$。 類似的論證可知:若 $m \gt a_{d,i}$, 則 $m = a_{d,i} + 1$; 但若 $m \lt a_{i,1}$ (這只會在 $d$ 為偶數時發生), 則 $m = a_{1,i}-1$。 故 $m$ 出現在下面的名單中: $$ a_{d,i}+1, a_{d-1,i}-1, \dots, a_{2,i} + (-1)^d, a_{1,i}-(-1)^d. $$ 這份名單中最多有 $d$ 個不同整數。 由此可以引申出, 若 $n_{i+1} \gt d-2$, 則必有 $$ P(a_{d,i}+1) = p_{i+1} = P(a_{d-1,i}-1), $$ 或 $$ P(a_{2,i}+(-1)^d) = p_{i+1} = P(a_{1,i}-(-1)^d) $$ 其中還有 $a_{2,i} + (-1)^d \ne a_{1,i} - (-1)^d$。 我們有 $$ |P(a_{1,i} \pm 1) - p_i| = 1 \cdot |a_{1,i} \pm 1 - a_{2,i}| \cdot \prod_{j=3}^d |a_{1,i} \pm 1 - a_{j,i}| $$ 以及 $$ |P(a_{2,i} \mp 1) - p_i| = |a_{2,i} \mp 1 - a_{1,i}| \cdot 1 \cdot \prod_{j=3}^d |a_{2,i} \mp 1 - a_{j,i}|. $$ 由於 $a_{1,i} \lt a_{2,i} \lt \cdots \lt a_{d,i}$, 得不等式 $|a_{1,i} \pm 1 - a_{j,i}| \geqslant |a_{2,i} \mp 1 - a_{j,i}|$, 且等號只有在 $a_{1,i}+1 = a_{2,i}-1$ 時成立。 也有 $|a_{1,i} \pm 1 - a_{2,i}| = |a_{2,i} \mp 1 - a_{1,i}|$, 且只有在 $a_{1,i} + 1 = a_{2,i} - 1$ 時會等於 $0$。 故我們得到:$|P(a_{1,i} \pm 1) - p_i| \gt |P(a_{2,i} \mp 1) - p_i|$ 或是 $a_{1,i} + 1 = a_{2,i} - 1$。 用同樣的方式看另外一端, 有 $$ | P(a_{d-1,i}-1) - p_i| = 1 \cdot |a_{d-1,i} - 1 - a_{d,i}| \cdot \prod_{j=1}^{d-2} | a_{d-1,i} - 1 - a_{j,i} | $$ 以及 $$ | P(a_{d,i} + 1) - p_i| = |a_{d,i} + 1 - a_{d-1,i}| \cdot 1 \cdot \prod_{j=1}^{d-2} | a_{d,i} + 1 - a_{j,i}|. $$ 上面兩式中, 連乘積符號之外的共同因式之值至少為 2 而不是 0。 而在連乘積符號之內, 對每一個 $j = 1, 2, \dots, d-2$, 都有 $|a_{d,i}+1-a_{j,i}| \gt |a_{d-1,i}-1-a_{j,i}|$。 因此有 $| P(a_{d,i}+1)-p_i | \gt | P(a_{d-1,i}-1)-p_i |$。Claim 1 證明完畢。 $\Diamond$ 回到原題。 對每一個 $i = 1, 2, \dots, d-1$, 現在有三種可能性: • $n_i, n_{i+1} \leqslant d-1$ 以上各情況, 皆有 $n_i + n_{i+1} \leqslant 2d-2$。 當 $d$ 為偶數時, 會得到 $$ d^2 - d + 1 = (n_1 + n_2) + \cdots + (n_{d-1} + n_d) \leqslant \frac{d}{2} (2d-2) = d^2 - d, $$ 矛盾!故我們證明了當 $d \geqslant 4$ 為偶數時, 不存在滿足題設條件的多項式 $P$。 自此開始, 假設 $d \geqslant 5$ 為奇數。 一樣有 $$ d^2 - d + 1 = (n_1 + n_2) + \cdots + (n_{d-2} + n_{d-1}) + n_d \leqslant \frac{d-1}{2} (2d-2) + d = d^2 - d + 1. $$ 因為前後相同, 所以中間的不等式全部變成等式。 由於 $\sum_{i=1}^d a_i$ 也可以分組為 $$ d^2 - d + 1 = n_1 + (n_2 + n_3) + \cdots + (n_{d-1} + n_d), $$ 一起考慮即得: 當 $i$ 為奇數時有 $a_i = d$, 而當 $i$ 為偶數時 $a_i = d-2$。 由此, 我們來證明一個比 Claim 1 更強的結果。 Claim 2. 設 $d \geqslant 5$ 為奇數, $n_i = d$, $n_{i+1} = d-2$ 對某一個 $i$ 成立。 則 $P$ 取值為 $p_{i+1}$ 之處恰發生在以下 $d-2$ 個點: $$ a_{2,i}-1, a_{3,i}+1, \dots, a_{d-2,i}+1, a_{d-1,i}-1. $$ Claim 2 的證明: 利用歸謬法, 假設 $a_{1,i}+1 \ne a_{2,i}-1$ 且 $P(a_{1,i}+1) = p_{i+1}$。 由於 $a_{1,i} \lt a_{2,i}$, 故 $a_{1,i}+1 \lt a_{2,i}-1$ 或是 $a_{1,i} = a_{2,i}-1$。 後者會導致 $P(a_{1,i}+1) = P(a_{2,i}) = p_i$, 不合。 而由 Claim 1 的證明過程, 在前者的情況會有 $$ |P(a_{2,i}-1) - p_i| \lt |P(a_{1,i}+1) - p_i| = |p_{i+1}-p_i| = p_{i+1}-p_i. $$ 故 $P(a_{2,i}-1) \lt p_{i+1}$。多項式 $P$ 在區間 $(a_{2,i}-1, a_{2,i})$ 中遞減, 所以 $p_i \lt P(a_{2,i}-1) \lt p_{i+1}$, 不合。 所以 $P(a_{1,i}+1) \ne p_{i+1}$。同理 $P(a_{d,i}+1) \ne p_{i+1}$。 所以結合 Claim 1, 得 Claim 2 的結論成立。 $\Diamond$ 由 Claim 2, 我們得知 $P(a_{2,d})$ 到 $P(a_{d-1,1})$ 的值依序形成兩組 $p_d, p_{d-1}, \dots, p_1$ 及 $p_1, p_2, \dots, p_d$ 交互組成的交錯遞減遞增數列。 此數列的前 $3d+1$ 項, 分別是 $P(a_{2,d})$ 到 $P(a_{4,1}+1)$, 依序為 $$ p_d, p_{d-1}, \dots, p_1, p_1, p_2, \dots, p_d, p_d, p_{d-1}, \dots, p_1, p_1. $$ (這裡用到了 $d - 1 \geqslant 4$)。仔細看會發現 $p_d, p_{d-1}, \dots, p_1, p_1$ 這 $d+1$ 項會是 $P$ 在兩組不同的 $d+1$ 個連續整數上的取值。 因為 $P$ 為 $d$ 次多項式, 故存在一常數 $c$ 滿足 $P(X) = P(X+c)$ 對所有 $X$ 均成立, 此在 $P$ 不為常數多項式時為矛盾。 故滿足題設的多項式 $P$ 在次數 $d \geqslant 5$ 為奇數時並不存在。 全題證明完畢。 $\Box$ 評註: 本題為非常困難的代數問題, 難度已達 IMO 的三、六題水準。 全場僅有一人得到 6 分, 其餘選手得分皆不超過 3 分。 很容易找到一次及二次多項式滿足題設, 但找出可行的三次多項式就是挑戰了。 而更困難的是證明四次以上的多項式不可能滿足題設, 證明過程中需要掌握多項式遞增遞減的行為, 並且對於每一取值發生的點有很好的估計。 本題對於多項式變化行為的刻劃極為深刻, 應可繼續探究下去。 本工作小組係由教育部委託國立台灣師範大學, 於「中華民國參加 2024 年第 36 屆亞太數學、第 13 屆歐洲女子數學及第 65 屆國際數學奧林匹亞競賽計畫」下成立。本文的主要作者為林延輯副教授, 任教於國立台灣師範大學數學系。 |
2024年9月 48卷3期
2024年第13屆歐洲女子數學奧林匹亞競賽試題解答

