| 發刊日期 |
2024年9月
|
|---|---|
| 標題 | 一道幾何趣題的探討及其推廣 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
1. 問題呈現及解筆者(指第二作者林開亮, 下同)曾在"好玩的數學"微信公眾號上分享了一道有趣的幾何題, 引起了大家的廣泛關注和討論。 問題如下: 在如圖1的矩形中, 已知三個角上的三角形的面積分別為 3, 4, 5, 求中間三角形的面積。 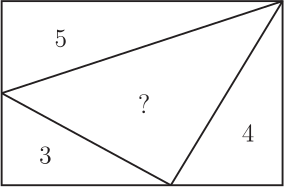 這是 1998 年筆者讀初三時在同學李明的一本中考復習書上見到的。 當時筆者想破了腦殼也沒想出來, 翻了書後的參考答案, 才恍然大悟。 它的解法完全是代數的, 如下。 1.1. 代數解法如圖2所示, 設邊長 $a, b$, 並根據面積得其他各邊的長, 於是有相等關係 $$ \frac{10}{a}=b+\frac{8}{a+\frac{6}{b}}, $$ 化簡, 整理得 $ (ab)^2+4ab-60=0 $, 即 $ (ab+10)(ab-6)=0 $, 從而 $ab=6$。 故中間三角形的面積為 $$ S=(a+\frac{6}{b})\cdot \frac{10}{a}-12=\frac{60}{ab}-2=8. $$ 以上的解法完全是代數的, 那麼這題有沒有幾何解法呢? 幾年前, 當筆者把這個問題作為思考題分享到網上時, 沒想到引起了南開大學陳省身數學所的唐梓洲教授和清華大學的扶磊教授的關注, 並給出了一個優美的幾何解法。 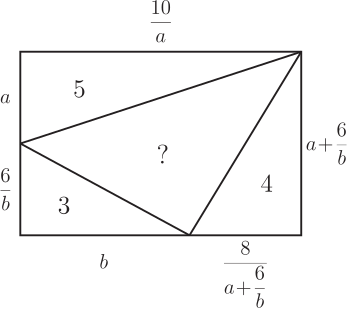 1.2. 幾何解法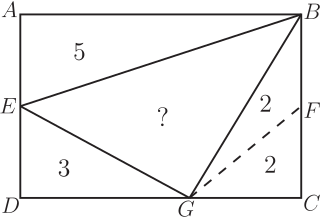 如圖 3 所示, 設 $F$ 是 $\overline{BC}$ 的中點。 由於 $$ 5 = 3 + 2, $$ 這就意味著, $ \triangle AEB $ 的面積等於 $ \triangle EGD $ 的面積與 $ \triangle GCF $ 的面積之和, 即 $$ S_{\triangle AEB}=S_{\triangle EGD}+S_{\triangle GCF}. $$ 注意到 $ \overline{AB} = \overline{DG} + \overline{GC} $。 若 $ \overline{AE}\gt\overline{ED} $, 則 $ \overline{ED}\lt\overline{CF}\lt\overline{AE} $, 從而 \begin{align*} S_{\triangle EGD}+S_{\triangle GCF} & =\frac{1}{2}\overline{ED}\cdot \overline{DG} +\frac{1}{2}\overline{CF}\cdot \overline{GC} \\ & \lt \frac{1}{2}\overline{AE}\cdot \overline{DG} +\frac{1}{2}\overline{AE}\cdot \overline{GC} \\ & =\frac{1}{2}\overline{AE}\cdot \overline{AB}=S_{\triangle AEB}, \end{align*} 矛盾。 於是 $\overline{AE}$ 大於 $\overline{ED}$ 不可能, 同樣 $\overline{AE}$ 小於 $\overline{ED}$ 也不可能, 從而必定有 $\overline{AE} = \overline{ED}$。 故 \begin{align*} S_{ABCD} =\,& 4S_{\triangle ABE} = 4 \times 5 = 20.\\ {\hbox{進而}} S_{\triangle BEG} =\,& 20 -(3 + 4 + 5) = 8. \end{align*} 解後思考: 以上的代數解法和幾何解法都很巧妙, 但問題是如果將問題中的 3, 4, 5 換成其他的數, 這兩種解法是否還適用呢? 1.3. 問題的一個變形唐梓洲教授就給出了這個問題的一個變形: 在如圖4的矩形中, 已知三個角上的三角形的面積分別為 2, 3, 6, 求中間三角形的面積。 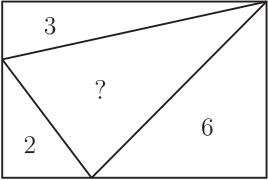 有興趣的讀者不妨試著解一下, 答案為 7。 你會發現 1.1 的代數解法仍然適用, 但 1.2 的幾何解法並不適用。 進一步思考: 這個問題能否推廣到更一般的情形, 即如果將問題中的 3, 4, 5 換成任意數 $ A, B, C $, 那麼問題是否一定有解? 是否有更一般的結論? 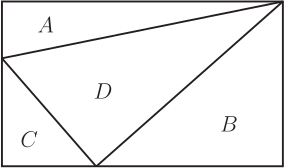 2. 問題推廣福建師範大學的王長平校長給出了肯定的回答, 並將以上兩個問題推廣到了一般的情形: 如圖5所示, 四邊形為矩形, $ A, B, C, D $ 分別為四個三角形的面積, 則 $$ D=\sqrt{(A+B+C)^2-4AB}.$$ 對於推廣後的問題, 你會發現 1.1 中的代數解法也不適用了, 這就要求我們尋求新的解法。 其中, 唐梓洲教授給我們分享了一個代數證明和一個幾何證明, 福建寧德師範學院的蔣劍劍博士則分享了另一個優美的幾何證明。 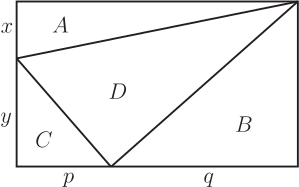 2.1. 代數證明(唐梓洲)如圖 {6} 所示, 設邊長 $ x, y, p, q $, 則 $$ \left\{ \begin{aligned} & 2A=(p+q)x \\ & 2B=q(x+y) \\ & 2C=py \\ \end{aligned} \right. $$ 設矩形的面積為 $S$, 則 \begin{align*} D=\,&S-(A+B+C)=(p+q)(x+y)-(A+B+C). \\ {\hbox{從而}} D^2=\,&(A+B+C)^2+(p+q)^2(x+y)^2-2(A+B+C)(p+q)(x+y). \end{align*} 注意到下述等式 \begin{align*} & (p+q)^2(x+y)^2-2(A+B+C)(p+q)(x+y) \\ = & (p+q)(x+y)[(p+q)(x+y)-2(A+B+C)] \\ = & (p+q)(x+y)[(p+q)(x+y)-(p+q)x-q(x+y)-py] \\ = & -(p+q)(x+y)qx \\ = & -(p+q)x\cdot (x+y)q \\ = & -4AB,\\ {\hbox{所以}} D^2=&(A+B+C)^2-4AB, \\ {\hbox{進而}} D=&\sqrt{(A+B+C)^2-4AB}. \end{align*} 單墫教授在 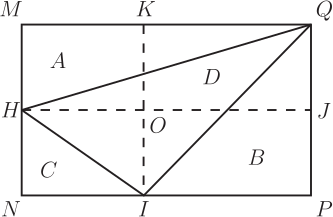 2.2. 幾何證明1(唐梓洲)如圖7所示, 過分點 $H,I$ 分別作 $\overline{NP},\overline{MN}$ 的平行線交 $\overline{PQ},\overline{MQ}$ 於點 $J,K$, 設 $\overline{HJ}$ 和 $\overline{IK}$ 交於點 $ O $, 於是 $$ A+B+C-D=S_{\triangle HQJ}+S_{\triangle KIQ}+S_{\triangle HOI}-S_{\triangle HIQ}=S_{KOJQ}. $$ 因此 \begin{align*} &\hskip -20pt \frac{2A}{A+B+C+D}=\frac{\overline{QJ}}{\overline{PQ}}=\frac{S_{KOJQ}}{2B}=\frac{A+B+C-D}{2B},\\ {\hbox{從而}} 4AB=\,&(A+B+C+D)(A+B+C-D)=(A+B+C)^2-D^2,\\ D^2=\,&(A+B+C)^2-4AB,\\ {\hbox{故}} D=\,&\sqrt{(A+B+C)^2-4AB}. \end{align*} 這個證明最關鍵的一步是發現了 $ A+B+C-D $ 恰好等於右上角小矩形的面積。 2.3. 幾何證明2(蔣劍劍)如圖8所示, 過左邊豎直邊的分點引矩形水準邊的平行線, 記圖中陰影部分的面積為 $S$, 則 $$ \frac{B}{S}=\frac{A+B+C+D}{2A}. $$ 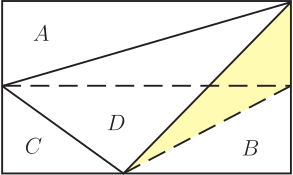 注意到 $ A+C+(B-S) $ 恰好是整個矩形面積的一半, 即有 $$2(A+B+C-S)=A+B+C+D,$$ 從而 $$2S=A+B+C-D,$$ 於是 $$\frac{B}{S}=\frac{2B}{A+B+C-D},$$ 因此 $$\frac{2B}{A+B+C-D}=\frac{A+B+C+D}{2A},$$ 從而 $$4AB=(A+B+C+D)(A+B+C-D)=(A+B+C)^2-D^2,$$ 所以 $$D^2=(A+B+C)^2-4AB,$$ 故 $$D=\sqrt{(A+B+C)^2-4AB}.$$ 這個證明最關鍵的一步是發現了 $ A+B+C-S $ 恰好是整個矩形面積的一半這一關係。 更一般地, 王長平校長還指出, 以上定理可以從矩形推廣到平行四邊形。 聰明的讀者不難發現, 在代數證明中, 適當的地方補充因數 $\sin \theta =\sin(\pi-\theta) $ (其中 $\theta$ 為平行四邊形的一個內角), 則論證一字不變地有效。 而在兩個幾何證明中, 則一個字都不需要改。 3. 問題再推廣對於該問題, 筆者提出了另一種推廣思路: 這個問題能不能推廣為求矩形的內接四邊形的面積? 遺憾的是, 這個推廣的答案是"否定"的, 一個反例即是證明畢氏定理時所用到的趙爽弦圖。 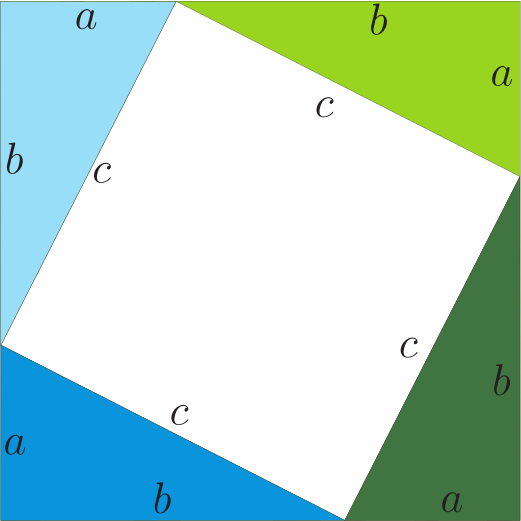 如圖9, 在邊長為 $a+b$ 的正方形中, 四個角上的小三角形面積都是 $ \frac{1}{2}ab $, 中間的正方形面積為 $ c^2 $, 依據畢氏定理, 它恰好是 $ a^2+b^2 $。 但顯然, $ a^2+b^2 $ 的值並非由 $ ab $ 的值所唯一確定。 雖然將問題推廣至矩形內接四邊形的面積失敗了, 但是王長平校長發現, 可以求出了內接四邊形面積的最小值。 因此, 該問題可以推廣為求矩形內接四邊形面積的最小值問題。 為了能讓你更好地理解該問題, 現將推廣後的問題重新表述如下: 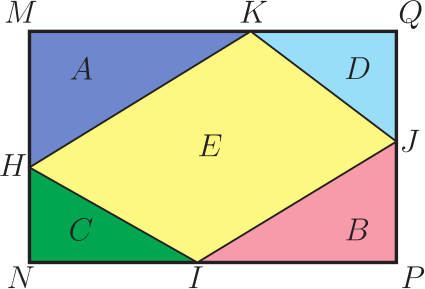 如圖10, $ HIJK $ 是矩形$ MNPQ $ 的內接四邊形, 已知四個角上的三角形面積分別為 $A, B, C, D $, 求內接四邊形 $ HIJK $ 的面積 $ E $的最小值。 通過計算, 王長平校長給出矩形內接四邊形面積 $E$ 的最小值為: $$ \sqrt{(A+B+C+D)^2-4(\sqrt{AB}-\sqrt{CD})^2}. $$ 其中的關鍵是證明以下不等式: $$ a^2b^2-2ab(A+B+C+D)+4(AB+CD) \geq 8\sqrt{ABCD}, $$ 這裡 $ a, b $ 分別是矩形的長和寬。 下面我們將王長平校長的證明過程整理如下。 3.1. 證明(王長平) 設矩形的長和寬分別為 $a$ 和 $b$, 並按如圖 {11} 所示設各條線段的長。 依題意, 我們有 $$ \left\{ \begin{aligned} & 2A=(a-z)(b-x) \\ & 2B=(a-y)(b-w) \\ & 2C=xy \\ & 2D=zw \\ \end{aligned},\right. $$ 則 \begin{align*} & a^2b^2-2ab(A+B+C+D)+4(AB+CD) \\ = & a^2b^2-2ab(A+B)+4AB-2ab(C+D)+4CD \\ = & (ab-2A)(ab-2B)-2ab(C+D)+4CD \\ = & [ab-(a-z)(b-x)][ab-(a-y)(b-w)]-ab(xy+zw)+xyzw \\ = & (ax+bz-xz)(aw+by-yw)-ab(xy+zw)+xyzw \\ = & a^2xw-axyw+b^2yz-byzw-axzw-bxyz+2xyzw \\ = & (a^2xw-axyw-axzw+xyzw)+(b^2yz-byzw-bxyz+xyzw) \\ = & xw(a^2-ay-za+yz)+yz(b^2-bw-bx+xw) \\ = & xw(a-y)(a-z)+yz(b-x)(b-w) \end{align*} 對最後一步使用均值(算幾)不等式就得到: \begin{align*} & xw(a-y)(a-z)+yz(b-x)(b-w) \\ \geq & 2\sqrt{(a-z)(b-x)\cdot (a-y)(b-w) \cdot (xy) \cdot (zw)} \\ = & 2\sqrt{2A \cdot 2B \cdot 2C \cdot 2D} \\ = & 8\sqrt{ABCD}. \end{align*} 即 $$ a^2b^2-2ab(A+B+C+D)+4(AB+CD) \geq 8\sqrt{ABCD}. $$ 其中等號取得當且僅當 $ xw(a-y)(a-z)=yz(b-x)(b-w) $。 所以 \begin{align*} E^2 & =[ab-(A+B+C+D)]^2 \\ & =a^2b^2-2ab(A+B+C+D)+(A+B+C+D)^2 \\ & \geq 8\sqrt{ABCD}-4(AB+CD)+(A+B+C+D)^2 \\ & =(A+B+C+D)^2-4(\sqrt{AB}-\sqrt{CD})^2.\\ {\hbox{故}} E &\geq \sqrt{(A+B+C+D)^2-4(\sqrt{AB}-\sqrt{CD})^2} . \end{align*} 其中等號取得當且僅當 $ xw(a-y)(a-z)=yz(b-x)(b-w) $, 即 $ \overline{HN}\cdot \overline{IP}\cdot \overline{JQ}\cdot \overline{KM} =\overline{NI}\cdot \overline{PJ}\cdot \overline{QK}\cdot \overline{MH} $。 下面我們來看兩個特例。 3.2. 兩個特例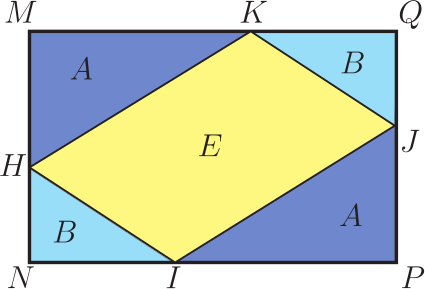 特例1: 如圖12, 假設在矩形 $ MNPQ $ 中, $ \overline{NP}=\overline{MQ}=a $, $ \overline{MN}=\overline{PQ}=b $, $ HIJK $ 是矩形的內接四邊形, 如果矩形四個角上的三角形面積分別為 $ A, B, A, B $, 那麼當矩形的內接四形邊 $ HIJK $ 的面積取最小值時, $ HIJK $是平行四邊形, 且 \begin{align*} \overline{IP}=\,&\overline{KM}=\frac{\sqrt{A}}{\sqrt{A}+\sqrt{B}}a,\; \overline{NI}=\overline{QK}=\frac{\sqrt{B}}{\sqrt{A}+\sqrt{B}}a,\\ \overline{MH}=\,&\overline{PJ}=\frac{\sqrt{A}}{\sqrt{A}+\sqrt{B}}b,\quad \overline{HN}=\overline{JQ}=\frac{\sqrt{B}}{\sqrt{A}+\sqrt{B}}b. \end{align*} 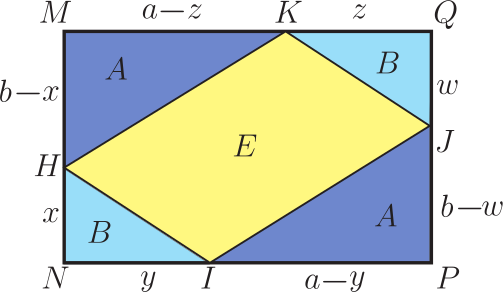 證明: 設矩形的長和寬分別為 $a, b $, 並按圖13所示設各條線段的長。 根據前述結果, 可得矩形內接四邊形 $ HIJK $ 的面積的最小值為 $$ E=\sqrt{(2A+2B)^2-4(\sqrt{A \cdot A}-\sqrt{B \cdot B})^2}=4\sqrt{AB}. $$ 此時, 矩形 $ MNPQ $ 的面積 $$ ab=2A+2B+4\sqrt{AB}=2(\sqrt{A}+\sqrt{B})^2. $$ 依題意, 我們有 \begin{align} & (a-z)(b-x)=2A, \label{1}\\ & (a-y)(b-w)=2A, \label{2}\\ & xy=2B, \label{3}\\ & zw=2B, \label{4}\\ & ab=2(\sqrt{A}+\sqrt{B})^2. \label{5} \end{align} 由 \eqref{1} 和 \eqref{5}, 得 \begin{align} ax+bz-xz=2B+4\sqrt{AB}, \label{6} \end{align} 由 \eqref{3} 和 \eqref{4}, 有 $ y=\frac{2B}{x}, w=\frac{2B}{z} $, 代入 \eqref{2} 並化簡整理得 \begin{align} ax+bz-(1+2\sqrt{\frac{A}{B}})xz=2B, \label{7} \end{align} \eqref{6}$-$\eqref{7}, 得 \begin{align} xz=2B, \label{8} \end{align} 由 \eqref{3} \eqref{4} \eqref{8}, 得 $$ y=z, x=w $$ 從而 $$ a-y=a-z, b-x=b-w, $$ 可得, $ HIJK $ 是平行四邊形。 將 \eqref{8} 代回 \eqref{6}, 得 $$ ax+bz=4\sqrt{B}(\sqrt{A}+\sqrt{B}), $$ 即 $$ ax+\frac{2(\sqrt{A}+\sqrt{B})^2}{a}\cdot \frac{2B}{x}=4\sqrt{B}(\sqrt{A}+\sqrt{B}), $$ 化簡, 得 $$ [ax-2\sqrt{B}(\sqrt{A}+\sqrt{B})]^2=0, $$ 故 \begin{align} ax=2\sqrt{B}(\sqrt{A}+\sqrt{B}),\label{9} \end{align} 由 \eqref{5} 和 \eqref{9}, 即得 $$ x=\frac{\sqrt{B}}{\sqrt{A}+\sqrt{B}}b, $$ 由 \eqref{5} 和 \eqref{8}, 可得 $$ z=\frac{\sqrt{B}}{\sqrt{A}+\sqrt{B}}a, $$ 故 $$ x=w=\frac{\sqrt{B}}{\sqrt{A}+\sqrt{B}}b,\qquad b-x=b-w=\frac{\sqrt{A}}{\sqrt{A}+\sqrt{B}}b, $$ $$ y=z=\frac{\sqrt{B}}{\sqrt{A}+\sqrt{B}}a,\qquad a-y=a-z=\frac{\sqrt{A}}{\sqrt{A}+\sqrt{B}}a. $$ 特例2: 如圖14, 假設在矩形 $ MNPQ $ 中, $ \overline{NP}=\overline{MQ}=a $, $ \overline{MN}=\overline{PQ}=b $, $ HIJK $ 是矩形的內接四邊形, 如果矩形四個角上的三角形面積分別為 $ A, A, B, B $, 那麼當矩形的內接四邊形 $ HIJK $ 的面積取最小值時, $ HIJK $ 是箏形, 且 $$\overline{MH}=\overline{HN}=\overline{PJ}=\overline{JQ}=\frac{1}{2}a,$$ $$\overline{NI}=\overline{KM}=\frac{A}{A+B}b,\quad \overline{IP}=\overline{QK}=\frac{B}{A+B}b.$$ 至於特例 2 的證明就留給親愛的讀者朋友們自行完成吧。 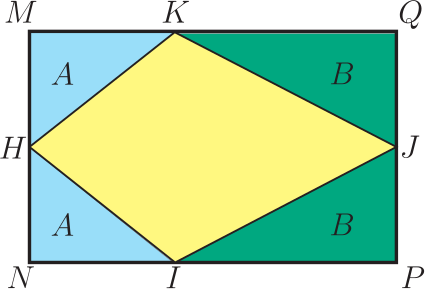 致謝及說明感謝南開大學陳省身數學所唐梓洲教授、 清華大學扶磊教授、 福建師範大學王長平校長、 寧德師範學院蔣劍劍博士、 單墫教授等對該問題的討論, 感謝他們積極分享對該問題的見解! 本題只是一道平常的初中數學練習題, 但引起了諸多大學教授的興趣和討論, 說明本題有一定的思考價值。 本文旨在記錄和整理大家對該問題的思考及討論過程, 以期給讀者提供一個思考問題的範本, 一窺數學專家們思考問題的獨特視角。 參考文獻本文作者孫志躍任教中國江西省吉水中學, 林開亮任教中國西北農林科技大學理學院 |
2024年9月 48卷3期
一道幾何趣題的探討及其推廣

