| 發刊日期 |
2025年3月
|
|---|---|
| 標題 | 四邊形的蝴蝶定理 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
關鍵字: 蝴蝶定理、坎迪定理、四邊形。 一、前言關於蝴蝶定理 (Butterfly Theorem), 如圖 1, 過圓內弦 $\overline{PQ}$ 的中點 $M$ 任作兩弦 $\overline{AB} $ 和 $\overline{CD} $, 連接 $A$、 $D$ 和 $C$、 $B$ 分別交弦 $\overline{PQ}$ 於 $X$、 $Y$ 兩點, 則 $\overline{XM} = \overline{MY} $。 除此之外, 文獻也針對蝴蝶形的連接方式、 弦 $\overline{PQ}$、 $M$ 點的位置和外接其他圓錐曲線作發想, 而有一些推廣的性質。 如圖 2, 若將蝴蝶形外接的圓形改成四邊形, 那蝴蝶形是否也會有類似的性質? 於是我們決定繼續推廣蝴蝶定理, 看能否有更多不一樣的發現。 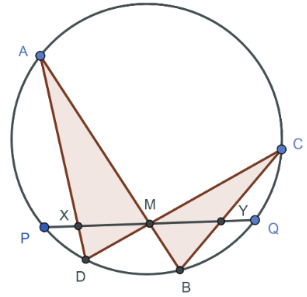 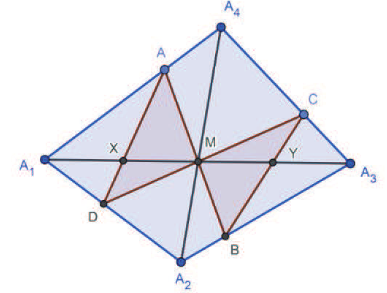 二、名詞定義(一) 蝴蝶形: 如圖 3, 凸四邊形的對角線相連, 所產生四個角形, 兩個不相鄰的三角形所構成。 (參 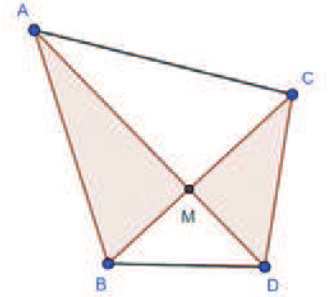 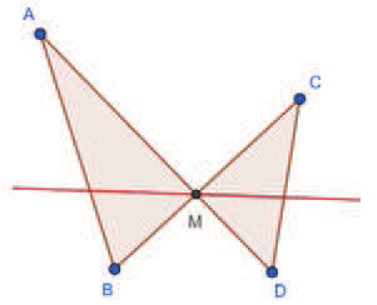 (四) 坎迪定理 (Candy Theorem) (參 如圖 5, 設 $\overline{PQ}$ 為圓內一條弦, 過 $\overline{PQ}$ 上一點 $M$ 任作兩弦 $\overline{AB}$ 和 $\overline{CD}$, 若連接 $A$、 $D$ 和 $C$、 $B$ 分別與 $\overline{PQ}$ 交於 $X$、 $Y$ 兩點, 則 $\dfrac{1}{\overline{XM}}-\dfrac 1 {\overline{YM}} =\dfrac 1{\overline{PM}}-\dfrac 1{\overline{QM}}$。 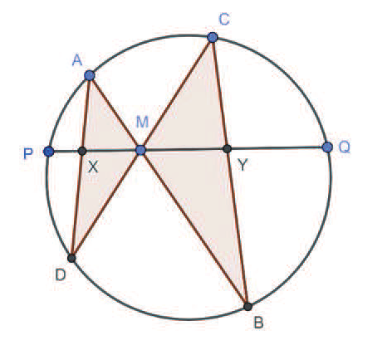 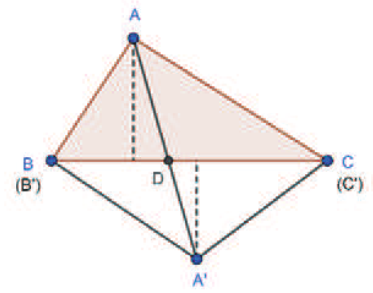 (五) 共邊定理 (參 如圖 6, 設 $\triangle ABC$ 和 $\triangle A'B'C'$ 共邊 $(\overline{BC} = \overline{B'C'})$, 且 $D$ 是 $\overline{BC}$ 和 $\overline{AA'}$ 的交點, $A'\not=D$, 則 $\dfrac{\triangle ABC}{\triangle A'B'C'}=\dfrac{\overline{AD}}{\overline{A'D}}$。 這裡 $\triangle ABC$ 表示 $\triangle ABC$ 的面積。 (六) 共角定理 (參 如圖 7 和 8, 設 $\angle ABC$ 和 $\angle A' B' C'$ 相等或互補, 即 $\angle ABC= \angle A' B' C'$ 或 $\angle ABC+ \angle A' B' C'\!=\! 180^\circ $, 則 $\dfrac{\triangle ABC}{\triangle A'B'C'}\!=\!\dfrac{\overline{AB} \!\times\! \overline{BC}}{\overline{A'B'}\!\times\!\overline{B'C'}}$。 這裡 $\triangle ABC$ 表示 $\triangle ABC$ 的面積。 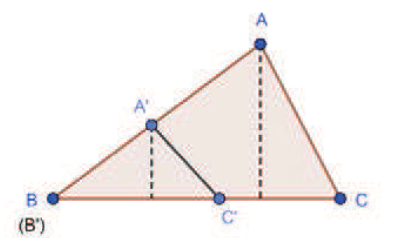 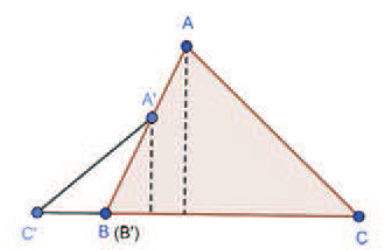 三、四邊形的蝴蝶定理根據四邊形對邊是否平行與對角線是否平分, 分成梯形、 平行四邊形、 一條對角線被平分的四邊形、 任意四邊形做討論, 而有以下的定理: (一) 定理 1 (參 設四邊形 $A_1 A_2 A_3 A_4$ 為梯形, $\overline{PQ}$ 為平行上下底 $\overline{A_1 A_2}$、 $\overline{A_3 A_4}$ 的截線段, 以 $\overline{PQ}$ 為蝴蝶線, $\overline{PQ}$ 上任一點 $M$ 為蝴蝶中心, 若蝴蝶形 $ABCD$ 的頂點分別落在上下底, 且連接 $A$、 $D$ 和 $C$、 $B$ 分別交 $\overline{PQ}$ 於 $X$、 $Y$ 兩點, 則 $\overline{MX}= \overline{MY}$。 (梯形之蝴蝶定理) (此定理是作者的創見) 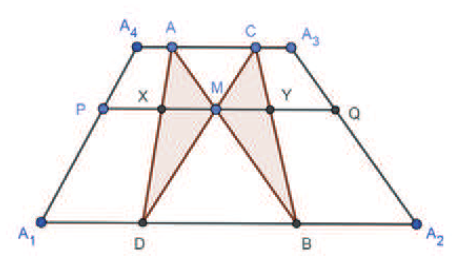 證明: 如圖 9, 因為 $\overline{PQ} //\overline{A_1 A_2}//\overline{A_3 A_4}$, 所以 $\dfrac{\overline{XM}}{\overline{DB}}=\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{CM}}{\overline{CD}}=\dfrac{\overline{MY}}{\overline{DB}}$, 從而 $\overline{MX}=\overline{MY}$。 (二) 定理 2 (參 設四邊形 $A_1 A_2 A_3 A_4$ 為平行四邊形, 以對角線的交點 $M$ 為蝴蝶中心, 一組對邊 $\overline{A_1 A_4}$、 $\overline{A_2 A_3}$ 的中點連線 $\overline{PQ}$ 為蝴蝶線, 若蝴蝶形ABCD的頂點不全落在一組對邊上, 且連接 $A$、 $D$ 和 $C$、 $B$ 分別交 $\overline{PQ}$ 於 $X$、 $Y$ 兩點, 則 $\overline{MX}=\overline{MY}$。 若進一步以M為中心將蝴蝶線 $\overline{PQ}$ 旋轉成蝴蝶線 $\overline{P'Q'}$, 且 $\overline{AD}$ 和 $\overline{CB}$ 分別交 $\overline{P'Q'}$ 於 $X'$、 $Y'$ 兩點, 則 $\overline{MX'}=\overline{MY'}$。 (平行四邊形之蝴蝶定理) (此定理是作者的創見) 證明: 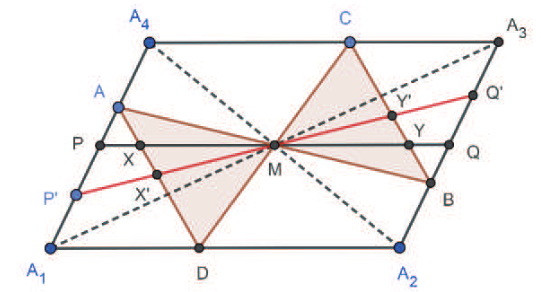 (1) 如圖 10, 因為 $\overline{A_1 A_4}//\overline{A_2 A_3}$, 所以 $\angle APM= \angle BQM$, $\overline{PM} = \overline{QM} $, $\angle AMP= \angle BMQ$, 推得 $\triangle AMP\simeq \triangle BMQ$ (ASA), 從而 $\overline{AM}=\overline{MB}$。 又 $\overline{PQ} //\overline{A_1 A_2}//$ $\overline{A_3 A_4}$, 所以 $\overline{CM}=\overline{MD}$, 且 $\angle AMD= \angle BMC$, 推得 $\triangle AMD\simeq \triangle BMC$ (SAS), 從而 $\angle MAX= \angle MBY$, 推得 $\triangle AMX\simeq \triangle BMY$ (ASA), 故 $\overline{MX}=\overline{MY}$。 (2) 因為 $\angle MAD= \angle MBC$, 所以 $\overline{AD} //\overline{CB}$, 從而 $\angle MXX'= \angle MYY'$, 且 $\overline{MX}= \overline{MY}$、 $\angle XMX'= \angle YMY'$, 推得 $\triangle MXX'\simeq \triangle MYY'$ (ASA), 故 $\overline{MX'}=\overline{MY'}$。 (三) 定理 3 (參 設四邊形 $A_1 A_2 A_3 A_4$ 為一條對角線 $\overline{A_1 A_3}$ 被另一條 $\overline{A_2 A_4}$ 平分的四邊形, 以 $\overline{A_1 A_3}$ 為蝴蝶線, $\overline{A_1 A_3}$ 的中點 $M$ 為蝴蝶中心, 若蝴蝶形 $ABCD$ 的頂點分別落在四邊形的四條邊或邊的延長線上, 且連接 $A$、 $D$ 和 $C$、 $B$ 分別交 $\overleftrightarrow{A_1A_3}$ 於 $X$、 $Y$ 兩點, 則 $\overline{MX}=\overline{MY}$。 (四邊形之蝴蝶定理) 證明: (參考資料 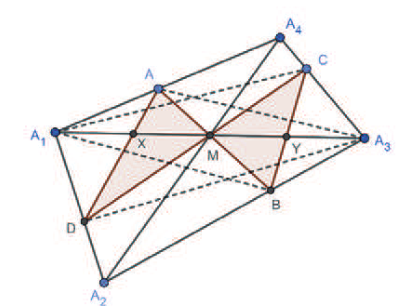 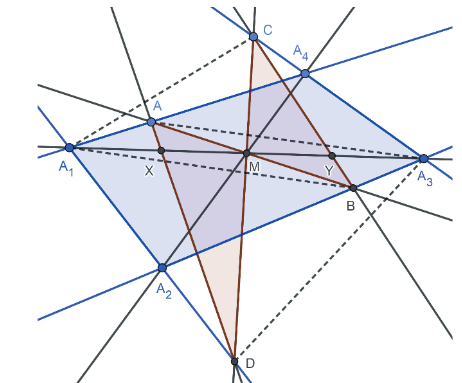 如圖 11 和 12, 由共邊、 共角定理, 及 $\overline{A_1M} = \overline{A_3M}$ 可得 \begin{align*} \frac{\overline{MX}}{\overline{A_1X}}=& \frac{\triangle MAD}{\triangle A_1AD}= \frac{\triangle MAD}{\triangle MBC}\!\times\! \frac{\triangle MBC}{ \triangle A_3BC} \!\times\! \frac{\triangle A_3BC}{\triangle A_3 A_2 A_4}\!\times\! \frac{\triangle A_3 A_2 A_4}{\triangle A_1 A_2 A_4}\!\times\! \frac{\triangle A_1 A_2 A_4}{\triangle A_1 DA}\\ =&\frac{\overline{MA} \times \overline{MD}}{\overline{MB}\times\overline{MC}}\times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3B} \times \overline{A_3C}}{\overline{A_3A_2} \times \overline{A_3A_4}}\times \frac{\overline{A_3M}}{\overline{A_1M}} \times \frac{\overline{A_1A_2}\times \overline{A_1A_4}}{\overline{A_1D} \times \overline{A_1A}}\\ =&\frac{\overline{MA}}{\overline{MB}} \times \frac{\overline{MD}}{\overline{MC}}\times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3B}}{\overline{A_3A_2}}\times \frac{\overline{A_3C}}{\overline{A_3A_4}} \times 1\times \frac{\overline{A_1A_2}}{\overline{A_1D}} \times \frac{\overline{A_1A_4}}{\overline{A_1A}} \\ =&\frac{\triangle A_1A_3A}{\triangle A_1A_3B}\!\times\! \frac{\triangle A_1A_3D}{\triangle A_1A_3C} \!\times\! \frac{\overline{MY}}{\overline{A_3Y}} \!\times\! \frac{\triangle A_1A_3B}{\triangle A_1A_3A_2}\!\times\! \frac{\triangle A_1A_3C}{\triangle A_1A_3A_4} \!\times\! \frac{\triangle A_1A_3A_2}{\triangle A_1A_3D}\\ &\!\times\! \frac{\triangle A_1A_3A_4}{\triangle A_1A_3A}=\frac{\overline{MY}}{\overline{A_3Y}}, \end{align*} 由合比性質得 $\dfrac{\overline{MX}}{\overline{A_1X}}=\dfrac{\overline{MY}}{\overline{A_3Y}}\Longrightarrow\dfrac{\overline{MX}}{\overline{MX} + \overline{A_1X}} = \dfrac{\overline{MY}}{\overline{MY}\!+\!\overline{A_3Y}}$, $\dfrac{\overline{MX}}{\overline{A_1M}} = \dfrac{\overline{MY}}{\overline{A_3M}}$, 故 $\overline{MX} = \overline{MY}$。 (四) 定理 4 (參 設四邊形 $A_1 A_2 A_3 A_4$ 為一條對角線 $\overline{A_1 A_3}$ 被另一條 $\overline{A_2 A_4}$ 平分於 $O$ 的四邊形, $\overline{A_1 O}=\overline{A_3 O}$, 以 $\overline{A_1 A_3}$ 為蝴蝶線, $\overline{A_1 A_3}$ 上一點 $M$ 為蝴蝶中心, 若蝴蝶形 $ABCD$ 的頂點分別落在四邊形的四條邊或邊的延長線上, 且連接 $A$、 $D$ 和 $C$、 $B$ 分別交 $\overleftrightarrow{A_1A_3}$ 於 $X$、 $Y$ 兩點, 則 $\dfrac{\overline{MX}}{\overline{MA_1}}= \dfrac{\overline{MY}}{\overline{MA_3}}$。 可改寫成 $\dfrac{\overline{A_1X}}{\overline{XM}}\times \dfrac{\overline{MY}}{\overline{YA_3}}=1$。 (四邊形之蝴蝶延伸定理) (此定理是作者的創見) 證明: 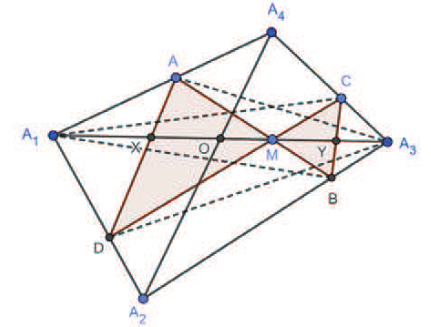 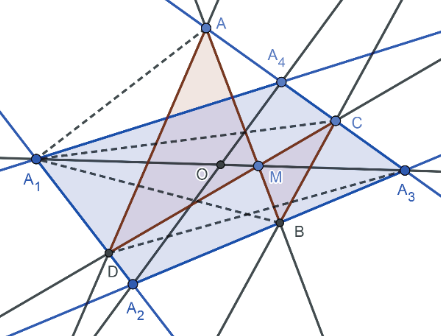 如圖 13 和 14, 由共邊、 共角定理, 及 $\overline{A_1 O}=\overline{A_3 O}$ 可得 \begin{align*} \dfrac{\overline{MX}}{\overline{A_1X}}=&\frac{\triangle MAD}{\triangle A_1AD} \!=\!\frac{\triangle MAD}{\triangle MBC}\!\times\! \frac{\triangle MBC}{\triangle A_3BC} \!\times\! \frac{\triangle A_3BC}{\triangle A_3 A_2 A_4}\!\times\! \frac{\triangle A_3 A_2 A_4} {\triangle A_1 A_2 A_4}\!\times\! \frac{\triangle A_1A_2 A_4}{\triangle A_1 DA}\\[5pt] =&\frac{\overline{MA} \times \overline{MD}}{\overline{MB} \times \overline{MC}}\times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3B} \times \overline{A_3C}} {\overline{A_3A_2}\times \overline{A_3A_4}}\times \frac{\overline{A_3O}}{\overline{A_1O}} \times \frac{\overline{A_1A_2} \times \overline{A_1A_4}}{\overline{A_1D} \times \overline{A_1A}}\\[5pt] =& \frac{\overline{MA}}{\overline{MB}}\times \frac{\overline{MD}}{\overline{MC}} \times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3B}}{\overline{A_3A_2}}\times \frac{\overline{A_3C}}{\overline{A_3A_4}} \times 1\times \frac{\overline{A_1A_2}}{\overline{A_1D}} \times \frac{\overline{A_1A_4}}{ \overline{A_1A}}\\[5pt] =&\frac{\triangle A_1A_3A}{\triangle A_1A_3B}\times \frac{\triangle A_1A_3D}{\triangle A_1A_3C} \times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\triangle A_1A_3B}{\triangle A_1A_3A_2}\times \frac{\triangle A_1A_3C} {\triangle A_1A_3A_4}\times \frac{\triangle A_1A_3A_2}{\triangle A_1A_3D}\\[5pt] &\times \frac{\triangle A_1A_3A_4}{\triangle A_1A_3A}= \frac{\overline{MY}}{\overline{A_3Y}}, \end{align*} 由合比性質得 $\dfrac{\overline{MX}}{\overline{A_1X}}= \dfrac{\overline{MY}}{\overline{A_3Y}}\Longrightarrow \dfrac{\overline{MX}}{\overline{MX} \!+\! \overline{A_1X}} = \dfrac{\overline{MY}}{\overline{MY} \!+\! \overline{A_3Y}}$, 故 $\dfrac{\overline{MX}}{\overline{MA_1}}= \dfrac{\overline{MY}}{MA_3}$。 若將原式的左式移項, 可得 $\dfrac{\overline{A_1X}}{\overline{XM}} \times \dfrac{\overline{MY}}{YA_3}=1$。 (五) 定理 5 (參 設四邊形 $A_1 A_2 A_3 A_4$ 為任意四邊形, 以 $\overline{A_1 A_3}$ 為蝴蝶線, 兩對角線交點 $M$ 為蝴蝶中心, 若蝴蝶形 $ABCD$ 的頂點分別落在四邊形的四條邊或邊的延長線上, 且連接 $A$、 $D$ 和 $C$、 $B$ 分別交 $\overleftrightarrow{A_1A_3}$ 於 $X$、 $Y$ 兩點, 則 $\dfrac 1{\overline{MX}}-\dfrac 1{\overline{MY}}=\dfrac 1{\overline{MA_1}}-\dfrac 1{\overline{MA_3}}$。 可改寫成 $\dfrac{\overline{A_1X}}{\overline{XM}}\times \dfrac{\overline{MY}}{\overline{YA_3}}\times \dfrac{\overline{A_3M}}{\overline{MA_1}}=1$。 (四邊形之坎迪定理)
證明: (參考資料 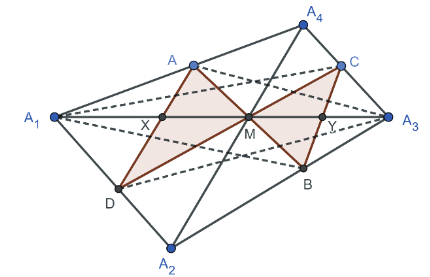 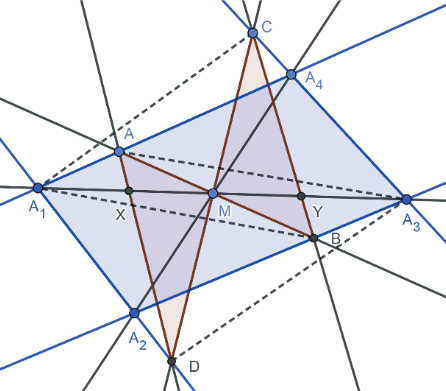 如圖 15 和 16, 由共邊、 共角定理可得 \begin{align*} \frac{\overline{MX}}{\overline{A_1X}}=&\frac{\triangle MAD}{\triangle A_1AD}= \frac{\triangle MAD}{\triangle MBC}\times \frac{\triangle MBC}{\triangle A_3BC}\times \frac{\triangle A_3BC}{\triangle A_3 A_2 A_4} \times \frac{\triangle A_3 A_2 A_4}{\triangle A_1 A_2 A_4}\times \frac{\triangle A_1 A_2 A_4}{\triangle A_1 DA}\\ =&\frac{\overline{MA} \times \overline{MD}}{\overline{MB} \times \overline{MC}}\times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3B} \!\times\!\overline{A_3C}} {\overline{A_3A_2} \!\times\! \overline{A_3A_4}}\times \frac{\overline{A_3M}}{\overline{A_1M}}\times \frac{\overline{A_1A_2} \!\times\! \overline{A_1A_4}}{\overline{A_1D} \!\times\! \overline{A_1A}}\\ =& \frac{\overline{MA}}{\overline{MB}} \times \frac{\overline{MD}}{\overline{MC}} \times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3B}}{\overline{A_3A_2}} \times \frac{\overline{A_3C}}{\overline{A_3A_4}} \times \frac{\overline{A_3M}}{\overline{A_1M}} \times \frac{\overline{A_1A_2}}{\overline{A_1D}}\times \frac{\overline{A_1A_4}}{\overline{A_1A}}\\ =&\frac{\triangle A_1A_3A}{\triangle A_1A_3B}\times \frac{\triangle A_1A_3D}{\triangle A_1A_3C} \times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\triangle A_1A_3B}{\triangle A_1A_3A_2}\times \frac{\triangle A_1A_3C}{\triangle A_1A_3A_4}\times \frac{\overline{A_3M}}{\overline{A_1M}} \\ &\times \frac{\triangle A_1A_3A_2}{\triangle A_1A_3D}\times \frac{\triangle A_1A_3A_4}{\triangle A_1A_3A}= \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3M}}{\overline{A_1M}}, \end{align*} 推得 $\dfrac{\overline{MX}}{\overline{A_1X}} = \dfrac{\overline{MY}}{\overline{A_3Y}} \times \dfrac{\overline{A_3M}}{\overline{A_1M}}\Longrightarrow \dfrac{\overline{MX}}{\overline{MA_1}- \overline{MX}} = \dfrac{\overline{MY}}{\overline{MA_3}\!-\!\overline{MY}}\times \dfrac{\overline{MA_3}}{\overline{MA_1}}$, 取倒數 $\dfrac{\overline{MA_1}\!-\!\overline{MX}}{\overline{MX}}=\dfrac{\overline{MA_3}\!-\!\overline{MY}}{\overline{MY}} \times \dfrac{\overline{MA_1}}{\overline{MA_3}}$ 化簡 $\dfrac{\overline{MA_1}}{\overline{MX}}-1=\big(\dfrac{\overline{MA_3}}{\overline{MY}}-1\big)\times \dfrac{\overline{MA_1}}{\overline{MA_3}}$, 推得 $\dfrac 1{\overline{MX}}-\dfrac 1{\overline{MA_1}}=\dfrac 1{\overline{MY}}-\dfrac 1{\overline{MA_3}}$, 即 $\dfrac 1{\overline{MX}}-\dfrac 1{\overline{MY}}=\dfrac 1{\overline{MA_1}} -\dfrac 1{\overline{MA_3}}$。 若將原式的左式移項, 可得 $\dfrac{\overline{A_1X}}{\overline{XM}}\times \dfrac{\overline{MY}}{\overline{YA_3}} \times \dfrac{\overline{A_3M}}{\overline{MA_1}}=1$。 (六) 定理 6 (參 設四邊形 $A_1 A_2 A_3 A_4$ 為任意四邊形, 以 $\overline{A_1 A_3}$ 為蝴蝶線, $\overline{A_1 A_3}$ 上一點 $M$ 為蝴蝶中心, 若蝴蝶形 $ABCD$ 的頂點分別落在四邊形的四條邊或邊的延長線上, 且連接 $A$、$D$ 和 $C$、$B$ 分別交 $\overleftrightarrow{A_1A_3}$ 於 $X$、$Y$ 兩點, 則 $\dfrac{\overline{A_1X}}{\overline{XM}}\!\times\! \dfrac{\overline{MY}}{\overline{YA_3}} \! \times\! \dfrac{\overline{A_3O}}{\overline{OA_1}}\!=\!1$。 (四邊形之坎迪延伸定理 1) 證明: (參考資料 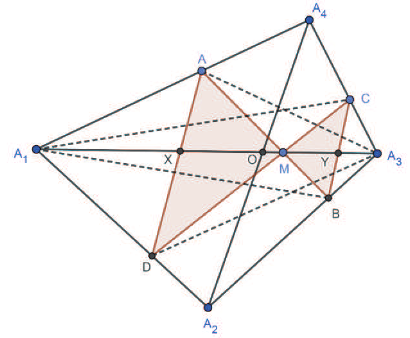 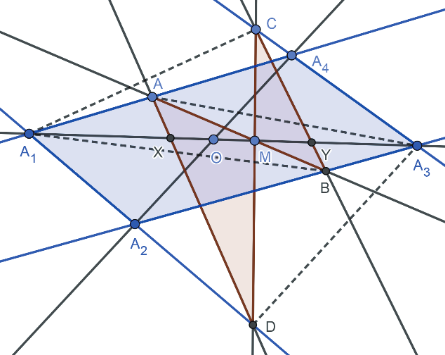 如圖 17 和 18, 由共邊、 共角定理可得 \begin{align*} \frac{\overline{MX}}{\overline{A_1X}} =& \frac{\triangle MAD}{\triangle A_1AD}\!=\! \frac{\triangle MAD}{\triangle MBC} \!\times\!\frac{\triangle MBC}{\triangle A_3BC}\!\times\! \frac{\triangle A_3BC}{\triangle A_3 A_2 A_4} \!\times\!\frac{\triangle A_3 A_2 A_4}{\triangle A_1 A_2 A_4}\!\times\! \frac{\triangle A_1 A_2 A_4}{\triangle A_1 DA}\\[5pt] =&\frac{\overline{MA} \!\times\!\overline{MD}}{\overline{MB} \!\times\!\overline{MC}}\times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3B} \!\times\! \overline{A_3C}}{\overline{A_3A_2} \!\times\! \overline{A_3A_4}}\times \frac{\overline{A_3O}}{\overline{A_1O}} \times \frac{\overline{A_1A_2} \!\times\! \overline{A_1A_4}}{\overline{A_1D} \!\times\! \overline{A_1A}}\\[5pt] =&\frac{\overline{MA}}{\overline{MB}} \times \frac{\overline{MD}}{\overline{MC}} \times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3B}}{\overline{A_3A_2}} \times \frac{\overline{A_3C}}{\overline{A_3A_4}} \times \frac{\overline{A_3O}}{\overline{A_1O}} \times \frac{\overline{A_1A_2}}{\overline{A_1D}} \times \frac{\overline{A_1A_4}}{\overline{A_1A}}\\[5pt] =&\frac{\triangle A_1A_3A}{\triangle A_1A_3B}\times \frac{\triangle A_1A_3D}{\triangle A_1A_3C} \times \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\triangle A_1A_3B}{\triangle A_1A_3A_2} \times \frac{\triangle A_1A_3C}{\triangle A_1A_3A_4}\times \frac{\overline{A_3O}}{\overline{A_1O}} \\[5pt] &\times \frac{\triangle A_1A_3A_2}{\triangle A_1A_3D} \times \frac{\triangle A_1A_3A_4}{\triangle A_1A_3A} = \frac{\overline{MY}}{\overline{A_3Y}} \times \frac{\overline{A_3O}}{\overline{A_1O}}, \end{align*} 推得 $\dfrac{\overline{MX}}{\overline{A_1X}}=\dfrac{\overline{MY}}{\overline{A_3Y}} \times \dfrac{\overline{A_3O}}{\overline{A_1O}}$, 從而 $\dfrac{\overline{A_1X}}{\overline{XM}}\times \dfrac{\overline{MY}}{\overline{A_3Y}} \times \dfrac{\overline{A_3O}}{\overline{OA_1}}=1$。 (七) 定理 7 (參 設四邊形 $A_1 A_2 A_3 A_4$ 為任意四邊形, 以 $\overline{A_1A_3}$ 為蝴蝶割線, $\overline{A_2A_4}$ 上一點 $N$ 為蝴蝶中心, 若蝴蝶形 $ABCD$ 的頂點分別落在四邊形的四條邊或邊的延長線上, 且連接 $A$、 $D$ 和 $C$、 $B$ 分別交 $\overleftrightarrow{A_1A_3}$ 於 $X$、 $Y$ 兩點, 再連接 $A$、 $B$ 和 $C$、 $D$ 分別交 $\overleftrightarrow{A_1A_3}$ 於 $T$、 $S$ 兩點, 則 $$\dfrac{\overline{A_1X}}{\overline{XS}}\times \frac{\overline{TY}}{\overline{YA_3}}\times \frac{\overline{A_3 S}}{\overline{TA_1}}=1\,\hbox{。}\ \hbox{可改寫成}\ \dfrac{\big(\frac{\overline{A_1 S}}{\overline{A_1 T}}\big)}{\overline{XS}} -\dfrac{\big(\frac{\overline{A_3 T}}{\overline{A_3S}}\big)}{\overline{YT}}=\dfrac{1}{\overline{A_1T}}-\frac{1}{\overline{A_3S}}\,\hbox{。}$$ (四邊形之坎迪延伸定理2) 證明: (以下證法是作者的創見) 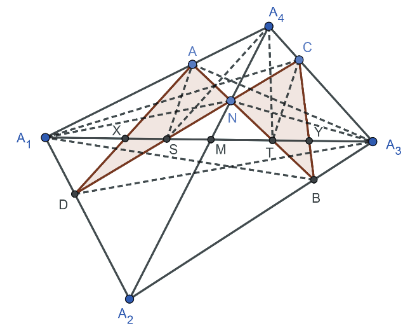 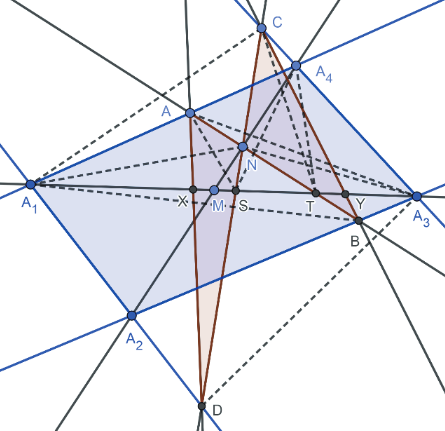 如圖 19 和 20, 由共邊、 共角定理可得 \begin{align*} (1)\frac{\overline{SX}}{\overline{A_1X}} =&\frac{\triangle SAD}{\triangle A_1AD}=\frac{\triangle SAD}{\triangle NAD}\times \frac{\triangle NAD}{\triangle NBC} \times \frac{\triangle NBC}{\triangle TBC}\times \frac{\triangle TBC}{\triangle A_3BC} \times \frac{\triangle A_3BC}{\triangle A_3 A_2 A_4}\\[5pt] &\times \frac{\triangle A_3 A_2 A_4}{\triangle A_1 A_2 A_4} \times \frac{\triangle A_1 A_2 A_4}{\triangle A_1 DA}\\[5pt] =&\frac{\overline{SD}}{\overline{ND}}\!\times\! \frac{\overline{NA} \!\!\times\!\! \overline{ND}}{\overline{NB} \!\!\times\!\! \overline{NC}} \!\times\! \frac{\overline{NB}}{\overline{TB}} \!\times\! \frac{\overline{TY}}{\overline{A_3Y}} \!\times\! \frac{\overline{A_3B} \!\times\! \overline{A_3C}}{\overline{A_3A_2} \!\times\! \overline{A_3A_4}}\!\times\! \frac{\overline{A_3M}}{\overline{A_1M}}\!\times\! \frac{\overline{A_1A_2} \!\times\! \overline{A_1A_4}} {\overline{A_1D} \!\times\! \overline{A_1A}}\\[5pt] =&\frac{\overline{SD} \times \overline{NA}}{\overline{NC} \times \overline{TB}}\times \frac{\overline{TY}}{\overline{A_3Y}} \times \frac{\overline{A_3B}}{\overline{A_3A_2}} \times \frac{\overline{A_3C}}{\overline{A_3A_4}} \times \frac{\overline{A_3M}}{\overline{A_1M}} \times \frac{\overline{A_1A_2}}{\overline{A_1D}}\times \frac{\overline{A_1A_4}}{\overline{A_1A}}\\[5pt] =&\frac{\overline{SD} \times \overline{NA}}{\overline{NC} \times \overline{TB}}\times \frac{\overline{TY}}{\overline{A_3Y}} \times \frac{\triangle A_1A_3B}{\triangle A_1A_3A_2}\times \frac{\triangle A_1A_3C}{\triangle A_1A_3A_4} \times \frac{\overline{A_3M}}{\overline{A_1M}}\\[5pt] &\times \frac{\triangle A_1A_3A_2}{\triangle A_1A_3D} \times \frac{\triangle A_1A_3A_4}{\triangle A_1A_3A}\\[5pt] =&\frac{\overline{SD} \times \overline{NA}}{\overline{NC} \times \overline{TB}} \times \frac{\overline{TY}}{\overline{A_3Y}} \times \frac{\triangle A_1A_3B}{\triangle A_1A_3A} \times \frac{\triangle A_1A_3C}{\triangle A_1A_3D} \times \frac{\overline{A_3M}}{\overline{A_1M}}\\[5pt] =&\frac{\overline{SD} \times \overline{NA}}{\overline{NC} \times \overline{TB}}\times \frac{\overline{TY}}{\overline{A_3Y}} \times \frac{\overline{TB}}{\overline{TA}} \times \frac{\overline{SC}}{\overline{SD}} \times \frac{\overline{A_3M}}{\overline{A_1M}}\\[5pt] =&\frac{\overline{NA} \times \overline{SC}}{\overline{NC} \times \overline{TA}}\times \frac{\overline{A_3M}}{\overline{A_1M}} \times \frac{\overline{TY}}{\overline{A_3Y}}. \end{align*} \begin{align*} (2)\ \hbox{欲證}\ \frac{\overline{NA} \!\times\!\overline{SC}}{\overline{NC}\!\times\!\overline{TA}}\!\times\! \frac{\overline{A_3M}}{\overline{A_1M}} \!=\!\frac{\overline{A_3S}}{\overline{A_1T}}\!\Leftrightarrow& \frac{\overline{NA}}{\overline{TA}}\times\frac{\overline{SC}}{\overline{NC}} =\frac{\overline{A_3S}}{\overline{A_3M}}\times \frac{\overline{A_1M}}{\overline{A_1T}}\\ &\hskip -35pt \Leftrightarrow \frac{\triangle A_1 A_4 N}{\triangle A_1 A_4 T}\!\times\! \frac{\triangle A_3 A_4 S}{\triangle A_3 A_4 N} \!=\!\frac{\triangle A_3 A_4 S}{\triangle A_3 A_4 M}\!\times\! \frac{\triangle A_1 A_4 M}{\triangle A_1 A_4 T}\\ &\hskip -35pt \Leftrightarrow \frac{\triangle A_1 A_4 N}{\triangle A_3 A_4 N}\!=\!\frac{\triangle A_1 A_4 M}{\triangle A_3 A_4 M} \Leftrightarrow \frac{\overline{A_1M}}{\overline{A_3M}}\!=\! \frac{\overline{A_1M}}{\overline{A_3M}}, \hbox{得證。} \end{align*} 由 (1)(2) 可知: $\dfrac{\overline{SX}}{\overline{A_1X}} =\dfrac{\overline{A_3S}}{\overline{A_1T}}\times \dfrac{\overline{TY}}{\overline{A_3Y}}$, 推得 $\dfrac{\overline{SX}}{\overline{A_1 S}-\overline{SX}}=\dfrac{\overline{A_3S}}{\overline{A_1T}}\times \dfrac{\overline{TY}}{\overline{A_3 T}\!-\!\overline{TY}}$, 取倒數 $\dfrac{\overline{A_1 S}\!-\!\overline{SX}}{\overline{SX}}=\dfrac{\overline{A_1 T}}{\overline{A_3S}} \times \dfrac{\overline{A_3 T}\!-\!\overline{TY}} {\overline{TY}}$, 化簡 $\dfrac{\overline{A_1 S}}{\overline{SX}}-1=\dfrac{\overline{A_1 T}}{\overline{A_3S}} \times \Big(\dfrac{\overline{A_3 T}}{\overline{TY}}-1\Big) \Rightarrow $ $\dfrac{\big(\frac{\overline{A_1 S}}{\overline{A_1T}}\big)}{\overline{SX}}-\dfrac{1}{\overline{A_1T}} =\dfrac{\big(\frac{\overline{A_3T}}{\overline{A_3S}}\big)}{\overline{TY}}-\dfrac{1}{\overline{A_3S}}$, 即 $\dfrac{\big(\frac{\overline{A_1 S}}{\overline{A_1T}}\big)}{\overline{XS}}-\dfrac{\big(\frac{\overline{A_3T}}{\overline{A_3S}}\big)}{\overline{YT}} =\dfrac{1}{\overline{A_1T}}-\dfrac{1}{\overline{A_3S}}$。 若將原式的左式移項, 可得 $\dfrac{\overline{A_1X}}{\overline{XS}}\times \dfrac{\overline{TY}}{\overline{YA_3}}\times \dfrac{\overline{A_3S}}{\overline{TA_1}}=1$。 四、四邊形的蝴蝶定理之一般化一般四邊形的蝴蝶線不一定要侷限於對角線, 也可能是四邊形任意兩邊的截線段, 於是分成對邊、 鄰邊的截線段做討論, 而有以下的定理: (一) 以對邊的截線段為蝴蝶線 定理 8 (參 設四邊形 $A_1 A_2 A_3 A_4$ 為任意四邊形, $\overline{PQ}$ 為和對邊 $\overline{A_1A_4}$、 $\overline{A_2 A_3}$ 相交的截線段, 以 $\overline{PQ}$ 為蝴蝶線, $\overline{PQ}$ 上任一點 $M$ 為蝴蝶中心, 設 $\overleftrightarrow{A_1A_4}$ 和 $\overleftrightarrow{A_2A_3}$ 相交於 $E$ 點, 過 $M$ 點作一截線段 $\overline{AB}$, 連接 $\overleftrightarrow{EM}$、 $\overleftrightarrow{QB}$ 相交於 $F$ 點, 並連接 $\overleftrightarrow{PF}$ 交 $\overline{A_1A_2}$ 於 $D$ 點, 再連接 $\overleftrightarrow{DM}$ 交 $\overleftrightarrow{A_2A_3}$ 於 $C$ 點, 且連接 $A$、 $D$ 和 $C$、 $B$ 分別交 $\overline{PQ}$ 於 $X$、 $Y$ 兩點, 則 $\dfrac 1{\overline{MX}}-\dfrac 1{\overline{MY}}=\dfrac 1{\overline{MP}}-\dfrac 1{\overline{MQ}}$。 (坎迪定理) 若 $\overline{MP}=\overline{MQ}$, 則 $\overline{MX} = \overline{MY}$。 (蝴蝶定理) (此定理是作者的創見) 證明: 如圖 21, 蝴蝶形 $ABCD$ 可以視為以兩對角線交點 $M$ 為中心的四邊形 $PEQF$ 之蝴蝶形, 故由定理 5 可知: $\dfrac 1{\overline{MX}}-\dfrac 1{\overline{MY}}=\dfrac 1{\overline{MP}} -\dfrac 1{\overline{MQ}}$。 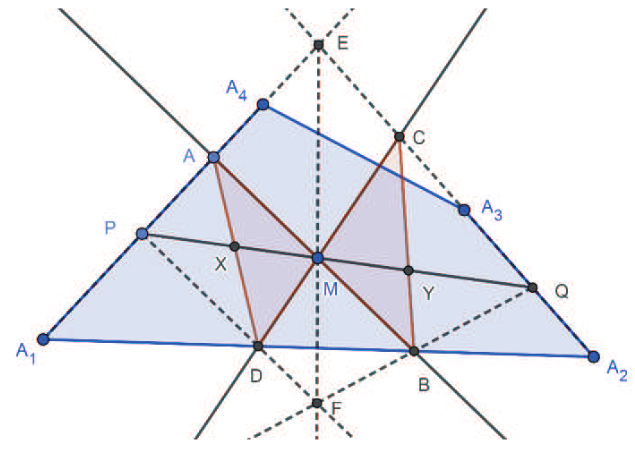 (二) 以鄰邊的截線段為蝴蝶線 定理 9 (參 設四邊形 $A_1 A_2 A_3 A_4$ 為任意四邊形, $\overline{PQ}$ 為和鄰邊 $\overline{A_1A_4}$、 $\overline{A_3 A_4}$ 相交的截線段, 以 $\overline{PQ}$ 為蝴蝶線, $\overline{PQ}$ 上任一點 $M$ 為蝴蝶中心, 過 $M$ 點作一截線段 $\overline{AB}$, 連接 $\overleftrightarrow{A_4M}$、 $\overleftrightarrow{QB}$ 相交於 $F$ 點, 並連接 $\overleftrightarrow{PF}$ 交 $\overline{A_1A_2}$ 於 $D$ 點, 再連接 $\overleftrightarrow{DM}$ 交 $\overleftrightarrow{A_3A_4}$ 於 $C$ 點, 且連接 $A$、 $D$ 和 $C$、 $B$分別交 $\overline{PQ}$ 於 $X$、 $Y$ 兩點, 則 $\dfrac 1{\overline{MX}}-\dfrac 1{\overline{MY}}=\dfrac 1{\overline{MP}}-\dfrac 1{\overline{MQ}}$。 (坎迪定理) 若 $\overline{MP}=\overline{MQ}$, 則 $\overline{MX} = \overline{MY}$。 (蝴蝶定理) (此定理是作者的創見) 證明: 如圖 22, 蝴蝶形 $ABCD$ 可以視為以兩對角線交點 $M$ 為中心的四邊形 $PA_4 QF$ 之蝴蝶形, 故由定理 5 可知: $\dfrac 1{\overline{MX}}-\dfrac 1{\overline{MY}}=\dfrac 1{\overline{MP}} -\dfrac 1{\overline{MQ}}$。 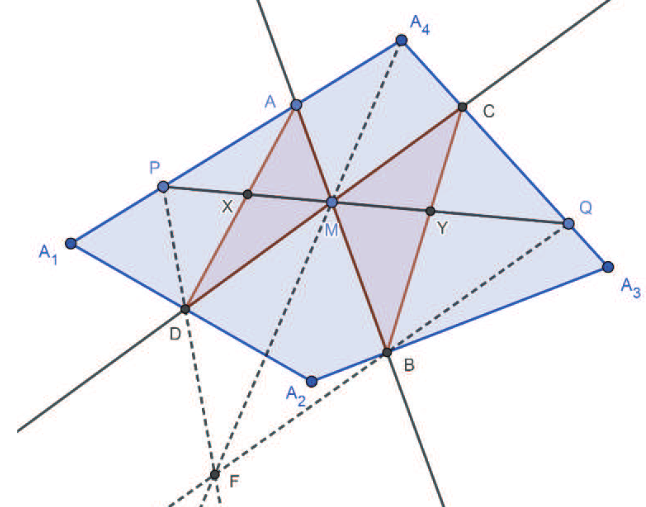 最後利用三線共點的作圖法, 我們成功將四邊形蝴蝶定理一般化, 只是此時蝴蝶形不一定內接在四邊形的邊上, 也可能接在邊之延長線上。 參考資料本文作者群為國立金門高級中學師生 |
| 頁碼 | 69-79 |
2025年3月 49卷1期
四邊形的蝴蝶定理

