| 發刊日期 |
2025年3月
|
|---|---|
| 標題 | 一個由指數函數加總的函數之探討 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
摘要: 本篇研究旨在討論 $y=f(x)=\Big(\sum\limits_{i=1}^n a_i^x\Big)^{\frac 1x}$, $n\ge 2$ 的相關性質, 其中 $x,a_1,\ldots,a_n\in {\Bbb R}^+$。 本文第一章首先, 我們從 $y=g(x)= \sum\limits_{i=1}^n a_i^x$, $x,a_1,\ldots,a_n\in {\Bbb R}^+$, 開始討論。 性質 1-1: (1) $y=g(x)= \sum\limits_{i=1}^n a_i^x$, $x\in {\Bbb R}^+$, $a_1,\ldots,a_n\gt 1$, 為嚴格遞增函數。 證明: (1) 若 $x_1\lt x_2$, 則 $a_i^{x_1}\lt a_i^{x_2},\ \forall\ i=1,2,\ldots,n\ \Rightarrow \ \sum\limits_{i=1}^n a_i^{x_1}\lt \sum\limits_{i=1}^n a_i^{x_2}$, 故 $g(x_1)\lt g(x_2)$, 因此 $y=g(x)= \sum\limits_{i=1}^n a_i^x$ 為嚴格遞增函數。 (2) 若 $x_1\lt x_2$, 則 $a_i^{x_1}\gt a_i^{x_2},\ \forall\ i=1,2,\ldots,n\ \ \Rightarrow \ \sum\limits_{i=1}^n a_i^{x_1}\gt \sum\limits_{i=1}^n a_i^{x_2}$, 故 $g(x_1)\gt g(x_2)$, 因此 $y=g(x)= \sum\limits_{i=1}^n a_i^x$ 為嚴格遞減函數。 (3) 我們證明: 若 $y=g_1(x)$, $y=g_2(x)$ 為凸函數, $y=G(x)=g_1(x)+g_2(x)$ 亦為凸函數。 \begin{align*} &\left\{\begin{array}{l} g_1\Big(\dfrac{x_1+x_2}2\Big)\le \dfrac 12g_1(x_1)+\dfrac 12 g_1(x_2)\\[7pt] g_2\Big(\dfrac{x_1+x_2}2\Big)\le \dfrac 12g_2(x_1)+\dfrac 12 g_2(x_2) \end{array}\right.\ \\ &\Rightarrow\ g_1\Big(\frac{x_1+x_2}2\Big)+g_2\Big(\frac{x_1+x_2}2\Big)\le \frac 12[g_1(x_1)+g_2(x_1)]+ \frac 12[g_1(x_2)+g_2(x_2)]\\ &\Rightarrow\ G\Big(\frac{x_1+x_2}2\Big)\le \frac 12G(x_1)+\frac 12G(x_2),\ \hbox{其中 $G(x)=g_1(x)+g_2(x)$,} \end{align*} 故 $y=G(x)$ 亦為凸函數。 而 $\because\ y=a_i^x$ 為凸函數, $\forall\ i=1,2,\ldots,n\ \Rightarrow\ y=g(x)=\sum\limits_{i=1}^n a_i^x$ 為凸函數。 $\Box$ 有了 $y=g(x)$ 當基礎, 我們懷疑 $y=f(x)$ 是否也有類似的性質, 我們先使用 Geogebra 進行繪圖發現幾個現象, 說明如後。 以 $y=f(x)=(1.2^x+1.9^x+0.2^x)^{\frac 1x}$, $x\in {\Bbb R}^+$ 為例子, 圖形如下: 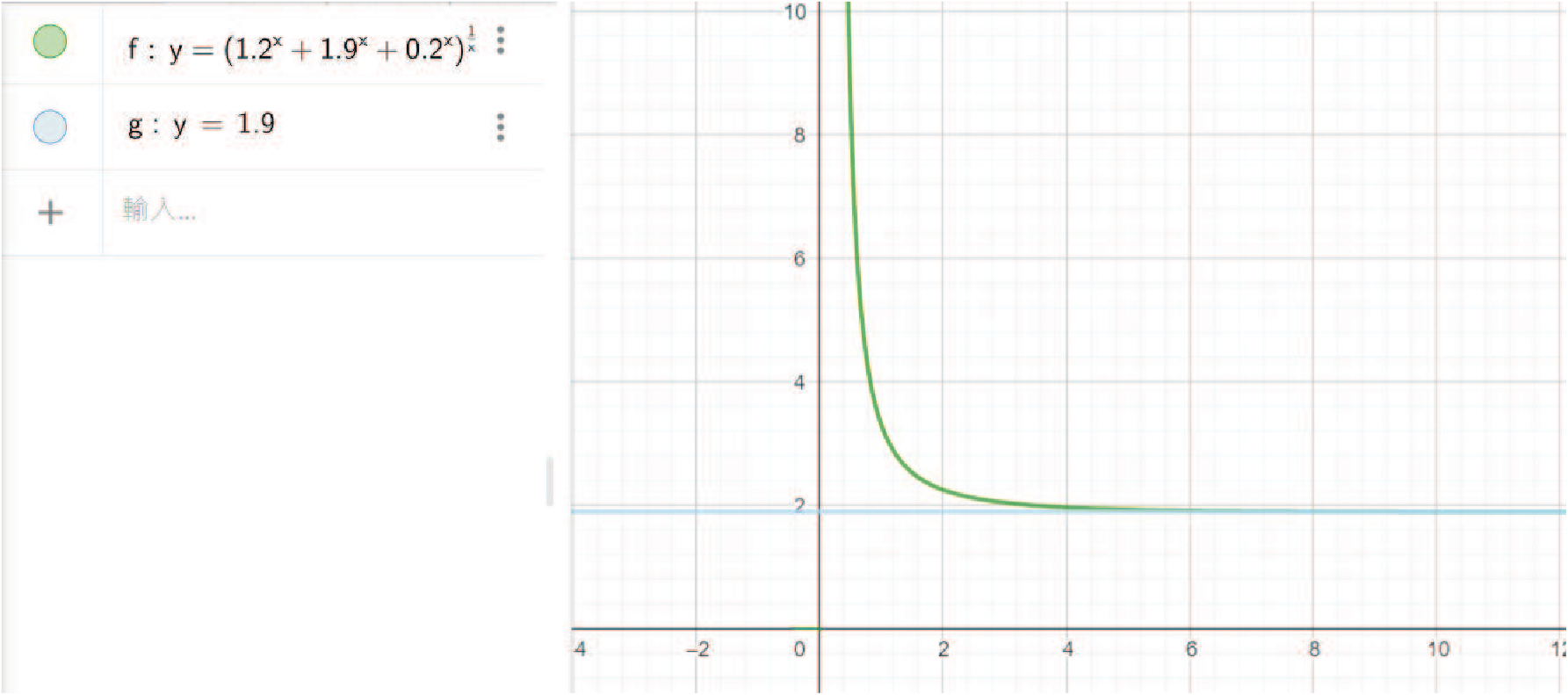 觀察圖形, $y=f(x)$ 除了嚴格遞減的現象, 圖形似乎有水平漸近線, 且也呈現凸函數的感覺。 性質 1-2: $y=f(x)$ 為嚴格遞減函數。 證明: 我們證明 $\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{\frac 1p}\gt \bigg(\sum\limits_{i=1}^n a_i^q\bigg)^{\frac 1q}$, $p\lt q$。 令 ${\rm max}\,\{a_1,\ldots,a_n\}=M$ 且 $q=p+x$, $x\gt 0$, 則 \begin{align*} \dfrac{\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{q}}{\bigg(\sum\limits_{i=1}^n a_i^q\bigg)^{p}} =\,&\dfrac{\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{p+x}}{\bigg(\sum\limits_{i=1}^n a_i^{p+x}\bigg)^{p}} =\dfrac{\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{p}\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{x}} {\bigg(\sum\limits_{i=1}^n a_i^x a_i^p\bigg)^{p}} \ge\dfrac{\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{p}\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{x}} {\bigg(\sum\limits_{i=1}^n M^xa_i^p\bigg)^{p}}\\ =\,&\dfrac{\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{p}\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{x}} {M^{px}\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{p}} =\dfrac{\bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{x}}{M^{px}}=\Bigg(\frac{\sum\limits_{i=1}^n a_i^p}{M^p}\Bigg)^x\gt 1\\ \Rightarrow\quad &\ \bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{q}\gt \bigg(\sum\limits_{i=1}^n a_i^q\bigg)^{p}\ \Rightarrow\ \bigg(\sum\limits_{i=1}^n a_i^p\bigg)^{\frac 1p}\gt \bigg(\sum\limits_{i=1}^n a_i^q\bigg)^{\frac 1q}\\ \Rightarrow\quad &\ f(p)\gt f(q),\ p\lt q. \end{align*} 因此, $y=f(x)=\bigg(\sum\limits_{i=1}^n a_i^x\bigg)^{\frac 1x}$, $x,a_1,\ldots,a_n\in {\Bbb R}^+$, 為嚴格遞減函數。 $\Box$ 性質 1-3: $\lim\limits_{x\to\infty} f(x)=M$, 其中 $\max\{a_1,\ldots,a_n\}=M$。 證明: \begin{align*} (M^x)^{\frac 1x}\le \,&\bigg(\sum\limits_{i=1}^n a_i^x\bigg)^{\frac 1x}\le \bigg(\sum\limits_{i=1}^n M^x\bigg)^{\frac 1x} \ \Rightarrow\ M\le \bigg(\sum\limits_{i=1}^n a_i^x\bigg)^{\frac 1x}\le (n\cdot M^x)^{\frac 1x}\\ \ \Rightarrow\ &\lim\limits_{x\to\infty} M\le \lim\limits_{x\to\infty}\bigg(\sum\limits_{i=1}^n a_i^x\bigg)^{\frac 1x} \le \lim\limits_{x\to\infty}(n\cdot M^x)^{\frac 1x}\\ \ \Rightarrow\ &\lim\limits_{x\to\infty} M\le \lim\limits_{x\to\infty}\bigg(\sum\limits_{i=1}^n a_i^x\bigg)^{\frac 1x} \le \lim\limits_{x\to\infty}(n)^{\frac 1x}\cdot M\\ \ \Rightarrow\ &M\le \lim\limits_{x\to\infty}\bigg(\sum\limits_{i=1}^n a_i^x\bigg)^{\frac 1x}\le M. \end{align*} 由夾擠定理可得 $\lim\limits_{x\to\infty}\bigg(\sum\limits_{i=1}^n a_i^x\bigg)^{\frac 1x}= M$。 因此 $y=f(x)$ 的水平漸近線為 $y=M$。 $\Box$ 性質 1-4: $y=f(x)$ 為凸函數。 證明: 我們證明 $f\Big(\dfrac{x_1+x_2}{2}\Big)\lt \dfrac 12f(x_1)+\dfrac 12f(x_2)$, $x_1\lt x_2$。 \begin{align*} \hbox{(I)}\quad \log f\Big(\dfrac{x_1+x_2}{2}\Big)=\,&\log \bigg(\sum\limits_{i=1}^n a_i^{\frac{x_1+x_2}{2}}\bigg)^{\frac 2{x_1+x_2}} =\dfrac{2}{x_1+x_2}\log \bigg(\sum\limits_{i=1}^n a_i^{\frac{x_1+x_2}{2}}\bigg)\hskip 2cm~\notag\\ =\,&\dfrac{2}{x_1+x_2}\log \bigg(\sum\limits_{i=1}^n a_i^{\frac{x_1}{2}}a_i^{\frac{x_2}{2}}\bigg). \end{align*} 利用柯西不等式得 $\sum\limits_{i=1}^n A_iB_i\le \bigg(\sum\limits_{i=1}^n A_i^{2}\bigg)^{\frac 12}\bigg(\sum\limits_{i=1}^n B_i^{2}\bigg)^{\frac 12}$, $A_i,B_i\in {\Bbb R},\ \forall\ i=1,2,\ldots,n$。 令 $A_i=a_i^{\frac{x_1}{2}}$, $B_i=a_i^{\frac{x_2}{2}}$, 則可得 $\sum\limits_{i=1}^n a_i^{\frac{x_1}{2}}a_i^{\frac{x_2}{2}} \le \bigg(\sum\limits_{i=1}^n (a_i^{\frac{x_1}{2}})^2\bigg)^{\frac{1}{2}} \bigg(\sum\limits_{i=1}^n (a_i^{\frac{x_2}{2}})^2\bigg)^{\frac{1}{2}}$。 \begin{align} &\hskip -25pt \hbox{故}\ \log f\Big(\dfrac{x_1+x_2}{2}\Big)\le\dfrac{2}{x_1+x_2}\log \left[\bigg(\sum\limits_{i=1}^n (a_i^{\frac{x_1}{2}})^2\bigg)^{\frac{1}{2}} \bigg(\sum\limits_{i=1}^n (a_i^{\frac{x_2}{2}})^2\bigg)^{\frac{1}{2}}\right]\notag\\ =\,&\dfrac{2}{x_1+x_2}\log\left[\bigg(\sum\limits_{i=1}^n a_i^{x_1}\bigg)^{\frac{1}{2}} \bigg(\sum\limits_{i=1}^n a_i^{x_2}\bigg)^{\frac{1}{2}}\right]\notag\\ =\,&\dfrac{2}{x_1+x_2}\log\left[ \bigg(\sum\limits_{i=1}^n a_i^{x_1}\bigg) \bigg(\sum\limits_{i=1}^n a_i^{x_2}\bigg)\right]^{\frac{1}{2}}=\dfrac{1}{x_1+x_2}\log\left[ \bigg(\sum\limits_{i=1}^n a_i^{x_1}\bigg)\bigg(\sum\limits_{i=1}^n a_i^{x_2}\bigg)\right]\notag\\ =\,&\dfrac{1}{x_1+x_2}\log\bigg(\sum\limits_{i=1}^n a_i^{x_1}\bigg) +\dfrac{1}{x_1+x_2}\log\bigg(\sum\limits_{i=1}^n a_i^{x_2}\bigg).\label{1} \end{align} (II) 利用算幾不等式得 $\dfrac{f(x_1)+f(x_2)}{2}\ge [f(x_1)f(x_2)]^{\frac 12}$, \begin{align} \hbox{則}\ &\log \bigg[\frac 12 f(x_1)+\frac 12 f(x_2)\bigg]\ge \log[f(x_1)f(x_2)]^{\frac 12}\notag\\ =\,&\log\left[\bigg(\sum\limits_{i=1}^n a_i^{x_1}\bigg)^{\frac{1}{x_1}} \bigg(\sum\limits_{i=1}^n a_i^{x_2}\bigg)^{\frac{1}{x_2}}\right]^{\frac{1}{2}}=\frac 12 \log \bigg(\sum\limits_{i=1}^n a_i^{x_1}\bigg)^{\frac{1}{x_1}}+\frac 12 \log \bigg(\sum\limits_{i=1}^n a_i^{x_2}\bigg)^{\frac{1}{x_2}}\qquad~\notag\\ =\,&\frac 1{2x_1}\log\Big(\sum_{i=1}^n a_i^{x_1}\Big)+\frac 1{2x_2}\log\Big(\sum_{i=1}^n a_i^{x_2}\Big).\label{2} \end{align} (III) 將 \eqref{2} 減掉 \eqref{1}, \begin{align*} &\hskip -15pt \frac 1{2x_1}\log\Big(\sum_{i=1}^n a_i^{x_1}\Big)\!+\!\frac 1{2x_2}\log\Big(\sum_{i=1}^n a_i^{x_2}\Big)\!-\!\frac 1{x_1\!+\!x_2}\log\Big(\sum_{i=1}^n a_i^{x_1}\Big) \!-\!\frac 1{x_1\!+\!x_2}\log\Big(\sum_{i=1}^n a_i^{x_2}\Big)\\ =\,&\Big(\frac 1{2x_1}-\frac 1{x_1+x_2}\Big)\log\Big(\sum_{i=1}^n a_i^{x_1}\Big)+\Big(\frac 1{2x_2}-\frac 1{x_1+x_2}\Big)\log\Big(\sum_{i=1}^n a_i^{x_2}\Big)\\ =\,&\frac {x_2-x_1}{2x_1(x_1+x_2)}\log\Big(\sum_{i=1}^n a_i^{x_1}\Big)+\frac {x_1-x_2}{2x_2(x_1+x_2)}\log\Big(\sum_{i=1}^n a_i^{x_2}\Big)\\ =\,&\frac {x_2-x_1}{2(x_1+x_2)}\bigg[\log\bigg(\sum\limits_{i=1}^n a_i^{x_1}\bigg)^{\frac{1}{x_1}}- \log \bigg(\sum\limits_{i=1}^n a_i^{x_2}\bigg)^{\frac{1}{x_2}}\bigg]. \end{align*} 由性質 1-2 得 $y\!=\!f(x)$ 為嚴格遞減函數, 故 $\log\bigg(\sum\limits_{i=1}^n a_i^{x_1}\bigg)^{\frac{1}{x_1}}\!-\! \log \bigg(\sum\limits_{i=1}^n a_i^{x_2}\bigg)^{\frac{1}{x_2}}\gt 0$, 因此 $$ \log f\Big(\dfrac{x_1+x_2}{2}\Big)\lt \log\Big[\frac 12 f(x_1)+\frac 12f(x_2)\Big]\Rightarrow f\Big(\dfrac{x_1+x_2}{2}\Big)\lt \frac 12 f(x_1)+\frac 12f(x_2), x_1\lt x_2 ,$$ 即 $y=f(x)$ 為凸函數。 $\Box$ 定理 1-5: 若 $0\!\lt \!p\!\lt \!q\!\lt \!r$, 則存在不等式 $\bigg(\sum\limits_{i=1}^n a_i^{q}\bigg)^{\frac{1}{q}} \!\lt \!\dfrac{r\!-\!q}{r\!-\!p}\bigg(\sum\limits_{i=1}^n a_i^{p}\bigg)^{\frac{1}{p}} \!+\!\dfrac{q\!-\!p}{r\!-\!p}\bigg(\sum\limits_{i=1}^n a_i^{r}\bigg)^{\frac{1}{r}}$。 證明: 根據性質 1-4 可得 $y\!=\!f(x)$ 為凸函數, $\therefore$ $f(tx_1+(1-t)x_2)\lt tf(x_1)+(1-t)f(x_2)$, $0\lt t\lt 1$, 令 $x_1=p$, $tx_1+(1-t)x_2=q$, $x_2=r$, 則 $t\!=\!\frac{r\!-\!q}{r\!-\!p}$, $1\!-\!t=\frac{q-p}{r-p}$, 因此 \begin{align*} f(q)\lt tf(p)+(1-t)f(r)\Rightarrow & \bigg(\sum\limits_{i=1}^n a_i^{q}\bigg)^{\frac{1}{q}}\lt t\bigg(\sum\limits_{i=1}^n a_i^{p}\bigg)^{\frac{1}{p}} +(1-t)\bigg(\sum\limits_{i=1}^n a_i^{r}\bigg)^{\frac{1}{r}}\\ \Rightarrow& \bigg(\sum\limits_{i=1}^n a_i^{q}\bigg)^{\frac{1}{q}}\lt \frac{r-q}{r-p}\bigg(\sum\limits_{i=1}^n a_i^{p}\bigg)^{\frac{1}{p}} +\frac{q-p}{r-p}\bigg(\sum\limits_{i=1}^n a_i^{r}\bigg)^{\frac{1}{r}}.\tag*{$\Box$} \end{align*} 定理 1-6: (1) 若 $y=h(x)\gt 0$, $x\in {\Bbb R}^+$ 在 $(a,b)$ 為連續嚴格遞增函數, 則 $y=f\circ h(x)=\bigg(\sum\limits_{i=1}^n a_i^{h(x)}\bigg)^{\frac{1}{h(x)}}$, $x\in{\Bbb R}^+$, $a_1,\ldots,a_n\in{\Bbb R}^+$, 在 $(a,b)$ 為嚴格遞減函數。 (2) 若 $y=h(x)\gt 0$, $x\in {\Bbb R}^+$ 在 $(a,b)$ 為連續嚴格遞減函數, 則 $y=f\circ h(x)=\bigg(\sum\limits_{i=1}^n a_i^{h(x)}\bigg)^{\frac{1}{h(x)}}$, $x\in{\Bbb R}^+$, $a_1,\ldots,a_n\in{\Bbb R}^+$, 在 $(a,b)$ 為嚴格遞增函數。 證明: (1) 若 $a\!\lt \!x_1\!\lt \!x_2\lt b$, 則 $h(x_1)\!\lt \!h(x_2)$, 且 $h(x_2)\!=\!h(x_1)+k$, $k\!\gt \!0$, $\max\{a_1,\ldots,a_n\}\!=\!M$。 \begin{align*} &\hskip -20pt \dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{{h(x_2)}}}{\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{{h(x_1)}}} =\,\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{{h(x_1)}+k}}{\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)+k}\bigg)^{{h(x_1)}}} =\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{k}\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{{h(x_1)}}} {\bigg(\sum\limits_{i=1}^n a_i^k a_i^{h(x_1)}\bigg)^{{h(x_1)}}}\\ \ge \,&\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{k}\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{{h(x_1)}}} {\bigg(\sum\limits_{i=1}^n M^k a_i^{h(x_1)}\bigg)^{{h(x_1)}}} =\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{k}\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{{h(x_1)}}} {M^{h(x_1)k} \bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{{h(x_1)}}}\\ =\,&\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{k}}{M^{h(x_1)k}} =\Bigg(\dfrac{\sum\limits_{i=1}^n a_i^{h(x_1)}}{M^{h(x_1)}}\Bigg)^k \gt \Big(\frac{M^{h(x_1)}}{M^{h(x_1)}}\Big)^k=1\\ \Rightarrow\,& \bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{h(x_2)}\gt \bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{h(x_1)} \Rightarrow \bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{\frac{1}{h(x_1)}}\gt \bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{\frac{1}{h(x_2)}}\\ \Rightarrow\,& f\circ h(x_1)\gt f\circ h(x_2),\ \hbox{故 $f\circ h(x)$ 在 $(a,b)$ 為嚴格遞減函數。} \end{align*} (2) 若 $a\lt x_1\lt x_2\lt b$, 則 $h(x_1)\gt h(x_2)$, 且 $h(x_1)=h(x_2)+k$, $k\gt 0$, $\max\{a_1,\ldots,a_n\}=M$。 \begin{align*} &\hskip -20pt \dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{{h(x_1)}}}{\bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{{h(x_2)}}} =\,\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{{h(x_2)}+k}}{\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)+k}\bigg)^{{h(x_2)}}} =\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{k}\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{{h(x_2)}}} {\bigg(\sum\limits_{i=1}^n a_i^k a_i^{h(x_2)}\bigg)^{{h(x_2)}}}\\ \ge \,&\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{k}\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{{h(x_2)}}} {\bigg(\sum\limits_{i=1}^n M^k a_i^{h(x_2)}\bigg)^{{h(x_2)}}} =\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{k}\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{{h(x_2)}}} {M^{h(x_2)k} \bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{{h(x_2)}}}\\ =\,&\dfrac{\bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{k}}{M^{h(x_2)k}} =\Bigg(\dfrac{\sum\limits_{i=1}^n a_i^{h(x_2)}}{M^{h(x_2)}}\Bigg)^k \gt \Big(\frac{M^{h(x_2)}}{M^{h(x_2)}}\Big)^k=1\\ \Rightarrow\,& \bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{h(x_1)}\gt \bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{h(x_2)} \Rightarrow \bigg(\sum\limits_{i=1}^n a_i^{h(x_2)}\bigg)^{\frac{1}{h(x_2)}}\gt \bigg(\sum\limits_{i=1}^n a_i^{h(x_1)}\bigg)^{\frac{1}{h(x_1)}}\\ \Rightarrow\,& f\circ h(x_2)\gt f\circ h(x_1), \hbox{故 $f\circ h(x)$ 在 $(a,b)$ 為嚴格遞增函數。}\tag*{$\Box$} \end{align*} 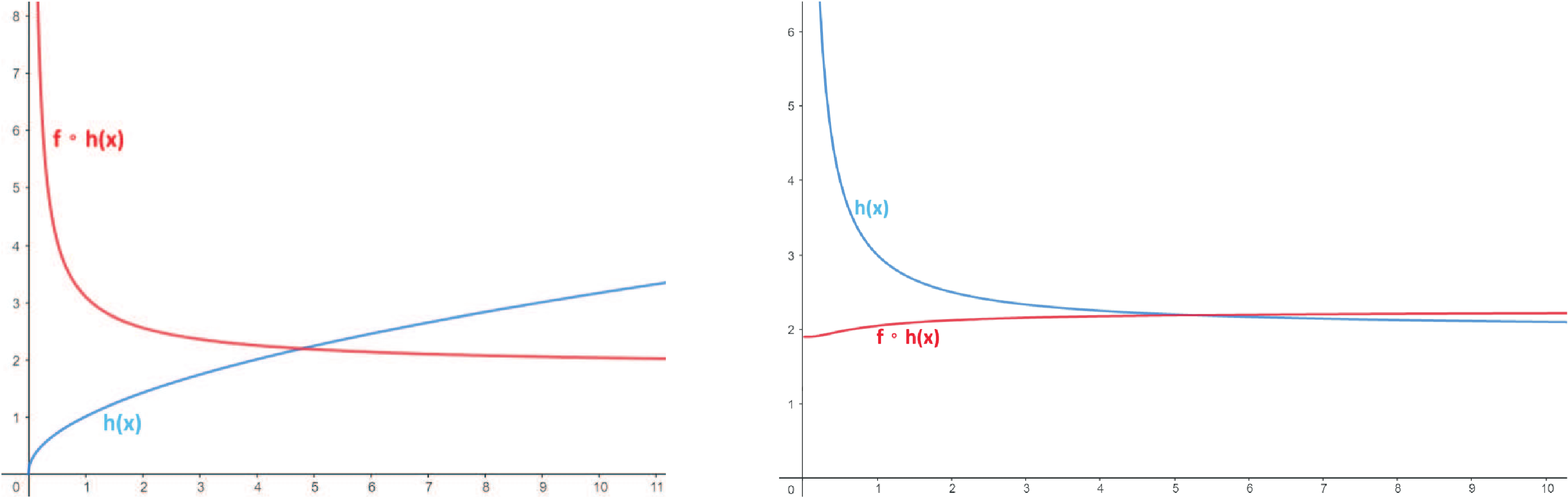 定理 1-7: 設 $y=h(x)\gt 0$, $x\in {\Bbb R}^+$ 且 $y=f\circ h(x)=\bigg(\sum\limits_{i=1}^n a_i^{h(x)}\bigg)^{\frac{1}{h(x)}}$, $x\in {\Bbb R}^+, a_1\ldots,a_n\in{\Bbb R}^+$。 若 $y=h(x)$ 在 $x=x_0$ 有極大值, 則 $y=f\circ h(x)$ 在 $x=x_0$ 有極小值。 證明: 由性質 1-6 即可得。 $\Box$ 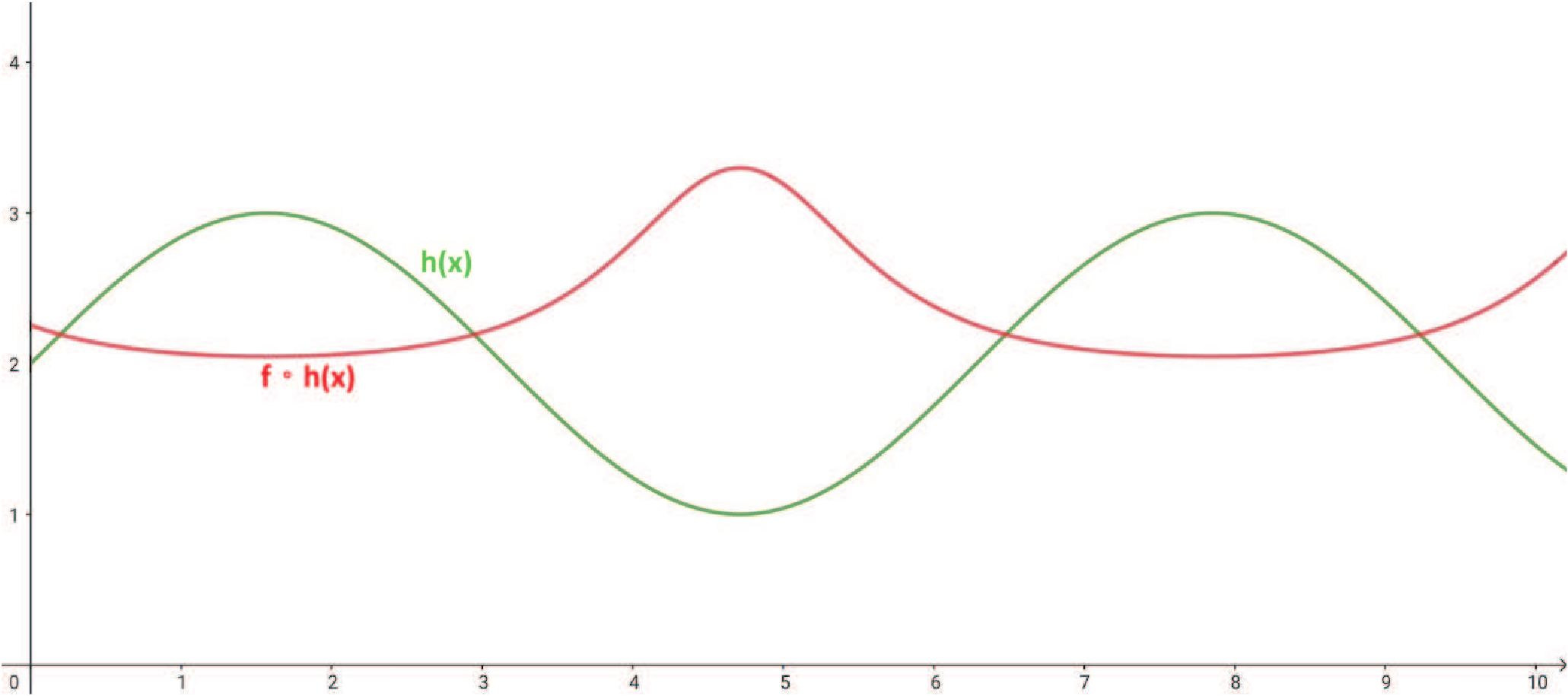 定理 1-8: 設 $y=h(x)\gt 0$, $x\in{\Bbb R}^+$ 為凹函數, 則 $y=f\circ h(x)=\bigg(\sum\limits_{i=1}^n a_i^{h(x)}\bigg)^{\frac{1}{h(x)}}$, $x\in {\Bbb R}^+, a_1\ldots,a_n\in{\Bbb R}^+$, 為凸函數。 證明: 令 $x_1\lt x_2$, 則 $h(\lambda x_1+(1-\lambda)x_2)\ge \lambda h(x_1)+(1-\lambda)h(x_2)$, $0\lt \lambda\lt 1$。 由性質 1-2 可知 $f(x)$ 為嚴格遞減函數, 即 $$f\big(h(\lambda x_1+(1-\lambda)x_2)\big)\le f(\lambda h(x_1)+(1-\lambda)h(x_2)),$$ 由性質 1-4 可知 $f(x)$ 為凸函數, 即 \begin{align*} &\hskip -20pt f\big(\lambda h(x_1)+(1-\lambda)h(x_2)\big)\le \lambda f\big(h(x_1)\big)+(1-\lambda)f\big(h(x_2)\big)\\ \Rightarrow \,&f\big(h(\lambda x_1+(1-\lambda)x_2)\big)\le \lambda f\big(h(x_1)\big)+(1-\lambda)f\big(h(x_2)\big), \end{align*} 故可得 $y=f\circ h(x)=\bigg(\sum\limits_{i=1}^n a_i^{h(x)}\bigg)^{\frac{1}{h(x)}}$, $x\in {\Bbb R}^+, a_1\ldots,a_n\in{\Bbb R}^+$, 也為凸函數。 $\Box$ 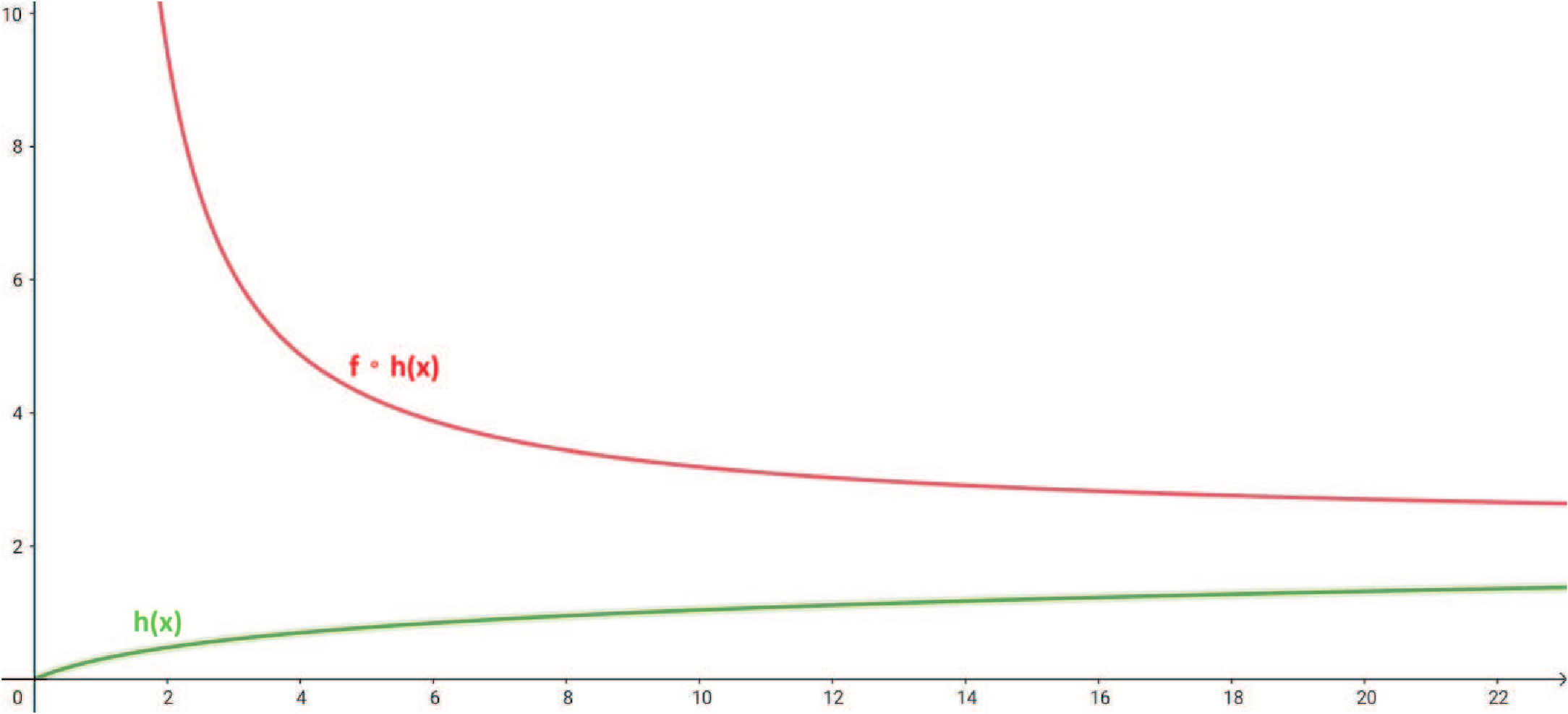 目前為止我們已經確定了 $y=f(x)$ 的基本性質, 接下來我們要依此性質更進一步討論。 第二章確定了 $y=f\circ h(x)$ 的走勢後, 我們開始思考 $y=f\circ f(x)$、 $y=f\circ f\circ f(x)$ 等, 甚至是 $\underbrace{f\circ\cdots\circ f(x)}_{n \hbox{次合成函數}}$ 的走勢, 為了方便, 我們定義 $\underbrace{f\circ\cdots\circ f(x)}_{n \hbox{次合成函數}}=\, _nf(x)$ 且 $f(x)=\, _1f(x)$, $x=\, _0f(x)$。 為了探討 $y=_nf(x)$ 的規律, 我們先嘗試用 Excel 來計算並觀察他們的相關性, 下列是計算 $y=f(x)=(1.2^x+1.9^x)^{\frac 1x}$ 近似值的表格(四捨五入到小數點第四位)。 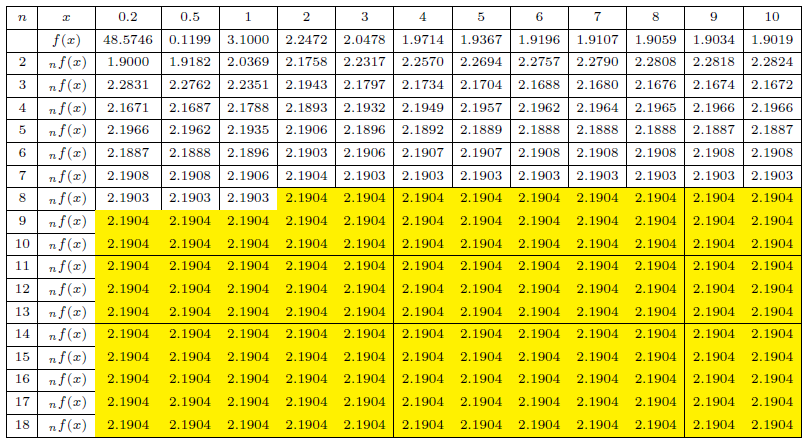 仔細觀察 $n=1,\ldots,7$ 發現, 似乎 $n$ 為奇數時, 函數嚴格遞減; $n$ 為偶數時, 函數則嚴格遞增。 且觀察表格中黃色區域, 函數值似乎會趨近於一定值。 這兩件事我們感到非常好奇, 於是我們展開下列討論。 性質 2-1: $\max\{a_1,\ldots,a_m\}=M$ 且 $x=\mu$ 為 $f(x)=x$ 的實根。 (1) 若 $n$ 為偶數, 則 $\langle 1\rangle$ $y=_n\!f(x)$ 為嚴格遞增函數。 (2) 若 $n$ 為奇數, 則 $\langle 1\rangle$ $y=_n\!f(x)$ 為嚴格遞減函數。 (3) $x=\mu$ 為 $\,_nf(x)=x$ 的實根。 (4) $M\lt _2\!f(M)\lt _4\!f(M)\lt \cdots\lt \mu\lt \cdots\lt _5\!f(M)\lt _3\!f(M)\lt f(M)$。 證明: (1) $\langle 1\rangle$ 由性質 1-6, $y=_2\!f(x)=f\big(f(x)\big)$ 為嚴格遞增函數, 依此類推, 可得 $y=_nf(x)$ 為嚴格遞增函數。 $\langle 2\rangle$ 由性質 1-3 可知 \begin{align*} \lim\limits_{x\to\infty} f(x)\!=\!M\Rightarrow \,&\lim\limits_{x\to\infty} \,_2f(x)=\lim\limits_{x\to\infty} f\big(f(x)\big)=f\big(\lim\limits_{x\to\infty} f(x)\big)=f(M)\\ &\hskip -37pt \Rightarrow\,\lim\limits_{x\to\infty} \,_3f(x)\!=\!\lim\limits_{x\to\infty} f\big(_2f(x)\big)\!=\!f\big(\lim\limits_{x\to\infty} \,_2f(x)\big) \!=\!f\big(f(M)\big)\!=\!\,_2f(M). \end{align*} 依此類推, 可得 $\lim\limits_{x\to\infty}\,_n f(x)=_{n-1} f(M)$。 \begin{align*} \lim\limits_{x\to 0} f(x)\!\to \infty\Rightarrow \,&\lim\limits_{x\to 0} \,_2f(x)=\lim\limits_{x\to0} f\big(f(x)\big)=\lim\limits_{z\to\infty} f(z)=M\\ \Rightarrow\,& \lim\limits_{x\to 0} \,_3f(x)\!=\!\lim\limits_{x\to 0} f\big(_2f(x)\big)\!=\!f\big(\lim\limits_{x\to 0} \,_2f(x)\big)\!=\!f(M). \end{align*} 依此類推, 可得 $\lim\limits_{x\to 0} \,_nf(x)\!=_{n-2} f(M)$。 $$\left\{\begin{array}{l} \,_2f(x_0)=f\big(f(x_0)\big)\gt M\\[4pt] f(x_0)\gt M\Rightarrow \,_2f(x_0)=f\big(f(x_0)\big)\lt f(M). \end{array}\right.$$ 由此可得 $M\lt _2\!f(x_0)\lt f(M)$。 \begin{align*} \hbox{由}\ &M\lt _2\!f(x_0)\lt f(M)\\ \Rightarrow\,& f(M)\gt f(\,_2f(x_0))\gt f\big(f(M)\big)\\ \Rightarrow\,& f(M)\gt _3f(x_0)\gt _2f(M)\\ \Rightarrow\,& f\big(f(M)\big)f\lt f(\,_3f(x_0))\lt f(\,_2f(M))\hskip 6cm~\\ \Rightarrow\,&\,_2f(M)\lt _4\!f(x_0)\lt _3\!f(M). \end{align*} 依此類推, 由此可得$_{n-2}\!f(M)\lt _nf(x_0)\lt _{n-1}\!f(M)$, $n\ge 4$。 $\langle 3\rangle$ \begin{align*} x_0\gt \mu\,\Rightarrow&\,f(x_0)\lt f(\mu)=\mu\,\Rightarrow\,_2f(x_0)\gt f(\mu)=\mu\\ \Rightarrow&\,_3f(x_0)\lt f(\mu)=\mu\,\Rightarrow\,_4f(x_0)\gt f(\mu)=\mu. \end{align*} 依此類推, 由此可得$_{n}f(x_0)\gt \mu$。 \begin{align*} x_0\lt \mu\,\Rightarrow&\,f(x_0)\gt f(\mu)=\mu\,\Rightarrow\,_2f(x_0)\lt f(\mu)=\mu\\ \Rightarrow&\,_3f(x_0)\gt f(\mu)=\mu\,\Rightarrow\,_4f(x_0)\lt f(\mu)=\mu. \end{align*} 依此類推, 由此可得$_{n}f(x_0)\lt \mu$。 (2) 由 (1) 可得。 (3) $f(\mu)=\mu\,\Rightarrow\,_2f(\mu)=f\big(f(\mu)\big)=f(\mu)=\mu\,\Rightarrow\,_3f(\mu)=f\big(_2f(\mu)\big)=f(\mu)=\mu$. 以此類推, $x=\mu$ 為 $\,_nf(x)=x$ 的實根。 (4) 由 (1) $\langle 2\rangle$ 及 (2) $\langle 2\rangle$ 可得。 性質 2-1 清楚說明 $y=\, _nf(x)$ 及其漸近線的圖形結構, 為更增加印象, 我們手繪一張示意圖如下 (手繪的原因是要特別凸顯函數跟漸近線之間的關係, 故不會符合真實比例): 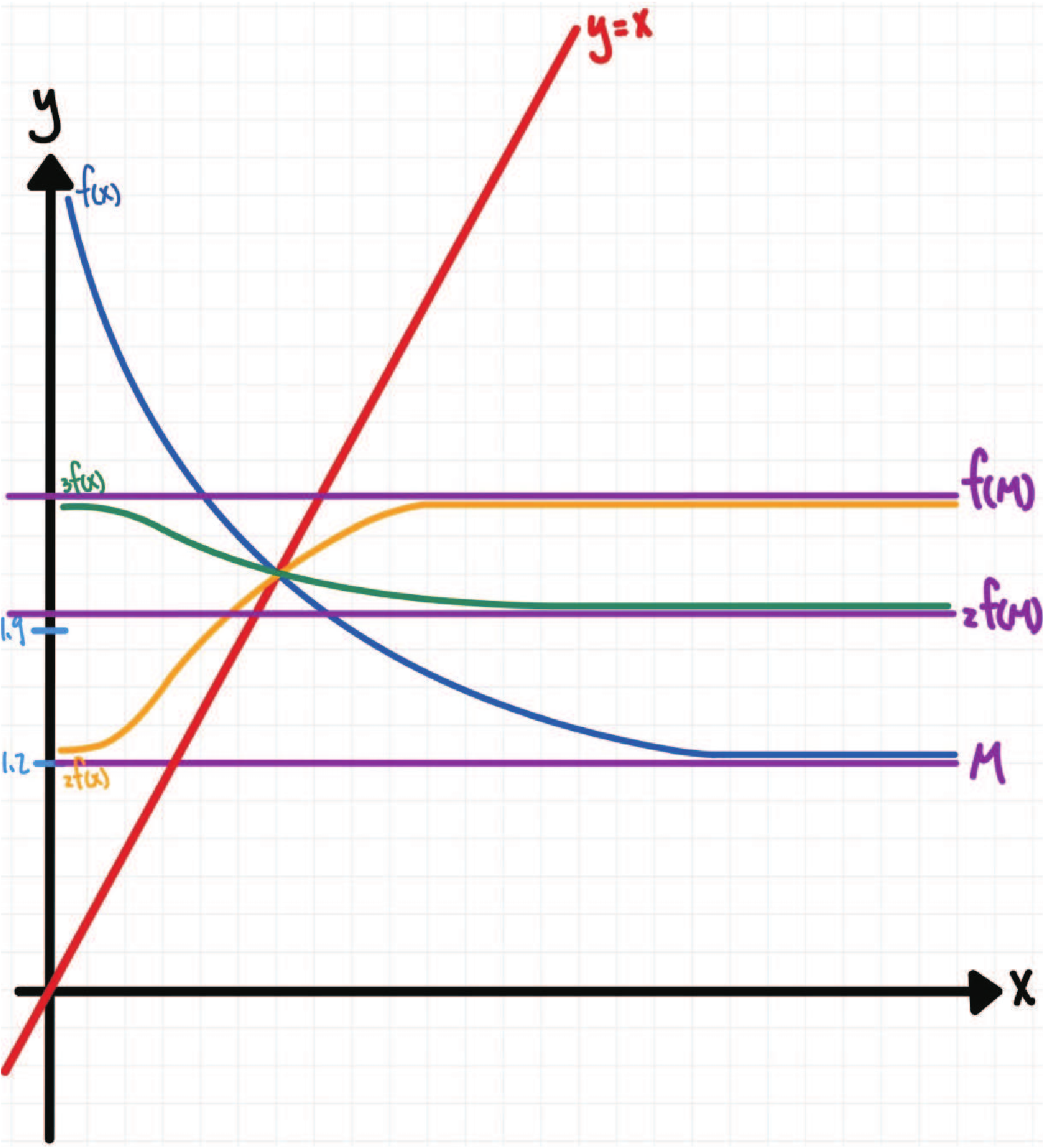 性質 2-2: $\max\{a_1,\ldots,a_n\}=M$, 則 $\lim\limits_{k\to\infty}\,_{2k} f(M)$ 及 $\lim\limits_{k\to\infty}\,_{2k+1} f(M)$ 收斂。 證明: $\{_{2k}f(M)\}$ 遞增有上界, 故 $\lim\limits_{k\to\infty}\,_{2k} f(M)$ 收斂。 $\{_{2k+1}f(M)\}$ 遞減有下界, 故 $\lim\limits_{k\to\infty}\,_{2k+1} f(M)$收斂。 定理 2-3: $\max\{a_1,\ldots,a_n\}=M$, 且 $x=\mu$ 為 $f(x)=x$ 的實根。 若 $\lim\limits_{n\to\infty}\,_{n} f(M)$ 收斂, 則 $\lim\limits_{n\to\infty}\,_{n} f(M)=\mu$ 且 $\lim\limits_{n\to\infty}\,_{n} f(x)=\mu$。 證明: 由性質 2-1 $\langle 4\rangle$ 及性質 2-2 可得。 $\Box$ 下列為 $y=f(x)=(0.1^x+0.2^x)^{\frac 1x}$ 的表格, 似乎 $\lim\limits_{k\to\infty}\,_{2k} f(M)\not=\lim\limits_{k\to\infty}\,_{2k+1} f(M)$, 即 $\lim\limits_{n\to\infty}\,_{n} f(M)$ 會發散, 故並非任意 $y=f(x)$ 均符合定理 2-3。 因此我們進一步想知道定理 2-3 的「$\lim\limits_{n\to\infty}\,_{n} f(M)$ 收斂」代表的意義是什麼。 我們從反面思考「若 $\lim\limits_{n\to\infty}\,_{n} f(M)$ 發散」有什麼意義。 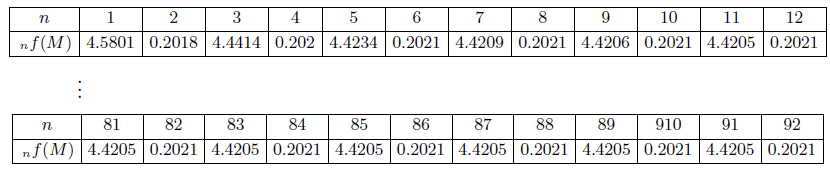 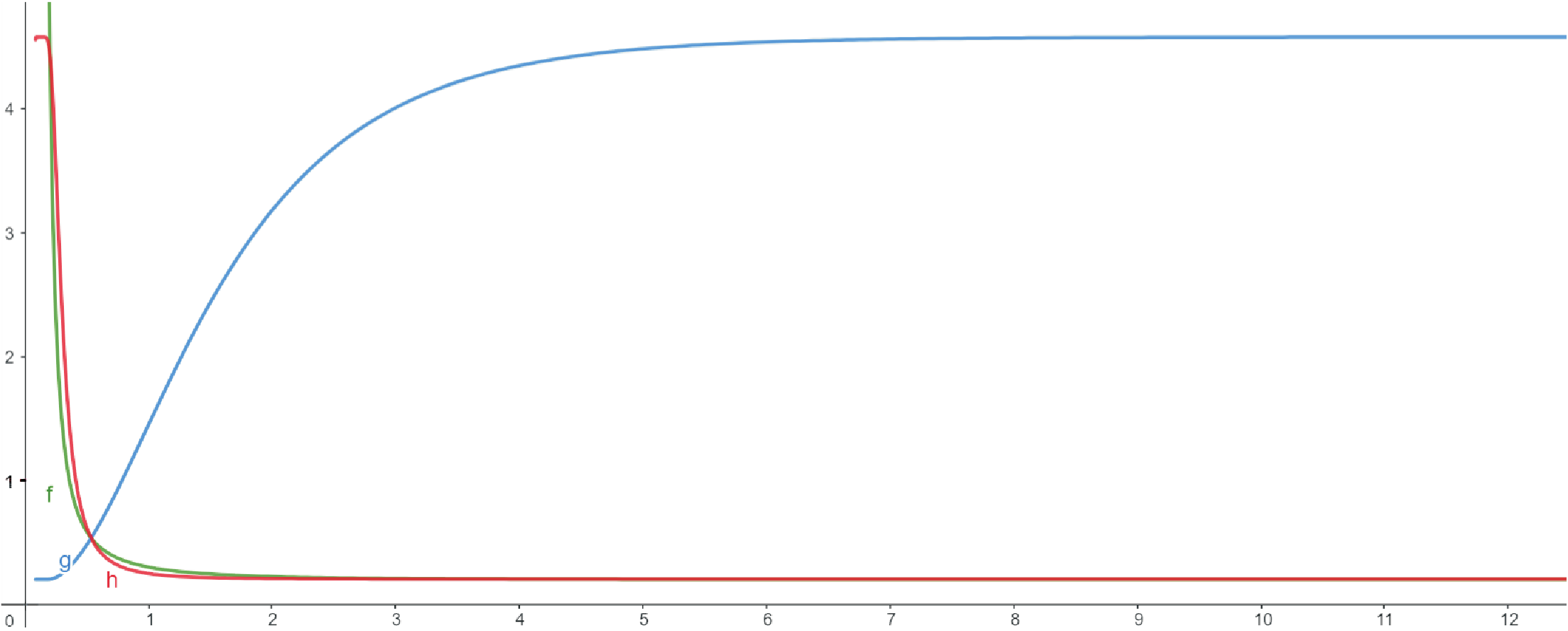 性質 2-4: 若 $\lim\limits_{n\to\infty}\,_{n} f(M)$ 發散 $\Leftrightarrow$ 存在 $\alpha\lt \mu\lt \beta$, 使得 $f(\alpha)=\beta$ 及 $f(\beta)=\alpha$。 證明: (1) ($\Rightarrow$) 令 $\lim\limits_{k\to\infty}\,_{2k} f(M)=\alpha$, $\lim\limits_{k\to\infty}\,_{2k+1}f(M)=\beta$, $\alpha\lt \beta$。 即當 $k$ 夠大時, $$\left\{\!\begin{array}{l} \,_{2k}f(M)\to \alpha\\[3pt] \,_{2k+1}f(M)\to \beta \end{array}\right. \!\Rightarrow\! \left\{\!\begin{array}{l} f\big(_{2k}f(M)\big)\to f(\alpha)\\[3pt] f\big(_{2k+1}f(M)\big)\to f(\beta) \end{array}\right. \!\Rightarrow\! \left\{\!\begin{array}{l} \,_{2k+1}f(M)\to f(\alpha)\\[3pt] \,_{2k+2}f(M)\to f(\beta) \end{array}\right. \!\Rightarrow\! \left\{\!\begin{array}{l} \beta=f(\alpha)\\[3pt] \alpha= f(\beta) \end{array}\right..$$ 由此可得, 若 $\lim\limits_{n\to\infty}\,_{n} f(M)$ 發散 $\Rightarrow$ 存在 $\alpha\lt \mu\lt \beta$, 使得 $f(\alpha)=\beta$ 及 $f(\beta)=\alpha$。 (2) ($\Leftarrow$) 若 $f(\beta)=\alpha$, 則 $f\big(f(\beta)\big)=f(\alpha)\, \Rightarrow\, _2f(\beta)=f(\alpha)=\beta$, $$\left\{\!\begin{array}{l} \,_{2k}f(\beta)=\beta\\[3pt] \,_{2k+1}f(\beta)\to \alpha \end{array}\right. \hbox{且由性質 2-1 可知} \ \left\{\!\begin{array}{l} \,_{2k}f(\beta)\lt _{2k-1}f(M)\\[3pt] \,_{2k+1}f(\beta)\gt _{2k}f(M) \end{array}\right. \!\!\Rightarrow\!\! \left\{\!\begin{array}{l} \beta\lt \lim\limits_{k\to\infty}\,_{2k-1}f(M)\\[3pt] \alpha\gt \lim\limits_{k\to\infty}\,_{2k}f(M) \end{array}\right..$$ $\therefore$ $\lim\limits_{k\to\infty}\,_{2k}f(M)\lt \alpha\lt \beta\lt \lim\limits_{k\to\infty}\,_{2k-1}f(M) \Rightarrow \lim\limits_{n\to\infty}\,_{n}f(M)$ 發散。 由此可得, 若存在 $\alpha\lt \mu\lt \beta$, 使得 $f(\alpha)=\beta$ 及 $f(\beta)=\alpha$, 則 $\lim\limits_{n\to\infty}\,_{n}f(M)$ 發散。 定理 2-5: $x=\mu$ 為 $f(x)=x$ 的實根, $y=f(x)$ 滿足下列任一條件則 $\lim\limits_{n\to\infty}\,_{n}f(x)=\mu$。 (1) 不存在 $\alpha\lt \mu\lt \beta$, 使得 $f(\alpha)=\beta$ 及 $f(\beta)=\alpha$。 證明: (1) 由性質 2-4 可得。 因此, 若$\,_2f(x)=x$ 除了 $x=\mu$ 之外無其他實根, 則 $\lim\limits_{n\to\infty}\,_{n}f(x)=\mu$。 $\Box$ 研究完定理 2-5 後, 我們懷疑任意 $\omega\in{\Bbb R}^+$, 是否存在一個 $y=f(x)$, 使得 $\lim\limits_{n\to\infty}\,_{n}f(x)=\omega$, 且 $y=f(x)$ 是否唯一。 更進一步討論, 任意正實數 $\omega$ 只要是某一個方程式 $f(x)=x$ 的實根且$\,_2f(x)=x$ 僅有一實根, 則 $\lim\limits_{n\to\infty}\,_{n}f(x)=\omega$, 接下來我們要試著找出這個 $y=f(x)$。 我們考慮 $\omega$ 是否為 $(a_1^x+a_2^x)^{\frac 1x}=x$ 的實根, 即為 $a_1^x+a_2^x=x^x$ 的實根, 且 $\omega\gt \max\{a_1,a_2\}$。 \begin{align*} &\hbox{令 $a_1\lt \omega$, 則 $a_1^\omega+a_2^\omega=\omega^\omega\Rightarrow a_2=(\omega^\omega-a_1^\omega)^{\frac 1\omega}$},\\ &\hskip .9cm\therefore\ f(x)=\Big[a_1^x+\Big((\omega^\omega-a_1^\omega)^{\frac {1}{\omega}}\Big)^x\Big]^{\frac 1 x} \end{align*} 對任意 $a_1\lt \omega$, 則可得 $f(x)=\Big[a_1^x+\Big((\omega^\omega-a_1^\omega)^{\frac {1}{\omega}}\Big)^x\Big]^{\frac 1 x}$, 但 $\lim\limits_{n\to\infty}\,_{n}f(x)$ 不一定能收斂, 也就是雖然我們找到了函數, 還需更進一步確認收斂的正確性。 性質 2-6: (1) 任意兩正實數 $\lambda\lt \omega$, 若 $f(x)_\lambda=\Big[\lambda^x+\Big((\omega^\omega-\lambda^\omega)^{\frac {1}{\omega}}\Big)^x\Big]^{\frac 1 x}$, 則 $f(\omega)=\omega$。 證明: (1) $f(\omega)=\Big[\lambda^x+\Big((\omega^\omega-\lambda^\omega)^{\frac {1}{\omega}}\Big)^\omega\Big]^{\frac 1 \omega}=[\lambda^\omega+\omega^\omega-\lambda^\omega]^{\frac 1\omega}= \omega$, 且 $x=\omega$ 為$\,_2f(x)=x$ 的實根。 (2) 由定理 2-5 可得。 $\Box$ 以 $\lambda=1.3$, $\omega=2.1$ 為例, $f(x)_{1.3}=\Big[1.3^x+\Big((2.1^{2.1}-1.3^{2.1})^{\frac {1}{2.1}}\Big)^x\Big]^{\frac 1 x}$ 圖形如下:   可從 Excel 表格看出 $\lim\limits_{n\to\infty}\,_{n}f(x)_{1.3}=2.1$。 第三章目前為止我們知道此類函數只要滿足定理 2-5, $\{_nf(x)\}$ 就會收斂, 我們懷疑除了此類函數, 其他函數是否也有這樣的收斂特性。 以 $y=f(x)=1+\frac 1{x+1}$ 為例, 下列是計算近似值的表格(四捨五入到小數點第四位)及圖形。 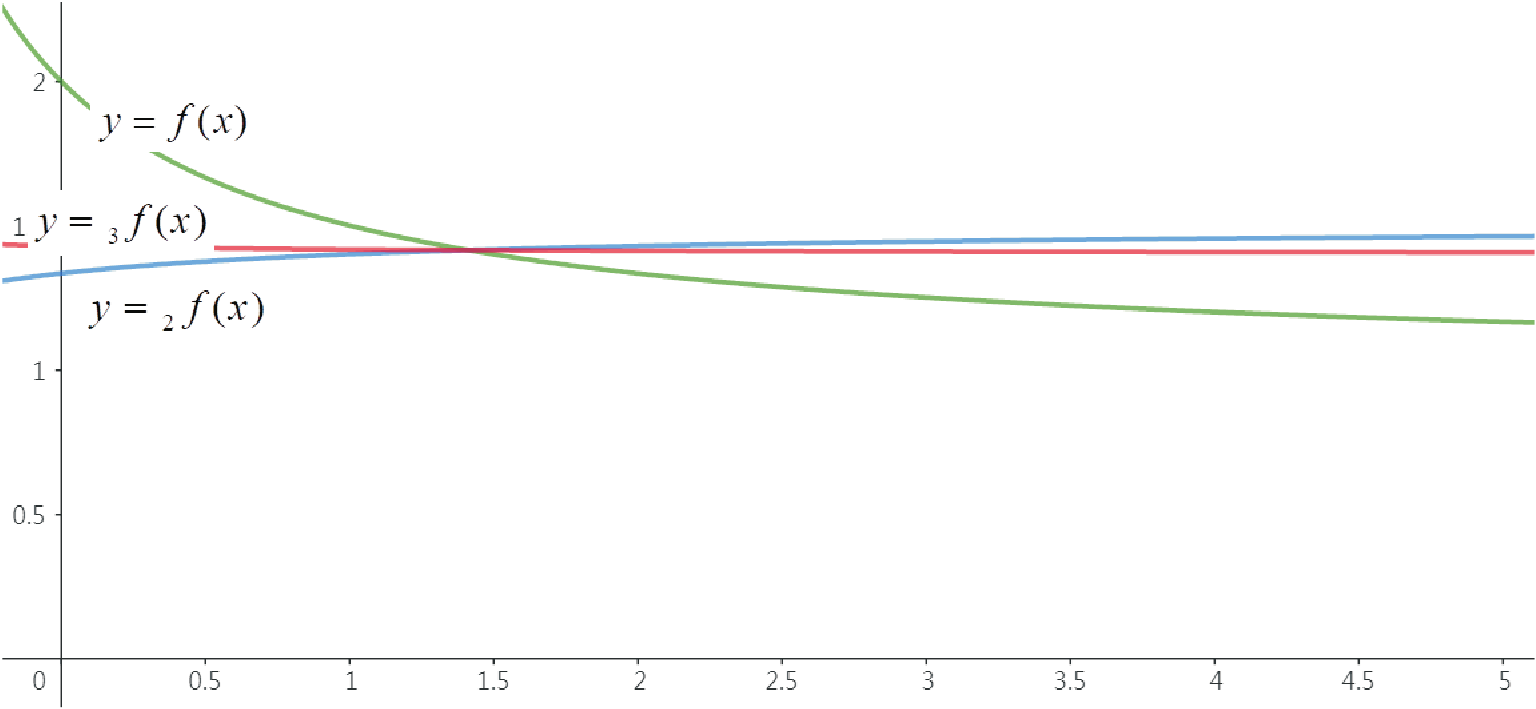 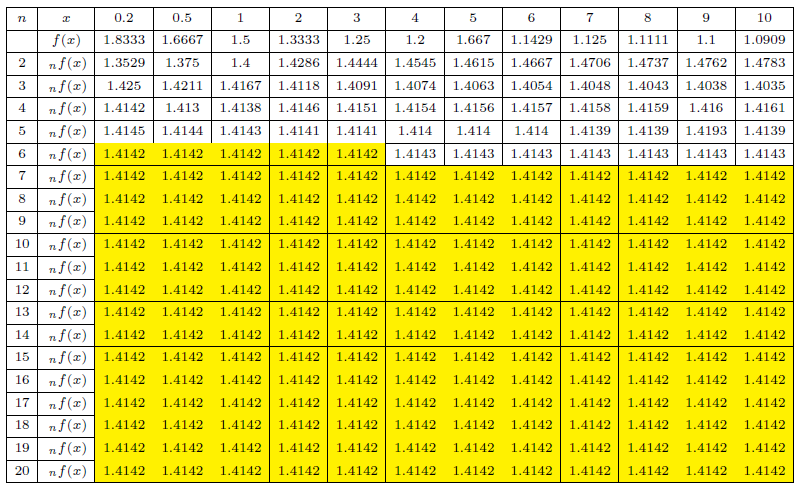 經由上述表格及圖形我們發現此函數和上述函數一樣也能收斂, 於是我們展開了下列的討論。 下列的 $y=f(x)$ 不一定為上述函數, 但 $y=f(x)\gt 0$, $x\in{\Bbb R}^+$。 性質 3-1: (1) 若 $y=f(x)$ 為嚴格遞減連續函數, $y=h(x)$ 為嚴格單調連續函數, 則 $y=f\circ h(x)$ 的單調性跟 $y=h(x)$ 相反。 證明: (1) 令 $y=h(x)$ 為嚴格遞增連續函數。 $$\hbox{若 $x_1\lt x_2$, 則 }\ h(x_1)\lt h(x_2)\Rightarrow f\big(h(x_1)\big)\gt f\big(h(x_2)\big)\Rightarrow f\circ h(x_1)\gt f\circ h(x_2)\hbox{。}$$ 令 $y=h(x)$ 為嚴格遞減連續函數。 $$\hbox{若 $x_1\lt x_2$, 則 }\ h(x_1)\gt h(x_2)\Rightarrow f\big(h(x_1)\big)\lt f\big(h(x_2)\big)\Rightarrow f\circ h(x_1)\lt f\circ h(x_2)\hbox{。}$$ 由此可知, $y=f\circ h(x)$ 的單調性與 $y=h(x)$ 相反。 (2) 令 $y=h(x)$ 為嚴格遞增連續函數。 $$\hbox{若 $x_1\lt x_2$, 則 }\ h(x_1)\lt h(x_2)\Rightarrow f\big(h(x_1)\big)\lt f\big(h(x_2)\big)\Rightarrow f\circ h(x_1)\lt f\circ h(x_2)\hbox{。}$$ 令 $y=h(x)$ 為嚴格遞減連續函數。 $$\hbox{若 $x_1\lt x_2$, 則 }\ h(x_1)\gt h(x_2)\Rightarrow f\big(h(x_1)\big)\gt f\big(h(x_2)\big)\Rightarrow f\circ h(x_1)\gt f\circ h(x_2)\hbox{。}$$ 由此可知, $y=f\circ h(x)$ 的單調性與 $y=h(x)$ 一致。 $\Box$ 性質 3-2: $y=f(x)$ 為嚴格遞減連續函數, 若 $\left\{\!\begin{array}{l} \lim\limits_{x\to\infty}f(x)=M\gt 0\\[3pt] \hbox{或} \lim\limits_{x\to\infty}f(x)=M\ \hbox{且}\ \lim\limits_{x\to0}f(x)\lt \infty \end{array}\right.,$ $x=\mu$ 為 $f(x)=x$ 的實根。 (1) 若 $n$ 為偶數, 則 $\langle 1\rangle$ $y=_n\!f(x)$ 為嚴格遞增函數。 (2) 若 $n$ 為奇數, 則 $\langle 1\rangle$ $y=_n\!f(x)$ 為嚴格遞減函數。 (3) $x=\mu$ 為$_nf(x)=x$ 的實根。 (4) $M\lt _2\!f(M)\lt _4\!f(M)\lt \cdots\lt \mu\lt \cdots\lt _5\!f(M)\lt _3\!f(M)\lt f(M)$。 證明: 由性質 2-1可得。 $\Box$ 定理 3-3: 設 $x=\mu$ 為 $f(x)=x$ 的正實根, 若$_2f(x)=x$ 除了 $x=\mu$ 之外無其他實根, 則 $\lim\limits_{n\to\infty} \,_nf(x)=\mu$。 證明: 由定理 2-5 可得。 $\Box$ 研究結果1. $y=f(x)$ 為嚴格遞減函數。 2. $y=f(x)$ 的水平漸近線為 $y=M$, 且 $M=\lim\limits_{x\to\infty} f(x)$, 其中 $\max\{a_1,\ldots,a_n\}=M$。 3. $y=f(x)$ 為凸函數。 4. (1) 若 $y=h(x)\gt 0$, $x\in {\Bbb R}^+$ 在 $(a,b)$ 為連續嚴格遞增函數, 則 $y\!=\!f\circ h(x)\!=\!\bigg(\sum\limits_{i=1}^n a_i^{h(x)}\bigg)^{\frac{1}{h(x)}}$, $x\!\in\! {\Bbb R}^+$, $a_1,\ldots,a_n\!\in\! {\Bbb R}^+$, 在 $(a,b)$ 為嚴格遞減函數。 (2) 若 $y\!=\!h(x)\!\gt \!0$, $x\!\in\! {\Bbb R}^+$ 在 $(a,b)$ 為連續嚴格遞減函數, 則 $y\!=\!f\circ h(x)\!=\!\bigg(\sum\limits_{i=1}^n a_i^{h(x)}\bigg)^{\frac{1}{h(x)}}$, $x\!\in\! {\Bbb R}^+$, $a_1,\ldots,a_n\!\in\! {\Bbb R}^+$, 在 $(a,b)$ 為嚴格遞增函數。 5. $x=\mu$ 為 $f(x)\!=\!x$ 的實根, 若$\,_2f(x)\!=\!x$ 除了 $x\!=\!\mu$ 之外無其他實根, 則 $\lim\limits_{n\to\infty} \,_nf(x)\!=\!\mu$。 6. 任意兩正實數 $\lambda\lt \omega$, 若 $f(x)_\lambda=\bigg[\lambda^x +\bigg(\big(\omega^\omega-\lambda^\omega\big)^{\frac{1}{\omega}}\bigg)^x\bigg]^{\frac{1}{x}}$, 若$\,_2f(x)_\lambda=x$ 僅有一實根 $\omega$, 則 $\lim\limits_{n\to\infty} \,_nf(x)_\lambda=\omega$。 7. $y=f(x)$ 為嚴格遞減連續函數, $x=\mu$ 為 $f(x)=x$ 的實根, 若$\,_2f(x)=x$ 除了 $x=\mu$ 之外無其他實根, 則 $\lim\limits_{n\to\infty} \,_nf(x)=\mu$。 結論在這次的研究中, 我們透過不同層面的數學知識, 利用各項相關不等式證明出函數的性質, 雖然在研究過程中, 我們遇到許多問題, 像是溝通上的困難、 時間緊迫、 抑或是對全新領域的陌生, 但也因為如此學習到了很多, 增進了做書面報告的能力, 也在其中學習到許多高中課程裡沒有的數學知識, 這一切全都需要團隊的努力和互相磨合, 尤其在途中會出現意見或看法的不同, 但經過每次的討論, 我們的觀念也逐漸統一, 這是在許多合作中體會不到的。 本文作者張庭毓、 盧彥綾、 林珈伃投稿時為彰化女中三年級學生, 指導老師盧俊豪老師 |
| 頁碼 | 80-95 |
2025年3月 49卷1期
一個由指數函數加總的函數之探討

