| 發刊日期 |
2025年3月
|
|---|---|
| 標題 | 3x+1猜想與x±1定理 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
摘要: 本文介紹了 $3x+1$ 問題的研究概況。 給出了 $nx\pm k$ ($n, k=1,2, ...$) 新方法: 把任意自然數 $x$ 經過計算得到"1"的快速方法, 定義了"對偶解"及"全對偶解"。 比傳統的 $3x+1$ 法簡單、 快捷。 $3x+1$ 問題簡介「曾有一個風靡世界的數字遊戲問題, 從小學生到大學生, 從平民到官員, 從歐洲到亞非拉, 人人都會做這個遊戲, 但要弄清它的道理卻非易事。 這個問題已變成世界難題」 $3x+1$ 問題是 20 世紀提出來的猜想, 被列入數論四大猜想之一。 這個問題有很多名字: 在 20 世紀 30 年代, 德國漢堡大學學生考拉茲 (Collatz) 就研究這個問題, 因此被稱為"考拉茲猜想"。 又, 這個問題是在美國的雪城大學被研究的, 所以在西方被稱為雪城 (Syracuse)猜想。 也有人稱為"角谷猜想", "烏拉姆問題", "冰雹猜想"等等。  《科學美國人》雜誌"數學遊戲"專欄編輯馬丁$\cdot$加德納 (Martin Gardner (1914年10月21日$\sim$2010年5月22日)), 撰寫了浩如煙海的數學科普文章, 據不完全統計已寫了五十本以上的科普讀物, 並多次獲獎, 在國際學術界影響之大無人能及。 他在《科學美國人》雜誌介紹了這個猜想, 加速了這個猜想的傳播, 讓這個猜想風靡全球!美國一位數學家說道: 「曾經有一個時期, 在美國大學裡, 這個猜想成了最熱門的話題, 數學系和電腦系的大學生, 差不多人人都在研究。」 據傳, 當時幾乎有文化又感興趣的男女老幼, 紛紛被捲入"猜想"的旋渦之中, 對於這個猜想的討論熱烈到頂峰, 人人期盼攻克, 一夜成名。 結果令美國中央情報局產生疑惑, 誤認為是蘇聯國家安全委員會 (KGB, 情報機關) 所使用的"特務"詭計, 企圖使美國人把寶貴時間陷入這個數字遊戲之中, 不務正業。 直到蘇聯解體, 才消除了美國人的疑慮。 目前, 已經發表了很多關於 $3x+1$ 問題的文章, 對這個問題進行了多方面的探討, 可是這個問題的本身始終沒有被解決, 至今還是不知道, "到底是不是總會得到1"? 基本定義任取一個自然數 $x$, 如果它是奇數, 就把它乘以 3 再加上 1; 如果是偶數, 就把它除以 2, 經過這樣的變換, 就得到一個新數。 如果反復使用這種變換進行計算, 就會得到一串數, 直到得到 1 為止。 因此猜想, 經過有限次計算, 最後得到的結果為 1。 直到現在也沒有被證明, 所以仍為猜想。 為便於介紹, 我們約定: 定義1(初始數) : 從第一個數"$x$"開始, 進行計算, 第一個數就叫"初始數"。 定義2: 從初始數開始進行計算, 每進行一次變換, 稱為"1步"。 直到 $x=1$, 所進行的變換次數, 稱為"步數", 簡稱"步"。 定義3 (對偶解): 利用演算法 $3x+1$ 與 $3x-1$, 合併為 $3x\pm 1$ 模式。 如果都能得到從初始數開始變換到 $x=1$。 稱這兩組解互為"對偶解"。 如果只能得到 1 組解 ($3x+1$ 或者 $3x-1$), 而另一組出現"循環數", 則稱為"非對偶解"。 定義4 (全對偶解): 若 $nx\pm k$ ($n, k=1,2, ...$) 經過變換, 無論是 $nx+k$ 或是 $nx-k$ 都能得到 $x=1$, 稱為"全對偶解"。 定義5 (循環數): 在計算 $3x\pm 1$ 的一串數字中, 如果出現了相同的數字, 就叫"循環數"。 對於 $3x+1$ 問題的探討道德經曰: 「天下難事, 必作於易;天下大事, 必作於細」。 對於 $3x+1$ 問題, 既是難事, 又是大事。 在《數學猜想與發現》 (科學出版社) 一書中, 把 $3x+1$ 問題列入第一項, 著名的哥德巴赫猜想被列入第二項, 其重要性非同一般。 所以我們不妨對其認真、細緻的探討一番, 尋找 $3x+1$ 的奧秘到底隱藏在哪裡? 眾所周知, 把一個奇數"$x$"變成偶數有兩種方法: $x+1=$偶數, $x-1=$偶數。 以本文為例, 當 $x$ 為奇數時, 經過 $3x+1$ 計算, 就得到一個偶數。 對 $3x-1$ 計算也應該得到一個偶數。 那麼問題來了: 問題1: 為什麼在文獻中只出現 $3x+1$ 模式, 而不見 $3x-1$ 模式呢? 下面我們對幾個較小的奇數進行"$3x\pm 1$"模式的計算, 檢驗得到什麼結果? 當初始數 $x=3$ 時, 表格中的數字表示每計算一步的變化情況, 例如 $3x+1=10$, $10/2=5$, $5\times 3+1=16$, $16/2=8$, $8/2=4$, $4/2=2$, $2/2=1$。 為方便計, 把 3, 10, 5, 16, 8, 4, 2, 1 直接填入下邊表格中: 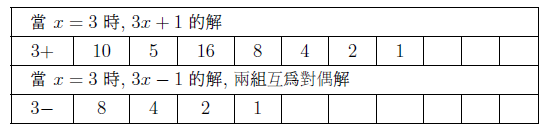 初始數後面的"$+$,$-$"符號, 表示對初始數及後面的奇數進行 $3x+1$ 或者 $3x-1$ 計算。 下同。 當 $x=5$、 7、 15 的例: 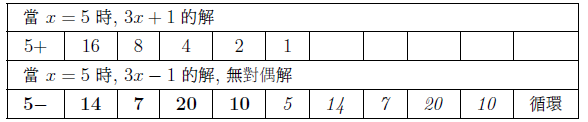   我們發現: 1. 當對奇數實施 $3x+1$ 模式計算時得到的結果, 最後 4 個數都是 8, 4, 2, 1。 是 8/2/2/2 得到的結果, 好像直達列車一樣, 一氣呵成! 2. 當初始數為 5 與 7 時, 對 5 與 7 實施 $3x-1$ 模式的計算時, 最後邊 5 個數與前面相鄰 5 個數相同。 當初始數等於 5 時, 粗體字 5, 14, 7, 20, 10 與斜體字 5, 14, 7, 20, 10。 就是循環數。 當初始數等於 7 時的粗體字 7, 20, 10, 5, 14 與斜體字 7, 20, 10, 5, 14 也是循環數。 3. 當初始數 $x=3$ 及初始數 $x=15$ 時, 無論用 $3x+1$ 模式計算或者用 $3x-1$ 模式計算得到的結果都等於 8, 4, 2, 1。 沒有循環數, 我們稱這兩組解為"對偶解"。 4. 我們還發現 18 個數的循環數, 下面是初始數為 17 時, 按照 $3x-1$ 模式運算, 得到的結果: 前面的 18 個粗體字 (17, 50, 25, ..., 136, 68, 34) 與後面的 18 個斜體字 (17, 50, 25, ..., 136, 68, 34.) 為 18 個數的循環數。 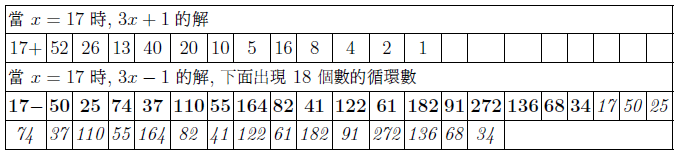 當初始數 $x=33$ 時, 用 $3x-1$ 模式計算, 得到 18 個循環數的例子 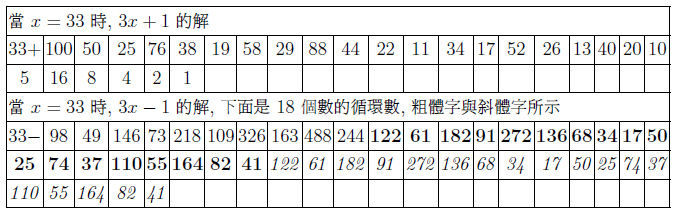 由上例發現, 當對奇數進行 $3x-1$ 模式計算時, 得到的結果不一定全部都有對偶解, 所以對 $3x-1$ 的計算被棄之不用, 其中的道理不言而喻。 探討 $3x+1$ 模式得到 1 的解與 $3x-1$ 模式出現循環數的例。下圖藍線與粗體字連接的數字, 表示用$3x+1$模式計算得到的從初始數到1的結果路線圖。 綠線與紅線所連接的表示用 $3x-1$ 模式計算得到的從初始數及兩段循環數。 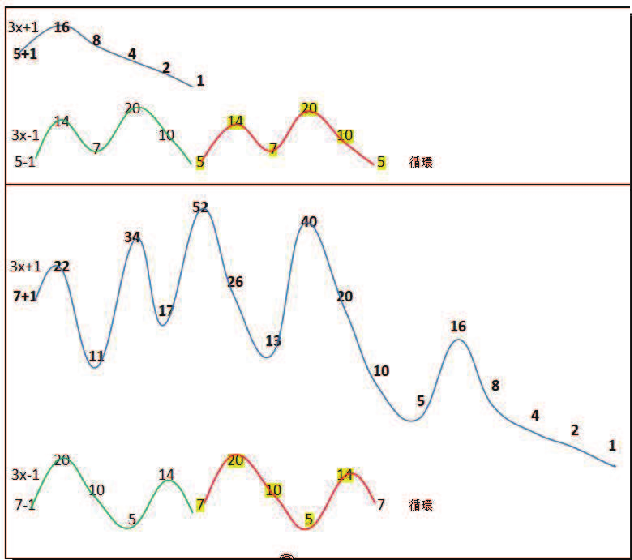 由以上 $3x-1$ 模式所示, 發現有循環數, 所以不能滿足 $3x\pm 1$ 模式的"全對偶解"。 那麼問題又來了: 問題2: 是否存在 $nx\pm k$ 模式滿足"全對偶解"的數組呢? 事實是最有力的證明: 方法一, 對於奇數實施$x\pm 1$計算, 對於偶數仍然除以2, 可以得到等於1的結果。下面是 $x=3,5,7$ 的例: 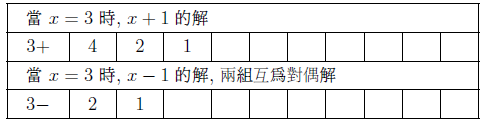 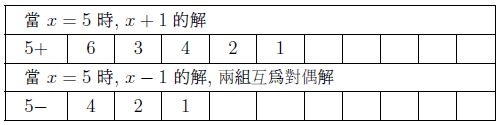 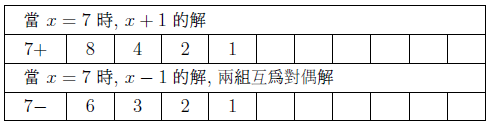 這裡我們給出初始數為 53, 55, 57, 59, 61, 63 的例子: 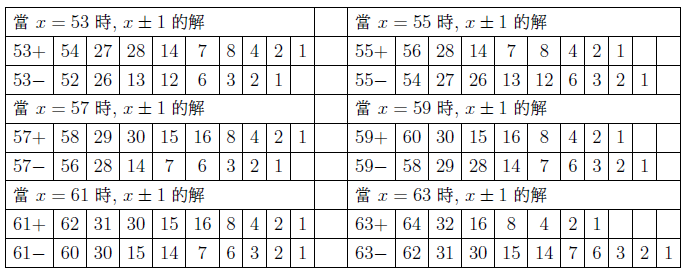 我們發現當對於奇數用 $x\pm 1$ 計算時, 都能得到對偶解。 並且每個解的最後 4 個數分別是 3,4,2,1; 5,4,2,1; 6,3,2,1; 8,4,2,1. 綜上, 我們有 定理1: 對於奇數實施 $x\pm 1$ 計算, 對於偶數實施 $x/2$ 計算, 按照這個演算法繼續進行計算, 得到的數列沒有重複循環元素。 最後可以得到 $2/2=1$。 證明: 用3個引理來證明: 引理1: 先證明按照"$x+1$ 模式"計算的數列 $x_1$, $x_2$, $x_3, ..., 2,1$, 中, 無循環數。 設: $x_1$ (奇數), $x_2$, $x_3$, $x_4, ..., 2,1$ 為"$x+1$ 模式"的元素數列 (表1), 由構作方法知, $x_1$ 為奇數時, 按照"$x+1$ 模式"計算, $x_2$ 應為 $x_1+1$。 接著 $x_3$ 應該是 $(x_1+1) /2$, 這時 $x_3$ 比 $x_2$ 小。 相鄰兩數 $x_1$ 與 $x_2$ (由奇數變偶數) 的差距為 1, 由偶數變奇數 (或偶數) 時, $x_2$ 是 $x_3$ 的 2 倍, 它們相鄰兩個數的差是: 差 1, 是後邊數的 2 倍; 差 1, 是後邊數的 2 倍; 是後邊數的 2 倍, ..., 永遠不會相等, 所以不會出現重複循環數。 引理 1 證畢。 引理2: 對於"$x-1$ 模式"計算的數列, $x_1, x_2, x_3, ..., 2,1$, 中, 無循環元素。 由構作方法知, $x_2=x_1-1$ (可知 $x_1 \gt x_2$)。 接著 $x_3=x_2/2$ (可知 $x_2 \gt x_3$)。 若 $x_3$ 為奇數則 $x_4 =x_3 -1$; 若 $x_3$ 為偶數則 $x_4=x_3/2 $, 無論 $x_3$ 為奇、 為偶, 必有 $x_3 \gt x_4$。 若 $x_4$ 為奇數則 $x_5=x_4-1$; 若 $x_4$ 為偶數則 $x_5=x_4/2$, 無論 $x_4$ 為奇、 為偶, 必有 $x_4 \gt x_5$。 所以都不會出現相等元素的現象。 當"$x-1$ 模式"時, 從 $x_1, x_2, ...,$ 至 4, 2, 1, 都是用大於符號 $x_1 \gt x_2 \gt x_3 \gt x_4 \gt x_5 \gt ... \gt 4 \gt 2 \gt 1$ 連接起來的, 所以沒有相等的循環數。 引理2證畢。 由引理 1 與引理 2, 證明對奇數實施 $x\pm 1$, 得到的數列無循環數。 引理3: 當 $x/2\!=$奇數時, 我們可以用 $x\!\pm\! 1$ 的方法使其變為 $x\!=\!2^m$ ($m = 2,3, ...$) 的偶數。 當 $x=2^m$ ($m = 2,3, ...$) 時, 最後的結果只能 $x/2/2, ..., 2/2=1$。 當 $x=6$ 時, $6/2=3$, 用 $x-1$ 模式, $3-1=2$, 再 $2/2=1$。 引理 3 證畢。 由引理1、2、3, 定理1證畢。 初始數為 69 與 97 的兩個例子: 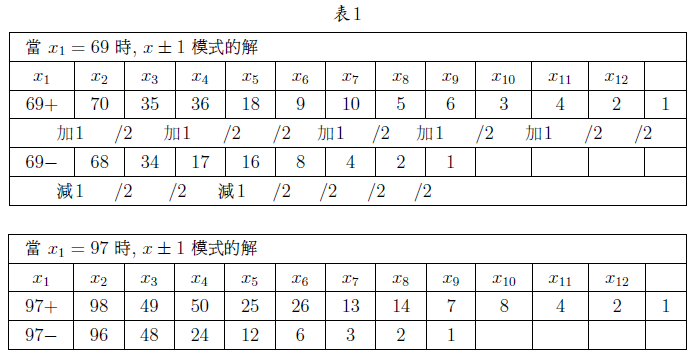 圖解定理1: $x\pm 1$ 模式元素變化示意圖 下圖顯示了初始數分別為 69, 19, 97 用 $x\pm 1$ 模式計算的示意圖, 既不循環重複, 又不互相交叉, 各自走完從初始數到 1 的路程。 藍色線 $(x+1)$、 綠色線 $(x-1)$ 清晰明瞭, 毫不混淆。 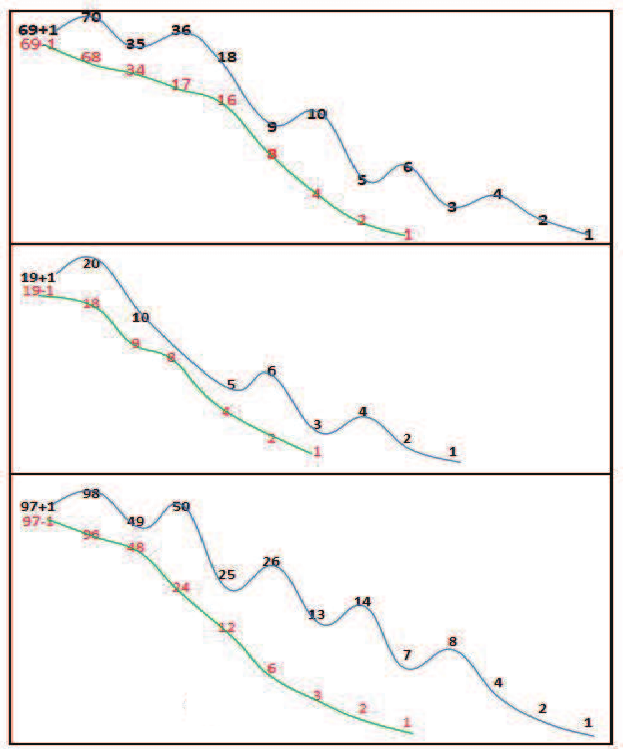 藍線連接的黑色粗體字, 表示 $x+1$ 模式的元素走向。 綠色線連接的紅色字, 表示 $x-1$ 模式的元素走向。 不存在重複元素。 此路不通另闢蹊徑: 一個謎語指點迷津整天除了吃飯、睡覺、就是想難題。 整天胡思亂想, 想得不著邊際, 想起了"男"字, 凡是男人就應該到田地裡去出力, 天經地義呀, 不得違抗。 再仔細想一想也不完全對, 還有"思"字呢?在田地裡也要用"心"呢, 還要有思想。想得兩眼發直, 想得目瞪口呆, 想出一個"方"法 ('方'為萬點選一), 想到"精當"處, 自己對自己嘿嘿一聲傻笑, 沒人理會。 只有搞幻方、 搞文字、 搞研究的"癡友"們才能體會其間的"樂趣"! 一天晚上, 孫子的同學小磊來找他玩耍, 平常我給他們出謎語讓他們猜, 這一次小磊跟別人學到一個謎語, 想難倒爺爺, 小磊主動出擊說: "爺爺我給你出個謎語。 一半大, 一半小。 猜一個字。" 我指著他的鼻子說: "是這個!"小磊說:"不對, 不對, 你猜錯啦!"小磊洋洋得意。 我說:"一二三, 鼻、 子、 尖, 就是這個尖"。 之後, 我想起 $3x+1$, 能不能把3變大或者變小呢? 天下萬物有大就有小, 世界上很難找到兩個一樣大的樹葉。 我在想, 如果把3變小, 只有2與1, 當 $x=2$ 時, $2x+1=$ 奇數, 顯然不符合題意。 那麼 $1x+1$ 呢? 即 $x+1$, 經過試驗竟然成功啦! 哈哈! 又做了很多例題, 無一不成功 --- 笨貓逮住個瘸老鼠。 於是突發奇想, 何不用 $x-1$ 試試呢? 乘勝追擊, 一鼓作氣檢驗了幾十組也都成功! 哈哈哈! 小孩子的謎語竟然與數學難題搭配上了, 真是天作之合呀! 想當年搞幻方時, 也是孩子們背誦的乘法口訣, 一二得二, 使我茅塞頓開, 找到解決雙重幻方的關鍵環節, 構造出新的雙重幻方。 看來我的老師是"童生"啊! 本文使用的 $x+1$ 法就是從構造幻方得到啟發的, 這一次, 小學生的謎語, 使我陡然醒悟。 一把鑰匙能開幾把鎖?解決了 $x\pm 1$ 的問題之後, 是否存在其他模式滿足全部對偶解的條件呢? 我們對下列問題 $$2x\pm 2,\ 4x\pm 4,\ 8x\pm 8,\ 16x\pm 16,\ 32x\pm 32,\ 64x\pm 64$$ 進行了探討, 都得到正確的結果, 最後一個數為"1"。 下面給出 $2x\pm 2$ 的 2 個例子: 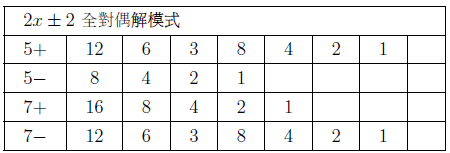 再給出 $4x\pm 4$ 的 2 個例子 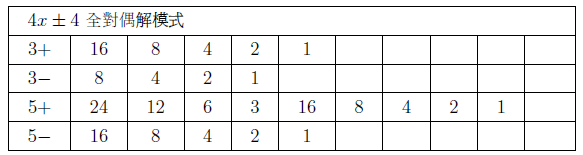 我們對$8x\pm 8$、$16x\pm 16$、$32x\pm 32$、$64x\pm 64$ 做了部分驗算 (從略), 都得到了正確的結果"1"。 因此, 我們有 猜想1: 存在 $2^m\pm 2^m$ ($m=1,2,3, ...$) 模式, 能得到正確的結果"1"。 我們又對初始數為偶數時做了研究發現 猜想2: 初始數為偶數時, 經過運算也可以得到"1"。 分兩種情況討論: 情況1: 當初始數為 $2^m$ 的偶數時, 可以直接除以 2, 一氣呵成而得到"1"。 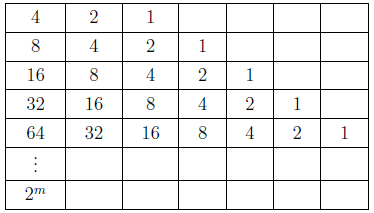 情況2: 當初始數為 $4k$ ($k=3,5,7, ..., 2n+1$) 時, 都能得到"1"。 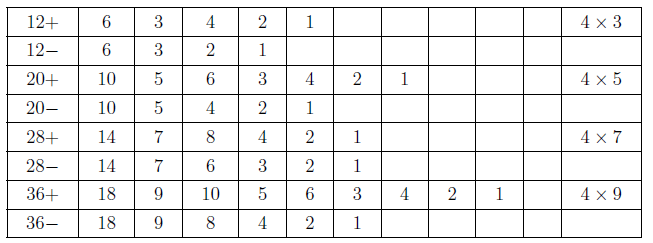 反其道而行之, 尋找全循環數假如我們討論的問題是: 對一個奇數實施 $nx\pm k$, 對於偶數仍然用除以2的規則, 使得它們得到的結果都有循環數。 是否有解呢? 這樣, 我們就把前面的問題顛倒過來了, 反其道而行之: 猜想3: 是否存在 $x\pm k$ 模式的全循環數呢? 全循環就是無論 $x+k$ 還是 $x-k$, 經過計算, 都只能得到循環數。 我們發現在 $12x\pm 12$ 及 $20x\pm 20$ 的全循環數的解如下: 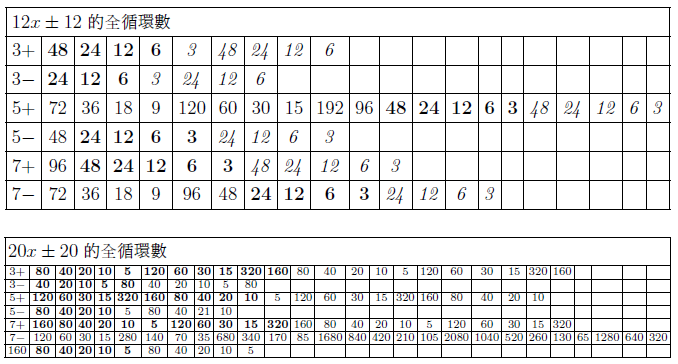 結語:$3x+1$ 是一個有趣的大難題, 筆者不揣淺陋異想天開, 給出一個對於奇數實施 $x\pm 1$ 的算法, 對於偶數仍然用 $x/2$ 的算法, 得到了一些結果。 請行家裡手不吝賜教。 嚶其鳴矣, 求其友聲。 鳴謝!感謝審稿老師的辛苦勞作, 提出很多中肯的建議和需要修改之處。 感謝編輯部主編及編輯老師, 一如既往重視鄙人的稿件, 本人共發表 13 篇小文, 其中有些問題幫助解決, 例如"反幻方定理"一文中, 主編親自添加了一個"推論", 有些錯誤之處, 也及時修改。 特致以誠摯的感謝! 參考文獻本文作者梁培基任職於中國君子故里梁培基數學工作室, 梁欽任職於中國北京在前線傳媒工作室 |
| 頁碼 | 96-106 |
2025年3月 49卷1期
3x+1猜想與x±1定理

