引潮力三講

楊維哲

2025年6月 49卷2期

引潮力三講

發刊日期	2025年6月
標題	引潮力三講
作者	楊維哲
關鍵字	天體力學, 天文曆法, 沈括
檔案下載	Download PDF
全文	獻詞與前言這個演講是因為閱讀了摯友莫宗堅伉儷的一篇有趣的文章 ¹ ¹ '潮汐現象與沈括定律', 數學傳播 48 卷 4 期 (pp. 22-34)。以下簡稱之為莫文。而引起的。因此我也學他, 將本文獻給當年台中一中高三物理課的恩師石克剛先生 ² ² 石先生在台中一中教了兩年書。老莫受教是在 1957$\sim$1958。筆者早了一年受到恩惠。石先生允許我: 上課可以低頭看課外的物理書, 習題不用做, 可以拿任何課外書的題目來做來交。。本文的第 0 節, 解釋了何謂引潮力場。在第 1 節, 我們用初等幾何 (作圖) 的辦法解決了引潮力場的固有問題。在第 2 節, 我們用簡單的 (微積分) 向量分析 ³ ³ 記得我進大一時, 石先生借給我一本美麗的精裝書, Philip Franklin: Methods of Advanced Calculus. 我大概讀了七成, 最少做了兩三百個磨練題, 因此對於向量分析與變分法的初等操作, 非常熟練。謝謝老師! 得到引潮位勢定理。在第 3 節, 我們以月球與日球的數據, 做估計與比較。在莫文中, 最主要的兩個計算議題是: (1) 引潮力的極大點, (2) 引潮力的靜水壓力。我們這兩節, 就對應地給以簡潔的補充。雖然兩文互相獨立成篇, 但是我當然特別要謝謝 ⁴ ⁴ 一邊寫, 一邊就想起往時相聚的美麗時光。 (拾貝齋主) 老莫。 0. 引潮力場 0.1. 向量 [空間的坐標系]: 假設我們在這個歐氏三維中已經設置好一個坐標系, 於是, 空間中的一點 $P$, 就可以寫為 $P= (x,y,z)$。如果 $Q= (\xi,\eta,\zeta)$ 是另外一點, 我們就得出其間的距離 \begin{equation} \rm{dist} (P,Q) := \sqrt{ (\xi-x)^2+ (\eta-y)^2+ (\zeta-z)^2}. \label{1} \end{equation} 這就是線段 $\overline{PQ}$ 之長 $ \|\overline{PQ}\|$, 通常也就簡寫為 $\overline{PQ}$。我們以點 $Q= (\xi,\eta,\zeta)$ 為中心, 以 $r$ 為半徑, 畫出一個 (閉)球體 $I\kern-0.35em B (r;Q)$, 其表面記為 $\mathbb{S} (r;Q)$: \begin{equation} \begin{array}{rl} I\kern-0.35em B (r;Q) & := \{P: \rm{dist} (P;Q) \leq r\}\\ & \equiv \{ (x,y,z): (\xi-x)^2+ (\eta-y)^2+ (\zeta-z)^2 \leq r^2\};\\ \mathbb{S} (r;Q) & := \{P: \rm{dist} (P;Q) = r \}\\ & \equiv \{ (x,y,z): (\xi-x)^2+ (\eta-y)^2+ (\zeta-z)^2 = r^2\}. \end{array} \label{2} \end{equation} [向量]: 在物理科學中, 我們經常遇到具有方向性的物理量, 即向量。我們把 x,y,z, 三軸方向上的單位向量, 依序記成 (W. Gibbs 的) $\mathbf{i},\mathbf{j},\mathbf{k}, $ 於是一個向量 $\mathbf{u}$, 就可以利用它的三個成分 $u,v,w, $ 而表達成 \begin{equation} \mathbf{u}=u \mathbf{i} +v \mathbf{j} +w \mathbf{k}.\label{3}\end{equation} 這向量的 (絕對)值 (或'大小' magnitude, '量度')就是 \begin{equation} \|\mathbf{u}\| := \sqrt{u ^2+v^2+w^2}. \label{4}\end{equation} 只要 $\|\mathbf{u}\| \gt0$, ($\mathbf{u}$ 是個非零向量, $\mathbf{u} \neq 0$,)我們就把 $\mathbf{u}$ 的方向 ⁵ ⁵ 記號 sgn = signum. (用萬國音標的讀法!) 對於一維的向量, 即實數 $x$, 其方向就是其正負號 $\rm{sgn} (x) \equiv \frac{x}{\|x\|}$. 解釋為單位向量 \begin{equation} \rm{sgn} (\mathbf{u}) := \frac{\mathbf{u}}{\|\mathbf{u}\|} \equiv \frac{u \mathbf{i} +v \mathbf{j} +w \mathbf{k}}{\sqrt{u ^2+v^2+w^2}}. \label{5}\end{equation} 因此,任何一個 (非零) 向量就是由它的 (方)向與量 (度) (= (絕對)值) 結合 (相乘)而成的: \begin{equation} \mathbf{u} =\rm{sgn} (\mathbf{u})\|\mathbf{u}\| \equiv \|\mathbf{u}\| \rm{sgn} (\mathbf{u}). \label{6}\end{equation} 兩個非零向量 $\mathbf{u},\mathbf{p}$, 狹義地同向, 是指 $\rm{sgn} (\mathbf{u})=\rm{sgn} (\mathbf{p})$; 而廣義地同向, 即'平行' $\mathbf{u} \parallel \mathbf{v}$ ,則是指 $\rm{sgn} (\mathbf{u})=\pm \rm{sgn} (\mathbf{p})$。零向量 $0$, 是迷向的 (isotropic), 無方向可言, 我們可以規定: \begin{equation} \rm{sgn} (0) \equiv 0.\label{7}\end{equation} 並且規定: 零向量和任何向量 $\mathbf{u}$, 都是'平行' (廣義地同向)。對於空間中的兩點 $P= (x,y,z)$ 與 $Q= (\xi,\eta,\zeta)$, 我們就說其間的位移向量為 \begin{equation} \overrightarrow{PQ} := (\xi-x) \mathbf{i}+ (\eta-y) \mathbf{j}+ (\zeta-z) \mathbf{k}.\label{8}\end{equation} 於是, 此兩點 $P,Q$ 間的距離, 其實也就是位移向量的值 $\|\overrightarrow{PQ}\|$; 通常所說的「由 $P$ 往 $Q$ 的方向」, 就是位移向量的方向 $\rm{sgn} (\overrightarrow{PQ})$。 [規約]: 我們用 $O= (0,0,0)$ 表記原點。於是我們經常就可以把點 $P$ 和向量 $\overrightarrow{OP}$ 混為一談。尤其是: \begin{equation} \rm{sgn} (P) := \rm{sgn} (\overrightarrow{OP}). \label{9}\end{equation} 0.2. 作用在質粒集團上的一股勢力 [質粒的集團]: 這一小節我們要討論的問題是: 「集團中的個體之行為, 相對於整個集團來說, 是否勻諧?」更精確地問, 「個體相對於整個集團來說的崎差, 如何定義?」其實這樣的問題, 在運動學 (kinematics)中, 已經很自然地出現過, 而且有簡單自然的答案。此地就做一點點複習, 順便介紹我們 (並不流行) 的記號。考慮由許多個質粒 (particle)所集成的一個 (有窮,不空的)集合 $A$。以下我們用 $i$ 當作 $A$ 中的活動的元素之標籤。我們把一個質粒 $i \in A$ 的質量記為 $m_i$。於是記集團 $A$ 的 \begin{equation} \underline{總質量} \hbox{ 為}\hspace{3mm} M := \sum\limits_{i \in A} m_i; \label{10} \end{equation} 現在我們把時間凍結在某一個時刻, 記那一瞬間質粒 $i$ 的位置為 $\mathbf{x}_i$, 速度為 $\mathbf{v}_i$。於是我們就說, (同樣在這一瞬間,) 集團 $A$ 的 \begin{equation} \begin{array}{rl} \hbox{平均位置} & \mathbf{x}_A:= \frac{1}{M} \sum\limits_{i \in A} m_i* \mathbf{x}_i,\\ \hbox{平均速度} & \mathbf{v}_A:= \frac{1}{M} \sum\limits_{i \in A} m_i* \mathbf{v}_i,\\[10pt] \hline\\[-15pt] \hbox{總位置矩} & \mathbf{x}^A:= \sum\limits_{i \in A} m_i* \mathbf{x}_i \equiv M* \mathbf{x}_A,\\ \hbox{總動量} & \mathbf{v}^A:= \sum\limits_{i \in A} m_i* \mathbf{v}_i \equiv M* \mathbf{v}_A\hbox{。}\\ \end{array} \label{11}\end{equation} 我們先解釋一下: 前兩個詞是很常見的。它們是很自然的概念。要點當然是: 所謂平均, 是加權 (weighted) ⁶ ⁶ 權=重=質量 (mass), 在漢文中, 原本是混用的。平均,是「要把'質量'的因素, '加進來'考慮」的意思。後兩個詞, 質粒 $i$ 的位置矩為 $m_i\mathbf{x}_i$, 這是非常罕見罕聞的一詞, 但質粒 $i$ 的動量為 $m_i \mathbf{v}_i$, 這是很熟悉的。我們'複習' (介紹)這兩個詞, 只不過是用它們來表達 \begin{equation} \begin{array}{rl} \mathbf{x}_A &= \mathbf{x}^A \div M;\\ \mathbf{v}_A &= \mathbf{v}^A \div M;\end{array} \label{12}\end{equation} [崎差]: 有了平均的定義之後, 於是我們定義: 質粒 $i$ 相對於整個集團 $A$ 而言的 \begin{equation} \begin{array}{rll} \hbox{崎差位置} & (\Delta_A \mathbf{x})_i &:= \mathbf{x}_i -\mathbf{x}_A;\\ \hbox{崎差速度} & (\Delta_A \mathbf{v})_i &:= \mathbf{v}_i -\mathbf{v}_A;\end{array} \label{13}\end{equation} 在普通物理學裡面, 平均位置, 平均速度, 的'平均'這個形容詞也常常被形容詞質心的 (mass-center)代替。而'崎差位置'與 '崎差速度' 其實就是「相對於質心的位置」, 與「相對於質心的速度 ⁷ ⁷ 以下, 我們就不再談論速度了! 因為本文並不討論動力學。記號 $\mathbf{v}$ 從此恢復自由! 」。 [一股勢力的崎攤]: 假設有某個勢力, 作用在質粒集團 $A$ 之上。意思就是它對於質粒 $i \in A$ 就給以力量 $m_i{\frak{g}}_i$。依我們這樣的記號, ${\frak{g}}_i$ 的意思是: 「對於質粒 $i$, 每單位質量的施力」。所以, 在量綱上, 它是'加速度', (用的國際單位是 '牛頓每公斤'), 而不是力 (用的國際單位是 '牛頓')。所以, 質粒集團 $A$ 所受自那個來源的 \begin{equation} \begin{array}{rl} \underline{總力} \hbox{ 為}\ ~ & {\frak{g}}^A := \sum\limits_{i \in A} (m_i {\frak{g}}_i);\hskip 2cm~\\ \hbox{每單位質量受的 } \underline{平均'力'為}\ ~ & {\frak{g}}_A := \frac{{\frak{g}}^A}{M}.\end{array}\label{14} \end{equation} 如果將總力量 ${\frak{g}}^A$ 依照質量來公平比例分攤的話, 質粒 $i$ (勻平地)攤受到的力量, 應該是 $\frac{m_i}{M}* {\frak{g}}^A$。然而它實際上受到的力量則是 $m_i{\frak{g}}_i$, 這就算出兩者間的差額 (=「不公平地分配到的力」) $$ m_i (\Delta_A {\frak{g}})_i := m_i{\frak{g}}_i - \frac{m_i}{M} {\frak{g}}^A = m_i* ({\frak{g}}_i - {\frak{g}}_A ).$$ 將這個差額, 除以 $m_i$: \begin{equation} (\Delta_A {\frak{g}})_i :={\frak{g}}_i - {\frak{g}}_A \equiv {\frak{g}}_i - \frac{{\frak{g}}^A}{M}.\label{15}\end{equation} 這是質粒 $i$ 每單位質量所受到的 '力'之崎差部分, 簡稱為這股勢力的崎差力。 [記號]: 以下我們就用 \begin{equation} m \oslash \mathbf{x} \hspace{5mm} \hbox{表示: 將質量 $m$ 放置於 $\mathbf{x}$ 處, 所得的一個抽象的質粒。}\label{16}\end{equation} 然後, 我們就把前此講過的質粒集團 $A$, 寫成 \begin{equation} A \equiv \sum\limits_{i \in A} \;\;\; m_i \oslash \mathbf{x}_i.\label{17}\end{equation} 本來並不需要新的記號, 單單寫成集合 $$ A \equiv \{ m_i \oslash \mathbf{x}_i: i \in A\} $$ 就好了。但是現在我們規定, \eqref{17} 式的右側, 含括了一個位置的明辨性條件: \begin{equation} \hbox{「$i$ 不同, $\mathbf{x}_i$ 就不同。」} \label{18}\end{equation} 這體現了物之理 ⁸ ⁸ 既然「時間已經凍結在那一瞬間」, 這個條件 \eqref{18} 式,非常自然! : 「同時同地, 不可以有兩物共存」。把集團中所有質粒的位置之集合, 稱為 (在那瞬間,) $A$ 的載體 (carrier) \begin{equation} {\rm carr} (A) := \{ \mathbf{x}_i: i \in A \}.\label{19}\end{equation} 所以, 位置的明辨性, 意思就是: 把 $i \in A$ 變換成 $\mathbf{x}_i \in {\rm carr} (A)$ 的映射 $\mathbf{x}_{\star}$, 是由 $A$ 到 ${\rm carr} (A)$ 的一個對射 (bijection)。注意到: 由定義, 載體 ${\rm carr} (A)$ 只與這個映射 $\mathbf{x}_{\star}$ 有關, 而與 $m_{\star}$ 無關。這裡, $m_{\star}$ 指的是由 $i \in A$, 得到 $m_i$ 的秤重映射 ⁹ ⁹ 我們是要求 $m_i\gt0$。。但是: 平均位置 $\mathbf{x}_{A}$ 就同時牽涉到位置映射 $\mathbf{x}_{\star}$ 與秤重映射 $m_{\star}$。最後, 我們定義: 集團 $A$ 的湊聚質粒為 ¹⁰ ¹⁰ 「將集團總質量放置在質心位置處, 所得的抽象質粒」。但質心位置不必在載體內。 \begin{equation} \hat{A} := M \oslash \mathbf{x}_A.\label{20}\end{equation} [兩個質粒集團間的簡單交涉作用]: 現在假設: 在上述的質粒集團 $A$ 之外, 還有一個質粒集團 \begin{equation} B \equiv \sum\limits_{j \in B} \;\; \mu_j \oslash \mathfrak{x}_j.\label{21}\end{equation} 我們要求: 不但 $B$ 自身也要滿足位置的明辨性條件, 而且兩個集團的載體也是互斥的: \begin{equation} {\rm carr} (A) \cap {\rm carr} (B) = \emptyset. \label{22}\end{equation} 於是 Newton 就思考這兩個集團間可能的簡單交涉作用。意思是: $B$ 的一個質粒 $j \equiv \mu_j \oslash \mathfrak{x}_j$ 對於 $A$ 的一個質粒 $m_i \oslash \mathbf{x}_i$ 的作用力是 \begin{equation} \mathbf{N} (m_i \oslash \mathbf{x}_i; \mu_j \oslash \mathfrak{x}_j) \equiv (m_i \mu_j)* \mathbf{n} (\mathbf{x}_i; \mathfrak{x}_j).\label{23}\end{equation} 也就是說, 此作用力, 與兩個質粒的質量都成正比, 而且剩下來的因子 $\mathbf{n} (\mathbf{x}_i; \mathfrak{x}_j)$ 只與兩個質粒的位置有關。當然我們知道: 依據 Newton 的 (作用與反作用的)第三定律,這個因子有交錯性: \begin{equation} \mathbf{n} (\mathbf{x}_i; \mathfrak{x}_j)=-\mathbf{n} (\mathfrak{x}_j; \mathbf{x}_i).\label{24}\end{equation} 然後 Newton 要求此種交涉作用是可加的 (additive), 也就是說: 整個集團 $B$ 對於 $A$ 的單一個質粒 $m_i \oslash \mathbf{x}_i$ 的作用力是 \begin{equation} m_i {\frak{g}}_i := \mathbf{N} (m_i \oslash \mathbf{x}_i; B)= \sum\limits_{j \in B} \mathbf{N} (m_i \oslash \mathbf{x}_i; \mu_j \oslash \mathfrak{x}_j) \equiv \sum\limits_{j \in B} (m_i \mu_j) \mathbf{n} (\mathbf{x}_i; \mathfrak{x}_j).\label{25}\end{equation} 因此, 對於此質粒 $i$, 它的每單位質量所受的力是 \begin{equation} {\frak{g}}_i \equiv \sum\limits_{j \in B} \mu_j* \mathbf{n} (\mathbf{x}_i; \mathfrak{x}_j).\label{26}\end{equation} 整個集團 $B$ 對於集團 $A$ 的所有的質粒的作用力總和則是 \begin{equation} {\frak{g}}^A := \mathbf{N} (A;B) \equiv \sum\limits_{i \in A} \sum\limits_{j \in B} (m_i \mu_j)* \mathbf{n} (\mathbf{x}_i; \mathfrak{x}_j).\label{27}\end{equation} 依照 \eqref{15} 式, 崎差力 $\Delta_A {\frak{g}}$ 的計算, 就歸結到 \eqref{26}, \eqref{27} 這兩個式子中的和分。這就引起了 [Newton 的大哉問]: 丙 (\eqref{27} 式?) $A,B$ 間的力, 等於把兩者各自湊聚成單一質粒時的力? \begin{equation} \mathbf{N} (A;B) \stackrel{?}{=} \mathbf{N} (\hat{A}; \hat{B}) \equiv M W \mathbf{n} (\mathbf{x}_A;\mathfrak{x}_B).\label{28}\end{equation} 甲 (\eqref{25} 式?) $B$ 施之於一質粒的力, 會等於其湊聚質粒 $\hat{B}$ 單個之所施? \begin{equation} \mathbf{N} (m \circ \mathbf{x};B) \stackrel{?}{=} \mathbf{N} (m \circ \mathbf{x}; \hat{B}).\label{29}\end{equation} 乙 $A$ 受自於一質粒的引力, 會等於湊聚質粒 $\hat{A}$ 之所受? \begin{equation} \mathbf{N} (A; \mu \circ \mathfrak{x}) \stackrel{?}{=} \mathbf{N} (\hat{A};\mu \circ \mathfrak{x}).\label{30}\end{equation} 這完全類似問題甲, 只是顛倒'施'與'受'的方向。要點是: 如果甲乙兩個疑問都有肯定的解答, 當然丙就被解決了。當然 Newton 想得更為深入, 把題目修改成更有意義: 甲': 找出一個針對集團 $B$ 的充分條件, 使得: (我們約掉因數 $m$,) \begin{equation} \sum\limits_{j \in B} \mu_j \mathbf{n} (\mathbf{x};\mathfrak{x}_j)= W \mathbf{n} (\mathbf{x};\mathfrak{x}_B).\label{31} \end{equation} 乙': 找出一個針對集團 $A$ 的充分條件, 使得: (我們約掉因數 $\mu$,) \begin{equation} \sum\limits_{i \in A} m_i \mathbf{n} (\mathbf{x}_i; \mathfrak{x})= M \mathbf{n} (\mathbf{x}_A; \mathfrak{x}).\label{32}\end{equation} 丙': 找出一個針對兩集團 $A,B$ 的充分條件, 使得: \begin{equation} \sum\limits_{i \in A}\sum\limits_{j \in B} m_i \mu_j \mathbf{n} (\mathbf{x}_i;\mathfrak{x}_j) = M W \mathbf{n} (\mathbf{x}_A; \mathfrak{x}_B).\label{33}\end{equation} 0.3. 作用在物體上的力這一小節, 我們把前述有關於質粒集團間的概念, 轉譯成有關於物體的概念。基本上這是用積分 (integration) 代替和分 (summation)。 [物體]: 以下假設: $\mathcal{A}$ 是三維空間的一個有界閉領域, $\rho (\mathbf{x})$ 是定義在其上的一個連續 (當然有界)的 (狹義)正值的函數。那麼以密度 $\rho$ 把質量分佈在 $\mathcal{A}$ 上, 我們就得到了一個 \begin{equation} \begin{aligned} \hbox{ (三維)物體}\ ~& A := \int_{\mathcal{A}} [\rho (\mathbf{x}) \circ \mathbf{x} ] d^3 \mathbf{x}; \\ \hbox{而其載體記為}\ ~& {\rm carr} (A):= \mathcal{A}; \\ \hbox{物體 $A$ 的總質量為}\ ~& M := \int_{\mathcal{A}} \rho (\mathbf{x}) d^3 \mathbf{x};\\ \hbox{ $A$ 的平均位置為}\ ~ &\mathbf{x}_A := \frac{1}{M} \int_{\mathcal{A}} \mathbf{x}* \rho (\mathbf{x}) d^3 \mathbf{x}; \\ \hbox{ $A$ 的湊聚質粒為}\ ~ & \hat{A} := M \oslash \mathbf{x}_A. \end{aligned} \label{34}\end{equation} [注意]: 把 $\mathcal{A}$ 改為三維空間中的一個緊緻曲面, (具緣或不具緣都可以,) 而 $\rho (\mathbf{x})$ 是定義在其上的一個連續且 (狹義)正值的函數, 又把 $d^2 \mathbf{x}$ 解釋為曲面上的微分面積, 於是我們就得到一個二維物體 \begin{equation} A := \int_{\mathcal{A}} [\rho (\mathbf{x}) \circ \mathbf{x} ] d^2 \mathbf{x}. \label{35}\end{equation} 而下面的敘述幾乎都照樣成立。當然在必要時, 我們會小心地分別敘述。首先, 對於 $\mathbf{x} \in \mathcal{A}$, 我們 (參考 \eqref{13} 式,)定義其處之 $$ \hbox{崎差位置} \;\;\;\; (\Delta_A \mathbf{x})_i := \mathbf{x} -\mathbf{x}_A.$$ [作用於物體上的力]: 假設有某個勢力來源, 作用於物體 $A$ 之上: \begin{equation} \hbox{它對於 $\mathbf{x} \in \mathcal{A}$ 處的微分質量 $\rho (\mathbf{x}) d^3 \mathbf{x}$, 施力}\; {\frak{g}} (\mathbf{x})* \rho (\mathbf{x}) d^3 \mathbf{x}.\label{36}\end{equation} 這裡的 ${\frak{g}} (\mathbf{x})$ 是「力除以質量」, (force per unit mass), 其實具有加速度的量綱。但是我們就把這股勢力稱為: 「作用在物體 $A$ 上的勢'力' ${\frak{g}}$」。而我們定義這股勢力的 \begin{equation} \begin{aligned} \hbox{合力}\ ~ {\frak{g}}^A &:= \int_{\mathcal{A}} {\frak{g}} (\mathbf{x})* \rho (\mathbf{x}) d^3 \mathbf{x};\\ \hbox{平均'力'} \ ~ {\frak{g}}_A &:= \frac{{\frak{g}}^A}{M} \equiv \frac{1}{M} \int_{\mathcal{A}} {\frak{g}} (\mathbf{x})* \rho (\mathbf{x}) d^3 \mathbf{x};\\ \hbox{崎差'力'} \ ~ (\Delta_A {\frak{g}}) (\mathbf{x}) &:= {\frak{g}} (\mathbf{x}) -{\frak{g}}_A. \end{aligned} \label{37} \end{equation} 如果將總力量 ${\frak{g}}^A$ 依照質量來公平分攤的話, 位於 $\mathbf{x} \in \mathcal{A}$ 處的微分質量 $\rho (\mathbf{x}) d^3 \mathbf{x}$, 勻平攤受到的力量應該是 $\frac{{\frak{g}}^A}{M}\rho (\mathbf{x}) d^3 \mathbf{x}$, 而它實際上受到的力, 則是 ${\frak{g}} (\mathbf{x}) \rho (\mathbf{x}) d^3 \mathbf{x}$; 這就算出差額 $$ {\frak{g}} (\mathbf{x})* \rho (\mathbf{x}) d^3 \mathbf{x} - \frac{{\frak{g}}^A}{M}\rho (\mathbf{x}) d^3 \mathbf{x} = (\Delta_A {\frak{g}}) (\mathbf{x}) \rho (\mathbf{x}) d^3 \mathbf{x} ; $$ 這就是崎差'力'一詞之由來。 0.4. 兩物體間的 Newton 引力 [兩物體間的簡單交涉]:* 現在起假設: 有兩個物體 $A$ 與 $B$。第一個物體 $A := \int_{\mathcal{A}} [\rho_1 (\mathbf{x}) \circ \mathbf{x} ] d^3 \mathbf{x};$ 是如 \eqref{28}, \eqref{29} 兩式所描寫, 但是要把彼處之 $\rho$ 改為此地之 $\rho_1$, 而其總質量為 $M$, 平均位置為 $\mathbf{x}_A$。另外的 \begin{equation} \begin{aligned} \hbox{第二個物體}\ ~ & B := \int_{\mathcal{B}} [\rho_2 (\mathfrak{x}) \circ \mathfrak{x} ] d^3 \mathbf{x}; \\ \hbox{$B$ 的總質量為}\ ~ & W \equiv \int_{\mathcal{B}} \rho_2 (\mathfrak{x}) d^3 \mathfrak{x};\\ \hbox{$B$ 的平均位置為}\ ~ & \mathfrak{x}_B \equiv \frac{1}{W} \int_{\mathcal{B}} \mathfrak{x}\rho_2 (\mathfrak{x}) d^3 \mathfrak{x};\\ \hbox{$B$ 的湊聚質粒}\ ~& \hat{B} \equiv (W \circ \mathfrak{x}_B). \end{aligned} \label{38} \end{equation} 我們還假設: $A, B$ 的兩個載集 ${\rm carr} (A) \equiv \mathcal{A}$ 與 ${\rm carr} (B) \equiv \mathcal{B}$ 互斥: \begin{equation} \mathcal{A} \cap \mathcal{B} =\emptyset. \label{39}\end{equation} 要描寫兩物體 $A$ 與 $B$ 間的簡單交涉, 我們先把 \eqref{25} 式翻譯如下: 整個集團 $B$ 對於 $A$ 的微分的質粒 $ \rho_1 (\mathbf{x}) d^3 \mathbf{x} \oslash \mathbf{x}$ 的作用力是 \begin{equation} \rho_1 (\mathbf{x}) d^3 \mathbf{x} {\frak{g}} (\mathbf{x};B) := \mathbf{N} (\rho_1 (\mathbf{x}) d^3 \mathbf{x} \oslash \mathbf{x}; B)= \rho_1 (\mathbf{x}) d^3 \mathbf{x} \int_{\mathcal{B}} \mathbf{n} (\mathbf{x}; \mathfrak{x}) \rho_2 (\mathfrak{x}) d^3 \mathfrak{x}. \label{40}\end{equation} 因此, 此微分的質粒, 每單位質量所受的力是 (參看 \eqref{26} 式) \begin{equation} {\frak{g}} (\mathbf{x};B) \equiv \int_{\mathcal{B}} \mathbf{n} (\mathbf{x}; \mathfrak{x}) \rho_2 (\mathfrak{x}) d^3 \mathfrak{x} \label{41}.\end{equation} 整個集團 $B$ 對於集團 $A$ 的總和力是 (參看 \eqref{27} 式) \begin{equation} {\frak{g}}^A (;B) := \mathbf{N} (A;B) \equiv \int_{\mathcal{A}} \rho_1 (\mathbf{x}) d^3 \mathbf{x} \int_{\mathcal{B}} \mathbf{n} (\mathbf{x}; \mathfrak{x}) \rho_2 (\mathfrak{x}) d^3 \mathfrak{x} .\label{42}\end{equation} 根據 \eqref{37} 式, $B$ 施之於 $A$ 的崎差力場 $$ (\Delta_A {\frak{g}}) (\mathbf{x};B) := {\frak{g}} (\mathbf{x};B) -{\frak{g}}_A (;B) $$ 之計算, 就歸結到上面最後這兩個式子中的積分。 [萬有引力]: Newton 假定: 質粒 $\mu \circ \mathfrak{x}$ 對質粒 $m \circ \mathbf{x}$ 所施的引力是 \begin{equation} \mathbf{N} (m \circ \mathbf{x};\mu \circ \mathfrak{x}) \equiv \frac{Gm \mu}{\|\mathfrak{x}-\mathbf{x}\|^2}* \rm{sgn} (\mathfrak{x}-\mathbf{x}) =(m \mu)* \mathbf{n} (\mathbf{x};\mathfrak{x}).\label{43}\end{equation} 引力的方向 $\rm{sgn} (\mathfrak{x}-\mathbf{x})$ 是由 $\mathbf{x}$ 向 $\mathfrak{x}$。引力的大小是與兩個質量都正比, 而與距離的平方反比。比例常數是 (Newton 的萬有引力常數) \begin{equation} G \equiv 6.67310^{-11} \hbox{米}^3/ \hbox{公斤秒}. \label{44}\end{equation} 注意到, 上式中, 我們已經引入純幾何的 \begin{equation} \mathbf{n} (\mathbf{x};\mathfrak{x}) := \frac{G}{\|\mathfrak{x}-\mathbf{x}\|^2} \rm{sgn} (\mathfrak{x}-\mathbf{x}).\label{45}\end{equation} [Newton 的問題]: 將 \eqref{31}, \eqref{32}, \eqref{33} 諸式翻譯過來, 問題就是: 甲' 找出很好的物體 $B=\int_{\mathcal{B}} \rho_2 (\mathfrak{x}) \oslash \mathfrak{x} d^3 \mathfrak{x}$, 使得: \begin{equation} \int_{\mathcal{B}} \rho_2 (\mathfrak{x}) \mathbf{n} (\mathbf{x};\mathfrak{x}) d^3 \mathfrak{x} = W \mathbf{n} (\mathbf{x};\mathfrak{x}_B) \equiv \Big (\int_{\mathcal{B}} \rho_2 (\mathfrak{x}) d^3 \mathfrak{x}\Big)* \mathbf{n} (\mathbf{x};\mathfrak{x}_B). \label{46}\end{equation} 乙' 找出很好的物體 $A=\int_{\mathcal{A}} \rho_1 (\mathbf{x}) \oslash \mathbf{x} d^3 \mathbf{x}$, 使得: \begin{equation} \int_{\mathcal{A}} \rho_1 (\mathbf{x}) \mathbf{n} (\mathbf{x};\mathfrak{x}) d^3 \mathbf{x} = M \mathbf{n} (\mathbf{x}_A; \mathfrak{x}) \equiv \Big (\int_{\mathcal{A}} \rho_1 (\mathbf{x}) d^3 \mathbf{x}\Big)* \mathbf{n} (\mathbf{x}_A;\mathfrak{x}).\label{47}\end{equation} 丙' 於是, 對於很好的兩個物體 $A$ 與 $B$ 如上, 就會有: \begin{align} \int_{\mathcal{A}}\!\!\int_{\mathcal{B}}\!\! \rho_1 (\mathbf{x}) \rho_2 (\mathfrak{x}) \mathbf{n} (\mathbf{x};\mathfrak{x}) d^3 \mathfrak{x} d^3 \mathbf{x} =\,& M W \mathbf{n} (\mathbf{x}_A; \mathfrak{x}_B) \equiv \Big(\!\int_{\mathcal{A}} \!\rho_1 (\mathbf{x}) d^3 \mathbf{x} \Big)\!\! \Big(\!\int_{\mathcal{B}}\!\rho_2 (\mathfrak{x}) d^3 \mathfrak{x} \Big) \mathbf{n} (\mathbf{x}_A;\mathfrak{x}_B). \label{48} \end{align} [Newton 球體積分定理]: 假設: 常數 $\rho_1,\rho_2,r_1,r_2$ 都是正的, 兩個定點 $\mathbf{a},\mathbf{b}$ 的距離 $\|\mathbf{a}-\mathbf{b}\|$ $\gt r_1+r_2$。那麼 \begin{equation} \begin{aligned} A &= \int_{B (r_1;\mathbf{a})} \rho_1 \oslash \mathbf{x} d^3 \mathbf{x};\\ B &= \int_{B (r_2;\mathbf{b})} \rho_2 \oslash \mathfrak{x} d^3 \mathfrak{x}; \end{aligned}\label{49} \end{equation} 都是很好的物體, 而且 $\mathbf{x}_A = \mathbf{a}; \;\;\; \mathfrak{x}_B=\mathbf{b}$, 而 \eqref{46}$-$\eqref{48} 式都是恆等式 ¹¹ ¹¹ 注意到: 體積 $\|I\kern-0.35em B (r_1;\mathbf{a})\| = \frac{4 \pi}{3} r_1^3$, $\|I\kern-0.35em B (r_2;\mathbf{b})\|=\frac{4\pi}{3} r_2^3$, 因而質量 $M= \rho_1\frac{4 \pi}{3} r_1^3$, $W = \rho_2\frac{4\pi}{3} r_2^3$。。 \begin{equation} {\frak{g}} (\mathbf{x};B) \equiv \int_{B (r_2;\mathbf{b})} \rho_2 \mathbf{n} (\mathbf{x};\mathfrak{x}) d^3 \mathfrak{x} = W* \mathbf{n} (\mathbf{x};\mathbf{b}).\label{50}\end{equation} \begin{equation} \frac{1}{\mu}\mathbf{N} (A;\mu \circ \mathfrak{x}) \equiv \int_{B (r_1;\mathbf{a})} \rho_1\mathbf{n} (\mathbf{x};\mathfrak{x}) d^3 \mathbf{x} = M* \mathbf{n} (\mathbf{a};\mathfrak{x}).\label{51}\end{equation} \begin{align} \mathbf{N} (A;B) \equiv& \int_{B (r_1;\mathbf{a})} \int_{B (r_2;\mathbf{b})} (\rho_1\rho_2) \mathbf{n} (\mathbf{x};\mathfrak{x}) d^3 \mathbf{x} d^3 \mathfrak{x} = (MW) \mathbf{n} (\mathbf{a};\mathbf{b}). \label{52} \end{align} [註解]: 事實上, 這個超卓的定理 (The Superb Theorem) ¹² ¹² 在 (自然哲學的數學)原理出版後兩百年的紀念會上, Glaisher 的用詞。 , 是 Newton 遲至 1685 的初春, 才完成證明的。稍微精進一點點的話, 就得到 Newton 球殼層定理。它的意義是說: 上述的「密度函數 $\rho_1,\rho_2$, 為常數函數」, 不是必要條件。其實, 「只要它們是球狀對稱的, 就夠了」。這在物理應用上非常有意義! 定理的主要等式為 \eqref{46}$=$\eqref{50}, (或者顛倒腳色所成的 \eqref{47}$=$\eqref{51},) 出現在原理卷 1 命題 74。次要等式 \eqref{48}$=$\eqref{52} 出現在原理卷 3 命題 8。比球殼層定理更為激進些的球面定理 ¹³ ¹³ 意思是: 把球體 $I\kern-0.35em B$ 改為球面 $\mathbb{S}$, (而 $d^3 \mathbf{x}$ 改為 $d^2 \mathbf{x}$ 等,) 把均勻的體密度, 改為均勻的面密度。結論仍然成立。出現在原理卷 1 命題 71, 當然這是指: $\mathbf{x}$ 在球外 ¹⁴ ¹⁴ 球內的情形, 與我們這裡的討論沒有關涉。出現在原理卷 1 命題 70, 這是指: 當 ($\mathbf{x}$ 在球內,) $\|\mathbf{x}-\mathbf{b}\|\lt r_2$ 時, \eqref{46} 式右側要改成零。。 [星球]: 滿足了上述 Newton 定理的假設的物體稱為星球。以下我們假設: $A$ 與 $B$ 都是星球。 [星球 $A=$地球]: 其載體的球心 $\mathbf{x}_A \equiv \mathbf{a} \equiv O=$ 原點, 半徑為 $r_1 \equiv R$; 這個 (閉) 球就簡單寫為 $I\kern-0.35em B \equiv I\kern-0.35em B (R;O)$, 其表面也就簡寫為 $\mathbb{S} \equiv \mathbb{S} (R;O)$。我們先明確固定三個常數: $G,R,M.$ \begin{align} \hbox{萬有引力常數}\ ~&G \approx 6.67310^{-11} \hbox{米}^3/ \hbox{公斤* 秒};\\ \hbox{地球質量}\ ~&M \approx 5.97410^{24} \hbox{公斤};\\ \hbox{地球半徑}\ ~&R \approx 6.37810^6 \hbox{米。}\end{align} 因此, 地表的重力加速度是 $$g \equiv \frac{GM}{R^2} \approx 9.8\;\; \hbox{米}/ \hbox{秒}^2\hbox{。} $$ [星球 $B$]: 載體是 $\mathcal{B} \equiv I\kern-0.35em B (r_2,\mathfrak{x}_B)$。其半徑 $r_2$ 在以下就不用再出現了。我們把星球 $B$ 的平均位置 $\xi_B$ 即 $\mathcal{B}$ 的球心, 記為 $Q \equiv \mathbf{b}$, 把兩個球心的距離, 用地球半徑來比, 這個比 $\alpha$ 稱為星球 $B$ 的據比。 \begin{equation} \|\overline{OQ}\| \equiv \|\mathbf{b}\| = \alphaR.\label{53}\end{equation} 我們把星球 $B$ 的質量 $W$ 用地球質量 $M$ 來比, 這個比 $\beta$ 稱為星球 $B$ 的權比。 \begin{equation} W \equiv \betaM. \label{54}\end{equation} 於是重新寫下, 由 $B$ 所生的最重要的兩個場與一個常數。星球 $B$ 所生的引力場是 \begin{equation} \mathbf{g} (\mathbf{x}) \equiv \mathbf{g} (\mathbf{x};B) = W\mathbf{n} (\mathbf{x};\mathbf{b}) \equiv \frac{g \beta R^2 }{\|\mathbf{b}-\mathbf{x}\|^2} \rm{sgn} (\mathbf{b}-\mathbf{x}).\label{55}\end{equation} 星球 $B$ 對地球 $A$ 上 (每單位質量的) 的引力之平均為 (常數!) \begin{equation} \mathbf{g} (O) \equiv \mathbf{g} (O;B) = W \mathbf{n} (O;\mathbf{b})= \frac{\beta g}{\alpha^2} \rm{sgn} (\mathbf{b}).\label{56}\end{equation} 星球 $B$ 在星球 $A$ 上的引潮力場為 \begin{equation} \mathbf{f} (\mathbf{x}) := (\Delta_A \mathbf{g}) (\mathbf{x};B) = g \beta R^2* \left (\frac{ \rm{sgn} (\mathbf{b}-\mathbf{x}) }{\|\mathbf{b}-\mathbf{x}\|^2} - \frac{ \rm{sgn} (\mathbf{b}) }{\|\mathbf{b}\|^2} \right).\label{57}\end{equation} [規約]: 以下, 「分號後面附寫 $B$」就省略掉! 用據比 $\alpha$ 與權比 $\beta$ 來表達, 則: \begin{equation} \begin{aligned} \|\mathbf{N} (A;B)\| & = \frac{\beta}{\alpha^2}M g;\\ \|\mathbf{g} (O)\| & = \frac{\beta}{\alpha^2} g. \end{aligned}\label{58} \end{equation} 由平方反比律, 我們馬上得到: \begin{equation} \frac{\| \mathbf{g} (P)\|}{ \|\mathbf{g} (O)\|}=\frac{ \overline{OQ}^2}{ \overline{PQ}^2};\label{59}\end{equation} 以下, 我們在強調幾何性的時候, 常常要把 $\mathbf{b}$ 轉換成 $Q$, 把 $\mathbb{S}$ (或 $I\kern-0.35em B$) 上的點 $\mathbf{x}$ 轉換成 $P$。那麼 \eqref{56} 式, \eqref{55} 式, \eqref{57} 式, (依此順序!)成為 \begin{align} \mathbf{g} (O) =\,& \left (\frac{\beta}{\alpha^2} g\right) \rm{sgn} (\overrightarrow{OQ}).\label{60}\\ \mathbf{g} (P) =\,& \left (\frac{\beta}{\alpha^2} g \right) * \frac{ \overline{OQ}^2}{ \overline{PQ}^2} \rm{sgn} (\overrightarrow{PQ}).\label{61}\\ \mathbf{f} (P) =\mathbf{g} (P)-\mathbf{g} (O)=\,& \left (\frac{\beta}{\alpha^2} g\right) \left (\frac{ \overline{OQ}^2}{ \overline{PQ}^2} \rm{sgn} (\overrightarrow{PQ})- \rm{sgn} (\overrightarrow{OQ}) \right).\label{62} \end{align} 1. 引潮力場的固有問題 1.1. 引潮力場的固有點 [鉛垂方向]:* 對於地表面上的一點 $P$, '鉛垂方向'這個詞有一點點曖昧。也許是指 '鉛垂向上'的 $\rm{sgn} (P) \equiv \rm{sgn} (\overrightarrow{OP})$, 也許是指 '鉛垂向下'的 $\rm{sgn} (-\overrightarrow{OP}) \equiv \rm{sgn} (\overrightarrow{PO})= - \rm{sgn} (P)$。 [固有點]: 當 $P\in \mathbb{S}$ 點處的引潮力 $\mathbf{f} (P)$ 是在'鉛垂方向'時: \begin{equation} (\spadesuit:) \left (\begin{array}{rl} \mathbf{f} (P) & \parallel \overrightarrow{OP}, \hbox{或即, 存在一個實數 $\lambda$, 使得}\\[6pt] \mathbf{f} (P) & = \lambda* \rm{sgn} (P) \equiv \lambda* \rm{sgn} (\overrightarrow{OP}), \end{array} \right. \label{63}\end{equation} 我們就說: $P$ 是引潮力場的固有點, $\lambda$ 是其對應的 (引潮力) 固有值。 $\theta := \angle QOP$ 是其對應的固有餘緯度。這一節中, 我們要解出 $ (\spadesuit)\;$ 中, 全部的固有問題。先注意對稱性。稱地星的連心線 $OQ$ 為 (對星的)極軸。在繞極軸的迴轉之下, 引潮力場是不變的, 那麼, 所有上述這些涉及'固有'的概念, 在繞極軸的迴轉之下, 顯然也是不變的。特別地說: 如果某一點 $P_0$ 是個固有點, 那麼, 將它繞極軸迴轉任何角度 $\varphi$ 所得的點 $P_0^{\varphi}$, 顯然也是固有點。這樣子說, 只要有一個固有點 $P_0$, 就有一圈的,無窮多的固有點。 [特異的固有點]: 最後那句話唯一的瑕疵是: 如果固有點是在迴轉軸上, 那麼它是特異的 (singular) 固有點, 因為它怎麼迴轉都還是自己。極軸與地球面 $\mathbb{S}$ 有兩個交點, 即近星點 $P_1$ 與遠星點 $P_2$, 它們 (幾乎不得不)都是引潮力場的固有點。事實上, 這很容易計算! [規約]: 從此開始, (重獲自由的) 足碼 $j$ 只取值 1 或 2。因為 \begin{equation} \overline{OQ}=\alpha R; \overline{P_1Q}= (\alpha-1)R, \overline{P_2Q}= (\alpha+1)R. \label{64}\end{equation} 那麼, 由平方反比定律 \eqref{59} 式, 及 \eqref{58} 式, 星球在 $P_j, (j=1,2,)$ 處的引力之大小是 \begin{equation} \|{\frak{g}} (P_1)\| =\frac{g \beta}{ (\alpha-1)^2}; \hspace{5mm} \|{\frak{g}} (P_2)\| =\frac{g \beta}{ (\alpha+1)^2}; \label{65}\end{equation} 注意到 $\overrightarrow{OP_j}$ 與 $\overrightarrow{P_jQ}$ 的方向: $$ \rm{sgn} (\overrightarrow{P_2Q})= \rm{sgn} (\overrightarrow{P_1Q})= \rm{sgn} (\overrightarrow{OQ})=\rm{sgn} (\overrightarrow{OP_1}) =-\rm{sgn} (\overrightarrow{OP_2});$$ 於是, 固有點 $P_j$ 處的引潮力固有值 $\lambda_j$ 與固有餘緯度 $\theta_j$ 都知道了: \begin{equation} \begin{aligned} \mathbf{f} (P_j) =\,& \lambda_j* \rm{sgn} (\overline{OP_j}), & \angle QOP_j =\theta_j;\\ \lambda_1=\,&g \beta* \left (\frac{1}{ (\alpha-1)^2}-\frac{1}{\alpha^2}\right);& \theta_1=0^{\circ};\\ \lambda_2=\,&g \beta* \left (\frac{1}{\alpha^2}-\frac{1}{ (\alpha+1)^2}\right);& \theta_2=180^{\circ}. \end{aligned}\label{66} \end{equation} 1.2. 平面幾何的模擬 [幾何上的相似性]: 我們先問: 如何把地球 $I\kern-0.35em B$, 地心 $O$, 星 (心) $Q$ 以及點 $P$ 等等東西的純粹幾何的關係, 表達出來 ? 立體幾何學我們不熟悉. 很難想像如何畫圖思考。所以最簡易的著手法, 就是把問題侷限成平面幾何學的題材。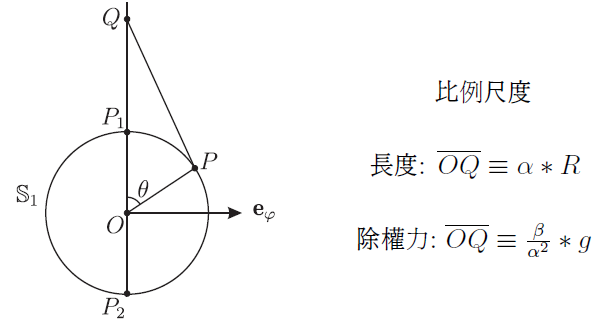我們在此就先假設 $P$ 不在 $OQ$ 連線上, 那麼, 通過不共面的這三點 $O,Q,P$, 就可畫出唯一的一個平面 $I\kern-0.35em P$。平面 $I\kern-0.35em P$ 與地球面 $\mathbb{S}$ 的交截就是一個圓 $\mathbb{S}_1$, 稱為地圓。它和連線 $OQ$ ((對星的)極軸) 的兩個交點是近星點 $P_1$ 與遠星點 $P_2$。所有以上談到的諸點 $O,Q,P$, $P_1$ 與 $P_2$, 以及圓 $\mathbb{S}_1$, 都是物理真實平面 $I\kern-0.35em P$ 中的幾何物件。現在就可以在桌子上, 放一張白紙。我們把這張紙, 叫做平面 $I\kern-0.35em P'$。然後在白紙 $I\kern-0.35em P'$ 上, 以適當的大小位置, 畫出一個相似三角形 \begin{equation} \triangle O'P'Q' \sim \triangle OPQ. \end{equation} 於是, 以 $O'$ 為心, 畫一個圓 $\mathbb{S}_1'$ 通過 $P'$ 點。圓 $\mathbb{S}_1'$ 與直線 $O'Q'$ 有兩個交點 $P_1',P_2', $ 取在 $\overline{O'Q'}$ 內的,記為 $P_1'$。現在, 物理真實平面 $I\kern-0.35em P$ 中所有的我們有興趣的幾何物件, 在平面 $I\kern-0.35em P'$ 上, 都有對應的相似物件, 都是加上了一撇。反過來說, $I\kern-0.35em P'$ 上的物件, 只要把撇號拿掉, 就成了 $I\kern-0.35em P$ 中的物件。這張白紙平面 $I\kern-0.35em P'$ 其實就是上圖左。圖中所有的點的標記, 本來都應該加上撇號, 但是我們全部刪掉撇號! 我們就是以加了撇的世界去模擬沒有撇的世界。在這個世界中的三點共一線, 就等於另一個世界中的三點共一線; 這一方的四點共圓, 在那一方對應的四點也就共圓。或許更重要的是: 兩個平面上的幾何度量, 互相有簡單的換算: $\bullet$ 對應角的角度相等。 $\bullet$ 對應線段的長度有固定的比例。真實平面 $I\kern-0.35em P$ 中的線段長 $\overline{OQ}=\alphaR$, 被加了撇的世界 $I\kern-0.35em P'$ 中的線段長 $\overline{O'Q'}$ 模擬了。以我們現在所討論的例子來說, 我們是取了 $\alpha \equiv \|\overline{OQ}\| \div \|\overline{OP}\| \equiv 2.4$ 來畫圖的。所以我們的標示, 可以是 (如圖所寫的) $$ \overline{OQ} \equiv \alphaR (\equiv 1.5307210^7 \hbox{米}) ;$$ 也可以是 ¹⁵ ¹⁵ 但是, 只准寫一個! 因為, 原則上, $\alpha$ 是可以由實測的 $\|\overline{OQ}\|$ 與 $\|\overline{OP}\|$ 而算出來的。寫了兩個, 就等於規定 $g= 9.8$ SI., 然後又規定 $g=10.0$, 那就讓人莫知所從了。 (更常見的寫法!) $$ \overline{OP_1} \equiv (R=) 6.37810^6 \hbox{米。}$$ 1.3. 圖解引潮力 [物理向量的圖解: 方向與尺度]: 回到原來的問題: 如何圖解引潮力 \eqref{62} $$ \mathbf{f} (P) = {\frak{g}} (P)- {\frak{g}} (O)? $$ 問題的前半是: 「兩個向量 ${\frak{g}} (P)$ 與 ${\frak{g}} (O)$ , 個別地說, 要如何圖解?」後半則是: 「如何 (由這兩個向量去)做加 (減)法的圖解?」先說前半。古時學者 (如 S. Stevinus) 掌握到「力是向量」時, 已經知道這樣的圖解法的意義了: 基本上, 向量是要用一個有向線段來代表的! 所以我們是要在這個紙面 $I\kern-0.35em P'$ 上, 適當地找到兩點, (暫時記為) $U,V, $ 用有向線段 $\overrightarrow{UV}$ 來代表 ${\frak{g}} (P)$, 我們就寫成 \begin{equation} \overrightarrow{UV} \propto {\frak{g}} (P); \label{68}\end{equation} 向量是有方向與大小的量。上面這個式子的意思就是說: 就方向而言, 上式的左右側的方向 (狹義地)相同 \begin{equation} \rm{sgn} (\overrightarrow{UV})=\rm{sgn} ({\frak{g}} (P)); \label{69}\end{equation} 就大小而言, 上式的左右側的大小, 也是成比例的 \begin{equation} \|\overrightarrow{UV}\| \propto \|{\frak{g}} (P)\|.\label{70}\end{equation} 同樣地, 我們又必須適當地找到兩點, (暫時記為) $U_0,V_0, $ 用有向線段 $\overrightarrow{U_0V_0}$ 來代表 ${\frak{g}} (O)$, 也就是說: \begin{equation} \hspace{35mm} \overrightarrow{U_0V_0} \propto {\frak{g}} (O); \hspace{50mm} (68'=) \label{71}\end{equation} 而上面這個式子的意思就是說: 不但有 (如同 \eqref{69} 式的) $$\rm{sgn} (\overrightarrow{U_0V_0})=\rm{sgn} ({\frak{g}} (O)); (69')$$ 而且有 (如同 \eqref{70} 式的) $$\|\overrightarrow{U_0V_0}\| \propto \|{\frak{g}} (O)\|; (70')$$ 上述的 \eqref{68} 式 $\cong$ \eqref{69} 式 + \eqref{70} 式, 及 \eqref{71} 式 $\equiv$ (68') 式 $\cong$ (69') 式 + (70') 式, 都是有兩個面向, 一是關於方向的, 一是關於大小的。 $\bullet$ 關於方向的, 即 \eqref{69} 式及 (69') 式, 很容易解決! 事實上, 只要 ¹⁶ ¹⁶ 當然還要注意'正負號': 要讓, 由 $U$ 向 $V$, 等於由 $P$ 向 $Q$。讓兩點 $U,V$ 就都在直線 $PQ$ 上, (69)式就成立; 同樣地, 只要讓 ¹⁷ ¹⁷ 當然還要注意'正負號': 要讓, 由 $U_0$ 向 $V_0$, 等於由 $O$ 向 $Q$。兩點 $U_0,V_0$ 在直線 $OQ$ 上, (69') 式也就成立。在此, 兩個式子 $(69)$ 式及 $(69')$ 式, 互不相干! $\bullet$ 關於大小的, 即 $ (70) \hbox{ 式}$, 及 $ (70') \hbox{ 式}$, 卻必須合併起來讀, 而解釋成 ¹⁸ ¹⁸ 或者寫成 \begin{equation} \|\overrightarrow{UV}\| : \|\overrightarrow{U_0V_0}\| \equiv \|{\frak{g}} (P)\| : \|{\frak{g}} (O)\|. \label{72}\end{equation} 這樣寫的好處是: 讓上式的左側是線段長度相除, 右側是除權力之大小相除, 都得到無量綱的純實數。 : \begin{equation} \frac{\|\overline{UV}\|}{ \|{\frak{g}} (P)\|} = \frac{ \|\overline{U_0V_0}\|}{ \|{\frak{g}} (O)\|}; \label{73}\end{equation} 這個比例, 就是在這個向量圖解法之中的尺度換算比。當 $O$ 與 $P$ 已經確定時, 兩個線段長 $\overline{UV}$ 與 $\overline{U_0V_0}$ 的比, 已經確定, 那麼, 這兩個線段長之中, 一個自由, 另一個不自由。我們在此就取定 $$ U_0 \equiv O,V_0 \equiv Q.$$ 因而確定了 \eqref{71} 式, 也就是 \begin{equation} \overrightarrow{OQ} \propto {\frak{g}} (O). \label{74}\end{equation} 我們必須在紙面 $I\kern-0.35em P'$ 的適當的空白處, 顯示出 \eqref{73} 式這個比例尺度 \begin{equation} \overline{OQ} \equiv \frac{\beta}{\alpha^2}g={\frak{g}} (O).\label{75} \end{equation} 關鍵性的思考是: 為什麼一張紙上可以出現兩個不同的比例尺度標示? 這是因為: 兩個不同的比例尺度, 分別用於兩種不同的物理量度, 用於不同的量綱, 一個是'長度', 一個是'(除權)力' (即加速度)。選定了 \eqref{74} 式之後, 對於 $\mathbb{S}_1$ 上的點 $P$, 要代表 ${\frak{g}} (P)$ 的有向線段 $\overrightarrow{UV}$, 其長度就沒有自由了。 (必須滿足 \eqref{72} 式。) 其方向本來就需要滿足 \eqref{69} 式。所以要確定這個有向線段, 就只需要擇定其一端。我們這裡就選定: $$ \hbox{終端點} \hspace{8mm} V \equiv V_0 \equiv Q .$$ 理由就是下述的銜接性。 [物理向量加法的圖解]:* 有了以上這樣的理解之後, 我們就可以把 Stevinus 的力量的加法之三角形定律, 用到我們這個引潮力的圖解問題來! 現在, $\mathbf{f} (P) = {\frak{g}} (P) + (- {\frak{g}} (O)) $ 是兩個除權的力 ${\frak{g}} (P)$ 與 $ (- {\frak{g}} (O)) $ 相加, 假定: 前一項是用有向線段 $\overrightarrow{UV}$ 代表, 如 \eqref{68} 式, 後一項則是, 將 \eqref{71} 式變號, 用有向線段 $\overrightarrow{V_0U_0}\equiv \overrightarrow{QO}$ 代表: \begin{equation} \overrightarrow{V_0U_0} \propto (-{\frak{g}} (O)).\label{76} \end{equation} Stevinus 說: 只要讓前一個有向線段 $\overrightarrow{UV}$ 的終端 $V$ 與後一個有向線段 $\overrightarrow{V_0U_0}$ 的始端 $V_0$ 重合, (即: 這兩個有向線段前後銜接,) $$V_0 \equiv V, $$ 然則, 這兩個線段, $\overline{UV}$ 與 $\overline{V_0U_0}$, 就是單獨一個三角形 $\triangle UVU_0$ 的兩邊。而第三邊是 $\overline{UU_0}$, 是由 ($\overrightarrow{UV}$ 的始端) $U$ 連結到 ($\overrightarrow{V_0U_0}$ 的終端) $U_0$ 的線段。那麼, (將 (68) 式與 (76) 式相加!) 有向線段 $\overrightarrow{UU_0}$ 就代表了這兩項相加的結果: \begin{equation} \overrightarrow{UU_0} \propto \left ({\frak{g}} (P) + (- {\frak{g}} (O)) \right) \equiv \mathbf{f} (P). \label{77}\end{equation} [圖解 ${\frak{g}} (O)$]: 現在要找出代表 ${\frak{g}} (O)$ 的有向線段 $\overrightarrow{UV}$ 如 \eqref{68} 式。我們已確定要讓兩端點 $U,V$ 就都在直線 $PQ$ 上, 而且由於銜接性: $V=V_0 \equiv Q$, 只需要知道線段長度 ¹⁹ ¹⁹ 這句話稍有語病: 因為距離是絕對值, 我們還需要考慮正負號, 也就是 $U$ 在直線 $PQ$ 上的哪個方向上。但因為 ${\frak{g}} (P)$ 的方向是由 $P$ 向 $Q$, 所以 $U$ 必定是在由 $Q$ 向 $P$ 的半線上。 $\overline{UV}$, 就可以找出開端 $U$ 了。以下, 為了後述作圖題中標記的明辨, 我們把 $U$ 改寫為 $T$。於是, 總而言之, 引潮力 $\mathbf{f} (P)$ 的圖解法, 就歸結到如下這個 [平面幾何作圖題]: 已給了: 圓心 $O$, 半徑 $R$ 的一圓 $\mathbb{S}_1$, 及圓 (盤)外一點 $Q$。任意取一點 $P \in \mathbb{S}_1$, 請畫圖找出半線 $QP$ 上的一點 $T$, 使得: \begin{equation} \overline{QT}: \overline{QO}= \overline{QO}^2 : \overline{QP}^2. \label{78}\end{equation} [補助命題]: 任給了平面上的'四'點 $K,L,M,N, $ 而 $K$ 與後三點相異, 那麼, 只用希臘規矩, 就可以找到半線 $KN$ 上 (唯一的一點) $I$, 使得: $$ \overline{KI}:\overline{KL}=\overline{KM}:\overline{KN};$$ 也可以找到半線 $KM$ 上 (唯一的一點) $J$, 使得: $$ \overline{KJ}:\overline{KL}=\overline{KM}:\overline{KN}.$$ [作圖題的解法]: 我們利用這個補題, 先對於'四'點 $Q,O,O,P$, 在 $QP$ 半線上, 找到點 $Z \neq P$, 使得: $$ (i:)\;\;\;\; \overline{QZ}:\overline{QO}=\overline{QO}:\overline{QP}.$$ 再對於'四'點 $Q,O,Z,P$, 在 $QZ$ 半線 (= $QP$ 半線)上, 找到點 $T$, 使得: $$ \overline{QT}:\overline{QO}=\overline{QZ}:\overline{QP};\ \hbox{ 即}\;\hspace{5mm} (ii:)\;\;\;\; \overline{QT}:\overline{QZ}=\overline{QO}:\overline{QP}; $$ 於是 $ (i), (ii)$ 兩式相乘而得 (參見 \eqref{78} 式): $$ \overline{TQ}: \overline{OQ}= \overline{QO}^2: \overline{QP}^2=\|{\frak{g}} (P)\|: \|{\frak{g}} (O)\|.$$ [圖解法的總結]: 這就證明了, 在我們的圖解法中: $$ \begin{array}{rrl} (\heartsuit:) & \overrightarrow{TQ} \propto& {\frak{g}} (P);\\ (\diamondsuit:) & \overrightarrow{QO} \propto& (-{\frak{g}} (O)); \hbox{因而}\\ (\clubsuit:) &\overrightarrow{TO} \propto& \mathbf{f} (P) \equiv {\frak{g}} (P) - {\frak{g}} (O).\\ \hbox{問題在} \;\;\; (\spadesuit:) & \overrightarrow{OP} \parallel& \overline{TO}. \end{array} $$ 注意到: 動影點 $T$ 會隨著地圓 $\mathbb{S}_1$ 上的動點 $P$ 而變。如何找出這樣子配合的點 $P$ 與 $T$ ? 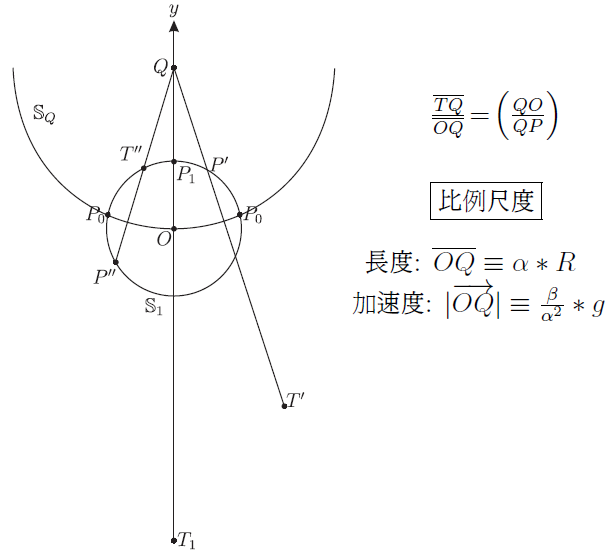現在 (如上圖,) 以 $Q$ 為圓心, $\overline{QO}$ 為半徑,畫圓 $\mathbb{S}_Q$。於是,由於平方反比定律 \eqref{78} 式, 當 $P$ 在圓 $\mathbb{S}_Q$ 內,如圖中的 $P'$, 則其影點 $T$ 在圓 $\mathbb{S}_Q$ 外, 如圖中的 $T'$; 當 $P$ 在圓 $\mathbb{S}_Q$ 外,如圖中的 $P''$, 則其影點 $T$ 在圓 $\mathbb{S}_Q$ 內, 如圖中的 $T''$。圖中有畫出近星點 $P_1$ 及其影點 $T_1$, 但是沒畫出遠星點 $P_2$ 及其影。點 $T$ 與點 $P$ 重合時, 就只有在兩圓 $\mathbb{S}_1$ 與 $\mathbb{S}_Q$ 的交點 $P_0$ 處。 1.4. 引潮力的固有點所以, 我們這個圖解法, 已經解決了上面提到的固有問題 \eqref{63} 式 $$ (\spadesuit:) \hspace{3mm} \mathbf{f} (P) = \lambda* \rm{sgn} (\overrightarrow{OP}).$$ 由於 $ (\clubsuit)$,這式子的解釋是: $O,T,P$ 三點共線。但是, 依照我們的建構, $ (\heartsuit)$, $\overrightarrow{TQ} \parallel \overrightarrow{PQ}$, 故 $Q,P,T$ 三點共線。所以, 有一種情況是: $T \neq P$, 而 $Q,O,P,T$ 四點共線, $P$ 在 $\overline{OQ}$ 上。那麼 $P$ 就只能是近日點 $P_1$ 或者遠日點 $P_2$ (即: 特異的固有點); 另一種情況是: $T=P$. 這就是上述的狀況: $P$ 是 $\mathbb{S}_Q$ 與 $\mathbb{S}_1$ 的交點 $P_0$。此時, $\overrightarrow{TO} = -\overrightarrow{OP_0}$, 而且 $\overline{TO}:\overline{OQ}=1:\alpha$, 換算成 $\|\mathbf{f} (P_0)\|=\frac{1}{\alpha}* \frac{\beta}{\alpha^2}g$, 就得到固有值 $\lambda_0 = \frac{-1}{\alpha} \frac{\beta}{\alpha^2}g$。固有餘緯度 $\theta_0=\angle QOP_0$ 是等腰三角形 $\triangle QOP_0$ 的底角 (如下圖), 這個等腰三角形的腰與底邊的長度之比為 $\alpha:1$ (依三角學, $ \theta_0= \arccos (\frac{1}{ 2 \alpha })$。) 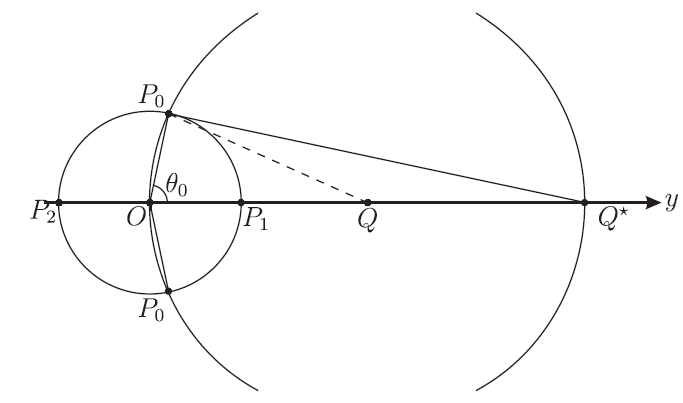[固有值的比較]: 現在我們設置一個正實值狹義凸性且遞降的函數 $$ h (x) := \frac{g \beta}{x^2}.$$ 把這個 $ \lambda_0=\frac{-\beta g}{\alpha^3}$ 的負的兩倍, 以及 \eqref{66} 式的那兩個固有值, 表達為 \begin{equation} \begin{array}{rll} \lambda_1 &=h (\alpha-1)-h (\alpha)&=g \beta \left (\frac{2 \alpha-1}{ (\alpha-1)^2 \alpha^2}\right);\\ \lambda_2 &=h (\alpha)-h (\alpha+1)&=g \beta \left (\frac{2 \alpha+1}{ (\alpha+1)^2 \alpha^2}\right);~\qquad~\\ (-2\lambda_0) &= - h' (\alpha)&= g \beta \left (\frac{2 }{ \alpha^3}\right); \end{array} \label{79}\end{equation} 就得到: \begin{equation} \lambda_1 \gtrapprox (-2 \lambda_0)= \frac{2 \beta}{\alpha^3} g \gtrapprox \lambda_2 \gt0; \label{80}\end{equation} 由固有值的正負號來談, 近月點 $P_1$ 與遠月點 $P_2$ 都是揚潮點, 因為此兩地的引潮力, 都是揚昇 (離開地心)的; 而所有的 $P_0$ 都是陷潮點, 因為其處的引潮力都是陷降 (向著地心)的。揚昇的大小,差不多是陷降的兩倍。 (以 $\alpha \gg 1$ 來考慮。) 2. 引潮力的位勢場 [問題]:* 求: 在地球表面 $\mathbb{S}$ 上的一條路徑 (或即有號 (oriented) 平滑的曲線) $\Gamma$, 使得, 引潮力場 $\mathbf{f}$ 沿著它的循線積分 \begin{equation} \mathcal{P} (\Gamma) := \int_{\Gamma} \mathbf{f} (\mathbf{x}) \cdot d \mathbf{x} \label{81}\end{equation} 有極大值。照定義, 把路徑 $\Gamma$ 反號 (reverse the orientation), 就會讓這個泛函 (functional) 反號: \begin{equation} \mathcal{P} (-\Gamma) \equiv (-1)* \int_{\Gamma} \mathbf{f} (\mathbf{x}) \cdot d \mathbf{x}. \label{82}\end{equation} 因此, 泛函的極大問題的解答,反號之後, 自動就是極小問題的解答。解法很簡單! 這個引潮力向量場是保守的 (conservative), 也就是說: 存在一個標量的 (scalar)場 $\Phi$, 使得: \begin{equation} \mathbf{f} (x,y,z) = -\nabla \Phi (x,y,z);\;\; \hbox{此地 } \underline{梯度算子} \;\;\; \nabla \equiv \mathbf{i}\frac{\partial}{\partial x}+\mathbf{j}\frac{\partial}{\partial y}+\mathbf{k}\frac{\partial}{\partial z}. \label{83}\end{equation} 這個場 $\Phi$,如果存在, 那就幾乎是唯一的: 最多只會相差一個積分常數。我們稱它為星球在地球 $I\kern-0.35em B$ 上的引潮力位勢, 由 \eqref{57} 式及上式, 就得知 \begin{equation} \Phi (\mathbf{x}) := G W \left (\frac{y}{\|\mathfrak{x}_B-\mathbf{x}_A\|^2} -\frac{1}{\|\mathfrak{x}_B-\mathbf{x}\|} \right).\label{84}\end{equation} 根據向量分析中的梯度積分定理, 若路徑 $\Gamma$ 的起端為 $P_a$, 終端為 $P_b$,則: \begin{equation} \int_{\Gamma} \mathbf{f} (\mathbf{x}) \cdot d \mathbf{x} =\Phi (P_a)-\Phi (P_b). \label{85}\end{equation} 泛函 $\mathcal{P} (\Gamma)$ 的極大問題, 變成兩點函數的極大問題: 「求 $\mathbb{S}$ 上的兩點 $P_a$ 與 $P_b$, 使得: 上式右側為極大」。換句話說: 求函數 $\Phi$ 在 $\mathbb{S}$ 上的極大點 $P_a$ 與極小點 $P_b$, 使得: \begin{equation} \hbox{對於一切 $\mathbf{x} \in \mathbb{S}$,}\;\; \Phi (P_b) \leq \Phi (\mathbf{x}) \leq \Phi (P_a).\label{86}\end{equation} 因為 $\mathbb{S}$ 是個無邊緣的曲面, 極大點 $P_a$ 也好, 極小點 $P_b$ 也好, 都必然是 $\Phi$ 在 $\mathbb{S}$ 上的臨界點 ²⁰ ²⁰ 於此點, $\Phi$在任何方向上的導數 (directional derivative) 恆為零。。問題變成: 「找出所有的 $\Phi$ 的臨界點」。這個微分學的問題, 有兩種常見的解法。 $\bullet$ 把函數 $\Phi$ 的定義域擴張為遮住 $I\kern-0.35em B$ 的一個開領域。則 $\mathbb{S}$ 只是其內的一個無邊緣的曲面, 那麼, 根據 Lagrange 的處方, 上述的臨界點就是指這樣的點 $P\in \mathbb{S}$, 讓 $\Phi$ 在此處的梯度 $\nabla \Phi (P)=-\mathbf{f} (P)$ 與 $\mathbb{S}$ 的切面垂直, 換句話說: $-\mathbf{f} (P) \parallel \overrightarrow{OP}$。臨界點 $P\in \mathbb{S}$ 就是引潮力場的固有點! 這是上一節已經處理過的。 $\bullet$ 純粹就限制在 $\mathbb{S}$ 上, 找出函數 $\Phi$ 的極值點。那麼, 最簡單的辦法就是: 在二維的球面上, 採用指向此星 $B$ 的球極坐標系 $ (\theta,\varphi)$, 此即 ²¹ ²¹ 唯一的抱歉是: 極軸是 $y$ 軸, (或者 $\mathbf{j}$ 軸), 因為被莫文綁住了。 : \begin{equation} y \equiv R \cos (\theta), x \equiv R \sin (\theta)\cos (\varphi), z \equiv R \sin (\theta)\sin (\varphi); \label{87}\end{equation} 這裡 $\theta := \angle QOP$ 是 $P$ 點的 (對星球 $B$ 的) 餘緯度 (co-latitude) ²² ²² 其範圍是 $ 0 \leq \theta \leq \pi$; 兩個端點 $\theta_1=0$ 與 $\theta_2=\pi$ 永遠需要特別考慮! 。而 $\varphi$ 是 $P$ 點的 (對星球 $B$ 的)經度, 而以 $2\pi$ 為週期, 並無邊緣點。 \begin{align} \Phi (x,y,z) \equiv\,& \frac{-G W}{ \sqrt{ (y-\alpha R)^2+x^2+z^2} }+\frac{G W}{ (\alpha R)^2}y \equiv g \beta R \left (\frac{-1}{\sqrt{\alpha^2+1-2 \alpha \cos (\theta)}} + \frac{\cos (\theta)}{\alpha^2} \right). \label{88} \end{align} [臨界的(對星)餘緯度]:* 讓我們思考在閉區間 $0 \leq \theta \leq \pi$ 上的函數 $$ V (\theta) \equiv \frac{-1}{\sqrt{\alpha^2+1-2 \alpha \cos (\theta)}} + \frac{\cos (\theta)}{\alpha^2} $$ 的極值問題: $$ \min\limits_{0 \leq \theta \leq \pi} V (\theta)=? \hspace{8mm} \max\limits_{0 \leq \theta \leq \pi} V (\theta)=? $$ 令 $\eta \equiv \cos (\theta)$, 則問題變成閉區間 $1 \geq \eta \geq -1$ 上的函數 $$ \tilde{V} (\eta) \equiv \frac{-1}{\sqrt{\alpha^2+1-2 \alpha \eta}} + \frac{\eta}{\alpha^2} $$ 的極值問題: $$ \min\limits_{-1 \leq \eta \leq 1} \tilde{V} (\eta) =? \hspace{4mm} \max\limits_{-1 \leq \eta \leq 1} \tilde{V} (\eta) =? $$ 此時, 極值點的候補者, 除了兩個端點 $\eta_1=1$ 與 $\eta_2=-1$ 之外, 就是函數 $\tilde{V}$ 的臨界點。因為導函數 $$ \tilde{V}' (\eta) = \frac{-\alpha }{\sqrt{\alpha^2+1-2 \alpha \eta}^3} + \frac{1}{\alpha^2} $$ 所以 $\tilde{V}' (\eta) =0$ 的唯一解, 就是 $$ \eta \equiv \frac{1}{2 \alpha}.$$ 因此函數 $V$ 唯一的臨界點 (critical point) 就是 $$ \theta_0 \equiv \arccos \Big(\frac{1}{2 \alpha}\Big).$$ 以上兩種解法當然得到相同的答案。現在接續剛剛的計算, 對於臨界點 $ \theta_0$ 與兩端點 $\theta_1=0$, $\theta_2=\pi$, 計算 $V$ 的函數值, 就得到: $$ V (0)=\frac{-1}{\alpha-1}+\frac{1}{\alpha^2}; V (\pi) = \frac{-1}{\alpha+1}-\frac{1}{\alpha^2}; V (\theta_0)=\frac{1-2 \alpha^2}{2 \alpha^3}.$$ 因為 $V (\theta_0) \gt V (\pi) \gt V (0)$, 所以 $V$ 的極大點是 $\theta_0=\arccos (\frac{1}{2 \alpha})$, 而極小點是 $\theta_1=0$,不是 $\theta_2=\pi$。總之: \eqref{81} 式泛函極大問題的最佳 (optimal)路徑 $\Gamma_0$, 就是要: 讓路徑 $\Gamma_0$ 的起端是上面算出的 $P_0$, 具有臨界的 (對星) 餘緯度 ²³ ²³ 但經度 $\varphi$ 隨意而不唯一! 當經度 $\varphi$ 繞了一週角時, $P_0$ 就在 ($\mathbb{S}$ 的) 臨界緯線上繞一圈。 $\theta=\theta_0$, 而終端是近星點 $P_1= (0,R,0)$。 (唯一!) 如此所得的 (引潮力位勢差) 泛函的極大值, 就是莫文所說的近星點的靜水壓力 \begin{equation} \mathcal{P} (\Gamma_0) = g R \beta\left ( (\frac{1}{\alpha-1}- \frac{1}{\alpha})- \frac{1}{\alpha^2} + \frac{1}{2 \alpha^3} \right)= g R \beta\frac{3 \alpha -1}{2 \alpha^3 (\alpha-1)}.\label{89}\end{equation} 3. 討論事實上,我們心目中只在意兩個案例: $B=$月球 (moon)或日球 (sun)。那麼, 採用簡化方便的數據, 我們將設定: 日地距 (所謂天文單位 =A.U.) $\approx 1.50110^{11} \hbox{米}$; 也就是 $\alpha_s \approx 23456$; 日球的質量 $W_s \approx 1.98910^{30} \hbox{公斤}$;也就是 $\beta_s \approx 10^6/3$; 月地距 $ \approx 3.8410^8 \hbox{米}$;也就是 $\alpha_m \approx 60$; 月球的質量 $W_m \approx 7.375310^{22} \hbox{公斤}$; 也就是 $\beta_m \approx \frac{1}{81}$。於是我們將把這兩個案例的數據, 代入 $7$ $(=3+3+1)$ 個公式, 就三個地點 $P_k, (k=0,1,2,)$, 計算 ($B$ 所生的) 引力 $\|{\frak{g}} (P_k)\|$; 引潮力 $ \|\mathbf{f} (P_k)\|=\|\lambda_k\| $, 然後再計算 $\mathcal{P} (\Gamma_0)$。我們先看月球 $B=B_m$。依照引力 $\|{\frak{g}} (P_k)\|$ 的公式 \eqref{58}, \eqref{65}, 有 \begin{equation} \|{\frak{g}} (P_1)\|=\frac{\beta g}{ (\alpha-1)^2} \gt \|{\frak{g}} (P_0)\|=\frac{\beta g}{\alpha^2}\gt \|{\frak{g}} (P_2)\| = \frac{\beta g}{ (\alpha+1)^2}; \label{90}\end{equation} 因此我把計算的結果, (用國際單位,) 就橫排成一列, 也把莫文 p.28 (8) 式以下的前三個數據, 並列在其下, 以供對照。 \begin{equation} \begin{array}{c\|\|c\|c\|c\|} & \|{\frak{g}} (P_1)\| & \|{\frak{g}} (P_0)\| & \|{\frak{g}} (P_2)\| \\ \hline \hbox{本文} & 3.47610^{-5} & 3.36110^{-5} & 3.25110^{-5} \\ \hline \hbox{莫文} & 3.59710^{-5} & 3.47610^{-5} & 3.36110^{-5} \\ \hline\end{array}\label{91} \end{equation} 所用的公式相同 (!) 答案當然應該相同 (?) 哈哈! 差別就在於: 我用 $\alpha =\alpha_m \equiv 60$, 他用 $\alpha=59$。所以我的 $\|{\frak{g}} (P_0)\|$ 是他的 $ \|{\frak{g}} (P_2)\| $; 而我的 $\|{\frak{g}} (P_1)\|$ 是他的 $ \|{\frak{g}} (P_0)\| $。 [月球對地表的 (固有) 引潮力之估算]: 我們根據公式 \eqref{79} 計算出來的結果 ²⁴ ²⁴ 用國際單位。 , 就列在下面。也把莫文 p.28 的後面兩個數據, 並列對照。請特別注意到 (參見 \eqref{80} 式,) 固有陷潮力 $\mathbf{f} (P_0)$ 之大小, 即 $\|\mathbf{f} (P_0)\|=-\lambda_0$, 而且其兩倍, 就是介於兩個特異固有值之間。所以才有表中的因子 $ (-2)$。而且這樣一來, 這個表就與上面這個表, 有顯然的對比! \begin{equation} \begin{array}{c\|\|c\|c\|c\|} & \|\mathbf{f} (P_1)\|=\lambda_1 & 2\|\mathbf{f} (P_0)\|= -2 \lambda_0 & \|\mathbf{f} (P_2)\|=\lambda_2 \\ \hline \hbox{本文} & 1.14910^{-6} & 1.12010^{-6} & 1.09310^{-6} \\ \hline \hbox{莫文} & 1.2110^{-6} & (??) & 1.1510^{-6} \\ \hline\end{array} \label{92}\end{equation} 除了表中莫文出現的空白問號之外, 莫文所給的這兩個數據, 其實就是遵照此地的公式。只是莫文用 $\alpha_m=59$, 而我們用 $\alpha_m=60$。為什麼莫文出現了空白? 這是因為莫文對於引潮力所給的定義, 不夠周全。莫文 ²⁵ ²⁵ 這是在其 p.28 幾乎中間的位置。把引潮力記為 $F_m (\mathbf{x})$, (其中 $\mathbf{x} \equiv (x,y,z) \in \mathbb{S}, $ 或者 $I\kern-0.35em B$ 也可以! ) 定義成 \begin{equation} F_m (\mathbf{x}) := \rm{sgn} (y) * \mathbf{f} (\mathbf{x}). \label{93}\end{equation} 切記: 莫文的 $y$ 軸是由 $O$ 指向 $Q$, 即: $\mathbf{j} := \rm{sgn} (\overline{OQ})$。所以, 對於 $P_1 \equiv (0,R,0),P_2 \equiv (0,-R,0)$ 這兩個固有點 $P_j, (j=1,2)$ 來說, 當然是: $$ \begin{array}{rrl} F_m (P_1) \equiv& \mathbf{f} (P_1) &=\lambda_1\mathbf{j};\\ F_m (P_2) \equiv& (-1) \mathbf{f} (P_2) &= - \lambda_2* (-\mathbf{j})= \lambda_2* \mathbf{j}. \end{array} $$ 莫文的定義, 主要的目的似乎就是要讓這兩個特異的引潮力固有點 (即近月點與遠月點) $P_1,P_2$ 處的'引潮力'的值, 同號。所以他們才在定義式中,引入這個因子 $\rm{sgn} (y)$。這個因子, 讓他們與我們的引潮力在近月點 $P_1$ 處完全一致; 但是在遠月點 $P_2$ 處差個負號。注意到他們定義的引潮力場 $F_m$, 在有定義且不是零值處, 與我們定義的引潮力場 $\mathbf{f}$, 都有相同的絕對值, (其實, 最多只差個正負號,) 既然我們定義的引潮力場 $\mathbf{f}$, 在 $\mathbb{S}$ 上, (其實是在 $I\kern-0.35em B$ 上 )處處有定義而且連續, 那麼, 當動點 $\mathbf{x}$ 沿著任何一條 (對月的!)經線, 由 $P_1$ 走向 $P_2$ 時, 必定要經過某個零值點 $F_m (\mathbf{x})=0=\mathbf{f} (\mathbf{x})$, 或者是 $F_m$ 的不連續的跳躍點。事實上, 他們根本就對於 $y=0$ 這條曲線 ²⁶ ²⁶ 這是對於星球 $B$ 而言的赤道。上的點 $\mathbf{x}$, 不去定義 $F_m (\mathbf{x})$。此地定義式 \eqref{93} 中的 $\rm{sgn} (y)$ 這個因子, 其實是我們幫忙加上去的。在莫文中, (p.30-p.31, (9-12) 諸式,)一再地出現 $y=y_0 \equiv \frac{R}{118}$, 那其實 ²⁷ ²⁷ 因為莫文採用的數據是 $\alpha \equiv 59$。就是 $y_0=\frac{R}{2 \alpha}$, 也就是我們此處所說的固有陷潮點的, (對月的)緯線。如果莫文中有完整的引潮力場的概念, 應該就會去想要定義我們這裡所說的引潮力的固有點, 引潮力的固有值等等吧。 [近月點的靜水壓力之估算]: 現在考慮 $\mathcal{P} (\Gamma_0)$ 如 \eqref{89} 式。我先算出來 $$ \frac{3 \alpha-1}{2 \alpha^3 (\alpha-1)} \approx 7.022910^{-6},$$ 於是 \begin{equation} \mathcal{P} (\Gamma_0) \approx 0.5523 g \approx 5.4193.\label{94}\end{equation} 以上是用我的 $\alpha=60,R=6.37810^6$, 如果用他們的 $\alpha=59,R=6.56010^6$, 所得到的將是 $$ \begin{array}{rl} \frac{3 \alpha-1}{2 \alpha^3 (\alpha-1)} &\approx 7.3875210^{-6};\\ \mathcal{P} (\Gamma_0) & \approx 7.3875210^{-6}* g \beta R \approx 0.5983 g \approx 5.8633.\end{array} $$ 現在看莫文怎麼計算。他們把循線積分 \eqref{81} 式, 用近似積分 ²⁸ ²⁸ 莫文 p.31, (11-12) 式。 $$ \begin{array}{rl} \mathcal{P} (\Gamma_0) &\approx \int_{y_0}^R \|\mathbf{f} (\mathbf{x})\| d y \equiv (\beta g) \int_{y_0}^R d y \left (\frac{1}{ \alpha^2+1 - 2 \alpha \frac{y}{R}}-\frac{1}{\alpha^2} \right)\\ &=g\beta R \left (\frac{1}{\alpha} \ln (\frac{\alpha}{\alpha -1}) - \frac{1}{\alpha^2} (1-\frac{1}{2 \alpha}) \right) \\ & \approx 4.8969110^{-6}* g* \beta R \\ & \approx 3.8866. \end{array} $$ 最後的答案在莫文 p.31 的最下面。這樣的近似積分, 顯得低估, 誤差太大了。現在考慮 $B=$ 日球。我們看看日球所生於地球 $I\kern-0.35em B$ 上的引力場 ${\frak{B}} (\mathbf{x})$。我們看 \eqref{90} 式的三個'力', 它們變化的幅度, 相對於中央值來比, 就是 $$ \frac{ \|{\frak{g}} (P_1)\|-\|{\frak{g}} (P_2)\| }{\| {\frak{g}} (O)\|} \approx \frac{4}{\alpha}. $$ 對於 $\alpha_s=23456$ 來說, 約為 $\frac{4}{\alpha_s}= \frac{1}{5864}$。太小了! 這和月球的情況 $\frac{4}{\alpha_m}= \frac{1}{15}$ 大不相同, 彼時三個力需要分別估算, 而現在我們只要計算一個。我們就計算中間那一個: $$ {\frak{g}} (O) \equiv \frac{\beta_s}{\alpha_s^2} g \approx 6.05910^{-4} g \approx 5.9410^{-3}.$$ $\bullet$ 日球的引'力'與 $g$ 相比, 只有 $\frac{\beta_s}{\alpha_s^2} \approx \frac{1}{1651}$, 很小; $\bullet$ 月球的引'力' 與 $g$ 相比, 只有 $\frac{\beta_m}{\alpha_m^2} \approx \frac{1}{2.91610^5}$, 更小; $\bullet$ 事實上, 月球引力只有日球引力的 $\frac{ (\beta_m / \beta_s)}{ (\alpha_m / \alpha_s)^2} \approx \frac{1}{177}$, (接近但)不到 $0.006$。現在看看日球所生於地球 $I\kern-0.35em B$ 上的引潮力場 $\mathbf{f} (\mathbf{x})$, 或者說, 我們把 \eqref{80} 式講得更精準些, 利用 \eqref{79} 式, 就得到 \begin{equation} \begin{aligned} \lambda_1 - \lambda_2 =\,& \frac{2 (3 \alpha^2-1)}{\alpha^2 (\alpha^2-1)^2} \approx \frac{6 \beta}{\alpha^4}. \\ \frac{ \lambda_1 - \lambda_2}{ -2 \lambda_0} &\approx \frac{3}{\alpha}.\end{aligned}\label{95}\end{equation} 對於日球的引潮力來說, 相對變化幅度, $\frac{3}{\alpha_s} \lt \frac{1}{8000}$, 是太小了。我們只要計算中間那一個: \begin{equation} (-2 \lambda_0)=\frac{2 \beta_s}{\alpha_s^3}g \approx 5.16610^{-8}g \approx 5.062610^{-7}.\label{96}\end{equation} 那麼,我們從日月之 \begin{align} \hbox{軌道半徑比} =\,& \frac{\alpha_s}{\alpha_m} \approx 391; \\ \hbox{質量比} =\,& \frac{\beta_s}{\beta_m} \approx 2.710^7; \end{align} 得到日球對月球之 \begin{align} \hbox{對地引力比} =\,& \frac{\beta_s}{\beta_m} \div (\frac{\alpha_s}{\alpha_m})^2 \approx 176.6;\\ \hbox{引潮力比} =\,& \frac{\beta_s}{\beta_m} \div (\frac{\alpha_s}{\alpha_m})^3 \approx 0.452 \approx \frac{9}{20};\\ \hbox{引潮靜水壓力比} =\,& \frac{\beta_s}{\beta_m} \div (\frac{\alpha_s}{\alpha_m})^3 \approx \frac{9}{20}. \end{align*} 極為有趣的事實是: 雖然對地的引力, 月球不到日球的千分之六, 可是, 對於地球的潮汐之影響, 日球不如月球, 不到一半。大約月球的 $\frac{9}{20}$。如果考慮的是近星點 (近月點與近日點)處的引潮力 $\mathbf{f} (P_1)$, 那麼日球大約是月球的 $0.44\approx \frac{26}{59}$。莫文 p.32 末段的估計則是 $\frac{27}{59}$。本文作者為國立台灣大學數學系退休教授
頁碼	8-32

獻詞與前言

0. 引潮力場

0.1. 向量

0.2. 作用在質粒集團上的一股勢力

0.3. 作用在物體上的力

0.4. 兩物體間的 Newton 引力

1. 引潮力場的固有問題

1.1. 引潮力場的固有點

1.2. 平面幾何的模擬

1.3. 圖解引潮力

1.4. 引潮力的固有點

2. 引潮力的位勢場

3. 討論