| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | 從向量觀點探討最小平方法 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
壹、前言對於二維數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 與 $Y\!=\!\langle y_i\rangle_{i=1}^n$, 以最小平方法所決定 $Y$ 對 $X$ 的迴歸直線, 其直線方程式的推導過程, 在現行的教科書中皆呈現在附錄當中。 最小平方法是以殘差平方和最小為標的, 求迴歸直線方程式事實上可視為一個雙變量函數求極值的問題, 在參考文獻中, 已提供許多不同的推導方式, 可以利用代數技巧同時配出兩個完全平方項 (參考文獻 貳、先備知識與符號令 $\vec u=(u_1,u_2,\ldots,u_n)$ 與 $\vec v=(v_1,v_2,\ldots,v_n)$ 皆為 $n$ 維向量, 定義 $\vec u$ 與 $\vec v$ 的內積為 $\vec u\cdot \vec v=\sum\limits_{i=1}^n u_iv_i$, 定義 $\vec u$ 的長度為 $\|\vec u\|=\sqrt{\vec u\cdot \vec u}=\sqrt{u_1^2+u_2^2+\cdots+u_n^2}$。 若 $\vec u\cdot \vec v=0$, 則稱 $\vec u$ 與 $\vec v$ 為正交向量 (以三維向量的觀點來看, 就是向量垂直的意思)。 考慮二維數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 與 $Y\!=\!\langle y_i\rangle_{i=1}^n$, 兩者的算術平均數分別為 $\mu_x$ 與 $\mu_y$, 若直線 $L:y=a+bx$ 能使得所有樣本點的殘差平方和 $\sum\limits_{i=1}^n e_i^2$ 最小, 則稱 $L$ 為以『最小平方法』所求得的『$Y$ 對 $X$ 的迴歸直線』, 其中 $e_i=y_i-(a+bx_i)$ 稱為第 $i$ 組的殘差。 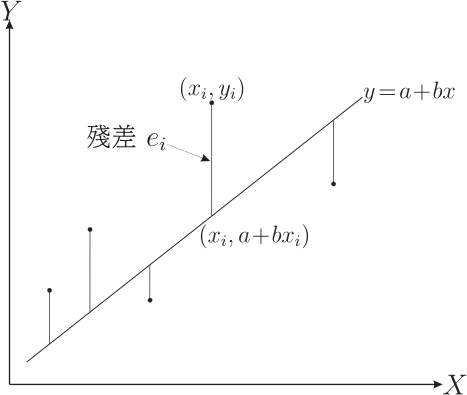 若數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 皆為相同的值, 則散布圖上的點全落在一條鉛直線上, 此時沒有討論迴歸直線的必要, 因此本文提及的 $X\!=\!\langle x_i\rangle_{i=1}^n$ 為數值不全相同的數據, 所以 $\sum\limits_{i=1}^n(x_i-\mu_x)^2\not=0$。 已知迴歸直線通過數據平均點 $(\mu_x,\mu_y)$ 且斜率 $b=\dfrac{\sum\limits_{i=1}^n (x_i-\mu_x)(y_i-\mu_y)}{\sum\limits_{i=1}^n (x_i-\mu_x)^2}$。 因為 $\sum\limits_{i=1}^n (x_i-\mu_x)^2=\sum\limits_{i=1}^n x_i^2-n\mu_x^2$ 與 $\sum\limits_{i=1}^n (x_i-\mu_x)(y_i-\mu_y)=\sum\limits_{i=1}^n x_iy_i-n\mu_x\mu_y$, 所以斜率 $b$ 亦可表示為 $\dfrac{\sum\limits_{i=1}^n x_iy_i-n\mu_x\mu_y}{\sum\limits_{i=1}^n x_i^2-n\mu_x^2}$。 參、利用正交向量的觀點求迴歸直線將二維數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 與 $Y\!=\!\langle y_i\rangle_{i=1}^n$ 分別視為 $n$ 維向量 $\vec x=(x_1,x_2,\ldots,x_n)$ 與 $\vec y=(y_1,y_2,\ldots,y_n)$, 令 $\vec 1=(1,1,\ldots,1)$ 為分量皆是 1 的 $n$ 維向量, 則 $\sum\limits_{i=1}^n x_iy_i=\vec x\cdot \vec y$, $\sum\limits_{i=1}^n x_i^2=\vec x\cdot \vec x=\|\vec x\|^2$, $\mu_x=\dfrac{\vec x\cdot \vec 1}{n}$ 與 $\mu_y=\dfrac{\vec y\cdot \vec 1}{n}$, 由此可知斜率 $b=\dfrac{\sum\limits_{i=1}^n x_iy_i-n\mu_x\mu_y}{\sum\limits_{i=1}^n x_i^2-n\mu_x^2}$ 亦可以用向量 $\vec x$、 $\vec y$ 與 $\vec 1$ 的內積來表示, 以下將從正交向量的觀點, 在滿足殘差平方和為最小值的條件下, 推論出迴歸直線的斜率。 利用正射影的概念, 首先可獲得以下引理。 引理1: 令 $\vec\alpha$, $\vec\beta$ 與 $\vec \gamma$ 為 $n$ 維向量 ($n\ge 3$), 考慮 $\vec v=a\vec \alpha+b\vec\beta-\vec \gamma$, 當實數 $a,b$ 能使得 $\vec v$ 滿足 $\vec v\cdot \vec\alpha=\vec v\cdot\vec\beta=0$ 時, $\|\vec v\|$ 為最小值。 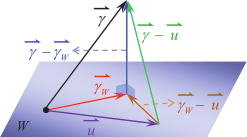 證明: 令 $\vec\alpha$ 與 $\vec\beta$ 所展開的子空間為 $W=span(\vec\alpha,\vec\beta)$ 且 $\vec\gamma$ 在 $W$ 上的正射影為 $\vec \gamma_W$。 令 $\vec u=a\vec\alpha+b\vec\beta\in W$, 則 \begin{align*} \|\vec v\|^2=\,&\|-\vec v\|^2=\|\vec \gamma-\vec u\|^2=\|\vec \gamma-\vec \gamma_W+\vec \gamma_W-\vec u\|^2\\ =\,&(\vec \gamma-\vec \gamma_W+\vec \gamma_W-\vec u)\cdot(\vec \gamma-\vec \gamma_W+\vec \gamma_W-\vec u)\\ =\,&\|\vec \gamma-\vec \gamma_W\|^2+\|\vec \gamma_W-\vec u\|^2 +2\underbrace{(\vec \gamma-\vec \gamma_W)}_{\hbox{ 屬於 $W^\bot$}}\cdot\underbrace{(\vec \gamma_W-\vec u)}_{\hbox{ 屬於 $W$}}. \end{align*} 因為 $\vec \gamma-\vec \gamma_W$ 屬於與 $W$ 正交的子空間 $W^\bot$, 且 $\vec \gamma_W-\vec u\in W$, 所以 $(\vec \gamma-\vec \gamma_W)\cdot(\vec \gamma_W-\vec u)=0$。 因此上述關係式可整理為 $\|\vec v\|^2=\|\vec \gamma-\vec \gamma_W\|^2+\|\vec \gamma_W-\vec u\|^2\ge \|\vec \gamma-\vec \gamma_W\|^2$, 所以當 $\vec u=\vec \gamma_W$ 時, $\|\vec v\|$ 有最小值 $\|\vec \gamma-\vec \gamma_W\|$。 此時 $\vec v=\vec u-\vec\gamma=\vec \gamma_W-\vec\gamma$ 與 $W$ 中所有向量皆正交, 所以 $\vec v\cdot \vec\alpha=\vec v\cdot\vec\beta=0$。 $\Box$ 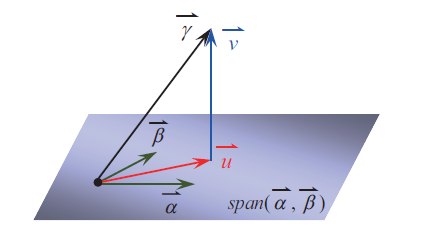 令數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 與 $Y\!=\!\langle y_i\rangle_{i=1}^n$, 其 $Y$ 對 $X$ 的迴歸直線為 $L:y=a+bx$。 以下我們利用正交向量的概念, 以最小平方法的原則, 求得迴歸直線的斜率 $b$ 與 $y$ 的截距 $a$。 定理1: $Y$ 對 $X$ 的迴歸直線必通過數據平均點 $(\mu_x,\mu_y)$ 且斜率為 $\dfrac{\sum\limits_{i=1}^n (x_i-\mu_x)(y_i-\mu_y)}{\sum\limits_{i=1}^n (x_i-\mu_x)^2}$。 證明: 已知殘差平方和 $\sum\limits_{i=1}^n e_i^2=\sum\limits_{i=1}^n \big((a+bx_i)-y_i\big)^2$, 定義 $\vec v=a\vec 1+b\vec x-\vec y$, 則殘差平方和即為向量 $\vec v$ 的長度平方, 意即 $\sum\limits_{i=1}^n e_i^2=\|\vec v\|^2$。 根據引理 1 可知, 欲使殘差平方和最小等價於 $\|\vec v\|$ 為最小值, 則實數 $a,b$ 必滿足 $\vec v\cdot \vec 1=\vec v\cdot\vec x=0$。 考慮方程組 $ \left\{\begin{array}{l} \vec v\cdot \vec 1=0\\ \vec v\cdot\vec x=0 \end{array}\right.\ \Leftrightarrow\ \left\{\begin{array}{l} (a\vec 1+b\vec x-\vec y)\cdot \vec 1=0\\ (a\vec 1+b\vec x-\vec y)\cdot \vec x=0 \end{array}\right., \Leftrightarrow\ \left\{\begin{array}{l} na+n\mu_xb=n\mu_y , (1)\\ n\mu_xa+\|\vec x\|^2b=\vec x\cdot\vec y. (2) \end{array}\right. $ 將第 (1) 式約分後可得 $a+\mu_xb=\mu_y$, 可知 $a=\mu_y-\mu_x b$, 故迴歸直線 $L:y=(\mu_y-\mu_x b)+bx$, 移項後可得 $y-\mu_y=b(x-\mu_x)$, 由此推得迴歸直線必通過數據平均點 $(\mu_x,\mu_y)$。 此外, 將第 (1) 式乘以 $\mu_x$ 後可得方程組 $\left\{\begin{array}{l} n\mu_xa+n\mu_x^2b=n\mu_x\mu_y\\ n\mu_xa+\|\vec x\|^2b=\vec x\cdot \vec y\\ \end{array}\right.$, 兩式相減可得 $(\|\vec x\|^2-n\mu_x^2)b=\vec x\cdot \vec y-n\mu_x\mu_y$, 故 $$b=\frac{\vec x\cdot \vec y-n\mu_x\mu_y}{\|\vec x\|^2-n\mu_x^2}=\dfrac{\sum\limits_{i=1}^n x_iy_i-n\mu_x\mu_y} {\sum\limits_{i=1}^n x_i^2-n\mu_x^2}=\frac{\sum\limits_{i=1}^n(x_i-\mu_x)(y_i-\mu_y)}{\sum\limits_{i=1}^n (x_i-\mu_x)^2}\hbox{。}$$ 由此可知, 迴歸直線的斜率 $b=\dfrac{\sum\limits_{i=1}^n(x_i\!-\!\mu_x)(y_i\!-\!\mu_y)}{\sum\limits_{i=1}^n (x_i-\mu_x)^2}$, 則直線 $L$ 的殘差平方和 $\sum\limits_{i=1}^n e_i^2$ 最小。 $\Box$ 肆、利用矩陣的觀點求迴歸直線從定理 1 的推論過程中可知, 既然利用向量內積的觀點可以求得迴歸直線, 那麼也可以試著使用矩陣的方式來表達。 對於一個 $n$ 維向量 $\vec s\!=\!(s_1,s_2,\ldots,s_n)$, $n\times 1$ 的行矩陣 $S=\left[\begin{array}{c} s_1\\ s_2\\ \vdots\\ s_n \end{array}\right]$ 可表示為 $S=\big[\vec s\big]_{n\times 1}$, 其中定義 $\|S\|\!=\!\|\vec s\|$。 對於 $n$ 維向量 $\vec x\!=\!(x_1,x_2,\ldots,x_n)$, $n\times 2$ 矩陣 $A\!=\!\left[\begin{array}{cc} 1&x_1\\ 1&x_2\\ \vdots&\vdots\\ 1&x_n \end{array}\right]_{n\times 2}$ 可表示為 $A=\big[\vec 1\quad \vec x\big]_{n\times 2}$, 其轉置矩陣 $A^T=\left[\begin{array}{cccc} 1&1&\cdots&1\\ x_1&x_2&\cdots&x_n\end{array}\right]_{2\times n}$ 可表示為 $A^T=\left[\begin{array}{c} \vec 1\\ \vec x\end{array}\right]_{2\times n}$。 針對數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 所決定的矩陣 $A$, 則有以下引理。 引理2: 若數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 有相異的數值, 則二階方陣 $A^TA$ 為可逆矩陣。 證明: 因為 $A^TA=\left[\begin{array}{c} \vec 1\\ \vec x\end{array}\right]\big[\vec 1\quad \vec x\big]=\left[\begin{array}{cc} n&\sum\limits_{i=1}^n x_i\\ \sum\limits_{i=1}^n x_i&\sum\limits_{i=1}^n x_i^2 \end{array}\right]$, 考慮 $A^TA$ 的行列式值可知 $\det(A^TA)=n\sum\limits_{i=1}^n x_i^2-\Big(\sum\limits_{i=1}^n x_i\Big)^2=\sum\limits_{1\le j\lt k\le n}(x_j-x_k)^2$。 因為 $X\!=\!\langle x_i\rangle_{i=1}^n$ 有相異的數值, 所以存在 $j\lt k$ 使得 $x_j-x_k\not=0$, 故 $\det(A^TA)\not=0$, 意即 $A^TA$ 為可逆矩陣。 $\Box$ 根據迴歸直線 $y=a+bx$ 的係數定義矩陣 $C=\left[\begin{array}{c} a\\ b\end{array}\right]_{2\times 1}$, 根據數據 $\langle y_i\rangle_{i=1}^n$ 定義矩陣 $Y=\big[\vec y\big]_{n\times 1}$, 因為 $\vec v=a\vec 1+b\vec x-\vec y$, 所以矩陣 $V=\big[\vec v\big]_{n\times 1}=\big[\vec 1\quad \vec x\big]\left[\begin{array}{c} a\\ b\end{array}\right]-\big[\vec y\big]=AC-Y$, 故殘差平方和 $\sum\limits_{i=1}^n e_i^2=\|\vec v\|^2=\|AC-Y\|^2$。 我們的目標是希望能利用 $\vec x$ 與 $\vec y$ 求得矩陣 $C$ 使得 $\|AC-Y\|$ 為最小值, 故有以下定理。 定理2: 若迴歸直線 $y=a+bx$, 則 $\left[\begin{array}{c} a\\ b\end{array}\right]=(A^TA)^{-1}A^TY$, 其中 $A=\big[\vec 1\quad \vec x\big]$。 證明: 根據引理 1 可知, 欲使 $\|\vec v\|$ 為最小值, 則 $\vec v\cdot\vec 1=\vec v\cdot \vec x=0$。 因為這個條件等價於矩陣關係式 $\left[\begin{array}{c} \vec 1\\ \vec x\end{array}\right](AC-Y)=\left[\begin{array}{c} 0\\ 0\end{array}\right]$, 意即 $A^T(AC-Y)=\left[\begin{array}{c} 0\\ 0\end{array}\right]$, 整理後可得 $A^TAC=A^TY$。 根據引理 2 可知 $A^TA$ 為可逆矩陣, 利用反矩陣即可推得 $C=(A^TA)^{-1}A^TY$。 $\Box$ 例1: 考慮二維數據 $\{(1,3),(2,5),(3,6),(4,10)\}$, 試求迴歸直線方程式。 可知 $Y\!=\!\left[\begin{array}{c} 3\\ 5\\ 6\\ 10\end{array}\right]_{4\times 1}$、 $A\!=\!\left[\begin{array}{cc} 1&1\\ 1&2\\ 1&3\\ 1&4\end{array}\right]_{4\times 2}$、 $A^TA\!=\!\left[\begin{array}{cccc} 1&1&1&1\\ 1&2&3&4\end{array}\right] \left[\begin{array}{cc} 1&1\\ 1&2\\ 1&3\\ 1&4\end{array}\right]\!=\!\left[\begin{array}{cc} 4&10\\ 10&30\end{array}\right]$ 與 $(A^TA)^{-1}=\left[\begin{array}{cc} \dfrac 32&\dfrac{-1}{2}\\[4pt] \dfrac{-1}{2}&\dfrac 15\end{array}\right]$。 所以 $C\!=\!(A^TA)^{-1}A^TY=\left[\begin{array}{cc} \dfrac 32&\dfrac{-1}{2}\\[4pt] \dfrac{-1}{2}&\dfrac 15\end{array}\right]\left[\begin{array}{cccc} 1&1&1&1\\ 1&2&3&4\end{array}\right]\left[\begin{array}{c} 3\\ 5\\ 6\\ 10\end{array}\right]\!=\!\left[\begin{array}{c} \dfrac 12\\[5pt] \dfrac {11}5\end{array}\right]$, 故迴歸直線為 $y\!=\!\dfrac 12+\dfrac{11}{5}x$。 $\Box$ 伍、多項式函數擬合與最小平方法考慮二維數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 與 $Y\!=\!\langle y_i\rangle_{i=1}^n$, 除了使用直線來分析兩數據的直線相關性, 也可以用 $k$ 次多項式函數 $f(x)$ 來擬合數據, 觀察曲線相關的程度, 一樣以殘差平方和最小為標的, 欲求出多項式 $f(x)$, 使得殘差平方和 $\sum\limits_{i=1}^n e_i^2=\sum\limits_{i=1}^n\big(f(x_i)-y_i\big)^2$ 為最小值。 對於數據 $X\!=\!\langle x_i\rangle_{i=1}^n$, 定義 $n$ 維向量 $\vec{x^t}=(x^t_1,x^t_2,\ldots,x^t_n)$ 其中 $t=0,1,2,\ldots,k$, 特別的, $\vec{x^0}=\vec 1=(1,1,\ldots,1)$ 與 $\vec{x^1}=\vec x=(x_1,x_2,\ldots,x_n)$。 運用類似的想法, 以正射影的概念, 我們可以將引理1的結論直接推廣如下: 引理3: 令 $\vec {\alpha_0},\vec {\alpha_1},\vec {\alpha_2},\ldots,\vec {\alpha_k}$ 與 $\vec \gamma$ 皆為 $n$ 維向量 $(n\ge 3)$, 考慮 $\vec v=\sum\limits_{t=0}^k a_t\vec{\alpha_t}-\vec \gamma$, 當實數 $a_0,a_1,a_2,\ldots,a_k$ 能使得 $\vec v$ 滿足對任意 $t\!=\!0,1,2,\ldots,k$, $\vec v\cdot \vec{\alpha_t}\!=\!0$ 皆成立時, $\|\vec v\|$ 為最小值。 引理 3 說明了若要在 $span(\vec {\alpha_0},\vec {\alpha_1}, \ldots,\vec {\alpha_k})$ 中尋找一個向量 $\vec u$ 使得 $\vec u-\vec \gamma$ 長度最小, 則 $\vec u-\vec\gamma$ 必定與 $\vec u$ 正交。 意即, 當 $\sum\limits_{t=0}^k a_t\vec{\alpha_t}$ 為 $\vec \gamma$ 在子空間 $span(\vec {\alpha_0},\vec {\alpha_1}, \ldots,\vec {\alpha_k})$ 上的正射影時, 則 $\vec v=\sum\limits_{t=0}^k a_t\vec{\alpha_t}-\vec\gamma$ 為長度最小, 此時 $\vec v$ 屬於 $W^\bot$。 接著使用 $k$ 次多項式來擬合二維數據。 令多項式 $f(x)=a_0+a_1x+a_2x^2+\cdots+a_kx^k$, 則殘差平方和 $\sum\limits_{i=1}^n e_i^2=\sum\limits_{i=1}^n\big(f(x_i)-y_i\big)^2=\|\vec v\|^2$, 其中 $\vec v=\sum\limits_{t=0}^ka_t\vec{x^t}-\vec y$。 定義矩陣 $A=\big[\vec 1\quad \vec x\quad \vec{x^2}\ \cdots\ \vec{x^k}\big]_{n\times (k+1)}$, 可以將引理 2 推廣如下。 引理4: 若數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 至少有 $k+1$ 個相異的數值, 則 證明: 不失一般性, 令 $x_1,x_2\ldots,x_{k+1}$ 為相異的數值。 (1) 假設存在實數 $c_0,c_1,c_2,\ldots,c_k$ 滿足 $c_0\vec 1+c_1\vec x+c_2\vec{x^2}+\cdots+c_k\vec{x^k}=\vec 0$, 則對應 $x_1,x_2,\ldots,x_{k+1}$ 可獲得齊次方程組 $\left\{\!\begin{array}{llclcl} c_0+c_1x_1&+c_2x_1^2&+\cdots&+c_kx_1^k&=&0\\ c_0+c_1x_2&+c_2x_2^2&+\cdots&+c_kx_2^k&=&0\\ &~\quad \vdots&&&&\\ c_0+c_1x_k&+c_2x_k^2&+\cdots&+c_kx_k^k&=&0\\ c_0+c_1x_{k+1}&+c_2x_{k+1}^2&+\cdots&+c_kx_{k+1}^k&=&0\end{array}\right.$。 將 $c_0,c_1$, $c_2,\ldots,c_k$ 視為變數, 各項係數所決定的行列式 $\Delta=\left|\begin{array}{ccccc} 1&x_1&x_1^2&\cdots&x_1^k\\ 1&x_2&x_2^2&\cdots&x_2^k\\ \vdots&\vdots&\vdots&\cdots&\vdots\\ 1&x_k&x_k^2&\cdots&x_k^k\\ 1&x_{k+1}&x_{k+1}^2&\cdots&x_{k+1}^k \end{array}\right|\!=\!\!\!\prod\limits_{1\le i\lt j\le k+1}(x_j\!-\!x_i)$ 為著名的范德蒙行列式 (Vandermonde determinant), 因為 $x_1,x_2,\ldots,x_{k+1}$ 為相異的值, 所以 $\Delta\not=0$。 由克拉碼公式可知, 齊次方程組有唯一解 $c_0=c_1=c_2=\cdots=c_k=0$, 故 $\vec 1,\vec x,\vec{x^2},\ldots,\vec{x^k}$ 為線性獨立。 (2) 令 $P$ 為階數 $(k+1)\times 1$ 的行矩陣, 使得 $(A^TA)P=O$, 其中 $O$ 為階數 $(k+1)\times 1$ 的零矩陣。 同時左乘 $P^T$ 後, 整理可得 $\|AP\|^2=(AP)^T(AP)=P^T(A^TA)P=P^TO=0$, 意即 $\|AP\|=0$。 由結論 (1) 可知 $A$ 的所有行向量為線性獨立, 故 $P=O$。 由此可知 $A^TA$ 為可逆矩陣。 $\Box$ 利用引理3與引理4, 可將定理2的結論推廣為一般多項式函數的版本。 定理3: 對於二維數據 $X\!=\!\langle x_i\rangle_{i=1}^n$ 與 $Y\!=\!\langle y_i\rangle_{i=1}^n$, 若數據 $X$ 至少有 $k+1$ 個相異的數值且多項式 $f(x)=a_0+a_1x+a_2x^2+\cdots+a_kx^k$ 為以最小平方法所求得的擬合函數, 則 $C\!=\!\left[\begin{array}{c} a_0\\ a_1\\ \vdots\\ a_k\end{array}\right]=(A^TA)^{-1}A^TY$。 證明: 殘差平方和 $\sum\limits_{i=1}^n e_i^2=\sum\limits_{i=1}^n\big(f(x_i)-y_i\big)^2=\|\vec v\|^2$, 其中 $\vec v=\sum\limits_{t=0}^k a_t\vec{x^t}-\vec y$, 所以 $\big[\vec v\big]_{n\times 1}=AC-Y$。 根據引理 3 可知, 欲使 $\|\vec v\|$ 為最小值, 則對任意 $t=0,1,2,\ldots,k$, $\vec v\cdot\vec{x^t}=0$ 皆需成立。 因為這個條件等價於 $A^T(AC-Y)=O$, 整理後可得 $A^TAC=A^TY$。 根據引理 4 可知 $A^TA$ 為可逆矩陣, 利用反矩陣即可推得 $C=(A^TA)^{-1}A^TY$。 $\Box$ 定理 3 說明了, 若要用 $k$ 次多項式來擬合數據, 則數據 $X$ 中相異的數值要足夠的多 (至少有 $k+1$ 個相異的數值), 才能保證有唯一解。 例2: 考慮二維數據 $\{(-1,-1),(0,0),(1,2),(2,0),(3,-2)\}$, 令 $f(x)=a_0+a_1x+a_2x^2$ 為最佳擬合二次函數。 可知 $Y\!=\!\!\left[\begin{array}{c} -1\\ 0\\ 2\\ 0\\ -2\end{array}\right]_{5\times 1}$、 $A\!=\!\!\left[\begin{array}{ccc} 1&-1&1\\ 1&0&0\\ 1&1&1\\ 1&2&4\\ 1&3&9\end{array}\right]_{5\times 3}$ 。 $A^TA\!=\!\!\left[\begin{array}{ccccc} 1&1&1&1&1\\ -1&0&1&2&3\\ 1&0&1&4&9\end{array}\right]\left[\begin{array}{ccc} 1&-1&1\\ 1&0&0\\ 1&1&1\\ 1&2&4\\ 1&3&9\end{array}\right]$ $=\left[\begin{array}{ccc} 5&5&15\\ 5&15&35\\ 15&35&99 \end{array}\right]$ 與 $(A^TA)^{-1}=\dfrac 1{70}\left[\begin{array}{ccc} 26&3&-5\\ 3&27&-10\\ -5&-10&5 \end{array}\right]$。 所以 $C=(A^TA)^{-1}A^TY$ $=\!\dfrac 1{70}\left[\begin{array}{ccc} 26&3&-5\\ 3&27&-10\\ -5&-10&5 \end{array}\right]\left[\begin{array}{ccccc} 1&1&1&1&1\\ -1&0&1&2&3\\ 1&0&1&4&9\end{array}\right]\left[\begin{array}{c} -1\\ 0\\ 2\\ 0\\ -2\end{array}\right]\!=\!\left[\begin{array}{c} \dfrac 57\\[5pt] \dfrac{43}{35}\\[5pt] -\dfrac 57\end{array}\right]$ 故以最小平方法所擬合的二次函數為 $y=\dfrac 57+\dfrac{43}{35}x-\dfrac 57x^2$。 $\Box$ 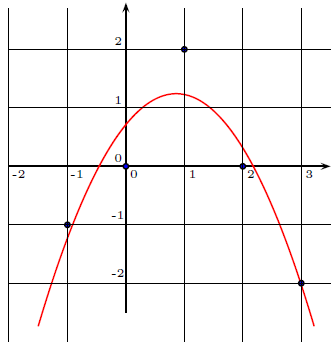 將二維數據 $\langle x_i\rangle_{i=1}^n,\langle y_i\rangle_{i=1}^n$ 分別視為向量 $\vec x=(x_1,x_2,\ldots,x_n)$ 與 $\vec y=(y_1,y_2,\ldots,y_n)$, 若要以最小平方法, 使用 $k$ 次多項式 $f(x)=\sum\limits_{t=0}^k a_t\vec{x^t}$ 來求得 $Y$ 對 $X$ 的最佳擬合函數, 則殘差平方和 $\sum\limits_{i=1}^n e_i^2$ 即可視為某個特殊向量 $\vec v=\sum\limits_{t=0}^k a_t\vec{x^t}-\vec y$ 的長度平方, 這是一種量化誤差的概念。 以向量的觀點來看, 在 $\vec y$ 是已知的情況下, 考慮 $\{\vec 1,\vec x,\vec {x^2},\ldots,\vec{x^k}\}$ 所生成的子空間 $W$, 我們欲從 $W$ 中挑選向量 $\vec u=\sum\limits_{t=0}^k a_t\vec{x^t}$ 來逼近 $\vec y$, 而 $\|\vec u-\vec y\|^2$ 即為誤差。 最小平方法就是希望從 $W$ 中尋找 $\vec u$ 使得 $\|\vec u-\vec y\|^2$ 為最小值, 此時 $\vec u-\vec y$ 即屬於 $W^\bot$, 而 $\vec u$ 即為 $\vec y$ 在 $W$ 上的正射影, 因此對任意 $t=0,1,2,\ldots,k$, $\Big(\sum\limits_{t=0}^k a_t\vec{x^t}-\vec y\Big)\cdot\vec{x^t}=0$ 皆成立。 若數據 $\langle x_i\rangle_{i=1}^n$ 至少有 $k+1$ 個相異的數值, 則這樣的聯立方程組可以透過克拉瑪公式來求得唯一的多項式係數 $a_0,a_1,a_2,\ldots,a_k$, 同時這些內積等於零的條件亦可轉換為矩陣關係, 運用定理 3 的結論來求得係數。  柒、結語高中學生在課堂中習得了向量與矩陣的基礎知識, 而筆者於高三開設線性代數選修課, 提供學生接觸更多實際應用, 在擴充知識領域後, 讓學生從向量與矩陣的觀點再一次理解最小平方法所得的迴歸直線方程式, 讓最小平方法的結論不只是一個公式而已, 而是具有向量的圖像概念 (將向量長度的平方視為誤差), 持續推廣到多項式函數的擬和, 將這樣的思路, 整理成這篇文章, 以循序漸進的方式呈現, 提供有興趣的教育先進作為補充教材的參考, 讓數據擬和的結論, 不單單是一個軟體輸出的結果, 而是可以理解背後的數學內涵。 參考資料本文作者楊宗穎任教於臺北市立第一女子高級中學, 林信安任教於臺北市立建國高級中學 |
| 頁碼 | 63-70 |
2025年6月 49卷2期
從向量觀點探討最小平方法

