| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | 兩個數學遊戲問題的等價分析 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
以圓形鐘面的 12 個整點為端點, 只能作出 6 種長度不同的弦。 (即 1 到 6 個單位的弧長)。 如果要求每個整點只當一次端點, 卻始終無法完成這 6 條弦。 這對多數喜愛 12 這個吉祥數的人來說, 可能不太能接受。 但一個簡單的問題無解, 一定有學理上的說法, 才不會形成遺憾。 最近在 YouTube Math & Logic 的影片中, 也提出一個類似的數學遊戲問題: "圓周上均勻分布的 20 個點, 能不能在每一個點各用一次的條件下, 恰好連出 10 條長度互不相等的弦?" 影片中分析得十分漂亮, 從 2 點、 4 點、 6 點 $\cdots$ 逐步探討到形成一個數學命題: 圓周上均勻分布的 $2n$ 個點, 能不能恰好連出 $n$ 條長度互不相等的弦? 把圓上的點編上序號, 弦兩端的序號差 (弧長差) 看成弦長的差, 就可以把這個命題變成一個適合中小學生的數學遊戲: 在下列算式的方格中, 填入 1 到 $2n$ 的正整數, 每數恰用一次, 使所有的算式都成立。 $$\left\{\begin{array}{c} \fbox{ }-\fbox{ }=1\\ \fbox{ }-\fbox{ }=2\\ \fbox{ }-\fbox{ }=3\\ \vdots\\ \fbox{ }-\fbox{ }=n \end{array}\right.$$ 或改為集合的講法: 將 1 到 $2n$ 的正整數平分成兩組, 是否存在 $A$、 $B$ 兩個有序集, $A = \{a_1, a_2,\ldots, a_n\}$, $B = \{b_1, b_2,\ldots, b_n\}$, 使對所有從 1 到 $n$, $a_i-b_i = i$ 都成立。 為了討論方便, 把原問題稱為"連弦問題", 修改後的問題稱為"等式問題", 再來探討這兩個數學問題, 具不具有等價的條件。  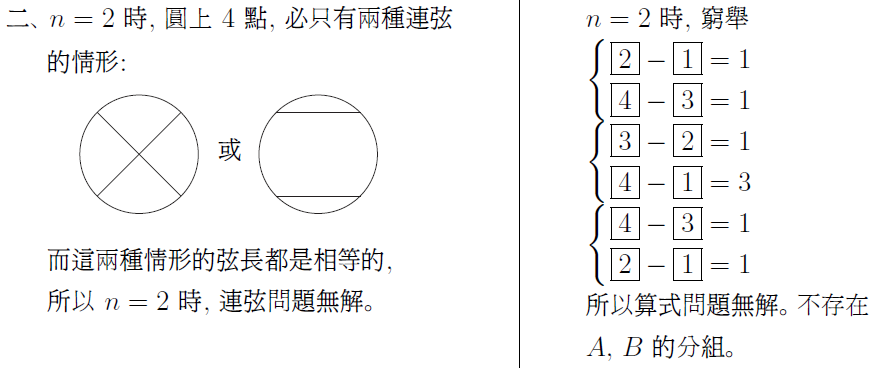 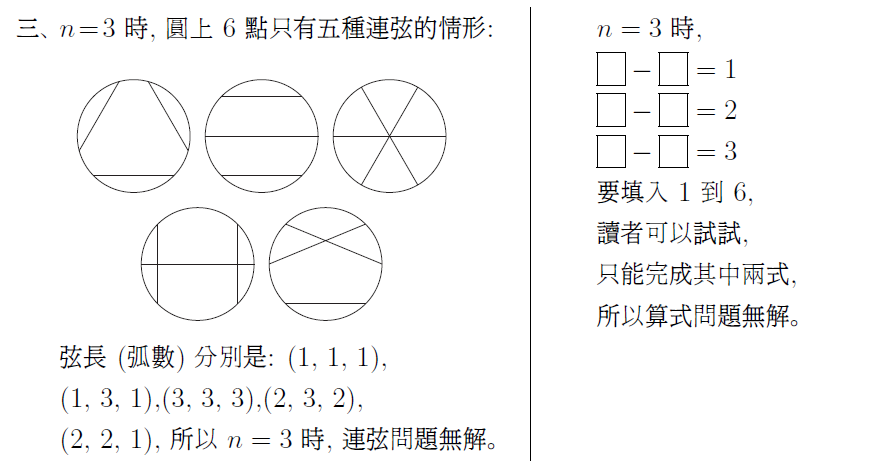 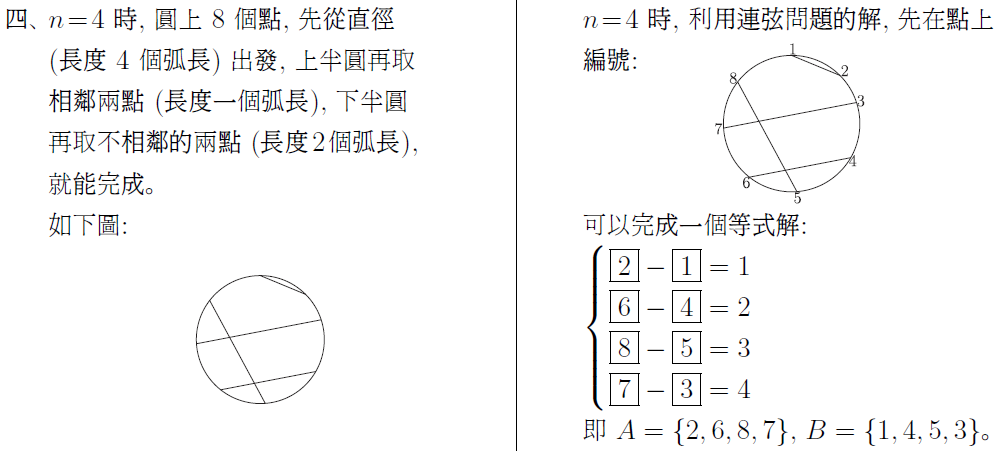 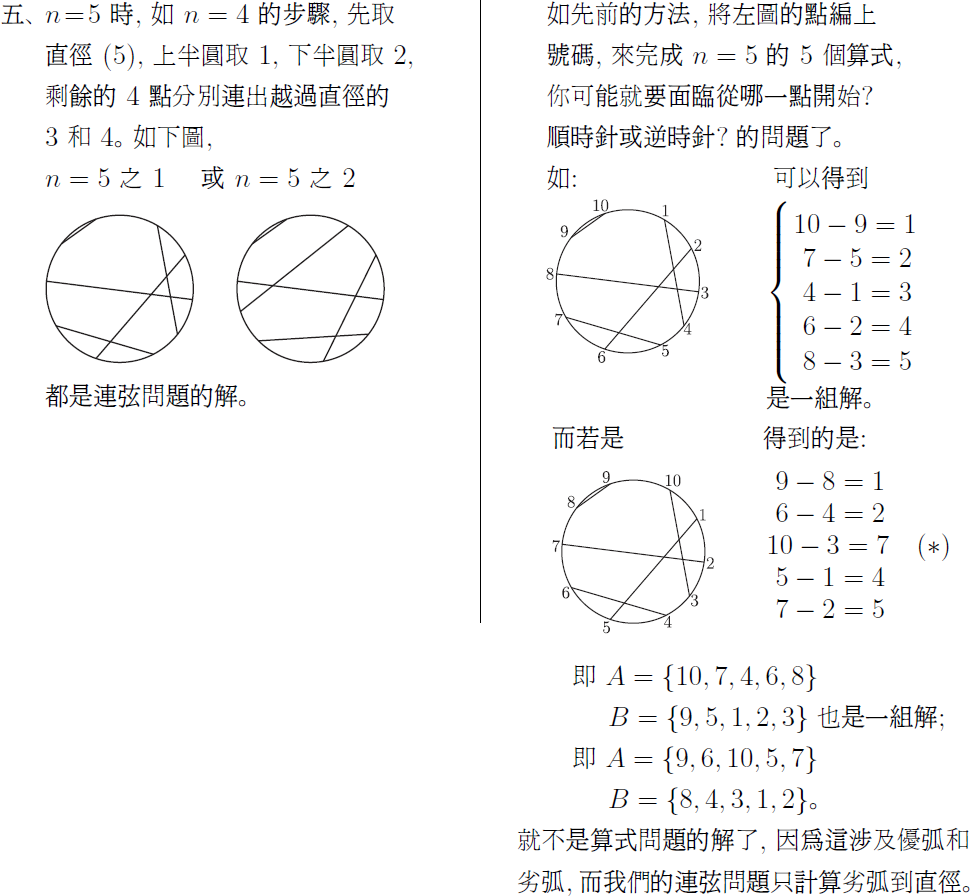 簡單地分析到 $n = 5$, 現在要進入本文的主題, 這兩個問題等價嗎? 我們目前的資訊是: 一. 有解無解的 $n$ 是一樣的, 1, 4, 5 有解, 2, 3 無解。 經過初步的探討, 這兩個問題無解的 $n$, 它的一般式是一樣的, 當 $n = 4k$, $n = 4k + 1$ 時, 兩個問題都有解; $n = 4k + 2$, $n = 4k + 3$ 時, 這兩個問題都無解, 而且無解的證明方法也是一樣的 --- 利用整數的奇偶性質。 命題: $n = 4k + 2$ 及 $n = 4k + 3$ 時, 連弦問題和等式問題都無解。 證明: 圓上均勻分布的 $2n$ 個點, 自任選之點順 (或逆) 時針方向依序編成 $1, 2,\ldots, 2n$, 當一弦被連接成時, 以劣弧的段落數記為一算式: $a_i-b_i = c_i$, 若 $c_i \gt n$, 則為優弧的段落數, 再以 $2n - c_i \lt n$ 取代之。 當一連弦問題有解時, 即下列等式成立。 $$\left\{\begin{array}{l} a_1 - b_1 = 1\\ a_2 - b_2 = 2\\ \quad \vdots\\ a_n - b_n = n \end{array}\right.$$ 恰形成一個聯立的等式, 此時等式左邊累加為: \begin{align*} \sum_{i=1}^n(a_i-b_i)=\,&\sum_{i=1}^n a_i-\sum_{i=1}^n b_i\equiv \sum_{i=1}^n a_i+\sum_{i=1}^n b_i\ (\hbox{mod}\, 2)\\ \equiv\,&\sum_{i=1}^n (a_i+b_i)\equiv \sum_{i=1}^{2n} i\equiv \frac{2n(2n+1)}{2}\ (\hbox{mod}\, 2). \end{align*} 這裡還包括 $a_i - b_i = c_i \gt n$ 時, $c_i \equiv 2n - c_i (\hbox{mod}\,2)$。 而等式右邊的累加是: $\sum\limits_{i=1}^n i= \dfrac{n(n+1)}2$, 當 $n = 4k + 2$ 時, 等式 \begin{align*} \hbox{左邊為:}\ \frac{2n(2n+1)}2=\,&\frac{(8k+4)(8k+4+1)}2 = (4k+2)(8k+5) \equiv 0\ (\hbox{mod}\,2),\\ \hbox{右邊為:}\ \frac{n(n+1)}2=\,&\frac{(4k+2)(4k+2+1)}2 = (2k+1)(4k+3) \equiv 1\ (\hbox{mod}\,2). \end{align*} 即等式左右兩邊的奇偶性不同。 當 $n = 4k + 3$ 時, 等式 \begin{align*} \hbox{左邊:}\ &\frac{2n(2n+1)}2=\frac{(8k+6)(8k+6+1)}2 = (4k+3)(8k+7) \equiv 1\ (\hbox{mod}\,2),\\ \hbox{右邊:}\ &\frac{n(n+1)}2=\frac{(4k+3)(4k+3+1)}2 = (4k+3)(2k+2) \equiv 0\ (\hbox{mod}\,2). \end{align*} 證明當 $n = 4k + 2$ 及 $4k + 3$ 時, 這組等式左右不能同時成立, 即連弦問題及等式問題在 $n = 4k + 2$ 及 $n = 4k + 3$ 時無解。 再看 $n = 4k$ 的情形: \begin{align*} \hbox{左邊:}\ &\frac{2n(2n+1)}2=\frac{8k(8k+1)}2 = 4k(8k+1) \equiv 0\ (\hbox{mod}\,2),\hskip 2.8cm~\\ \hbox{右邊:}\ &\frac{n(n+1)}2=\frac{4k(4k+1)}2 = 2k(4k+1) \equiv 0\ (\hbox{mod}\,2). \end{align*} 當 $n = 4k+1$ 時, \begin{align*} \hbox{左邊:}\ &\frac{2n(2n+1)}2=\frac{(8k+2)(8k+2+1)}2 = (4k+1)(8k+3) \equiv 1\ (\hbox{mod}\,2),\\ \hbox{右邊:}\ &\frac{n(n+1)}2=\frac{(4k+1)(4k+1+1)}2 = (4k+1)(2k+1) \equiv 1\ (\hbox{mod}\,2). \end{align*} 即 $n = 4k$ 及 $4k + 1$ 時等式兩邊的奇偶性相同, 可能有解。 當 $n = 4k$ 或 $4k + 1$, 且 $n$ 不太大時, 等式問題和連弦問題都可以用樹狀圖來窮舉, 由 $a - b = n$ 開始, 下一層是 $a - b = n - 1$, 由大到小會比由小到大簡單, 下圖是 $n = 4$ 時的樹狀圖, 當 $a - b = d \gt 4$ 時, 以 $\langle\langle a - b\rangle\rangle$ 表示優弧。 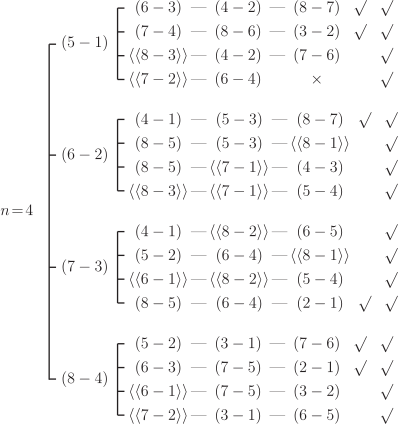 顯然連弦問題因為有優弧和劣弧的弦長相等的優勢, 所以分枝較多。 但是把 $n = 4$ 的 6 組等式解, 用固定編號畫成連弦的圖, 如下圖, 6 個圖形全部可以經旋轉或翻轉而重合, 嚴格說來只是一組連弦的解而已。 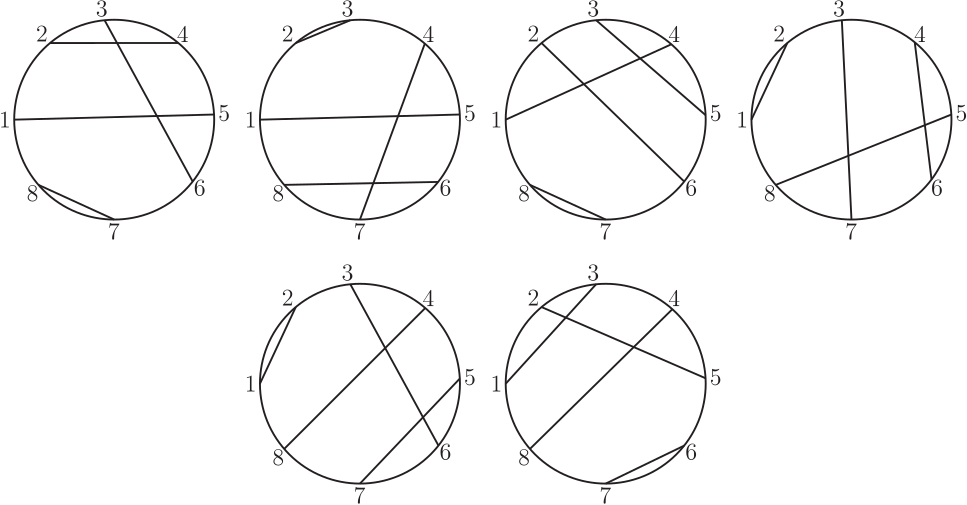 如果把 $n = 4$ 的 9 組含有優弧而成立的解, 也用固定編號畫成連弦圖, 這 9 個圖形仍然可以經旋轉或翻轉而重合。 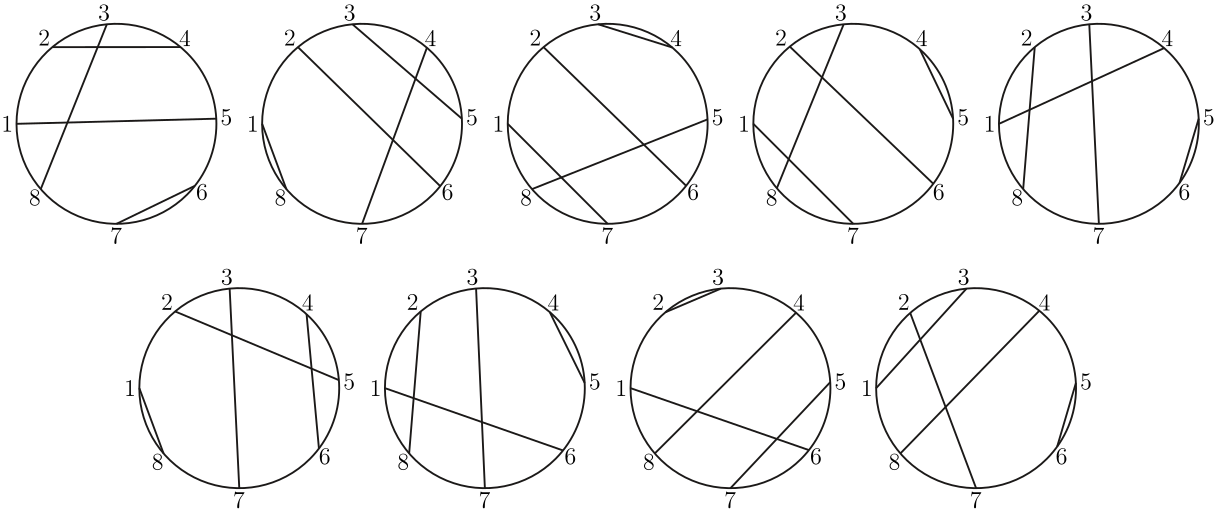 將上述結果合併討論, 等式問題因為數字是有序的, $5 - 1$ 的 4 當然不同於 $6 - 2$ 的 4, 所以樹狀圖的每一枝, 都可以看成不同的解; 但是連弦問題一開始是沒有編碼的, 所以圖形若能經旋轉或翻轉而重合, 應該視為同一解。 我們觀察上述 15 個圖, 似乎可以確定一個基準點, 就是連弦圖中的 $a - b = 4$ 的弦, 如果以最長的弦當赤道, 連弦問題的解才能最簡化, 且便於分析對稱問題。 在 YouTube Math & Logic 的影片中, 對 $n = 4k$ 及 $n = 4k + 1$ 的連弦問題提出一個建構式的解法, 因為影片以動畫方式呈現, 並沒有說明完整的步驟, 及討論其中 $k$ 值在建構解法中的地位, 以下將以最長弦當赤道及 $k$ 值的地位, 逐步重建連弦問題的建構式解法: 以 $n = 4k$ 為例, 圓上標示均勻的 $2n$ 個點, 如圖。 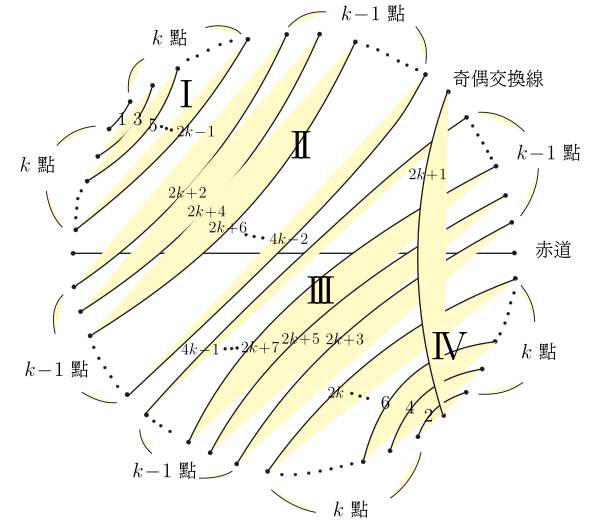 一. 連出赤道, 弦長為 $n$ 個弧長, 將圓平分成上下半圓。 二. 從左上角的連續 $2k$ 個點連出 $1, 3, 5,\ldots, 2k - 1$ 等弧長的弦, 這 $k$ 條弦會互相平行, 如圖中的 I 區, 我們稱此區為小奇數區。 (註一)。 三. 從右下角的連續 $2k + 1$ 個點, 連出 $2, 4, 6,\ldots, 2k$ 弧長的弦, 這些弦也會互相平行, 如圖中的 IV 區, 單位 2 個弦中會空出一點, 這區稱為小偶數區。 (註二)。 四. 從單位 2 的弦空出的點越過赤道, 作出長 $2k + 1$ 的弦, 這條弦是奇偶交換的關鍵, 稱它為奇偶交換線。 五. 如圖中之 II 區, 可作出 $k - 1$ 條平行弦, 弦長分別是 $2k + 2, 2k + 4, 2k + 6,\ldots, 4k - 2$, 此區稱為大偶數區。 六. 如圖中之 III 區, 可作出 $k - 1$ 條平行弦, 弦長分別是 $2k + 3, 2k + 5, 2k + 7,\ldots, 4k - 1$, 此區稱為大奇數區。 七. 如果 $n = 4k$, 此時圓上已無未連弦的點, 且依序共連出 $1 + k + k + 1 + (k-1) + (k-1) = 4k$ 條長度不等的弦, 完成一個連弦的解。 八. 如果 $n = 4k + 1$, 在第 II 區還可作出一條 $k$ 的弦。 仍然滿足題目要求。 由於 $n = 4k + 2$ 及 $n = 4k + 3$ 的連弦問題已證明無解, 如果也用這個建構法連弦, 前六個步驟都不成問題, 但最後必是留下兩條 $n - 1$ 或兩條 $n$ 的弦, 無法滿足題目要求, 讀者可以自行嘗試。 這樣建構出來的連弦圖, 如果隨意任選起點, 依序編號寫成算式, 並不一定是等式問題的解, 原因就是優弧的問題。 所幸透過編號起點的調整就可以解決。 但是要調整到每一組算式都沒有優弧的問題, 就另有玄機。 技巧是: 找一條直徑, 只跟赤道有交點, 不跟其餘的弦相交, 再以這條直徑的兩端, 順時針或逆時針方向重新編號, 恰好避開優弧問題, 就可以得到 4 組等式問題的解。 以 $n = 9$ 為例: 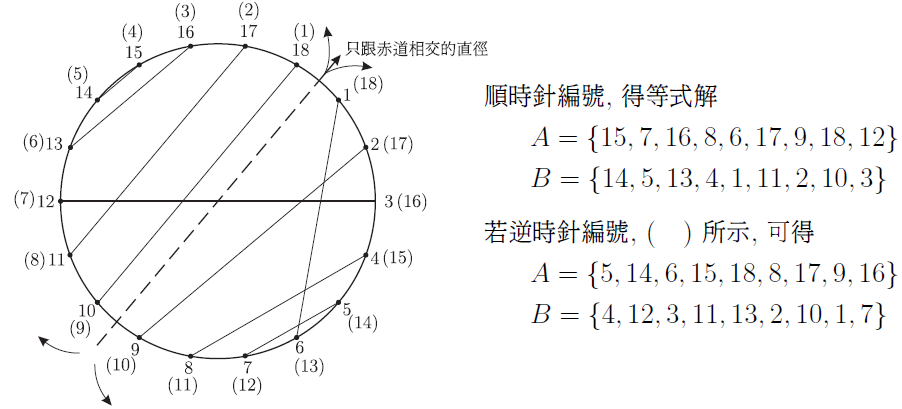 很明顯的, 這條直徑會出現在步驟五所作的大偶數區和步驟六所作的大奇數區之間。 或者簡單的說, 以步驟四所作的 $2k + 1$ (奇偶交換線)的末端 (即非單位2的弦中間) 點開始, 順時針或逆時針方向依序編號, 就各能得到一組等式解, 也可從這條直徑的另一端開始編號, 也能得到另二組等式解。 綜合上述的研究, 可以得到下列幾點結論: 一、 連弦問題如果只在圖上嘗試, 很難證明在 $n = 4k + 2$ 及 $n = 4k + 3$, $k \ge 0$ 無解。 Math & Logic 的作者巧妙的轉換成: 大數的和減小數的和等於 1 到 $n$ 的整數和, 大數的和加小數的和等於 1 到 $2n$ 的整數和, 就回到中小學生熟悉的和差問題: $\left\{\begin{array}{l} x+y=a\\ x-y=b\end{array}\right.,$ 兩式相減得 $2y = a - b$, 在 $x, y$ 都是整數的情況下, $2y$ 一定是偶數, 如果 $a - b$ 是奇數, $x, y$ 必無整數解。 利用這個必要條件的不成立, 輕易的證明 $n = 4k + 2$, 及 $n = 4k + 3$ 時, 連弦問題無解, 很適合中學以上的學生溫故而知新。 二、 等式問題用樹狀圖由大到小分析, 較易窮舉所有的解, 若是連弦問題, 必須加上優弧差的分析, 會更複雜。 但對於較大的 $n$, 如 $n = 10$, 第一層有 10 分枝, 第二層有 8 分枝, 若加上優弧會有 16 分枝, 雖然愈往後會逐漸減少, 但其分枝節點數將呈指數或階乘成長, 除非以電腦程式列出, 否則不容易呈現。 三、 每一組等式問題的解, 都可以對應一個連弦的圖, 但不同的解對應出來的圖可能可以經旋轉或翻轉變成同一個連弦的圖。 四、 即使考慮優弧問題的樹狀圖, 作出來的連弦圖也可能經旋轉或翻轉得到相同的連弦圖, 例如 $n = 4$ 的 15 個樹狀圖解, 竟全部是同一個連弦圖, 所以連弦問題的解數, 可能沒有我們當初的想像那麼多。 五、 $n = 4k$ 和 $n = 4k + 1$, $k\ge 0$ 的連弦問題, 都有相同的建構式解法。 特別的是 $n = 1$ 時, $k = 0$, 小奇數區 0, 小偶數區 0, 奇偶交換的 $2k + 1 = 1$, 恰是赤道。 $n = 4$ 時, $k = 1$, 小奇數區 $k = 1$ 條, 小偶數區 $k = 1$ 條, 大偶數區 $k - 1 = 0$ 條, 大奇數區 $k - 1 = 0$ 條, 奇偶交換 $2k + 1 = 3$, 已是 $n - 1$, 加上赤道 $n = 4$, 簡單明瞭。 六、 利用建構式解法及序號重編, 至少可得到 4 組等式問題的解, 可見這 4 組等式問題的解轉換成連弦圖時, 一定可以經旋轉翻轉而重合。 七、 連弦問題的建構式解法並非唯一解, 如本文中 $n = 5$ 之 2 是建構式解法, $n = 5$ 之 1 不是建構式解法。 八、 建構式解法中, 提供一個連弦圖是否可以經旋轉或翻轉 (對稱)的方法, 就是對最長的弦轉成赤道 $n$, 並將最短的弦 1 轉或翻到同一象限, 即可判斷是否重合。 總結而言, 連弦問題和等式問題在 $n = 4k + 2$ 和 $n = 4k + 3$ 時無解是充分且必要條件。 在 $n = 4k$ 和 $n = 4k + 1$ 時有解, 且等式問題的解是連弦問題解的充分非必要條件; 連弦問題的解是等式問題解的必要非充分條件。 所以這兩個問題並不等價。 如果把等式問題的要求改為 $a_i - b_i = i\ (\hbox{mod}\,2n)$, 這兩個問題顯然是等價的, 只是如此一來, 不懂負數的小學生和不懂同餘的中學生, 就無法享受這個等式的挑戰了, 不知道數學傳播的讀者, 同不同意我這樣的看法? 註一: 這裡以左上角開始, 當然也可以選擇從右上, 右下或左下開始。 參考資料本文作者為高雄市中正高中退休教師 |
| 頁碼 | 71-79 |
2025年6月 49卷2期
兩個數學遊戲問題的等價分析

