把一張地圖, 等比例縮小數倍 (如 $1/5 \times 1/5$) 成一張小的圖。 把小圖任意丟在大圖上, 則必可找到重疊的一點, 是地圖上相同的地點。

問題是如何找到這一點？

用國中幾何的觀念其實就可以找得到的。 茲解釋如下： 大圖 $ABCD$, 小圖 $abcd$, 小圖旋轉某個角度疊在大圖上(圖一):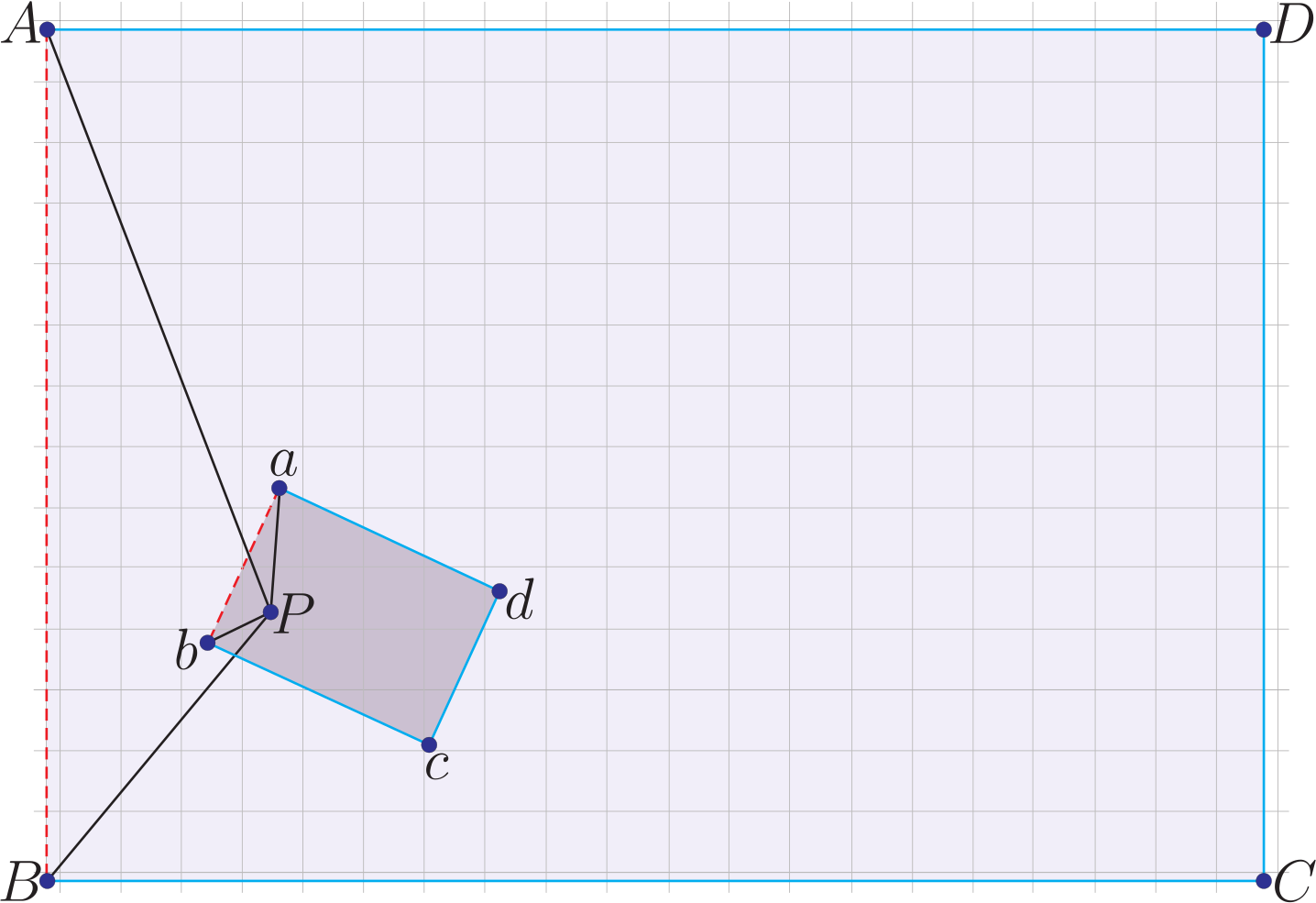

 

若那重疊的一點令為 $P$, 那麼以大小圖的對應點相連 $\triangle APB$ 與 $\triangle aPb$ 是相似三角形。 $\angle BAP$ 與 $\angle baP$ 全等, 用圓周角全等的定理。 我們把 $\overline{ab}$ 延長與 $\overleftrightarrow{AB}$ 相交於 $E$, 那麼 $AaPE$ 會四點共圓, 如圖二: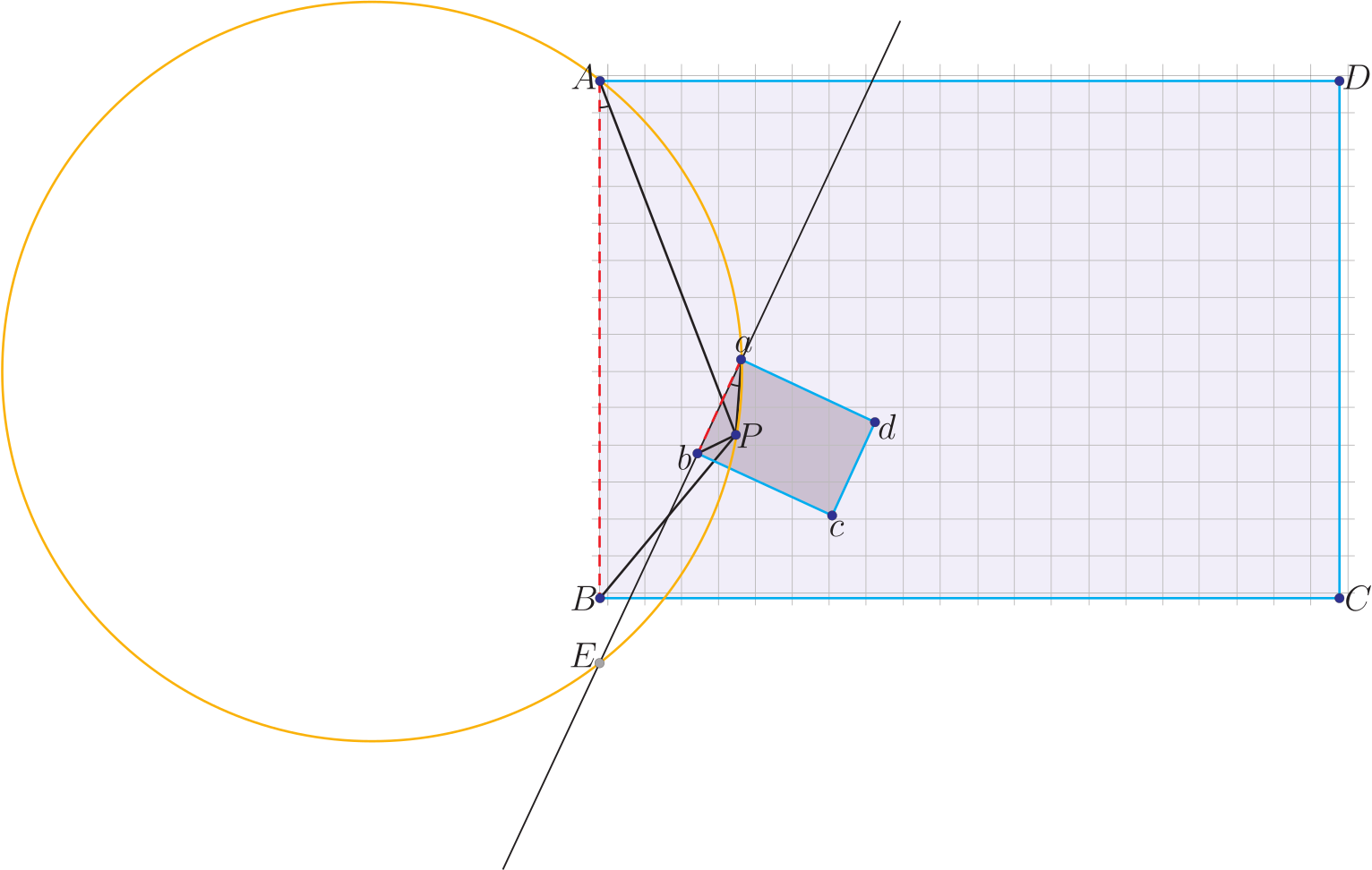

 

用相同的方式, 選擇對應邊 $\overline{BC}$ 與 $\overline{bc}$ ($\overline{bc}$ 延長線交 $\overline{BC}$ 於 $H$) 畫通過 $BbH$ 的圓, 這個圓內的圓周角 $PBC$ 與 $Pbc$ 是全等的。 顯然這個重疊的 $P$ 點也會在這個圓上。 (圖三)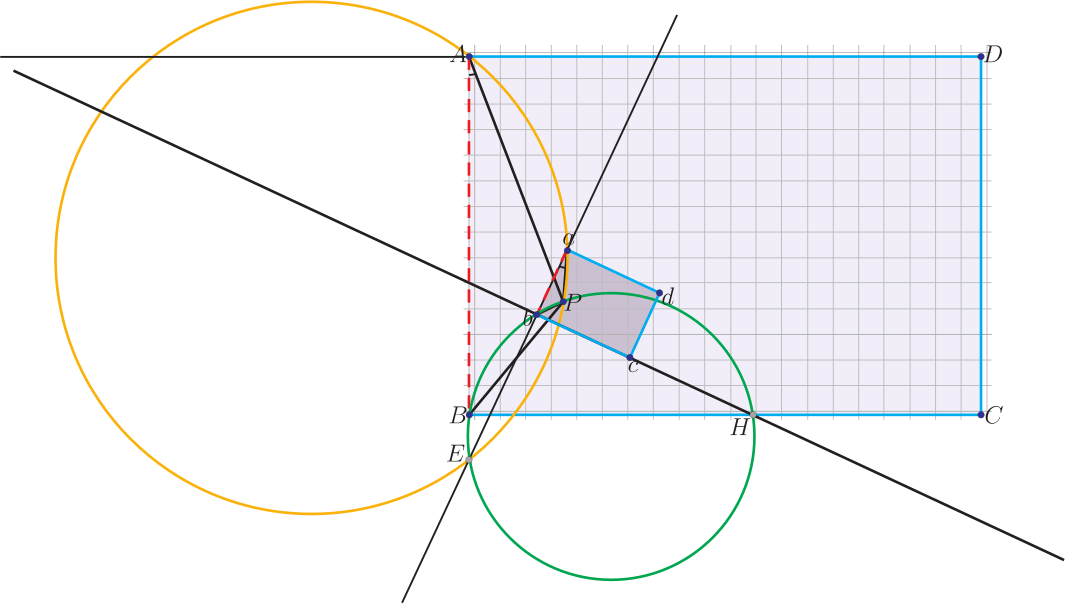

 

通過作圖方式來畫這兩個圓, 可找到兩個圓的交點。 這個交點就是我們要找的重疊的那一點。

總結來說

大小圖代表相同地點重疊的那一點的找法就是

1. 找某個對應邊, 小圖的對應邊延長到與大圖的對應邊找到交點, 用通過大小圖對應點與那個交點(三個點可決定一個圓)畫圓。
2. 找另一個對應邊, 同樣的方式延長小圖對應邊與大圖的對應邊找到交點, 再畫出另一個圓。
3. 這兩個圓的交點就是重疊的那一點。

本文作者任職璺到底皮膚專科診所