| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | 圓內接四邊形內部矩形的面積討論 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
摘要: 本文主要推導圓內接四邊形日本定理的內部矩形函數(與角度有關的三變數函數), 再藉此函數來討論此特殊矩形的相關性質, 並提出未來可以討論的方向。 壹、前言根據圓內接四邊形的日本定理, 其內部可以形成一特別的矩形。 劉步松先生也於《數學傳播》第 34 卷 4 期 首先我們先引用劉步松先生於《數學傳播》第 34 卷 4 期 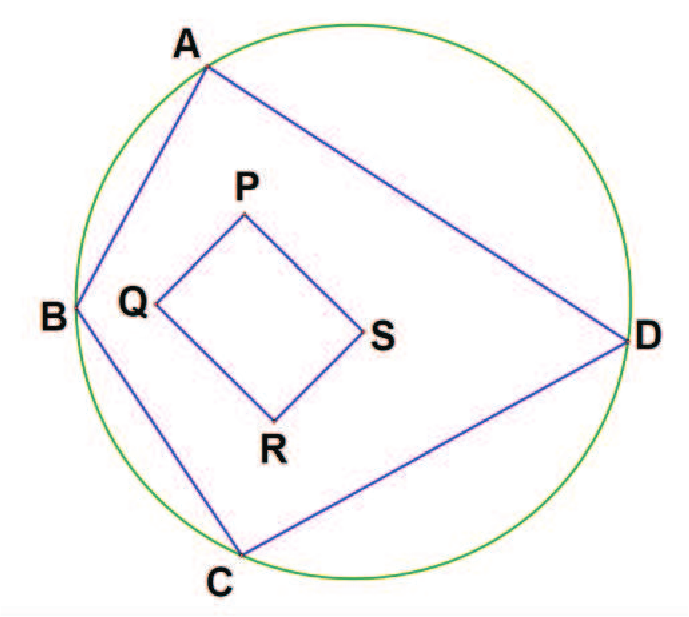 如[圖1], 有下列二種性質: 性質一: (圓內接四邊形的日本定理) 圓內接四邊形 $ABCD$, 兩對角線所分成的四個三角形, 其中 $P$、 $Q$、 $R$、 $S$ 為分別為 $\triangle ABD$、 $\triangle ABC$、 $\triangle BCD$、 $\triangle ACD$ 的內心, 其內心連線 $PQRS$ 為一個矩形。 性質二: (圓內接四邊形的日本定理) $A$、 $P$、 $Q$、 $B$ 四點共圓, 依此類推 $B$、 $Q$、 $R$、 $C$ 與 $C$、 $R$、 $S$、 $D$ 與 $D$、 $S$、 $P$、 $A$ 四點共圓。 為了方便後續討論, 引入[性質三] : $$\sin (X+Y) \sin (X-Y)=\sin^2(X)-\sin^2(Y).$$ 貳、主要結果接著我們從鳶形出發, 一步步推廣到圓內接任意四邊形。 第一步:內接鳶形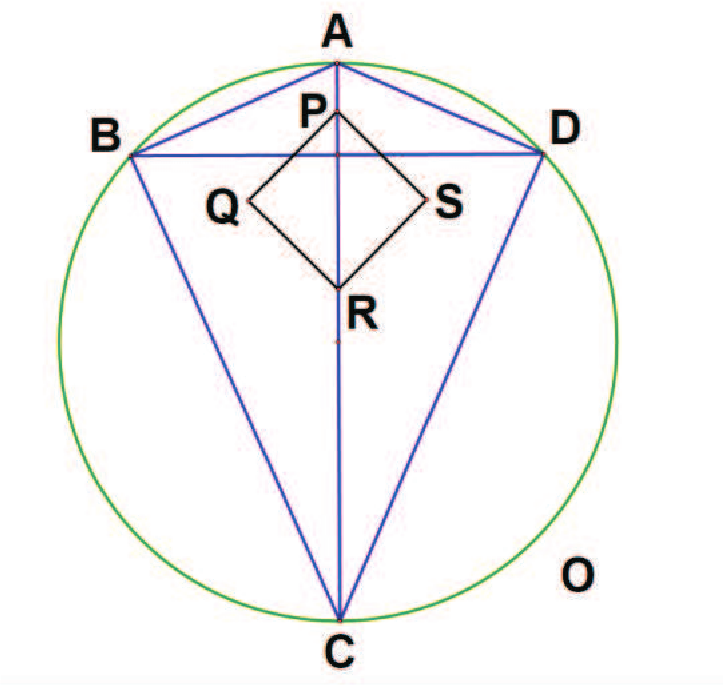 一個圓 $O$ 半徑為 $r$, 如[圖2], 作一內接鳶形 $ABCD$, 其中 $\overline{AC}$ 為單位圓的直徑 (故 $ABCD$ 左右對稱), 令 $\angle BAC= \angle DAC=\alpha $, 故 $\overline{AB}= \overline{AD}=2r \cos \alpha $, $\overline{CB}= \overline{CD}=2r \sin \alpha$。 針對 $\triangle ABD$、 $\triangle ABC$、 $\triangle BCD$、 $\triangle ACD$, 分別作其內心 $P$、 $Q$、 $R$、 $S$。 而 $P$、 $R$ 在直徑上, $Q$、 $S$ 以 $\overline{AC}$ 為軸左右對稱, 故顯然內部矩形 $PQRS$ 的對角線 $\overline{PR}\bot\overline{QS}$, 因此 $PQRS$ 為一正方形。 由直角三角形與內切圓半徑的基本性質, 可得對角線 $\overline{PR}= \overline{QS}=2r \cos \alpha +2r \sin \alpha -2r$ (內切圓半徑的 2 倍), 故 $PQRS$ 面積為 \begin{align} \frac 12 \overline{PR}^2=\frac 12 (2r \sin \alpha +2r \cos \alpha -2r)^2.\label{1} \end{align} 第二步:將 $D$ 點順時針方向在圓周上移動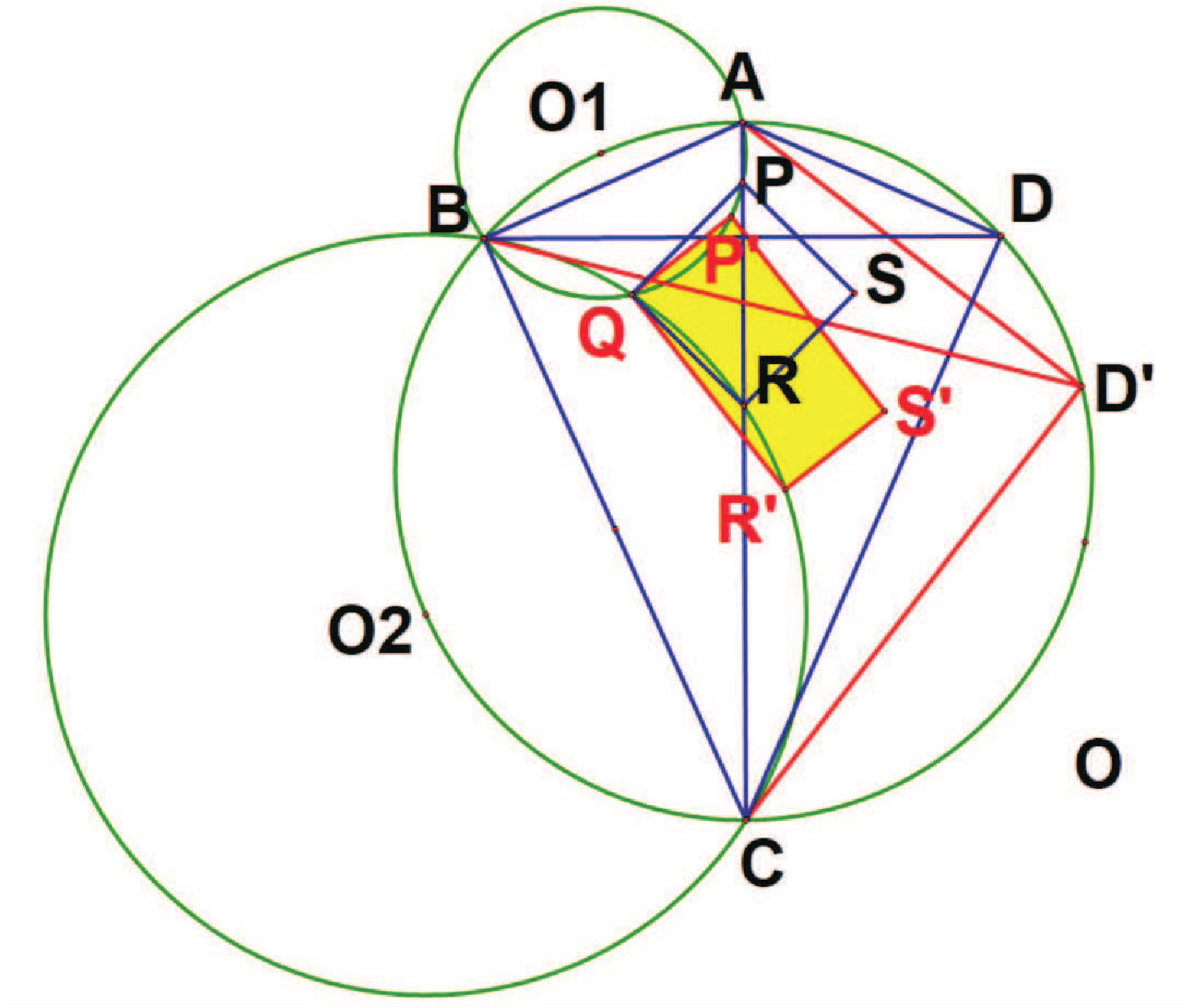 將[圖 2]中的 $D$ 點在圓周上順時針移動到 $D'$ ($D'$ 在 圓弧$CD$ 之間), 如[圖 3]。 使得 $\angle DAD'=\beta $。 此時四邊形由 $ABCD$ 變成 $ABCD'$, 所對應到的內心形成的內部矩形由 $PQRS$ 變為 $P' QR' S'$。 由[性質二]知 $A$、 $P$、 $P'$、 $Q$、 $B$ 五點共圓, 令此圓為 $O_1$, $O_1$ 半徑為 $r_1$; 同理, $B$、 $Q$、 $R$、 $R' $、 $C$ 五點共圓, 令此圓為 $O_2$, $O_2$ 半徑為 $r_2$。 又 $\angle PQP'= \angle PAP'= \angle P' AD'- \angle PAD'=(\alpha -\frac \beta 2)-(\alpha -\beta )=\frac \beta 2$, 而 $PQRS$ 與 $P' QR' S'$ 同為矩形, 因此 $\angle RQR'$亦為 $\frac \beta 2$, 即矩形 $PQRS$ 以 $Q$ 為中心旋轉 $\frac \beta 2$, 並伸縮長寬變為 $P' QR' S'$, 接下來我們繼續討論伸縮的方式。 由正弦定理知, 我們有 $\dfrac{\overline{AB}}{\sin \big(\frac \pi 2-\alpha \big)} =2r$ (在 $O$)且 $\dfrac{\overline{AB}}{\sin \big(\frac {3\pi}4-\frac \alpha 2\big)} =2r_1$ (在 $O_1$); $\dfrac{\overline{QB}}{\sin \big(\frac \alpha 2\big)} =2r_1$ (在 $O_1$)且 $\dfrac{\overline{QB}}{\sin \big(\frac \pi 4-\frac \alpha 2\big)} =2r_2$ (在 $O_2$)。 故三圓的半徑為 \begin{align*} r_1=\,&\dfrac{\sin \big(\frac \pi 2-\alpha \big)}{\sin\big(\frac{3\pi}4-\frac \alpha 2\big)}\cdot r =\dfrac{\cos (\alpha )}{\cos\big(\frac\pi 4-\frac \alpha 2\big)}\cdot r,\\ r_2=\,&\dfrac{\sin \big(\frac\alpha 2\big)}{\sin \big(\frac\pi 4-\frac \alpha 2\big)}\cdot r_1 =\frac{\sin \big(\frac\alpha 2\big)} {\sin \big(\frac\pi 4-\frac \alpha 2\big)} \frac{\cos(\alpha )}{\cos\big(\frac\pi 4-\frac \alpha 2\big)}\cdot r =\frac{2\sin\big(\frac\alpha 2\big)}{2 \sin \big(\frac\pi 4-\frac \alpha 2\big)} \frac{\cos(\alpha )}{\cos\big(\frac\pi 4-\frac \alpha 2\big)}\cdot r\\ =\,&\frac{2\sin\big(\frac\alpha 2\big)\cos (\alpha )}{\sin \big(\frac \pi 2-\alpha \big)}\cdot r=2 \sin \big(\frac\alpha 2\big)\cdot r. \end{align*} 而 $P'QR'S'$ 內部矩形的 $\overline{QP'}$ 與 $\overline{QR'}$ 其所對應的角度分別在 $O_1$ 的 $\angle QAP'$ 與 $O_2$ 的 $\angle QCR'$, 其中 $\angle QAP'= \angle QAP- \angle PAP'=\frac \alpha 2- \angle PQP'=\frac \alpha 2-\frac \beta 2$, $\angle QCR'= \angle QCR+ \angle RCR'=\frac \pi 4-\frac \alpha 2 + \angle RQR'=\frac \pi 4-\frac \alpha 2+\frac \beta 2$。 由正弦定理 $\dfrac{\overline{QP'}}{\sin \big(\frac\alpha 2-\frac \beta 2\big)} =2r_1$, $\dfrac{\overline{QR'}}{\sin \big(\frac\pi 4-\frac \alpha 2+\frac \beta 2\big)} =2r_2$, 得 \begin{align*} \overline{QP'}=\,&\dfrac{2 \cos(\alpha)\sin \big(\frac\alpha 2-\frac \beta 2\big)}{\cos\big(\frac\pi 4-\frac \alpha 2\big)}\cdot r =\frac{4 \cos (\alpha ) \sin\big(\frac\alpha 2-\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big)} {2 \sin \big(\frac\pi 4-\frac \alpha 2\big)\cos \big(\frac\pi 4-\frac \alpha 2\big)}\cdot r\\ =\,&\dfrac{4 \cos (\alpha ) \sin \big(\frac\alpha 2-\frac \beta 2\big)\sin \big(\frac\pi 4-\frac \alpha 2\big)} {\sin \big(\frac \pi 2-\alpha \big)}\cdot r=4 \sin \big(\frac\alpha 2-\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) \cdot r,\\ \overline{QR'}=\,&4 \sin \big(\frac\alpha 2\big) \sin \big(\frac\pi 4-\frac \alpha 2+\frac \beta 2\big)\cdot r. \end{align*} 故矩形 $$P' QR' S'=\overline{QP'}\cdot \overline{QR'}=16 \sin \big(\frac\alpha 2\big) \sin \big(\frac\alpha 2-\frac \beta 2\big)\sin \big(\frac\pi 4-\frac \alpha 2+\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2.$$ 若 $D$ 點在圓周上移動的方向為逆時針, 仿照同樣方式可得到矩形面積為 \begin{align} 16 \sin \big(\frac\alpha 2\big)\sin \big(\frac\alpha 2+\frac \beta 2\big)\sin\big(\frac\pi 4-\frac \alpha 2-\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big)\cdot r^2, \label{2} %……(公式2) \end{align} 即 $D$ 點移動方向相反, 針對式子 $\beta$ 作變號即可。 我們以此式子為主以符合廣義角逆正順負的習慣 (移動後的 $D'$需在 圓弧$ADC$ 之間)。 第三步:將 $C$ 點順時針方向在圓周上移動在[圖 3]中, 將 $C$ 點在圓周上順時針移動到 $C'$ ($C'$ 在 圓弧$BC$ 之間), 使得 $\angle CAC'=\gamma $, 如[圖 4]。 此時四邊形由 $ABCD'$ 變成 $ABC' D'$, 所對應到的內心形成的內部矩形由 $P' QR' S'$ 變為 $P' Q' R'' S''$。 由[性質二]知 $A$、$P' $、 $Q$、 $Q'$、 $B$ 五點共圓(與 [圖 3]的 $O_1$ 相同); 同理, $A$、 $P'$、 $S''$、 $S' $、 $D'$ 五點共圓, 令此圓為 $O_3$, $O_3$ 半徑為 $r_3$。 又 $\angle Q' P' Q= \angle Q' BQ= \angle Q' BA- \angle QBA=\big(\frac\pi 4+\frac \gamma 2\big)-\frac \pi 4=\frac \gamma 2$, 而 $P' QR' S'$ 與 $P' Q' R''S''$ 同為矩形, 因此 $\angle S' P' S''$ 亦為 $\frac \gamma 2$, 即矩形 $P' QR' S'$ 以 $P'$ 為中心旋轉 $\frac \gamma 2$, 並伸縮長寬為 $P' Q' R'' S''$, 我們同樣繼續討論伸縮的方式。 由正弦定理知, 我們有 $\dfrac{\overline{AP'}}{\sin \big(\frac\pi 4-\frac \alpha 2+\frac \beta 2\big)} =2r_1$ (在 $O_1$) 且 $\dfrac{\overline{AP'}}{\sin \big(\frac\pi 4-\frac \alpha 2\big)} =2r_3$ (在 $O_3$), 故 $O_3$ 的半徑為 $r_3=2\sin\big(\frac\pi 4-\frac \alpha 2+\frac \beta 2\big)\cdot r$。 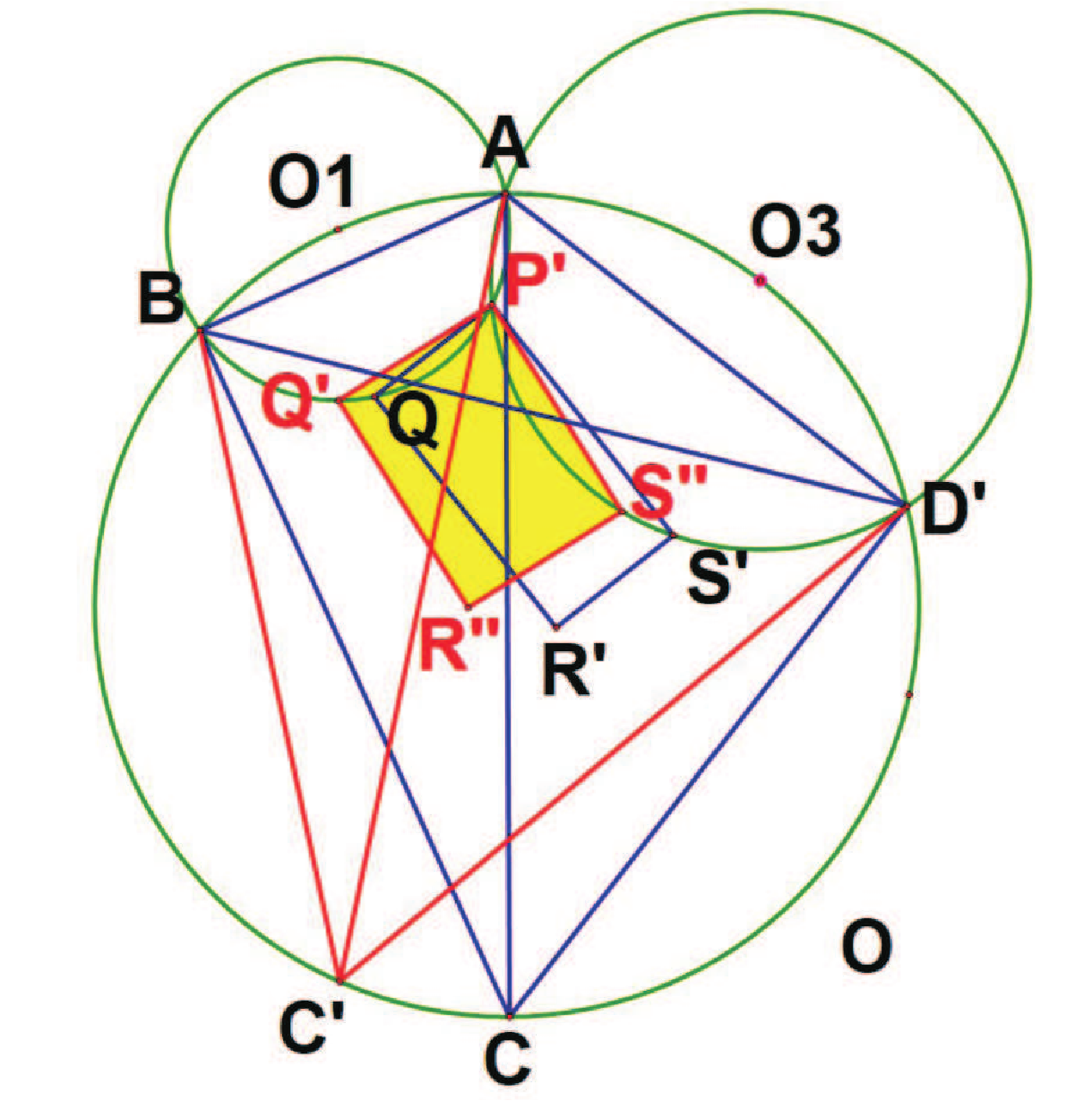 而 $P' Q' R'' S''$ 內部矩形的 $\overline{P'Q'}$ 與 $\overline{P' S''}$ 其所對應的角度分別在 $C_1$ 的 $\angle P' BQ'$ 與 $C_3$ 的 $\angle P' D' S''$, 其中 $\angle P' BQ'= \angle ABQ'- \angle ABP'=\big(\frac\pi 4+\frac \gamma 2\big)-\big(\frac\pi 4-\frac \alpha 2+\frac \beta 2\big)=\frac \alpha 2-\frac \beta 2 +\frac \gamma 2$, $ \angle P' D' S''= \angle AD' S''- \angle AD' P'=\big(\frac\pi 4-\frac \gamma 2\big)-\big(\frac\pi 4-\frac \alpha 2\big)= \frac \alpha 2-\frac \gamma 2$。 再由正弦定理 $\dfrac{\overline{P'Q'}}{\sin \big(\frac\alpha 2-\frac\beta 2+\frac \gamma 2\big)} =2r_1$, $\dfrac{\overline{P' S''}}{\sin \big(\frac\alpha 2-\frac \gamma 2\big)}=2r_3$, 得 \begin{align*} \overline{P'Q'}=\,&\frac{2 \cos (\alpha ) \sin \big(\frac\alpha 2-\frac\beta 2+\frac \gamma 2\big)}{\cos\big(\frac\pi 4-\frac \alpha 2\big)}\cdot r =\frac{4 \cos (\alpha )\sin\big(\frac\alpha 2-\frac\beta 2+\frac \gamma 2\big)\sin \big(\frac\pi 4-\frac \alpha 2\big)} {2 \sin \big(\frac\pi 4-\frac \alpha 2\big) \cos \big(\frac\pi 4-\frac \alpha 2\big)}\\ =\,&\frac{4\cos (\alpha ) \sin\big(\frac\alpha 2-\frac\beta 2+\frac \gamma 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big)}{\sin \big(\frac\pi 2-\alpha\big)} =4 \sin \big(\frac\alpha 2-\frac\beta 2+\frac \gamma 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big), \end{align*} $$\overline{P' S''}=4 \sin \big(\frac\alpha 2-\frac \gamma 2\big) \sin \big(\frac\pi 4-\frac \alpha 2+\frac \beta 2\big)\cdot r.$$ 故矩形 $P' Q' R'' S''=\overline{P'Q'}\cdot \overline{P'R''}=16 \sin \big(\frac\alpha 2-\frac \gamma 2\big)\sin \big(\frac\alpha 2-\frac\beta 2+\frac \gamma 2\big) \sin \big(\frac\pi 4-\frac \alpha 2+\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2$。 若 $C$ 點在圓周上移動方向為逆時針, 仿照上述方式可得到矩形面積為 $$16 \sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2-\frac\beta 2-\frac \gamma 2\big) \sin \big(\frac\pi 4-\frac \alpha 2+\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2,$$ 即 $C$ 點移動方向相反, 針對式子 $\gamma$ 作變號即可 (移動後的 $C'$ 需在 圓弧$BCD'$ 之間)。 搭配 \eqref{2}, 同樣為了符合逆正順負的習慣, 我們將式子改成 \begin{align} 16 \sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2+\frac\beta 2-\frac \gamma 2\big) \sin\big(\frac\pi 4-\frac \alpha 2-\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2. %……(公式3) \label{3}\end{align} 參、應用與討論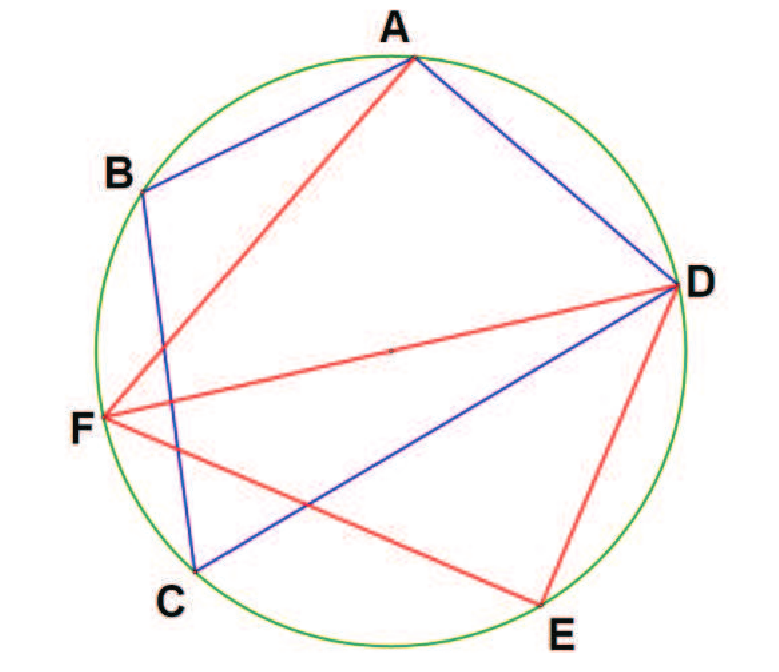 應用一: 利用推導的矩形面積公式, 透過角度的變化來計算內部矩形面積。 如[圖 5], 任意四邊形 $ABCD$, 過 $D$ 作圓的直徑 $\overline{DF}$, 以 $\overline{DF}$ 為軸, 作 $A$ 的對稱點 $E$, 此時得到四邊形(鳶形) $ADEF$。 從鳶形 $ADEF$ 與四邊形 $ABCD$ 相比較, 即可得到 $\alpha = \angle ADF$, $\beta = \angle EDC$, $\gamma = \angle FDB$, 代入 \eqref{3} 即可得到內部矩形面積。 應用二: 觀察 \eqref{3} $16 \sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2+\frac\beta 2-\frac \gamma 2\big) \sin\big(\frac\pi 4-\frac \alpha 2-\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2$, 當 $\gamma =0$, 即可得到 $16 \sin \big(\frac\alpha 2\big) \sin \big(\frac\alpha 2+\frac \beta 2\big) \sin\big(\frac\pi 4-\frac \alpha 2-\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2$, 此即為 \eqref{2} ; 當 $\beta =\gamma =0$, 即可得到 $\frac 12 (2r \cos \alpha +2r \sin \alpha -2r)^2$, 此為 \eqref{1}。 故 \eqref{1} 、 \eqref{2} 為 \eqref{3} 的特例。 應用三: 我們觀察 \eqref{1} $\frac 12 (2r \sin \alpha +2r \cos \alpha -2r)^2$, 顯然 \eqref{1} 有最大值 $(6-4\sqrt{2})r^2$。 應用四: 再來我們觀察 \eqref{2} $$16 \sin \big(\frac\alpha 2\big) \sin \big(\frac\alpha 2+\frac \beta 2\big) \sin\big(\frac\pi 4-\frac \alpha 2-\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2.$$ 利用[性質三], 令 $X+Y=\frac \alpha 2$, $X-Y=\frac \pi 4-\frac \alpha 2$, 故其中 $\sin \big(\frac\alpha 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big)=\sin (X+Y)\sin (X-Y)=\sin^2(X)-\sin^2(Y)=\sin^2\big(\frac\pi 8\big) -\sin^2 \big(\frac\alpha 2-\frac \pi 8\big)$, 顯然當 $\frac \alpha 2=\frac \pi 8$, $\sin \big(\frac\alpha 2\big)\sin \big(\frac\pi 4-\frac \alpha 2\big)$ 有最大值 $\sin^2\big(\frac\pi 8\big)=\dfrac{2-\sqrt{2}}4$; 同理 $\sin \big(\frac\alpha 2+\frac \beta 2\big)\sin\big(\frac\pi 4-\frac \alpha 2-\frac \beta 2\big)$, 當 $\frac \alpha 2+\frac \beta 2=\frac \pi 4$ 會有最大值 $\dfrac{2-\sqrt{2}}4$。 故 \eqref{2} 會在 $\frac \alpha 2=\frac \pi 8$ 且 $\frac \alpha 2+\frac \beta 2=\frac \pi 8$ 會有最大值, 即 $\alpha =\frac \pi 4$, $\beta =0$, 會有最大值 $(6-4\sqrt{2}) r^2$。 應用五: 進一步觀察 \eqref{3} $$16 \sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2+\frac\beta 2 -\frac \gamma 2\big)\sin\big(\frac\pi 4-\frac \alpha 2-\frac \beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2,$$ 顯然與 \eqref{2} 差在 $\sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2+\frac\beta 2-\frac \gamma 2\big)$, 因此我們將 $\alpha $、 $\beta$ 視為常數, $\gamma$ 為變數來討論 $\sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2+\frac\beta 2-\frac \gamma 2\big)$。 同前述類似手法, 令 $X+Y=\frac \alpha 2+\frac \gamma 2$, $X-Y=\frac \alpha 2+\frac \beta 2-\frac \gamma 2$, 則 $\sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2+\frac\beta 2-\frac \gamma 2\big)=\sin (X+Y) \sin (X-Y)=\sin^2(X)-\sin^2(Y)=\sin^2\big(\frac\alpha 2+\frac \beta 4\big)-\sin^2\big(-\frac\beta 4+\frac \gamma 2\big)$, 顯然在 $\gamma =\frac \beta 2$, $\sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2+\frac\beta 2-\frac \gamma 2\big)$ 會有最大值 $\sin \big(\frac\alpha 2+\frac \beta 4\big) \sin \big(\frac\alpha 2+\frac \beta 4\big)$。 即 $16 \sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2+\frac\beta 2-\frac \gamma 2\big) \sin \big(\frac \pi 4-\frac\alpha 2-\frac\beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2 \le 16 \sin \big(\frac\alpha 2+\frac \beta 4\big) \sin \big(\frac\alpha 2+\frac \beta 4\big) \sin \big(\frac \pi 4-\frac\alpha 2-\frac\beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2$。 從不等關係可知道, 在主要結果的第三步驟, 當 $C'$ 移動所形成的矩形中, 會在 $\gamma =\frac \beta 2$ 會有最大矩形面積。 應用六: 接著我們繼續前述「應用五」的不等關係: \begin{align*} &\hskip -15pt 16 \sin \big(\frac\alpha 2+\frac \gamma 2\big) \sin \big(\frac\alpha 2+\frac\beta 2-\frac \gamma 2\big) \sin\big(\frac \pi 4-\frac\alpha 2-\frac\beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2\\ \le \,&16 \sin\big(\frac\alpha 2+\frac \beta 4\big) \sin \big(\frac\alpha 2+\frac \beta 4\big)\sin \big(\frac \pi 4-\frac\alpha 2-\frac\beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big) r^2\\ =\,&16 \sin^2\big(\frac\alpha 2+\frac \beta 4\big)\big[\sin\big(\frac \pi 4-\frac\alpha 2-\frac\beta 2\big) \sin \big(\frac\pi 4-\frac \alpha 2\big)\big] r^2, \end{align*} 再利用[性質三]技巧, 令 $X+Y=\frac \pi 4-\frac \alpha 2-\frac \beta 2$, $X-Y=\frac \pi 4-\frac \alpha 2$, 我們有 \begin{align*} &\hskip -15pt 16\sin^2 \big(\frac\alpha 2+\frac \beta 4\big)\big[\sin \big(\frac \pi 4-\frac\alpha 2-\frac\beta 2\big)\sin \big(\frac\pi 4-\frac \alpha 2\big)\big]r^2\\ =\,&16\sin^2 \big(\frac\alpha 2+\frac \beta 4\big)\big[\sin^2 \big(\frac \pi 4-\frac\alpha 2-\frac\beta 4\big)-\sin^2(-\frac \beta 4) \big] r^2\\ =\,&16\Big\{\big[\sin \big(\frac\alpha 2+\frac \beta 4\big) \sin\big(\frac \pi 4-\frac\alpha 2-\frac\beta 4\big)\big]^2 -\big[\sin \big(\frac\alpha 2+\frac \beta 4\big) \sin (-\frac \beta 4) \big]^2 \Big\} r^2\\ =\,&16\Big\{\big[\sin^2 \big(\frac\pi 8\big)-\sin^2 \big(\frac\alpha 2+\frac\beta 4-\frac \pi 8\big)\big]^2 -\big[\sin^2 (\frac \alpha 4)-\sin^2 \big(\frac\alpha 4+\frac\beta 4\big)\big]^2 \Big\} r^2.\\ &\quad \hbox{(此處一樣以[性質三]的技巧處理, 在此就不贅述)} \end{align*} 可以觀察得到, 當 $\frac\alpha 2+\frac\beta 4-\frac \pi 8=0$ 且 $\frac \alpha 4=\frac \alpha 4+\frac \beta 4$, 即當 $\alpha =\frac \pi 4$, $\beta =0$, $$16\Big\{\big[\sin^2 \big(\frac\pi 8\big)-\sin^2\big(\frac\alpha 2+\frac\beta 4-\frac \pi 8\big)\big]^2-[\sin^2 (\frac \alpha 4) -\sin^2\big(\frac\alpha 4+\frac\beta 4\big) \big]^2 \Big\} r^2$$ 有最大值 $(6-4\sqrt{2}) r^2$。 又由於 $\beta =\gamma =0$ 符合 $\gamma =\frac \beta 2$ (應用五最後的不等式), 因此 \eqref{3} 會有最大值 $(6-4\sqrt{2}) r^2$。 從「應用二」至「應用六」, 我們可以知道任意圓內接四邊形在 $\alpha =\frac \pi 4$, $\beta =0$, $\gamma =0$ 有最大面積為 $(6-4\sqrt{2}) r^2$ (即圓內接四邊形為正方形, 內部矩形面積最大)。 這裡提供圖形的測量與式子計算作驗證, 如[圖 6], 供讀者參考。 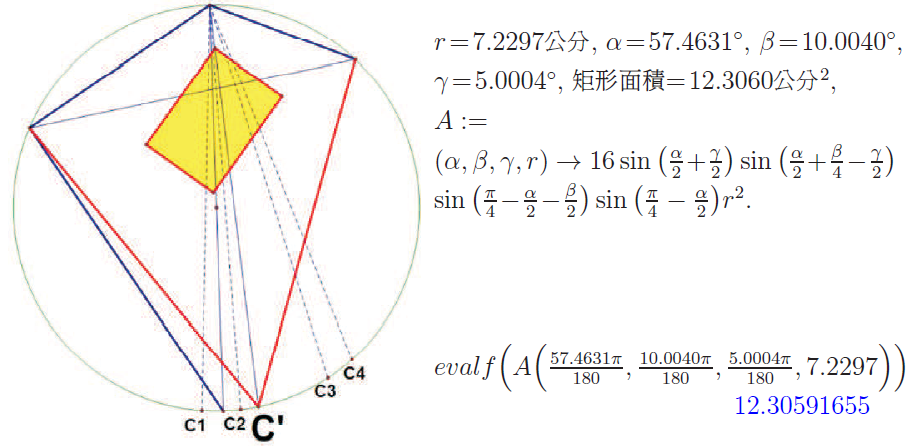 肆、後記與其他針對「圓內部的所有任意矩形, 是否都能對應到一圓內接四邊形?」 可做為另一個可討論的議題。 而筆者透過尺規作圖的操作, 猜測「並非圓內任意的矩形都可以有一個對應的圓內接四邊形」, 故後續應可以再繼續討論何種條件的矩形才會有相對應的圓內接四邊形。 而隨著內接四邊形頂點的移動, 內部矩形會繞著某個頂點作旋轉, 同時改變長寬, 透過此特性, 可作內部矩形的堆疊, 亦可討論圓周上頂點的移動與矩形堆疊方式的關係。 針對此類相關問題, 筆者以本文拋磚引玉, 期望未來有數學先進前輩能在此類問題上給予更多有趣的延伸討論。 致謝感謝審稿委員們的建議及指教, 也感謝編輯委員們不厭其煩協助修正。 參考文獻本文作者為新北市立清水高中數學科教師, 亦為參考文獻中科展作品指導教師 |
| 頁碼 | 83-90 |
2025年6月 49卷2期
圓內接四邊形內部矩形的面積討論

