| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | 一道組合恆等式的另證 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
一、前言在數學傳播第 164 期《關於初等對稱多項式的一類恆等式》一文當中(請參考 推論: \begin{equation} \left(\sum_{k=0}^{\left[\frac n2\right]}(-1)^k C_{2k}^n\right)^2+\left(\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k+1}^n\right)^2=2^n .\label{1} \end{equation} 上述推論結果與組合數有關, 不妨稱其為一道組合恆等式。 筆者進行研究過後, 對於組合恆等式 \eqref{1} 找出了兩個另證, 兩者皆不需透過 $$S_n=\sum_{k=0}^{\left[\frac n2\right]}(-1)^k C_{2k}^n,\qquad T_n=\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k+1}^n,$$ 接著再求出數列 $\langle S_n\rangle$, $\langle T_n\rangle $ 所滿足的遞迴式, 以完成證明。 在底下的第二與第三小節中, 筆者將依序介紹上面所提到的兩個證明。 而在接著的第四小節中, 筆者將會延續第二個證明, 進一步介紹自己將上述 $S_n$, $T_n$ 兩表達式化簡的過程以及所得到的一些相關推論結果。 二、第一個證明首先, 由二項式定理可知 \begin{equation} (1+x)^n=C_0^n+C_1^n x+\cdots+C_n^n x^n.\label{2} \end{equation} 我們考慮將 \eqref{2} 式改寫, 改寫方式為: 在 \eqref{2} 右式具備 $C_k^n x^k$ 形式的 $n+1$ 項之中, 將所有 $k$ 為偶數的項放在一起, 並將其餘 $k$ 為奇數的項也放在一起。 改寫之後的結果如下: \begin{eqnarray} (1+x)^n&=&(C_0^n+C_2^n x^2+\cdots+C_{2a}^n x^{2a} )+(C_1^n x+C_3^n x^3+\cdots+C_{2b+1}^n x^{2b+1} )\nonumber\\ &=&\sum_{k=0}^aC_{2k}^n x^{2k} +\sum_{k=0}^b C_{2k+1}^n x^{2k+1}, \label{3} \end{eqnarray} 其中令 $2a$ 是不超過 $n$ 的最大偶數, 而 $2b+1$ 則是不超過 $n$ 的最大奇數。 在 \eqref{3} 式中, 由於 $2a$ 是小於或等於 $n$ 的最大偶數, 因此在大於 $2a$ 的偶數中, 最小的 $2a+2$ 必須比 $n$ 大, 從而可知 $2a\le n$ 且 $2a+2\gt n$, 合起來寫就是 \begin{equation} 2a\le n\lt2a+2. \label{4} \end{equation} 因此得 $$a\le \frac n2\lt a+1,$$ 所以有 \begin{equation} \left[\frac n2\right ]=a,\label{5} \end{equation} 其中高斯符號 $[x]$ 表示不超過 $x$ 的最大整數。 又因為 $2b+1$ 是小於或等於 $n$ 的最大奇數, 仿照寫下 \eqref{4} 式之前的討論過程, 可知 $$2b+1\le n\lt2b+3.$$ 因此得 $$b\le \frac{n-1}2\lt b+1,$$ 所以有 \begin{equation} \left[\frac {n-1}2\right ]=b .\label{6} \end{equation} 將 \eqref{5}, \eqref{6} 兩式的推論結果代入 \eqref{3} 式, 可知 \begin{eqnarray} (1+x)^n&=&\sum_{k=0}^{\left[\frac n2\right]}C_{2k}^n x^{2k}+\sum_{k=0}^{\left[\frac {n-1}2\right]} C_{2k+1}^n x^{2k+1} \nonumber\\ &=&\sum_{k=0}^{\left[\frac n2\right]}C_{2k}^n x^{2k} +x\cdot \sum_{k=0}^{\left[\frac {n-1}2\right]}C_{2k+1}^n x^{2k}.\label{7} \end{eqnarray} 接著分別以 $x=i$ 與 $x=-i$ 代入 \eqref{7} 式, 其中 $i$ 為虛數單位, 則可得底下兩式 : \begin{eqnarray} (1+i)^n&=&\sum_{k=0}^{\left[\frac n2\right]}(-1)^k C_{2k}^n +i\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k+1}^n, \label{8}\\ (1-i)^n&=&\sum_{k=0}^{\left[\frac n2\right]}(-1)^k C_{2k}^n -i\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k+1}^n. \label{9} \end{eqnarray} 最後只要將 \eqref{8}, \eqref{9} 兩式相乘, 即得 $$2^n=\left(\sum_{k=0}^{\left[\frac n2\right]}(-1)^k C_{2k}^n \right)^2+\left(\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k+1}^n \right)^2,$$ 這樣我們就證明了 \eqref{1} 式。 三、第二個證明在第一節中, 我們介紹了底下 $S_n$ 與 $T_n$ 的表達式: \begin{eqnarray} S_n&=&\sum_{k=0}^{\left[\frac n2\right]}(-1)^k C_{2k}^n =C_0^n-C_2^n+\cdots+(-1)^{[n/2]} C_{2[n/2]}^n,\label{10}\\ T_n&=&\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k+1}^n =C_1^n-C_3^n+\cdots+(-1)^{[(n-1)/2]} C_{2[(n-1)/2]+1}^n,\label{11} \end{eqnarray} 注意我們有初始值 $S_1=T_1=1$。 利用上述兩式, 我們可將所證明的 \eqref{1} 式改寫為 \begin{equation} {S_n}^2+{T_n}^2=2^n. \label{12} \end{equation} 在底下的內容中, 筆者將會證明 \eqref{12} 式成立。 在證明 \eqref{12} 式之前, 筆者先證明數列 $\langle S_n\rangle$, $\langle T_n\rangle $ 滿足底下兩遞迴式 : \begin{eqnarray} S_n&=&S_{n-1}-T_{n-1},\label{13}\\ T_n&=& S_{n-1}+T_{n-1},\label{14} \end{eqnarray} 其中 $n\ge 2$, 證明如下: 證明: 對 $n$ 為偶數與 $n$ 為奇數的兩種情形, 我們分開討論如下: (a) 當 $n$ 為偶數時, 令 $n=2m$, 其中 $m\ge 1$, 則此時有 $$\left[\frac n 2\right]=m,\qquad \left[\frac{n-1}2\right]= \left[\frac{n-2}2\right]=m-1.$$ 利用巴斯卡定理, 由 \eqref{10}, \eqref{11} 兩式可知 \begin{eqnarray*} S_n=S_{2m}&=&\sum_{k=0}^m(-1)^k C_{2k}^{2m}=C_0^{2m}+\sum_{k=1}^{m-1}(-1)^k C_{2k}^{2m}+(-1)^m C_{2m}^{2m}\\ &=&C_0^{2m-1}+\sum_{k=1}^{m-1}(-1)^k (C_{2k-1}^{2m-1}+C_{2k}^{2m-1} )+(-1)^m C_{2m-1}^{2m-1}\\ &=&\sum_{k=0}^{m-1}(-1)^k C_{2k}^{2m-1}+\sum_{k=0}^{m-2}(-1)^{k+1} C_{2k+1}^{2m-1}+(-1)^m C_{2m-1}^{2m-1}\\ &=&\sum_{k=0}^{m-1}(-1)^k C_{2k}^{2m-1}+\sum_{k=0}^{m-1}(-1)^{k+1} C_{2k+1}^{2m-1}\\ &=&\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k}^{n-1}-\sum_{k=0}^{\left[\frac{n-2}2\right]}(-1)^k C_{2k+1}^{n-1}=S_{n-1}-T_{n-1},\\ T_n=T_{2m}&=&\sum_{k=0}^{m-1}(-1)^k C_{2k+1}^{2m}=\sum_{k=0}^{m-1}(-1)^k (C_{2k}^{2m-1}+C_{2k+1}^{2m-1} )\\ &=&\sum_{k=0}^{m-1}(-1)^k C_{2k}^{2m-1} +\sum_{k=0}^{m-1}(-1)^k C_{2k+1}^{2m-1}\\ &=&\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k}^{n-1}+\sum_{k=0}^{\left[\frac{n-2}2\right]}(-1)^k C_{2k+1}^{n-1} =S_{n-1}+T_{n-1}, \end{eqnarray*} 因此知此情形下 \eqref{13}, \eqref{14} 兩式成立。 (b) 當 $n$ 為奇數時, 令 $n=2m+1$, 其中 $m\ge 1$, 則此時有 $$\left[\frac n 2\right]=\left[\frac{n-1}2\right]=m,\qquad \left[\frac{n-2}2\right]=m-1.$$ 再次利用巴斯卡定理, 由 \eqref{10}, \eqref{11} 兩式可知 \begin{eqnarray*} S_n=S_{2m+1}&=&\sum_{k=0}^m(-1)^k C_{2k}^{2m+1}=C_0^{2m+1}+\sum_{k=1}^m(-1)^k C_{2k}^{2m+1}\\ &=&C_0^{2m}+\sum_{k=1}^m(-1)^k (C_{2k-1}^{2m}+C_{2k}^{2m} )\\ &=&\sum_{k=0}^m(-1)^k C_{2k}^{2m} +\sum_{k=0}^{m-1}(-1)^{k+1} C_{2k+1}^{2m}\\ &=&\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k}^{n-1} -\sum_{k=0}^{\left[\frac{n-2}2\right]}(-1)^k C_{2k+1}^{n-1}=S_{n-1}-T_{n-1},\\ T_n=T_{2m+1}&=&\sum_{k=0}^m(-1)^k C_{2k+1}^{2m+1}=\sum_{k=0}^{m-1}(-1)^k C_{2k+1}^{2m+1}+(-1)^m C_{2m+1}^{2m+1}\\ &=&\sum_{k=0}^{m-1}(-1)^k (C_{2k}^{2m}+C_{2k+1}^{2m} )+(-1)^m C_{2m}^{2m}\\ &=&\sum_{k=0}^m(-1)^k C_{2k}^{2m}+\sum_{k=0}^{m-1}(-1)^k C_{2k+1}^{2m} \\ &=&\sum_{k=0}^{\left[\frac {n-1}2\right]}(-1)^k C_{2k}^{n-1}+\sum_{k=0}^{\left[\frac{n-2}2\right]}(-1)^k C_{2k+1}^{n-1}=S_{n-1}+T_{n-1}, \end{eqnarray*} 因此知此情形下 \eqref{13}, \eqref{14} 兩式亦成立。 由以上 (a), (b) 兩項目的討論結果可知當 $n\ge 2$ 時 \eqref{13}, \eqref{14} 兩式恆成立, 證明完畢。 接下來, 當 $n\ge 2$ 時, 利用 \eqref{13}, \eqref{14} 兩式可推得 $${S_n}^2+{T_n}^2=(S_{n-1}-T_{n-1} )^2+(S_{n-1}+T_{n-1} )^2=2({S_{n-1}}^2+{T_{n-1}}^2 ).$$ 若令 $D_n={S_n}^2+{T_n}^2$, 其中 $n$ 為正整數, 則上式可改寫為 $$D_n=2D_{n-1}.$$ 注意 $D_1={S_1}^2+{T_1}^2=2$, 而當 $n\ge 2$ 時, 可推得 \begin{equation} D_n=2D_{n-1}=\cdots=2^{n-1} D_1=2^n ,\label{15} \end{equation} 從而對任意正整數 $n$ 均有 $${S_n}^2+{T_n}^2=D_n=2^n.$$ 至此我們就證明了 \eqref{12} 式, 而它就是 \eqref{1} 式, 故我們得到 \eqref{1} 式的第二個證明。 四、進一步的探討我們知道底下的二項式定理展開式: $$(x+y)^n=C_0^n y^n+C_1^n xy^{n-1}+\cdots+C_{n-1}^n x^{n-1} y+C_n^n x^n.$$ 在上式中, 若取 $x=y=1$, 可得 \begin{equation} C_0^n+C_1^n+\cdots+C_{n-1}^n+C_n^n=2^n;\label{16} \end{equation} 若另取 $x=-1$, $y=1$, 可得 $$C_0^n-C_1^n +\cdots+C_{n-1}^n (-1)^{n-1}+C_n^n (-1)^n=0.$$ 把上式中帶有負號的項移到等號右側, 只要參考前面把 \eqref{3} 式改寫成 \eqref{7} 式的過程, 可知移項後將得到 \begin{equation} C_0^n+C_2^n+\cdots+C_{2[n/2]}^n=C_1^n+C_3^n+\cdots+C_{2[(n-1)/2]+1}^n.\label{17} \end{equation} 注意上式等號兩側的所有項, 分別是 \eqref{16} 左式一般項 $C_k^n$ 中 $k$ 為偶數以及 $k$ 為奇數的所有項, 因此 \eqref{17} 式等號兩側所有項之和各占 $2^n$ 的一半, 即 \begin{equation} C_0^n+C_2^n+\cdots+C_{2[n/2]}^n=C_1^n+C_3^n+\cdots+C_{2[(n-1)/2]+1}^n=\frac{2^n}2=2^{n-1}.\label{18} \end{equation} 回顧 \eqref{10}, \eqref{11} 兩式中的 $S_n$ 與 $T_n$, 它們是否像 \eqref{17} 式等號兩側的表達式那樣, 可化簡為如同 \eqref{18} 式最後的 $2^{n-1}$ 那樣簡單的結果呢? 底下筆者將予以探討。 首先, 在 \eqref{13}, \eqref{14} 兩式所介紹的兩遞迴式, 可將其合併改寫成底下的矩陣形式: \begin{equation} \left[\begin{array}{c} S_n\\ T_n \end{array}\right]=\left[\begin{array}{ccc}1&\ ~&-1\\ 1&&1\end{array}\right] \left[\begin{array}{c}S_{n-1}\\ T_{n-1} \end{array}\right].\label{19} \end{equation} 如果令 $$V_n=\left[\begin{array}{c} S_n\\ T_n \end{array}\right], \qquad A=\left[\begin{array}{ccc} 1&&-1\\ 1&\ ~ &1\end{array}\right],$$ 則 \eqref{19} 式可改寫為 \begin{equation} V_n=AV_{n-1}.\label{20} \end{equation} 當 $n=1$ 時, 我們有 $$V_1=\left[\begin{array}{c} S_1\\ T_1 \end{array}\right]=\left[\begin{array}{c}1\\ 1\end{array}\right].$$ 而當 $n\ge 2$ 時只要利用 \eqref{20} 式, 如同 \eqref{15} 式那樣, 我們可寫下 $$V_n=AV_{n-1}=\cdots=A^{n-1} V_1,$$ 因此有 \begin{equation} \left[\begin{array}{c} S_n\\ T_n \end{array}\right]=A^{n-1} \left[\begin{array}{c} 1\\ 1\end{array}\right].\label{21} \end{equation} 由上式可知, 只要能寫出 $A^{n-1}$ 的表達式, 就可以寫下 $S_n$ 與 $T_n$ 的表達式。 為了求得 \eqref{21} 式中 $A^{n-1}$ 的表達式, 我們先寫下方陣 $A$ 的特徵方程式 $$\det(A-xI)=x^2-2x+2=0,$$ 並求解上式中的 $x$, 即可求得 $A$ 的兩特徵值為 $1\pm i$, 此時不妨令 $$\lambda_1=1+i,\quad \lambda_2=1-i.$$ 假設 $\lambda_1,\lambda_2$ 所對應的特徵向量分別為 $v_1,v_2$, 由 $Av_1=\lambda_1 v_1$ 與 $Av_2=\lambda_2 v_2$ 可求出 $$v_1=\left[\begin{array}{c} i\\ 1\end{array}\right] ,\qquad v_2=\left[\begin{array}{c} -i\\ 1\end{array}\right]$$ 為矩陣 $A$ 的一組特徵向量, 因此有 $$A\left[\begin{array}{c} i\\ 1\end{array}\right]=\lambda_1 \left[\begin{array}{c} i\\ 1\end{array}\right],\qquad A\left[\begin{array}{c} -i\\ 1\end{array}\right]=\lambda_2 \left[\begin{array}{c} -i\\ 1\end{array}\right].$$ 將上面兩式合併寫成 $$A\left[\begin{array}{ccc} i&\ ~&-i\\ 1&&1\end{array}\right]=\left[\begin{array}{ccc} i&\ ~&-i\\ 1&&1\end{array}\right] \left[\begin{array}{ccc}\lambda_1&\ ~&0\\ 0&&\lambda_2 \end{array}\right],$$ 因此得 $$A=\left[\begin{array}{ccc} i&\ ~&-i\\ 1&&1\end{array}\right]\left[\begin{array}{ccc}\lambda_1&\ ~&0\\ 0&&\lambda_2 \end{array}\right] \left[\begin{array}{ccc} i&\ ~&-i\\ 1&&1\end{array}\right]^{-1}.$$ 若以上式計算 $A^k=\underbrace{A\cdot A\cdots A}_{k\hbox{個}}$ 的話, 相乘時可消去中間許多方陣而得 \begin{equation} A^k=\left[\begin{array}{ccc} i&\ ~&-i\\ 1&&1\end{array}\right] \left[\begin{array}{ccc} {\lambda_1}^k&~&0\\ 0&&{\lambda_2}^k \end{array}\right] \left[\begin{array}{ccc} i&\ ~&-i\\ 1&&1\end{array}\right]^{-1}.\label{22} \end{equation} 假設方陣 $B=\left[\begin{array}{ccc} i&\ &-i\\ 1&&1\end{array}\right]$ 且設其反矩陣為 $B^{-1}=\left[\begin{array}{ccc} x&\ &y\\ z&&u\end{array}\right]$, 兩者代入關係式 $BB^{-1}=I$ 並求解 $x,y,z,u$ 四數後(其中 $I$ 為二階單位方陣), 可得 $$B^{-1}=\left[\begin{array}{ccc} i&\ ~&-i\\ 1&&1\end{array}\right]^{-1}=\frac 12 \left[\begin{array}{ccc} -i&&1\\ i&\ ~&1\end{array}\right].$$ 將上式代入 \eqref{22} 式可得 \begin{eqnarray} A^k&=&\frac 12 \left[\begin{array}{ccc} i&\ ~&-i\\ 1&&1\end{array}\right] \left[\begin{array}{ccc} {\lambda_1}^k&&0\\ 0&&{\lambda_2}^k \end{array}\right] \left[\begin{array}{ccc}-i&\ ~&1\\ i&&1\end{array}\right]=\frac 12 \left[\begin{array}{ccc}i&\ ~&-i\\ 1&&1\end{array}\right] \left[\begin{array}{ccc}-i{\lambda_1}^k&\ ~&{\lambda_1}^k\\ i{\lambda_2}^k&&{\lambda_2}^k \end{array}\right]\nonumber\\ &=&\frac 12 \left[\begin{array}{cc} {\lambda_1}^k+{\lambda_2}^k&i({\lambda_1}^k-{\lambda_2}^k )\\ -i({\lambda_1}^k-{\lambda_2}^k )&{\lambda_1}^k+{\lambda_2}^k \end{array}\right].\label{23} \end{eqnarray} 此時, 注意前面求出的兩特徵根 $\lambda_1,\lambda_2$, 其值滿足 \begin{eqnarray*} \lambda_1&=&\sqrt{2} \Big(\cos \frac{\pi}4+i\sin \frac{\pi}4 \Big),\\ \lambda_2&=&\sqrt{2} \Big(\cos \frac{-\pi}4+i\sin \frac{-\pi}4 \Big). \end{eqnarray*} 根據隸美佛定理, 可知 \begin{eqnarray*} {\lambda_1}^k&=&(\sqrt{2})^k \Big(\cos \frac{k\pi}4+i \sin \frac{k\pi}4 \Big),\\ {\lambda_2}^k&=&(\sqrt{2})^k \Big(\cos \frac{-k\pi}4+i \sin \frac{-k\pi}4 \Big)=(\sqrt{2})^k \Big(\cos \frac{k\pi}4-i \sin \frac{k\pi}4 \Big). \end{eqnarray*} 接著, 由上兩式可得 \begin{eqnarray} {\lambda_1}^k+{\lambda_2}^k&=&(\sqrt{2})^k\cdot 2 \cos \frac{k\pi}4,\label{24}\\ {\lambda_1}^k-{\lambda_2}^k&=&(\sqrt{2})^k\cdot 2i\cdot \sin \frac{k\pi}4. \label{25} \end{eqnarray} 將 \eqref{24}, \eqref{25} 兩式代入 \eqref{23} 式後就有 $$ A^k=(\sqrt{2})^k\cdot \left[\begin{array}{ccc} \cos \dfrac{k\pi}4&\ &-\sin \dfrac{k\pi}4 \\[6pt] \sin \dfrac{k\pi}4&&\cos \dfrac{k\pi}4 \end{array}\right]. $$ 在上式中令 $k=n-1$ 後, 再將其結果代入 \eqref{21} 式, 可得 \begin{eqnarray} \left[\begin{array}{c}S_n\\ T_n \end{array}\right]&=&(\sqrt{2})^{n-1}\cdot \left[\begin{array}{ccc} \cos \dfrac{(n-1)\pi}4 &\ ~&-\sin \dfrac{(n-1)\pi}4 \nonumber\\ \sin \dfrac{(n-1)\pi}4&&\cos \dfrac{(n-1)\pi}4 \end{array}\right] \left[\begin{array}{c} 1\\ 1\end{array}\right]\nonumber\\ &=&(\sqrt{2})^{n-1}\cdot \left[\begin{array}{c} \cos \dfrac{(n-1)\pi}4-\sin \dfrac{(n-1)\pi}4\nonumber\\[8pt] \cos \dfrac{(n-1)\pi}4+\sin \dfrac{(n-1)\pi}4 \end{array}\right]\nonumber\\ &=&(\sqrt{2})^n\cdot \left[\begin{array}{c}\cos \dfrac{\pi}4 \cos \dfrac{(n-1)\pi}4-\sin \dfrac{\pi}4 \sin \dfrac{(n-1)\pi}4\nonumber\\[8pt] \sin \dfrac{\pi}4 \cos \dfrac{(n-1)\pi}4+\cos \dfrac{\pi}4 \sin \dfrac{(n-1)\pi}4 \end{array}\right]\nonumber\\ &=&(\sqrt{2})^n\cdot \left[\begin{array}{c}\cos \dfrac{n\pi}4\\[8pt] \sin \dfrac{n\pi}4 \end{array}\right].\label{25a} \end{eqnarray} 注意在上式第三個等號處, 我們用上了 $\cos \dfrac{\pi}4=\sin \dfrac{\pi}4=\dfrac 1{\sqrt{2}}$ 的條件。 因此由 \eqref{25a} 式可得 \begin{eqnarray} S_n=(\sqrt{2})^n \cos \frac{n\pi}4,\label{26}\\ T_n=(\sqrt{2})^n \sin \frac{n\pi}4\label{27} \end{eqnarray} 這兩個簡單的表達式。 至此, 我們就完成了 \eqref{10}, \eqref{11} 兩式中 $S_n,T_n$ 兩表達式的化簡。 此外, 將 \eqref{26}, \eqref{27} 兩式代入 \eqref{12} 的左式, 還可再次確認 \eqref{12} 式成立。 若仔細觀察 \eqref{26}, \eqref{27} 兩式, 可發現如下結果: (i) 當 $n$ 為奇數時, 令 $n=2k+1$, 此時 $S_n,T_n$ 之值為 $2^k$ 或 $-2^k$ (其中 $k=\dfrac{n-1}2$); (ii) 當 $n$ 為偶數時, 令 $n=2k$, 此時 $S_n,T_n$ 之值為 $2^k$, $-2^k$ 或 0 (其中 $k=\dfrac n2$)。 因此, 可確定 $n \ge 1$ 時 $S_n,T_n$ 必為整數。 雖然說, 由 \eqref{10}, \eqref{11} 兩式也可看出 $S_n,T_n$ 必為整數, 但是卻不易看出 $S_n,T_n$ 之值為 $2^k$, $-2^k$ 或 0, 這可說是求出 \eqref{26}, \eqref{27} 兩式的好處之一。 如果把 $(S_k,T_k )$ 當成坐標平面上的點 $P_k (S_k,T_k )$, 並且另定 $P_0$ 的坐標為 $(1,0)$, 則可證明所有的三角形 $\triangle OP_k P_{k+1}$ 均為等腰直角三角形 (其中 $k\ge 0$)。 怎麼說呢? 首先由 \eqref{25a}, \eqref{26}, \eqref{27} 三式可求出 $$\overline{OP_{k+1}}=(\sqrt{2})^{k+1}=\sqrt{2}\cdot (\sqrt{2})^k=\sqrt{2}\cdot \overline{OP_{k}},$$ $$\angle P_k OP_{k+1}=\frac{(k+1)\pi}{4}-\frac{k\pi}{4}=\frac{\pi}{4},$$ 其中後者是透過(以直線 $OP_{k+1}$ 與 $OP_{k}$ 為终邊的) 兩廣義角相減而得。 因此可畫出底下的參考圖形: 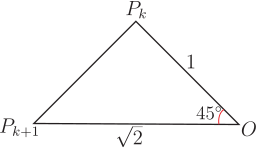 注意上圖中的 1 與 $\sqrt{2}$ 是用來標示出 $\overline{OP_{k}}$, $\overline{OP_{k+1}}$ 兩邊之長度比為 $1:\sqrt{2}$。 利用上圖, 使用餘弦定理可推得 $\overline{P_k P_{k+1}}=\overline{OP_{k}}$, 因此 $\triangle OP_k P_{k+1}$ 為等腰直角三角形, 而 $\overline{OP_{k+1}}$ 的對角 $\angle OP_kP_{k+1}$ 為直角。 不妨看看 $P_k (S_k,T_k )$ 前幾個點的坐標, 如下: $$P_0 (1,0),P_1 (1,1),P_2 (0,2),P_3 (-2,2),P_4 (-4,0),$$ $$P_5 (-4,-4),P_6 (0,-8),P_7 (8,-8),P_8 (16,0),P_9 (16,16).$$ 若把前幾個 $\triangle OP_k P_{k+1}$ 畫在坐標平面上, 結果將如下圖所示。 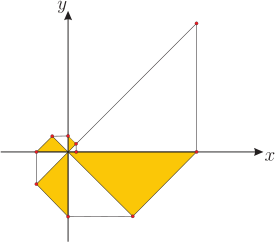 除了考慮圖 2 之外, 其實所有的點 $P_k (S_k,T_k )$ 都會落在同一條對數螺線上, 此對數螺線的極坐標方程式為 \begin{equation} r(\theta )=(\sqrt{2})^{4\theta/{\pi}}. \label{28} \end{equation} 應如何確認上述事實呢? 我們只要在上述方程式中取 $\theta =\dfrac{k\pi}{4}$, 則有 $r\Big(\frac{k\pi}{4}\Big)=(\sqrt{2})^k$, 故得極坐標上的點 $(\theta ,r)=\Big(\dfrac{k\pi}{4},(\sqrt{2})^k \Big)$, 它在直角坐標上對應的點正好就是 $P_k$, 這是因為 $$\Big((\sqrt{2})^k \cos \frac{k\pi}4,(\sqrt{2})^k \sin \frac{k\pi}4 \Big)=(S_k,T_k ).$$ 透過上式, 我們知道所有的點 $P_k(S_k,T_k)$ 都會落在方程式 \eqref{28} 所代表的曲線上。 注意 \eqref{28} 式可改寫為 $r(\theta )=e^{(\frac 2\pi \ln 2)\cdot \theta}$, 這樣的寫法, 就符合參考資料 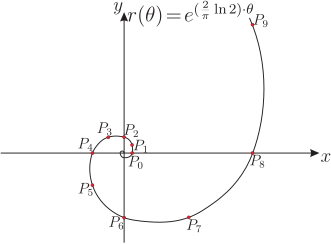 五、結語本文寫作的動機, 是出自筆者對於 \eqref{1} 式的好奇心, 想找出有別於 本文對 \eqref{1} 式所介紹的第二個證明則是以遞迴數列的想法來貫穿, 雖然其證明過程較長, 但是在完成證明之後卻還能帶我們繼續探索本文第四節內容所介紹的一些推論結果, 這應是第一個證明所無法辦到的, 或許可說是好事多磨吧。 無論如何, 希望本文能帶給讀者一些閱讀上的樂趣。 最後筆者想感謝 參考資料本文作者投稿時任職適園有限公司(人力派遣) |
| 頁碼 | 102-112 |
2025年6月 49卷2期
一道組合恆等式的另證

