有過搬家經歷的人都有這樣的感受, 移動大型傢俱通過轉角是件不很容易的事情。 也許是受此啟發, 加拿大數學家裏奧$\cdot$莫澤 (Leo Moser) 在 1966 年提出了下述有趣問題。

沙發移動問題 (the Moving Sofa Problem) : 在單位寬度的走廊中, 可圍繞直角移動的最大面積的平面形狀是什麼？

1. 通過拐角的最大沙發

一般意義上的沙發移動問題看似簡單, 徹底解決卻極為困難。 為方便起見, 數學家把繞過直角走廊的沙發截面積稱為"沙發常數" (sofa constant)。

當沙發截面為直徑是 1 的半圓 (在直轉角處, 可繞直拐角頂點旋轉通過) 時, 沙發常數 $s_1=\dfrac \pi 2=1.570796 \cdots $ 顯然, 這不是最優的沙發常數。 因為半圓形沙發在拐角處轉動時, 還存在一定的"區域浪費"。 據此我們設想, 能否把半圓形沙發"拉長些", 然後在其中間的下方挖去一個半圓, 以便在直拐角頂點"繞著"半圓轉動的過程中能讓沙發順利通過拐角 (圖1)。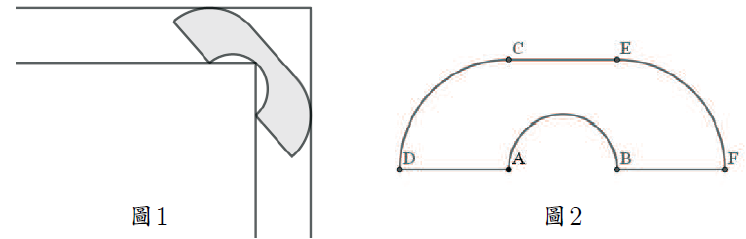

如圖 2 所示, 此時的沙發形狀類似於老式電話筒。 它的兩側是半徑為 1 的四分之一圓, 中間為挖去半圓的矩形。 我們設挖去的半圓半徑為 $r$, 則矩形的相鄰兩邊長分別為 $2r$ 和 1。 於是沙發面積為

$$s=\frac 12\cdot \pi\cdot 1^2+2r\cdot 1-\frac 12\cdot \pi\cdot r^2=-\frac\pi 2r^2+2r+\frac\pi 2.$$

$s$ 為 $r$ 的二次函數, 易知, 當 $r=\dfrac 2\pi$ 時, $s$ 取得最大值 $s_2=\dfrac \pi 2+\dfrac 2 \pi =2.207416 \cdots $。 顯然, 電話筒形沙發的沙發常數 $s_2$ 較 $s_1$ 有了很大進展, 但是 $s_2$ 仍然不是最優沙發常數。 1992 年, 數學家 Joseph Gerver 構造出了一個更大的"沙發", 其沙發常數約為 2.2195, 將 $s_2$ 往上又提升了0.5%。 該沙發的形狀 (被稱為 Gerver 沙發) 仍然類似於電話筒, 但其構造要比圖 3 複雜得多。 它由三條線段與 18 條曲線段構成, 其中涉及到圓的漸開線等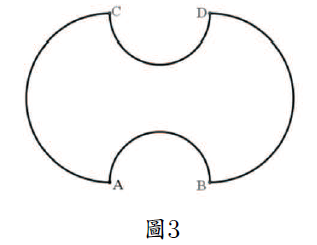。 此沙發是否為最優沙發曲線, Gerver 也不得而知, 但他表示最完美的沙發常數應該在 $2.2195 \sim 2.37$ 之間。

如果沙發要連續通過兩個直角走廊, 那麼, 上述沙發在第二個拐角處都會被卡。 為了連續通過兩個直拐角, 我們考慮將圖 2 中兩側的四分之一圓弧改為半圓, 並從中間矩形的上部、 下部各挖去一個半圓, 我們就得到了一個啞鈴形沙發, 如圖 3 所示。 其中 圓弧$AC$ 和 圓弧$DB$ 為直徑是 1 的半圓, 圓弧$DC$ 和 圓弧$AB$ 是半徑為 $r$ 的半圓。 我們來探究這種沙發對應的沙發常數。

$$s'=\pi\cdot\Big(\frac 12\Big)^2+2r\cdot 1-\pi\cdot r^2=-\pi r^2+2r+\frac\pi 4.$$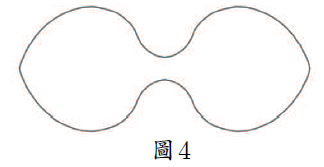

$s'$ 為 $r$ 的二次函數, 易知, 當 $r=\dfrac 1 \pi$ 時, 啞鈴形沙發的面積取得最大值。 於是, 這種沙發的最優沙發常數為

$$s_3=-\pi\Big(\frac 1\pi\Big)^2+2\cdot\dfrac 1\pi+\frac \pi 4=\dfrac 1\pi+\frac \pi 4=1.103708 \cdots .$$

很明顯, 這種啞鈴形沙發並不是可通過連續直拐彎的最優沙發。 美國加州大學戴維斯分校數學系教授 Dan Romik 在 Gerver 沙發的基礎上構造出了一種眼鏡形沙發, 其形狀如圖 4。 它由 16 條曲線段構成, 其中涉及到圓弧等四種類型的曲線 。 其沙發常數 $s_4=1.644955 \cdots $, 將 $s_3$ 提高了近 50%！

特別巧合！ 就在這篇短文完稿之時, 筆者從網路上得知 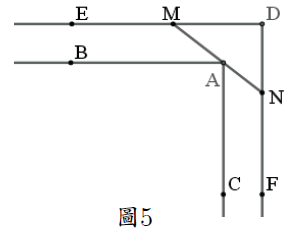, 韓國學者 Jineon Baek 發表了 1 篇包含 8 章、 共計 119 頁的最新論文 《Optimality of Gerver's Sofa》 (文章地址： https://arxiv.org/pdf/2411.19826)。 文章摘要為"通過證明具有 18 個曲線段的沙發的確達到了最大面積 2.2195, 進而解決了移動沙發問題。"

2. 通過拐角的最長細棍

我們將問題中的"沙發"更換成"細棍", 即探求能通過拐角的細棍的最大長度。

如圖 5, 不難得知, 所求細棍的最大長度, 即為經過直拐角內頂點 $A$, 且端點分別落在 $ED$ 和 $DF$上的線段 $MN$ 長度的最小值。

我們設 $\angle MAB=x$, 則線段 $MN$ 的長度

\begin{align*} |MN|=\,&|MA|+|NA|=f(x)=\frac 1{\sin x}+\frac 1{\cos x}\\ =\,&2\left(\dfrac 2{\dfrac 1{\sin x}+\dfrac 1{\cos x}}\right)^{-1}\ge 2\left(\sqrt{\dfrac{\sin^2 x+\cos^2x}{2}}\right)^{-1}=2\sqrt 2. \end{align*}

其中, 等號取到的條件為 $\sin x=\cos x$。 這裡, 用到了不等式 $\dfrac 2{\dfrac 1a+\dfrac 1b}\le\sqrt{\dfrac{a^2+b^2}{2}}$

($a,b\gt0$)。 所以, 通過單位寬度直拐角的最長細棍的長度為 $2\sqrt 2$。

如果拐角不是直角, 則情況如何呢？ 如圖 6, 我們設拐角的夾角為 $\alpha$。 則 $\angle MAB$ 和 $\angle NAC$ 的平均值為 $\beta=\dfrac{\pi-\alpha}2$。 於是, 我們可設 $\angle MAB=\beta+x$, 則 $\angle NAC=\beta-x$。 從而, 經過點 $A$, 且聯結 $EF$、 $FD$ 上兩點的線段 $MN$ 的長度

\begin{align*} |MN|=\,&|MA|+|NA|=\frac 1{\sin (\beta+x)}+\frac 1{\sin(\beta-x)}\\ =\,&\dfrac{\sin(\beta+x)+\sin(\beta-x)}{\sin(\beta+x)\sin(\beta-x)}=\frac{2\sin \beta\cos x}{\sin^2\beta\cos^2x-\cos^2\beta\sin^2 x}\\ =\,&\frac{2\sin\beta\cos x}{\cos^2 x-\cos^2\beta}=\dfrac{2\sin\beta}{\cos x-\dfrac{\cos^2\beta}{\cos x}} \end{align*}

由函數 $y=x-\dfrac a x\ (a\gt0)$ 的單調性可知, 當 $\cos x=1$, 即 $x=0$ 時,

$$L_{\rm min}=\frac 2{\sin\beta}=\dfrac 2{\sin\dfrac{\pi-\alpha}2}=\dfrac 2{\cos \dfrac \alpha 2}.$$

特殊的, 當 $\alpha=\dfrac\pi 2$ 時, $L_{\rm min}=\dfrac 2{\cos\dfrac \pi 4}=2\sqrt 2$, 與前述討論一致。 至此, 我們有下述結論。

定理： 若單位寬度的拐角夾角為 $\alpha$, 則可通過此拐角的細棍最大長度為 $2\csc\dfrac \alpha 2$。

3. 通過拐角的最大矩形

我們討論可以通過單位寬度拐角的最大矩形。 如圖 7, 設拐角的角度為 $\alpha$, 我們研究一邊架在 $A$ 上, 且對邊兩個端點分別落在 $EF$、 $DF$ 上的矩形 $MNPQ$ 面積的最小值。 我們設矩形的一邊 $|MQ|=a$, 令 $\beta=\dfrac{\pi-\alpha}2$, $\angle QAB=\beta+x$, 則 $\angle PAC=\beta-x$, 於是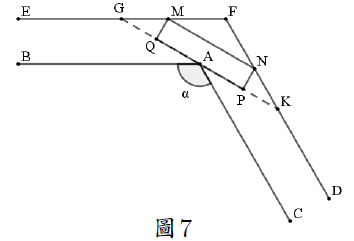

\begin{align*} b=\,&|MN|=|PQ|=|GA|+|KA|-|GQ|-|KP|\\ =\,&\frac 1{\sin(\beta+x)}+\frac 1{\sin(\beta-x)}-a\cot(\beta+x)-a\cot(\beta-x)\\ =\,&\frac{\sin(\beta+x)+\sin(\beta-x)-a[\sin(\beta+x)\cos(\beta-x)+\cos(\beta+x)\sin(\beta-x)]}{\sin(\beta+x)\sin(\beta-x)}\\ =\,&\frac{2\sin\beta\cos x-2a\sin\beta\cos\beta}{\cos^2x-\cos^2\beta}=\frac{2\sin\beta[\cos x-\cos\beta+(1-a)\cos\beta]}{\cos^2x-\cos^2\beta}\\ =\,&2\sin\beta\Big[\frac 1{\cos x+\cos\beta}+\frac{(1-a)\cos\beta}{\cos^2x-\cos^2\beta}\Big]. \end{align*}

注意到 $0\lt a\lt1$, 由此可知, 當 $\cos x=1$, 即 $x=0$ 時,

$$|MN|_{\rm min}=\frac{2\sin\beta-2a\sin\beta\cos\beta}{1-\cos^2\beta}=\frac{2-2a\cos\beta}{\sin\beta}=\dfrac{2-2a\sin\dfrac \alpha 2}{\cos\dfrac{\alpha}2}.$$

這即為可以通過拐角的矩形另一條邊長 $b$ 的最大值, 此時, 矩形的面積

$S=ab=g(a)=\dfrac{a\Big(2-2a\sin\dfrac\alpha 2\Big)}{\cos\dfrac \alpha 2}$, $S$ 為 $a$ 的二次函數, 對稱軸為 $a=\dfrac 1{2\sin\dfrac \alpha 2}$。 注意到 $a\le 1$。 於是, 若 $0\lt\alpha\le \dfrac \pi 3$, 則當 $a=1$ 時, 矩形面積取得最大值

$$S_{\rm max}=g(1)=\dfrac{2-2\sin\dfrac \alpha 2}{\cos\dfrac \alpha 2};$$

若 $\dfrac\pi 3\lt\alpha\lt\pi$, 則當 $a=\dfrac{1}{2\sin\dfrac \alpha 2}$ 時,

$$S_{\rm max}=g\Big(\dfrac{1}{2\sin\dfrac \alpha 2}\Big)=\dfrac{\dfrac{1}{2\sin\dfrac \alpha 2}(2-1)}{\cos\dfrac\alpha 2}=\frac 1{\sin\alpha}.$$

於是, 我們有下屬一般結論。

定理： 若單位寬度的拐角夾角為 $\alpha$, 則可通過此拐角的矩形的最大面積為

$$S_{\rm max}=\left\{\begin{array}{lcl} 2\sec\dfrac \alpha 2\Big(1-\sin\dfrac \alpha 2\Big),&&0\lt\alpha\le \dfrac \pi 3;\\[6pt] \csc\alpha,&~~&\dfrac \pi 3\lt\alpha\lt\pi. \end{array}\right.$$

數學家哈爾莫斯 (P. Halmos) 曾說, "問題是數學的心臟。" 好的問題是數學發展的源動力。好的問題也是數學學習與探究的驅動力。沙發移動問題及其變式就是一個很好的例證。

參考文獻

本文作者任教中國陝西省西安中學