| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | 三角形旁切圓的幾個有趣的性質 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
摘要: 本文旨在給出與三角形旁切圓相關的7個性質。 旁切圓是指和三角形的一邊及其他兩邊的延長線相切的圓。 每個三角形都有 3 個旁切圓, 各與三角形其中一邊和另外兩邊的延長線相切。 它們的圓心稱為旁心, 旁心是三角形一內角平分線和另外兩外角平分線的交點, 每個三角形有三個旁心。 本文旨在給出與三角形旁切圓相關的 7 個有趣的性質。 為了行文方便, 我們約定 $\triangle ABC$ 的三個內角 $\angle BAC=A$, $\angle ABC=B$, $\angle ACB=C$, 對應的三邊分別為 $BC=a$, $CA=b$, $AB=c$, 對應的旁切圓圓心分別為 $D,E,F$, 外接圓, 內切圓的半徑分別為 $R$, $r$, 面積為 $s$, 半周長為 $p$, 對應的角平分線長為 $f_a$, $f_b$, $f_c$。 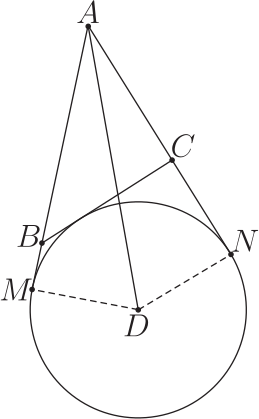 性質1: $\dfrac{AD^2}{bc}+\dfrac{BE^2}{ca}+\dfrac{CF^2}{ab}=\dfrac{4R}{r}+1.$ 證明: 如圖, 設 $\angle BAC$ 對應的旁切圓 $\odot D$ 和直線 $AB$, $AC$ 相切於點 $M,N$, 由圓中切線定理得 $AM+AN=AB+BC+CA=a+b+c$, 則 $AM=AN=\dfrac{a+b+c}{2}=p$. 在 $Rt\triangle AMD$ 中, 由 $AM=AD\cos\dfrac A2$ 得 $AD=\dfrac{AM}{\cos\dfrac A2}=\dfrac p{\cos\dfrac A2}$. 同理得 $BE=\dfrac p{\cos\dfrac B2}$, $CF=\dfrac p{\cos\dfrac C2}$. 於是 \begin{align*} &\hskip -5pt \dfrac{AD^2}{bc}+\dfrac{BE^2}{ca}+\dfrac{CF^2}{ab}=\dfrac {p^2}{bc\cos^2\dfrac A2}+\dfrac {p^2}{ca\cos^2\dfrac B2}+\dfrac {p^2}{ab\cos^2\dfrac C2}\\ &=\dfrac {2p^2}{bc(1+\cos A)}+\dfrac {2p^2}{ca(1+\cos B)}+\dfrac {2p^2}{ab(1+\cos C)}\\ &=\dfrac {4p^2}{(b+c)^2-a^2}+\dfrac {4p^2}{(c+a)^2-b^2}+\dfrac {4p^2}{(a+b)^2-c^2}\\ &=\dfrac {2p}{b+c-a}+\dfrac {2p}{c+a-b}+\dfrac {2p}{a+b-c}=\dfrac {4p^2[2(ab+bc+ca)-(a^2+b^2+c^2)]}{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}. \end{align*} 把海龍-秦九韶公式 $16p^2r^2=16s^2={(a+b+c)(b+c-a)(c+a-b)(a+b-c)}$, $a^2+b^2+c^2=2(p^2-4Rr-r^2)$ 和 $bc+ca+ab=p^2+4Rr+r^2$ 等代入上式並整理得 $$\dfrac{AD^2}{bc}+\dfrac{BE^2}{ca}+\dfrac{CF^2}{ab}=\dfrac{4R}{r}+1.$$ 性質2: $\dfrac{bc}{AD^2}+\dfrac{ca}{BE^2}+\dfrac{ab}{CF^2}=1.$ 證明: 由性質 1 的證明得 \begin{align*} &AD=\frac{AM}{\cos\dfrac A2}=\frac{p}{\cos\dfrac A2},\quad BE=\frac{p}{\cos\dfrac B2},\quad CF=\frac{p}{\cos\dfrac C2}.\\ {\hbox{則}} &\hskip 3pt \dfrac{bc}{AD^2}+\dfrac{ca}{BE^2}+\dfrac{ab}{CF^2}=\dfrac {bc\cos^2\dfrac A2}{p^2}+\dfrac {ca\cos^2\dfrac B2}{p^2}+\dfrac {ab\cos^2\dfrac C2}{p^2}\\ &=\dfrac {bc(1+\cos A)}{2p^2}+\dfrac {ca(1+\cos B)}{2p^2}+\dfrac{ab(1+\cos C)} {2p^2}\\ &=\dfrac {2bc+b^2+c^2-a^2}{4p^2}+\dfrac {2ca+c^2+a^2-b^2}{4p^2}+\dfrac {2ab+a^2+b^2-c^2}{4p^2}\\ &=\dfrac {(b+c)^2-a^2}{4p^2}+\dfrac{(c+a)^2-b^2}{4p^2}+\dfrac{(a+b)^2-c^2}{4p^2}\\ &=\dfrac {(b+c+a)(b+c-a)}{4p^2}+\dfrac{(c+a+b)(c+a-b)}{4p^2}+\dfrac{(a+b+c)(a+b-c)}{4p^2}\\ &=\dfrac {(a+b+c)^2}{4p^2}=1, \hbox{故} \dfrac{bc}{AD^2}+\dfrac{ca}{BE^2}+\dfrac{ab}{CF^2}=1. \end{align*} 性質3: $AD\cdot DE\cdot CF\ge 3\sqrt{3}abc$. 證明: 由性質 1 的證明得 \begin{align*} AD=\frac{p}{\cos\dfrac A2},&\quad DE=\frac{p}{\cos\dfrac B2},\quad CF=\frac{p}{\cos\dfrac C2}.\\ {\hbox{則}} AD\cdot DE\cdot CF=\,&\dfrac{p^3}{{\cos\dfrac A2}{\cos\dfrac B2}{\cos\dfrac C2}}=\dfrac{(a+b+c)^3}{8{\cos\dfrac A2}{\cos\dfrac B2}{\cos\dfrac C2}}\\ \ge\,&\dfrac{(3{\root 3\of {abc}})^3}{8{\cos\dfrac A2}{\cos\dfrac B2}{\cos\dfrac C2}}= \dfrac{27 abc}{8{\cos\dfrac A2}{\cos\dfrac B2}{\cos\dfrac C2}}. \end{align*} 又由熟悉的不等式 ${\cos\dfrac A2}{\cos\dfrac B2}{\cos\dfrac C2}\le \dfrac {3\sqrt{3}}8$ 得 $AD\cdot DE\cdot CF\ge 3\sqrt{3}abc$. 性質4: $AD+BE+CF\ge 2\sqrt{3}p$. 證明: 由性質 1 的證明得 \begin{align*} AD=\frac{p}{\cos\dfrac A2},\quad &BE=\frac{p}{\cos\dfrac B2},\quad CF=\frac{p}{\cos\dfrac C2}.\\ {\hbox{則}} AD+ BE+ CF=\,&p\Big(\dfrac{1}{\cos\dfrac A2}+\dfrac{1}{\cos\dfrac B2}+\dfrac{1}{\cos\dfrac C2}\Big)\ge \dfrac{9p}{{\cos\dfrac A2}+{\cos\dfrac B2}+{\cos\dfrac C2}}. \end{align*} 由 ${\cos\dfrac A2}+{\cos\dfrac B2}+{\cos\dfrac C2}\le \dfrac{3\sqrt 3}{2}$ 得 $AD+BE+CF\ge\dfrac{9p}{\dfrac{3\sqrt 3}{2}}= 2\sqrt{3}p$, 故 $AD+BE+CF\ge 2\sqrt{3}p$. 性質5: $a\cdot AD+b\cdot BE+c\cdot CF\ge 12s$. 證明: 由性質 1 的證明得 \begin{align*} AD=\frac{p}{\cos\dfrac A2},\quad &BE=\frac{p}{\cos\dfrac B2},\quad CF=\frac{p}{\cos\dfrac C2}. \end{align*} 結合正弦定律(law of sine)得 \begin{align*} &\hskip -20pt a\cdot AD+b\cdot BE+c\cdot CF\\ =\,&\frac{ap}{\cos\dfrac A2}+\frac{bp}{\cos\dfrac B2}+\frac{cp}{\cos\dfrac C2}=\frac{2pR\sin A}{\cos\dfrac A2}+\frac{2pR\sin B}{\cos\dfrac B2}+\frac{2pR\sin C}{\cos\dfrac C2}\\ =\,&4pR\sin \dfrac A2+4pR\sin \dfrac B2+4pR\sin \dfrac C2=4pR\Big(\sin \dfrac A2+\sin \dfrac B2+\sin \dfrac C2\Big). \end{align*} 由 ${\sin\dfrac A2}+{\sin\dfrac B2}+{\sin\dfrac C2}\ge 1+\dfrac{3\sqrt 3r}{2p}$ (見文 $$a\cdot AD+b\cdot BE+c\cdot CF\ge 4pR\Big(1+\dfrac{3\sqrt 3 r}{2p}\Big)=4pR+6\sqrt 3 Rr.$$ 又由 $R\ge 2r$ 和 $2p\le 3\sqrt 3 R$ 得 $a\cdot AD+b\cdot BE+c\cdot CF\ge 8pr+4pr=12s$. 故 $a\cdot AD+b\cdot BE+c\cdot CF\ge 12s$. 性質6: $\dfrac 1{AD}+\dfrac 1{BE}+\dfrac 1{CF}\le \dfrac{3\sqrt 3}{2p}$. 證明: 由性質 1 的證明得 \begin{align*} AD=\frac{p}{\cos\dfrac A2},\quad BE=\,&\frac{p}{\cos\dfrac B2},\quad CF=\frac{p}{\cos\dfrac C2}.\\ {\hbox{則}} \dfrac 1{AD}+\dfrac 1{BE}+\dfrac 1{CF}=\,&\dfrac{{\cos\dfrac A2}+{\cos\dfrac B2}+{\cos\dfrac C2}}{p}. \end{align*} 由 ${\cos\dfrac A2}+{\cos\dfrac B2}+{\cos\dfrac C2}\le \dfrac{3\sqrt 3}{2}$ 得 $\dfrac 1{AD}+\dfrac 1{BE}+\dfrac 1{CF}\le \dfrac{3\sqrt 3}{2p}$. 性質7: $\dfrac {f_a}{AD}+\dfrac {f_b}{BE}+\dfrac {f_c}{CF}\le \dfrac{3}{2}$. 證明: 由三角形內角平分線公式得 $$f_a=\dfrac{2bc\cos \dfrac A2}{b+c},\quad f_b=\dfrac{2ca\cos \dfrac B2}{c+a},\quad f_c=\dfrac{2ab\cos \dfrac C2}{a+b}.$$ 由性質 1 的證明得 \begin{align*} AD=\frac{p}{\cos\dfrac A2},\quad &BE=\frac{p}{\cos\dfrac B2},\quad CF=\frac{p}{\cos\dfrac C2}.\\ {\hbox{則}} \dfrac {f_a}{AD}+\dfrac {f_b}{BE}+\dfrac {f_c}{CF}=\,&\dfrac{2bc\cos^2 \dfrac A2}{(b+c)p}+\dfrac{2ca\cos^2 \dfrac B2}{(c+a)p} +\dfrac{2ab\cos^2 \dfrac C2}{(a+b)p}\\ =\,&\dfrac{bc(1+\cos A)}{(b+c)p}+\dfrac{ca(1+\cos B)}{(c+a)p}+\dfrac{ab(1+\cos C)}{(a+b)p}\\ =\,&\dfrac{2bc+b^2+c^2-a^2}{2(b+c)p}+\dfrac{2ca+c^2+a^2-b^2}{2(c+a)p}+\dfrac{2ab+a^2+b^2-c^2}{2(a+b)p}\\ =\,&\dfrac{b+c-a}{b+c}+\dfrac{c+a-b}{c+a}+\dfrac{a+b-c}{a+b}\\ =\,&3-\Big(\dfrac a{b+c}+\dfrac b{c+a}+\dfrac c{a+b}\Big). \end{align*} 由 $\dfrac a{b+c}+\dfrac b{c+a}+\dfrac c{a+b}\ge \dfrac 32+\dfrac 14\sum \Big(\dfrac{b-c}{b+c}\Big)^2$ (見文 $$\dfrac {f_a}{AD}+\dfrac {f_b}{BE}+\dfrac {f_c}{CF}=3-\Big(\dfrac a{b+c}+\dfrac b{c+a}+\dfrac c{a+b}\Big)\le \dfrac 32, $$ 故 $\dfrac {f_a}{AD}+\dfrac {f_b}{BE}+\dfrac {f_c}{CF}\le \dfrac{3}{2}$. 讀者可以進一步去開發更加有趣的性質。 參考文獻本文作者任教中國山東省泰安市甯陽縣第一中學 |
2025年6月 49卷2期
三角形旁切圓的幾個有趣的性質

