| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | 第 31 屆 USAMTS 數學競賽 (第二輪) 試題賞析 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
一、前言美國數學天才選拔賽 (USAMTS) 是一項針對所有美國初、 高中學生進行的免費、 開放性的數學競賽。 數學競賽試題從易到難, 目的是選拔最優秀的學生。 USAMTS 是 Art of Problem Solving Initiative 的子項目, 主要由美國國家安全局 (National Security Agency) 等贊助。 該項比賽分三輪 --- 初賽、 複賽和決賽, 所有參賽學生必須在一個月之內完成, 學生可查閱相關資料, 借助計算器和電腦等, 但所有問題的解決必須是獨自完成, 不能求助其他人。 該項比賽主要訓練參賽學生的分析問題、 解決問題和規範表達的能力, 同時對學生的洞察力、 創造力和毅力等都有很高的要求, 這些能力、 品質和意志的形成對將來的科學研究有很大的幫助。 本文選取第 31 屆 (2019$\sim$2020) 第二輪比賽的全部 5 道題, 並給出解答過程和點評。 本文旨在讓讀者對 USAMTS 競賽及其試題特色有大致瞭解, 文章最後對第 31 屆 USAMTS 數學競賽試題 (第二輪) 的特色進行了歸納和總結。 二、試題賞析試題1: 如圖 1, 記每個小正方形的四個頂點上的數字按順時針方向分別為 $a,b,c,d$, 將數字 $1,2, \ldots ,16$ 填入圓圈中 (每個數字只能用一次), 使 $(a+c)(b+d)$ 的值與小正方形內部數相等。 圖中給出了一部分小正方形內和頂點上的數字, 請將圓圈內餘下的數字補充完整。 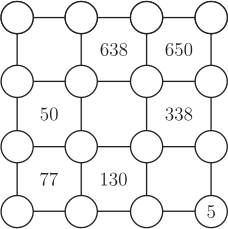 解析: 答案如圖 2 所示。  觀察圖形發現, 第一行靠右的兩個小正方形內部的數字較大 (相對其他四個數字來說), 第二行的靠最右邊的小正方形内部的數字 (338) 相比其他三個數字 (50,77,130) 也大很多, 因此不妨猜測三個小正方形的公共頂點處的數字最大, 即為"16", 圖中的數據用矩陣的結構表示為 $\left[\begin{array}{cccc} ~a_{11}~&~a_{12}~&~a_{13}~&~a_{14}~\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ a_{41}&a_{42}&a_{43}&a_{44}\end{array}\right]$, 則有 $a_{23}=16$, $a_{44}=5$。因為 $a_{23}=16$, 且 $650=(a_{23}+a_{14})(a_{13}+a_{24})$, 又因為 $650=25\times 26$, 因此 $a_{23}+a_{14}=25$ 或 $a_{23}+a_{14}=26$。 若 $a_{23}+a_{14}=26$, 則 $a_{14}=10$。 又因為 $(a_{23}+a_{34})(a_{33}+a_{24})=338=13\times 26$, 所以只能 $a_{33}+a_{24}=26$ (若 $a_{23}+a_{34}=26$, 則 $a_{34}=10=a_{14}$, 矛盾), 因此 $a_{23}+a_{34}=13\lt a_{23}=16$, 矛盾, 因此 $a_{23}+a_{14}=25$。 因為 $a_{23}+a_{14}=25$, 則 $a_{14}=9$, $a_{13}+a_{24}=26$, $a_{23}+a_{34}=26$, 所以 $a_{34}=10$。 因為 $a_{24}+a_{23}=13$, 又因為 $26=10+16=11+15=12+14$, 則 $a_{24}\lt13$, 所以 $a_{24}=11$ 或 12。 當 $a_{24}=12$ 時, 則 $a_{33}=1$。 因為 $130=(a_{32}+a_{43})(a_{42}+a_{33})=5\times 26=10\times 13$, 若 $a_{42}=4$, 則 $a_{32}=11$ 或 15, 與 $(a_{41}+a_{32})(a_{31}+a_{42})=77=7\times 11$ 矛盾 ($a_{32}$ 必小於 7 或 11); 若 $a_{42}=9$, 又與 $a_{14}=9$ 矛盾, 所以 $a_{24}=11$, $a_{13}=15$, $a_{33}=2$。 因為 $a_{33}+a_{42}$ 的值只可能為 5, 10, 13, 26, 顯然其值不可能為 26、 13 和 5。 若值為 26, 則 $a_{42}=26-a_{33}=24\gt16$, 矛盾; 若值為 13, 則 $a_{42}=13-2=11=a_{24}$ (矛盾); 若值為 5, 則 $a_{42}=3$, 因為 $a_{32}+a_{43}=26=11+15$, 所以 $a_{32}=11$ 或 15, 又因為 $a_{32}\lt11$, 因此 $a_{33}+a_{42}=10$, 故 $a_{42}=10-2=8$, $a_{31}=11-8=3$。 因為 $a_{31}+a_{22}=5$ 或 11, 顯然 $a_{22}\not=2$ (因為 $a_{33}=2$), 因此 $a_{22}=7$, $a_{12}=\dfrac{638}{15+7}-16=13$。 因為 $a_{32}+a_{43}=13$, $a_{32}+a_{41}=7$, 所以 $a_{43}-a_{41}=6=7-1=8-2=9-3=10-4=11-5=12-6=13-7=14-8=15-9=16-10$, 因為數字 "3, 7, 8, 9, 10, 11" 均已找出, 所以 $a_{43}-a_{41}=12-6$, 即 $a_{43}=12$, $a_{41}=6$, 因此 $a_{32}=1$, $a_{21}=\dfrac{50}{3+7}-1=4$。 發現只有數字"14"未被填入, 所以 $a_{11}=14$。 點評: 本題答案唯一, 且不要求解答過程, 答案正確即可。若圓圈中的數字沒有一個正確, 給零分, 否則根據圓圈中所填數字正確的多少來給分。 本題的關鍵是憑考生的數感 (設 $a_{23}=16$), 再通過步步推理得出空白部分各元素的值, 類似於走迷宮 (發現問題後立即調整策略), 直到走出迷宮 (即解決了問題, 尋找到一條解決問題的方案)。 試題2: 如圖3, 甲將一個 $3\times 3$ 的方格表用1, 2, $\ldots$, 9 共 9 個數字標識 (如圖 3 中表格 $A$ 所示), 並用柑橘橙和檸檬黃兩種顏色中的一種隨機地給每個格子染色 (每個格子被染成兩種顏色之一的概率為 $\dfrac 12$), 隨後乙將甲染好色的方格表進行處理, 乙有兩種處理方法: (1) 將最上面的一行移到最下面, 如圖 3 所示 (表格 $A\to $ 表格 $A'$)。 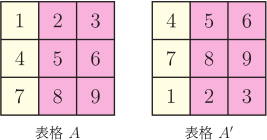 (2) 將最左邊的一列移到最右邊, 如圖 4 所示 (表格 $B\to$ 表格 $B'$)。 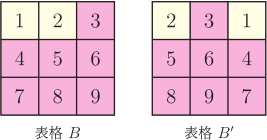 若乙能夠通過上面兩種變換, 得到與甲染色後的顏色相同, 但數字不同的方格表, 則稱甲染好色的方格表為"好玩"的方格表。 若乙不能通過上面兩種變換, 得到與甲染好色後的顏色相同, 數字不同的方格表, 則稱甲染好色的方格表為"酸酸"的方格表。 圖 3 所示的表就是一個"好玩"的方格表, 而圖 4 所示的表則是一個"酸酸"的方格表。 請問乙得到一個"酸酸"的方格表的概率是多少? 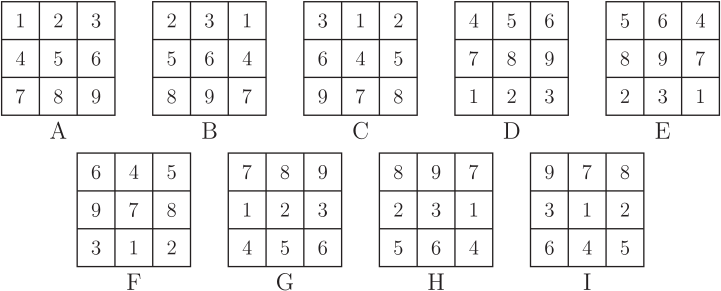 解析: 方法1. 代數的方法 根據移動規則可知, 數字1、2、3 (4、5、6, 7、8、9) 始終在同一行, 數字1、4、7 (2、5、8, 3、6、9) 始終在同一列 (只是位置相互之間發生變化), 且整行、 整列可以互換位置, 故共有 $3\times 3=9$ (種) 不同的置換 (排列) 方式, 如圖5所示。 若能夠找出不是"酸酸"的方格表的數量, 即"好玩"的方格表的數量, 問題就解決了。 因為 $3\times 3$ 的方格表共有 $2^9=512$ (種) 不同的著色方法, 對於某個方格表 $X$ 來說, 若方格表 $Y$ 與方格表 $X$ 具有相同的顏色, 即方格表中的每個小單元格 (共9個) 顏色必須全部相同。 按照這種方式來考慮, 甲染好的方格表是"好玩"的方格表的染色方式必須是以下 4 種 (有且僅有) 方式之一, 如圖 6 所示。  其中 $a,b,c$ 表示柑橘橙或檸檬黃兩種顏色。 因為 $W,X,Y,Z$ 四種中的任意一種著色方法, 乙都可通過兩種移動方式, 將表格變成顏色與甲所染好色的方格表相同, 但數字不同的方格表。 對於圖 6 所示的每一種著色方式, 因為 $a,b,c$ 各有 2 種顏色可以選取, 又因為每一種方式均包含整個方格表是同一種顏色的 2 種情形, 因此, 每一種方式包含有 $2^3-2=6$ (種) 不同顏色的著色方法。 因為四種著色方法中的每一種著色方法都與其他三種著色方法不同, 再加上全部同一種顏色的2種著色方法, 因此共有 $2+4\times 6=26$ (種) "好玩"的方格表著色方法, 即"好玩"的方格表的著色方法共有 26 種, 因此乙收到甲染的"酸酸"的方格表的概率為 $\dfrac{512-26}{512}=\dfrac{243}{256}$。 方法2: 群論的方法 (利用伯恩賽德引理) 令 $S$ 為 $3\times 3$ 方格表的共 $2^9$ 種不同著色方法的集合, 所以集合 $S$ 共有 $2^9=512$ (個) 元素。 $G$ 表示移動變換的 9 階置換群, 即共有 9 種變換方式 (如圖 5 中的 A 到 I)。 兩種著色方法一致, 就是指 $S$ 中元素在群 $G$ 的作用下屬於同一軌道。 作用在集合 $S$ 上的群 $G$ 將集合 $S$ 劃分為 3 個軌道, 其中軌道的大小 (即軌道中元素的個數) 只有 1, 3, 9個, 共三種情形。 軌道大小為 9 的軌道中元素的個數, 即對應"酸酸"的方格表的個數。 利用伯恩賽德 (Burnside's) 引理可以求出軌道的數量, 軌道數為 $L=\dfrac{1}{|G|}\sum\limits_{g\in G}|S_g|$, 其中 $S_g$ 表示在變換 $g\in G$ 的作用下 $S$ 中不變的元素個數, $|G|$ 表示變換群 $G$ 中的元素個數, 即 $|G|=9$, $G$ 中的恒等置換 (圖5中 A 所示) 下, $S$ 中有 512 個元素顏色不變, 群 $G$ 中的其他 8 種變換 (如圖 5 中的 $B\to I$ 所示), 每種變換下, $S$ 中均有 $2^3=8$ (個) 元素 (如在表格 $B$ 表示的置換下, 即要求每列顏色相同, 每行的顏色各有 2 種選擇, 共 3 行, 即 $2^3=8$) 的顏色相同且數字不同, 因此總軌道數為 $\dfrac 19\times(512+8\times 8)=64$ (個), 即共有 64 個軌道。 在群 $G$ 的作用下, 含有 1 個元的軌道有 2 個, 即整個方格表為柑橘橙或者檸檬黃色, 且位於 2 個不同的軌道中。 令 $x$ 為含有 3 個元的軌道個數, $y$ 為含有 9 個元的軌道個數, 因此還有 $512-2=510$ (個) 元素和 $64-2=62$ (個) 軌道剩餘, 所以有 $\left\{\begin{array}{l} 3x+9y=510,\\ x+y=62,\end{array}\right.$ 解得 $y=54$, 因此有 $54\times 9=486$ (個) 元素位於軌道大小為 9 的軌道中, 即有 486 個"酸酸"的方格表, 所以, 乙收到的表格為"酸酸"的方格表的概率為 $\dfrac{486}{512}=\dfrac{243}{256}$。 點評: 本題給出了兩種解答方法, 即代數的方法和群論的方法, 當然本題可能還有其他的方法。 兩種方法的思路不同, 方法 1 是直接求出"好玩"的方格表的數量, 利用總的染色方法的方格表的數量減去"好玩"的方格表的數量, 即得到"酸酸"的方格表的數量, 從而求得概率。 方法 2 則利用群論的知識, 關鍵求出軌道大小為 9 的軌道個數 $y$, 從而求得軌道大小為 9 的所有元素的個數 $9y$, 即對應於"酸酸"的表格的數量。 方法 2 雖然簡單, 但涉及群論知識, 特別是 Burnside's 引理, 對於未接觸過該知識的考生較難且抽象。 試題3: 對四元正整數組 $(a,b,c,d)$, 若存在無窮個正整數 $m$ 使得 $\gcd(am+b,cm+d)=2019$, 則稱這個四元整數組 $(a,b,c,d)$ 是"水果味"的。 請求出"水果味"四元正整數組 $(a,b,c,d)$ 的所有 $|ad-bc|$值。 解析: 因為 $2019=\gcd(am+b,cm+d)$, 所以 $2019\mid (a(cm+d)-c(am+b))$, 又因為 $$a(cm+d)-c(am+b)=ad-bc,$$所以有 $|ad-bc|=2019k$, 其中 $k$ 為非負整數。 考察 $(a,b,c,d)=(k,2019,k,4038)$ 的情况, 當 $k$ 為正整數時, 有 $|ad-bc|=|k\cdot 4038-k\cdot 2019|=2019k$, 且有 $$\gcd((am+b,cm+d)=\gcd(km+2019,km+4038)=\gcd(km+2019,2019)$$若 $m$ 為 2019 的倍數, 則有 $\gcd(km+2019,2019)=2019$, 又因為 2019 的倍數有無窮多個, 也就是說存在無窮多個正整數 $m$, 使得 $\gcd(am+b,cm+d)=2019$, 所以 $(k,2019,k,4038)$ 是滿足要求的"水果味"四元正整數组, 因此 $|ad-bc|$ 的所有可能值為 2019 的任一正整數倍。 當 $|ad-bc|=0$, 即 $ad-bc=0$ 時, 若其中 $a=c=k=0$, 與 $a,b,c,d$為正整數矛盾; 若 $a,b,c,d$ 為全不為零的正整數時, 有 $\dfrac ab=\dfrac cd=\dfrac ef$, 其中 $(e,f)=1$。 即存在正整數 $x,y$ 滿足 $a=ex$, $b=fx$, $c=ey$, $d=fy$, 所以 $$\gcd(am+b,em+f)=\gcd(emx+fx,em+f)=\gcd(x(em+f),em+f)=em+f$$同理, $\gcd(cm+d,em+f)=em+f$, 因此有 $\gcd(am+b,cm+d)$ 為 $em+f$ 的倍數。 因為 $e,f,m$ 均為正整數, 所以 $em+f$ 的值隨著 $m$ 的值增加而嚴格遞增, 因此必定在某個 $m=m_0$ 時, 有 $em_0+f\gt2019$, 當 $m\gt m_0+1$ 時, 不再有 $\gcd(am+b,cm+d)=2019$, 因此, 若 $|ad-bc|=0$, 則 $(a,b,c,d)$ 不是"水果味"的四元正整數組。 因此, $|ad-bc|$ 的值只能為 2019 的任意正整數倍。 點評: 本題的關鍵是觀察到 $a(cm+d)-c(am+b)=ad-bc$, 並得出 $|ad-bc|=2019k$。 本題考查的思想和能力並不少, 比如求最大公約數的"減損術"和運算推理的能力。 本題需要特別注意的是, 一定還要討論當 $a,b,c,d$ 部分為 0 和全不為 0 兩種情況, 說明當 $|ad-bc|=0$ 時, 不存在無窮多個正整數 $m$, 使得 $\gcd(am+b,cm+d)=2019$, 這樣解答才算完整。 因此 $|ad-bc|$ 的所有可能值只能為 2019 的任意正整數倍。 試題4: 梨公主有 100 個身高分別為 1 英寸, 2 英寸, $\cdots$, 100 英寸的小丑。 在第 $n$ 天 $(1\le n\le 100)$, 梨公主召集身高不超過 $n$ 英寸的小丑開會, 每 6 個身高的中位數為 $n-50$ 英寸的小丑們組成一組 (小丑們可以重複參加不同的小組, 直到所有符合要求的小組都組建完畢, 不能再組建符合要求的小組為止), 每組要求給梨公主 2 個櫻桃蜜餞。 第 101 天, 梨公主召集所有的 100 個小丑進行最後一次會議。 這次, 要求身高的中位數為 50.5 英寸的小丑組成的 6 人小組 (同樣, 小丑可以重複參加不同小組, 直到不能再組建成符合要求的小組為止), 每個小組都給梨公主 1 個櫻桃蜜餞。 請問梨公主最後總共收到了多少個小丑們所給的櫻桃蜜餞? 解析: 方法 1. 代數的方法 在前100天, 對於任何一個身高為 $\{a_1,a_2,\ldots,a_6\}$ (單位:英寸), 其中 $a_1\!\lt\!a_2\!\lt\!\cdots\!\lt\!a_6$ 的小組來說, 第三矮的小丑的身高至少為 3 英寸, 即 $a_3\ge 3$, 又因為 $a_3+a_4=2n-100\ge 7$, 解得 $n\ge 54$, 也就是說, 直到第 54 天後, 梨公主才會收到小丑們所給的櫻桃蜜餞, 在 1$\sim$53 天, 梨公主是不會收到任何櫻桃蜜餞的。 設某個身高為 $\{b_1,b_2,\ldots,b_6\}$ 的小組的中位數為 $n-50$, 設 $b_3=n-50-x$, 則 $b_4=n-50+x$, 其中 $x$ 為正整數。 因為 $b_3\ge 3$, 所以 $n-50-x\ge 3$, 即 $x\le n-53$, 因此, 在第 $n$ ($54\le n\le 100$) 天, 有 ${n-51-x\choose 2}$ 種選擇最矮的 2 個小丑 $(b_1,b_2)$ 的方法和 ${n-(n-50+x)\choose 2}={50-x\choose 2}$ 種選擇最高的 2 個小丑 $(b_5,b_6)$ 的方法, 所以, 在開始的 100 天, 梨公主能共收到 $$2\sum_{n=54}^{100}\sum_{x=1}^{n-53}{n-51-x\choose 2}{50-x\choose 2}$$個櫻桃蜜餞。 在第 101 天, 設符合要求 (即小組中 6 個小丑的身高中位數為 50.5 英寸) 的小組為 $\{c_1,c_2,\ldots,c_6\}$, 設 $c_3=t$ $(3\le t\le 50)$ 英寸, 則 $c_4=(101-t)$ 英寸。 因此, 在該小組中共有 ${t-1\choose 2}$ 種選擇最矮的 2 個小丑的方法和 ${100-(101-t)\choose 2}={t-1\choose 2}$ 種選擇最高的 2 個小丑方法。所以, 在第 101 天, 梨公主能收到 $\sum\limits_{t=3}^{50}{t-1\choose 2}^2$ 個櫻桃蜜餞。 因此, 梨公主在 101 天之後, 共收到櫻桃蜜餞的數目為 \begin{align*} &\sum_{t=3}^{50}{t-1\choose 2}^2+2\cdot \sum_{n=54}^{100}\sum_{x=1}^{n-53}{n-51-x\choose 2}{50-x\choose 2}\\ &\quad =\sum_{t=2}^{49}{t\choose 2}^2 +2\cdot \sum_{x=1}^{47}\sum_{n=x+53}^{100}{n-51-x\choose 2}{50-x\choose 2} \end{align*}令 $t=50-x$, 則有 $$\sum\limits_{t=2}^{49}{t\choose 2}^2+2\cdot \sum\limits_{t=3}^{49}\sum_{n=103-t}^{100}{n+t-101\choose 2}{t\choose 2},$$再令 $s=n+t-101$, 有 $$\sum\limits_{t=2}^{49}{t\choose 2}^2+2\cdot \sum\limits_{t=3}^{49}\sum_{s=2}^{t-1}{s\choose 2}{t\choose 2}=\Bigg(\sum\limits_{t=2}^{49}{t\choose 2}\Bigg)^2\hbox{。}$$因為 $$\sum\limits_{t=2}^{49}{t\choose 2}^2={50\choose 3},$$所以 101 天後, 梨公主共收到 ${50\choose 3}^2=384160000$ (個) 櫻桃蜜餞。 方法2. 雙射法 根據方法 1 得到的結果, 猜測梨公主收到的櫻桃蜜餞數 ${50\choose 3}^2$ 能否與從身高不超過 50 英寸和身高不低於 51 英寸的小丑中各選取 3 個, 共 6 個小丑組成的小組建立一一對應關係。 根據題意, 設 6 個小丑的身高為 $a_1\lt a_2\lt\cdots\lt a_6$, 且身高的中位數為 $n-50$。 在第 $n$ 天, 該組應給梨公主 2 個櫻桃蜜餞。 梨公主收到的第 1 個櫻桃蜜餞, 可構造集合 $$A=\{a_1,a_2,a_3,100-n+a_4,100-n+a_5,100-n+a_6\}.$$因為 $a_1\lt a_2\lt a_3\le 50$, 又因為 $a_4\gt n-50$, 所以 $100-n+a_4\gt50$, 又因為 $n-50=\dfrac{a_3+a_4}{2}$, 則集合 $A$ 中數據的中位數為 $\dfrac{a_3+100-n+a_4}{2}=\dfrac{2n-100+100-n}{2}=\dfrac n2\hbox{。}$ 因為 $n\le 100$, 即該組數據的中位數總不超過 50。 梨公主收到的第 2 個櫻桃蜜餞, 可構造集合 $$B=\{n+1-a_6,n+1-a_5,n+1-a_4,101-a_3,101-a_2,101-a_1\}.$$因為 $a_3\le 50$, 所以 $101-a_3\ge 51$, 又因為 $a_4\gt n-50$, 所以 $n+1-a_4\le 50$, 則集合 $B$ 中數據的中位數為 $\dfrac{n+1\!-\!a_4+101\!-\!a_3}{2}=\dfrac{n+102\!-\!2n+100}{2}=101\!-\!\dfrac n2\hbox{。}$ 因為 $n\!\le\! 100$, 所以該組數據的中位數不小於 51 英寸。 通過上述兩種方式構造的集合 $A,B$, 其中位數除 $n=101$ 時才相等外, 其他始終不等, 即集合 $A,B$ 中的元素不全相同。 由圖 7 可知, 在第 $n$ ($54\le n\le 100$) 天, 6 個小丑組成的身高中位數為 $n-50$ 的組數與集合 $A,B$ 形成一一對應的關係。 另外, 由於任何一組身高的中位數為 50.5 英寸的 6 個小丑組成的集合, 必有 3 個小丑的身高位於集合 $\{1,2,\ldots,50\}$ 中, 另外 3 個小丑的身高位於 $\{51,52,\ldots,100\}$ 中, 這種情形在集合 $A,B$ 中已經包含, 無需另外計算。 所以, 梨公主收到的每一蜜餞也對應於從 50 個身高不超過 50 英寸和 50 個身高不低於 51 英寸的小丑中各選取 3 個小丑的一種選取方法。 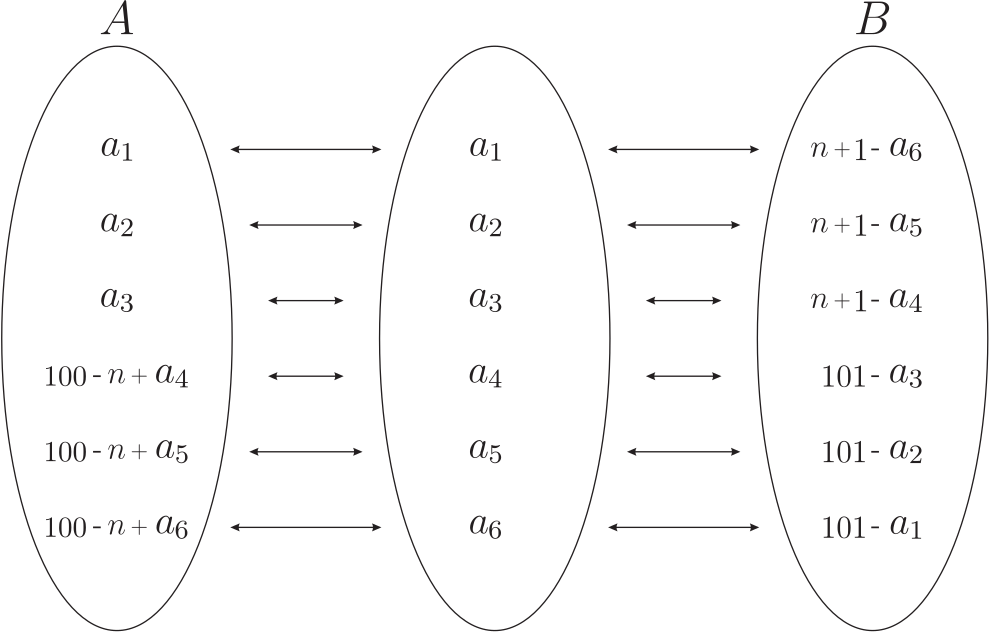 綜上所述, 梨公主收到的每個蜜餞均對應於從身高為 $\{1,2,\ldots,50\}$ 和 $\{51,52,\ldots,100\}$ 中各選取 3 個小丑的一種選取方法, 且過程是可逆的, 即每一個選取方法也可對應於梨公主收到的每個蜜餞, 且是一一對應關係。 所以, 梨公主收到的蜜餞總數, 也就是從 $\{1,2,\ldots,50\}$ 和 $\{51,52,\ldots,100\}$ 各選取 3 個小丑的總的方法數, 共有 ${50\choose 3}^2$ 種選取方法, 故梨公主共收到 ${50\choose 3}^2=384160000$ (個) 櫻桃蜜餞。 點評: 本題給出了兩種解答方法, 即代數法和雙射法。 "雙射法"很難被一般的學生想到, 要求較高。 第一種方法較為普通, 思路也比較自然, 即分別求出前 100 天和第 101 天梨公主分別得到的櫻桃蜜餞的數量, 求和即可得到總數, 但運算量和運算技巧較大, 較為複雜, 特別是雙重求和運算中有關變數替換來簡化運算, 以及求和中的有關恒等式 (如 $\sum\limits_{i=1}^n a_i^2+2\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n a_ia_j=\Big(\sum\limits_{i=1}^n a_i\Big)^2$) 的運用。 雙射法是組合數學中一種重要的證明方法, 常用來證明有限集合的元素數目相等。 當集合 $A$ 中元素的個數較難計數時, 構造一個與集合 $A$ 形成一一對應關係的集合 $B$, $B$ 中的元素個數較易計算, 通過計算集合 $B$ 中元素個數從而求得集合 $A$ 中元素的個數。 試題5: 如圖 8, $\triangle ABC$ 的外心為點 $O$, 點 $A,B,C$ 對應的旁心分別為 $I_A,I_B,I_C$, $\triangle ABC$ 內切圓分別與三邊 $BC$, $CA$, $AB$ 切於點 $D,E,F$, 直線 $I_BE$ 與直線 $I_CF$ 交於點 $P$。 若過點 $O$ 且與 $OP$ 垂直的直線經過點 $I_A$, 證明 $\angle BAC=60^\circ$。 證明: 令 $O_e$ 為三角形 $I_A,I_B,I_C$ 的外心, $EF, I_BI_C$ 均垂直於 $\angle BAC$ 的平分線 $AI_A$, 所以 $EF/\!/I_BI_C$。 同理, $FD/\!/ I_CI_A$, $DE/\!/I_AI_B$, 因此 $\triangle DEF$ 和 $\triangle I_AI_BI_C$ 位似, 位似中心為 $I_BE\cap I_CF=P$。 設點 $I$ 為 $\triangle DEF$ 的外心, 因為點 $O_e$ 為 $\triangle I_AI_BI_C$ 的外心, 所以點 $P$, $I$, $O_e$ 三點共線, 又因為點 $I$ 為 $\triangle ABC$ 的內心, 所以點 $I$ 也就是 $\triangle I_AI_BI_C$ 的垂心 (三角形內心是旁心三角形的垂心), 因此 $\overline{PIO_e}$ 是 $\triangle I_AI_BI_C$ 的歐拉線, $O$ 是 $\triangle I_AI_BI_C$ 的九點圓中心。 所以, 點 $O$ 也位於歐拉線上。 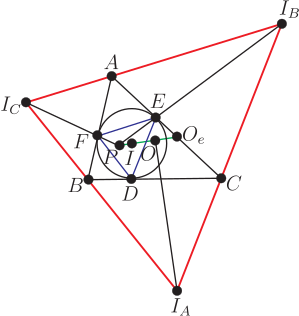 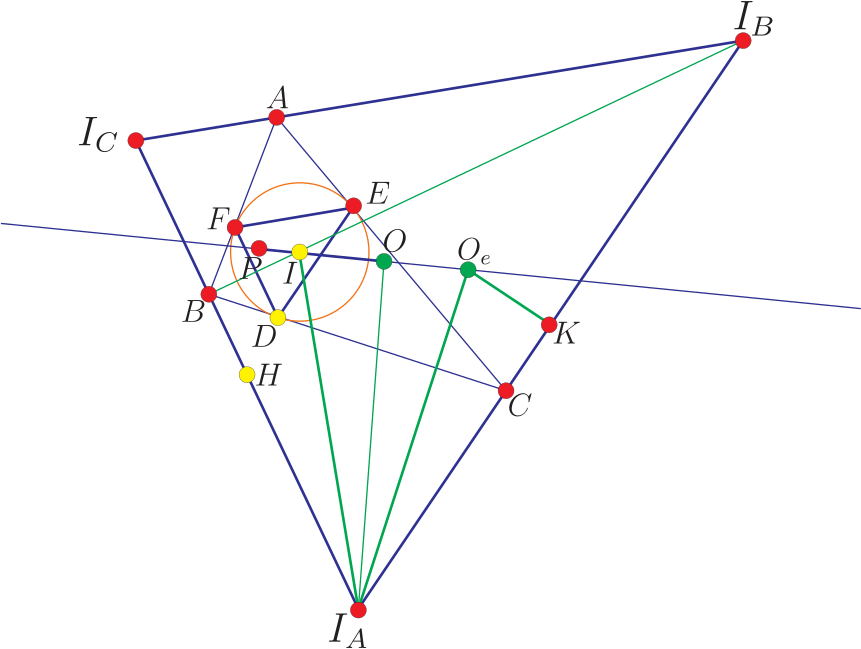 因為 $I_AO\bot OP$, 又因為 $IO=OO_e$, 所以有 $I_AO_e=I_AI$。 所以 $I_AO$ 必為 $\angle I_BI_AI_C$ 的角平分線, 如圖 9 所示 (讀者不妨試一試), 顯然有 $Rt\triangle BII_A\simeq Rt\triangle KO_eI_A$ (其中點 $B$ 為 $I_AI_C$ 邊上高的垂足, 點 $K$ 為線段 $I_AI_B$ 的中點), 所以 $I_AK=KI_B=BI_A$, 因此 $I_AB=2BI_A$。 又因為 $\angle I_BBI_A$ 為直角三角形, 所以 $\angle BI_BI_A=30^\circ$, 因此 $\angle I_CI_AI_B=60^\circ$, 所以 $\angle A=\angle BAC=180^\circ-2 \angle I_BI_AI_C=60^\circ$。 點評: 本題是一道幾何題, 完全解答需要考生有一定的幾何素養, 綜合考查了三角形的內心、 外心、 垂心、 旁心以及九點圓等知識。 首先, 考生要意識到 $\triangle DEF$ 和 $\triangle I_AI_BI_C$ 位似, 點 $P$ 為位似中心, 點 $O$ 是 $\triangle I_AI_BI_C$ 的九點圓的圓心; 其次, 考生還要知道點 $I$ 既是 $\triangle DEF$ 的外心, 又是 $\triangle ABC$ 的內心, 還是 $\triangle I_AI_BI_C$ 的垂心, 以及 $\triangle I_AI_BI_C$ 的內心必在直線 $I_AO$ 上的推導; 最後, 三角形的有關知識必須牢固掌握, 如歐拉線上垂心、 重心、 九點圓圓心和外心之間距離的比例以及三角形內心是旁心三角形的垂心等等。 三、評分標準USAMTS 數學競賽由 5 道題構成, 每道題 5 分, 共 25 分。 評分標準既是明確具體的, 又靈活多變.對於普通的解題方法, 可以根據關鍵步驟給分, 要考慮解決問題的完整性和連貫性。 對於少數創新性的解題方法, 考慮解題過程中的有意義的步驟或中間的結論, 以及距離解決問題的遠近來給分。 閱卷老師可以根據實際情況來扣除糟糕的書寫和不連貫的推理的考生分數。 利用電腦、 計算器、 代數系統解決問題的考生, 需要遞交原始程式碼和指定代數系統中調用的函數 (包括參數)。 若考生在有意義的步驟上跳步, 或者關鍵步驟論述不清楚, 均需要扣除一定的分數。 四、試題特點1. USAMTS 數學競賽一年進行三輪, 每一輪均由5道題構成, 涉及初、 高中數學的各個分支, 且已連續舉行了 31 屆。 考生必須在規定的時間, 按照規定的方式 (郵件郵寄或者通過E-mail) 郵寄結果, 所有結果必須用要求的 tex 範本排版列印, 且不接收數值結果, 需要解題的完整過程。 遞交日期結束後, 官方網站公佈詳細解答過程。 2. 充分利用現代資訊工具, 可以借助電腦或計算器解決問題, 與時代接軌。 數學中很多問題過於抽象、 複雜, 往往難以想像, 無從下筆。 但借助電腦和計算器, 可以幫助考生思考, 使用程式設計語言編寫代碼, 在電腦上進行調試和運行, 最後能夠得出答案, 甚至還可以利用電腦的高效率計算功能, 發現其他新的結論。 3. 通過上面 5 題發現, 題目素材新穎且有趣, 能夠提起學生的興趣, 考查考生的數學素養和能力。 考題通常沒有固定的出題方向和題型, 題目靈活多變, 形式多樣。 很多題目新穎, 解法獨特, 令人耳目一新, 且大部分題偏向於應用。 試題 1 通常給出的填圖和表, 考查觀察、 分析問題的能力及數感。 試題 2 是一道概率題, 考生要根據題意釐清"友好的"和"酸酸的"表格區別, 找出題中給出的變換 (置換) 的規律。 特別是方法2, 考生利用群論的有關知識, 可以減少運算, 達到解決問題的目的。 試題 3 為一道數論題, 考查了考生的推理和論證的能力, 特別是嚴謹、 全面考慮問題的能力; 試題 4 實際上是一道關於求計數個數的問題, 給出的兩種方法從不同的方向解決了問題。 實際上, 方法 2 可以從方法 1 得出的結論基礎上, 從結論聯想能否構造雙射, 可以得出答案, 思維層次較高; 第 5 題為一道純幾何題, 考查的知識點卻不少。 4. 培養考生的獨立分析、 解決問題以及數學寫作的能力。 一個月時間內, 要求考生通過查閱資料, 使用資訊技術等, 在獨立思考的前提下, 在規定的時間內將解答過程發至官方指定的郵箱, 並且規定使用固定的 tex 範本寫作, 對考生的要求較高, 是對考生的科研能力和毅力的一次很好的培養。 5. USAMTS 是一項個人數學競賽, 成績好的選手可以被邀請參加AIME (美國數學邀請賽), 甚至直接進入美國國家數學奧林匹克隊。 在被允許的情形下, 考生的姓名和地址可提供給大學和用人單位, 作為錄用時的一種參考。 本文作者任職中國湖南省長沙市湖南教育出版社 |
| 頁碼 | 123-133 |
2025年6月 49卷2期
第 31 屆 USAMTS 數學競賽 (第二輪) 試題賞析

