| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | 用複數法證明牛頓線定理 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
牛頓線定理: 完全四邊形 $ABCDEF$ 的三條對角線的中點共線。 如圖 1, 在完全四邊形 $ABCDEF$ 中, $M,N,P$ 分別為對角線 $AD,BF,CE$ 的中點, 求證: $M,N,P$ 共線。 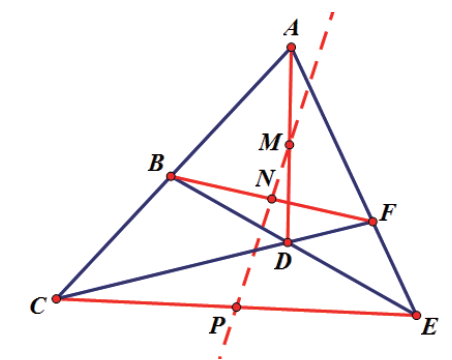 證明引理: 複平面上 $A,B,C$ 三點共線 (用字母本身表示該點所代表的複數) $$\Leftrightarrow \frac{A-B}{A-C}=k\in \mathbb{R}\ \Leftrightarrow \ \frac{A-B}{A-C}=\frac{\overline A-\overline B}{\overline A-\overline C}\ \Leftrightarrow \ A\overline B+B\overline C+C\overline A= \ \overline A B+\overline BC+\overline CA.$$ (引理非常顯然, 其證明在這裏不作贅述。) 在三角形所在的平面建立複平面, 用字母本身表示該點所代表的複數, 則: $$M=\frac{A+D}2,\quad N=\frac{B+F}{2},\quad P=\frac{C+E}{2}.$$ 欲證明 $M,N,P$ 共線, 由引理知只需證: $M\overline N+N\overline P+P\overline M= \ \overline M N+\overline NP+\overline PM$ \begin{align*} \Leftrightarrow\,& \frac{A+D}{2} \cdot \frac{\overline B+\overline F}{2}+ \frac{B+F}{2} \cdot \frac{\overline C+\overline E}{2}+\frac{C+E}{2} \cdot \frac{\overline A+\overline D}{2}\\ &=\frac{\overline A+\overline D}{2} \cdot \frac{B+F}{2}+ \frac{\overline B+\overline F}{2} \cdot \frac{C+E}{2}+\frac{\overline C+\overline E}{2} \cdot \frac{A+D}{2}\\ \Leftrightarrow\,& A\overline B+A\overline F+D\overline B+D\overline F +B\overline C+B\overline E+F\overline C+F\overline E+C\overline A+C\overline D+E\overline A+E\overline D\\ &= \overline AB+\overline AF+\overline DB+\overline DF +\overline BC+\overline BE+\overline FC+\overline FE+\overline CA+\overline CD+\overline EA+\overline ED,\\ \hbox{相加}&\Leftarrow\ \left\{\begin{array}{ll} A\overline B+B\overline C+C\overline A=\overline AB+\overline BC+\overline CA&\Leftarrow\ A,B,C\,\hbox{共線}\\ A\overline F+F\overline E+E\overline A=\overline AF+\overline FE+\overline EA&\Leftarrow\ A,F,E\,\hbox{共線}\\ D\overline B+B\overline E+E\overline D=D\overline B+B\overline E+E\overline D&\Leftarrow\ D,B,E\,\hbox{共線}\\ D\overline F+F\overline C+C\overline D=D\overline F+F\overline C+C\overline D&\Leftarrow\ D,F,C\,\hbox{共線。}\\ \end{array}\right. \end{align*} 即證。 總結: 牛頓線定理有很多純幾何的證明方法, 但這些純幾何的證明方法往往不好想, 用複數法就可以輕鬆的寫出。 一般地, 解決平面幾何問題可以用幾何法 (難想)、 建系法 (難算)、 三角硬演算法 (難想+難算)、 複數法, 筆者覺得有些難的幾何題只有通過複數才能秒殺! 參考文獻本文作者任教中國安徽省無為中學 |
| 頁碼 | 134-135 |
2025年6月 49卷2期
用複數法證明牛頓線定理

