| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | 再探一道壓軸題及其尺規作法 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
在解題教學中, 有部分教師只是教給學生問題的解法, 而對為什麼這樣解及解法的數學本質揭示得不夠。 在中考復習時遇到一道往年的壓軸題, 命題組給出的參考答案也是只說了具體的做法, 本文詳細說明為什麼這樣做, 並給出尺規作法及結論的應用, 供參考。 一、探究原題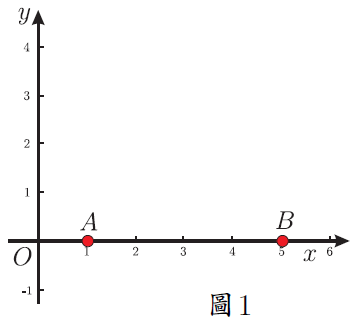 (2014年淄博中考數學壓軸題) 如圖 1, 點 $A$ 與點 $B$ 的座標分別是 (1,0)、 (5,0), 點 $P$ 是該直角坐標系內的一個動點。 (1) 使 $\angle APB=30^\circ$ 的點 $P$有 __________ 個; 說明 (1) (2)略。 (3) 原題給出的參考答案是「當過點 $A$、$B$ 的 $\odot E$ 與 $y$ 軸相切於點 $P$ 時, $\angle APB$ 最大 $\cdots\cdots$」。 為什麼過點 $A$、$B$ 的 $\odot E$ 與 $y$ 軸相切於點 $P$ 時, $\angle APB$ 最大? 尺規作圖如何作出這個圓? 我們不妨探究一番。 探究1: $\angle APB$ 最大時 $\odot E$ 與 $y$ 軸相切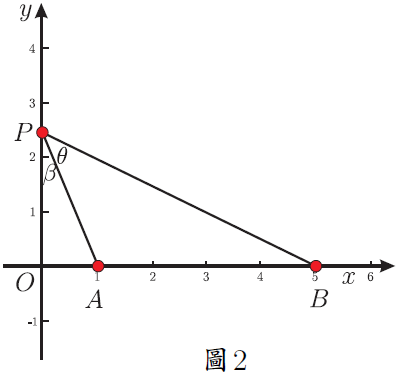 如圖 2, 點 $P$ 在 $y$ 軸上移動時, 有一個時刻 $\angle APB$ 最大 (只考慮 $y$ 軸正半軸的情況, $y$ 軸負半軸上的情況類似), 只要能求出 $\angle APB$ 最大時線段 $OP$ 的長度就可以了。 為方便接下來的計算, 不妨設 $OP=x$, $\angle APB=\theta$, $\angle OPA=\beta$, $\angle OPB=\alpha$。 當 $\angle APB$ 最大時, $\tan \angle APB$ 也最大, 也就是 $\tan\theta$ 最大。 $$\tan\angle \beta=\frac{OA}{OP}=\frac 1{x};\qquad \tan\angle \alpha=\frac{OB}{OP}=\frac 5{x}.$$ 而 $\tan\theta=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}$, 將 $\dfrac 1x$、 $\dfrac 5x$ 代入上式得 $\tan\theta=\dfrac4{x+\dfrac 5x}$, 當分母 $x+\dfrac 5x$ 最小時 $\tan\theta$ 最大。 $x+\dfrac 5x\ge 2\sqrt 5$, 當且僅當 $x=\dfrac 5x$ 時等號成立, 所以當 $x=\sqrt 5$ 時, $\tan\theta$ 最大。 下面說明當 $\angle APB$ 最大時, 過 $A$、$B$ 的圓與 $y$ 軸切於點 $P$。 可以有以下兩種思路。 思路1:根據圓的定義和切線的判定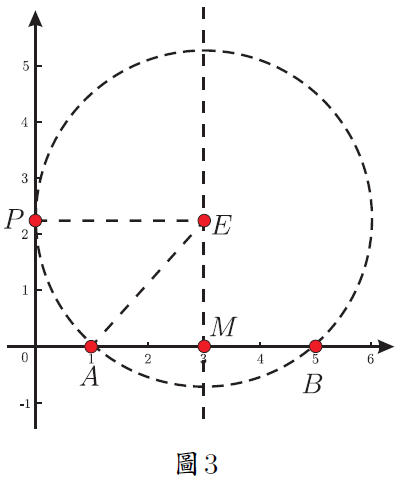 如圖3。 以 $AB$為弦的圓圓心在 $AB$ 的中垂線上, 作線段 $AB$ 的中垂線, 過點 $P(0,\sqrt 5)$ 作 $y$ 軸的垂線與 $AB$ 的中垂線相交於點 $E(3,\sqrt 5)$。 由畢氏定理可以計算出 $EA=3$。 此時有 $EA=EB=EP=3$, 所以 $A$、$B$、$P$ 在同一個圓上, 又 $EP\bot y$ 軸, 所以圓 $E$ 和 $y$ 軸相切於點 $P$。 思路2:根據切割線定理的逆定理如圖 3。 由 $OP=\sqrt 5$, $OA=1$, $OB=5$, 可以想到 $OP^2=OA\cdot OB$。 根據切割線定理的逆定理知道 當 $A$、$B$ 橫坐標變為任意數值 $m$、$n$ $(m,n\gt0)$ 時仍有類似的結論, 不再贅述。 探究2:圓 $E$ 與 $y$ 軸相切時 $\angle APB$ 最大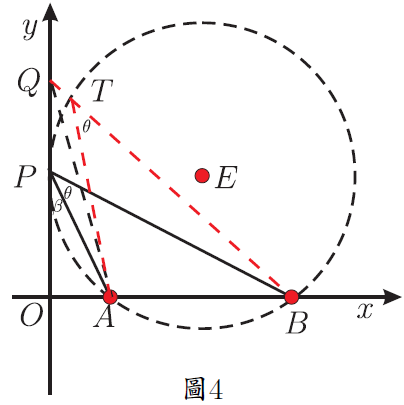 如圖 4。 以 $AB$ 為弦的圓 $E$ 與 $y$ 軸相切於點 $P$。 在 $y$ 軸上任找一點 $Q$ (不與 $P$ 重合), 連接 $AQ$ 和 $BQ$, $BQ$ 與圓交於點 $T$, 證明 $\angle APB\gt\angle AQB$ 即可。 不容易直接比較 $\angle APB$ 與 $\angle AQB$ 的大小。 觀察圖 4, $\angle APB$ 是圓周角, 連接 $AT$ 就有 $\angle ATB=\angle APB=\theta$, 而 $\angle ATB\gt\angle AQB$, 所以 $\angle APB\gt\angle AQB$。 所以, 以 $AB$ 為弦的圓與 $y$ 軸相切於點 $P$ 時, $\angle APB$ 最大。 並且, 此時根據切割線定理有 $OP^2=OA\cdot OB$。 二、尺規作法尺規作出圓 $E$ 的方法有多種, 限於篇幅, 在此只給出兩種容易想到的方法, 其餘的尺規作法讀者可以自行補充。 方法1:根據切線的定義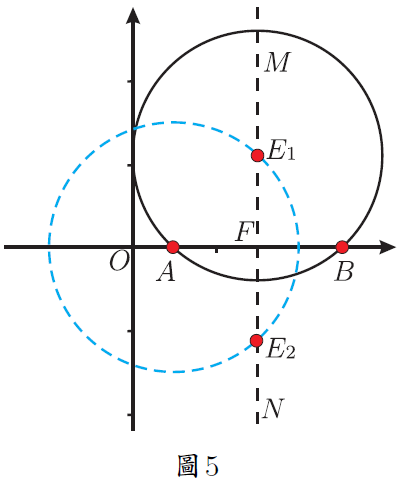 如圖 5, 過 $A$、$B$ 兩個點的圓, 其圓心 $E$ 線上段 $AB$ 的中垂線 $MN$ 上, 要實現圓 $E$ 與 $y$ 軸相切, 則點 $E$ 到 $y$ 軸的距離就是 $OF$ 的長, 再實現 $E$ 到點 $A$、$B$ 的距離是 $OF$ 就可以了。 以 $A$ 為圓心, $OF$ 的長為半徑作圓, 與 $AB$ 的垂直平分線 $MN$ 相交於點 $E_1$ 和 $E_2$, 再以 $E_1$ 為圓心 $E_1A$ 為半徑作圓 $E_1$, 圓 $E_1$ 就是求作的圓 (圓 $E_2$ 的作法類似, 略)。 作法:略。 方法2:根據射影定理在 $x$ 軸上有 $A$、$B$ 兩點, 過 $A$、$B$ 兩點作一個圓使其與 $y$ 軸相切。 根據切割線定理的逆定理 如何在 $y$ 軸上找出點 $P$? 思路1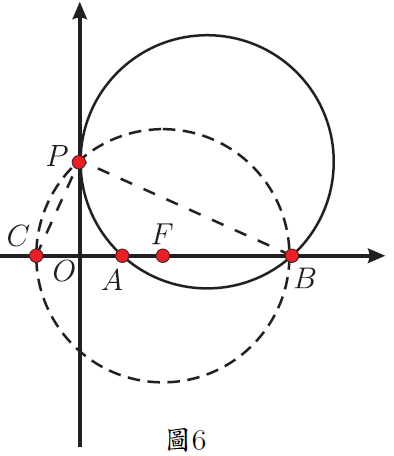 如圖6。 由 $OP^2=OA\cdot OB$, 可以想到射影定理, 作點 $A$ 關於 $y$ 軸的對稱點 $C$, 有 $OA=OC$, 只需在 $y$ 軸上找一個點 $P$, 使得 $OP^2=OC\cdot OB$ 即可。 以 $BC$ 為直徑作圓 $F$, 交 $y$ 軸於點 $P$ (只考慮正半軸的情況, 負半軸的情況讀者可自行補充)。 根據射影定理, 此時就有 $OP^2=OC\cdot OB$, 也就是 $OP^2=OA\cdot OB$。 過 $A$、$B$、$P$ 三個點的圓就是求作的圓。 思路2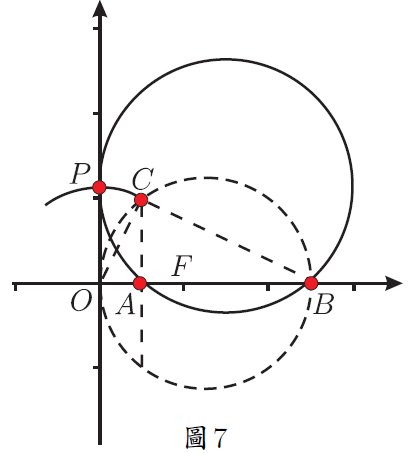 如圖 7, 根據思路 1 中的想法, 以 $OB$ 為直徑作圓 $F$, 過點 $A$ 作 $x$ 軸的垂線, 交圓 $F$ 與點 $C$, 根據射影定理, $OP^2=OA\cdot OB$, 再以 $O$ 為圓心, $OC$ 的長為半徑作弧, 交 $y$ 軸於點 $P$ (只作出 $y$ 軸正半軸的情況), 此時 $OP^2=OA\cdot OB$。 過 $A$、$B$、$P$ 三個點的圓就是求作的圓。 三、結論應用1.(2004年全國高中數學聯賽)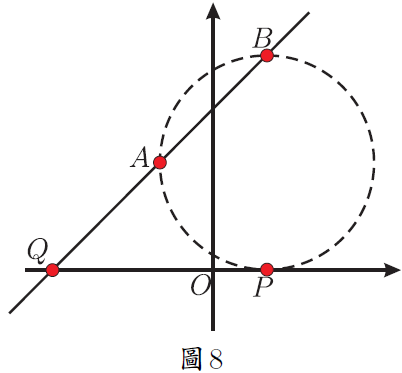 如圖 8, 在平面直角坐標系中, 給定兩點 $A(-1,2)$、 $B(1,4)$, 點 $P$ 在 $x$ 軸上移動, 當 $\angle APB$ 取最大值時, 點 $P$ 的橫坐標是多少? 思路分析由上文分析可以知道, 當以 $AB$ 為弦的圓與 $x$ 軸相切的時候, $\angle APB$ 最大, 如何作出與 $x$ 軸相切的圓可參考上文「尺規作法」。 由切割線定理知道, $QP^2=QA\cdot QB$, 所以 $PQ=4$, 所以點 $P$ 的橫坐標為 1 或 $-7$。 分別畫出圖形可以知道當點 $P$ 的橫坐標為 1 時, $\angle APB$ 取最大值。 2.(2015陝西中考數學壓軸題)如圖9, 在四邊形 $ABCD$ 中, 有 $AD//BC$, $CD\bot BC$, $\angle ABC=60^\circ $, $AD=8$, $BC=12$. 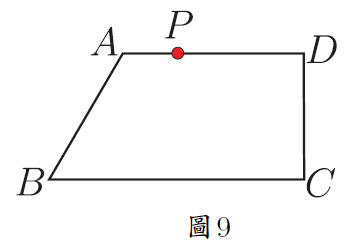 (1) 略; (2) 略; 思路分析(1) (2) 略. (3) 要使得 $\cos\angle BPC$ 最小, 只需要 $\angle BPC$ 最大就可以。 何時 $\angle BPC$ 最大? 以 $BC$ 為弦的圓與 $AD$ 相切於點 $P$ 時, $\angle BPC$ 最大。 具體解法, 略。 四、思考通過上文的探究和分析可以看出, 一道往年的壓軸題, 如果直接按照參考答案給出的思路進行教學, 學生只能知道相切時角最大, 不知道為什麼相切時圓最大, 也不會知道如何尺規作出這個圓, 因此在平時的課堂教學中, 可以重視對典型問題的深度探究, 在引導學生學好基礎知識、 掌握基本技能和方法的基礎上, 對典型問題進行深度探究, 揭示數學本質, 讓學生在探索中學會發現問題, 進而分析問題、 解決問題, 從而有效提升學生的數學素養。 參考文獻本文作者張小川任教中國山東淄博高青實驗中學,邢春林任職中國山東省高青縣教研室 |
| 頁碼 | 136-140 |
2025年6月 49卷2期
再探一道壓軸題及其尺規作法

