| 發刊日期 |
2025年9月
|
|---|---|
| 標題 | 道成肉身的表現定理 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
謹將此文獻給劉太平院士並祝他 80 歲生日快樂 1. 邏各斯(logos) --- 希臘、希伯來的精神『道成了肉身, 住在我們中間, 充充滿滿地有恩典有真理。我們也見過祂的榮光, 正是父獨生子的榮光。 約翰為祂作見證, 喊著說: 「這就是我曾說: 『那在我以後來的, 反成了在我以前的, 因祂本來在我以前。』」 從祂豐滿的恩典裡, 我們都領受了, 而且恩上加恩。 律法本是藉著摩西傳的;恩典和真理都是由耶穌基督來的。 從來沒有人看見神, 只有在父懷裡的獨生子將祂表明出來。』 --《約翰福音 1:14-18》-- 在西元前 560 年, 在以弗所 1 1 以弗所是古希臘人在小亞細亞建立的一個大城市, 位於加斯他河注入愛琴海的河口 (今天屬於土耳其)。 以弗所同時是新約聖經不時出現的城市, 聖經的新約全書裡面就有一卷是以弗所書。 的一名哲學家赫拉克利特 (Heraclitus, BC535$\sim$BC475), 他最著名的例子是《 人不可能踏進同一條河流兩次。》 他認為: 《每一樣東西時刻都在變動, 沒有停止不動的。》 既然每一樣事物都不斷變動, 那為何世界還不是完全的混亂呢? 他的答案是: 「萬物的發生都遵照邏各斯 (logos)。」這世界是有理性和心意的, 而這心意便是上帝的邏各斯 (logos)。 由於有 logos, 整個宇宙大自然也就有了規律。赫氏認為邏各斯 (logos)或翻譯為《道》、 就是秩序的原則, 整個宇宙都藉它而存在。這是赫拉克利特使用這個名詞時所指的東西, 他是第一個把這個詞運用到哲學上。 他以為邏各斯 (logos)是決定一切實在事務運動的規律。 這種心意、理性的概念, 統御世界的邏各斯 (logos)使希臘人為之著迷。 例如, 阿那克薩哥拉(Anaxagoras, BC 500$\sim$428)「精神」 (智性)的概念解釋自然變化, 超然獨立, 純淨無瑕, 引發變化。 並聲稱心意 (nous) 「管轄萬物」。 希臘哲學基本上就沿著這條《道》發展出來, 這就是邏各斯 (logos) 中心主義之濫觴。 柏拉圖申明它的整個學說都是基於邏各斯並宣稱: 上帝的邏各斯使行星運行在軌道上, 又按時帶回季節與年份。 邏各斯是判斷真與不真的根本標準(尺度), 所以就與《理念》聯繫起來。 在亞里斯多德 (Aristoteles, BC 384$\sim$322)的著作中, 邏各斯常常作為《言語》、《比例》, 但更多是作為《理性》來使用, 它日後發展為邏輯學 (logic) 也就順理成章了。 所有這些努力都朝一個方向前進, 就是利用《理性》的方式去探討宇宙或大自然的秩序與規律, 使宇宙和人類呈現理性 2 2 理性 (英語: reason) 最早源起於希臘語詞語"邏各斯" (希臘語:logos)。在羅馬時代, 譯成拉丁語: ratio, 拉丁語原意是計算金錢, 但在等同於邏各斯後, 成為哲學上廣泛使用的術語。 的是邏各斯 (logos), 而邏各斯正是上帝的心意。由於有邏各斯 (logos) 世界也就井然有序了。 這個概念後來由斐羅 (Philo, BC20$\sim$AD40) 發揮得淋漓盡致, 他是一位住在亞歷山大的猶太人, 他致力於融合猶太人與希臘人這個崇高的思想, 他認為上帝的邏各斯 (logos) 係「銘刻在萬物的構造之上」。 邏各斯 (logos)是將靈魂放在上帝面前的大祭司, 所以邏各斯 (logos) 是人和上帝之間的橋樑。 基督教源於猶太教, 當福音向外宣揚特別來到與希伯來思想迴異的希臘世界, 首先面對的是文化的差異。 在西元第一世紀左右, 在以弗所的約翰(約翰福音的作者)看到這問題但同時也找到解決方案。 他可能是教會初期最偉大的思想家, 他發現猶太人與希臘人都有《道》也就是邏各斯 (logos) 的概念, 它能聯繫猶太人與非猶太人的思想。 約翰福音的作者約翰, 使基督教穿上希臘人能夠瞭解的外衣, 讓基督教適應世界思潮, 並成長為普世的宗教成為可能。 他向世人介紹一種全新的《基督論》, 並稱耶穌是邏各斯 (Logos), 意思是: 耶穌是上帝在人間的創造力量, 同時也體現了上帝的心意。 約翰對於《道》的認知是獨特的, 所謂《道成肉身》 (incarnation) 意思是《道》就是耶穌基督, 直接翻譯可以這麼說: 「上帝的心意成了人, 耶穌完全表達了上帝對我們的思想。」《道成肉身》 (incarnation), 是基督教信仰的核心: 創造天地的全能上帝, 居然成為一名居住在拿撒勒的人 (神以人的形式出現)。 上帝不是高高在上, 而是甘願卑微, 親身降到世間, 在人群之中啟示自己。 在耶穌基督的獨特性裡面, 祂能將上帝的真相、榮耀表達出來。 透過邏各斯 (logos) 將兩希文明(希伯來與希臘)匯為西方文明的主要源泉。 因為上帝創造了有理性的世界和人類。 這種思維的含義, 是上帝和人的理性在某種程度上是相似的, 因此, 人能根據上帝的理性來思考。 因為人是上帝用以創造萬物的理性秩序的反照, 所以人能理解萬物的秩序。 簡言之, 大自然的可理解性, 是基於它的秩序和人的理性都來自同一位道 (Logos)。 數學起源於希臘, 自然大部分的字彙, 尤其與理性有關的必然是出自於邏各斯 (logos), 例如邏輯學 (logic) 與邏各斯 (logos) 同源, 意為: 詞語、 思想、 概念、 理念、 論據、 論點、 說明、 理由、 原則、 推理。 另外拓樸學 (topology) 3 3 簡單的說: 拓樸學是對幾何對象在連續變換下保持不變的性質之研究。 這個字來自希臘文的《topos》 和 《logos》, 前者意為《地方》或《位置》, 後者就是邏各斯 (logos) 意思是《學問》或《研究》, 基本上這是一門研究位置變換的學問。
數學中將這種希臘--希伯來精神(道成肉身)展現最淋漓盡致, 當屬 Riesz 表現定理 (Riesz representation theorem), 這是匈牙利數學家 Frigyes (Frederic) Riesz
(1880$\sim$1956) 於 1909 年得出的重要結果。
根據數學傳播 Peter Lax 的訪談  由 Riesz 表現定理 F. Riesz 引入了函數序列「弱收斂」的概念, 這對於微分方程弱解之研究有根本的重要貢獻。 由弱解 (weak solution) 自然就引進對偶空間 (dual space) 之研究。 任何向量空間都有其對應的對偶向量空間, 一個向量(線性)空間如果對它不清楚, 那麼我們可以先看看它的對偶空間, 而 Riesz 表現定理正是研究對偶空間最重要的工具。 F. Riesz 是泛函分析的創始人之一, 他的工作在物理學上有許多重要的應用。 在泛函分析的發展歷史離不開 Lebesgue (勒貝格) 積分, 在數學史這實在是令人驚訝的也是慶幸的, 只有在 Lebesgue (勒貝格) 積分發明之後, 才有可能提出令人滿意的正交函數級數理論, 而這個理論主要是 F. Riesz 的工作。 他以 Fréchet 提出的思想為基礎, 利用 Fréchet 的距離 (metric) 思想, 將勒貝格實變函數論的工作與 D. Hilbert (1862$\sim$1943) 及其學生 E. Schmidt (1876$\sim$1959) 發展的積分方程聯繫起來。 F. Riesz 的工作不僅因其成果的重要性而顯著, 還因其在數學品味和措辭方面的美學洞察力而聞名於世。 對他來說, 不存在單純為了結構理論而進行的抽象, 他總是回歸一些具體、 實際情形的應用。 F. Riesz 與他的弟弟 Marcel Riesz也是數學史出名的兄弟檔數學家, Marcel 主要是研究偏微分方程與調和分析, Riesz potential 還有 Riesz 變換是 Marcel Riesz 的貢獻。 他們兩人如何區別呢?通常我是教學生這麼看: 泛函是《F》所以在泛函分析的 Riesz 定理幾乎都是哥哥 F. Riesz 的成果。 雖然哥哥 F. Riesz 的名氣遠比弟弟 Marcel Riesz 來的大, 但後來 Marcel Riesz 在 Mittag--Leffler (1846$\sim$1927) 的邀請下於 1908 年起任教於瑞典, 對於瑞典的調和分析與偏微分方程學派有極深遠的影響。 例如著名的瑞典數學家, Lars Garding (1919$\sim$2014) 與 1962 年費爾茲獎得主 Lars Valter Hörmander (1931$\sim$2012) 都是他的學生 4 4 1952 年 M. Riesz 退休之後 L. Garding 自然就接替他成為 Hörmander 的指導教授。 。再加上近 30 年來由於調和分析 (harmonic analysis) 在偏微分方程研究的重大突破, 使得 Riesz 變換與相關研究變得重要, 無形中 Marcel Riesz 的歷史地位也提高不少。  2. 矩陣與線性變換
『要是沒有線性代數, 任何數學和初等數學都講不下去。』 --《數學概觀 (Lars Garding)》-- Riesz 表現定理的前身, 是線性代數中線性變換的矩陣表示論, 與此相關的是表現理論 (Representation Theory), 它的基本精神是將抽象的代數結構, 映射到具體的向量空間讓我們能夠看到數學內在的本質。 學線性代數最大的困難之一是分不清矩陣 (matrix) 與線性變換 (linear transformation)。 比較老的書是先介紹線性變換然後才講矩陣, 這種幾何方法的好處是避免在理論中使用座標, 但最終當需要計算時, 還是必須藉助於座標和矩陣。 在此我們就面對 $$ \hbox{抽象}\quad\Longleftrightarrow\quad\hbox{具體} $$的兩難, 這本質上是數學史著名的形式主義與直覺主義(intuitionism)之爭的延續。我們還是先回到主題, 線性變換源自於變數變換 \begin{align} \left\{ \begin{aligned} y_1&=\varphi_1(x_1,x_2,\ldots, x_n), \\[2mm] y_2&=\varphi_2(x_1,x_2,\ldots, x_n), \\[2mm] &\ \ \vdots \\[2mm] y_n&=\varphi_n(x_1,x_2,\ldots, x_n). \end{aligned} \right. \label{2.1} \end{align}如果 $\varphi_k, k=1,2,\ldots, n, $ 是平滑的則在小範圍內與(非齊次)線性變換 \begin{align} \left\{ \begin{aligned} y_1&=a_{11}x_1+a_{12}x_2+\cdots+a_{1n} x_n+b_1, \\[2mm] y_2&=a_{21}x_1+a_{22}x_2+\cdots+a_{2n} x_n+b_2, \\[2mm] &\ \ \vdots \\[2mm] y_n&=a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn} x_n+b_n. \end{aligned} \right. \label{2.2} \end{align}是相當接近的。 做個平移可以假設 $b_1=b_2=\cdots=b_n=0$, 所以對 \eqref{2.2} 的研究基本上可以轉化為具有相同係數的 (齊次) 線性變換 \begin{align} \left\{ \begin{aligned} y_1&=a_{11}x_1+a_{12}x_2+\cdots+a_{1n} x_n, \\[2mm] y_2&=a_{21}x_1+a_{22}x_2+\cdots+a_{2n} x_n, \\[2mm] &\ \ \vdots \\[2mm] y_n&=a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn} x_n. \end{aligned} \right. \label{2.3} \end{align}而且從此之後我們認定所謂的線性變換是沒有常數項的齊次線性變換 \eqref{2.3}, 這是學線性代數首先要分辨清楚的地方。 變數變換 \eqref{2.1} 與 \eqref{2.3} 的關係是透過全微分 (total differential) 來看 \begin{align} \left\{ \begin{aligned} d\varphi_1&={\partial \varphi_1\over \partial x_1} dx_1+{\partial \varphi_1\over \partial x_2} dx_2+\cdots+{\partial \varphi_1\over \partial x_n} dx_n, \\[2mm] d\varphi_2&={\partial \varphi_2\over \partial x_1} dx_1+{\partial \varphi_2\over \partial x_2} dx_2+\cdots+{\partial \varphi_2\over \partial x_n} dx_n, \\[2mm] &\ \ \vdots \\[2mm] d\varphi_n&={\partial \varphi_n\over \partial x_1} dx_1+{\partial \varphi_n\over \partial x_2} dx_2+\cdots+{\partial \varphi_n\over \partial x_n} dx_n. \end{aligned} \right. \label{2.4} \end{align}可知線性變換 \eqref{2.3} 的係數正是變數變換 \eqref{2.1} 之 Jacobian 矩陣的係數 \begin{align} a_{ij}\quad\Longleftrightarrow\quad {\partial \varphi_i\over \partial x_j} \quad \qquad i,j=1,2,\ldots, n. \label{2.5} \end{align}由此自然可以引進 $n\times n$ 矩陣 $A=[a_{ij}]$, $i,j=1,2,\ldots n$ 並將 \eqref{2.3} 表示為 \begin{align} \boldsymbol{y} = A\boldsymbol{x},\qquad y_i =\sum_{j=1}^n a_{ij} x_j,\qquad i=1,2,\ldots, n. \label{2.6} \end{align}所以 $A$ 可視為 $\mathbb{R}^n \mapsto \mathbb{R}^n$ 的一個映射 (map) 將 $\boldsymbol{x}\in \mathbb{R}^n$ 映射到 $\boldsymbol{y}=A\boldsymbol{x} \in \mathbb{R}^n$ 其中 $\boldsymbol{y}=A\boldsymbol{x}$ 的第 $i$ 個座標為 $$ y_i=\sum_{j=1}^n a_{ij} x_j,\qquad i=1,2,\ldots, n. $$根據這個定義容易驗證這個映射 $A$ 滿足 \begin{align} \left\{ \begin{array}{ccl} A(\boldsymbol{x}_1+\boldsymbol{x}_2)=A(\boldsymbol{x}_1) + A(\boldsymbol{x}_2),&~\qquad~& \forall\ \boldsymbol{x}_1, \boldsymbol{x}_2 \in \mathbb{R}^n,\\[2mm] A(\alpha \boldsymbol{x}) = \alpha A(\boldsymbol{x}),&\qquad& \forall\ \boldsymbol{x} \in \mathbb{R}^n,\quad \forall\ \alpha \in \mathbb{R}. \end{array} \right. \label{2.7} \end{align}我們稱這兩個性質為線性 (linear)。 $n$ 維空間的線性變換也可以用它的內秉 (intrinsic) 性質來定義, 而不用與之對應的座標公式 \eqref{2.3}。 這種不用座標的定義最大的好處是它與基底(basis)的選取無關。 定義 2.1: $n$ 維空間的線性變換 (linear transformation) 是一個函數 $\boldsymbol{y}=T(\boldsymbol{x})$, 其中變數 $\boldsymbol{x}\in \mathbb{R}^n$ 與函數值 $\boldsymbol{y}\in \mathbb{R}^n$ 都是向量, 這個函數滿足 \begin{align} \left\{ \begin{array}{ccl} T(\boldsymbol{x}_1+\boldsymbol{x}_2)=T(\boldsymbol{x}_1) + T(\boldsymbol{x}_2),&~\qquad~& \forall\ \boldsymbol{x}_1, \boldsymbol{x}_2 \in \mathbb{R}^n, \\[2mm] T(\alpha \boldsymbol{x})= \alpha T(\boldsymbol{x}),&\qquad& \forall\ \boldsymbol{x} \in \mathbb{R}^n,\quad \forall\ \alpha \in \mathbb{R}. \end{array} \right. \label{2.8} \end{align}或者兩者合併為線性組合之形式 \begin{align} T(\alpha_1\boldsymbol{x}_1+\alpha_2\boldsymbol{x}_2)=\alpha_1T(\boldsymbol{x}_1) + \alpha_2T(\boldsymbol{x}_2),\qquad \forall\ \boldsymbol{x}_1, \boldsymbol{x}_2 \in \mathbb{R}^n,\quad \forall\ \alpha_1, \alpha_2 \in \mathbb{R}. \label{2.9} \end{align}如果值域是實數 $$ T:\mathbb{R}^n\mapsto \mathbb{R}, \qquad y=T(\boldsymbol{x})\in \mathbb{R}, $$實數值函數 $y=T(\boldsymbol{x})$ 滿足 \eqref{2.8}, 我們稱這種特殊的線性變換為 線性泛函 (linear functional)。 註解: (i) \eqref{2.8} 這個定義雖然抽象卻對座標沒有特定的選擇, 甚至無窮維空間缺少座標表示的向量也沒有問題, 所以今後只要談到空間的線性變換時, 都是根據 \eqref{2.8} 或 \eqref{2.9} 這個定義來理解。 如果有人說分析的線性與線性代數的線性是不一樣的, 那絕對是錯的! (ii) 線性變換的幾何意義 : 假設向量 $\boldsymbol{x}_1, \boldsymbol{x}_2$ 相交有夾角, 用專業的術語也就是 $\{\boldsymbol{x}_1, \boldsymbol{x}_2\}$ 是線性獨立, 它們會形成一個平行四邊形。 現在的問題是邊長帶到邊長, 那麼對角線帶到哪裡去? $$ \boldsymbol{x}_1\to T(\boldsymbol{x}_1),\quad \boldsymbol{x}_2\to T(\boldsymbol{x}_2) \quad\Longrightarrow\quad \boldsymbol{x}_1+\boldsymbol{x}_2\to ? $$假設 $T$ 不是退化的也就是 $\{T(\boldsymbol{x}_1), T(\boldsymbol{x}_2)\}$ 仍然是線性獨立, 它們也會形成一個平行四邊形。 映射過去的對角線為 $T(\boldsymbol{x}_1)+ T(\boldsymbol{x}_2)$, 所以 \eqref{2.8}$_1$就回答了上述的問題 $$ \boldsymbol{x}_1\to T(\boldsymbol{x}_1),\quad \boldsymbol{x}_2\to T(\boldsymbol{x}_2) \quad\Longrightarrow\quad \boldsymbol{x}_1+\boldsymbol{x}_2\to T(\boldsymbol{x}_1+\boldsymbol{x}_2); $$一個線性變換把平行四邊形的對角線映射過去也是新的平行四邊形的對角線, 換句話說線性變換會《保持平行四邊形》。 這是向量加法的情形, 其次是純量的乘法 $$ \boldsymbol{x} \to \alpha \boldsymbol{x}; $$給定向量 $\boldsymbol{x}$ 然後在這條線上將 $\boldsymbol{x}$ 放大或縮小 $\alpha$ 倍(包括負號)成為 $\alpha \boldsymbol{x}$。 現在的問題是 $\boldsymbol{x}$ 帶到 $T(\boldsymbol{x})$, 那麼 $\alpha \boldsymbol{x}$ 帶到哪裡去? $$ \boldsymbol{x}\to T(\boldsymbol{x}) \quad\Longrightarrow\quad \alpha\boldsymbol{x}\to \ ? $$所以 \eqref{2.8}$_2$ 就回答了 $$ \boldsymbol{x} \to T(\boldsymbol{x}) \quad\Longrightarrow\quad \alpha\boldsymbol{x}\to \alpha T(\boldsymbol{x}), $$向量 $\boldsymbol{x}$ 放大或縮小 $\alpha$ 倍, 那麼映射過去的向量 $T(\boldsymbol{x})$ 也一樣放大或縮小 $\alpha$ 倍。 換句話說線性變換會《保持直線》。 如果兩者合併, \eqref{2.9} 則告訴我們線性變換會《保持線性組合》。 除此之外, 線性變換直觀來看就是分配律: 先加減再作用等於先作用再加減。 (iii) 線性變換的代數意義 : 向量空間的基本運算是向量的加法 (vector addition) 與純量的乘法 (scalar multiplication)。 為了方便雖然我們定義線性變換 $T: \mathbb{R}^n\mapsto \mathbb{R}^n$, 但實際上可以是 $T: \mathbb{R}^n\mapsto \mathbb{R}^m$ 或更一般的情形, $T: V\mapsto W$, 此時向量空間 $V$ 與 $W$ 的加法與純量的乘法不見得是一樣。 但 \eqref{2.8} 告訴我們一個將 $V$ 映射到 $W$ 的線性變換會將 $V$ 的加法帶到 $W$ 的加法, 同時也將 $V$ 的純量乘法帶到 $W$ 的純量乘法。 我們稱保持這種運算結構的映射為同態 (homomorphism) 5 5 英文的同態 (homomorphism) 源自希臘文 的 homo 與 morphism 意思分別是《相同》與《形象》, morphism (形象, image)這個字也常出現在聖經神學, 它特別指有形可見的樣式, 最具體的例子就是《道成肉身》。 。從代數的角度來看: 能夠保持這兩個運算(代數結構)的最好函數就是線性變換 (linear transformation)。 這不僅僅是線性代數更是數學與物理還有整個科學與科技最根本的概念。 (iv) 先講線性變換, 其深層的意義是想通過公理化來表述線性代數。 這源於歐幾里得 (Euclid) 的體系, 雖然嚴謹但也帶來教學上的困難。 由於將線性變換的研究視為抽象代數的一部分, 不少的人是將線性代數當成抽象代數在教, 以至於學生認為線性代數是純數學。 這實在是誤導也是極其不幸的! 這樣的教學導致學生在計算還有整體數學觀上是有欠缺的。 (v) 學線性代數 (linear algebra) 的矩陣理論 (matrix theory), 最常見的困難 是把矩陣當成數! 所以在觀念上很難接受矩陣的乘法不滿足交換律 $$ AB\not=BA,\qquad A, B \in M_n(\mathbb{R}). $$其實連量子力學的創始人之一的海森堡 (Werner Heisenberg, 1901$\sim$1976) 也碰見這問題。 如今有了線性變換的概念, 可以將矩陣視為函數 (線性變換) 則矩陣的乘法就相當於函數的合成, 那麼矩陣相乘的交換律自然不會成立。 (vi) 上面之討論並沒有限定在 $n\times n$ 方陣, \eqref{2.6} 這個關係式換成 $m\times n$ 矩陣也成立 $$ \boldsymbol{y} = A\boldsymbol{x},\qquad y_i =\sum_{j=1}^n a_{ij} x_j,\qquad i=1,2,\ldots, m. (2.6') $$整個證明是一樣的, 細節我們就省略了! $\Box$ 現在我們要問矩陣 $A$ 與線性變換 $T$ 之關係? 先引進標準基底 \begin{align} \boldsymbol{e}_j=(0,\ldots, 0,1,0,\ldots, 0)^{\rm T}\in \mathbb{R}^n,\qquad j=1,2,\ldots, n \label{2.10} \end{align}則由 \eqref{2.3} 或 \eqref{2.6} 得 \begin{align} A\boldsymbol{e}_j= \left[\begin{matrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{nj}\end{matrix}\right] = a_{1j} \boldsymbol{e}_1 + a_{2j} \boldsymbol{e}_2+\cdots + a_{nj} \boldsymbol{e}_n =\sum_{i=1}^n a_{ij} \boldsymbol{e}_i \label{2.11} \end{align}基底 $\boldsymbol{e}_j$ 經過 $A$ 之作用成為 $A\boldsymbol{e}_j$ 正是矩陣 $A$ 第 $j$ 個行向量 (column vector)。 原先矩陣只是一堆數字放在類似九宮格的方塊裡面, 現在則告訴我們矩陣的內在本質是函數, 而且這些數字代表座標而該座標是與選取的基底有關的。 反過來若 $\boldsymbol{y}=T(\boldsymbol{x})$ 是任意的線性變換, 而 $\mathscr{B}=\{\boldsymbol{e}_1, \boldsymbol{e}_2,\ldots, \boldsymbol{e}_n\}$ 是一組標準基底, 則根據線性 \eqref{2.8} 或 \eqref{2.9} 有 \begin{align} \boldsymbol{y}=\,&T(\boldsymbol{x})=T(x_1\boldsymbol{e}_1+ x_2\boldsymbol{e}_2+\cdots+x_n \boldsymbol{e}_n)=x_1T(\boldsymbol{e}_1)+ x_2T(\boldsymbol{e}_2)+\cdots+x_n T(\boldsymbol{e}_n).\label{2.12} \end{align}這個等式就是物理的疊加 (重疊) 原理 (principle of superposition), 線性變換將線性組合 (linear combination) 帶過去仍然是相同的線性組合, 由這等式推出整個空間在線性變換下轉換到由向量 $\{T(\boldsymbol{e}_1),T(\boldsymbol{e}_2),\ldots,T(\boldsymbol{e}_n)\}$ 所編織 (span) 而成的子空間。 對照 \eqref{2.3} 定義 $a_{ij}$ 是 $T(\boldsymbol{e}_j)$ 第 $i$ 個座標, 那麼向量 $\boldsymbol{y}=T(\boldsymbol{x})$ 的座標就是 \begin{align} y_i = a_{i1} x_1 + a_{i2} x_2+\cdots + a_{in} x_n,\qquad i=1,2,\ldots, n. \label{2.13} \end{align}而且藉由 \eqref{2.11} 可以證明 \begin{align} T(\boldsymbol{e}_j)= A\boldsymbol{e}_j,\qquad j=1,2,\ldots,n. \label{2.14} \end{align}對於任意 $\boldsymbol{x}\in \mathbb{R}^n$ $$ \boldsymbol{x}= x_1 \boldsymbol{e}_1 + x_2 \boldsymbol{e}_2 +\cdots+ x_n \boldsymbol{e}_n, $$藉由線性可得 \begin{align} A\boldsymbol{x} =\,& A\bigg(\sum_{j=1}^n x_j \boldsymbol{e}_j\bigg)=\sum_{j=1}^n x_j (A\boldsymbol{e}_j)=\sum_{j=1}^n x_j T(\boldsymbol{e}_j)=T\bigg(\sum_{j=1}^n x_j \boldsymbol{e}_j\bigg)= T(\boldsymbol{x}). \label{2.15} \end{align}根據這個規則線性空間 (也就是向量空間) 中每一個線性變換 $T$ 就對應一個矩陣 $A=[a_{ij}]$ \begin{align} [T]_\mathscr{B}=A=[a_{ij}]. \label{2.16} \end{align}一個抽象的線性變換透過基底可以具體地表示為矩陣。 這裡面有極為深刻的希臘哲學與希伯來神學之內涵, 我個人則將之類比為線性代數中的 《道成肉身》: $$ \hbox{線性變換, 道, (抽象)}\quad\Longleftrightarrow\quad\hbox{矩陣,肉身, (具體)}; $$抽象的線性變換必須透過具體的矩陣才能夠計算, 但是只有矩陣就好比瞎子摸象只是接觸到真理的一部分而不是全貌, 容易以偏概全, 如何維持理論與計算的平衡是線性代數學習的重點。 同理將標準基底換為一般的基底 $\mathscr{B}'=\{\boldsymbol{e}_1', \boldsymbol{e}_2',\ldots, \boldsymbol{e}_n'\}$, 並重複 \eqref{2.11}$-$\eqref{2.15} 的計算則相同的線性變換 $T$ 此時表示為 \begin{align} [T]_{\mathscr{B}'}=A'=[a_{ij}']. \label{2.17} \end{align}也就是不同的矩陣 $A, A'$ 卻代表同一個線性變換 $T$, 我們稱這兩個矩陣是相似的, 通常表示為 $A\sim A'$, 意思是存在可逆矩陣 $P$ 使得 $A=PA'P^{-1}$ \begin{align} A\sim A' \quad\Longleftrightarrow\quad A=PA'P^{-1}. \label{2.18} \end{align}類似於如何將一個圓錐曲線(conic section)化為標準式, 這裡自然就引進如何將一個線性變換對應的矩陣化為最簡單的形式, 也就是對角化成 Jordan 型標準矩陣這個問題。 實際上: 任意一個矩陣都可以化為與它相似的 Jordan 型標準矩陣。 這個定理在數學問題的應用, 特別在線性微分方程組的理論, 起著重大的作用。 3. Riesz 表現定理 (Hilbert 空間版本)我個人認為要談 Riesz 表現定理就應該從 Cauchy 函數方程開始! 例題 3.1: 已知 $T: \mathbb{R}\mapsto \mathbb{R}$ 是一個有界線性泛函 (bounded linear functional), 請問 $T$ 的長相為何? 解: 根據線性的定義 \eqref{2.8}, $T$ 滿足 $$ T(x+y)= T(x) +T(y),\qquad T(\alpha x)= \alpha T(x),\qquad \forall x,y,\alpha \in \mathbb{R}. $$但因為定義域是 $\mathbb{R}$ 可以將兩個條件降為一個 \begin{align} T(x+y)= T(x) +T(y),\qquad \forall x,y \in \mathbb{R}. \label{3.1} \end{align}這是著名的 Cauchy 函數方程 (functional equation), 是法國數學家 Augustin-Louis Cauchy (1789$\sim$1857) 於 1821 年在他巴黎高等理工著名的分析教程 (Cours d'analyse) 中所提, 他假設 $T$ 是一個連續函數。 之後 Jean Gaston Darboux (1842$\sim$1917) 則證明一個連續的線性算子在一點連續就可推論到處連續。 如果沒有連續這個條件, 則 \eqref{3.1} 這個問題並不是那麼明顯。 我們還是回到最簡單的情形, 分幾個情形(這個方法中學生也看得懂!) (1) $x=0$。 利用加法單位元素的性質可得 $$ T(0)= T(0+0)=T(0)+T(0) \quad\Longrightarrow\quad T(0)=0. $$一個線性變換一定將原點帶到原點。 (2) $x\in \mathbb{N}$。 假設 $T(1)=a\not=0$ 則簡單地歸納可得 $$ \begin{aligned} T(2)&=T(1+1)= T(1)+T(1)= 2T(1) = 2a, \\[2mm] T(3)&=T(2+1)= T(2)+T(1)= 3T(1) = 3a, \\[2mm] &\ \ \vdots \\[2mm] T(n)&=T(n-1+1)= T(n-1)+T(1)= nT(1) = na. \end{aligned} $$(3) $x\in \mathbb{Z}$。 要將一個正整數推廣到負整數, 一定要通過加法單位元素 $0$: $$ T(0)=T\big(n+(-n)\big)=T(n)+T(-n) \quad\Longrightarrow\quad T(-n)=-T(n) = -na, $$所以與 (2) 合併可以結論 $$ T(z)= za,\qquad \forall z\in \mathbb{Z}. $$(4) $x={m\over n}\in \mathbb{Q}, m,n\in \mathbb{Z}$。 要將一個正整數推廣到有理數, 一定要通過乘法單位元素 $1$: $$ T(1)= T\bigg({1\over n}\bigg) +\cdots +T\bigg({1\over n}\bigg)= n T\bigg({1\over n}\bigg) \quad\Longrightarrow\quad T\bigg({1\over n}\bigg)={1\over n}T(1) = {1\over n} a, $$ $$ T\bigg({m\over n}\bigg)= T\bigg({1\over n}\bigg) +\cdots +T\bigg({1\over n}\bigg)= m T\bigg({1\over n}\bigg) ={m\over n}T(1) = {m\over n} a, $$或者表示為更一般化 \begin{align} T(r)= r a,\qquad \forall r\in \mathbb{Q}. \label{3.2} \end{align}(5) $x\in \mathbb{R}$。 要將一個有理數推廣到實數, 這牽扯到實數是甚麼? 根據實數的構造給定任意一個實數 $x\in \mathbb{R}$ 總是可以取一串有理數 $\{x_n\}_n$ 來逼近 $x$。 這裡面是分析中所謂 《稠密性定理》, $\overline{\mathbb{Q}}=\mathbb{R}$, 也就是從有理數過渡到實數需要極限的概念。 由於 $T$ 是連續所以 \eqref{3.2} 對有理數成立自然對所有的實數也成立 \begin{align} T(x)= a x,\qquad \forall x\in \mathbb{R}. \label{3.3} \end{align}為了證明 \eqref{3.3} 我們需要引進極限的概念。 在分析中兩個數相等意思是兩數相減的絕對值是任意小, 現在 \eqref{3.3} 左右兩邊相減之後因為要與 $T(x)$ 比較, 所以減一項 $T(x_n)$ 加一項 $T(x_n)$ 再利用 \eqref{3.2} 有理數的結果得 \begin{align} |T(x)-ax| =\,& |T(x)-T(x_n)+T(x_n)-ax| =|T(x)-T(x_n)+a x_n-ax| \le |T(x)-T(x_n)|+|a| |x_n-x|\lt {\epsilon\over 2} +{\epsilon\over 2}. \label{3.4} \end{align}最後的兩項 ${\epsilon\over 2}$ 是 (人為) 事先設定好的 \begin{align} |a| |x_n-x|\lt{\epsilon\over 2} \quad\Longrightarrow\quad |x_n-x|\lt{\epsilon\over 2|a|}\overset{\rm def}{=}\delta\qquad a\not=0; \label{3.5} \end{align}在這裡清楚明白 $\delta$ 的選取。 至此我們的證明幾乎已經完成了! 如果有需要(例如考試或寫書)再把它寫為 $\epsilon$--$\delta$ 嚴格的形式, 但我認為沒有必要。 總之 $$ |T(x)-ax|\lt\epsilon,\quad\forall\ \epsilon\gt0 \quad\Longleftrightarrow\quad T(x) = ax,\quad \forall x\in \mathbb{R}. $$(6) $T(1)=a=0$。 這是退化的情形: $T(x)=0$, $\forall x\in \mathbb{R}$, 此時 $y=T(x)=0$ 正是 $x$-軸, 自然就沒有必要搬上 $\epsilon$--$\delta$ 這個技巧。 綜合上面的論述可以結論: 『一個定義在 $\mathbb{R}$ 上的有界線性泛函是平面上一條通過原點的直線。』 $\Box$ 註解: (i) 這個題目的論述方式就是典型的分析思想: $$ \hbox{正整數}\quad\Longrightarrow\quad\hbox{整數}\quad\Longrightarrow\quad\hbox{有理數}\quad\Longrightarrow\quad\hbox{實數。} $$以通俗的語言來說: 這個題目 (或定理) 如果 $x$ 是正整數 $x\in \mathbb{N}$ 對了, 那麼所有實數 $x\in \mathbb{R}$ 也差不多對了! 而證明的思路是: 一直到有理數, 由於它們的個數是可數的 (countable), 所以藉由歸納法所有 $x\in \mathbb{Q}$ 的問題都可以歸納為 $x=1$。 但是 $x\in \mathbb{R}$, 由於實數的個數是不可數的 (uncountable), 這個從 《可數》到《不可數》的過渡必須藉由極限 (limit) 才可以克服, 這就是數學分析的稠密性定理 (density theorem)。 對照實變函數論 (Real Analysis) 則為 $$ \hbox{特徵函數}\quad\Longrightarrow\quad\hbox{單純函數}\quad\Longrightarrow\quad\hbox{可積函數。} $$實分析的定理如果對特徵函數 (characteristic function) 成立, 那麼所有的可積函數也就對了! 只是最後這一步需要將實數上的極限定理提升為函數上的極限定理 (limit theorem), 例如, Fatou's 引理、 單調收斂定理與 Lebesgue 控制收斂定理, 使得積分與極限可以變換順序。我相信一旦有這概念, 學生就不會無奈且悲情地說: 『實變要讀十遍。』 (ii) \eqref{3.3} 這個結果的幾何意義如下: 一維空間只有一個方向, 通常直線 $\mathbb{R}$ 上的點都只寫座標而把方向向量忽略了。 所以要深入理解這個結果必須將《向量》拉回來。 令 $\boldsymbol{e}_1=(1,0)$ 是 $x$-軸的單位向量, $\boldsymbol{x}=x\boldsymbol{e}_1$, $\boldsymbol{y}=T(\boldsymbol{e}_1)\boldsymbol{e}_1=a\boldsymbol{e}_1$ 則線性泛函 $T$ 可以表示為內積 (inner product) \begin{align} T(\boldsymbol{x})=T(x\boldsymbol{e}_1)= x T(\boldsymbol{e}_1)= xa= \boldsymbol{x}\cdot \boldsymbol{y}=\langle \boldsymbol{x}, \boldsymbol{y}\rangle \label{3.6} \end{align}所以 $a=T(\boldsymbol{e}_1)$ 是 $T(\boldsymbol{e}_1)$ 在 $y$-軸上的座標, 由於線性泛函 $y=T(x)=ax$ 是一條通過原點且斜率等於 $a$ 的直線, 可以將它與 $y$-軸 1-1 對應。 其對應方式, 是將直線上的點 $(x,y)=(x,ax)$ 一對一且映成的映射到 $y$-軸的 $(0, ax)$。 簡單的估計得 $$ |T(x)|\le |a||x|\le |a|,\qquad \forall |x|\le 1. $$因為 $|a|$ 是一個上界, 由線性算子範數(最小上界)之定義這相當於 $$ \Vert T\Vert \overset{\rm def}{=}\sup_{|x|\le 1} |T(x)| \le |a|. $$另外取特殊的 $x=1$ 則 $$ |T(1)|=|a|\le \Vert T\Vert \quad\Longrightarrow\quad \Vert T\Vert =|a|. $$這告訴我們 $T$ 差不多就是 $a$, $T\approx a$, 一個抽象的線性泛函 $T$ 完完全全可以由實數軸上的一個點 $a\in \mathbb{R}$ 來刻劃! 從幾何的角度來看也是完全合理的, 決定平面上的曲線我們需要斜率 (slope) 與曲率 (curvature)。 但是線性泛函 $T$ 是一條直線 $y=T(x)=ax$ 其曲率等於 0, 再加上它必須通過原點, 所以斜率 $a$ 就完全決定了這條直線 (可以視為超平面 6 6 所謂的超平面 (hyperplane) 是指 $n$ 維空間中的 $n-1$ 維的子空間。 它是平面中的直線、 空間中的平面之推廣。 $\mathbb{R}^n$ 中的超平面是由方程式 $a_1x_1+ a_2x_2+\cdots + a_n x_n=b$ 定義的子集, 其中 $a_k\in \mathbb{R}^n, k=1,2,\ldots, n$ 是不全為零的常數。 hyper 翻作《超出》、《過度》, 意思是超出二維、三維我們習慣的維度, 不應過度詮釋! ), 也就是可以把線性泛函 $T$ 當作實數 $a$ 來看待。 這相當於說 $\mathbb{R}$ 的對偶空間 (dual space) 就是 $\mathbb{R}$ 本身, $\mathbb{R}^*=\mathbb{R}$。 (iii) 在 (ii) 的討論中知道 $a=T(\boldsymbol{e}_1)$ 是座標, 但座標是根據基底來決定的。 因此要推廣到更一般的空間勢必要先擺脫基底的限制。 首先藉由隱函數定理提高一個維度, 在二維空間看這個事實 $$ y=T(x)=ax \quad\Longleftrightarrow\quad F(x,y) = y-T(x)= y-ax =(x,y)\cdot (-a,1)=0. $$這條直線的法向量為 $$ \nabla F = (F_x, F_y)= (-a,1), $$所以 $a$ 這個值本質上是與法向量或投影有關的。 $\Box$ 定理 3.2: 已知 $V$ 是一 $n$ 維內積空間, $\dim V=n$, $T: V\mapsto \mathbb{R}$ 是一個有界線性泛函, 則存在唯一 $\boldsymbol{y} \in V$ 使得 \begin{align} T(\boldsymbol{x})=\langle \boldsymbol{x}, \boldsymbol{y}\rangle = \boldsymbol{x}\cdot \boldsymbol{y},\qquad \forall\ \boldsymbol{x} \in V. \label{3.7} \end{align}證明:存在性 根據 Gram-Schmidt 正交化程序造出一組內積空間 $V$ 的正交單位基底 $$ \mathscr{B}=\{\boldsymbol{e}_1, \boldsymbol{e}_2,\ldots, \boldsymbol{e}_n\}, $$再將 $\boldsymbol{x}\in V$ 表示為這組基底的線性組合 \begin{align} \boldsymbol{x} = x_1 \boldsymbol{e}_1 + x_2\boldsymbol{e}_2 +\cdots + x_n \boldsymbol{e}_n , x_1, x_2,\ldots, x_n \in \mathbb{R}, {\hbox{則}} T(\boldsymbol{x}) = T(x_1 \boldsymbol{e}_1 + x_2\boldsymbol{e}_2 +\cdots + x_n \boldsymbol{e}_n) = \sum_{j=1}^n x_j T(\boldsymbol{e}_j)= \sum_{j=1}^n x_j y_j, \label{3.8} \end{align}其中 $y_j=T(\boldsymbol{e}_j)$ 是 $T(\boldsymbol{e}_j)$ 在 $\boldsymbol{e}_j$-軸上的座標。 根據這組座標定義向量 \begin{align} \boldsymbol{y} = y_1\boldsymbol{e}_1+ y_2\boldsymbol{e}_2+\cdots +y_n \boldsymbol{e}_n, \label{3.9} \end{align}再由正交單位基底的性質可將座標乘積的和 \eqref{3.8} 重新化妝成內積的形式: \begin{align} T(\boldsymbol{x})= \sum_{j=1}^n x_j y_j =\langle \boldsymbol{x}, \boldsymbol{y}\rangle. \label{3.10} \end{align}唯一性 假設有兩點 $\boldsymbol{y}, \boldsymbol{z} \in V$ 滿足 $$ T(\boldsymbol{x})=\langle \boldsymbol{x}, \boldsymbol{y}\rangle = \langle \boldsymbol{x}, \boldsymbol{z}\rangle \quad\Longrightarrow\quad \langle \boldsymbol{x}, \boldsymbol{y}-\boldsymbol{z}\rangle =0,\qquad \forall\ \boldsymbol{x} \in V. $$取特殊的 $\boldsymbol{x}=\boldsymbol{y}-\boldsymbol{z}$, 則 $$ \langle \boldsymbol{y}-\boldsymbol{z}, \boldsymbol{y}-\boldsymbol{z}\rangle= \Vert \boldsymbol{y}-\boldsymbol{z}\Vert^2=0 \quad\Longrightarrow\quad \boldsymbol{y}-\boldsymbol{z}=\boldsymbol{0} \quad\Longrightarrow\quad \boldsymbol{y}=\boldsymbol{z}. $$綜合上面的論述可以結論: 『一個定義在 $\mathbb{R}^n$ 上的有界線性泛函是一個通過原點的超平面。』 註解: (i) 證明用到了座標這是典型線性代數的方法, 雖然很乾淨而且是簡潔的代數運算, 但是看不出背後的幾何意義。 如果向量空間沒有基底可用時, 我們不得不直接研究《向量》本身, 而不是它們的《座標》! 令 \begin{align} W=\hbox{Ker}\, T= \{\boldsymbol{x}\in V |\, T(\boldsymbol{x}) =0\}=T^{-1}(\{0\}). \label{3.11} \end{align}因為 $T$ 是連續 $\{ 0\}$ 是 $\mathbb{R}$ 上的單點集合, 而單點必然是一個閉集 (closed set), 而連續函數將值域的閉集帶回定義域也是閉集, 所以 $W$ 是一個閉集。 $V$ 有正交分解 (orthogonal decomposition) \begin{align} V= W\oplus W^\perp,\qquad \boldsymbol{x}= \boldsymbol{x}_h + \boldsymbol{x}_p, \label{3.12} \end{align}其中 $\boldsymbol{x}\in V$, $\boldsymbol{x}_h \in W$, $\boldsymbol{x}_p \in W^\perp$ 而且 $\dim V=\dim W+\dim W^\perp$。 根據定義 $T(\boldsymbol{x}_h)=0$ (齊次解!) 可以推得 \begin{align} T(\boldsymbol{x}) = T(\boldsymbol{x}_h + \boldsymbol{x}_p)=T(\boldsymbol{x}_p)= T({\cal P}(\boldsymbol{x})). \label{3.13} \end{align}這意思是 $T(\boldsymbol{x})$ 的值完全由 $\boldsymbol{x}$ 在 $W^\perp$ 的正交投影 $\boldsymbol{x}_p={\cal P}(\boldsymbol{x})$ 所決定。 那麼正交投影是甚麼? 為了方便討論, 最好將 $T$ 視為矩陣 $ [T]_{\mathscr{B}}=A, $ 則線性代數的基本定理告訴我們 \begin{align} \left\{ \begin{aligned} V&=N(A)\oplus R(A^{\rm T}), \\[2mm] \dim V&=\dim N(A) + \dim R(A^{\rm T}), \\[2mm] \hbox{rank}(A)&=\hbox{rank}(A^{\rm T})=\dim R(A^{\rm T}). \end{aligned} \right. \label{3.14} \end{align}因為 $A$ 不是退化的情形, $A\not=0$, 再加上 $T$ 是一線性泛函其值域是實數, 也就是 $$ \hbox{rank}(A)=\hbox{rank}(A^{\rm T})=\dim R(A^{\rm T})=1, $$再由 rank-nullity 定理得 \begin{align} \dim W = \dim V - \dim R(A^{\rm T})=n-1 \quad\Longrightarrow\quad \dim W^\perp = 1, \label{3.15} \end{align}所以存在一非零向量 $\boldsymbol{z}\in W^\perp$ 使得 $W^\perp=\hbox{span}\{\boldsymbol{z}\}$。 因此根據投影的公式 \begin{align} \boldsymbol{x}_p={\cal P}(\boldsymbol{x}) = {\langle \boldsymbol{x}, \boldsymbol{z}\rangle \over \langle \boldsymbol{z}, \boldsymbol{z}\rangle }\boldsymbol{z} = {\langle \boldsymbol{x}, \boldsymbol{z}\rangle \over \Vert \boldsymbol{z}\Vert^2 }\boldsymbol{z}, \label{3.16} \end{align}這裡, ${\cal P}$ 是投影變換, 帶回 \eqref{3.13} \begin{align} T(\boldsymbol{x})=\,&T(\boldsymbol{x}_p)=T\big({\cal P}(\boldsymbol{x})\big) = T\bigg({\langle \boldsymbol{x}, \boldsymbol{z}\rangle \over \Vert \boldsymbol{z}\Vert^2 }\boldsymbol{z}\bigg) ={\langle \boldsymbol{x}, \boldsymbol{z}\rangle \over \Vert\boldsymbol{z}\Vert^2}T(\boldsymbol{z})=\bigg\langle \boldsymbol{x}, {T(\boldsymbol{z})\over \Vert \boldsymbol{z}\Vert^2}\boldsymbol{z}\bigg\rangle=\langle \boldsymbol{x}, \boldsymbol{y}\rangle, \label{3.17} \end{align}其中 \begin{align} \boldsymbol{y}\overset{\rm def}{=}{T(\boldsymbol{z})\over \Vert \boldsymbol{z}\Vert^2}\boldsymbol{z}={T(\boldsymbol{z})\over \langle \boldsymbol{z}, \boldsymbol{z}\rangle}\boldsymbol{z} \label{3.18} \end{align}正是我們要找的《那個向量》! 這裡就清楚知道為何連續 (有界) 線性泛函是以內積的形式表現出來, 根本原因是投影 (projection) 也就是最短距離! (ii) 在中學兩個 $\mathbb{R}^n$ 上的向量 $\boldsymbol{x}, \boldsymbol{y}$ 的內積是以 $\boldsymbol{x}\cdot \boldsymbol{y}$ 表示, $$ \boldsymbol{x}\cdot \boldsymbol{y} = x_1y_1+x_2y_2+\cdots +x_n y_n, $$由此可以看得出來內積有時候也稱為點積 (dot product) 的緣由。 但在更一般的內積空間我們較喜歡用帶箭頭的括號 (arrow bracket) 來表示內積 $$ \langle \boldsymbol{x},\boldsymbol{y}\rangle = x_1y_1+x_2y_2+\cdots +x_n y_n. $$主要原因是內積的本質是角度(箭頭代表角度), 在內積空間才能夠談垂直, 這才是 Gram-Schmidt 正交化程序之所以成立的根本原因。 在一般的賦範空間 (normed space) 沒有內積無法定義垂直 (orthogonality), 取而代之的是 F. Riesz 著名《幾乎垂直》(almost orthogonality) 的成果, 我們稱之為 Riesz 引理 (Riesz Lemma)。 有興趣的讀者可以查閱泛函分析的著作, 但是研讀的時候要記得它的目的是要取代內積的垂直 (orthogonality), 以此為指引不要陷於證明中的技巧而模糊了目標。 $\Box$ 例題 3.3: 已知 $a,b,c\in \mathbb{R}$, 試以變換 $T: \mathbb{R}^3\mapsto \mathbb{R}$, 其中 $$ T(\boldsymbol{x})=T(x,y,z)=ax+by+cz, \qquad \forall\ \boldsymbol{x}=(x,y,z)\in \mathbb{R}^3 $$為例討論 Riesz 表現定理。 解: 這個問題可以拆解為底下幾個步驟: (1) $T$ 是有界線性泛函: 因為 $x,y,z$ 出現的都是一次而且常數項為 0, 所以 $T$ 是線性。 由 Cauchy 不等式 $$ \begin{aligned} |T(\boldsymbol{x})|&\le \sqrt{a^2+b^2+c^2}\sqrt{x^2+y^2+z^2} \\[2mm] &=\sqrt{a^2+b^2+c^2}\Vert \boldsymbol{x}\Vert, \qquad\forall\ \boldsymbol{x}=(x,y,z)\in \mathbb{R}^3, \end{aligned} $$所以 $T$ 為有界(連續) 且 $$ \Vert T\Vert =\sup_{\Vert \boldsymbol{x}\Vert\le 1} |T(\boldsymbol{x})|\le \sqrt{a^2+b^2+c^2}. $$更進一步取 $\tilde{\boldsymbol{x}}={(a,b,c)\over \sqrt{a^2+b^2+c^2}}, \Vert \tilde{\boldsymbol{x}}\Vert=1$ 則根據算子範數 (operator norm) 的定義 $$ \Vert T\Vert \ge |T(\tilde{\boldsymbol{x}})|= {1\over \sqrt{a^2+b^2+c^2}}|T(a,b,c)|=\sqrt{a^2+b^2+c^2}. $$這就證明了 $T$ 的範數為 $$ \Vert T\Vert =\sqrt{a^2+b^2+c^2}. $$(2) 核空間(零空間): $$ W=\hbox{Ker}\, T= \{(x,y,z)\in \mathbb{R}^3 \,|\, T(x,y,z)=ax+by+cz =0\} $$這是三維空間, 一個通過原點的平面可以表示為內積 $$ ax+by+cz= (a,b,c)\cdot (x,y,z)=0. $$(3) 法向量: 由 (2) 可得超平面的法向量 $\boldsymbol{z}\!=\!\nabla T\!=\!(a,b,c)\in W^\perp$, 因為 $\dim W^\perp \!=\!1$ 所以 $$ W^\perp =\hbox{span}\{\boldsymbol{z}\}=\hbox{span}\{(a,b,c)\}. $$(4) 投影: 由 \eqref{3.16} $\boldsymbol{x}=(x,y,z)\in \mathbb{R}^3$ 在$W^\perp$之投影為 $$ \boldsymbol{x}_p={\cal P}(\boldsymbol{x}) = {\langle \boldsymbol{x}, \boldsymbol{z}\rangle \over \langle \boldsymbol{z}, \boldsymbol{z}\rangle }\boldsymbol{z} = {\langle \boldsymbol{x}, \boldsymbol{z}\rangle \over \Vert \boldsymbol{z}\Vert^2 }\boldsymbol{z} ={ax+by+cz\over a^2+b^2+c^2} (a,b,c). $$(5) 對偶向量: 由 \eqref{3.18} 所要的那個向量為 $$ \boldsymbol{y} = {T(\boldsymbol{z})\over \Vert \boldsymbol{z}\Vert^2} \boldsymbol{z} = {a^2+b^2+c^2\over a^2+b^2+c^2}(a,b,c)=(a,b,c), $$所以 $T$ 可以表示為內積 $$ T(\boldsymbol{x})= ax+by+cz= \langle \boldsymbol{x}, \boldsymbol{y}\rangle,\qquad \forall\ \boldsymbol{x} \in \mathbb{R}^3. $$$\Box$ 定理 3.4: 已知 $H$ 是一 Hilbert 空間, $T_g: H\mapsto \mathbb{R}$ 是一個有界 $($連續$)$ 線性泛函, 則存在唯一的 $g \in H$ 使得 \begin{align} T_g(f)=\langle f, g\rangle,\qquad \forall \ f \in H; \label{3.19} \end{align}也就是說 Hilbert 空間上的有界$($連續$)$線性泛函完全由內積來刻劃, 並且 $$ \Vert T_g\Vert = \Vert g\Vert_H \overset{\rm def}{=} \sup\{ |g(x)|: x\in H\}. $$這相當於說 Hilbert 空間的對偶空間就是它自己, $H^*=H$。 證明: 我們分四段處理: (1) 假設 $H$ 是可分離的 (separable) 意思是存在 $H$ 的可數稠密子集 (countable dense subset) $$ B\subset H,\qquad \overline{B}=H. $$根據 $B$ 可以造一組可數的正交單位基底 (orthonormal basis), $ \mathscr{B}=\{f_1, f_2,\ldots, f_n, \cdots \}$ $\subseteq B$ 則定理 3.2 的證明可以直接搬過來, 唯一的差別是此時 $H$ 是無窮維空間, 我們只需將 $n\to \infty$, 這就是座標的好處。 有興趣的讀者可以自行演練, 我們在此就沒有必要重複。 (2) 如果不確定有基底可用 (也就是 $H$ 不見得是可分離的), 那麼就需要依據 \eqref{3.11}$-$\eqref{3.18} 透過投影直接討論向量本身而不是其座標。 首先是核空間 (零空間) $$ W=\hbox{Ker}\, T_g= \{f\in H \,|\, T_g(f)=0\}. $$顯然 $W$ 是一個閉集滿足投影定理的要求。 如果 $W=H$, 則 $T_g=0$, 直接取 $g=0\in H$ 即可。 由於 $W\not=H$ 我們有正交分解 $$ H= W\oplus W^\perp. $$對於任意 $f\in H$ 總是有 $f= f_h + f_p$, 其中 $f_h\in W, f_p\in W^\perp$, 也就是 $\langle f_h,f_p\rangle=0$。 \begin{align} T_g(f_h)=0 \quad\Longrightarrow\quad T_g(f)=T_g(f_p)= T_g({\cal P}(f)). \label{3.20} \end{align}由於 $\dim W^\perp = 1$, 所以存在一非零向量 $g_0\in W^\perp$ 使得 $W^\perp=\hbox{span}\{g_0\}$, 而且 $$ \langle f_h, g_0 \rangle=0,\qquad \forall \ f_h\in W, $$因此根據投影的公式 \begin{align} f_p={\cal P}(f) = {\langle f, g_0\rangle \over \langle g_0, g_0\rangle }g_0 = {\langle f, g_0\rangle \over \Vert g_0\Vert^2 }g_0, \label{3.21} \end{align}帶回 \eqref{3.20} \begin{align} T_g(f)=\,&T_g(f_p)=T\big({\cal P}(f)\big) = T_g\bigg({\langle f, g_0\rangle \over \Vert g_0\Vert^2 }g_0\bigg) ={\langle f, g_0\rangle \over \Vert g_0\Vert^2}T_g(g_0)=\bigg\langle f, {T_g(g_0)\over \Vert g_0\Vert^2}g_0\bigg\rangle=\langle f, g\rangle, \label{3.22} \end{align}其中 \begin{align} g={T_g(g_0)\over \Vert g_0\Vert^2}g_0\in W^\perp. \label{3.23} \end{align}(3) 我們證明由 \eqref{3.23} 所定義的 $g$就是《那個向量》。 首先 $$ f\in W\quad\Longrightarrow\quad T_g(f)=0, $$其次 $$ f\in W,\quad g\in W^\perp \quad\Longrightarrow\quad \langle f,g\rangle =0. $$由這兩式結論 $T_g(f)= \langle f,g\rangle =0$。 如果 $f\in W^\perp=\hbox{span}\{g_0\}$ 則存在 $\alpha\in \mathbb{R}$ 使得 $f=\alpha g_0$ \begin{align} \langle f, g\rangle= \langle \alpha g_0, g\rangle=\bigg\langle \alpha g_0, {T(g_0)\over \Vert g_0\Vert^2}g_0\bigg\rangle=\alpha T_g(g_0)= T_g(\alpha g_0)= T_g(f). \label{3.24} \end{align}最後, 對任意 $f\in H=W\oplus W^\perp$, 此時刻意將 $g_0$ 換為 $g$ 並把內積換為線性變換, 則由 \eqref{3.23} 得 $f$ 在 $g$ 之投影為 \begin{align} f_p ={\cal P}(f)= {\langle f, g\rangle \over \langle g, g\rangle }g= {T_g(f)\over T_g(g)} g,\qquad T_g(g)\not=0, \label{3.25} \end{align}所以$f$之正交分解為 \begin{align} f= (I-{\cal P})(f)+ {\cal P}(f)= \bigg(f-{T_g(f)\over T_g(g)} g\bigg) + {T_g(f)\over T_g(g)} g. \label{3.26} \end{align}顯然 \begin{align} T_g\bigg(f-{T_g(f)\over T_g(g)} g\bigg)= T_g(f)-{T_g(f)\over T_g(g)} T_g(g)=0. \label{3.27} \end{align}換言之 \begin{align} f-{T_g(f)\over T_g(g)} g\in W \quad\Longrightarrow\quad \bigg\langle f-{T_g(f)\over T_g(g)} g, g\bigg\rangle=0 \quad\Longrightarrow\quad T_g(f)=\langle f, g\rangle. \label{3.28} \end{align}(4) 由算子的範數與Cauchy-Schwarz 不等式得 $$ \Vert T_g\Vert \overset{\rm def}{=} \sup_{\Vert f\Vert_H\le 1} |T_g(f)| =\sup_{\Vert f\Vert_H\le 1}|\langle f, g\rangle| \le \sup_{\Vert f\Vert_H\le 1}|\Vert f\Vert_H \Vert g\Vert_H= \Vert g\Vert_H. $$另外取特別的 $f={g\over \Vert g\Vert_H}$ 則 $$ \Vert T_g\Vert = \sup_{\Vert f\Vert_H\le 1} |T_g(f)|\ge \bigg|T_g\bigg({g\over\Vert g\Vert_H}\bigg)\bigg| = \bigg|\bigg\langle {g\over \Vert g\Vert_H}, g\bigg\rangle\bigg|= \Vert g\Vert_H. $$兩者合併我們就證明了$\Vert T_g\Vert = \Vert g\Vert_H$。 $\Box$ 註解:
(i) 有不少書在證明這個定理時是直接從 \eqref{3.27} 出發, 而後得 \eqref{3.28}。
因為外表看起來非常對稱也不難, 於是學生就硬背下來以應付考試, 甚至不少人教書也就照本宣科, 一輩子從來沒有弄清楚過。
書上這麼寫如果作者不是抄的, 就是他先有答案, 然後再倒寫回來, 所以我們研讀證明的時候也要倒著看才看得清楚, 否則一定被別人牽著鼻子走。
正如 Cauchy-Schwarz 不等式 (請參閱 (ii) $L^2$ 或 $\ell^2$ (分別是連續型與離散型) 版本的 Riesz 表現定理, 實際上是 René Maurice Fréchet (1878$\sim$1973) 與 F. Riesz 分別獨立研究所得, 因此也稱為 Riesz-Frechet 表現定理。 $\Box$ 證明(變分學的角度): 既然 Riesz 表現定理證明的重點是投影, 也就是與最短距離有關, 這相當於說我們也可以藉由變分的角度來處理這定理。 若 $T\not=0$ 由 \eqref{3.18} 或 \eqref{3.25} 可以假設 $T(f)=1$, 並視此為一超平面 (hyperplane) \begin{align} \pi = \{f\in H \,|\, T_g(f) =1\}, \label{3.29} \end{align}則投影直接與此超平面的法向量有關。 假設 $f_1, f_2 \in \pi$ 則 $$\langle f_1- f_2, g\rangle=T_g(f_1-f_2)=T_g(f_1)-T_g(f_2)=0.$$所以 $g$ 可以詮釋為超平面 $\pi$ 的法向量, 而且是原點到超平面 $\pi$ 最短距離的方向。 實際上由 \eqref{3.25} 定義 $$ g^*\overset{\rm def}{=}{g\over T_g(g)}= {g\over \langle g,g\rangle} \quad\Longrightarrow\quad T_g(g^*)= 1 \quad\Longrightarrow\quad g^*\in \pi. $$對任意 $f\in \pi$ 因為 $$ \langle f-g^*, g^*\rangle={\langle f-g^*, g\rangle\over \langle g, g\rangle} ={T_g(f)-T_g(g^*)\over \langle g, g\rangle}=0, $$所以 $$ \Vert f\Vert_H= \Vert f-g^*+g^*\Vert_H=\Vert g^*\Vert_H +\Vert f- g^*\Vert_H +2\langle f-g^*, g^*\rangle \ge \Vert g^*\Vert_H, $$也就是 $g^*\in \pi$ 會取得到原點的最短距離! 利用這個極值特性也可以從變分學的角度來證明 Riesz 表現定理。 考慮子空間 \begin{align} E=\big\{ f\in H | T_g(f)=1\big\}\subset H. \label{3.30} \end{align}由於 $T_g$ 是連續, 所以 $E$ 是一個閉集 (closed set)。 但是 $H$ 是完備的 (complete), $E$ 也會是完備的, 另外利用 $T_g$ 是線性可以證明 $E$ 是一個凸集 (convex set)。 令 \begin{align} d= \inf_{f\in E} \Vert f\Vert_H, \label{3.31} \end{align}則根據 $d$ 的定義與變分學的直接法 (direct method) 我們可以取一串極小化序列 (minimizing sequence) $\{g_n\}\subset E$ 且 $\Vert g_n\Vert_H\to d$。 利用內積空間具有平行四邊形法則 7 7 一個在內積空間的平行四邊形法兩個對角線的平方和等於四個邊的平方和。 這是內積空間才擁有的性質, 也是判斷一個空間是否為內積空間的最好方法。 與 $E$ 是一個凸集可得 \begin{align} d^2\le \bigg\Vert {1 \over 2}(g_m + g_n)\bigg\Vert_H^2 ={1\over 2}\Vert g_m\Vert_H^2 + {1\over 2}\Vert g_n\Vert_H^2-{1\over 4}\Vert g_m -g_n \Vert_H^2. \label{3.32} \end{align}令 $m, n \to \infty$ $$ \bigg\Vert {1 \over 2}(g_m + g_n)\bigg\Vert_H^2\to d^2, \qquad {1\over 2}\Vert g_m\Vert_H^2 + {1\over 2}\Vert g_n\Vert_H^2\to d^2. $$由 \eqref{3.32} 得 $\Vert g_m -g_n \Vert_H\to 0$, 所以 $\{g_n\}\subset E$ 是一 Cauchy 數列。 但 $E$ 是完備的, 所以存在非零向量 $g^*\in E$ 使得 \begin{align} \lim_{n\to \infty} g_n =g^* \in E,\qquad T_g(g^*)=1,\qquad \Vert g^*\Vert_H=d. \label{3.33} \end{align}考慮核空間 (kernel) $$ W=\hbox{Ker}\, T_g= \{f\in H \,|\, T_g(f)=0\}. $$我們分兩個情形討論: (1) 如果 $T_g(f)=0$, $\forall \ f\in H$, 意即 $W=H$, 可以直接取 $g^*=0$, 則 $$T_g(f)=\langle f,\quad g^*\rangle= \langle f,\quad 0\rangle=0.$$(2) 若 $T_g(f)\not=0$, 也就是 $W\not=H$, 我們有正交分解 $$H= W\oplus W^\perp.$$由於 $\dim W^\perp = 1$, 所以存在一非零向量 $g^*\in W^\perp$ 使得 $W^\perp=\hbox{span}\{g^*\}$, 因此根據投影的公式 \begin{align} T_g(f)= T_g({\cal P} (f))=T_g\bigg({\langle f, g^*\rangle \over \Vert g^*\Vert_H^2}g^* \bigg) = {\langle f, g^*\rangle \over \Vert g^*\Vert_H^2} T_g(g^*) =\langle f, g\rangle,\quad g = {g^*\over d^2}. \label{3.34}\\ \tag*{$\Box$} \end{align}4. Hahn-Banach定理的前世 --- Riesz表現定理 (原始版本)為了定義我們所說的線性變換, 首先必須把函數域弄清楚。 我們考慮定義在兩個固定的數 (譬如說 0 與 1)之間的連續函數類 $\Omega$。 對於這個函數類, 我們可以用一致收斂性來定義極限函數。 對於 $\Omega$ 中的每一個元素, 都使之對應於一個實數, 這樣就定義了一個泛函算子 $A[f(x)]$, 這個算子稱為連續的: 如果當 $f_i(x)$ 趨向於 $f(x)$ 時, $A(f)$ 是 $A(f_i)$ 的極限。 滿足分配律的連續變換稱為線性變換。 不難看出這樣的算子也是有界的, 也就是存在一個數 $M_A$ 使得對於每個元素 $f(x)$, 都有 $$ |A(f(x))|\le M_A \max_{x\in [0,1]} |f(x)|. $$阿達瑪 (Jacques Salomon Hadamard, 1864$\sim$1963) 證明了一個重要的事實, 即每個這樣的線性算子 $A(f(x))$ 都可以寫成 $$ \lim_{n\to \infty}\int_0^1 k_n(x) f(x) dx $$的形式, 其中 $k_n$ 是一列連續函數。 在本文中, 我們要給出線性泛函的一個新的解析表現式 , 其中只含有一個生成形式。 為此目的 $\cdots\cdots$。 於是我們便有下面的定理: 任給一個線性泛函 $A[f(x)]$, 我們總可以定義一個有界變差函數 $\alpha(x)$, 使得對於任意的連續函數 $f(x)$, 恆有} $$ A[f(x)]=\int_0^1 f(x) d\alpha(x). $$---《On Linear Functional Operators, 1909》, F. Riesz (1886$\sim$1955)--- Riemann-Stieltjes 積分是數學中的一種「積分」概念, 是 Riemann 積分的推廣。 自 1894 年荷蘭數學家 Thomas Joannes Stieltjes (1856$\sim$1894) 提出之後的 15 年間, 人們只是把它當成是 Riemann 積分的一種推廣而已。 當數學界對此積分趨於冷淡與遺忘之際, 1909 年匈牙利數學家 F. Riesz 指出任意連續線性泛函 $T: C[a,b]\mapsto \mathbb{R}$ 都能被唯一表示為 Riemann-Stieltjes 積分 $$ T(f)=\int_a^b f(x) d\alpha(x),\qquad \forall \ f\in C[a,b], $$其中 $\alpha(x)$ 是一個定義在區間 $[a,b]$ 上的有界變差函數 (function of bounded variation), 並且滿足附加條件 $\alpha(x)$ 在 $[a,b]$ 上是左連續且 $\alpha(a)=0$。 這就是著名的 Riesz 表現定理最原始的版本, 也因為 F. Riesz 這個發現, 讓 Riemann-Stieltjes 積分得到新生, 也激起數學界對它的重視, 後來並在物理與機 (概) 率等眾多領域獲得重大的應用, 特別這個積分所對應的 BV 函數(有界變差函數) 在最小曲面 (minimal surface) 與守恆律方程 (conservation law) 的成果最令人矚目。 例題 4.1: 已知 $\alpha \in BV[a,b]$ 且 $\beta(x)= V_a^x(\alpha)$ 是一有界變差函數, 定義 $T: C[a,b]\mapsto \mathbb{R}$ \begin{align} T(f)= \int_a^b f(x) d\alpha(x),\qquad \forall \ f\in C[a,b], \label{4.1} \end{align}則 $T$ 是一個有界線性泛函, 而且 \begin{align} |T(f)|\le \Vert f\Vert V_a^b(\alpha) \quad\Longleftrightarrow\quad \Vert T\Vert \le V_a^b(\alpha). \label{4.2} \end{align}解: 由積分的性質容易證明 $T$ 是線性。 另外直接由範數與 $\beta(x)$ 的定義可得 $$ \int_a^b |f(x)|d\beta \le \int_a^b \Vert f \Vert d\beta = \Vert f \Vert \int_a^b d\beta= \Vert f \Vert [\beta(b) -\beta (a)], $$因此 $$ |T(f)|=\bigg|\int_a^b f(x) d\alpha(x) \bigg| \le \int_a^b |f(x)| d\beta(x)=\Vert f\Vert V_a^b(\alpha), $$所以 $T$ 是 $C[a,b]$ 上的連續 (有界) 線性泛函, 也就是 $T\in \big(C[a,b]\big)^*$。 $\Box$ 這是一個好的題目也是常見資格考的標準考題, 自然會問: 反過來也會成立嗎? 答案是肯定的就是著名的 Riesz 表現定理。 定理 4.2: 已知 $[a,b]\subset \mathbb{R}$ 是一閉區間而且 $T: C[a,b]\mapsto \mathbb{R}$ 是一個有界線性泛函, 也就是 $T\in (C[a,b])^*$, 則存在 $\alpha \in BV[a,b]$ 使得 \begin{align} T(f)=\int_a^b f(x) d\alpha(x),\qquad \forall \ f \in C[a,b],\label{4.3} \end{align}而且 \begin{align} \Vert T\Vert = V_a^b(\alpha) \quad\Longleftrightarrow\quad \big(C[a,b]\big)^*\approx BV[a,b]. \label{4.4} \end{align}
證明:
詳細的證明有興趣的讀者可以參考林義雄與林紹雄; 理論分析(下) (1) 連續函數在最大值的範數下並不是一個內積空間, 沒有正交投影可資運用, F. Riesz 的想法, 同時也是後來整個實變函數論的典型方法, 就是先考慮特徵函數 (characteristic function) \begin{align} f(x)=\chi_s(x) =\chi_{[a,s]}(x)=\left\{ \begin{aligned} 1,\qquad &a\le x\le s, \\ 0,\qquad &s\lt x\le b. \end{aligned} \right. \label{4.5} \end{align}如果 $\alpha$ 在 $x$ 點是連續而且 $\alpha(a)=0$, 則 \begin{align} T(\chi_s)=\int_a^s d\alpha(x) = \alpha(s). \label{4.6} \end{align}接著就是證明 $\alpha\in BV[a,b]$。 藉由特徵函數我們已經得到答案, 但是不幸的是, $f=\chi_s$ 並不是連續函數(除非 $s=b$)! 所以整個 Riesz 表現定理的重點在將 $T$ 的定義域 $C[a,b]$ 擴充到有界函數 (bounded function) $B[a,b]$ 的子空間, 其中必須包含特徵函數: \begin{align} C[a,b]\subseteq C_1[a,b]\subseteq B[a,b],\qquad \chi_s\in C_1[a,b]. \label{4.7} \end{align}一旦 $T$ 的延拓 (extension) 在 $C_1[a,b]$ 存在, \begin{align} T_2: C_1[a,b]\mapsto \mathbb{R},\qquad T_2(f)= T(f),\qquad \forall \ f\in C[a,b], \label{4.8} \end{align}我們就可以根據 \eqref{4.6} 定義 \begin{align} \alpha(x) \overset{\rm def}{=} T_2(\chi_s(x)). \label{4.9} \end{align}(2) 如何造出 $C_1[a,b]$ 這個子空間? 首先考慮造一串遞減連續函數 $f_n\in C[a,b]$ 來逐點逼近特徵函數 $f=\chi_s$ (參考圖 3!) \begin{align} \left\{ \begin{aligned} &f_1\ge f_2\ge \cdots \ge f_n\ge f_{n+1}\ge \cdots\qquad n=1,2,\ldots, \\[2mm] &\lim_{n\to \infty} f_n(x) = \chi_s(x), \qquad \forall x\in [a,b], \end{aligned} \right. \label{4.10} \end{align}而後根據這個極限來定義 $T$ 的延拓 \begin{align} T_2(\chi_s) \overset{\rm def}{=} \lim_{n\to \infty} T(f_n). \label{4.11} \end{align}(3) 根據 (2) 的想法, 可以將特徵函數推廣為一般的有界函數: 也就是 $C_1[a,b]$ 這個子空間是所有定義在 $[a,b]$ 的有界函數 $f$ 的集合且$f$是一串滿足 \eqref{4.10} 遞減連續函數 $f_n$ 的逐點收斂極限 $$ \lim_{n\to \infty} f_n(x) = f(x)\qquad \forall x\in [a,b]. $$顯然 $C[a,b]\subseteq C_1[a,b]$ 而且 $$ \begin{aligned} f,g \in C_1[a,b] &\quad\Longrightarrow\quad f+g \in C_1[a,b], \\[2mm] f\in C_1[a,b],\quad c\ge 0 &\quad\Longrightarrow\quad cf\in C_1[a,b], \end{aligned} $$所以 $C_1 [a,b]$ 看起來很像一個向量空間, 然而$C_1 [a,b]$並不是!例如 $ -\chi_a\not\in C_1[a,b]$。 這個困難可以透過將 $C_1[a,b]$ 擴張到大一點的空間來解決。 幸運的是, 將負號也考慮進來, 定義 \begin{align} C_2[a,b] =\big\{ f-g | f,g\in C_1[a,b]\big\},\label{4.12} \end{align}則 $C_2[a,b]$ 真的是一個向量空間而且 $$ C[a,b]\subseteq C_1[a,b]\subseteq C_2[a,b] \subseteq B[a,b]. $$$\Box$ 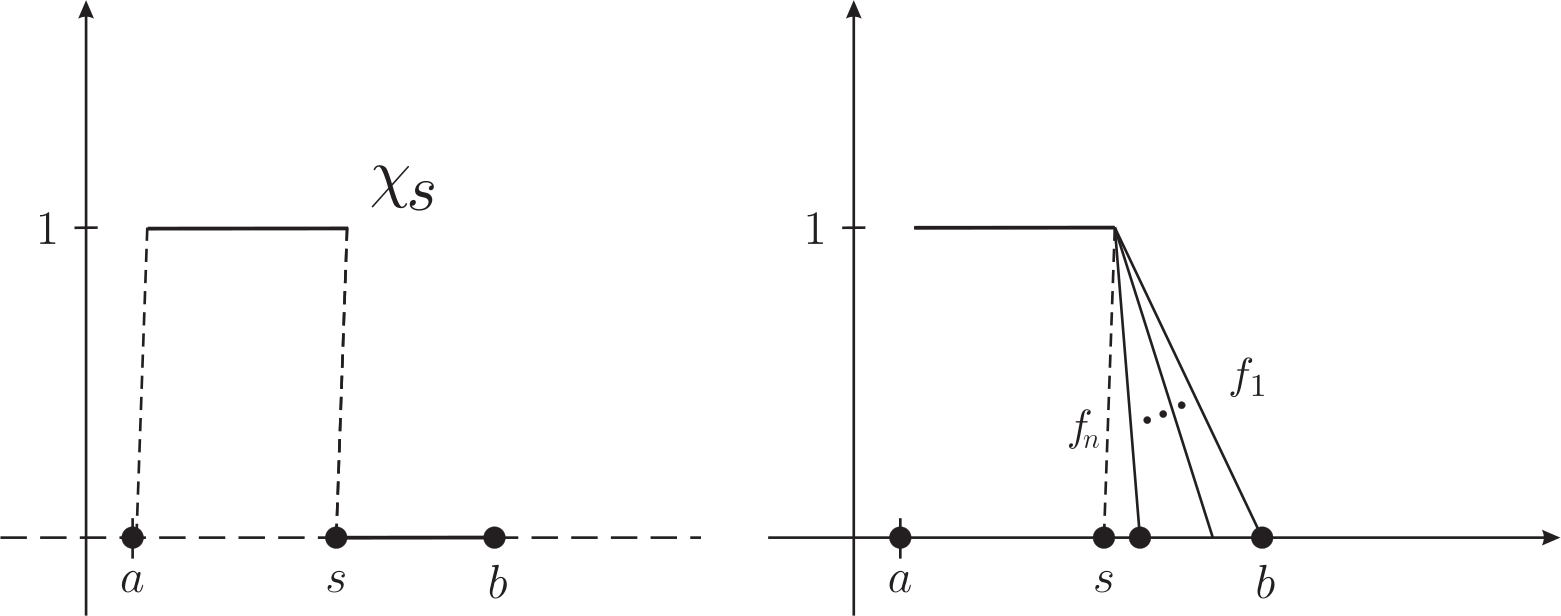 註解: (i) 為何有界線性泛函 (bounded linear functional)是積分? 這是一個極其有趣且核心的問題。 在內積空間它必然是在某一特定向量之投影, 而投影本質上是內積! 如果是 $L^2[a,b]$ 空間其內積自然是積分, 所以 $L^2[a,b]$ 版本的 Riesz 表現定理為 \begin{align} T_g(f)=\langle f, g\rangle \overset{\rm def}{=}\int_a^b f(x) g(x) dx, \qquad \Vert T_g\Vert = \Vert g\Vert_2, \label{4.13} \end{align}$\forall \ f\in L^2[a,b]$。 更進一步假設 $p$ 滿足 ${1\over p} +{1\over q}=1$ 與 $1\le p\lt\infty$ 則 $L^p[a,b]$ 版本的 Riesz 表現定理也是 \eqref{4.13} 的形式 \begin{align} T_g(f)=\int_a^b f(x) g(x) dx, \qquad \Vert T_g\Vert = \Vert g\Vert_q,\qquad \forall \ f\in L^p[a,b]. \label{4.14} \end{align}但 $p\not=2$ 時 $L^p[a,b]$ 並不是一個內積空間, 所以第三節的方法派不上用場。 這時候我們就需要實變函數論的根本思想: 『一個定理如果特徵函數對了、那麼它差不多就對了!』 正如 \eqref{4.6}, 對於 $L^p$ 空間也如法泡製: 給定 $s\in [a,b]$ 得 $T_g(\chi_s)\in \mathbb{R}$ 是一個數, 我們依此定義新的函數 \begin{align} \Phi(s) \overset{\rm def}{=} T_g(\chi_s),\qquad s\in [a,b], \label{4.15} \end{align}並且證明 $\Phi$ 是絕對連續 (absolutely continuous), 而絕對連續函數必定是一個不定積分 \begin{align} \Phi(s) = \int_a^s g(x) dx \quad\Longrightarrow\quad T_g(\chi_s)=\int_a^b \chi_s(x) g(x) dx. \label{4.16} \end{align}所以 $L^p$ 版本的 Riesz 表現定理是一個積分的緣由, 那是因為 $L^p[a,b]$ 空間 ($1\le p\lt\infty$)的有界線性泛函是《絕對連續》! 由於是絕對連續自然可推廣至抽象的測度, 此時 Radon-Nikodym 定理的出現就是水到渠成的事了。 (ii) 對於原版的 Riesz 表現定理, 也就是 $C[a,b]$ 的情形 (可以視為 $L^\infty$ 的子空間), 因為特徵函數不是連續, 上述的討論是有落差的。 這也是 F. Riesz 苦心孤詣要將連續函數空間 $C[a,b]$ 擴張 (延拓, extension) 到有界函數空間 $B[a,b]$ 的原因。 事實上, F. Riesz 的證明已經蘊含了將定義在某個向量空間上的有界線性算子擴張到整個空間, 這就是後來 1920 年左右出現的 Hahn--Banach 定理。 換句話說: Hahn-Banach定理就是有界線性泛函的擴張或延拓定理, 其目的是研究對偶空間 (dual space), 它是泛函分析最重要的定理之一。 按歷史發展而言, 第一個 Hahn-Banach 定理也就是連續函數 $C[a,b]$ 的情形, 是 Eduard Helly (1884$\sim$1943) 於 1912 年證明的。 (iii) 在 \eqref{4.12} 這一步引進的空間 $C_2[a,b]$ 感覺上有點突兀! 但是對於實變函數論稍有認知的讀者會發覺這是自然的。 如何定義 Lebesgue 積分? 我們是從特徵函數開始、 然後是單純函數, 接著是{非負可測函數} (nonnegative measurable function), 而一般可測函數的積分則是分解為兩個非負可測函數之差來定義: $f = f^+ - f^-$, 其中 $$ f^+(x) = \max\{ f(x), 0\}, \qquad f^-(x) = \max\{ -f(x), 0\}. $$若不是 Lebesgue 積分, 泛函分析的發展不會那麼快也不會那麼順利!
(iv) 不少泛函分析的書 ( (v) 正如 Riemann--Lebesgue 引理, 雖然 Lebesgue 利用稠密性 (density) 的證明比較簡單易懂, 但 B. Riemann 的方法才是更有創意。 利用 Riemann 和 (Riemann sum)不僅可以得到 Riemann--Lebesgue 引理之極限的明確公式, 還為後來的發展, 例如, Young 測度與弱收斂等鋪設好了道路, 也就是說 Riemann 的思想更具開創性, 才是我們該學的數學。
(vi) Riesz 表現定理最好的應用, 是證明 Poisson 方程 Dirichlet 問題之弱解的存在性, 如果 Laplace
算子推廣為更一般的橢圓算子, 這相當於將單位矩陣換為正定的對稱矩陣, 此時 Riesz 表現定理的內積必須推廣為二次型
(quadratic form), 對應的 Riesz 表現定理就推廣為 Lax--Milgram 定理。
關於這段歷史在 Peter Lax的訪談 誌謝: 從研究所開始由於研究的主題是與流體力學相關的非線性偏微分方程, 自然而然就接觸了守恆律方程 $($Conservation Law$)$ 與震波 $($Shock Wave$)$ 理論。同時也理解這個理論離不開一個來自台灣的數學家 --- 劉太平 $($Taiping Liu$)$。 1985 年由於劉太平的大力支持與奔走台灣數學界, 第一次在國立交通大學應用數學系舉辦「中美微分方程研討會」, 美方代表有六人, 除了他之外會中還邀請了 L. Nirenberg, James Glimm, Paul Rabinowitz, Daniel Stroock 當然還有第一次來台灣的丘成桐, 真是星光熠熠。 那時我讀研究所有幸躬逢盛會, 讓人覺得當數學家是一件榮耀的事。 會中讓人印象最深刻的是在閒談中劉太平老師大聲疾呼: 「我們應該聽學生的心聲。 如果要對學生有影響, 應該先走向學生而不是在研究室等學生來 $!$」 由於這次會議的成功使得台灣數學界信心大增, 猶如武俠小說所言打通任督二脈, 對於後來台灣微分方程的發展有深遠的影響。 我相信這是交通大學應用數學系特別是鄭國順、 林松山與許世壁三位前輩對於台灣數學界特別是微分方程最重要的貢獻。 2007 年我轉到交通大學應用數學系任教, 此時劉太平院士已長期在中研院任職, 並固定在每個星期一舉行分析研討會。 我詢問博士班學生吳恭儉$($目前任教成功大學數學系$)$ 有沒有興趣去參加 $?$ 於是星期一待在中研院數學所就成為我在交大任教期間生活的一部分。 由於近距離的接觸, 可以感受太平老師頗有 Richard Courant 的風範, 除了數學之外, 數學人文與歷史都有深入的研究。 每個星期一參加分析研討會跟他聊天是最快樂的時光。 在此謹將此文獻給劉太平教授並祝他 80歲生日快樂。 參考文獻在這裡, 在作者本人撰寫的前半部分, 我們發現這位大師以藝術家敏銳的眼光, 充滿愛意、 從容不迫地向我們描繪了他所看到的《實分析》。 我毫不懷疑, 這本書將成為數學文獻寶庫中的經典。 這部作品以及他的其它作品將使 F. Riesz 作為一位偉大而多產的數學家永遠活在我們的(數學)藝術史上。 --- W. W. Rogosinski 的書評 --- 我記得台大數學系退休教授張海潮老師曾經以這本書為教材上過泛函分析, 他問過我的意見(那時我當他的助教)。 我回答: 好像古老了一些, 還有文字敘述比較多不容易閱讀。 但是海潮老師告訴我所謂的經典就是經得起時間的淬鍊, 裡面有一些永恆的東西是別的書沒有的, 還有這類書更接近原創可以看見最開始的想法。 當學生的時候心浮氣燥, 閱讀比較膚淺, 很難體會張老師的說法, 畢業拿了學位在大學教書之後比較能夠享受閱讀的樂趣逐漸有此感受。 如今我會說: 《一本好書要慢慢的讀!》 Stewart 的書都值得看, 他是我最喜歡的數學科普作家之一, 基本上他的書只要有中文翻譯我一定購買且詳細閱讀。 看過他的幾本書之後才發現讀大學時就已經研讀過 Stewart 的書: I. Stewart, Galois theory, Chapman and Hall/CRC Press, Boca Raton, FL, 2022 大部分的學校(大學部)都很難開出這種課, 但 Stewart 卻針對大學部學生寫了這本歷時 50 年仍然還會再版的教科書。 Galois 理論我是透過這本書 (1973 年版) 自學的。 Stewart 的書簡潔優雅而且還有 Galois 理論的歷史介紹, 就算英文不是頂尖也容易閱讀, 這是本書讓人愛不釋手的原因。 作者雖然是學代數卻有本事寫通俗數學讓普羅大眾更喜歡數學。 這種人才在缺少人文素養的華人數學圈實在是太難得了。 『連超級電腦都不會想要解反(逆)矩陣: 太慢了。 反 (逆) 矩陣給出了最簡單的公式 $\boldsymbol{x}=A^{-1}{{\boldsymbol{b}}}$, 可是這不是最快的解法。 大家還應該知道, 行列式甚至比反(逆)矩陣還要更慢, 因此一門線性代數課程没有任何理由以求解一個 $n\times n$ 的行列式開始。 那玩意兒應該占有一席之地, 但不是在開篇。』 任何一本書一定要讀前言! 看到作者在前言講了這段話, 就知道這是一本好書。 麻省理工 (MIT) 的開放式課程有 Gilbert Strang 教授完整的線性代數教學影片, 有興趣的讀者可上網學習, 我確信你會對線性代數有更健康的看法。
閱讀 American Mathematical Monthly 是我上大學之後就培養的習慣, 後來教書與寫作都會鼓勵學生與讀者趁年輕的時候就養成這個好習慣。
對於 Gilbert Strang 教授的認識我是從這篇文章開始的, 讀懂且完全消化這篇文章之後我還以此為藍本寫了一篇《線性代數的基本定理》 本文作者為國立交通大學應用數學系退休教授 |
| 頁碼 | 61-88 |
2025年9月 49卷3期
道成肉身的表現定理

