本文於 2025 年 4 月 15 日刊載於中研院訊漫步科研專欄, 作者及中研院訊同意本刊轉載。 ^{* *} * 英文版請見： https://staff.stat.sinica.edu.tw/htsai/Pricing_Asian_Options.pdf

在自然界中, 我們經常遇見充滿隨機性的現象。 統計學家透過數學工具來解析這些隨機性, 其中「機率分佈」是最常見的描述方式。 簡單來說, 機率分佈用來表示各種可能結果發生的機率, 幫助我們了解資料的整體結構, 包括哪些數值常見、 哪些則較罕見。 尋找適合的機率分佈通常包括兩個步驟: 首先, 進行視覺化, 例如使用直方圖或密度圖觀察數據的分佈型態； 其次, 將這些圖像與已知的理論分佈 (如常態分佈) 比對, 找出最相符的模型。

然而, 有時最能描述資料特性的分佈過於複雜, 不易用來進行後續計算。 此時, 動差匹配法 (moment matching) 提供了一個實用的解法: 利用較簡單的分佈, 如高斯 (Gaussian)、 伽瑪 (Gamma) 或皮爾森 (Pearson) 分佈來近似原始分佈, 同時保留其關鍵特徵。

動差匹配的基本理念, 是讓簡化後的分佈在下列特徵上與原始分佈一致:

$\bullet$ 平均值 (mean) : 代表數據的整體趨勢或重心位置
$\bullet$ 變異數 (variance) : 衡量數據的離散程度
$\bullet$ 偏度 (skewness) : 反映分佈的對稱性
$\bullet$ 峰度 (kurtosis) : 描述分佈尾部厚度與尖峰程度

透過匹配這些動差, 我們可以使用更容易處理的分佈來近似原始分佈, 同時保留其關鍵特徵。

本文將介紹一種基於動差匹配的簡便方法, 用以推估標的資產在特定期間內的平均價格分佈, 進而評估亞式選擇權的合理價值。 正式進入主題之前, 我們先簡要回顧股票市場的基本概念, 並介紹幾種常見的價格動態模型。

一、市場模型

股票價格代表市場對公司價值的即時評估, 受到公司營運表現、 產業趨勢與整體經濟情勢等多重因素的影響, 因此價格會在交易期間持續波動。 例如：

$\bullet$ 公司消息 : 如財報表現亮眼、新產品發佈或醜聞爆發
$\bullet$ 市場趨勢 : 如通膨、經濟成長或景氣衰退
$\bullet$ 供需變化 : 如大量買盤推升價格, 或賣壓導致下跌

圖一呈現台積電 (TSMC) 自 2024 年 2 月 14 日至 2025 年 2 月 10 日的股價走勢。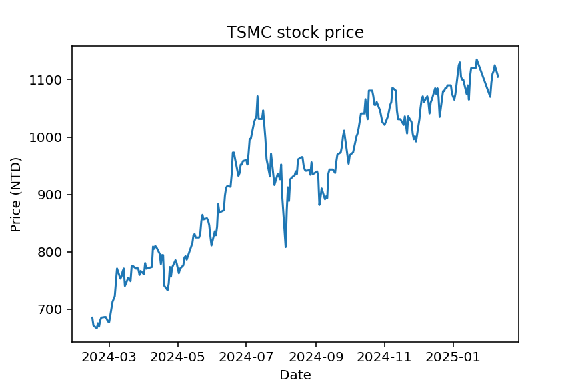

股票價格雖然難以準確預測, 但若能建構合理的數學模型, 仍可提供有用資訊, 包括：

$\bullet$ 風險評估：潛在獲利與損失範圍
$\bullet$ 決策支援：何時進場或退場
$\bullet$ 情境模擬：不同市場條件下的反應

雖然價格表面上呈現隨機性, 但實際上可能存在某些可預測的結構。 以下介紹幾種常見的模型：

(i) 隨機漫步理論 (Random Walk Theory) ： 股價變動視為完全隨機, 如擲硬幣決定漲跌, 無趨勢可循。
(ii) 幾何布朗運動 (Geometric Brownian Motion, GBM) ： 在隨機性之外加入平均增長趨勢, 是 Black-Scholes 模型的基礎。
(iii) 均值回歸 (Mean Reversion) ：假設股價若偏離某一長期均衡值, 會逐步修正回該水準。

圖二展示這三種模型的模擬路徑, 有助讀者對其差異建立直觀印象。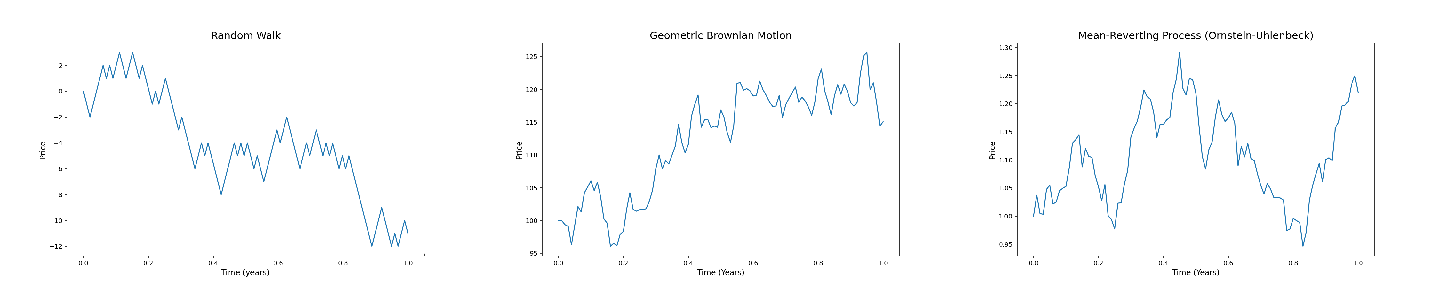

在介紹亞式選擇權定價方法之前, 下一節將說明本文所依據的數學工具 --- 連續時間馬可夫鏈 (Continuous-Time Markov Chain, CTMC) 的基本概念。

二、連續時間馬可夫鏈模型簡介與應用

想像一下, 股票價格在一天之內不斷跳動, 上下波動, 這種看似隨機的行為, 是否能透過模型來理解與預測? 馬可夫鏈 (Markov Chain) 提供了一種簡潔的描述方式: 系統當前的狀態僅取決於前一個時刻的狀態, 而與更早的歷史無關。 若將這樣的系統延伸至連續時間, 則可得到連續時間馬可夫鏈, 其允許在任意時刻進行狀態轉移, 更貼近股價這類隨時變動的現象。

Mijatović 和 Pistorius (2013) 指出, 對於某些複雜的資產價格模型 $S$, 可以以用一個較簡單的連續時間馬可夫鏈 $X$ 進行近似。 儘管 $X$ 的結構較為簡化, 卻能保留 $S$ 的核心機率特性, 讓原本難以處理的模型轉化為可分析的形式。

在金融市場中, CTMC 可透過以下步驟應用於股價建模：

$\bullet$ 狀態 (States) ： 將股價劃分為不同的離散狀態, 例如「低於 100」、 「介於100$\sim$110」、 「介於 110$\sim$120」等。 每個區間對應一個特定狀態。
$\bullet$ 轉移 (Transitions) ： 股價在不同區間間跳動, 反映其漲跌。 例如, 從「100$\sim$110」跳至「110$\sim$120」代表價格上升； 跳至「低於 100」則代表下跌。
$\bullet$ 轉移率 (Transition Rates) ： 描述從一個狀態跳至另一狀態的頻率。例如, 若從「100$\sim$110」跳至「110$\sim$120」的機率高於跳至「低於 100」, 則代表市場有上升趨勢。 這些轉移率可透過歷史數據與原始模型 $S$ 進行估計。
$\bullet$ 近似 (Approximation) ： 結合上述狀態劃分與轉移率, 即可建立一個連續時間馬可夫鏈作為資產價格的近似模型。 雖無法完全模擬真實市場行為, 但提供一個可處理且具有分析性的架構, 對理解與預測價格行為具有實用價值。

為何使用 CTMC 模型近似?

真實世界的資產價格行為極為複雜, 幾乎無法以完整模型精確描述。 作為一種有效的近似工具, CTMC 擁有以下幾項優勢：

$\bullet$ 預測能力 (Make predictions) ： 可估算未來某一時間點資產價格落在特定區間的機率, 輔助投資或風險管理決策。
$\bullet$ 風險評估 (Assess risk) ： 可衡量資產價格劇烈波動的可能性, 幫助投資者制定對應策略。
$\bullet$ 簡化計算 (Simplify calculations) ： 與全面模擬所有市場因子相比, CTMC是一個更具數學處理性的模型, 能在維持分析價值的同時, 大幅提升運算效率。

當然, CTMC 的準確性仍仰賴狀態劃分的細緻度與轉移率估計的品質。 通常需結合統計方法與歷史資料推估模型參數。

但整體而言, CTMC 是一項強大的建模工具, 廣泛應用於理解金融市場中的隨機行為。

三、亞式選擇權 (Asian Option) 價格

假設我們希望在未來某個時間點購買一支股票, 但又擔心價格波動過大, 此時亞式選擇權便是一項理想的工具。 亞式選擇權的報酬 (payoff) 取決於標的資產在一段期間內的平均價格, 而非到期當日的單一價格。因此, 它能有效平滑市場短期波動, 降低價格操縱風險, 進而提升投資的穩定性。

歐式選擇權 vs. 亞式選擇權

1. 歐式選擇權 (European Option)
例如, 我們約定在一個月後以 100 元買入某支股票:
$\bullet$ 若屆時市場價格為110元, 則可獲利10元；
$\bullet$ 若價格跌至 90 元, 仍需以 100 元買入, 將導致損失。

2. 亞式選擇權 (Asian Option)
改為以未來一個月內的平均價格買入該股票:
$\bullet$ 即使期間內價格劇烈波動, 平均價格可有效分散風險；
$\bullet$ 即使最後一日價格急劇下跌, 其影響也會被整體平均所稀釋。

亞式選擇權特別適合波動性高的資產, 如大宗商品與外匯市場。從本質上來看, 它提供一種以「平滑後價格」進行交易的方式, 有助於降低整體投資風險。

選擇權定價的數學原理

選擇權定價的核心在於評估其「公平價值」, 亦即持有該權力在理論上的預期收益。首先, 需以下幾個關鍵參數：
$\bullet$ $S$ ：當前股價
$\bullet$ $K$ ：行權價 (合約中約定的價格)
$\bullet$ $T$ ：到期時間 (距到期的期間)
$\bullet$ $\sigma$ ： 波動率 (股價變化幅度)
$\bullet$ $r$ ：無風險利率 (如政府公債)

這些因素可代入數學模型 (如 Black-Scholes 公式或蒙地卡羅模擬) 來估算選擇權價格。 選擇權的價值, 取決於未來可能的報酬, 根據時間價值原則 (Time Value of Money), 未來的現金流需以折現方式處理。 例如, 歐式買權 (European Call Option) 之理論價格 $C(S)$ 表示為：

$$C(S)=E[e^{-rT} \max \{S(T)-K,0\}]$$

其中$S(T)$為到期時的股價, $E$表示期望值。 若已知$S(T)$的機率分佈, 則此期望值可直接計算。

對亞式選擇權而言, 報酬取決於期間平均價格。以算術平均為例, 其理論價格為：

$$C(S)=E\Big[e^{-rT} \max\Big\{\frac 1T \int_0^T S(t)dt-K,0\Big\}\Big]$$

因此, 問題核心在於估算平均價格

$$A=\frac 1T \int_0^T S(t) dt$$

的機率分佈。 這項分佈在理論上非常難以解析, 因此需要額外工具加以近似。

動差母函數與分布近似

針對這項挑戰, 先前已有學者運用連續時間馬可夫鏈演算法來模擬標的資產價格的路徑, 以進行亞式選擇權的定價。 Cai et al.~(2015) 更進一步推導出平均價格 $A$ 的動差母函數 (Moment Generating Function, MGF), 為此問題提供了重要的數學基礎。 動差母函數是機率與統計中的核心工具, 可用來導出隨機變數的各階動差, 例如平均值、 變異數、 偏度與峰度。 只需針對 MGF 做對應階次的微分, 即可取得這些動差資訊。

在 Das et al. (2022) 的研究中, 我們基於 Cai 等人的 MGF 結果, 提出一套高效方法來精確計算 $A$ 的各階動差, 並進一步透過動差匹配法來近似其分佈情形。 我們選用皮爾森分佈作為近似分佈模型, 因其在處理偏斜與厚尾結構方面表現優異。

模擬結果與比較

為驗證所提出方法的準確性與效率, 我們選用幾何布朗運動模型作為基礎資產價格模型, 並採用下列五種參數組合:

$$\{(0.02, 0.1, 2), (0.18, 0.3, 2), (0.05, 0.5, 1.9), (0.05, 0.5, 2), (0.05, 0.5, 2.1)\}$$

其中 $r$、 $\sigma$、 $S_0$ 分別表示利率、 波動率與初始價格。 我們計算每組參數下的亞式選擇權價格, 並與既有基準方法比較, 結果如表一所示。 表一顯示, 我們的動差匹配法與 benchmark 相比誤差極小, 顯示高度準確性。 此外, 我們亦評估不同方法的計算效率。 圖三為計算時間比較圖。 實驗結果顯示, 我們的方法不僅在準確度方面表現優異, 在計算速度上亦具顯著優勢, 展現出兼顧實務應用中效率與準確度的潛力。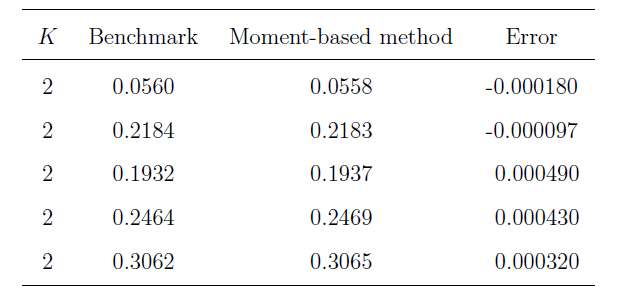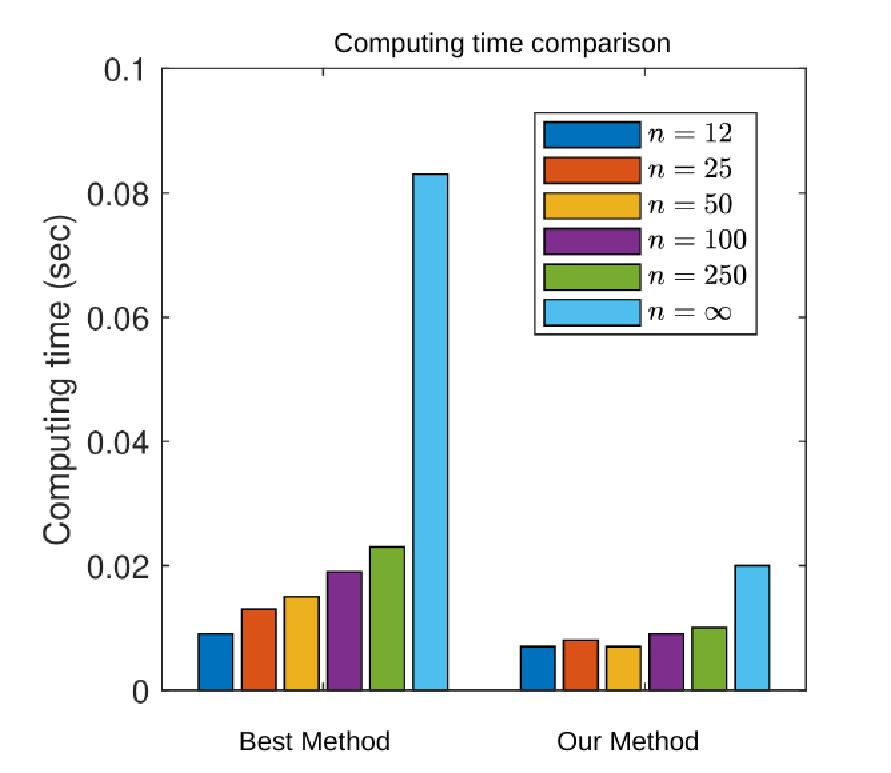

四、結論

本文從機率論的基本觀念出發, 介紹了模擬技術 (特別是連續時間馬可夫鏈演算法) 與選擇權定價理論之間的結合應用。 儘管篇幅有限, 我們未能深入展開所有數學細節, 但目標在於提供一套直觀且實用的說明架構, 協助讀者理解這些工具在金融市場中的潛在應用價值。

我們提出的方法, 結合了:
$\bullet$ 連續時間馬可夫鍊對資產價格路徑的建模能力；
$\bullet$ 動差母函數在分佈資訊提取上的數理基礎；
$\bullet$ 以及動差匹配法在分佈近似上的實務效率。

透過這些技術的整合, 我們發展出一套高效且準確的計算方法, 用以近似亞式選擇權的價格分布。 根據表一與圖三的結果, 此方法在效率與準確度間取得良好平衡, 並可推廣至金融工程中其他具有路徑相依性的定價問題。

特別感謝江妙真博士生 (國立臺灣大學資料科學博士學位學程) 協助排版。

參考文獻

本文作者蔡恆修任職中央研究院統計科學研究所, 白英輝任職中央研究院統計科學研究所博士後研究人員