| 發刊日期 |
2025年9月
|
|---|---|
| 標題 | 艾狄胥等人的一個加性數論定理——由模算術談起 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
1. 緣起 --- 話說 1961 年匈牙利數學家保羅$\cdot$艾狄胥 (英文姓名 Paul Erdős, 匈牙利原名 Erdős Pál, 匈牙利人和華人一樣, 姓在先名在後) 出生於 1913 年, 在 1996 年以八十三歲高齡去世, 一生寫過的數學論文多達 1525 篇 (包括與 511人合寫的), 遠遠超過之前數百年來由 Leonhard Euler 所維持的紀錄, 成為數學史上第一名。 更可貴的是, 這些著作不只是數目多, 份量也很紮實, 其中有許多影響後來的發展十分深遠。 有關他的傳記, 請參見柴契特 [1999] 和霍夫曼 [2001] 的書。 這篇文章要談的是他和 Ginzburg 及 Ziv [1961] 合作寫的有關加性數論的一個定理。 定理 1. (Erdős, Ginzburg and Ziv [1961]). 對於正整數 $n$, 任意整數列 $a_1, a_2, \ldots, a_{2n-1}$ 恆存在 $n$ 項 $a_{i_1}, a_{i_2}, \ldots, a_{i_n}$, 其和為 $n$ 的倍數。 定理中的項數 $2n-1$ 是最小可能, 也就是, 如果把它換成 $2n-2$, 定理就不對了。 舉例來說, 如果 $a_1=a_2=\cdots=a_{n-1}=0\lt1=a_n=a_{n+1}=\cdots=a_{2n-2}$, 就找不到 $n$ 項, 其和為 $n$ 的倍數。 本文要用模算術證明這個定理。 我們準備由模算術的定義和基本性質說起。 2. 模算術的基本定義模算術 (modular arithmetic) 或稱同餘算術, 是一種整數的算術系統, 其中數字超過某一個定值後會「捲回」到較小的數值, 稱為模或餘數。 模算術最早出現在德國數學家高斯 (Johann Carl Friedrich Gauss, 1777 年 4 月30日$\sim$1855 年 2 月 23 日) 在 1801 年出版的《算術研究》 (Disquisitiones Arithmeticae)一書中。 在日常生活中, 我們每天都在使用模算數, 例如計時制度, 時鐘或手錶採用的是十二小時制。 假設現在是九點, 八小時後會是五點。 用一般的算術加法, 會得到 $9+8=17$, 但在十二小時制中, 超過十二小時會歸零, 所以「十七點」其實就是「五點」。 同樣的道理, 如果現在是十點, 那麼二十小時後的三十點會說是六點。 小時數超過十二後會再回到一, 就是模 12 的模算術系統。 實務上, 我們把一天分為上午和下午各十二小時。 按照定義, 12 和 12 本身同餘, 也和 0 同餘, 所以十二點也可以說是零點;但是實際上, 人們還是常用十二點。 這會產生一點小小困惑, 上午十二點到底指的是何時? 按照直觀的感覺, 上午應該是 0:00, 1:00, $\ldots$, 11:00, 接下來似乎應該是 12:00。 經查, 上午其實是以數字 $12,1,2,3,4,5,6,7,8,9,10,11$ 依次序表示。 所以, 上午 12:00 其實是在半夜; 為免混淆, 常稱為午夜 12:00、或子夜 12:00 或凌晨 12:00。 類似的, 下午 12:00 最好稱為中午 12:00 或正午 12:00。 現在也有許多人用二十四小時制, 這些困擾就自然消失。 對於正整數 $n$, 兩個整數 $a$ 和 $b$ 在模 $n$ 下同餘的意思是指 $a-b$ 為 $n$ 的倍數, 或是說 $n$ 為 $a-b$ 的因數, 也就是存在整數 $c$ 滿足 $a-b=nc$, 記為 $$ a \equiv b~({\rm mod}~n)\,\mbox{。} $$ 例如, 因為 $28-7=21=7\times 3$ 是 7 的倍數, 所以 $ 28 \equiv 7~({\rm mod}~7)\,\mbox{。} $ 整數的加法、減法、乘法都具有封閉性, 也就是兩個整數經過這三種運算都會得到整數, 但是除法卻沒有這種特性, 而具有下面性質。 定理 2 (除法原理). 對於正整數 $n$ 及整數 $a$, 存在唯一的整數 $q$ 使得 $$ a = nq + r\mbox{, } $$ 其中 $0\le r\lt n$。 這裡的 $q$ 稱為商, $r$ 稱為餘數。 根據除法原理, 任意整數 $a$ 在模 $n$ 下同餘於唯一的 $r\in \mathbb{Z}_n := \{0, 1, \ldots, n-1\}$。 有時, 為了特殊的應用, 我們會要求在除法原理的 $r$ 滿足 $1\le r\le n$, 有時會要求滿足 $-n/2 \lt r \le n/2$。 整數的同餘運算和普通運算有類似的規律。 首先, 同餘是一個等價關係, 也就是, 對於正整數 $n$ 和整數 $a, b, c$, 下列關係恆成立: (ER1) 成立是因為 $a-a=0$ 是 $n$ 的倍數。 (ER2) 成立是因為, 如果 $a-b$ 是 $n$ 的倍數, 則 $b-a=-(a-b)$ 也是 $n$ 的倍數。 (ER3) 成立是因為, 如果 $a-b$ 和 $b-c$ 都是 $n$ 的倍數, 則 $a-c=(a-b)+(b-c)$ 也是 $n$ 的倍數。 其次, 對於正整數 $n$ 和非負整數 $e$, 若整數 $a, b, c, d$ 滿足 $a \equiv b~({\rm mod}~n)$ 及 $c \equiv d~({\rm mod}~n)$, 則下列運算規律恆成立: 首先 $a-b$ 和 $c-d$ 都是 $n$ 的倍數。 (O1) 成立是因為 $(a+c)-(b+d)=(a-b)+(c-d)$ 也是 $n$ 的倍數。 (O2) 成立是因為 $(a-c)-(b-d)=(a-b)-(c-d)$ 也是 $n$ 的倍數。 (O3) 成立是因為 $ac-bd=(a-b)c+b(c-d)$ 也是 $n$ 的倍數。 (O4) 成立是因為 $a^e-b^e=(a-b)(a^{e-1}+a^{e-2}b+\cdots+ab^{e-2}+b^{e-1})$ 也是 $n$ 的倍數。 在進入更多的數學性質之前, 讓我們看一些模算術有趣的應用。 3. 奇偶原理 --- 翻轉杯子的應用任意一個整數模 2 之後, 不是與 1 就是與 0 同餘, 與 1 同餘的稱為奇數, 例如 $\pm 1, \pm 3$, $\pm 5, \ldots$, 與 0 同餘的稱為偶數, 例如 $0, \pm 2, \pm 4, \pm 6, \ldots$。 換句話說, 奇數就是可以表示為 $2k+1$ 的整數, 偶數就是可以表示為 $2k$ 的整數, 其中 $k$ 為整數。 奇數和偶數有一些基本的運算性質: 奇數與奇數的和是偶數, 奇數與偶數的和是奇數, 偶數與偶數的和是偶數; 用同餘的方式來寫就是: $1+1 \equiv 0~({\rm mod}~2)\mbox{, }$ $1+0 \equiv 1~({\rm mod}~2)\mbox{, }$ $0+0 \equiv 0~({\rm mod}~2)\mbox{;}$ 寫成表格就是:  接著來看一些奇偶原理、也就是模 2 算術的應用。 例 1. 將 6 隻杯子排成一排, 一開始所有杯子的杯口都朝上, 每次操作是指將其中任意 4 隻杯子同時翻轉。請經過若干次操作, 將所有杯口全部朝下。 解析: 經過三次操作之後所有杯口都朝下 (每次將有星號的 4 隻杯子同時翻轉)。 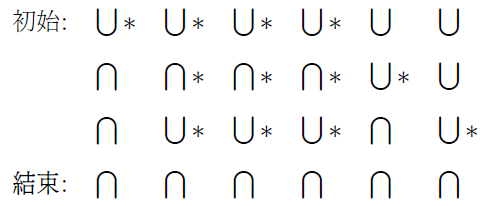 $\Box$ 例 2. 將 7 隻杯子排成一排, 一開始所有杯子的杯口都朝上, 每次操作是指將其中任意 4 隻杯子同時翻轉。請經過若干次操作, 將所有杯口全部朝下。 解析: 這是做不到的, 理由如下所述。 用 $a_i$ 表示第 $i$ 時間時, 杯口朝上的杯子數, 所以在一開始的時候 $a_0=7$。 如果第 $i$ 時間時把 $r$ 隻杯口朝上的杯子翻轉、同時把 $4-r$ 隻杯口朝下的杯子翻轉, 則 $$ a_{i+1} = a_i - r + (4-r)= a_i + 4 - 2r\mbox{, 即 } a_{i+1} \equiv a_i~({\rm mod}~2)\mbox{, } $$ 由於 $a_0$ 是奇數, 所以任何 $a_i$ 都是奇數, 不可能是 0, 所以不管怎樣翻轉, 都不可能讓所有杯口全部朝下。 $\Box$ 習題 1. 將 $n$ 隻杯子排成一排, 一開始所有杯子的杯口都朝上, 每次操作是指將其中任意 $m$ 隻杯子同時翻轉。請經過若干次操作, 將所有杯口全部朝下。 如果被翻轉的杯子都要連續, 則結論如何? 例 3. 將 16 隻杯子排成四行四列, 一開始對角線的 4 隻杯子的杯口都朝上, 其餘 12 隻杯子的杯口都朝下, 每次操作是指將其中某一行或某一列的 4 隻杯子同時翻轉。請經過若干次操作, 將所有杯口全部朝下。  解析: 這是做不到的, 理由如下所述。 將這 16 隻杯子標號如下所示。  用 $a,b,c,d$ 分別表示標號為 $A,B,C,D$ 的杯子杯口朝上的數目, 所以一開始有 $(a,b,c,d)=(1,1,2,0)$。 每一次操作把某一行或一列的 4 隻杯子同時翻轉, 因為被翻轉的杯子包含四種不同標號杯子各恰好一隻, 所以 $a,b,c,d$ 各數中, 原來是奇數的變為偶數, 原來偶數的變為奇數。 因為 $a,b,c,d$ 這四個數中, 原來有兩個奇數、兩個偶數, 所以任何時刻還是保留為兩個奇數、兩個偶數, 不可能變為 $(a,b,c,d)=(0,0,0,0)$。 也就是, 永遠不可能讓所有杯口全部朝下。 $\Box$ 習題 2. 將 16 隻杯子排成四行四列, 一開始對角線的 4 隻杯子中的 2 隻的杯口都朝上, 其餘 14 隻杯子的杯口都朝下, 每次操作是指將其中某一行、某一列、或某一對角線的 4 隻杯子同時翻轉。請經過若干次操作, 將所有杯口全部朝下。  4. 模算術再應用 --- 骨牌在拼盤上的排列一個 $n$ 格骨牌是用 $n$ 個單位正方形合成的連通圖形, 圖 1 是所有的一格骨牌、二格骨牌、三格骨牌、四格骨牌。 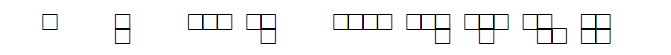 小心排列, 可以發現五格骨牌共有 12 種。 而六格骨牌很快就增加到 35 種。 一般來說, $n$格骨牌隨著 $n$ 的增加而快速增多, 要很有系統並且很小心才能正確將它們不重複地列出來。 市面上販售一種益智盤, 玩具有 12 個塑膠做成的五格骨牌, 及一個 $6 \times 10$ 拼盤, 問題是要把這 12 個五格骨牌放進 $6 \times 10$ 拼盤中。 如果把對稱 (包括翻轉後相同)的算作同一種, 答案就高達幾千種, 這要依賴計算機的幫忙才容易列出所有答案。 也可以考慮 $5 \times 12$ 拼盤、$4 \times 15$ 拼盤、$3 \times 20$ 拼盤, 但是顯然不能考慮 $2 \times 30$ 拼盤及$1 \times 60$ 拼盤。 拼盤越瘦長的, 放的彈性就越小, 答案的數目就越少, 例如 $3 \times 20$ 拼盤, 扣除對稱就只有兩種。 圖 2 顯示一些排法。 為何沒有考慮四格骨牌的拼盤? 理由並不是因為只有 5 種四格骨牌而使得問題太簡單, 而是根本無解。 不管是考慮 $4 \times 5$ 拼盤或是 $2 \times 10$ 拼盤。 將拼盤的 20 格黑白相間著色, 會有 10 個黑格、10 個白格。 再把 5 種四格骨牌也各自黑白相間著色, 則會有 4 種四格骨牌各自含有 2 個黑格及 2 個白格, 但是有一個 T 形狀的四格骨牌含有 1 個黑格及 3 個白格 (也可以著成 3 個黑格及 1 個白格), 參見圖 3。  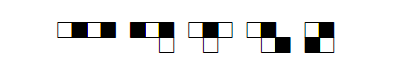 如果能夠將這 5 個四格骨牌拼進拼盤, 則 T 型骨牌會占用 1 個或 3 個黑格, 其他的 4 個四格骨牌各自占用 2 個黑格, 所以總共占用了 $1+2\times 4=9$ 或 $3+2\times 4=11$ 個黑格, 但這是不可能的, 因為拼盤有 10 個黑格。 將 35 個六格骨牌放進拼盤也是做不到的, 理由類似。 不管是用哪一種 $m \times n$ 拼盤, 將拼盤的 $mn=210$ 格黑白相間著色, 會有 105 個黑格、105 個白格。 再把 35 種六格骨牌也各自黑白相間著色, 則會有 24 種六格骨牌各自含有 3 個黑格及 3 個白格, 稱為奇六格骨牌, 如圖 4 所示。 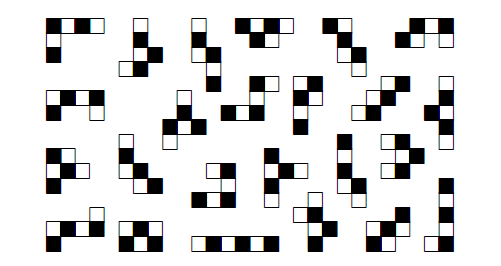 另有 11 種六格骨牌各自含有 2 個黑格及 4 個白格 (也可以著成 4 個黑格及 2 個白格), 稱為偶六格骨牌, 如圖 5 所示。 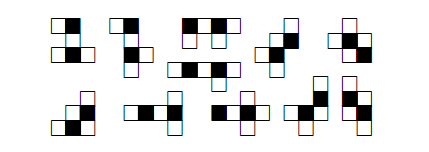 如果能夠將這 35 個六格骨牌放進拼盤, 則 24 個奇六格骨牌各占用 3 個黑格, 11 個偶六格骨牌各占用 2 個或 4 個黑格, 假設有 $a$ 個占用 2 個黑格、$11-a$ 個占用 4 個黑格, 所以總共占用了 $24 \times 3+ a \times 2+ (11-a)\times 4=116-2a$ 個黑格, 這個數是一個偶數, 不可能等於拼盤所有的黑格數 105。 一個可能不是很容易的問題如下。 問題 1. 共有多少種七格骨牌? 所有這些七格骨牌能不能放進一個長方形拼盤? 我們之所以只問七格骨牌, 是因為, 從八格骨牌開始, 就存在有洞的骨牌。 下面來談一個利用模 3 解決問題的例子。 考慮一個 $8 \times 8$ 拼盤 (一般常稱為西洋棋盤)。大家熟知的問題是: 現在考慮長條形三格骨牌 $L$。 因為 $64=21\times 3+1$, 我們只能問「能不能將 21 個 $L$ 放入 $8 \times 8$ 拼盤?」當然最後會剩下一格沒被骨牌覆蓋到。 答案是可以的, 如圖 6 所示, 其中 $(3,3)$ 位置的方格未被覆蓋。 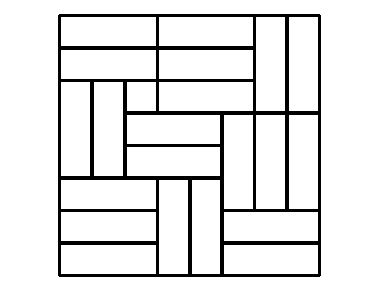 如果現在把問題改為 「能不能將 21 個 $L$ 放入 $8 \times 8$ 拼盤, 使得被指定的某一方格 $(a,b)$ 未被覆蓋?」 前面已經給出了 $(a,b)=(3,3)$ 的答案, 對稱來說 $(a,b)$ 為 $(3, 5)$、$(5, 3)$ 或 $(5, 5)$ 也會有答案。 那麼, 除了這四種情況以外的 $(a,b)$ 要如何解呢? 答案是, 那就不可能了! 這要用到模 3 來協助論證。 將 $8 \times 8$ 拼盤用兩種方法著三色, 分別以 $0,1,2$ 表示。 圖 7 左是第一種方法。著色的方法是由 $(1, 1)$ 的位置開始, 由左往右、由上往下, 循環著 $0,1,2$。 圖 7 右是第二種方法。著色的方法是由 $(1, 8)$ 的位置開始, 由右往左、由上往下, 循環著 $0,1,2$。 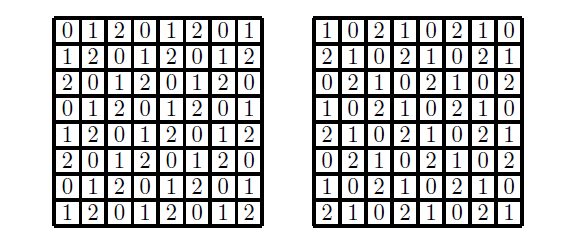 不管是哪一種著色法, 有 21 格著 0、 22 格著 1、 21 格著 2。 將 21 個 $L$ 放入拼盤, 每一個都占用了著 0 的一格、著 1 的一格、 著 2 的一格, 所以最後會剩下著 1 的一格未被覆蓋; 而這一格, 不管是在圖 7 左還是圖 7 右都要著 1, 那就只有可能是在 $(3,3), (3,5), (5,3)$ 或 $(5,5)$ 中的一格。 一般可以考慮下面的問題。 問題 2. 如果要將最多可能數目的長條形三格骨牌放入一般的 $m \times n$ 拼盤, 答案為何? 如果要將最多可能數目的某一種 $k$ 格骨牌放入一般的 $m \times n$ 拼盤, 答案為何? 5. 從費馬小定理到歐拉公式在整數中, 如同減法是加法的反運算, 除法是乘法的反運算。 不同的是, 整數減整數得到整數, 但是整數除以整數, 有時候會得到整數, 但是有時候不一定得到整數, 也就是在除法原理中餘數 $r$ 不為 0 的時候, 這和把一個整數分解成整數相乘有關。 考慮一個大於 1 的正整數 $n$, 有一種可能是它不能被分解成兩個比它小 (因此都大於 1) 的正整數的乘積, 這時候我們把它叫做一個質數。 如果 $n$ 不是質數, 我們就可以把它分解成兩個比它小 (因此都大於 1) 的正整數的乘積 $n=ab$, 其中 $1\lt a, b\lt n$; 如果 $a$ 或 $b$ 不是質數, 可以繼續把它分解成兩個比它小 (因此都大於 1) 的正整數的乘積; 繼續下去, 到頭來可以把 $n$ 分解成一些質數的乘積。 命題 1 (質因數分解). 大於 1 的正整數都可以分解成一些質數的乘積。也可以說, 大於 1 的正整數都有質因數。 舉例來說, $2100=2\times 2\times 3\times 5\times 5\times 7$\,。 直觀來看, 這樣的分解應該只有一種方法, 但是要說明清楚其實是要費一些力氣的。 其實, 的確有一些整數環並不是唯一分解的, 舉例來說, 若 $\mathbb{Z}$ 表示所有整數的集合, 則 $$ \mathbb{Z}[\sqrt{-5}] := \{m+n\sqrt{-5}: m,n\in \mathbb{Z}\} $$ 就不具有唯一分解的性質, 例如 $$ 6 = 2 \cdot 3 = (1+\sqrt{-5})\cdot(1-\sqrt{-5})\,\mbox{。} $$ 大於 1 的正整數可以唯一分解成質數乘積, 其關鍵是下面這個性質。 命題 2. 如果兩個正整數 $a$ 和 $b$ 的乘積 $ab$ 是質數 $p$ 的倍數, 則 $a$ 是 $p$ 的倍數或者 $b$ 是 $p$ 的倍數。 也就是, 若 $ab \equiv 0$ (mod $p$), 則 $a \equiv 0$ (mod $p$) 或 $b \equiv 0$ (mod $p$)。 證明: 選取最小正整數 $m$ 使得 $am$ 是 $p$ 的倍數。 如果 $m=1$,則 $a$ 是 $p$ 的倍數, 性質得證。 所以假設 $m\ge 2$。 根據除法原理 $$ b = m q + r\mbox{, 其中 $q$ 和 $r$ 都是整數、而且}0\le r\lt m\,\mbox{。} $$ 如果 $r\gt0$, 則因為 $ar=a(b-mq)=ab-amq$ 也是 $p$ 的倍數, 這和 $m$ 的最小性矛盾, 所以事實上 $r=0$, 也就是 $b=mq$。 因為 $ap$ 是 $p$ 的倍數, 和上面的論述一樣 (以 $p$ 代替 $b$ 的位置), 就有 $p=mq'$。 但因為 $2\le m\le p$、而 $p$ 是質數, 所以 $m=p$。 從而 $b=mq=pq$, 也就是 $b$ 是 $p$ 的倍數。 $\Box$ 有了這樣的性質, 就會有正整數的唯一分解定理。 定理 3 (算術基本定理). 大於 1 的正整數 $n$ 都可以唯一分解成一些質數的乘積。 也就是, $n$ 可以分解成質數的乘積 $p_1 p_2 \cdots p_r$。 而且, 如果 $n = p_1 p_2 \cdots p_r = q_1 q_2 \cdots q_s$, 其中 $p_1 \le p_2 \le \cdots \le p_r, q_1 \le q_2 \le \cdots \le q_s$ 是質數, 則 $r=s$ 且對 $1\le i\le r$ 恆有 $p_i=q_i$; 或是, 如果 $n = p_1^{a_1} p_2^{a_2} \cdots p_r^{a_r} = q_1^{b_1} q_2^{b_2} \cdots q_s^{b_s}$, 其中 $p_1 \lt p_2 \lt \cdots \lt p_r, q_1 \lt q_2 \lt \cdots \lt q_s$ 是質數, 且 $a_1, a_2, \ldots, a_r, b_1, b_2, \ldots, b_s$ 是正整數, 則 $r=s$ 且對 $1\le i\le r$ 恆有 $p_i=q_i$ 及 $a_i=b_i$。 證明: 由質因數分解性質知道 $n$ 可以分解成質數的乘積。 唯一性可由數學歸納法證明。 當 $r=1$ 時, 如果 $s\gt1$ 則 $p_1$ 是兩個大於 1 的整數 $q_1$ 和 $q_2 q_3 \cdots q_s$ 的乘積, 矛盾, 所以 $s=1$, 因此唯一性成立。 假設 $r\ge 2$ 且 $s \ge 2$。 因為 $p_1 p_2 \cdots p_r$ 是 $q_1$ 的倍數, 連續使用命題 2 得知 $q_1$ 是某個 $p_i$ 的因數, 但是因為 $q_1\gt1$ 所以事實上 $q_1=p_i$, 就有 $q_1\ge p_1$。 同理可證 $p_1 \ge q_1$, 而有 $p_1=q_1$。 因此 $p_2 p_3 \cdots p_r = q_2 q_3 \cdots q_s$, 由歸納法假設 $r-1=s-1$、即 $r=s$, 而且對於 $2\le i\le r$ 恆有 $p_i=q_i$。 唯一性得證。 $\Box$ 命題 2 還有一個乘法消去律的面向。這和一般整數的消去律類似: $$ \mbox{對於整數 $a, b, c$, 若 $a\ne 0$ 且 $ab=ac$, 則 $b=c$。} $$ 命題 3 (模質數消去律). 對於整數 $a, b, c$ 及質數 $p$, 若 $a\not\equiv 0$ (mod $p$) 且 $ab \equiv ac$ (mod $p$), 則 $b \equiv c$ (mod $p$)。 模質數消去律在模算術中扮演基礎的角色。 先來看費馬小定理。 定理 4 (費馬小定理). 若 $p$ 為質數且整數 $a$ 不是 $p$ 的倍數, 則 $$ \mbox{ $a^{p-1}-1$ 是 $p$ 的倍數, 也就是 $a^{p-1} \equiv 1$ (mod $p$)。} $$ 證明: 考慮 $\mathbb{Z}_p = \{0,1,\ldots, p-1\}$ 中的元素, 對於 $i,j\in \mathbb{Z}_p$, 若 $ai \equiv aj$ (mod $p$), 則由模質數消去律得知 $i \equiv j$ (mod $p$) 也就是 $\{(ai$ mod $p): i \in \mathbb{Z}_p\} = \mathbb{Z}_p$, 其中 ($ai$ mod $p$) 表示 $ai$ 除以 $p$ 的餘數。 因此 $$ (a\cdot 1) \cdot (a \cdot 2) \cdot \cdots \cdot (a \cdot (p-1)) \equiv 1 \cdot 2 \cdot \cdots \cdot (p-1) ~({\rm mod}~p) $$ 利用模質數消去律將 $1,2,\dots,p-1$ 逐一消去就會有 $a^{p-1} \equiv 1$ (mod $p$)。 $\Box$ 歐拉 $\varphi$ 函數定義為: 對於大於 1 的正整數 $n$ $$ \varphi(n) = |\{i \in \mathbb{Z}_n: \mbox{~$i$ 和 $n$ 互質。}\}| $$ 例如 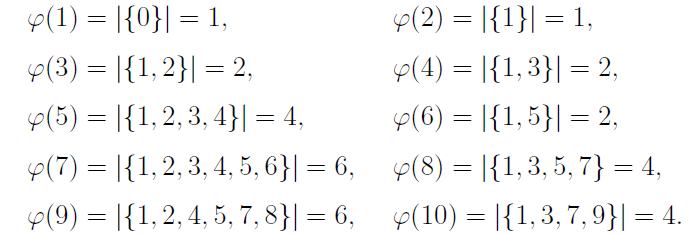 當 $p$ 是質數時, $\varphi(p)=p-1$。 費馬小定理可以推廣到一般的模 $n$。 首先要把模質數消去律推廣。 命題 4 (模$n$消去律). 對於整數 $a, b, c$ 及正整數 $n$, 若 $a$ 和 $n$ 互質且 $ab \equiv ac$ (mod $n$), 則 $b \equiv c$ (mod $n$)。 證明: 若 $b=c$, 則性質顯然成立。不妨假設 $b\gt c$。 由已知可見存在整數 $d$ 使得 $a(b-c)=nd$, 不妨假設 $a\gt0, d\gt0$。 在 $a, b-c, n, d$ 的質因數分解中, 由算術基本定理可得分解的唯一性, 由於 $a$ 和 $n$ 互質, $n$ 分解出來的質因數不發生在 $a$ 分解出來的質因數中, 所以必定全部發生在 $b-c$ 分解出來的質因數中, 所以 $b-c$ 是 $n$ 的倍數, 也就是 $b \equiv c$ (mod $n$)。 $\Box$ 定理 5 (歐拉$\varphi$函數定理). 若 $n$ 為正整數且整數 $a$ 和 $n$ 的互質, 則 $$ \mbox{ $a^{\varphi(n)}-1$ 是 $n$ 的倍數, 也就是 $a^{\varphi(n)} \equiv 1$ (mod $n$)。} $$ 證明: 考慮 $A:=\{i \in \mathbb{Z}_n: i$ 和 $n$ 互質。} 中的元素, 對於 $i,j\in A$, 若 $ai \equiv aj$ (mod $n$), 則由模$n$消去律得知 $i \equiv j$ (mod $n$) 也就是 $\{(ai$ mod $n): i \in A\} = A$, 其中 ($ai$ mod $p$) 表示 $ai$ 除以 $p$ 的餘數。 因此 $$ \prod_{i\in A} (a \cdot i) \equiv \prod_{i\in A} i ~({\rm mod}~n) $$ 利用模 $n$ 消去律將 $A$ 中的 $i$ 逐一消去就會有 $a^{\varphi(n)} \equiv 1$ (mod $n$)。 $\Box$ 6. 證明 Erdős-Ginzburg-Ziv 定理最後來證明 Erdős-Ginzburg-Ziv 定理: 對於正整數 $n$, 任意整數列 $a_1, a_2, \ldots, a_{2n-1}$ 恆存在 $n$ 項 $a_{i_1}, a_{i_2}, \ldots, a_{i_n}$, 其和為 $n$ 的倍數。 定理對於 $n=1$ 顯然成立。 假設 $n \ge 2$。 首先討論 $n=p$ 是質數的情況。 先證明一個引理。 引理 1. 若 $p$ 為質數, $b_1,b_2,\ldots,b_s$ 是 $s$ 個不是 $p$ 倍數的整數, 其中 $2\le s\lt p$ 而且 $b_1\not\equiv b_2$ (mod $p$), 則最少有 $s+1$ 個模 $p$ 不同餘的 $\sum_{i=1}^s \varepsilon_i b_i$, 其中各 $\varepsilon_i =0$ 或 1。 證明: 用歸納法證明。 如果 $s=2$, 則 $b_1, b_2, b_1+b_2$ 模 $p$ 不同餘 (這是因為 $b_1 \not\equiv b_2$, $b_1\not\equiv 0$, $b_2\not\equiv 0$)。 假設 $s\ge 3$, 而且引理對 $s-1$ 成立。 令 $c_1,c_2,\ldots,c_k$ 是所有模 $p$ 不同餘的 $\sum_{i=1}^{s-1} \varepsilon_i b_i$。 由歸納法假設 $k\ge s$\,。 如果 $k\ge s+1$, 引理成立。現假設 $k=s\lt p$。 如果對 $1\le i\le k$ 都存在 $i_r$ 使得 $c_i+b_s \equiv c_{i_r}$ (mod $p$), 因為 $i_r=j_r$ 時 $c_i+b_s \equiv c_{i_r} \equiv c_{j_r} \equiv c_j+b_s$ (mod $p$), 而有 $c_i \equiv c_j$ (mod $p$), 也就是 $i=j$。 所以 $$ \sum_{i=1}^s (c_i+b_s) \equiv \sum_{i=1}^s c_i\mbox{, } $$ 遂有 $s b_s \equiv 0$ (mod $p$), 這與 $s \not\equiv 0$ (mod $p$) 及 $b_s \not\equiv 0$ (mod $p$) 矛盾。 所以有某一個 $c_i+b_s$ 模 $p$ 時不與任何 $b_j$ 同餘。引理得證。 $\Box$ 回到定理的證明。 不妨假設 $0\le a_1\le a_2\le\cdots\le a_{2p-1}\lt p$。 首先, 可以假設 $a_i\ne a_{i+p-1}$ (不然的話 $a_i+a_{i+1}+\cdots+a_{i+p-1}=p a_i\equiv 0$ (mod $p$)), 以及 $a_1+a_2+\cdots+a_p \equiv c \not\equiv 0$ (mod $p$), 不然定理就成立了。 令 $b_i=a_{p+i}-a_{i+1}$, $1\le i\le p-1$, 則各 $b_i\not\equiv 0$ (mod $p$)。 此時 $-c\equiv \sum_{i=1} \varepsilon_i b_i$ (mod ($p))$, $\varepsilon_i=0$ 或 1 有解;這是因為如果有兩個 $b_i$ 模 $p$ 不同餘時, 可由前述引理推得;而當所有 $b_i$ 模 $p$ 都同餘時, $\{b_2, 2b_2,\ldots,(p-1)b_2\}=\{1,2,\ldots,p-1\}$ 而存在某個 $1\le j\le p-1$ 滿足 $-c=j b_2$, 此時 $-c=\sum_{i=1}^j b_i$。 顯然 $$ \sum_{i=1}^p a_i + \sum_{i=1}^{p-1} \varepsilon_i b_i \equiv 0 ~({\rm mod}~ p) $$ 是 $p$ 個 $a_i$ 的和。 所以定理對 $n=p$ 成立。 對於一般的 $n$, 只要證明, 若 $n=u$ 及 $n=v$ 時定理成立, 則 $n=uv$ 時定理也成立。 考慮 $2uv-1$ 個整數 $a_1,a_2,\ldots,a_{2uv-1}$。 因為定理對 $u$ 成立, 可以選取其中 $u$ 個和為 $u$ 倍數的 $a_i$, 去掉這 $u$ 個數並重複同樣的步驟, 如果重複了 $2v-2$ 次, 還會剩下 $2uv-1-(2v-2)u=2u-1$ 個 $a_i$, 所以還可以選出 $u$ 個和為 $u$ 倍數的 $a_i$。 總結來說, 存在 $2v-1$ 組 $a_1^{(i)},a_2^{(i)},\ldots,a_u^{(i)}$, $1\le i\le 2v-1$ 滿足 $\sum_{j=1}^u a_j^{(i)}=c_i u$, $1\le i\le 2v-1$。 因為定理對 $v$ 成立, 所以存在 $c_{i_1},c_{i_2},\ldots,c_{i_v}$ 使得 $\sum_{r=1}^v c_{i_r}\equiv 0$ (mod $v$)。 所以 $$ \sum_{r=1}^v \sum_{j=1}^u a_j^{i_r} = u \sum_{r=1}^v c_{i_r} \equiv 0~({\rm mod}~uv)\,\mbox{。} $$ 所以定理成立。 $\Box$ 參考文獻本文作者為臺灣大學數學系名譽教授 |
| 頁碼 | 96-107 |
2025年9月 49卷3期
艾狄胥等人的一個加性數論定理——由模算術談起

