| 發刊日期 |
2025年9月
|
|---|---|
| 標題 | 強連通圖中封閉道路的邊數期望值 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
壹、前言考慮一個正四面體, 頂點分別為 $v_1,v_2,v_3,v_4$, 若一隻螞蟻由 $v_1$ 出發, 在機率均等的原則下, 每次皆以 $\dfrac 13$ 的機率選擇下一條邊行走到相鄰的點, 過程中點與邊都可以重複, 直到第一次走回 $v_1$ 後即停止。 整個過程, 若螞蟻走了 $k$ 條邊, 則共有 $3\times 2^{k-2}$ 種走法, 而每一種走法發生的機率為 $\Big(\dfrac 13\Big)^k$, 透過無窮級數的處理技巧, 可知螞蟻行走邊數的期望值為 $$\sum_{k=2}^\infty k\Big(\dfrac 13\Big)^k\times(3\times 2^{k-2})=\frac 13\sum_{k=2}^\infty k\Big(\dfrac 23\Big)^{k-2}=4,$$ 意即螞蟻要走回出發點平均要走 4 條邊。  本文將上述的問題一般化, 用圖論的語言來重新詮釋這樣的邊數期望值問題, 研究的對象為具有強連通性的有向圖, 螞蟻必須遵循有向邊的方向性來進行隨機漫步, 而從一個點選擇哪一條有向邊來行走的機率則是以函數來決定 (不限制機率均等), 再利用線性代數的觀點刻畫封閉道路的邊數期望值, 並試著探討與圖形結構之關係。 貳、基本知識與符號一個圖 $G$ 是由點集合 $V(G)$ 與邊集合 $E(G)$ 構成, 令 $V(G)=\{v_1,v_2,\ldots,v_n\}$, 若 $G$ 的每一條邊都具有方向性, 則稱為『有向圖 (directed graph)』。 若 $v_i$ 與 $v_j$ 有邊相連且為 $v_i$ 指向 $v_j$, 則將此有向邊記為序對『$(v_i,v_j)$』。 本文所討論的有向圖, 對於任意相連的兩點 $v_i$ 與 $v_j$, 有向邊 $(v_i,v_j)$ 與 $(v_j,v_i)$ 是可以同時存在的 (在圖示上使用雙向箭頭來表示這兩條有向邊)。 考慮 $v\in V(G)$, 令 $v$ 的『外鄰居 (out-neighbor)』為存在有向邊由 $v$ 指向的點所形成的集合, 以符號記為『$N^+(v)$』; 令 $v$ 的『內鄰居 (in-neighbor)』為存在有向邊指向 $v$ 的點所形成的集合, 以符號記為『$N^-(v)$』。 換句話說 $N^+(v)=\{u:(v,u)\in E(G)\}$ 與 $N^-(v)=\{u:(u,v)\in E(G)\}$。 此外, $|N^+(v)|$ 與$|N^-(v)|$ 分別稱為點 $v$ 的『外度數 (out-degree)』與『內度數 (in-degree)』, 符號依序記為『$d^+(v)$』與『$d^-(v)$ 』。 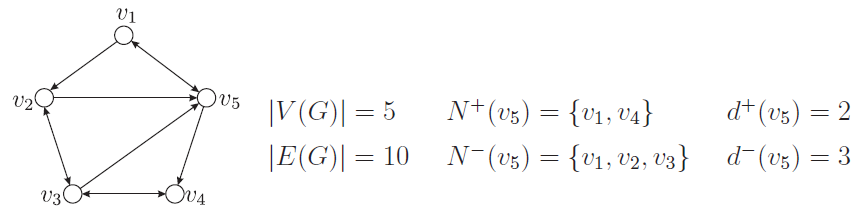 對於有向圖 $G$, 若任意兩點 $v_i$ 與 $v_j$, 皆存在一系列的有向邊使得 $v_i$ 能行走到 $v_j$, 則稱此有向圖為『強連通圖 (strongly connected graph)』, 本文所討論的圖 $G$ 皆為強連通圖。 強連通圖的結構, 能保證螞蟻在出發後, 依循有向邊來進行隨機漫步, 不會有無法走回出發點的狀況。 因為螞蟻行走的方式, 是完全依循有向邊的存在與否, 進行下一步的選擇, 假設螞蟻從一個點選擇哪一條邊直接行走到外鄰居時, 皆有固定的選邊機率。 對 $(v_i,v_j)\in E(G)$, 定義 $v_i$ 直接走到 $v_j$ 的選邊機率為『$P(i.j)$』, 其中函數 $P$ 滿足 $0\lt P(i,j)\le 1$ 且 $\sum\limits_{v_j\in N^+(v_i)} P(i,j)=1$。 若 $v_i$ 與 $v_j$ 為圖形上的任意點, 考慮由 $v_i$ 出發第一次走到 $v_j$ 所產生的道路, 將此道路的邊數期望值記為『$E(i\to j)$』。 特別的, 將 $E(i\to i)$ 的值記為『$E(i)$』。 圖 $G$ 的點集合預設為 $V(G)=\{v_1,v_2,\ldots,v_n\}$, 因此 $\{E(i\to j):1\le i,j\le n\}$ 共有 $n^2$ 個期望值, 我們想要探討的是對任意 $v_i\in V(G)$, $E(i)$ 的值關於圖 $G$ 與函數 $P$ 是否有特殊關聯性。 參、期望值 $E(i\to j)$ 的線性關係考慮由 $v_i$ 出發行走一條邊抵達外鄰居 $v_k$ 後 (其中 $v_k\not=v_j$), 再考慮由 $v_k$ 繼續行走, 第一次抵達 $v_j$ 所經過的邊數期望值, 則可以建立 $E(i\to j)$ 的線性關係式, 故有以下引理。 引理 1: 對任意 $v_i$ 與 $v_j$, 則 $E(i\to j)=1+\sum\limits_{v_k\in N^+(v_i)\atop v_k\not=v_j}P(i,k)\cdot E(k\to j)$。 證明: 若 $v_j\in N^+(v_i)$, 由於 $v_i$ 有 $P(i,j)$ 的機率走一條邊即可走到 $v_j$, 也有 $P(i,k)$ 的機率走到 $v_k\in N^+(v_i)\backslash \{v_j\}$, 而 $v_k$ 後續要第一次走到 $v_j$ 的邊數期望值為 $E(k\to j)$, 故 $E(i\to j)=P(i,j)\times 1+\sum\limits_{v_k\in N^+(v_i)\atop v_k\not=v_j}P(i,k)\big(E(k\to j)+1\big) =\sum\limits_{v_k\in N^+(v_i)}P(i,k)+\sum\limits_{v_k\in N^+(v_i)\atop v_k\not=v_j}P(i,k)\cdot E(k\to j)$, 整理後可得 $E(i\to j)=1+\sum\limits_{v_k\in N^+(v_i)\atop v_k\not=v_j}P(i,k)\cdot E(k\to j)$。 同理, 若 $v_j\not\in N^+(v_i)$, 則 $E(i\to j)=\sum\limits_{v_k\in N^+(v_i)\atop v_k\not=v_j}P(i,k)\big(E(k\to j)+1\big) =\sum\limits_{v_k\in N^+(v_i)}P(i,k)+\sum\limits_{v_k\in N^+(v_i)\atop v_k\not=v_j}P(i,k)\cdot E(k\to j)$, 亦可得知 $E(i\to j)=1+\sum\limits_{v_k\in N^+(v_i)\atop v_k\not=v_j}P(i,k)\cdot E(k\to j)$。 $\Box$ 讓我們用一個例子來說明如何透過引理1來求得邊數期望值 $E(1)$。 例 1: 給定圖 $G$, 如下圖所示, 其中頂點周圍的數字代表該點走到其外鄰居的機率, 函數 $P$ 定義為: $$\left\{\begin{array}{l} P(1,2)=\frac 14\\[3pt] P(1,5)=\frac 34\end{array}\right., \left\{\begin{array}{l} P(2,1)=\frac 7{12}\\[3pt] P(2,3)=\frac 13\\[3pt] P(2,5)=\frac 1{12} \end{array}\right., \left\{\begin{array}{l} P(3,2)=\frac 16\\[3pt] P(3,4)=\frac 14\\[3pt] P(3,5)=\frac 7{12} \end{array}\right., \left\{\begin{array}{l} P(4,3)=\frac 34\\[3pt] P(4,5)=\frac 14\end{array}\right., \left\{\begin{array}{l} P(5,1)=\frac 1{16}\\[2pt] P(5,2)=\frac 1{2}\\[2pt] P(5,3)=\frac 18\\[2pt] P(5,4)=\frac 5{16} \end{array}\right.. $$考慮 $j=1$, 利用引理 1 則可建立出五條關係式如下:  將上述關係式視為聯立方程組, 則可利用克拉瑪公式求得每一個期望值。 特別的, 當我們將每一條 $E(i\to 1)$ 的關係式乘上 $v_i$ 的外度數 $d^+(v_i)$ 時, 則聯立方程組可改寫如下:  可以發現, 將 5 式相加之後, 除了 $E(1\to 1)$ 以外, 其餘的變數都會被抵銷掉, 因此可以求得 $E(1\to 1)=E(1)=7$。 事實上, 對於這個例子, 利用一樣的手法, 也能夠求得 $E(2)$、 $E(3)$、 $E(4)$ 與 $E(5)$ 的值依序為 $\dfrac {14}3$、 $\dfrac {14}3$、 7 與 $\dfrac 72$。 因為外度數總和即為圖的邊數, 因此這五個期望值皆可表示為『圖的邊數』與『該點外度數』的比值, 也就是對任意 $v_i\in V(G)$, $E(i)=\dfrac{\sum\limits_{v\in V(G)}d^+(v)}{d^+(v_i)}=\dfrac{|E(G)|}{d^+(v_i)}$。 $\Box$ 例 1 能有這樣巧妙的結論取決於圖 $G$ 的結構與函數 $P$ 的設定, 其關鍵原因在於對任意 $v_i\in V(G)$, 關係式 $\sum\limits_{v_k\in N^-(v_i)}d^+(v_k)\cdot P(k,i)=d^+(v_i)$ 恆成立。 有關這樣的性質, 我們試著將結論一般化, 並嘗試刻畫出期望值的通式。 肆、方程組係數的分析對於一個 $n$ 個點的圖 $G$ 與邊的機率函數 $P$, 考慮一個正實數數列 $\langle a_i\rangle_{i=1}^n$, 設計特殊向量如下: 1. 定義 $\vec \alpha\in {\Bbb R}^n$, 其中第 $j$ 個分量為 $\sum\limits_{v_k\in N^-(v_j)}a_k\cdot P(k,j)-a_j$; 2. 對任意 $i\in \{1,2,\ldots,n\}$, 定義 $\vec{e_i}\in{\Bbb R}^n$, 其中第 $j$ 個分量為 $e_{ji}=\left\{\begin{array}{ccl} E(j\to i)&,&\hbox{當}\ j\not=i\\[4pt] 0&,&\hbox{當}\ j=i \end{array}\right.$。 利用這兩個特殊向量的符號, 我們可以將 $E(i)$ 表示成向量內積相關的型態, 故有以下引理。 引理 2: 令 $G$ 為強連通圖, 則對任意 $v_i\in V(G)$, $a_i\cdot E(i)=\sum\limits_{k=1}^n a_k+\vec{\alpha}\cdot \vec{e_i}$ 恆成立。 證明: 根據引理 1 可知 $E(k\to i)=1+\sum\limits_{v_j\in N^+(v_k)\atop v_j\not=v_i}P(k,j)\cdot E(j\to i)$, 其中 $k=1,2,\ldots,n$。 對任意 $k\in\{1,2,\ldots,n\}$, 將 $E(k\to i)$ 的線性關係式乘上 $a_k$, 則可得關係式 $a_k\cdot E(k\to i)=a_k+\sum\limits_{v_j\in N^+(v_k)\atop v_j\not=v_i}a_k\cdot P(k,j)\cdot E(j\to i)$。 將此 $n$ 條線性關係直接相加, 讓左式總和只保留變數 $a_i\cdot E(i\to i)$, 其餘變數都移項到右式, 整理後為 $$\sum_{k=1}^n a_k+\sum\limits_{v_j\in V(G)\backslash \{v_i\}}\Big(\sum_{v_k\in N^-(v_j)} a_k\cdot P(k,j)-a_j\Big)\cdot E(j\to i)=\sum_{k=1}^n a_k+\vec \alpha\cdot \vec{e_i}.$$由此可得 $a_i\cdot E(i\to i)=a_i\cdot E(i)=\sum\limits_{k=1}^na_k+\vec \alpha\cdot \vec{e_i}$。 $\Box$ 令 $G$ 為強連通圖, 考慮函數 $P$ 與正實數數列 $\langle a_i\rangle_{i=1}^n$, 運用引理 2, 則有以下定理。 定理 1: 若對任意 $v_i\!\in\! V(G)$, $\sum\limits_{v_k\in N^{-}(v_i)}\!\!a_k\!\cdot\! P(k,i)\!=\!a_i$, 則對任意 $v_i\!\in\! V(G)$, $E(i)\!=\!\dfrac{\sum\limits_{k=1}^n \!a_k}{a_i}$。 證明: 因為對任意 $v_i\in V(G)$, 皆滿足 $\sum\limits_{v_k\in N^{-}(v_i)}\!\!a_k\!\cdot\! P(k,i)\!=\!a_i$, 所以特殊向量 $\vec \alpha=\vec 0$, 故 $\vec \alpha\cdot \vec{e_i}=0$。 根據引理 2 的結論可知對任意 $v_i\in V(G)$, 關係式 $a_i\cdot E(i)=\sum\limits_{k=1}^n \!a_k$ 恆成立, 由此可知 $E(i)\!=\!\dfrac{\sum\limits_{k=1}^n \!a_k}{a_i}$。 $\Box$ 透過討論方程組的係數, 定理 1 的結論說明了, 對於函數 $P$ 而言, 只要能夠找到滿足條件的正實數數列 $\langle a_i\rangle_{i=1}^n$, 即可得知每一點的期望值 $E(i)$。 例 2: 考慮例 1 中的圖 $G$, 其中對任意 $(v_i,v_j)\in E(G)$, 若函數 $P$ 的值設定為 $P(i,j)=\dfrac 1{d^+(v_i)}$, 則正實數數列 $(a_1,a_2,a_3,a_4,a_5)=\big({d^+(v_1)},{d^+(v_2)},{d^+(v_3)},{d^+(v_4)},{d^+(v_5)}\big)$, 滿足對任意 $v_i\in V(G)$, $\sum\limits_{v_k\in N^{-}(v_i)}\!\!a_k\!\cdot\! P(k,i)\!=\!\sum\limits_{v_k\in N^{-}(v_i)}{d^+(v_k)}\cdot \dfrac 1{d^+(v_k)}\!=\!{d^-(v_i)}\!=\!{d^+(v_i)}\!=\!a_i$。 由定理 1 的結論可知, 對任意 $v_i\!\in\! V(G)$, 期望值 $E(i)\!=\!\dfrac{\sum\limits_{k=1}^n \!a_k}{a_i}\!=\!\dfrac{\sum\limits_{k=1}^n \! {d^+(v_k)}}{d^+(v_i)} =\dfrac{|E(G)|}{d^+(v_i)}$。 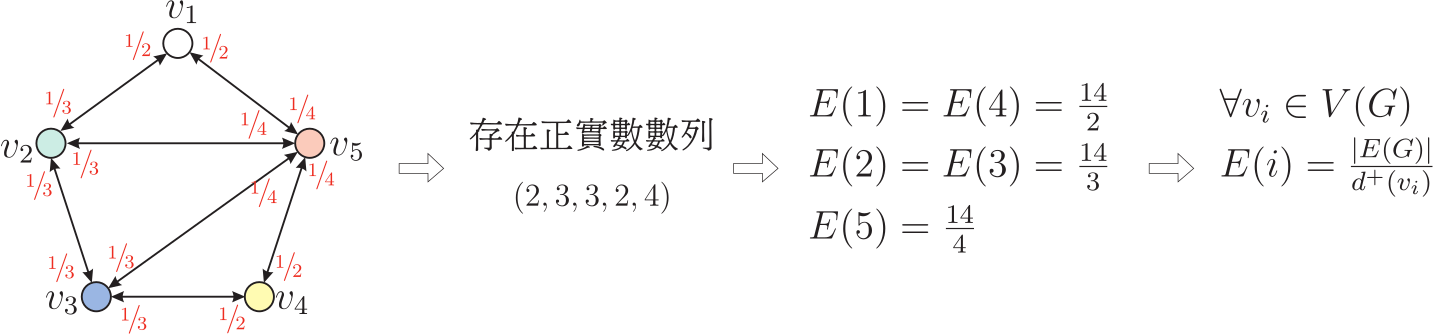 例 2 中函數 $P$ 的設定, 是每個點都以機率均等的原則, 選擇有向邊來進行隨機漫步, 在這種特殊的情況下, 符合定理 1 的正實數數列 $\langle a_i\rangle_{i=1}^n$ 即為各點所決定的外度數數列 $\langle d^+(v_i)\rangle_{i=1}^n$, 因此各點的期望值可由圖 $G$ 的結構來直接刻畫, 故例 2 可推廣為以下推論。 推論: 若對任意 $v_i\in V(G)$, $d^-(v_i)=d^+(v_i)$ 且對任意 $(v_i,v_j)\in E(G)$, $P(i,j)=\dfrac 1{d^+(v_i)}$, 則對任意 $v_i\in V(G)$, 期望值 $E(i)=\dfrac{|E(G)|}{d^+(v_i)}$。 因為當圖 $G$ 與函數 $P$ 確定之後, 各點的期望值都隨之確定, 所以我們想要探討的是, 符合定理 1 的正實數數列 $\langle a_i\rangle_{i=1}^n$ 是否必然存在呢? 後續我們將利用矩陣來說明其存在性, 意味著可以由數列 $\langle a_i\rangle_{i=1}^n$ 來決定各點的期望值。 至於例 1 與例 2, 為何針對不同的函數 $P$, 每個點 $v_i$ 的期望值皆可表示為 $E(i)=\dfrac{|E(G)|}{d^+(v_i)}$? 後續也將解釋其主要原因。 伍、矩陣觀點的分析接下來我們試著用矩陣的觀點來表示期望值的線性關係。 對於 $n$ 個點的圖 $G$, 根據引理 1 共可以建立出 $n^2$ 條關係式, 這些關係式透過轉移矩陣, 可以統一使用矩陣的乘法來表達。 以下我們用三個點的圖來說明, 考慮圖 $G$ (如下圖所示), 共可以建立 9 條關係式如下:  當 $v_1$ 為終點時, 則 $\left\{\begin{array}{l} E(1\!\to\! 1)\!=\!1\!+\!P(1,2)E(2\!\to\! 1)\!+\!P(1,3)E(3\!\to\! 1)\\[5pt] E(2\!\to\! 1)\!=\!1\!+\!P(2,3)E(3\!\to\! 1)\\[5pt] E(3\!\to\! 1)\!=\!1\!+\!P(3,2)E(2\!\to\! 1) \end{array}\right.$; 當 $v_2$ 為終點時, 則 $\left\{\begin{array}{l} E(1\!\to\! 2)\!=\!1\!+\!P(1,3)E(3\!\to\! 2)\\[5pt] E(2\!\to\! 2)\!=\!1\!+\!P(2,1)E(1\!\to\! 2)\!+\!P(2,3)E(3\!\to\! 2)\\[5pt] E(3\!\to\! 2)\!=\!1\!+\!P(3,1)E(1\!\to\! 2) \end{array}\right.$; 當 $v_3$ 為終點時, 則 $\left\{\begin{array}{l} E(1\!\to\! 3)\!=\!1\!+\!P(1,2)E(2\!\to\! 3)\\[5pt] E(2\!\to\! 3)\!=\!1\!+\!P(2,1)E(1\!\to\! 3)\\[5pt] E(3\!\to\! 3)\!=\!1\!+\!P(3,1)E(1\!\to\! 3)\!+\!P(3,2)E(2\!\to\! 3) \end{array}\right.$ 。 適當地移項後則可將 9 條關係式表示為以下的矩陣乘法 $H(M-I)=D-J$: 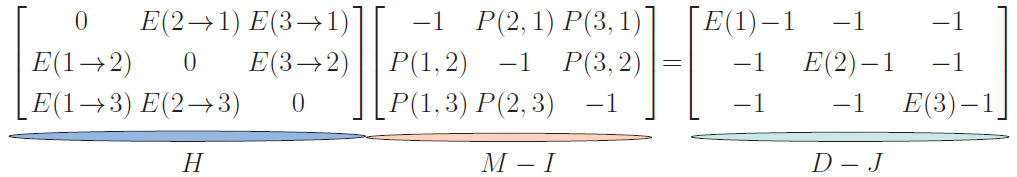 以下解釋矩陣 $H$、 $M$、 $D$ 與 $J$ 的定義。 事實上, 給定圖 $G$, 其中 $V(G)=\{v_1,v_2,\ldots,v_n\}$, 選邊機率為函數 $P$, 上述的矩陣關係式具有一般性, 以下定義矩陣: 1. $H=[h_{i,j}]$ 是由 $\vec{e_1},\vec{e_2},\ldots,\vec{e_n}$ 決定的矩陣, 其中 $h_{i,j}=\left\{\begin{array}{cl} E(j\to i)&,\ \hbox{當}\ i\not=j\\[4pt] 0&,\ \hbox{當}\ i=j\end{array}\right.$。 2. $M=[m_{i,j}]$ 為函數 $P$ 決定的轉移矩陣, 其中 $m_{i,j}=\left\{\begin{array}{cl} P(j,i)&,\ \hbox{當}\ (v_j,v_i)\in E(G)\\[4pt] 0&,\ \hbox{當}\ (v_j,v_i)\not\in E(G)\end{array}\right.$。 3. $D\!=\![d_{i,j}]$ 為期望值 $E(i)$, $i\!=\!1,2,\ldots,n$ 決定的對角矩陣, 其中 $d_{i,j}\!=\!\left\{\!\begin{array}{cl} E(i)&,\hbox{當}\ i=j\\[4pt] 0&,\hbox{當}\ i\not=j\end{array}\right.$。 4. $I$ 為 $n$ 階單位方陣, $J$ 為元素全為 1 的 $n$ 階全一方陣。 利用上述矩陣的概念, 則可得以下引理。 引理 3 (矩陣關係式): 令 $G$ 為強連通圖, 選邊機率為函數 $P$, 則 $H(M-I)=D-J$。 若 $n$ 階方陣滿足每一行與每一列皆恰有一個 1 且其餘元素皆為 0, 則將此方陣稱為『排列矩陣』。 例如所有的二階排列矩陣為 $\left[\begin{array}{cc} ~1~&~0~\\ ~0~&~1~\end{array}\right]$ 與 $\left[\begin{array}{cc} ~0~&~1~\\ ~1~&~0~\end{array}\right]$;所有的三階排列矩陣為 $\left[\begin{array}{ccc} ~1~&~0~&~0~\\ ~0~&~1~&~0~\\ ~0~&~0~&~1~ \end{array}\right]$、$\left[\begin{array}{ccc} ~1~&~0~&~0~\\ ~0~&~0~&~1~\\ ~0~&~1~&~0~ \end{array}\right]$、$\left[\begin{array}{ccc} ~0~&~1~&~0~\\ ~1~&~0~&~0~\\ ~0~&~0~&~1~ \end{array}\right]$、$\left[\begin{array}{ccc} ~0~&~0~&~1~\\ ~1~&~0~&~0~\\ ~0~&~1~&~0~ \end{array}\right]$、$\left[\begin{array}{ccc} ~0~&~1~&~0~\\ ~0~&~0~&~1~\\ ~1~&~0~&~0~ \end{array}\right]$ 與 $\left[\begin{array}{ccc} ~0~&~0~&~1~\\ ~0~&~1~&~0~\\ ~1~&~0~&~0~ \end{array}\right]$。 對於一個 $n$ 階方陣 $A$, 若存在一個 $n$ 階排列矩陣 $X$ 與其轉置矩陣 $X^T$ 能使得 $X^TAX=\left[\begin{array}{cc} ~B~&~C~\\ ~O~&~F~\end{array}\right]$, 則稱 $A$ 為『可分解 (reducible)』, 其中 $B$ 為 $r$ 階方陣 $(1\le r\le n-1)$、 $F$ 為 $n-r$ 階方陣、 $C$ 為 $r\times(n-r)$ 階矩陣且 $O$ 為 $(n-r)\times r$ 階零矩陣。 若 $A$ 不為可分解的方陣, 則稱為『不可分解 (irreducible)』。 例 3: 令 $A_1\!=\!\!\left[\begin{array}{ccc} ~4~&~6~&~2~\\ ~0~&~7~&~0~\\ ~2~&~3~&~1~ \end{array}\right]$, 則排列矩陣 $X\!=\!\!\left[\begin{array}{ccc} ~0~&~1~&~0~\\ ~0~&~0~&~1~\\ ~1~&~0~&~0~ \end{array}\right]$ 能使得 $X^TA_1X\!=\!\!\left[\begin{array}{ccc} ~1~&~2~&~3~\\ ~2~&~4~&~6~\\ ~0~&~0~&~9~ \end{array}\right]$, 故 $A_1$ 為可分解。 令 $A_2=\left[\begin{array}{ccc} ~1~&~2~&~3~\\ ~2~&~4~&~6~\\ ~3~&~6~&~0~ \end{array}\right]$, 則不存在排列矩陣 $X$ 使得 $X^TA_2X=\left[\begin{array}{cc} ~B~&~C~\\ ~O~&~F~ \end{array}\right]$, 故 $A_2$為不可分解。 $\Box$ 一個轉移矩陣若為不可分解, 就表示不存在一種狀態的重新排序, 使得各種狀態轉移的機率, 可被重新表現為左下方是一個零矩陣 $O_{(n-r)\times r}$ 的轉移矩陣, 其中 $1\le r\le n-1$。 有關圖 $G$ 與函數 $P$ 所決定的轉移矩陣 $M$, 透過 $M$ 中的各非零元素, 可以直接呈現圖 $G$ 的有向邊結構。 然而一個不可分解的轉移矩陣 $M$, 即能反映出圖 $G$ 為強連通圖, 反之亦然, 故有以下引理。 引理 4: $G$ 為強連通圖若且唯若轉移矩陣 $M$ 為不可分解。 證明: $(\Rightarrow)$ 假設 $M$ 為可分解, 則存在排列矩陣 $X$ 使得 $X^TMX=\left[\begin{array}{cc} ~B~&~C~\\ ~O~&~F~ \end{array}\right]$, 其中 $O$ 為 $(n-r)\times r$ 階零矩陣。 因此對任意 $1\le i\le r$ 與任意 $r+1\le j\le n$, $(v'_i,v'_j)\not\in E(G)$。 此與 $G$ 為強連通圖矛盾。 $(\Leftarrow)$ 假設 $G$ 非強連通圖, 不失一般性, 設 $v_1$ 所能連通的點所形成的集合為 $\{v_2,v_3,\ldots,v_r\}$, 則不存在有向邊從 $\{v_1,v_2,\ldots,v_r\}$ 指向 $\{v_{r+1},v_{r+2},\ldots,v_n\}$, 因此\\ $I^TMI=M=\left[\begin{array}{cc} ~B~&~C~\\ ~O~&~F~ \end{array}\right]$, 其中 $O$ 為 $(n-r)\times r$ 階零矩陣。 此與 $M$ 為不可分解矛盾。  若一個方陣的各項元素皆為非負, 則稱此矩陣為非負方陣。 Perron-Frobenius Theorem 提供了許多有關非負方陣的性質, 若 $A$ 為非負方陣, 則有以下四點性質:
性質1:
有一個實數特徵值 $\rho$, 且其它特徵值 $\lambda$ 都滿足 $|\lambda|\le \rho$, 其中 $\rho$ 稱為譜半徑。 因為轉移矩陣 $M$ 為非負方陣且滿足 $[1,1,\ldots,1]M=[1,1,\ldots,1]$, 所以 $M^T\!\left[\begin{array}{c} 1\\ 1\\ \vdots\\ 1\end{array}\right]=\left[\begin{array}{c} 1\\ 1\\ \vdots\\ 1\end{array}\right]$。 這表示非負方陣 $M^T$ 存在特徵值為 1 且存在各項分量都是正數的特徵向量, 根據性質 3, 可知 $M^T$ 的譜半徑 $\rho=1$。 因為 $\det(x\cdot I-M)=\det(x\cdot I-M)^T=\det(x\cdot I^T-M^T)=\det(x\cdot I-M^T)$, 所以 $M$ 與 $M^T$ 有一樣的特徵多項式, 因此具有完全相同的特徵值, 即 $M$ 亦有譜半徑 $\rho=1$。 因為 $M$ 是不可分解, 根據性質 2, 可知存在特徵值為 $\rho=1$ 的特徵向量 $\vec u=[u_1,u_2,\ldots,u_n]\gt0$, 其各項分量全為正數。 意即 $M$ 存在穩定狀態機率分布 $S=\dfrac 1{\sum\limits_{i=1}^n u_i}[u_1,u_2,\ldots,u_n]=[p_1,p_2,\ldots,p_n]\gt0$, 使得 $MS^T=S^T$。 因為 $M$ 是不可分解, 根據性質 4, 可知穩定狀態機率分布 $S=[p_1,p_2,\ldots,p_n]\gt0$ 是唯一的。 利用引理 3 的結論, 所有期望值的線性關係可用矩陣表示為 $H(M-I)=D-J$。 因為非負矩陣 $M$ 為強連通圖的轉移矩陣, 根據 Perron-Frobenius Theorem 可知轉移矩陣 $M$ 有唯一的穩定狀態機率分布 $S\gt0$, 將穩定狀態 $S$ 記為列矩陣 $S=[p_1,p_2,\ldots,p_n]$, 其中元素 $p_i$ 皆為正數。 定義 $R=(r_{i,j})=\left[\begin{array}{ccccccc} p_1^{-1}&&&&&\\ &p_2^{-1}&&&0&\\ &&&\ddots&&&\\ &&0&&&\ddots&\\ &&&&&&p_{n}^{-1}\end{array}\right]$, 是由穩定狀態的各項機率的倒數所決定的 $n$ 階方陣。 探討矩陣關係式與穩定狀態 $S$ 的關係, 我們可以發現, 期望值 $E(i)$ 與機率 $p_i$ 有密切關係, 故有以下定理。 定理 2: 令 $S=[p_1,p_2,\ldots,p_n]\gt0$ 為 $M$ 的穩定狀態機率分布, 則對任意 $v_i\in V(G)$, $E(i)=\dfrac 1{p_i}$。 證明: 因為 $MS^T=S^T$, 所以 $(M-I)S^T=O_{n\times 1}$ 為零行矩陣, 所以 $H(M-I)S^T=(D-J)S^T=O_{n\times 1}$ 亦為零行矩陣。 令 $d_i=d_{i,i}=E(i)$, 考慮 $D-J$ 的第 $i$ 列與 $S^T$ 的乘積, 可得 $d_ip_i-(p_1+p_2+\cdots +p_n)=0$, 整理後得 $d_ip_i=1$, 故 $d_i=\dfrac 1{p_i}$。 由此可知對任意 $v_i\in V(G)$, $E(i)=d_i=\dfrac 1{p_i}$。 $\Box$ 定理 2 說明了各點的期望值 $E(i)$ 是由轉移矩陣 $M$ 的穩定狀態機率分布 $S$ 所決定, 而 Perron-Frobenius Theorem 可保證這個穩定狀態機率分布是恆正、 存在且唯一的。 然而定理 2 的結論也可以有另一種直觀的解釋, 穩定狀態的機率分布說明著從 $v_1$ 出發, 長期下來會有 $p_1$ 的機率抵達 $v_1$, 會有 $1-p_1$ 的機率抵達其他點, 因此可以將整個行走過程整合成一個伯努利試驗 (Bernoulli trial), 當抵達 $v_1$ 時即視為成功, 其成功機率為 $p_1$。 令隨機變數 $X$ 表示第一次成功所試驗的次數, 則 $X$ 的機率分布即為參數 $p_1$ 的幾何分布 $X\sim G(p_1)$。 因為幾何分布 $X$ 的期望值公式為成功機率 $p_1$ 的倒數, 所以 $E(X)=\dfrac 1{p_1}$, 變異數 $\rm{Var}(X)=\dfrac{1-p_1}{p_1^2}$, 而第一次成功所需要試驗的次數即可視為螞蟻行走的邊數, 這樣的觀點可以作為定理 2 所展現的直觀意義。 當我們比較定理 1 與定理 2 的關係可以發現, 對於函數 $P$, 能夠滿足定理 1 條件的正實數數列 $(a_1,a_2,\ldots,a_n)$, 條件 『$\forall\ v_i\in V(G)$, $\sum\limits_{v_k\in N^-(v_i)}a_k\cdot P(k,i)=a_i$』 等價於滿足矩陣關係式 $M\!\left[\begin{array}{c} a_1\\ a_2\\ \vdots\\ a_n\end{array}\right]=\left[\begin{array}{c} a_1\\ a_2\\ \vdots\\ a_n\end{array}\right]$, 意即 $(a_1,a_2,\ldots,a_n)$ 必為轉移矩陣 $M$ 特徵值為 1 的特徵向量。 換句話說, 數列 $(a_1,a_2,\ldots,a_n)$ 必為穩定狀態機率分布 $S$ 的實數倍, 因此 $E(i)=\dfrac{\sum\limits_{k=1}^na_k}{a_i}=\dfrac 1{p_i}$。 定理 1 說明如果存在特殊的正實數數列, 則各點的期望值即可由此數列得知。 然而 Perron-Frobenius Theorem 保證這個特殊的正實數數列的存在性, 在各項比例上亦具有唯一性, 由此可以知定理 2 是定理 1 的推論。 特別的, 由建立聯立方程組並觀察係數, 定理 1 的充分條件即說明了, 當轉移矩陣 $M$ 存在唯一恆正的穩定狀態機率分布時, 則各點的期望值即各機率的倒數。 又因為 $G$ 為強連通圖, 所以轉移矩陣 $M$ 必為不可分解, 故能保證 $M$ 存在唯一恆正的穩定狀態機率分布, 這也突顯出定理 1 的充分條件事實上也會是必要條件, 而這樣的結果 Perron-Frobenius Theorem 居中扮演著重要的角色。 此外, 本文中的例 1 與例 2, 有關圖 $G$, 對於兩個不同的函數 $P$, 每個點 $v_i$ 的期望值竟然皆可表示為 $E(i)=\dfrac{|E(G)|}{d^+(v_i)}$。 根據定理 2 可知, 其主要的原因是外度數數列 $(d^+(v_1),d^+(v_2)$, $d^+(v_3),d^+(v_4),d^+(v_5))$ 為兩個轉移矩陣的特徵值為 1 的特徵向量。 陸、結語本文一開始透過期望值之間的關係式, 建立聯立方程組, 藉由分析係數之間的關係, 用比較通俗的方法獲得定理 1, 獲得一個刻畫期望值的充分條件。 然而轉移矩陣 $M$ 不僅具有選邊機率的資訊, 更蘊含著圖的有向邊結構, 運用 Perron-Frobenius Theorem 即可得知強連通圖的轉移矩陣 $M$ 必存在唯一的穩定狀態機率分布 $S\gt0$, 從中獲得各點的期望值, 支撐定理 1 的充分條件是具有存在性的, 因而獲得定理 2, 進一步理解定理 1 的充分條件其實亦為必要條件。 隨機漫步的研究與應用非常地廣泛, 希望本文的呈現方式有助於高中生閱讀理解, 可以成為學習隨機漫步的入門文章, 也可以作為高中課堂上的補充教材。 最後要感謝國立中山大學應用數學系林晉宏教授, 在線性代數的知識上提供我們許多實質上的建議與指導。 感謝審稿教授給予文章寫作上的提點, 方能讓此文章得以完整流暢地呈現。 參考資料本文作者曹爾秦投稿時為臺北市立第一女子高級中學高二學生, 楊宗穎任教於臺北市立第一女子高級中學 |
| 頁碼 | 120-130 |
2025年9月 49卷3期
強連通圖中封閉道路的邊數期望值

