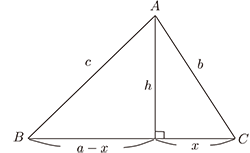
畢氏定理和相似形比例關係是處理幾何計量問題的兩大支柱。 從這兩大支柱又演化出正弦定律和餘弦定律, 應用起來更具威力。 然而眾所周知, 在利用正、餘弦定律解題的時候, 由於經常涉及三角恆等式, 因此代數的操作稍重。 本文嘗試只利用畢氏定理和相似形比例關係說明如何將三角形的高、中線、 分角線和外接圓半徑的長度一一表示成三角形邊長的函數, 藉以突顯這兩大支柱在幾何計量的核心地位。 為了方便解釋, 我們只談銳角三角形; 文末並附上以正、餘弦定律處理相同問題的簡要說明, 供讀者比較。

一. 求三角形高的長度

如圖一

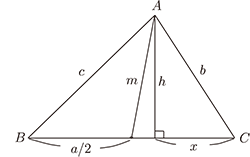
根據畢氏定理, 有 $b^2-x^2=c^2-(a-x)^2$, 因此解出 $x=a^2+b^2-c^2/2a$ $^{[ \hbox{註一}]}$。 又由 $h^2=b^2-x^2$, 得到 $$ h^2 = b^2 - \Big (\frac {a^2+b^2-c^2}{2a}\Big )^2 = \frac{1}{4a^2}(a+b+c)(a+b-c)(c+a-b)(b+c-a) ^{[ \hbox{註二}]} $$

二. 求三角形中線的長度

如圖二

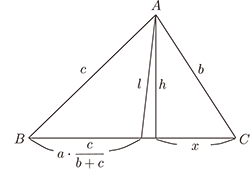
根據畢氏定理, \begin{eqnarray*} m^2 &=& h^2 + \Big (\frac{a}{2}-x \Big )^2 \\ &=& h^2 + x^2 - ax + \frac{a^2}{4} \\ &=& b^2 + \frac{a^2}{4} - a \cdot x \\ &=& b^2 + \frac{a^2}{4} - \frac{a^2+b^2-c^2}{2} \\ &=& \frac{2b^2+2c^2-a^2}{4} \end{eqnarray*}

三. 求三角形分角線的長度

如圖三 $^{[ \hbox{註三}]}$

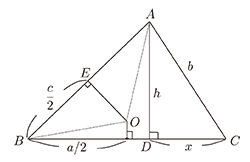
根據畢氏定理 \begin{eqnarray*} l^2 &=& h^2 + \Big (\frac{ab}{b+c}-x\Big )^2 \\ &=& h^2 + x^2 + \frac{a^2b^2}{(b+c)^2} - \frac{2ab}{b+c}x \\ &=& b^2 + \frac{a^2b^2}{(b+c)^2} - \frac{2ab}{b+c} \frac{a^2+b^2-c^2}{2a} \\ &=& b^2 + \frac{a^2b^2}{(b+c)^2} - \frac{b}{b+c}(a^2+b^2-c^2), \\ \end{eqnarray*} 化簡得 $$ l^2 = \frac{bc(b+c+a)(b+c-a)}{(b+c)^2} ~^{[ \hbox{註四}]} $$

四. 求外接圓半徑

如圖四

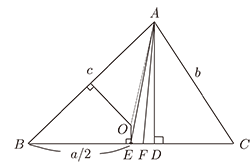
圖中, 點 $O$ 為外接圓圓心, $\overline {OB}=\overline {OA}=R$, 並且 $\angle BOE=\angle C$ $^{[ \hbox{註五}]}$, 所以 $\triangle BOE\sim \triangle ACD$。 由相似形比例關係: $$ R/b = \frac{c}{2} / h, \hbox { 得出 } R = bc / 2h \hbox{ 或者 } R = abc / 2ha $$ 亦即 $$ R = abc / 4\triangle ~^{[ \hbox{註六}]} $$

五. 利用正、餘弦定律解題

如圖五

圖中, $AD$ 是高, $AE$ 是中線, $AF$ 是分角線, $\overline{AO}=R$ 是外接圓半徑。

• (一) $\overline{AD}=b\sin C$, ${\overline{AD}}^2=b^2\sin^2 C=b^2(1-\cos^2 C)$ 再利用餘弦定律將 $\cos C$ 以 $a$, $b$, $c$ 的函數代入。
• (二) 根據餘弦定律, $$ {\overline {AE}}^2 = b^2 + \Big (\frac{a}{2}\Big )^2 - ab\cos C $$ 再將 $\cos C$ 以 $a$, $b$, $c$ 的函數代入。
• (三) 根據正弦定律 $$ c / \sin\angle{AFB} = \overline{BF} / \sin \Big (\frac{1}{2}A \Big ) $$ $$ b / \sin\angle{AFC} = \overline{CF} / \sin \Big (\frac{1}{2}A \Big ) $$ 所以 $$ c / b = \overline{BF} / ~\overline{CF} ~^{[ \hbox{註七}]} $$ 因此 $$ \overline{CF} = \frac{b}{b+c} \cdot a $$ 根據餘弦定律 $$ {\overline{AF}}^2 = b^2 + {\overline{CF}}^2 - 2b \overline{CF} \cos C $$ 再將 $\cos C$ 及 $\overline {CF}$ 以 $a$, $b$, $c$ 的函數代入。
• (四) 根據正弦定律 $$ c / \sin C = 2R $$ $$ abc / ab\sin C = 2R $$ 所以 $$ R = abc / 4\triangle $$

附註

• 註一: 此式相當於餘弦定律 $c^2=a^2+b^2-2ax$。
• 註二: 從此式立即導出海龍(Heron)公式: $$ {\triangle}^2=\frac {(a+b+c)(a+b-c)(c+a-b)(b+c-a)}{16} $$
• 註三: 此處用到角平分線把底邊分成二段, 其比值等於 $\displaystyle\frac{c}{b}$。
• 註四: 不難發現, 在 $a$ 邊上的中線或分角線的長度公式中, $b$, $c$ 以對稱的角色出現。
• 註五: $\angle {BOA}=2\angle {BOE}$ 是外接圓的一個圓心角, $\angle C$ 是相關的圓周角。
• 註六: $\triangle$ 代表三角形的面積, 請見註二。
• 註七: 同註三。

---本文作者為台大數學系退休教授---