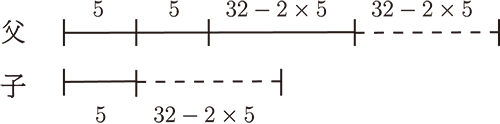| 發刊日期 |
2011年12月
|
|---|---|
| 標題 | 從代數到算術一獻給國中小的老師 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
我的老師項武義先生告訴我一件往事。他出生於抗戰之始, 童年在山裡躲日本人, 直到抗戰勝利, 才輾轉遷至上海。 12歲左右到上海一間初中寄讀。有一天在圖書館中發現一本講義, 題為《從代數到算術》。 大凡學算的程序都是從算術到代數, 因此這本反其道而行的小書立刻就引起他的注意。 當然武義師很快掌握了書中的要旨。原來, 這本書是說明如果一個題目可以用代數解題, 那麼, 如何還原成只用算術解題呢? 武義師告訴我當時書中所言, 只要將代數式逐步展開, 展開時保留數據的關係而不求出結果, 直到最後再將變數留在符號一邊, 然後觀察另一邊的式子, 就可以得出算術的解法。以下舉幾個例子來說明如何從代數到算術。 例一: 雞和兔共15頭, 雞腳加兔腳共38隻, 求雞、兔的頭數。 令 $X$ 為兔的頭數, 則有 \begin{eqnarray*} &&4X+2(15-X)=38\\ &&4X+2\times 15-2X=38\\ &&(4-2)X=38-2\times 15 \end{eqnarray*} 從上式可以解讀算術的方法。 $2\times 15$ 表示全部想成是雞, 那麼腳只有 $2\times 15=30$ 隻。 但是腳應有 38 隻, 所以少了 $38-2\times 15=8$ 隻。 這 8 隻是因為兔子而增加的, 每一頭兔子增加 $(4-2)$ 隻腳, 所以應該用 $38-2\times 15$ 去除以 $(4-2)$ 來得到兔子應有 4 頭。 例二: 今年父親 32 歲, 兒子 5 歲, 請問幾年後父親的年齡是兒子的 2 倍? 假設是 $X$ 年後, 則有 \begin{eqnarray*} &&2(5+X)=32+X\\ &&2\times 5+2X=32+X\\ &&2X-X=32-2\times 5 \end{eqnarray*} 所以算術的做法是用父親的年齡去扣掉兒子年齡的兩倍, 進一步可以用圖解釋:
例三: 全班同學出遊, 雇若干輛同型車子, 每一輛除駕駛外均有五個空位。 若每一輛均坐五人, 則總共留下 12 個空位, 若每一輛僅坐三人, 而用空位放行李, 則有 8 人無法上車, 請問車子幾輛, 人數幾人? 假設車子有 $C$ 輛, 全班有 $m$ 人, 則 \begin{eqnarray*} &&5C-12=m\\ &&3C+8=m\\ \hbox{所以}&~\qquad~&5C-12=3C+8\\ &&5C-3C=12+8\\ &&(5-3)C=12+8 \end{eqnarray*} 因此算術的解法是:第一種坐法比第二種坐法的容量多 $(12+8)$ 人, 這是因為每一輛車多坐 $(5-3)$ 人的關係, 所以用 $(12+8)\div (5-3)$ 得到車輛數是 10, 並求出人數是 38。 例四: 一個蘋果比一個橘子貴 4 元, 3 個蘋果和 5 個橘子等價, 問蘋果、橘子一個各幾元? 設橘子一個 $X$ 元, 則有 \begin{eqnarray*} &&3(X+4)=5X\\ &&3X+3\times 4=5X\\ &&3\times 4=5X-3X\\ &&3\times 4=(5-3)X \end{eqnarray*} 算術的解法是:若將 3 個蘋果換成橘子, 則 3 個蘋果相當於 3 個橘子多 $3\times 4$ 元, 因此 5 個橘子也相當於 3 個橘子多 $3\times 4$ 元, 所以一個橘子是 $3\times 4$ 除以 $(5-3)$, 即 6 元。 下例原出於中國古代《九章算術》卷7《盈不足》問題: 例五: 天平左邊有 12 個金塊, 天平右邊有 20 個銀塊, 左右等重。現在將金、銀交換一塊後, 左邊比右邊輕了 40 克, 問金塊、銀塊各重幾克? 設金塊一塊重 $g$ 克, 銀塊一塊重 $s$ 克, 則有 \begin{eqnarray} &~\qquad~&12g=20s\label{1}\\ &&11g+s=19s+g-40\label{2}\\ \eqref{1}-\eqref{2}&&(12g-11g)-s=(20s-19s)-g+40\nonumber\\ &&g-s+(12g-11g)-(20s-19s)=40\nonumber\\ \hbox{可得} &&g-s=20\nonumber \end{eqnarray} 因此算術的解法要從金塊、銀塊的重量差開始思考。 已知金比銀重, 並且天平左右兩邊原來是等重的, 因為金、銀交換了一塊而使兩邊的重量差了 40 克, 所以一塊金比一塊銀要重20克。 也就是說, 移一個金塊到右邊去, 比原來的銀塊重了20克, 而移一個銀塊到左邊來, 比原來的金塊輕了20克, 一重一輕才會左右差了40克。 明白了此點, 剩下的就是在 $g-s=20$ 之下怎麼解 $12g=20s$, 這又回到例四的方法, 可以解出 $s=30$, $g=50$。 上面這個例子看起來比較困難, 特別是 \eqref{1}-\eqref{2} 的代數操作。我們提供另一個更具啟發的解法。 設想自己是個沒學過代數的老夫, 在沒有時間壓力的情況下, 自我挑戰要幫孫子解答這道問題。於是有了以下的想法: 既然調換金、銀各一塊就減重40克, 調換二塊便減重80克, $\cdots$, 所以當調換至左邊是6金、6銀塊, 而右邊是6金、14銀塊, 便減重240克, 這相當於是14銀塊與6銀塊的差重, 因此, 銀塊一個重30克。同樣的道理, 當調換至左邊是10銀、2金塊, 而右邊是10銀、10金塊, 所減重量 400克便相當於是10金塊與2金塊之差重, 因此, 金塊一個重50克。 最後, 我們想提醒教學現場的老師, 用算術或圖解解算術應用題仍是較有趣味、較有深度, 且對學習思考者也比較有價值的。 若只是為求快圖便, 私下教孩子用代數法取代算術, 而剝奪了探索的機會, 這是短利之途, 對孩子不公平, 也將傷害到孩子。 不論在哪一階段, 學習之中, 直覺又自然的方法便是好方法, 也是最值得鼓勵的方法。 感謝審稿人對本文提出的寶貴意見與提醒。 ---本文作者為台大數學系退休教授--- |
2011年12月 35卷4期
從代數到算術一獻給國中小的老師