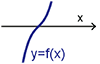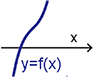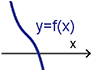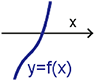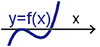剛從國中升上高中的學生, 有部分同學國中數學成績還算不錯, 但接觸到高中數學後, 成績一落千丈, 慘不忍睹。 或許是因為高中數學所學習的內容更深更廣, 學生理解的能力不足, 但本人更相信學生的求學方式出了問題, 學生們在國中階段的學習經驗裡, 數學就是背公式, 寫練習題, 考試不會考的就不去理會, 慢慢的學生就失去思考的能力, 只是把數學當背科, 頂多用大量的練習得到較好的分數, 違背了學習的意義。

本篇主要討論的內容為三次實係數多項式函數, 我們知道, 無論是95或是99課綱的高中數學教材設計, 微分到高三才會學習到, 學習後用來分析實係數多項式函數圖形當然不是問題, 但對於高一的學生, 我們不希望草草跟學生說: 「圖形的性質高三才會教$\cdots$」之類的話, 所以我們就用高一所學的知識來討論, 在討論的過程中, 教導學生如何循序漸進的看待問題, 並且以現有的知識來解決問題。

學生在國中時, 已經學過二次實係數多項式函數 $y=ax^2+bx+c$ 的圖形性質, 部分學生也會很熟練的運用配方法將函數寫成 $y=a\Big(x+\dfrac{b}{2a}\Big)^2+\dfrac{4ac-b^2}{4a}$ 並且知道當 $x=-\dfrac{b}{2a}$ 時, $y$ 有最大值或是最小值 $\dfrac{4ac-b^2}{4a}$, 並且知道圖形的對稱軸為直線 $x=-\dfrac{b}{2a}$, 參考圖(一)。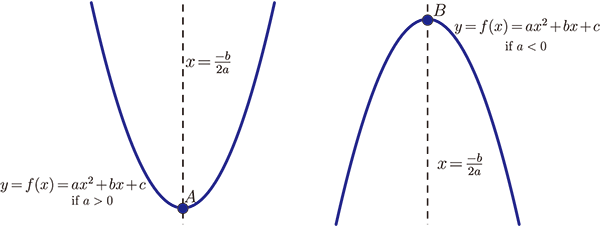

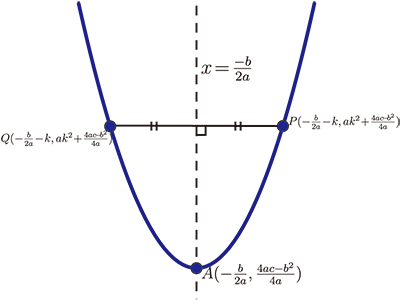
那何謂圖形的對稱軸, 簡單來說, 將此二次多項式函數圖形 $y=ax^2+bx+c$ 畫在白紙上, 若以直線 $x=-\dfrac{b}{2a}$ 當成摺線, 圖形會完全重疊。 若是以數學的方式說明, 在圖形上取任一點 $P$, 對直線 $x=-\dfrac{b}{2a}$ 做對稱點 $Q$, 而 $Q$ 點也在圖形上。如圖(二), 假設 $a\gt 0$。

有了對稱的概念, 接下來就可以討論三次實係數多項式函數 $y=ax^3+bx^2+cx+d$ 的圖形, 第一個問題是三次實係數多項式函數圖形有沒有對稱軸? 我們希望學生懂得去思考問題, 在思考問題之前一定要提出問題, 但學生往往只會照著課本所敘述的內容去做記憶的動作, 不去做任何質疑, 不去談 "為什麼"。 為何我會希望高中生去討論三次實係數多項式函數圖形有沒有對稱軸, 原因很簡單, 因為二次實係數多項式函數圖形有對稱軸, 那就應該拿來討論。

若是要討論一般形式的三次函數 $y=ax^3+bx^2+cx+d$ 可能對高一的學生比較吃力, 我們會鼓勵學生先討論最簡單的三次函數 $y=x^3$, 如果三次函數 $y=x^3$ 存在對稱軸 $L$, 代表在 $y=x^3$ 上取任意點 $P(t,t^3)$, 作 $P$ 點對 $L$ 的對稱點 $Q$, $Q$ 點也會在 $L$ 上。

首先, 我們先觀察 $y=x^3$, 大部分的學生觀察的結果, 都認為且肯定圖形沒有對稱軸, 但我問他們「為什麼沒有?」很多人都回答：「用看的就知道！」； 少部分的學生認為應該有, 只是還沒發現而已。事實上, 身為老師的我, 我反而比較欣賞那少部分的學生(雖然我早就知道此圖形沒有對稱軸), 因為他們做到了一件事 --- 『質疑』。

我們在圖形上取最簡單的一點 $A(1,1)$, 很顯然, 圖形若是有對稱軸, 大多數的學生們根據經驗, 認為對稱軸一定會過原點, 經過簡單的運算可以算出對稱軸應為直線 , $y=-x$ 且 $B(-1,-1)$ 為 $A$ 點對直線 $y=-x$ 的對稱點, $B$ 點也在 $y=x^3$ 的圖形上。所以我們可以說, 如果 $y=x^3$ 有過原點的對稱軸, 那一定是直線 $y=-x$。 但顯然的, 對稱軸並不是直線 $y=-x$, 因為我們可以在圖形上找一點 $C(\frac 43,\frac{64}{27})$, $C$ 點對直線 $y=-x$ 的對稱點 $C(-\frac{64}{27},-\frac 43)$並不在圖形 $y=x^3$ 上。如圖(三)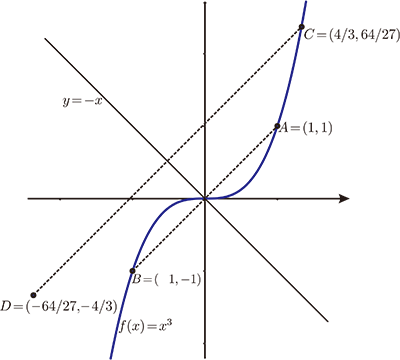

接下來可以請學生驗證, 任何一條不過原點的直線也不會是 $y=x^3$ 的對稱軸。 那我們就可以說 $y=x^3$ 沒有對稱軸, 並且延伸問題到一般類型的三次實係數多項式函數圖形, 也是沒有對稱軸的, 在此就不多加討論。

不過, 關於圖形 $y=x^3$ 的問題並沒有結束, 眼尖的學生們會發現, 原點在圖形 $y=x^3$ 裡應該是個關鍵的角色。

學生們發現, 函數圖形 $y=x^3$ 上的任一點 $P(t,t^3)$, $t\not=0$, 將 $P$ 點的 $x,y$ 座標同時加上負號得到 $Q(-t,-t^3)$, 而 $Q$ 點也在圖形 $y=x^3$ 上, 原點 $O$ 為線段 $\overline{PQ}$ 中點。如圖(四)。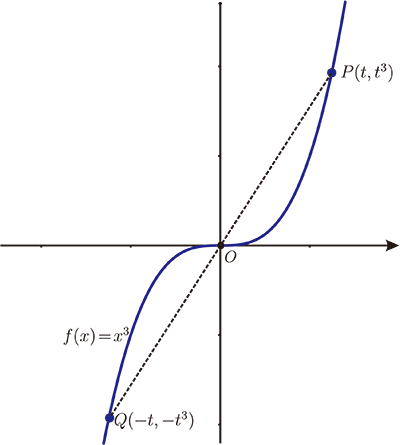

也就是說圖形 $y=x^3$ 上的任一點 $P$, 對於 $O$ 對稱點 $Q$ 也在圖形上, 那我們稱原點 $O$ 為圖形 $y=x^3$ 的對稱中心。

那對於一般形式的三次實係數多項式 $y=f(x)=ax^3+bx^2+cx+d$ 是否有對稱中心? 若 $O(t,f(t))$ 為其對稱中心, 則 $P(t+k,f(t+k))$ 與 $Q(t-k,f(t-k))$ 的中點為 $O$ 點, 如圖(五), 可以推導到 $f(t+k)+f(t-k)=2f(t)$, 其中 $k$ 為任意實數。

$f(t+k)+f(t-k)=2f(t)$
 $\Rightarrow (a(t+k)^3+b(t+k)^2+c(t+k)+d)+(a(t-k)^3+b(t-k)^2+c(t-k)+d)$
   $=2(at^3+bt^2+ct+d)$
 $\Rightarrow 2(at^3+bt^2+ct+d)+2(3atk^2+bk^2)=2(at^3+bt^2+ct+d)$
 $\Rightarrow 3atk^2+bk^2=0$

對任意實數 $k$ 皆成立, 可得 $t=\dfrac{-b}{3a}$。

那我們可以得到三次實係數多項式 $y=f(x)=ax^3+bx^2+cx+d$ 的對稱中心為 $O\Big(\frac{-b}{3a},f(\frac{-b}{3a})\Big)$。 接下來, 我們想將圖形的對稱中心平移到原點, 方便接下來的討論, 先將 $f(x)$ 表示成 $a'(x+\frac{b}{3a})^3+b'(x+\frac{b}{3a})^2+c'(x+\frac{b}{3a})+d'$, 可利用綜合除法：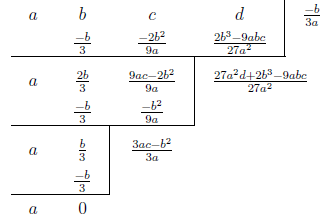

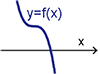
所以 $f(x)=a(x+\dfrac{b}{3a})^3+\dfrac{3ac-b^2}{3a}(x+\dfrac{b}{3a})+\dfrac{27a^2d+2b^3-9abc}{27a^2}$。

利用伸縮及平移(對稱中心為原點)方式得到新的函數為 $g(x)=x^3+(\dfrac{3ac-b^2}{3a^2})x$,

那麼 $y=g(x)$ 的圖形便是一個以原點為對稱中心且領導係數為 1 的三次實係數多項式函數圖形。 值得注意的是函數 $y=g(x)$ 的 $x^2$ 係數為 0, 也是因為如此更方便我們討論接下來的問題。

為了方便起見, 我們令 $p=\dfrac{3ac-b^2}{3a^2}$, 則 $g(x)=x^3+px$。

狀況一： $p\gt 0$ (即 $3ac-b^2\gt 0$), $g(x)=x(x^2+p)$, $g(x)=0$ 有一實根兩虛根, $f(x)\!=\!k$ 有一實根兩虛根 ($k$ 為任意實數), ($f(x)\!=\!0$ 有一實根兩虛根), 參考圖(六)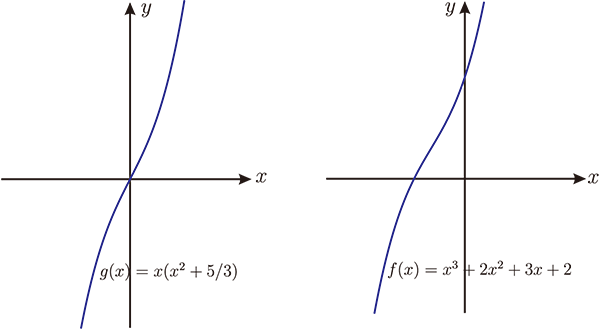

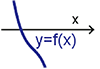
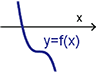
狀況二： $p=0$ (即 $3ac-b^2=0$), $g(x)=x^3$, $g(x)=0$ 有三實根(三重根), 經過推導可得 $f(x)=a\Big(x+\dfrac b{3a}\Big)^3+f\Big(\dfrac{-b}{3a}\Big)$ $$f(x)=0\left\{\begin{array}{lcl} \hbox{有三實根(三重根)}&~~&\hbox{if}\ (\frac{-b}{3a})=0\\[5pt] \hbox{有一實根兩虛根}&~~&\hbox{if}\ f(\frac{-b}{3a})\not=0 \end{array}\right.$$ 參考圖(七)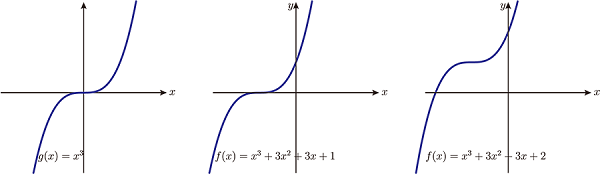

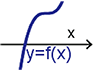
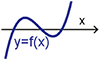
狀況三： $p\lt 0$ (即 $3ac-b^2\lt 0$) 令 $p=-d^2$ 且 $d\gt 0$ $g(x)=x(x^2+p)=x(x-d^2)=x(x-d)(x+d)$

代表 $y=g(x)$ 與 $x$ 軸交於 (0,0), $(d,0)$, $(-d,0)$ 相異三點。如圖(八)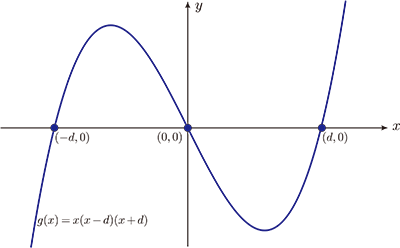

圖形很明顯, 會有一個波峰及一個波谷。接下來我們想求此三次函數的極大值與極小值。

• (i) 若 $0\lt k\lt d$, 我們有 $2k^2\gt 0$, $(d-k)(k+d)\gt 0$, 利用算幾不等式可得 $$\frac{2k^2+(d-k)(k+d)+(d-k)(k+d)}3=\frac{2d^2}3\ge {\root 3 \of {2(g(k))^2}}$$ $-\dfrac{2\sqrt 3d^3}{9}\le g(k)\lt 0$ 且算幾不等試的"等號"成立在 $k=\dfrac{\sqrt 3 d}3$ 時 所以, 當 $x=\dfrac{\sqrt 3 d}3$, $y=g(x)$ 有極小值 $\dfrac{-2\sqrt 3 d^3} 9$ (比較值得注意的是：算幾不等式在高一的課程裡僅介紹在 $a\gt 0$, $b\gt 0$ 的情況下, $\dfrac{a+b}2\ge \sqrt{ab}$, 在 $a=b$ 時等號才會成立。高中老師必須推廣到 $a\gt 0$, $b\gt 0$, $c\gt 0$ 的情況下, $\dfrac{a+b+c}3\ge \root 3 \of {abc}$, 在 $a=b=c$ 時等號才會成立。)
• (ii) 若 $-d\lt k\lt 0$, 同理可得 $0\lt g(k)\le\dfrac{2\sqrt 3 d^3}9$ 所以, 當 $x=\dfrac{-\sqrt 3 d}3$, $y=g(x)$ 有極大值 $\dfrac{2\sqrt 3 d^3}9$

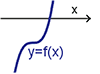
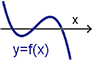
接下來, 我們想將問題還原成 $y=f(x)$ 與 $x$ 軸的相交情形, 以及其極值。

從 $p=\dfrac{}{}=-d^2$ 可得 $\dfrac{\sqrt 3d}{3}=\sqrt{\dfrac{b^2-3ac}{9a^2}}=\left\{\begin{array}{lcl} \dfrac{\sqrt{b^2-3ac}}{3a}&~~&\hbox{if}\ a\gt 0\\[5pt] \dfrac{-\sqrt{b^2-3ac}}{3a}&~~&\hbox{if}\ a\lt 0 \end{array}\right.,$

所以 $y=f(x)$ 的極值為 $f\Big(\dfrac{-b}{3a}\pm \dfrac{\sqrt{b^2-3ac}}{3a}\Big)$

寫到這邊, 高一的學生總有那麼幾個認為 $\dfrac{-b}{3a}\pm \dfrac{\sqrt{b^2-3ac}}{3a}$ 怎麼和國中一元二次方程 式 $ax^2+bx+c=0$ 的公式解很像, 於是我們做了以下的推導： \begin{eqnarray*} x=\frac{-b}{3a}\pm\dfrac{\sqrt{b^2-3ac}}{3a}&\Rightarrow& 3ax+b=\pm\sqrt{b^2-3ac}\Rightarrow (2ax+b)^2=b^2-3ac\\ &\Rightarrow& 9a^2x^2+6abx+3ac=0 \Rightarrow 3ax^2+2bx+c=0 \end{eqnarray*} 所以當 $x$ 為方程式 $3ax^2+2bx+c=0$ 的根時, $f(x)$ 會產生極值。 (而事實上, $3ax^2+2bx+c=f'(x)$)

接下來我們可以整理出一元三次方程式 $f(x)=0$ 的根的性質, 令 $$x_1=\frac{-b+\sqrt{b^2-3ac}}{3a},\qquad x_2=\frac{-b-\sqrt{b^2-3ac}}{3a}$$ $$f(x)=0\left\{\begin{array}{lcl} \hbox{有三相異實根}&~~&\hbox{if}\ f(x_1)f(x_2)\lt 0\\[5pt] \hbox{有三實根(有二重根)}&~~&\hbox{if}\ f(x_1)f(x_2)=0\\[5pt] \hbox{有一實根兩虛根}&~~&\hbox{if}\ f(x_1)f(x_2)\gt 0 \end{array}\right.$$ 參考圖(九)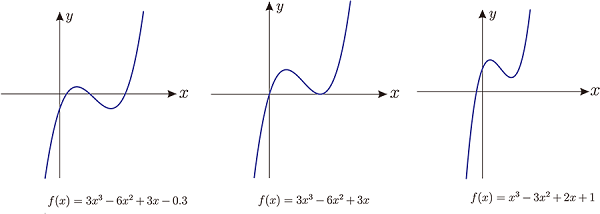

本篇文章著重在如何不用到微分工具跟高一學生討論三次實係數多項式函數的性質, 但也因為不使用微分工具, 本人才疏學淺, 尚還無法討論透徹, 日後會再跟工作夥伴或是數學教育先進討論, 期盼能在教學過程中, 給高中學生探討問題的方法。

關於三次多項式的圖形的相關文章在網路上亦可搜尋, 初次寫作, 本文論證應有不夠嚴謹之處, 敬請各界指證。

以下為函數 $y=f(x)=ax^3+bx^2+cx+d$ 整理結果：

$y=f(x)=ax^3+bx^2+cx+d$, $p=3ac-b^2$ 若 $p\lt 0$ 令 $x_1=\frac{-b+\sqrt{b^2-3ac}}{3a}, x_2=\frac{-b-\sqrt{b^2-3ac}}{3a}$
$p$ 值	$y=f(x)$ 圖形特徵	$f(x)=0$ 的解	圖例 $y=f(x)$ 與 $x$ 軸交點數
			$a\gt 0$	$a\lt 0$
$p\gt 0$	沒有波峰 及波谷	一個實根 兩個虛根
$p=0$	沒有波峰 及波谷	若 $f(\frac{-b}{3a})=0$ 三重實根
		若 $f(\frac{-b}{3a})\not=0$ 有一實根 兩虛根
$p\lt 0$	有一個波峰 及一個波谷	若 $f(x_1)f(x_2)\lt 0$ 有三相異重實根
		若 $f(x_1)f(x_2)=0$ 有三實根 (有二重根)
		若 $f(x_1)f(x_2)\gt 0$ 有一實根 兩虛根

參考文獻

---本文作者現職為國立竹東高中數學科教師---