前言：2014年春季, 洪萬生教授推薦我到李國鼎基金會為高中生講授「非歐幾何」。
為了讓高中生理解數學史上這一頁輝煌的成就, 我盡量以簡馭繁, 寫就這一個講稿。
講授過程中, 我的學生周哲偉自願擔任助教, 並協助打字及校對, 出了許多力氣, 在此致謝。
本課程共分五節。第一節回顧歐氏幾何的公設, 特別是平行公設; 第二節暫不考慮平行公設來指出非歐幾何的必要性; 第三節討論對圓的鏡射, 作為非歐運動的基石;
第四節定出在非歐運動之下的不變距離; 第五節是一個簡要的結論。
希望這份講稿能夠幫助願意在高中或大學開非歐幾何選修課的老師。
第一節 : 回顧
眾所周知, 歐幾里得《幾何原本》是以五條公設 (postulate) 作為演繹後續幾何命題的基礎。
這五條公設分別是 :
(一) 兩點決定(唯一的)一條直線。
(二) 線段可以延長。
(三) 以任意點為圓心, 任意長為半徑, 可以作一圓。
(四) 凡直角皆相等。
(五) 平行公設 : 過線外一點, 恰有唯一的一條平行線。
歷史上對這五條公設的檢討大致有兩個面向 :
第一是以為第五公設可以從前面四個公設推論而出, 但是這個希望被 19 世紀的數學家 Bolyai 和 Lobachevsky 粉碎, 他們發現了一種新的幾何,
滿足公設(一)到(四), 但是過線外一點, 可以有多於一條的平行線。
Bolyai 和 Lobachevsky 所發現的「新」幾何正是所謂的非歐幾何。
第二是認為這些公設不夠基本, 需要進一步把許多概念講清楚。
例如在第一章命題 4
證明 $S.A.S$ 全等判定時, 已知三角形 $ABC$ 和三角形 $DEF$ 之間有 $\overline{AB}=\overline{DE}$、
$\angle A=\angle D$、 $\overline{AC}=\overline{DF}$, 如圖一 :
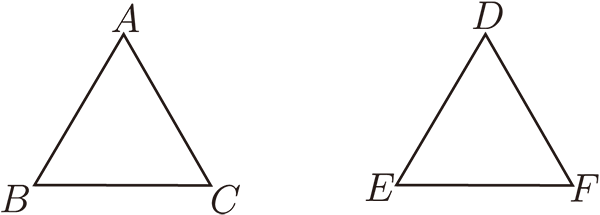
歐幾里得的證法是先平移三角形 $ABC$ 使 $A$ 和 $D$ 重合, 之後再利用對 $A$ 點的旋轉, 轉動 $\overline{AB}$ 與 $\overline{DE}$ 重合。
$A$ 與 $D$、 $B$ 與 $E$ 以及 $\overline{AB}$ 與 $\overline{DE}$ 重合之後, 如圖一的情形,
利用 $\angle A=\angle D$ 證明 $\overline{AC}$ 與 $\overline{DF}$ 重合。
既然 $A$ 與 $D$、 $B$ 與 $E$、 $C$ 與 $F$ 均已重合, 即可由公設一的唯一性證明兩三角形已完全重合, 是為全等。
不過, 歐幾里得忽略了另外一種可能的配置, 如圖二 :
在此圖的情形, 當 $\overline{AB}$ 與 $\overline{DE}$ 重合之後, $DF$ 和 $AC$ 分據 $\overline{AB}(\overline{DE})$ 之兩側,
因此下一步必須將圖形對 $\overline{AB}$ 鏡射, 才能將 $\overline{AC}$ 重合到 $\overline{DF}$。
在上面這段證明中, 用到的基本概念包括點、 線、 線段、 三角形、 角度、 線段之等長, 角與角之相等、 平移、 旋轉、 鏡射, 乃至兩點決定唯一的直線或線段,
似乎過於依賴幾何直覺, 因而引起「公設派」的質疑。
誠然, 一個完整的公設系統應該從無定義名詞出發, 以公設的方式來逐步建立它們之間的關係。
Hilbert 於是在 1899 年提出 13 條公設來重新鋪陳暫時去掉第五公設的平面幾何。
他首先假設有兩個集合, 一個是點集, 一個是由點集的某些子集所構成的線集。
然後用三條從屬(Incidence)公設來說明點集與線集之間的關係。
(從屬1) : 對點集之任二元素 $A$、$B$ 恆有唯一的線集之元素 $l$ 包含 $A$、$B$。
(從屬2) : 線集之任一 $l$, 至少包含點集之二元素。
(從屬3) : 存在三個點集之元素 $A$、$B$、$C$, 任一 $l$ 均不能同時包含 $A$、 $B$ 和 $C$。
明眼人當然立刻看出上面三條公設其實是照顧下面三個直觀的現象 :
(1) 平面上至少有三個不共線的點(否則何必談平面呢？)。 ..... (從屬3)
(2) 任一直線均由點構成, 並且至少含有兩個不同的點
(否則直線也不成其為直線了)。 ..... (從屬2)
(3) 兩點決定唯一的直線(這本是歐幾里得的公設之一)。 ..... (從屬1)
簡言之, Hilbert 的《
幾何學之基礎》成功地「再造」歐氏
幾何和非歐
幾何的基礎, 但是, 如果要通過 Hilbert 來了解歐氏
幾何或非歐
幾何, 可想而知一定是流於瑣碎,
並且疏離
幾何直觀, 工本未免太大。
這裡應該先提一件事情, 亦即在笛卡兒提出坐標幾何之後, 我們在高(國)中所學的平面坐標幾何正是歐氏幾何的一個模型, 當然滿足 Hilbert 13 條公設。
例如在坐標平面中點集指的是所有的實數對 $\{(x,y) \mid x\hbox{、} y \hbox{ 均為實數}\}$, 而線集就是一組特別的子集, 由下列 (1)、 (2) 兩類組成。
(1) $y=mx+b$ (指滿足 $y=mx+b$ 的所有實數對, 其中 $m$、$b$ 是給定實數)
(2) $x=c$ (指滿足 $x$ 坐標為 $c$ 的所有實數對, 其中 $c$ 是給定實數)
不難驗證這樣的點集和線集滿足 Hilbert 三條從屬公設 (以及後續另十條)
至於非歐幾何, 也有類似具體的模型可以理解為什麼平行公設與前四個公設之間其實是獨立的關係。
這個模型是由數學和物理學家 H. Poincare 所提出, 稱為 Poincare Upper Half-Plane (上半平面)
我們將在下一章仔細討論這個非歐模型。
第二節 : 暫不考慮平行公設
本節要說明在忘掉第五公設 (平行公設) 之下, 但保留 $S.A.S$ 判定可以得到三角形三內角和 $\le 180^\circ$。
定理1 :
三角形外角大於內對角。
證明 :
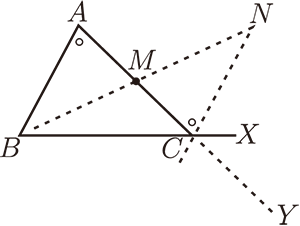取 $\overline{AC}$ 中點 $M$, 連 $\overline{BM}$ 延長到 $N$, 使 $\overline{BM}=\overline{MN}$; 連 $\overline{NC}$
(注意 $\overleftrightarrow{NC}$ 非 $\overleftrightarrow{BC}$, 因為如果是的話, $B$ 和 $C$ 就會決定兩條直線)
因此 $\angle ACN\lt \angle ACX$, 根據 $S.A.S$ $\angle ACN=\angle A$, 因此 $\angle ACX\gt \angle A$。
同理 $\angle BCY(=\angle ACX)\gt \angle B$, 因此, $\angle A,\angle B$ 均小於 $\angle ACX$。
定理2 :
三角形任二角之和均小於 $180^\circ$。
證明 :
上圖, $\angle A+\angle C\lt \angle ACX+\angle C=180^\circ$。
定理3 : 三角形三內角和 $\le 180^\circ$。
證明 :
如圖,
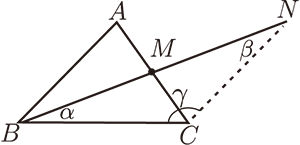設 $\angle B$ 為最小角, 仿定理 1 得 $\alpha+\beta+\gamma=\angle A+\angle B+\angle C$, $\alpha+\beta=\angle B$,
取 $\alpha$, $\beta$ 中較小者 $(\le \dfrac 12\angle B )$
再重覆作一次, 得 $\alpha'+\beta'+\gamma'$ 不變, 但最小者 $\le \dfrac 12\alpha,\dfrac 12\beta$,
如此繼續,
如果 $\angle A+\angle B+\angle C\gt 180^\circ$,
設為 $\angle A+\angle B+\angle C=180^\circ+\delta$ 則當取到三角 $\alpha'',\beta'',\gamma''$ 中有一小於 $\delta$ 時,
其餘兩角之和便會大於 $180^\circ$, 違背定理2。推廣 : 任意 $n$ 凸多邊形內角和 $\le(n-2)\times 180^\circ$。
定理4 :
如果有一個三角形三內角和 $=180^\circ$, 則所有三角形三內角和均 $=180^\circ$。
(一) 如果有一個三角形三內角和 $=180^\circ$, 則必存在一直角 $\triangle$, 三內角和 $=180^\circ$。
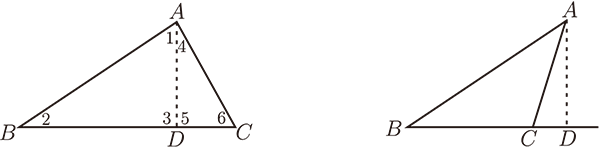因為取 $\angle C$, $\angle B$ 均小於 $90^\circ$ (因為至多只有一個角 $\ge 90^\circ$) 則從 $A$ 向 $BC$ 作高,
垂足必在 $BC$ 之間。
已知 : $(1+2+3)+(4+5+6)=360^\circ$, 但 $1+2+3\le 180^\circ$, $4+5+6\le 180^\circ$,
所以 $1+2+3=180^\circ$, $4+5+6=180^\circ$, 即得二直角 $\triangle$, 三內角和 $=180^\circ$。
(二)
設有一個直角三角形三內角和 $= 180^\circ$, 則可組裝一個任意大的長方形
(此長方形的四個角均為直角並且對邊相等)。
(三) 任予一直角三角形 123, 將之置於大長方形之一隅,
則 $1+2+3+4+8+5+6+7$
$=4\times 90^\circ+180^\circ\times 2=720^\circ$
但 $4+8+5+6+7\le 540^\circ$,
$1+2+3\le 180^\circ\ \Rightarrow\ 1+2+3=180^\circ$
(四) 已證任一直角三角形三內角和 $=180^\circ$, 當可證得任一三角形三內角和亦為 $180^\circ$。
結論 :
在不假設平行公設之下, 三角形三內角和 $\le 180^\circ$。
若是其中有一個三角形內角和等於 $180^\circ$, 則所有三角形的內角和均等於 $180^\circ$, 此即歐氏幾何的情形。
至於是否有一個系統, 其所有三角形之內角和均小於 $180^\circ$？
答案是肯定的, 這就是我們在下文要介紹的 Poincare upper half plane (上半平面), 亦即非歐幾何的模型。
在進入上半平面的討論之前, 我們略回顧歐氏幾何中基本的要素。
第一, 兩點之間有距離的概念, 此即兩點所決定線段的長度。
第二, 有三種基本的保距或保長的運動 :
(1) (對直線的) 鏡射;
(2) 繞一點的轉動;
(3) (沿某一方向的) 平移。
我們提醒讀者, 在這三種運動中, 以鏡射最為基本。
因為若是對兩相交直線 $L$ 和 $M$ 連續作鏡射, 便會得到對 $L\cap M$ 的旋轉, 而若對 $J,K$ 兩平行線連續作鏡射便會得到平移。
上述這三種(保距的)運動以及它們之間的接力運動構成一個群,
稱為歐幾里得運動 (Euclidean motions)。
正是因為有這些 (保距的) 運動, 我們才能定義圖形的全等。
同理, 在上半平面的模型裏, 也要有足夠多 (保距的) 運動。
而這些運動中最基本的就是對鉛垂線和對圓心在 $X$ 軸上的圓的鏡射。
我們將在下一節中討論對圓鏡射的定義和基本性質, 然後再在上半平面定一個在鏡射之下是保距的距離概念。
第三節 : 有關圓鏡射(Inversion)的基本定理
設平面上有一半徑為 $r$、 圓心在 $C$ 的圓, 對圓 $C$ 的鏡射 $I_{C,r}$ 或 $I_C$ 定義為 :
$I_C(P)=Q\ \Leftrightarrow$ $C$、 $P$、 $Q$ 三點共線, $P$、$Q$ 在 $C$ 之同側, 並且
$\overline{CP}\cdot\overline{CQ} =r^2$
。
注意 $I_C(C)$ 無定義, 但也可以想成是 $I_C(C)=$無窮遠點, 或 $I_C$(無窮遠點)$=C$。
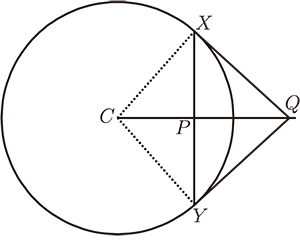
$C$、$P$、$Q$ 三點的關係如圖 :
$\overleftrightarrow{QX}$、$\overleftrightarrow{QY}$ 為切線, $X$、$Y$ 為切點
$\triangle CPX \sim \triangle CXQ\ \Rightarrow\ \dfrac{\overline{CP}}{\overline{CX}}
=\dfrac{\overline{CX}}{\overline{CQ}}$
$\therefore$ ${\overline{CP}}\cdot {\overline{CQ}}={\overline{CX}}^2=r^2$
定理 1 :
$I_C(P)=Q \Leftrightarrow I_C(Q)=P$
且圓 $C$ 上的任一點 $X$ 均有 $I_C(X)=X$ 亦即
$I_{C,r}\circ I_{C,r}=$Identity, 且若 $I_C(Y)=Y$ $\Leftrightarrow$ $Y\in $
圓 $C$。
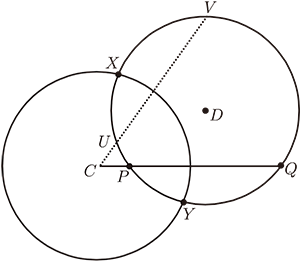
定理 2 :
如果 $I_C(P)=Q$ ($P\not=Q$), 且圓 $D$ 過 $P$、$Q$ 兩點, 則圓 $C$ 和圓 $D$ 正交
(從兩圓交點作任一圓之切線, 必過另一圓之圓心),
並且從 $C$ 發出的直線與圓 $D$ 相交的兩點 $U$、$V$ 互為鏡射。
證明 :
根據圓冪定理
$\because$ ${\overline{CP}}\cdot {\overline{CQ}}={\overline{CX}}^2$,
$\therefore$ $\overleftrightarrow {CX}$ 是圓 $D$ 的切線, 因此
$\overleftrightarrow {CX}$ 和 $\overleftrightarrow {DX}$ 垂直。
至於 $U$、$V$ 互為鏡射, 亦由圓冪定理。
定理 3 :
若圓 $C$ 與圓 $D$ 正交, 則 $I_C$ (圓 $D$)$=$圓 $D$ (圓冪定理),
反之, 若 $I_C$ (圓 $D$)$=$圓 $D$, 則圓 $D$ 不過 $C$, $\because$ $I_C(C)=$無窮遠點
,
如圖
連 $\overleftrightarrow {CD}$ 交圓 $D$ 於 $P$、$Q$, 顯然 $I_C(P)=Q$,
再由定理2, 圓 $D$ 含 $\overline{PQ}$ 為一弦(直徑), 所以圓 $D$ 與圓 $C$ 正交。
在以下的討論中, 我們把直線想成有無窮遠點 $\infty$, $I_C(\infty )=C$。
事實上對直線上的點 $P$ 而言,
$\lim\limits_{P\rightarrow\infty} I_C (P)$ 一定是 $C$ (留做習題)。
定理 4 :
(一) 若直線 $l$ 過 $C$, 則 $I_C(l)=l$ (簡單)。
(二) 若直線 $l$ 不過 $C$, 則 $I_C(l)$ 是一個過 $C$ 的圓 $D$, 且圓心 $D$ 與 $C$ 的連線垂直 $l$
。
證明 :
證明 (二)
(i) 若 $l$ 在圓外
過 $C$ 作 $l$ 的垂線, 垂足為 $P$, $I_C(P)=Q$,
則 $I_C(l)=$以 $\overline{CQ}$ 為直徑的圓。
(留作習題, 利用相似直角三角形)
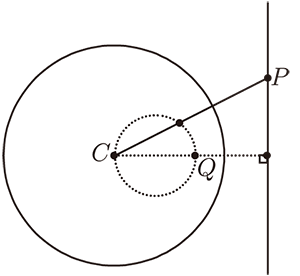
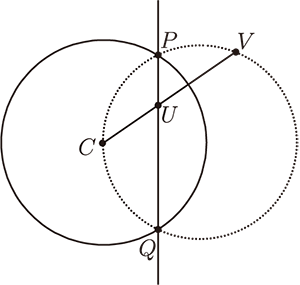
(ii) 若 $l$ 交圓 $C$ 於 $P$、 $Q$ 兩點
由於 $I_C(P)=P$、 $I_C(Q)=Q$,
則 $I_C(l)=$ 過 $C$、 $P$、 $Q$ 三點的圓。
(留作習題, 利用 $\widehat{CP}=\widehat {CQ}$, $\triangle CPU\sim \triangle CVP)$
(iii) 若 $l$ 切圓 $C$, 證明與 $l$ 在圓 $C$ 之外類似。
注意到 (1) 若 $l$ 在圓 $C$ 外, 則 $I_C(l)$ 在圓 $C$ 的內部, 與圓 $C$ 分離。
(2) 若 $l$ 切圓 $C$, 則 $I_C(l)$ 內切於圓 $C$。
(3) 若 $l$ 交圓 $C$ 於兩點, 則 $I_C(l)$ 與圓 $C$ 交同樣的兩點, 並且以 $C$ 為極限點。
由此可得逆定理。
定理 5 :
若圓 $D$ 過 $C$, 則 $I_C($圓D$)=$ 一條直線。
證明 :
分別討論圓 $D$ 在圓 $C$ 內部且分離, 圓 $D$ 在圓 $C$ 內部但內切, 圓 $D$ 與圓 $C$ 交於兩點。
(留作習題, 利用 $I_{C,r}\circ I_{C,r}=$Identity)
定理 6 :
若圓 $D$ 不過 $C$, 則 $I_C$(圓$D)=$ 一不過 $C$ 之圓。
證明 :
不妨設 $C$ 為原點, 半徑為 1, ${\bf D}$ 為一向量, ${\bf X}=(x,y)$
圓 $D$ 方程式為 $({\bf X}-{\bf D})\cdot ({\bf X}-{\bf D})=r^2$, 其中 $r$ 為圓 $D$ 之半徑, 圓 $D$ 不過 $C$, $r^2\not=|{\bf D}|^2$
而有
\begin{equation}
{\bf X}\cdot {\bf X}-2{\bf D}\cdot {\bf X}=r^2-|{\bf D}|^2
\label{1}
\end{equation}
如圖
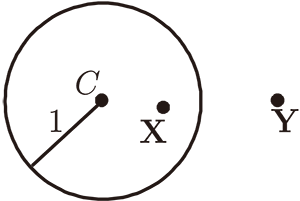若 $I_C({\bf X})={\bf Y}$, 則 ${\bf Y}=\dfrac{{\bf X}}{|{\bf X}|^2}$ ($\because$ ${\bf Y}$ 與 ${\bf X}$ 同方向,
$\Big|\dfrac{{\bf X}}{|{\bf X}|^2}\Big|\cdot |{\bf X}|=1^2=1$)
注意到 ${\bf Y}\cdot {\bf Y}=\dfrac{{\bf X}}{|{\bf X}|^2}\cdot \dfrac{{\bf X}}{|{\bf X}|^2}=\dfrac{{\bf 1}}{|{\bf X}|^2}$
\eqref{1} 式除以 $|{\bf X}|^2$ 得 $1-2{\bf D}\cdot \dfrac{{\bf X}}{|{\bf X}|^2} =\dfrac{{\bf 1}}{|{\bf X}|^2}(r^2-|{\bf D}|^2)$
再除以 $r^2-|{\bf D}|^2$, 得 $\dfrac{1}{r^2-|{\bf D}|^2}-2\dfrac{\bf D}{r^2-|{\bf D}|^2}\cdot {\bf Y}={\bf Y}\cdot {\bf Y}$
(注意 $r^2-|{\bf D}|^2\not=0$)
配方之後, 得一圓。
定理 7 :
保角性質(保持直線與直線, 直線與圓, 圓與圓的夾角)
證明 :
由於兩曲線之夾角即在交點之兩切線之夾角, 因此只需考慮過一點 $P$ 之兩直線相交之角, 不妨設 $P$ 在圓內, $P\not=C$, 或 $P$ 在圓上。
如圖在圓 $C$ 內有一點 $P$, $P\not=C$。
(一) 過 $P$ 有二直線方向 $k$、 $l$, $k$、 $l$ 均不過 $C$, 則 $I_C$ 保持 $k$、 $l$ 之夾角
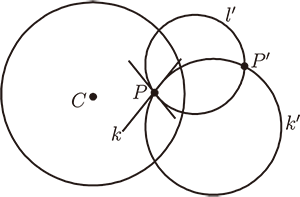作二圓, 均與圓 $C$ 正交, 分別切 $k$、 $l$ 於 $P$, 對此二圓作 $I_C$ (參考(附錄)作圖題 6)。
(二) 若 $k$ 過 $C$
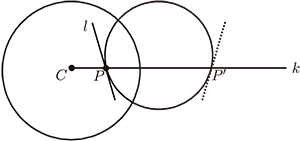作圓 $D$ 切 $l$ 於 $P$ 並與圓 $C$ 正交, 對圓 $D$ 及 $k$ 作 $I_C$, $k$ 不變, 圓 $D$ 亦不變, $I_C(P)=P$,
仍然保角。
(三) 若 $P$ 在圓 $C$ 上, 如圖
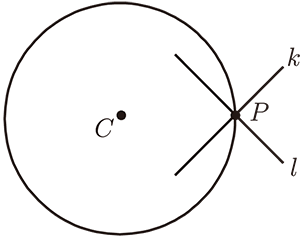則可考慮 $Q$ 在 $C$、 $P$ 之間
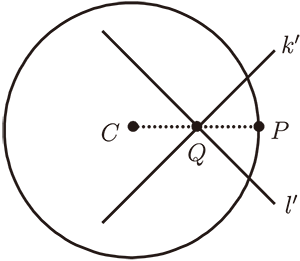$k'//k$, $l'//l$, 則由 (一), $I_C$ 對 $Q$、 $k'$、 $l'$ 保角。
因此, 令 $Q$ 趨近於 $P$, $k'\rightarrow k$、 $l'\rightarrow l$, $I_C$ 仍然對 $P$、 $k$、 $l$ 保角。
定理 8 : (縮放)
對同心圓連續鏡射 $=$ 縮放。
證明 :
$${\bf Y}=\frac{\bf X}{|{\bf X}|^2},\quad {\bf Z}=\frac{r^2\cdot{\bf Y}}{|{\bf Y}|^2}\qquad \therefore\ {\bf Z}
=\frac{r^2\cdot\frac{{\bf X}}{|{\bf X}|^2}}{\frac{1}{|{\bf X}|^2}}=r^2\cdot {\bf X}.$$
我們暫時思考一個問題 : 在這些鏡射運動, 以及它們的接力運動之下, 對 $y$ 軸有什麼影響？
例如, 在限制 $y$ 軸運動到 $y$ 軸的前提下, $y$ 軸上的坐標會有什麼變化？
由定理 8 (縮放定理), 如果涉及的兩個圓是圓心都在原點的圓, 則縮放將在 $y$ 軸的 $y$ 坐標上造成 $y\rightarrow py (p\gt 0)$ 的運動。
而另一方面, 若只是對半徑為 1 的單位圓(圓心在原點)進行鏡射, 顯然, $y$ 軸上 $y$ 坐標的變化是 $y\rightarrow \dfrac 1y$。
綜合這兩個影響, 一個在y軸上合理的不變距離 (Invariant metric), 即在運動下保持不變的距離至少應該是
$|\log a-\log b|$, 式中 $a$、 $b$ 是 $y$ 軸上的坐標。
我們暫時以 $|\log a-\log b|$ 來規範 $y$ 軸上的距離, 將來我們會給一個詳細的證明, 證明此一距離的概念可以推廣到上半平面上的任意兩點, 並且在所有的
「非歐」運動下是保持不變的。
在規範了 $y$ 軸上的距離後, 我們再來介紹單位圓上(圓心在原點)兩點的「非歐距離」。
利用圓心在 $(0, 1)$, 半徑為 2 的圓, 對它作鏡射, 就會把單位圓 (圓心在 $(0, 0)$, 半徑 1) 對到過 $(0,-1)$ 的鉛垂線, 從 $(0, 1)$ 連 $X$ 延長交 $l$ 於 $Y$, 則
\begin{eqnarray*}
\frac{\bf YZ}{2}&=&\tan \alpha,\qquad 2\alpha+\theta=180^\circ\\
\alpha&=&\frac{180^\circ-\theta}{2}=90^\circ-\frac \theta 2\\
{\bf YZ}&=&2\tan (90^\circ -\frac \theta 2)=2\cot \frac \theta 2\\
\cot \frac\theta 2&=&\frac{\cos \frac \theta 2}{\sin \frac \theta 2}=\frac{2\cos^2 \frac \theta 2}{2\sin \frac \theta 2\cos \frac \theta 2}\\
&=&\frac{\cos\theta+1}{\sin \theta}=\frac{\sin\theta}{1-\cos\theta}=\frac y{1-x}\hskip 8cm~\\
\log {\bf YZ}&=&\log 2+\log(\cot \frac \theta 2)\\
{\bf YY}'\hbox{的非歐距離}&=&\log \frac{\cot \frac \theta 2}{\cot \frac{\theta'}{2}}=\log\Big(\frac{y(1-x')}{y'(1-x)}\Big)
\end{eqnarray*}
進一步, 若圓半徑為 $r$, 則距離只與 $\theta$ 有關(？)
\begin{eqnarray*}
{\bf X}&=&(r\cos\theta, r\sin\theta)=(u, v)\\
{\bf X}'&=&(r\cos\theta', r\sin\theta')=(u',v')
\end{eqnarray*}
則令, $\dfrac ur=x$、 $\dfrac vr=y$
$${\bf XX}'\hbox{距離公式}=\log\Big(\frac{\frac vr(1-\frac {u'}{r})}{\frac {v'}r(1-\frac {u}{r})}\Big)
=\Big|\log\Big[\frac{v(r-u')}{v'(r-u)}\Big]\Big|\hbox{。}$$
假定我們已將上半平面的鉛垂線和圓心在 $x$ 軸的半圓看成是系統中的「直線」或「測地線」
,
則歐幾里得原本中第一、二個公設當然滿足 (注意到越靠近 $x$ 軸, 距離是以 log 的速度增加到 $\infty$)。
至於角度, 非歐的角度和歐的角度是定成一致的, 所以定理7的保角性質保證了歐氏所謂的「凡直角皆相等」, 亦即在運動過程中, 角度不變。
至於第三個公設 : 以任意點為圓心, 以任意長為半徑可作一圓, 請見下面定理9。
注意在非歐上半平面中的圓就是歐氏中的圓, 但是圓心的位置不同, 半徑也不同。
定理 9 :
如圖, 歐氏圓 $X$, 與 $y$ 軸交於 $B$、 $C$兩點, $B$ 點坐標為 $(0, a)$、 $C$ 點坐標為
$(0, \frac 1a)$、 $X$ 坐標為 $(0, \frac{a+\frac 1a}2)$。
$A$ 點坐標為 $(0, 1)$, 則歐氏圓 $X$ 是一個以 $A$ 為圓心的非歐圓, 其非歐半徑為 $\log a$。
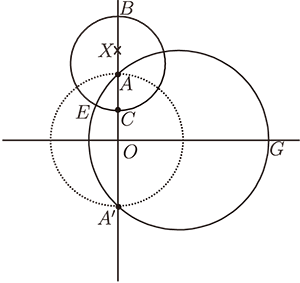
證明 :
$X$ 是 $B$、 $C$ 的歐氏中點, $\overline{OA}=1$、 $\overline{OC}=\frac 1a$、
$\overline{OB}=a$, $\overline{OX}=(a+\frac 1a)/2$
圓 $X$ 以 $X$ 為歐氏圓心, $\overline{CB}$ 為直徑
對圓 $O$, $I_{O,1}(C)=B$
($\because$ $\overline{OB}\cdot\overline{OC}=1^2=1$)
$\because$ 圓 $X$ 含 $\overline{CB}$ 為弦 (直徑)
$\therefore$ 圓 $X$ 與圓 $O$ 正交,
因此 $I_X$(圓$O)=$圓$O$,
可得 $I_X(A)=A'$ $\Rightarrow$ 凡含 $\overline{AA'}$ 為弦之歐氏圓,
其歐氏圓心均在 $x$ 軸上並與圓 $X$ 正交。 考慮任一含 $\overline{AA'}$ 為弦,
與 $x$ 軸交於 $G$, 並與圓 $X$ 交於 $E$ 的圓。
另外再作圓 $G($ 以 $G$ 為圓心)過 $\overline{AA'}$,
則 $I_G(\overleftrightarrow{AA^\prime})=$ 過 $G$、 $A$、 $A'$ 之圓; $I_G$(圓$X)=$圓$X$,
所以 $\overline{AA'}\cap $ 圓 $X=C$,
被 $I_G$ 對到過 $GAA'$ 之圓 $\cap$ 圓 $X=E$
$\therefore$ $\overline{AC} {\buildrel {I_G}\over \longrightarrow } \widehat {AE}$,
因此圓 $X$ 同時也是一個非歐圓。
非歐圓心在 $A$, 半徑為 $\log a$。
定理 10 :
三角形三內角和小於 $180^\circ$。
如圖, 只看直角三角形 $BCD$
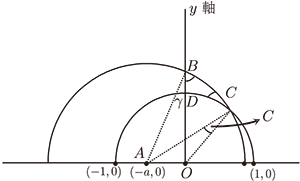圓 $A\cap Y$ 軸 $=B$、圓 $A$ 半徑 $R$
圓 $O\cap Y$ 軸 $=D$、 圓 $O$ 半徑 $1$, $\angle D=90^\circ$ (圓 $O$ 與 $Y$ 軸垂直)
要證 $\angle C+\angle B\lt 90^\circ$ 或 $\angle C\lt \angle \gamma $ ($AB$ 與圓 $A$ 垂直, $\angle B+\angle \gamma =90^\circ$)
$$\sin\gamma =\frac aR, \quad \cos^2\gamma =1-\frac{a^2}{R^2}=\frac{R^2-a^2}{R^2},\quad\hbox{又}\ \angle C=\angle ACO$$
根據餘弦定理 : $a^2=R^2+1^2-2R\cos C$ 或 $\cos C=\dfrac{R^2-a^2+1}{2R}$, 想證
$$\cos C\gt \cos\gamma\ \hbox{或}\ \frac{R^2-a^2+1}{2R}\gt \frac{\sqrt{R^2-a^2}}R\ \hbox{或} \ \frac{R^2-a^2+1}2\gt
\sqrt{R^2-a^2}$$
此為最基本的算幾不等式, 注意 $R^2-a^2(=\overline{OB}^2)\gt 1$, 因此"$\gt $" 成立。
因為此一定理, 推論三角形面積 $=\pi-(A+B+C)$。
(附錄)作圖題
1. 作圖 : 以圓 $C$ 外一點 $P$ 為圓心, 作圓 $P$ 與圓 $C$ 正交。
2. 作圖 : 過圓 $C$ 外一點 $P$, 作圓與圓 $C$ 正交。
3. 作圖 : 過圓 $C$ 內一點 $P'$, 作圓與圓 $C$ 正交。
4. 作圖 : $C$、$P$、$Q$ 三點不共線, 作圓過 $P$、$Q$ 並與圓 $C$ 正交。
5. 作圖 : 要求圓心在直線 $l$ 上, 作一圓過 $P$、 $Q$ 兩點 ($\overline{PQ}$ 與 $l$ 不垂直)。
6. 作圖 : $P$ 不在圓 $C$ 上, $P\not=C$, 直線 $l$ 過 $P$, 但不過 $C$, 求作一圓切 $l$ 於 $P$,
並與圓 $C$ 正交。
1. 解 : 過 $P$ 作圓 $C$ 之兩切線段, 以 $P$ 為圓心, 以此切線段為半徑作圓。
2. 解 : 令 $P'=I_C(P)$, 凡以 $\overline{PP^\prime}$ 為弦之圓皆與圓 $C$ 正交(定理2)。
3. 解 : 令 $P=I_C(P^\prime)$, 凡以 $\overline{PP^\prime}$ 為弦之圓皆與圓 $C$ 正交。
4. 解 : 令 $P'=I_C(P)$, 作圓過 $P$、 $Q$、 $P'$ 三點。
5. 解 : 作 $\overline{PQ}$ 之中垂線交 $l$ 於 $C$, 作圓 $C$, 半徑取 $\overline{CP}=\overline{CQ}$。
6. 解 : 令 $I_C(P)=P'$, 過 $P$ 作 $l$ 之垂線與 $\overline{PP^\prime}$ 之中垂線交於一點 $D$,
以 $D$ 為圓心, $\overline{DP}=\overline{DP^\prime}$ 為半徑作圓即為所求(定理2)。
第四節 : 所有的非歐運動及運動下之保距
在以上半平面為具體模型的非歐幾何中, 我們先行規定其中的
「直線」是鉛垂線以及圓心在 $x$ 軸上的上半圓。
此處所謂的直線乃是連接兩點之間最短距離的路徑。
至於距離的概念, 請參考第三節, 在 $y$ 軸上定義的距離 $|\log a-\log b|$。
我們在本節要解釋這樣的距離概念, 在所有的非歐運動之下是不變的。
至於什麼是非歐運動呢?
那就是以對鉛垂線或是對圓心在 $x$ 軸上的圓的鏡射, 以及這些鏡射之間所有的接力運動。
(見第二節及註
)
首先, 我們想要說明, 上半平面所有的非歐運動分屬甲、 乙兩類,
(甲) $z\rightarrow \frac{az+b}{cz+d}$, 式中 $z$ 為複數, $z=x+iy$, $a$、 $b$、 $c$、 $d$ 為實數, $ad-bc=1$
(乙) $z\rightarrow \frac{p\overline z+q}{r\overline z+s}$, $p$、 $q$、 $r$、 $s$ 為實數,
$ps-qr=-1$, $\overline z=x-iy$
我們先證明
定理 1 :
甲或乙類均將上半平面對應到上半平面。
證明 :
設 $F(z)=\dfrac{az+b}{cz+d}$, $z=x+iy$, $a$、 $b$、 $c$、 $d$ 為實數, $ad-bc=1$
(1) $F(x$軸$)=x$軸, $\because$ $x$ 軸即 $y=0$, 而 $\dfrac{a(x+iy)+b}{c(x+iy)+d}=\dfrac{ax+b}{cx+d}$ 全為實數
($x$軸)。
(2) $F(x+iy)=\dfrac{ax+b+iay}{cx+d+icy}=\dfrac{(ax+b+iay)(cx+d-icy)}{(cx+d)^2+c^2 y^2}$
因為 $ay(cx+d)-cy(ax+b)=(ad-bc)y=y$
所以 $F(z)$ 的虛部 $=\dfrac y{(cx+d)^2+c^2 y^2}$
上半平面即 $y\gt 0$, 而 $F(z)$ 的虛部也 $\gt 0$, 故 $F$ 將上半平面對應到上半平面。
(3) 乙類實際上相當於 $-\overline{F(z)}$, 亦即 $F(z)$ 的共軛加負號
$F(z)$ 在上半平面, 代表 $-\overline{F(z)}$ 也在上半平面。
我們再來觀察幾個現象
乙1 : 圓心在原點、半徑為 $R$ 的圓之鏡射, $z\rightarrow\dfrac{R^2 z}{|z|^2} =\dfrac{R^2}{\overline{z}}
=\dfrac{p\overline z+q}{r\overline z+s}$
$p=0$、 $q=R$、 $r=1/R$、 $s=0$, $ps-qr=-1$, 屬於乙類。
乙2 : 對 $y$ 軸的鏡射, $z\rightarrow -\overline z=\dfrac{-{\overline{z}}+0}{0\overline z+1}$
$p=-1$、 $q=0$、 $r=0$、 $s=1$, $ps-qr=-1$, 屬於乙類。
乙3 : 對任意鉛垂線 $x=b$ 的鏡射, $x\rightarrow 2b-x$ 或 $x+iy\rightarrow (2b-x)+iy=-\overline{x+iy}+2b$
可表成 $z\rightarrow -\overline z+2b=\dfrac{p\overline z+q}{r\overline z+s}$
$p=-1$、 $q=2b$、 $r=0$、 $s=1$, $ps-qr=-1$, 屬於乙類。
乙4 : 對圓心在 $x$ 軸上, 半徑為 $R$ 的任意圓的鏡射, 均屬於乙類
假定圓心在 $c$, 則先用乙3將 $z$ 對 $x=c/2$ 鏡射到 $\omega =-\overline z+c$,
然後對圓心在原點的對應圓鏡射, $\omega \rightarrow \dfrac{R^2 \omega}{|\omega |^2}=u$, 再將 $u$ 對 $x=c/2$ 鏡射回來 :
$u\rightarrow -\overline u+c$, 即得乙4, 如圖
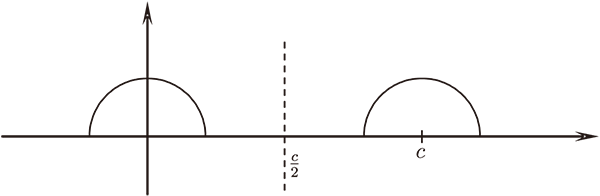
接下來, 是對甲類的理解
甲1 :
如果用乙3兩次, 即對兩條鉛垂線接力鏡射便會得到平移
$z\rightarrow z+b=\dfrac{az+b}{cz+d}$, $a=d=1$, $c=0$, $ad-bc=1$。
甲2 :
如果用乙1兩次, 就會得到以原點 $(0,0)$ 為中心的正向縮放(見第三節定理8)
$z\rightarrow pz=\dfrac{\sqrt p z+0}{\frac 1{\sqrt p}}$, $a=\sqrt p$, $b=c=0$, $d=\dfrac 1{\sqrt p}$,
其中 $p\gt 0$, $ad-bc=1$。
甲3 :
如果將對圓心在原點的單位圓鏡射(乙1)接力對 $y$ 軸的鏡射(乙2), 就會得到
$z\rightarrow \dfrac z{|z|^2} \rightarrow -\overline{\Big(\frac{z}{|z|^2}\Big)}=-\dfrac 1z
=\dfrac{0z-1}{z+0}$, $a=0$、 $b=-1$、 $c=1$、 $d=0$, $ad-bc=1$。
我們證明下面這個重要的定理
定理 2 :
甲 1、 2、 3 連續接力, 可以得出所有的甲類 $\dfrac{\alpha z+\beta}{\gamma z+\delta}$, $\gamma \not=0$,
$\alpha\delta-\beta \gamma =1$。
證明 :
$$z \mathop{\longrightarrow}\limits_{\hbox{甲1、2}}pz+b
\mathop{\longrightarrow}\limits_{\hbox{甲3}}-\frac 1{pz+b}
\mathop{\longrightarrow}\limits_{\hbox{甲1}}-\frac 1{pz+b}+c
=\frac{cpz+cb-1}{pz+b}=\frac{c\sqrt p z+\frac{cb-1}{\sqrt p}}{\sqrt p z+\frac b{\sqrt p}}
$$
則行列式值 $=1$, 不妨設 $\gamma \gt 0$
令 $\sqrt p=\gamma$, $\dfrac b{\sqrt p}=\delta$, $c\sqrt p=\alpha$, 則因行列式值=1, $\beta$ 自然等於
$\dfrac{cb-1}{\sqrt p}$。
定理 3 :
承定理2, 如果 $\gamma =0$, 甲類 : $\dfrac{\alpha z+\beta}{\delta}$, $\alpha\delta=1$ 可由甲 1、 2 接力而得。
證明 :
不妨設 $\alpha\gt 0$, 則甲1、 2 連續接力得
$$z\rightarrow pz+b=\dfrac{\sqrt p z+\frac {b}{\sqrt p}}{\frac{1}{\sqrt p}}$$
令 $\sqrt p=\alpha$, $\dfrac{b}{\sqrt p}=\beta$, $\delta$ 自然等於 $\dfrac{1}{\sqrt p}$。
一旦有了所有的甲類, 只要再與乙類的 $z\rightarrow -\overline z$ (對 $y$ 軸的鏡射) 接力, 便得到
$z\rightarrow \dfrac{az+b}{cz+d}\rightarrow \dfrac{-a\overline z-b}{c\overline z+d}$, $p=-a$、 $q=-b$、
$r=c$、 $s=d$, $ps-qr=-ad+bc=-1$ 即所有的乙類(見本節定理1(3))。
我們總結如下 :
(一) 對圓心在 $x$ 軸上的圓的鏡射屬於乙類(乙4)。
(二) 對鉛垂線的鏡射屬於乙類(乙3), 包含 $z\rightarrow -\overline z$。
(三) 上述 (一)、 (二) 之連續接力可得平移 (甲1)、 縮放(甲2) 及 $z\rightarrow -\frac 1z$ (甲3)。
(四)
甲1、2、3的連續接力可得甲類全體。
(五)
甲類與 $z\rightarrow -\overline z$ (乙3)之接力可得乙類全體。
(六)
甲、乙類混和接力均屬甲、乙類。
(七)
甲、乙類即所有的非歐運動, 由乙3、乙4連續接力完成。
(八)
甲類將順向 $A$、 $B$、 $C$ 對到順向 $A'$、 $B'$、 $C'$;
乙類將順向 $A$、 $B$、 $C$ 對到逆向 $D$、 $E$、 $F$, 如圖(留作習題)。
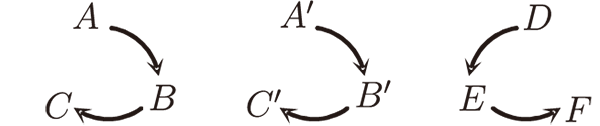
現在回頭來討論一個關鍵性的問題, 即為什麼
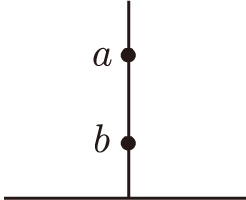必須要先行理解在所有非歐運動之下, 若是將 $y$ 軸 $(x=0)\rightarrow y$ 軸($x=0$), 則在 $y$軸上,
$y$ 坐標的變化為何?
現在,
$$z\rightarrow\frac{az+b}{cz+d}\qquad x=0\rightarrow\frac{aiy+b}{ciy+d}=\frac{(b+aiy)(d-ciy)}{(d+ciy)(d-ciy)}$$
右邊實部 $=0=bd+acy^2\ \Rightarrow\ bd=0=ac$
因為 $a$、$b$ 不能同時 $=0$, 且 $c$、$d$ 不能同時 $=0$, 所以 :
$$a=0=d\ \Rightarrow\ z\rightarrow \frac b{cz},\ (0,y)\rightarrow \frac b{c(iy)} =\frac{\alpha i}y=(0, \frac \alpha y),\ \alpha=-\frac bc\gt 0\qquad~\label{2}$$
$$\hbox{或}\quad c=0=b\ \Rightarrow\ z\rightarrow \frac {az}{d},\ (0,y)\rightarrow (0, \alpha y),\ \alpha=\frac ad\gt 0\label{3}$$
同理, 對 $z\rightarrow \dfrac{a\overline z\!+\!b}{c\overline z\!+\!d}$, $ad\!-\!bc\!=\!-1$ 以同樣的方法討論 $x\!=\!0\rightarrow x\!=\!0$ 的情形有類似的結果。
所以如果 (1) $y\rightarrow \dfrac \alpha y$, $\alpha\gt 0$, $\log y\rightarrow \log\alpha-\log y$
(2) $y\rightarrow \alpha y$, $\alpha\gt 0$, $\log y\rightarrow \log\alpha
+\log y$
由此看出所謂的非歐距離 $|\log a-\log b|$ 確實是在非歐運動之下保距的。
第五節 : 非歐幾何落實
(一) 我們利用上半平面, 先預設了「直線」是鉛垂線和圓心在 $x$ 軸的上半圓。
(二) 我們從對鉛垂線的鏡射和圓心在 $x$ 軸的圓的鏡射, 利用連續接力, 而定出所有的
「非歐」運動, 他們分屬甲、乙兩類。
甲 : $z\rightarrow \dfrac{az+b}{cz+d}$, $ad-bc=1$, $z=x+iy$, $y\gt 0$
乙 : $z\rightarrow \dfrac{p\overline z+q}{r\overline z+s}$, $ps-qr=-1$, ${\overline z}=x-iy$, $y\gt 0$
而對「直線」的鏡射屬於乙類。
(三) 甲類保持定向, 乙類翻轉定向。
(四) 在 $y$ 軸上定義測距 $|\log a-\log b|$, 若要了解其他「直線」上的測距, 只要將該直線以非歐運動對到 $y$ 軸, 以 $y$ 軸上的測距為測距。
若是以不同的運動對到 $y$ 軸, 相對應的測距是一樣的。(因為保距)
(五) 因為有充分的非歐運動, 因此「直線段」和角度均可以透過運動比較。
因此而有 $S.A.S$ 全等判定。
(六) 由 $S.A.S$ 而有等腰三角形兩底角相等, 以及三角形大角對大邊, 大邊對大角(見第二節)。
(七) 因此而有三角形兩邊之和大於第三邊。
(八) 由此重新驗證我們的「直線」均為測地線, 因為折線的長 $\gt $ 直線的長。
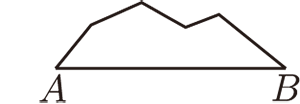
最後, 在上一節, 我們看到「過直線外一點, 有無窮多條平行線」。
並由第二節定理 10, 我們看到三角形三內角和小於 $180^\circ$。
---本文作者為台大數學系退休教授---
