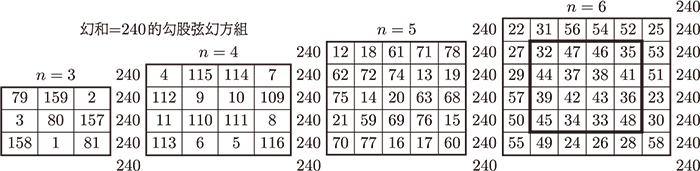| 發刊日期 |
2018年9月
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 標題 | 勾股弦幻方組的三種構造方法 |
|||||||||||
| 作者 | ||||||||||||
| 關鍵字 | ||||||||||||
| 檔案下載 | ||||||||||||
| 全文 |
一、前言
勾股弦數組是一個歷史悠久的古老數學問題, 近代將勾股弦數組代入幻方之中, 使得幻方的結果也滿足勾股弦數組的定義, 頗為有趣。
在此之前, 國外僅有2篇勾股弦幻方的文章, 介紹了2種方法。第一種是「R法」 (Royal Vale Heath) 「R法」與「EE法」研究的是 $K=2$ 次方勾股弦數組的勾股弦幻方組, 本文我們給出了 $K=3$、 4、 5 次方數組的勾股弦幻方組, 拓廣了勾股弦幻方組的研究範圍。 二、畢氏定理的來由及用途畢氏定理描述了直角三角形三條邊之間的關係, 我國古代把直角三角形中較短的直角邊叫做「勾」, 較長的直角邊叫做「股」, 斜邊叫做「弦」。 「平面上的直角三角形的兩條直角邊的長度 $a$, $b$ (古稱勾長、 股長) 的平方和等於斜邊長 $c$ (古稱弦長) 的平方。」 則畢氏定理的公式為 $a^2+b^2=c^2$。 $(a,b,c)$ 叫做勾股數組。 最早發現畢氏定理的國家是古巴比倫,在英國博物館保存的一塊相同時期的泥板上有這樣的記載: 「長是 4, 對角線是 5。 那麼寬是多少?
沒人知道。
這段文字說明古巴比倫人知道當直角三角形的斜邊是 5, 一條直角邊是 4 的時候, 另外一條直角邊一定是 3。
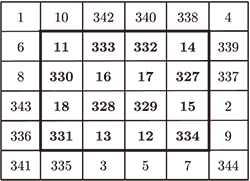
在美國哥倫比亞大學收藏的一塊編號為 PLIMPTON
322 的泥板上記錄了很多例子。
這塊泥板西元前 2000 年至西元前 1600 年的古巴比倫泥板,
總共有 15 行符號, 分成 5 列。
其中第四列相當於我們的「編號」兩個字, 第五列從第一行到最後一行依次是從 1 到 15 這 15 個數字。
所以說真正有意義的其實只有前 3 列。
第三列是斜邊長, 第二列是短的直角邊長。
最令人費解的是第一列, 這一列的數字從第一行的 $0.9834\ldots $逐漸減少到最後一行的$ 0.38716\ldots$。
關於這第一列的含義, 長期以來爭論不休。
美國威斯康星大學巴克教授於1980年寫了一篇膾炙人口的文章《夏洛克.福爾摩斯在巴比倫》。
這篇文章發表在《美國數學月刊》上。
巴克教授在這篇文章裏從大偵探福爾摩斯的角度出發來研究這些數字。其結論令人吃驚不已
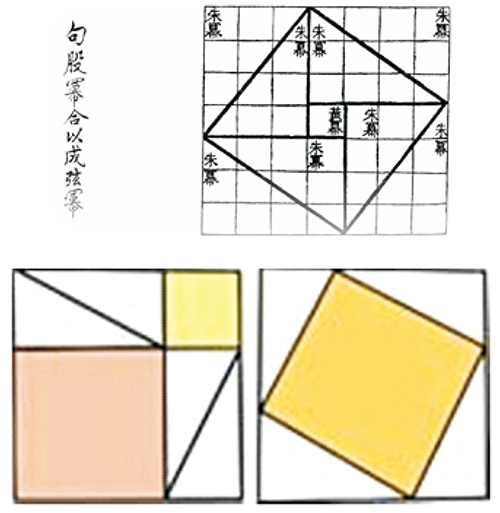
原來這一列的數字代表的是短的直角邊和長的直角邊比值的平方, 也就是 $(a/b)^{2}$。 如果以 $\theta$ 代表斜邊和長的直角邊的夾角, 那麼這第一列數字就是 $(\tan\theta)^{2}$。 更有趣的是這個 $\theta$, 從第一行開始, 幾乎是穩定的以 1 度的速度下降, 從大約 45 度, 下降到大約 30 度。 所以這個表還有可能是古巴比倫人的三角函數表呢。 巴克教授認為古巴比倫人不但知道很多勾股數組的例子, 而且還知道如何製造勾股數組。 也就是說他們知道勾股數組的那個一般公式: $$a=2mn,\quad b=m^{2}-n^{2},\quad c=m^{2}+n^{2}\hbox{。}$$ 巴克的結論是可信, 因為泥板涉及的最大的一個勾股數組是 (18541, 12709, 13500)。 這樣的例子是絕對不可能通過測量發現的, 也幾乎不可能通過湊巧得到。 而且 18541 還是個素數, 也就是說這組數字也不可能是通過較小的勾股數組放大得來。 所以我們確實有充分的理由相信古巴比倫人知道一般形式的畢氏定理。 正因為如此, 2002 年 1 月份的《美國數學會通告》封面登載了 YBC 7289 泥板的照片。 配的文字說明是比「畢達哥拉斯早一千年的畢達哥拉斯定理」。 約西元前一世紀的《周髀算經》相傳畢氏定理是商代由商高發現的, 全書第一節就記載著一個名叫商高的人, 對周公講了這樣一段話: 「折矩以為勾廣三, 股修四, 徑隅五。 既方其外, 半之一矩, 得成三四五。 兩矩共長二十有五, 是謂積矩。」 這段話毫無疑問是在談論畢氏定理, 而周公大約生活在西元前 11 世紀, 商高既和周公談話, 當然是周公的同時代人, 這就比畢達哥拉斯早了數百年, 所以商高理應獲得畢氏定理的榮譽。 故又有稱為商高定理, 明確記載了周公後人陳子敘述的畢氏定理公式: 「若求邪至日者, 以日下為勾, 日高為股, 勾股各自乘, 並而開方除之, 得邪至日」(圖2.2)。
表述為「勾股各自乘, 並之, 為弦實。開方除之, 即弦」。 法國稱為「驢橋定理」, 埃及稱為「埃及三角形」。 畢氏定理在幾何學中的實際應用非常廣泛。 相傳大禹在治水過程中, 「左準繩, 右規矩」。 (「規」就是圓規, 「矩」就是曲尺, 由長短兩尺在端部相交成直角合成, 短尺叫勾, 長尺叫股), 運用勾股測量術進行測量。 表明大禹已經知道用長為 3:4:5 的邊構成直角三角形。 陳子利用畢氏定理, 測量太陽高度等。 勾股弦定理廣泛應用在人民生活方面, 例如: 測量土地的面積、 測量距離、 測量山的高度、 太陽高度等。 畢氏定理把數學由計算與測量技術轉變為證明與推理科學。 畢氏定理中的公式是第一個不定方程, 也是最早得出完整解答的不定方程, 它一方面引導到各式各樣的不定方程, 包括著名的費爾馬大定理, 也為不定方程的解題程式樹立了一個規範的模式。 從畢氏定理出發開平方、 開立方、 求圓周率等。 古希臘的畢達哥拉斯證明了畢氏定理。 相傳畢達哥拉斯證明這個定理後, 殺了一百頭牛作慶祝, 故又稱「百牛定理」。 據有關資料報導, 僅畢氏定理的證明方法就有 500 多種, 是數學定理中證明方法最多的定理之一。 但他們發現的時間都比我國晚, 我國是世界上最早發現畢氏定理的證明。 三、最早提出構造勾股弦幻方組的學者Royal Vale Heath (1883 年$\sim$1960 年)是紐約城經紀人、 美國魔術師和數學謎題愛好者, 1930 年發表了一組幻方圖 3.1 在他的書《數學魔術 --- 數字的魔術, 謎題, 遊戲》(Mathemagic --- magic, puzzles, games with numbers, Dover 1953)
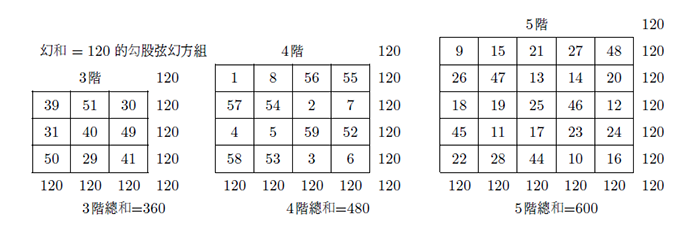
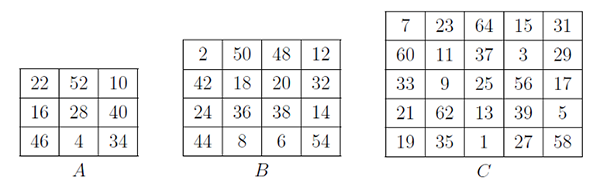
這組幻方分別由 3 階、 4 階與 5 階所組成, 奇怪的是, 這 3 個幻方的幻和都相同, 都等於 174。 而 3 階幻方幻和的總和是 $174\times 3=522$, 4 階幻方幻和的總和是 $174\times 4=696$, 5 階幻方幻和的總和是 $174\times 5=870$。 再求 3 個幻方總和的平方和, 得: $522^{2}+696^{2}=870^{2}=272484+484416=756900$。 這種方法稱為「R法」。 其特點是, 每個階數不同的幻方, 他們幻和相等, 再求 $n$ 個幻和的平方和, 使得 $A^{2}+B^{2}=C^{2}$. 又稱為「同幻和, 不同階數法」。 我們利用「R法」可以得到其幻和較小的 3, 4, 5 階勾股弦幻方組 (圖 3.2):
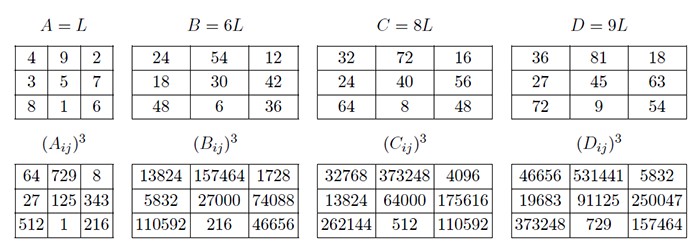
由 3、 4、 5 階幻方, 得到:$3^{2}+4^{2}=5^{2}$。 即 $360^{2}+480^{2} = 600^{2} = 360000$。 方陣外邊的數字分別是各個幻方的行、 列及對角線之和(下同)。 還可以拓廣到廣義勾股弦數組及 3 次冪和數組。 在洛書中我們發現兩個廣義 4 元素 3 次勾股弦數組。 第 1 組是 $A=3$, $B=4$, $C=5$, $D=6$, 第 2 組是 $A=1$, $B=6$, $C=8$, $D=9$, 用這兩個數組可以構造出廣義勾股弦幻方組, 圖 3.3 是 $A=3$, $B=4$, $C=5$, $D=6$ 的廣義勾股弦數組, 他們滿足: $$ A^{3}+B^{3}+C^{3}=D^{3}.$$ 這 4 個幻方的幻和都等於 240。 $A$, $B$, $C$, $D$ 各個子幻方的總和分別是 720,960,1200,1440。 計算得 $720^{3}+960^{3}+1200^{3}=1440^{3}$, 即: $373248000+884736000+1728000000=2985984000$。
圖 3.4 是利用第 2 組元素, 當 $A=1$, $B=6$, $C=8$, $D=9$ 時構造的廣義勾股弦幻方組, 仍然滿足 3 次方的性質: 對於拓廣勾股數組 1, 6, 8, 9, 我們可以造出 4 個幻方, 來滿足廣義勾股弦幻方組。 設 $S=1080$, 則 $(1080\times 1)^{3} +(1080\times 6)^{3} +(1080\times 8)^{3}=(1080\times 9)^{3}$. 在幻方的階數 1, 6, 8, 9 中, 第一個「1」, 代表 1 階幻方, 其幻和為 1080; 其餘的 6, 8, 9, 分別代表 6 階, 8 階, 9 階幻方。 我們造出的 1, 6, 8, 9 廣義勾股弦幻方組如圖 3.4, 1 階省略。 有意思的是, 8 階幻方與 9 階幻方都具有平方幻方的性質, 並且這兩個幻方的 1 次幻和相等, 即 $S_{8}=1080$; $S_{9}=1080$。 但是他們的 2 次幻和就分道揚鑣了 $S_8^2=227284$; $S_9^2=134520$。 經計算得: $$ 1080^{3}+6480^{3}+8640^{3}=9720^{3 }$$ 即:$1259712000+272097792000+644972544000=918330048000$。 四、 Emanuel Emanouilidis的勾股弦幻方組4.1.
「EE法」是Emanuel Emanouilidis 新澤西州 Kean
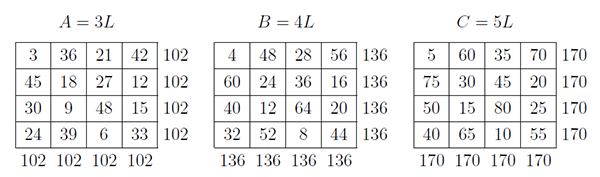
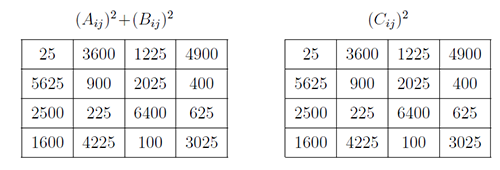
大學電腦科學系教授在 2005 年介紹的概念 定義: 如果 $n$ 階幻方 $A,B,C$ 滿足: $$(A_{ij})^{2}+(B_{ij})^{2}=(C_{ij})^{2}$$ 則稱 $A$、 $B$、 $C$ 為 EE 法勾股弦幻方組。 由於勾股弦幻方組的階數都相同, 又稱為「同階勾股弦幻方組」。 這一點與「R法」不同。 圖 4.1.1 上部的 $A,B,C$; 是滿足勾股弦幻方組的 3 個 3 階幻方; 再計算出他們各個元素的平方和, 如圖 4.1.1 下部的 $(A_{ij})^{2}$, $(B_{ij})^{2}$, $(C_{ij})^{2}$。
我們再把 $(A_{ij})^{2}+(B_{ij})^{2}$ 與 $(C_{ij})^{2}$ 計算出來, 如下圖4.1.2
他給出以下定理: 定理: 用 EE 法可以得到下面的勾股弦幻方組:
例如: $A$、 $B$、 $C$, EE 型勾股弦幻方組可由下面
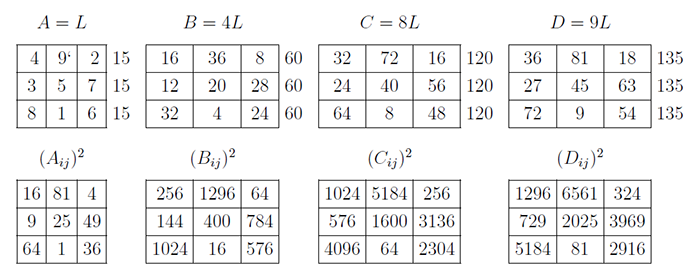
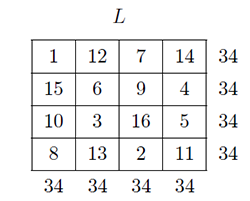
4.2. EE 型勾股弦幻方組的拓廣利用 EE 型勾股弦幻方的構造方法, 可以造出 4 元 2 次勾股幻方組, 例如 $A^{2}+B^{2}+C^{2}=D^{2}$。 我們從古老的洛書 (3 階幻方, 簡記為 L) 中找到兩組 4 元 2 次 (3:1型) 拓廣勾股數組: $1^{2}+4^{2}+8^{2}=9^{2}=81$; $2^{2}+3^{2}+6^{2}=7^{2}=49$。 用這兩個數組, 分別乘以洛書 $L$ 的各個元素, 可以構造 4 個 3 階幻方。 當 $A=1$, $B=4$, $C=8$ 及 $D=9$ 時, 用 $L$ 分別乘以 1, 4, 8, 9 得到的 4 個 3 階幻方,如圖 4.2.1 上部的 $A,B,C,D$; 再計算出他們各個元素的平方和, 如圖 4.2.1 下部的 $(A_{ij})^{2}$, $(B_{ij})^{2}$, $(C_{ij})^{2}$, $(A_{ij})^{2}$。
我們再把 $(A_{ij})^{2}+(B_{ij})^{2}+(C_{ij})^{2}$ 與 $(D_{ij})^{2}$ 計算出來, 如下圖 4.2.2。
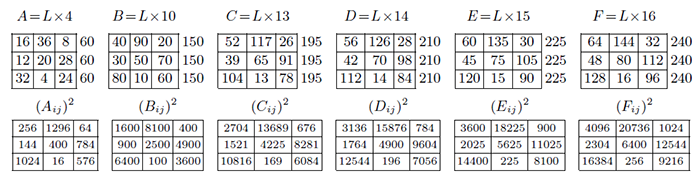
4.3. 拓廣勾股數組, 6 元 2 次勾股數幻方組 (4:2)存在 $(A_{ij})^{2}+(B_{ij})^{2}+(C_{ij})^{2}+(D_{ij})^{2}=(E_{ij})^{2}+(F_{ij})^{2}$ 拓廣勾股數組, 當 $A=4$, $B=10$, $C=13$, $D=14$ 及 $E=15$, $F=16$ 時, 用洛書方陣 $L$分別乘以 4, 10, 13, 14, 15, 16 得到 6 個 3 階幻方, 如圖 4.3.1 上部的 $A,B,C,D,E,F$; 再計算出他們各個元素的平方和如圖 4.3.1 下部的 $(A_{ij})^{2}$, $(B_{ij})^{2}$, $(C_{ij})^{2}$, $(D_{ij})^{2}$, $(E_{ij})^{2}$, $(F_{ij})^{2}$。
我們再把 $(A_{ij})^{2}+(B_{ij})^{2}+(C_{ij})^{2}+(D_{ij})^{2}$ 與 $(E_{ij})^{2}+(F_{ij})^{2}$ 計算出來, 如下圖 4.3.2:
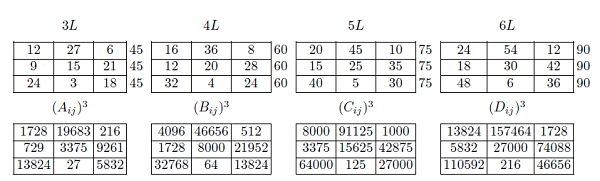
4.4. 拓廣勾股數組, 4 元 3 次勾股數幻方組 (3:1型)我們可以構造出 4 元 3 次勾股數幻方組 (3:1 型) , 首先找到滿足3次方勾股數組 $(A_{ij})^{3}+(B_{ij})^{3}+(C_{ij})^{3}=(D_{ij})^{3}$ 也就是說, 這3個子幻方任意相同位置上 $A^{3}+B^{3}+C^{3}$ 之和都等於 $D^{3}$。 下面給出用洛書 $L$ 分別乘以 3、 4、 5、 6 與分別乘以 1、 6、 8、 9 的兩個例子。 這兩個數組 $3^{3}+4^{3}+5^{3}=6^{3}$ 與 $1^{3}+6^{3}+8^{3}=9^{3}$, 來源於中國的洛書, 洛書中蘊藏的「珍寶」還多著呢, 等待著有興趣的人擷取和開發! 把 3, 4, 5, 6 分別乘以 $L$, 得到 4 個 3 階幻方如圖 4.4.1 上部的 $A,B,C,D$; 再計算出他們各個元素的立方和如圖 4.4.1 下部的 $(A_{ij})^{3}$, $(B_{ij})^{3}$, $(C_{ij})^{3}$, $(D_{ij})^{3}$。
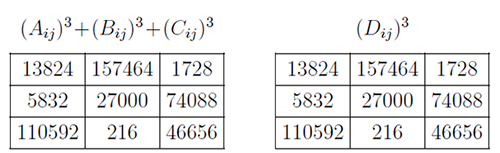
我們再把 $(A_{ij})^{3}+(B_{ij})^{3}+(C_{ij})^{3}$ 與 $(D_{ij})^{3}$ 計算出來, 如下圖 4.4.2:
把 1, 6, 8, 9 分別乘以 $L$, 得到 4 個 3 階幻方如圖 4.4.3 上部的 $A,B,C,D$; 再計算出他們各個元素的立方和如圖 4.4.3 下部的 $(A_{ij})^{3}$, $(B_{ij})^{3}$, $(C_{ij})^{3}$, $(D_{ij})^{3}$。
我們再把 $(A_{ij})^{3}+(B_{ij})^{3}+(C_{ij})^{3}$ 與 $(D_{ij})^{3}$ 計算出來, 如下圖 4.4.4
4.5. 拓廣勾股數組, 5元3次勾股數幻方組 (4:1型)存在數組滿足 $(A_{ij})^{3}+(B_{ij})^{3}+(C_{ij})^{3}+(D_{ij})^{3}=(E_{ij})^{3}$, 兩個滿足條件的數組如下: $$1^{3}+5^{3}+7^{3}+12^{3}=13^{3};$$ $$5^{3}+7^{3}+9^{3}+10^{3}=13^{3}.$$ 利用上述數組可以構造出 5 元 3 次勾股弦數幻方組 (4:1型) , 下面給出洛書 $L$ 分別乘以 1、 5、 7、 12、 13 及 $L$ 分別乘以 5、 7、 9、 10、 13 的兩個例子。 這兩個數組 $1^{3}+5^{3}+7^{3}+12^{3}=13^{3}=5^{3}+7^{3}+9^{3}+10^{3}$, 結果相同。 如圖 4.5.1 與圖 4.5.3。 計算結果分別在圖 4.5.2 與圖 4.5.4。
我們把 $(A_{ij})^{3}+(B_{ij})^{3}+(C_{ij})^{3}+(D_{ij})^{3}$ 計算出來, 圖 5.4.2 (左) , 再把 $(E_{ij})^{3}$ 計算出來, 圖 5.4.2 (右) 。
下面是 $5^{3}+7^{3}+9^{3}+10^{3}=13^{3}$ 的例子圖 4.5.3 :
我們把 $(A_{ij})^{3}+(B_{ij})^{3}+(C_{ij})^{3}+(D_{ij})^{3}$ 計算出來, 圖 4.5.4 (左), 再把 $(E_{ij})^{3}$ 計算出來, 圖 4.5.4 (右),
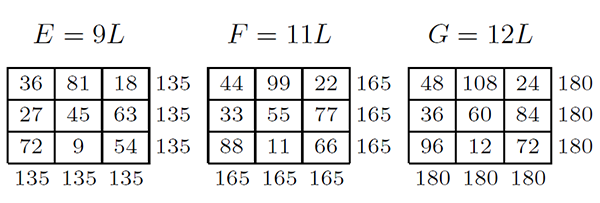
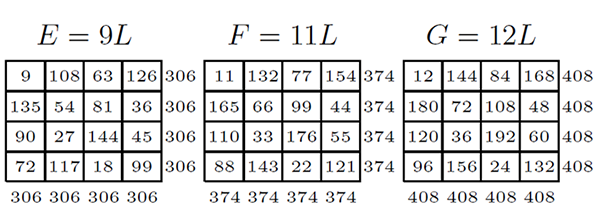
4.6. 拓廣勾股數組, 7 元 5 次勾股數幻方組 (6:1 型)存在 $(A_{ij})^{5}+(B_{ij})^{5}+(C_{ij})^{5}+(D_{ij})^{5}+ (E_{ij})^{5}+(F_{ij})^{5}=(G_{ij})^{5}$ 拓廣勾股數組 $$4^{5}+5^{5}+6^{5}+7^{5}+9^{5}+11^{5}= 12^{5} = 248832 .$$ 下面給出洛書 $L$ 分別乘以 4、 5、 6、 7、 9、 11、 12 的例子, 得到 7 個 3 階幻方如圖 4.6.1。
各個子陣幻和的 5 次方: $60^{5}+75^{5}+90^{5}+105^{5}+135^{5}+165^{5}= 188956800000=180^{5}=188956800000$ 相等。 把 6 個子幻方幻和的 5 次方和計算出來, 圖 4.6.2 (左) , 再把 $(G_{ij})^{5}$ 計算出來。
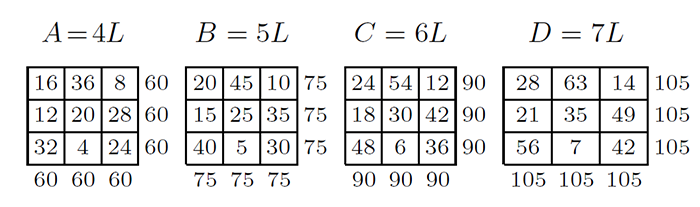
4.7. 用 4 階幻方為基圖擴大倍數得到勾股弦幻方組的嘗試前面所講述的是用 3 階幻方為「基圖」, 乘以勾股數組使得滿足勾股幻方的方法, 下面我們用 4 階幻方來探討這個問題: 我們把圖 4.7.1 的 4 階幻方稱為 $L$ 陣, 用 4 階幻方代替原來的 3 階幻方。 其他步驟同前。
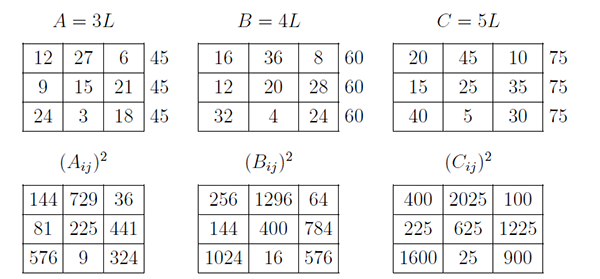
用 $A=3$, $B=4$, $C=5$ 的勾股數組分別乘以圖 4.7.1 的 4 階幻方 $L$, 得到另外 3 個 4 階幻方, 圖 4.7.2
經計算知: $(A_{ij})^{2}+(B_{ij})^{2}=(C_{ij})^{2}$, 即: $102^{2}+136^{2} =170^{2}=28900$。 我們把 $(A_{ij})^{2}+(B_{ij})^{2}$ 計算出來, 圖 4.7.3 (左); 再把 $(C_{ij})^{2}$ 計算出來, 圖 4.7.3 (右)。
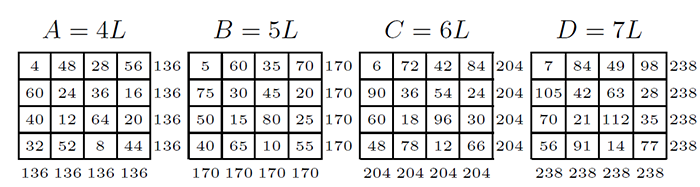
由此, 可以猜想用任意相同奇數的幻方作基圖, 都可以得到勾股弦幻方組。 4.8.用 4 階幻方構造 7 元 5 次方勾股弦幻方組 (6:1 型)$A^{5}+B^{5}+C^{5}+D^{5}+E^{5}+F^{5}= G^{5}$ 用 $A=4$, $B=5$, $C=6$, $D=7$, $E=9$, $F=11$, $G=12$ 的勾股數組分別乘以 圖 4.8.1 的 4 階幻方 $L$, 得到另外 7 個 4 階幻方, 圖 4.8.1
經過計算知: $A$、 $B$、 $C$、 $D$、 $E$、 $F$, 這 6 個幻方幻和的 5 次方和等於幻方 $G$ 的 5 次方和。 即: $136^{5}+170^{5}+204^{5}+238^{5}+306^{5}+374^{5}=408^{5}=11305787424768$。 我們把 $(A_{ij})^{5}+(B_{ij})^{5}+(C_{ij})^{5}+(D_{ij})^{5}+ (E_{ij})^{5}+(F_{ij})^{5}$ 計算出來, 圖 4.8.2 (左) ; 再把 $(G_{ij})^{5}$ 計算出來, 圖 4.8.2 (右) ,
五、用 LL 法構造的勾股弦幻方組用上述兩種方法得到的勾股弦幻方組, 各自的特點是: 「R法」是幻和相同, 幻方階數不相同;「EE法」是幻方的階數相同, 而幻和不相同。 我們另闢蹊徑, 用「幻方的幻和不相同, 幻方的階數也不相同」的方法得到勾股弦幻方組, 稱為「LL法」。 定義1: 由自然數 $A$, $B$, $C$ 構成的數組, 並且滿足方程: $$A^{2}+B^{2}=C^{2}$$ 則稱 $A$、 $B$、 $C$為勾股弦數組。 定義2: 如果勾股弦數組的三個元素兩兩互素 (即他們沒有公約數), 稱為「本原勾股弦數組」。 如果將一個本原勾股弦數組的各個元素同時乘以一個相同的數, 得到的有公約數的新勾股弦數組, 則稱為「倍數勾股弦數組」。
勾股弦數組是一個古老的數學問題, 勾股弦數組在測量和計算等方面有廣泛的應用, 勾股弦數組的實際應用, 導致了無理數的重大發現 奇妙勾股弦, 天下廣流傳, 成就冠寰宇, 萬古流芳遠! 5.1. 勾 3、 股 4、 弦 5 幻方組本文介紹以勾、 股、 弦數組為階次的三個幻方。 這三個幻方的階次是勾股弦數組, 並且他們的幻和也是勾股弦數組。 定義: 如果由 $A^{2}+B^{2}+C^{2}$ 個自然數構成的 $A$ 階、 $B$ 階與 $C$ 階幻方, 它們的幻和分別記作 $S_{A}$, $S_{B}$, $S_{C}$。 如果 $A$、 $B$、 $C$ 是勾股弦數組, 即 $A^{2}+B^{2}=C^{2}$。 並且滿足: $$S_A^2+S_B^2 = S_C^2$$ 則稱這 3 個幻方為「勾股弦幻方組」。 圖 5.1.1 是一個勾股弦幻方組。
上圖 $A$、 $B$、 $C$ 三個幻方是一組「勾股弦幻方組」, 其「幻和」分別為 $S_{3}=84$, $S_{4}=112$, $S_{5}=140$。 它們的階次 3、 4、 5 是一個勾股弦數組;它們幻和的平方和是: $$ 84^{2} + 112^{2} = 140^{2} ,$$ 即: $7056 + 12544 =19600$, 也是一個勾股弦數組。 所以 $A$、 $B$、 $C$ 是勾股弦幻方組。 其中:
對於勾股弦幻方組, 我們得到下面的結果:
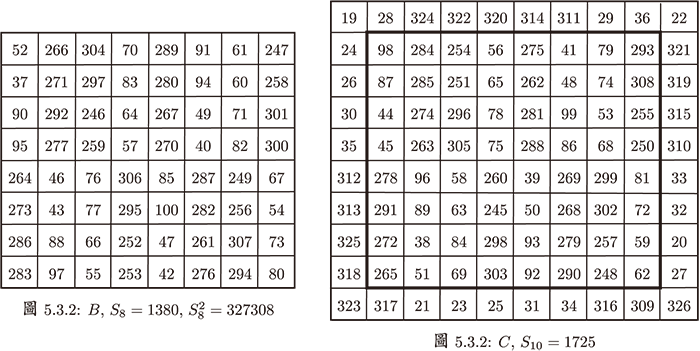
5.2. 倍數勾股弦數組 勾 6、 股 8、 弦 10 幻方組下面我們給出由連續自然數 1, 2, $\ldots$, 200 構作的 $A=6$, $B=8$, $C=10$ 的勾股弦幻方組 (圖 5.2.1, 圖 5.2.2, 圖 5.2.3)。 其中 $A$ 是一個分層幻方, 內心 (粗實線所圍的) 是一個 4 階全對稱幻方, 整體是一個 6 階幻方。 $C$ 也是一個分層幻方, 內心 (粗實線所圍的虛線部分) 的 $8\times 8$ 方陣與 $B$ 陣是一對「8 階同值平方幻方」。
$6^{2} + 8^{2} = 10 ^{2},\quad 603^{2}+804^{2}=1005^{2}.$ 對於勾股弦幻方組 $Z$ 陣元素的選擇, 有很多種方法, 請讀者自己發掘。 如果找到新的 $Z$ 陣元素, 構造出新的勾股弦幻方組, 將使您忘記疲勞和煩惱, 而帶來無窮的樂趣 ! 5.3. 勾股弦數組的拓廣 $A_{3}$、 $B_{4}$、 $C_{5}$、 $D_{6}$ 幻方組在洛書中, 有一組勾股弦數組, 即 $3^{2}+4^{2}=5^{2}$。 我們把他稱為 3 元數組, 因為該數組共有 3 個元素。 另有 3 次冪和相等的 4 元數組, 即: $3^{3}+4^{3}+5^{3}=6^{3}$。 我們稱為「拓廣勾股弦數組」。 下面我們討論 4 元幻方組。 圖 5.3.1: 是 $A=3$、 $B=4$、 $C=5$、 $D=6$ 的拓廣勾股弦幻方組。
各個幻方幻和的3次方之和, 即 $150^{3}+200^{3}+250^{3}=300^{3} = 27000000$。 我們可以造出由連續自然數 1$\sim$344 組成的 6、 8、 10、 12 階幻方組 (圖 5.3.2, $A$, $B$, $C$, $D$) 。
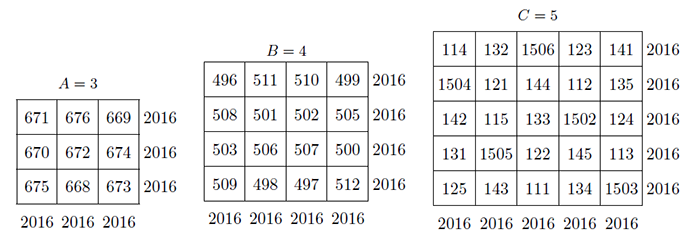
圖 5.3.2, $C$ 的中心部分 (粗實線所圍的) 是一個 8 階幻方平方幻方, 其 1 次、 2 次幻和與圖 5.3.2 $B$ 相同, 並且這兩個幻方的每行上 16 個元素的 $S_{16}=2760$, $S_{16}^2=654616$; $S_{16}^3=174509280$。 對於這類幻方, 我們稱為「同值平方幻方」。 真是: 同值幻方妙趣無窮, 幻和相等模樣相同, 數理蘊藏左右對稱, 誰大誰小難分伯仲。 圖 5.3.2. $D$ 的幻方由連續自然數 101$\sim$244 構成。 其兩條對角線上的 $S_{12}^4\!=\!14389435574$。 各個幻方幻和的3次方之和, 即 $1035^{3}+1380^{3}+1725^{3}=2070^{3} = 8,869,743,000$。 六、構造勾股弦幻方組的三種方法大薈萃截止目前, 有 3 種方法可以造出勾股弦幻方組。 李學數提議構造一組勾股弦幻方組 --- 使他們的幻和等於 2016, 或者與 2016 有關聯以示紀念。 這三個方法都可以造出其幻和等於 2016 的年份, 倘若錯過 2016 這個年份, 必須再等 12 年才能符合這個條件。 12 年, 對於年輕朋友來說, 只是瞬間而已, 但對於我們來說, 是非常漫長和艱辛的, 甚至是不可能的。 但我們渴望在有生之年再造幾次與年份有關的勾股弦幻方組 $\ldots\ldots$。 第一種方法, R 法:下面是用第一種 R 法, 造出幻和等於 2016 的 3 個幻方, 圖 6.1
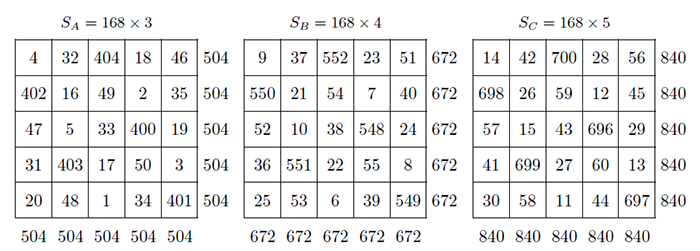
驗算: $6048^{2}+8064^{2} = 10080^{2}= 36578304+65028096 =101606400$。 第二種方法: 下面是用 EE 法, 構造 3 個 5 階幻方, 圖 6.2, 使他們的幻和之和等於 2016 的 (把原來 3 階或 4 階拓廣到 5 階)。 用 3 個 5 階幻方分別滿足勾股弦幻方組。
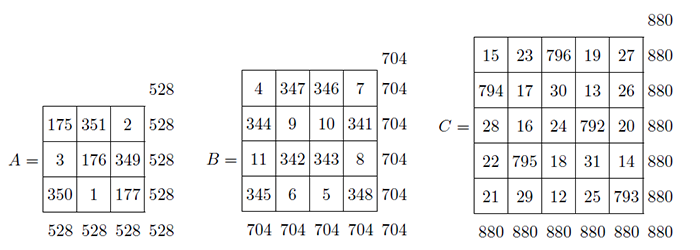
上面 3 個幻方的幻和分別用 $S_{A}$, $S_{B}$, $S_{C}$ 來表示, 他的幻和之和 $=S_{A}+S_{B}+S_{C}$ 即: $504+672+840= 2016$。 這 3 個 5 階幻方的平方和滿足勾股弦幻方組的關係: $$ S_A^2+ S_B^2 = S_C^2,\ \hbox{即}\ 504^{2}+672^{2}= 840^{2} = 254016+451584 =705600,$$ 3 個子幻方的 25 個元素之和分別等於 $504\times 5=2520$, $672\times 5=3360$, $840\times 5= 4200$, 他們也滿足勾股弦數組的性質, 即: $$ 2520^{2}+3360^{2}=4200^{2}= 6350400+ 11289600= 17640000.$$ 第三種方法: LL 法 在富蘭克林誕辰 310 周年 (1706$\sim$2016) 之際, 李學數教授提議設計一個「紀念富蘭克林誕辰 310 周年幻方」, 來紀念這位身兼多職的著名科學家, 待刊。 富蘭克林幻方是迄今為止奇妙性質最多的幻方, 《有趣的數論》一書 (潘承彪譯, 北大出版社出版) 稱為「最神奇的幻方」而享譽國際, 開「曲線幻方」研究之先河, 深受幻方愛好者所崇敬。 在這裏, 我們用 LL 法設計一組 (3 個) 幻方其幻和之和等於 2112 的勾股弦幻方組來等待「勾股弦幻方組」三種構造方法 96 周年的到來, 2112 是一個回文數, 頗有意義。 3 個幻方如下圖 6.3 之 $A$、 $B$、 $C$:
在上面 3 個幻方中, $528+704+880=2112$. 幻方的階數: $3^{2}+4^{2}=5^{2}=25$; 幻和的平方和: $S_A^2+ S_B^2 = S_C^2$ 即: $$ 528^{2}+704^{2}=880^{2} = 278784+495616 = 774400.$$ 七、結語
勾股弦幻方組的問世給幻方家族增添了新成員, 增加了活力, 豐富了幻方的研究內容。
在構造勾股弦幻方組中, 我們應用了多種方法 幻方遠景展望 俗話說:人生不滿百, 常懷千歲憂。 到了 2112 年, 要想造出新幻方, 就更加輕鬆。 由現在的「舉手」之勞, 就變成了「開口」之勞, 只要對電腦「說」出要求, 一切由「高智能電腦」來完成, 哪裡還用得著「撥打算盤珠子呢!」 不過, 即便是到了 3000 年, 也有電腦難以解決的幻方問題。 就現在的電腦而言, 僅僅是解決了「$k=1$、 2 次冪和幻方」的構造問題。 也有人用電腦搜索的方法得到了連作者自己也「不會構造」的高次冪和幻方。 對於 $k\gt 20$ 的冪和幻方尚未出現。 即便解決了 $k\gt 20$、 $k\gt 10000$ 的冪和幻方問題, 那在數字海洋裏也不過是滄海一粟而已。 並且, 目前的電腦對於雙重幻方尚無能為力, 如果給雙重幻方再加上一個冪和幻方的條件 --- 即:「$k$ 次冪和積幻方」 $(k=1,2,3\ldots{})$ , 更是「太平洋裏撈針」了。 這就是幻方研究能歷經幾千年而長興不衰的魅力,並且是一個永無止境的課題! 參考資料---本文作者梁培基任職中國河南省封丘縣科協, 李學數為美國聖荷西大學退休榮譽教授--- |
2018年9月 42卷3期
勾股弦幻方組的三種構造方法