| 全文 |
一、前言
在平面幾何中, 歐拉線是指過三角形的外心、 重心、 九點圓 (歐拉圓) 圓心和垂心的一條直線。
歐拉線上的四點中, 九點圓圓心到垂心和外心的距離相等, 而且重心到外心的距離是重心到垂心距離的一半。
換言之, 設三角形的外心為 $O$、 重心為 $G$、
九點圓圓心為 $K$ 和垂心為 $H$, 可以推得 $\overline{OG} : \overline{GK} : \overline{KH}=2 : 1 : 3$。
如果現在我們也可以定義圓內接多邊形的外心、 重心、 歐拉圓心和垂心, 那麼圓內接多邊形的四心是否依然共線?
又四心的距離比能否維持不變呢? 這兩者都是我們感興趣的。
二、圓內接多邊形四心的定義
(一)外心
一般定義多邊形的外接圓圓心即是外心, 因此圓內接多邊形必有外心。
(二) 重心
將三角形想像成在頂點位置各放一顆質量相等的質點, 則此三個質點的質心就是三角形的重心。
因此依據力矩平衡的概念, 先找出其中兩質點的質心, 再跟剩餘的質點, 就可以確定最後的質心位置, 也就是三角形重心的位置。
依此類推, 就可以定義任意多邊形的重心。
$~\qquad $ (本定義不同於參考資料 是利用多邊形中線定義其重心)
(三) 歐拉圓心
如果將圓上一弦的中點視為兩邊形的歐拉圓心, 那麼三角形的歐拉圓心就是過此三中點之圓的圓心。
圓內接四邊形四頂點中任取三頂點可得四個三角形, 因此可得四個三角形的歐拉圓心, 而此時這四個歐拉圓心會共圓,
不妨就定義圓內接四邊形的歐拉圓心就是過此四點之圓(歐拉圓)的圓心。
依此類推, 就可以定義圓內接多邊形的歐拉圓心。
$~\qquad $ (引用參考資料 的定義)
(四) 垂心
三角形的三條高線交於一點, 稱為三角形的垂心。
圓內接四邊形四頂點中任取三頂點可得四個三角形, 因此可得四個三角形的垂心, 而此時這四個垂心會共圓,
不妨就定義圓內接四邊形的垂心就是過此四點之圓(垂心圓)的圓心。
依此類推, 就可以定義圓內接多邊形的垂心。 (引用參考資料的定義)
三、圓內接多邊形的四心共線與距離比
定理:
設圓內接 $n$ ($n\ge 3$) 邊形 $A_1 A_2\cdots A_{n-1} A_n$ 中, 其外心為 $O$、 重心為 $G$、 歐拉圓心為
$K$、 垂心為 $H$, 則此四心會共線且 $\overline{OG} : \overline{GK} : \overline{KH}=2 : (n-2) : n$。
$\qquad~$ (此定理是作者個人的創見)
證明:
(一)如圖一, 設 $\triangle A_1 A_2 A_3$ 的三頂點坐標分別為 $A_1 (x_1,y_1 )$, $A_2 (x_2,y_2 )$, $A_3 (x_3,y_3 )$,
其外接圓半徑為 $r$, 外心為 $O$ $(0,0)$, 則 $x_1^2+y_1^2=r^2$, $x_2^2+y_2^2=r^2$, $x_3^2+y_3^2=r^2$。
(參考資料 的假設)
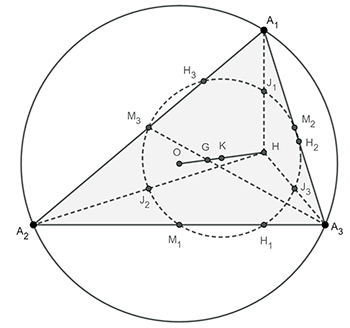 圖一
圖一
- 已知 $A_1$ 和 $A_2$ 的中點為 $M_3\Big(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\Big)$, 由前面三角形重心的定義可知 :
\begin{eqnarray*}
\triangle A_1 A_2 A_3 \ \hbox{的重心} \ G&=&\dfrac 23 \Big(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\Big)+\dfrac 13 (x_3,y_3)\\
&=&\Big(\dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}{3}\Big).\hskip 2cm~
\end{eqnarray*}
- 又 $A_2$ 和 $A_3$ 的中點為 $M_1\Big(\dfrac{x_2\!+\!x_3}{2},\dfrac{y_2\!+\!y_3}{2}\Big)$, $A_3$ 和 $A_1$ 的中點為
$M_2\Big(\dfrac{x_3\!+\!x_1}{2},\dfrac{y_3\!+\!y_1}{2}\Big)$,
由三角形各邊中點坐標之關係,
(參考資料 的證法)
易知 $\triangle A_1 A_2 A_3$ 的九點圓圓心
$K\Big(\dfrac{x_1+x_2+x_3}{2},\dfrac{y_1+y_2+y_3}{2}\Big)$,
且
$\overline{KM_1}=\dfrac 12\sqrt{x_1^2+y_1^2}=\dfrac 12 r$
$\overline{KM_2}=\dfrac 12\sqrt{x_2^2+y_2^2}=\dfrac 12 r$
$\overline{KM_3}=\dfrac 12\sqrt{x_3^2+y_3^2}=\dfrac 12 r$。
- 設 $\triangle A_1 A_2 A_3$ 的垂心 $H$ 為 $(x,y)$, 由三角形垂心的定義可知 :
$\overrightarrow{A_1 H}\cdot \overrightarrow{A_3 A_2}=0$,
$\overrightarrow{A_2 H}\cdot \overrightarrow{A_3 A_1}=0$, $\overrightarrow{A_3 H}\cdot \overrightarrow{A_2 A_1}=0$, (以下證法是作者個人的創見)
推得
\begin{eqnarray*}
(x-x_1 )(x_2-x_3 )+(y-y_1 )(y_2-y_3 )&=&0,\\
(x-x_2 )(x_1-x_3 )+(y-y_2 )(y_1-y_3 )&=&0,\\
(x-x_3 )(x_1-x_2 )+(y-y_3 )(y_1-y_2 )&=&0,\\
{\hbox{又}}
(x_2+x_3 )(x_2-x_3 )+(y_2+y_3 )(y_2-y_3 )&=&0\ \Leftrightarrow\ (x_2^2+y_2^2 )-(x_3^2+y_3^2 )=0,\\
(x_1+x_3 )(x_1-x_3 )+(y_1+y_3 )(y_1-y_3 )&=&0\ \Leftrightarrow\ (x_1^2+y_1^2 )-(x_3^2+y_3^2 )=0,\\
(x_1+x_2 )(x_1-x_2 )+(y_1+y_2 )(y_1-y_2 )&=&0\ \Leftrightarrow\ (x_1^2+y_1^2 )-(x_2^2+y_2^2 )=0,\hskip 1.6cm~
\end{eqnarray*}
故 $\triangle A_1 A_2 A_3$ 的垂心 $H(x,y)=(x_1+x_2+x_3,y_1+y_2+y_3 )$。
從而
$$\begin{array}{c}
\overrightarrow{OG}=\Big(\dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}{3}\Big),\qquad \overrightarrow{OK}=\Big(\dfrac{x_1+x_2+x_3}{2},\dfrac{y_1+y_2+y_3}{2}\Big),\\[12pt]
\overrightarrow{OH}=(x_1+x_2+x_3 , y_1+y_2+y_3 ),\end{array}$$
可推知 : $\overrightarrow{OG}//\overrightarrow{OK}//\overrightarrow{OH}$, 且
\begin{eqnarray*}
\overrightarrow{GK}=\overrightarrow{OK}-\overrightarrow{OG}&=&\Big(\dfrac{x_1+x_2+x_3}{6},\dfrac{y_1+y_2+y_3}{6}\Big),\\[8pt]
\overrightarrow{KH}=\overrightarrow{OH}-\overrightarrow{OK}&=&\Big(\dfrac{x_1+x_2+x_3}{2},\dfrac{y_1+y_2+y_3}{2}\Big),
\end{eqnarray*}
故 $\triangle A_1 A_2 A_3$ 的四心 $O$、 $G$、 $K$、 $H$ 共線且 $\overline{OG} : \overline{GK} : \overline{KH}=2 : 1 : 3$。
(二) 如圖二, 設圓內接四邊形 $A_1 A_2 A_3 A_4$ 的四頂點坐標分別為 $A_1 (x_1,y_1 )$, $A_2 (x_2,y_2 )$,
$A_3 (x_3,y_3 )$, $A_4 (x_4,y_4 )$, 其外接圓半徑為 $r$, 外心為 $O$ (0,0),
則 $x_1^2+y_1^2=r^2$,
$x_2^2+y_2^2=r^2$, $x_3^2+y_3^2=r^2$, $x_4^2+y_4^2=r^2$。 (參考資料 的假設)
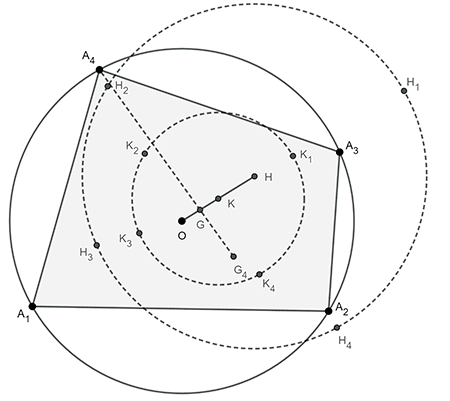 圖二
圖二
-
已知 $\triangle A_1 A_2 A_3$ 重心為 $G_4$ $\Big(\dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}{3}\Big)$, 由前面多邊形重心的定義可知 :
圓內接四邊形 $A_1 A_2 A_3 A_4$ 的重心為
\begin{eqnarray*}
G&=&\frac 34 \Big(\dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}{3}\Big)+\frac 14 (x_4,y_4)\\
&=&\Big(\dfrac{x_1+x_2+x_3+x_4}{4},\dfrac{y_1+y_2+y_3+y_4}{4}\Big).
\end{eqnarray*}
如圖三, 已知圓內接 $(n-1)$ 多邊形 $A_1 A_2 A_3\cdots A_{n-1}$ 的重心為
$$G_n \Big(\frac{x_1+x_2+x_3+\cdots+x_{n-1}}{n-1},
\frac{y_1+y_2+y_3+\cdots+y_{n-1}}{n-1}\Big),$$
則由多邊形重心的定義可知 :
圓內接 $n$ 多邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n$ 的重心為
\begin{eqnarray*}
G&=&\frac{n-1}n \Big(\frac{x_1+x_2+x_3+\cdots+x_{n-1}}{n-1},\frac{y_1+y_2+y_3+\cdots+y_{n-1}}{n-1}\Big)+\frac 1n (x_n,y_n )\\
&=&\Big(\frac{x_1+x_2+x_3+\cdots+x_{n-1}+x_n}n,\frac{y_1+y_2+y_3+\cdots+y_{n-1}+y_n}n\Big),
\end{eqnarray*}
故由數學歸納法得證此重心公式為真。
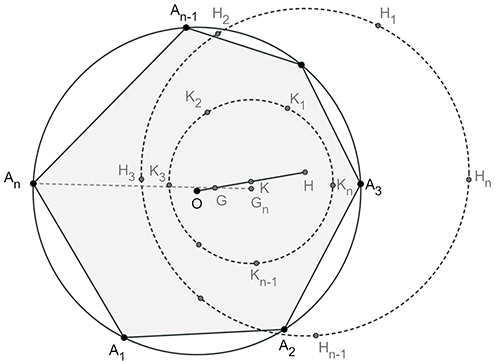 圖三
圖三
-
已知圓內接四邊形 $A_1 A_2 A_3 A_4$ 中, $\triangle A_1 A_2 A_3$、 $\triangle A_2 A_3 A_4$、 $\triangle A_3 A_4 A_1$、 $\triangle A_4 A_1 A_2$
的歐拉圓心分別為
$$K_4\Big(\dfrac{x_1+x_2+x_3}{2},\dfrac{y_1+y_2+y_3}{2}\Big)\hbox{、 }K_1 \Big(\frac{x_2+x_3+x_4}2,\frac{y_2+y_3+y_4}2\Big)\hbox{、}$$
$$K_2\Big(\frac{x_3+x_4+x_1}2,\frac {y_3+y_4+y_1}2\Big)\hbox{、 }K_3 \Big(\frac{x_4+x_1+x_2}2,\frac{y_4+y_1+y_2}2\Big),$$
則由這四個三角形歐拉圓心坐標之關係, (以下參考資料 的假設與證法)
易知圓內接四邊形 $A_1 A_2 A_3 A_4$ 的歐拉圓心為 $K\Big(\dfrac{x_1+x_2+x_3+x_4}{2},\dfrac{y_1+y_2+y_3+y_4}{2}\Big),$
\begin{eqnarray*}
\hbox{且}\qquad \overline{KK_1}&=&\frac 12 \sqrt{x_1^2+y_1^2}=\frac 12 r,\qquad \overline{KK_2}=\frac 12 \sqrt{x_2^2+y_2^2}=\frac 12 r,\\
\overline{KK_3}&=&\frac 12 \sqrt{x_3^2+y_3^2}=\frac 12 r,\qquad \overline{KK_4}=\frac 12 \sqrt{x_4^2+y_4^2}=\frac 12 r.
\end{eqnarray*}
如圖三, 設圓內接 $n$ 多邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n$ 的 $n$ 個頂點坐標分別為 $A_1 (x_1,y_1 )$,
$A_2 (x_2,y_2 )$, $A_3 (x_3,y_3 )$, $\ldots$, $A_{n-1} (x_{n-1},y_{n-1} )$, $A_n (x_n,y_n )$, 其外接圓半徑為 $r$,
外心為 $O$ (0,0), 則
$$x_1^2\!+\!y_1^2=r^2,\ x_2^2\!+\!y_2^2=r^2,\ x_3^2\!+\!y_3^2=r^2, \ldots, \ x_{n-1}^2\!+\!y_{n-1}^2=r^2,\
x_n^2\!+\!y_n^2=r^2.$$
已知圓內接 $n$ 多邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n$ 中, $n$ 個圓內接 $(n-1)$ 多邊形
$A_1 A_2 \cdots A_{n-1}$、 $A_2 A_3 \cdots A_n$ 、 $\ldots$ 、 $A_n A_1 A_2\cdots A_{n-2}$ 的歐拉圓心分別為
\begin{eqnarray*}
&&K_n \Big(\frac{x_1+x_2+x_3+\cdots+x_{n-1}}2,\frac{y_1+y_2+y_3+\cdots+y_{n-1}}2\Big),\\
&&K_1 \Big(\frac{x_2+x_3+x_4+\cdots+x_n}2,\frac{y_2+y_3+y_4+\cdots+y_n}2\Big),\ldots,\\
&&K_{n-1}\Big(\frac{x_n+x_1+x_2+\cdots+x_{n-2}}2,\frac{y_n+y_1+y_2+\cdots+y_{n-2}}2\Big),
\end{eqnarray*}
則由這 $n$ 個圓內接 $(n-1)$多邊形歐拉圓心坐標之關係,
易知圓內接 $n$ 多邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n$ 的歐拉圓心為
$$ K\Big(\frac{x_1+x_2+x_3+\cdots+x_{n-1}+x_n}2,\frac{y_1+y_2+y_3+\cdots+y_{n-1}+y_n}2\Big),$$
且 $$\overline{KK_1}=\frac 12 \sqrt{x_1^2+y_1^2}=\frac 12 r,\ \ldots\ , \overline{KK_{n-1}}=\frac 12 \sqrt{x_{n-1}^2+y_{n-1}^2}=\frac 12 r,$$
$$\overline{KK_n} ̅=\frac 12 \sqrt{x_n^2+y_n^2}=\frac 12 r.$$
故由數學歸納法得證此歐拉圓心公式為真。
- 已知圓內接四邊形 $A_1 A_2 A_3 A_4$ 中, $\triangle A_1 A_2 A_3$、 $\triangle A_2 A_3 A_4$、 $\triangle A_3 A_4 A_1$、 $\triangle A_4 A_1 A_2$
的垂心分別為
$$\begin{array}{ccc}
H_4 (x_1+x_2+x_3, y_1+y_2+y_3 )\hbox{、 }&\quad~&H_1 (x_2+x_3+x_4, y_2+y_3+y_4 )\hbox{、}\\[8pt]
H_2 (x_3+x_4+x_1, y_3+y_4+y_1 )\hbox{、 }&& H_3 (x_4+x_1+x_2, y_4+y_1+y_2 ),\end{array}$$
則由這四個三角形垂心坐標之關係, (以下證法是作者個人的創見)
易知圓內接四邊形 $A_1 A_2 A_3 A_4$ 的垂心為 $H(x_1+x_2+x_3+x_4, y_1+y_2+y_3+y_4 )$,
$$\begin{array}{rccccc}
\hbox{且}\qquad \overline{HH_1}&=&\sqrt{x_1^2+y_1^2}=r,\qquad~& \overline{HH_2}&=&\sqrt{x_2^2+y_2^2}=r,\\[8pt]
\overline{HH_3}&=&\sqrt{x_3^2+y_3^2}=r,\qquad~& \overline{HH_4}&=&\sqrt{x_4^2+y_4^2}=r.
\end{array}$$
如圖三, 已知圓內接 $n$ 多邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n$ 中, $n$ 個圓內接 $(n-1)$ 多邊形
$A_1 A_2 A_3\cdots A_{n-1}$、 $A_2 A_3 A_4\cdots A_n$、 $\ldots$ 、 $A_n A_1 A_2\cdots A_{n-2}$ 的垂心分別為
\begin{eqnarray*}
&&H_n (x_1+x_2+x_3+\cdots+x_{n-1}, y_1+y_2+y_3+\cdots+y_{n-1} ),\\
&&H_1 (x_2+x_3+x_4+\cdots+x_n, y_2+y_3+y_4+\cdots+y_n ),\ldots,\\
&&H_{n-1} (x_n+x_1+x_2+\cdots+x_{n-2}, y_n+y_1+y_2+\cdots+y_{n-2}),
\end{eqnarray*}
則由這 $n$ 個圓內接 $(n-1)$多邊形垂心坐標之關係, 易知圓內接 $n$ 多邊形 $A_1 A_2 \cdots A_n$ 的垂心為
$$H(x_1+x_2+\cdots+x_n, y_1+y_2+\cdots+y_n ),$$
$$\hbox{且}\ \overline{HH_1}\!=\!\sqrt{x_1^2\!+\!y_1^2}\!=\!r,\ \ldots\ ,\ \overline{HH_{n-1}}\!=\!\sqrt{x_{n-1}^2\!+\!y_{n-1}^2}\!=\!r, \quad
\overline{HH_n}\!=\!\sqrt{x_n^2\!+\!y_n^2}\!=\!r.$$
故由數學歸納法得證此垂心公式為真。
\begin{eqnarray*}
\hbox{從而}\ \overrightarrow{OG}&=&\Big(\frac{x_1+x_2+\cdots+x_n}n,\frac{y_1+y_2+\cdots+y_n}n\Big),\hskip 5cm~\\
\overrightarrow{OK}&=&\Big(\frac{x_1+x_2+\cdots+x_n}2,\frac{y_1+y_2+\cdots+y_n}2\Big),\\
\overrightarrow{OH}&=&(x_1+x_2+\cdots +x_n, y_1+y_2+\cdots+y_n ),
\end{eqnarray*}
可推知 : $\overrightarrow{OG}//\overrightarrow{OK}//\overrightarrow{OH}$,
\begin{eqnarray*}
\hbox{且}\qquad \overrightarrow{GK}=\overrightarrow{OK}-\overrightarrow{OG}&=&\frac{n-2}2 \Big(\frac{x_1+x_2+\cdots+x_n}n,\frac{y_1+y_2+\cdots+y_n}n\Big),\\
\overrightarrow{KH}=\overrightarrow{OH}-\overrightarrow{OK}&=&\frac n2 \Big(\frac{x_1+x_2+\cdots+x_n}n,\frac {y_1+y_2+\cdots+y_n}n\Big),
\end{eqnarray*}
故圓內接 $n$ ($n\ge 3$) 多邊形 $A_1 A_2 A_3\cdots A_{n-1} A_n$ 的四心 $O$、 $G$、 $K$、 $H$ 也會共線,
且 $$\overline{OG} : \overline{GK} : \overline{KH}=1 : \dfrac{n-2}2 : \dfrac n2=2 : (n-2) : n.$$
參考資料
李冬梅, 白世忠譯。 幾何學中的歸納法。 九章出版社, 開明(大陸)出版社, 101-119。
黃家禮編著。 幾何明珠。 九章出版社, 155-156。
---本文作者任教國立金門高級中學---
|




