| 發刊日期 |
2022年12月
|
|---|---|
| 標題 | 數學與現代科技 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
民國111年7月13日
崔茂培教授: 各位大家好, 我是現任數學系系主任。 非常感謝地主台大科教中心的協助, 讓我們能在這麼短的時間規劃這個活動; 特別是于宏燦主任, 還有中心同仁的協助。 大概兩個禮拜前, 我們來這裡拜訪于主任, 聊說要推動一些數學科普活動、一些交流。 因為剛好姚鴻澤回來, 又因為我們數學辦的這種科普活動好像相對比較少; 因為我們學數學的, 大部分好像是住在深山裡面的和尚, 做自己的事情。 剛好姚鴻澤最近因為院士會議回來, 正好在理論中心訪問, 就跟他聊了一下。 因為他有一些想法, 我就說「那你講給我們的高中生聽看看好了」。 他也很爽快, 在很短時間就答應辦這場演講。 所以其實他這幾天花很多時間在準備這演講, 我覺得好像比準備理論中心演講還花更多時間。 我才知道說, 要跟高中生講這些, 不是這麼容易。 我很快介紹一下姚鴻澤教授; 他是台大數學系 1980 年畢業的系友, 是台大的傑出校友, 目前是理論中心的 distinguished scholar。 我覺得他應該是什麼都會。 他專精領域是數學, 特別是數學物理, 早期是一些分析, 這幾年是比較偏重機率領域的研究。 他的工作影響這些機率論。 之後是隨機矩陣, 另外還有統計物理、量子力學等等很多方面。 他得過很多的獎項, 我就不再一一敘述。 其實我認識姚鴻澤很久了。 這個人還滿特別。 大家都知道他數學很好, 其實他運動也很好。 我記得他上次回來台灣, 為了精進他自己的桌球, 特別請教練來讓自己更厲害。 所以他其實做事非常認真, 也很會打羽球, 也很會滑雪。 他其實對台灣的教育也非常地關心, 因為台灣這幾年的一些政策$\cdots$, 如果沒記錯, 他前幾年有回來和政府有$\cdots$, 不過他也很低調, 所以很多事情他可能沒有講, 其實他幕後推動, 不過他都沒講, 我不好意思講。 所以說他其實非常關心台灣的教育。 這次回來, 他也提到一些數學現在的發展。 今天真的很高興特別請到他, 能夠跟我們分享「數學與現代科技」。 我們就歡迎姚鴻澤院士。 姚鴻澤院士: 非常謝謝讓我有這機會跟大家談這個話題。 我自己整個教育過程是滿特別的, 可能跟大家都不太一樣。 可是我看到現在很多人很擔心、很懷疑說:該不該學這些基礎科學, 或者該不該學數學; 擔心說這樣會不會走進一個非常純粹的方向$\cdots$。 就是會擔心這個事情。 像我, 我在當時根本就不擔心, 因為當時台灣的環境相對來說相當落後, 當時學了什麼都比我們爸爸媽媽還要好, 所以完全沒有這個顧慮。 我想, 因為我現在看到我小孩, 就知道他也會擔心說:他能不能比我們這一代還做得更好? 他會有這個疑問。 我這一代當然是絕對沒這問題, 因為我的祖父連他自己的名字都不會寫, 所以我要超過他是非常容易的。 牛頓力學、Maxwell方程組、統計力學、愛因斯坦方程、量子力學現在就先開始談一下我對數學與現代科技的一些看法。 主要先講一些歷史, 然後再談談比較近代的東西。 從以前, 從譬如說像牛頓力學, 寫做 $F=ma$, 其中 $a$ 是加速度, 是位置函數的二次導數, $a=\dfrac{d^2 x}{dt^2}$。 同學看到這件事情的時候, 要想到說, 我們現在教微積分通常是在高中第三年;可是你要知道, 牛頓寫下這些東西的時候, 到現在已經是幾百年了。 所以為什麼幾百年前的東西, 我們現在要到高三才開始學習? 這其實也是有點奇怪。 我們到高中三年級才要學習 300 年前發現、發明的東西, 倒是滿奇怪。 但我現在強調是說, 其實牛頓力學和微積分是不可分離的。 因為牛頓力學是寫成微積分的形式, 因為你要談什麼是加速度的話, 一定要知道什麼是微分。 再來是牛頓的萬有引力定律, 他寫出來的 force 剛好是這樣子: \begin{align*} F=G\frac{m_1 m_2}{|r_1-r_2 |^2},\qquad (\hbox{$G$: 重力常數}); \end{align*} 你看他把 force 放到前面。 牛頓力學裡, 他就可以算行星等等的運動。 當然更早之前還有別的東西, 但是在我這個演講, 我們要從這邊開始, 最原始的牛頓力學, 就是第一個就和數學是息息相關的。 再來第二個。 第二個講到的是電磁學的 Maxwell equations; 電場是 $E=(E^1,E^2,E^3)$, 磁場是 $B=(B^1,B^2,B^3)$, 電場跟磁場寫出來的方程式是這個樣子: \begin{align*} &\nabla \cdot E=0,\\ &\nabla \cdot B=0,\\ &\nabla \times B-\frac{\partial E}{\partial t}=0,\\ &\nabla \times E+\frac{\partial B}{\partial t}=0. \end{align*} 這個方程式其實不是全部是 Maxwell 發現的, 並且我在這裡只寫下它在真空的型態。 可是 Maxwell 找到 key equation, 所以現在大家都把這四個 equations 合在一起叫做 Maxwell equations。 你可以看到, 微積分絕對是裡面最最重要的一個東西。 下一個我要說的是波茲曼的統計物理 (Boltzmann's statistical physics)。統計物理有一個所謂的 probability measure, 就是一個概率, 寫成 exponential $e^{-\beta H(x)}$, 這裡 $\beta$ 是溫度 $T$ 的倒數 $\beta =\dfrac{1}{\kappa T}$ ($\kappa$: Boltzmann 常數)。 它告訴我們說, 譬如我們現在這間屋子裡面有一大堆的 particles, 有一大堆粒子, 那麼你發現說這些粒子在這個空間的概率是多少。 它告訴你說, 你有一個 $H$, 通常是叫做 Hamiltonian, 就是它的能量, 那麼它的概率是 $\exp(-\beta H)$。 當然寫下波茲曼統計物理的時候, 背後的很多很多都是現代的概率論; 它影響了很多概率論, 並且也用了很多概率論的技巧、工具。 接下來講的, 對非數學系的學生可能比較難看懂, 我只是稍微 show 一下。 我是要說 Maxwell's equations, 現在若用微分幾何的符號來寫的話, 其實寫起來非常簡單, 只是一個幾何上很簡單一個方程式: \begin{align*} &\hskip 2cm dF=0,\quad d*F=0,\\ \hbox{其中} &F=\sum_{\mu ,\nu}F^{\mu \nu} dx^\mu \wedge dx^\nu ,\qquad (x^\mu =(t,x)),\\ \hbox{而} &F^{\mu \nu} =-F^{\nu \mu}=\left(\begin{array}{ccccccc} 0&&-E^1&&-E^2&&-E^3\\ E^1&&0&&-B^3&&B^2\\ E^2&&B^3&&0&&-B^1\\ E^3&&-B^2&&B^1&&0 \end{array}\right).\end{align*} 下一個我們要談的, 是相對論的愛因斯坦方程式 (Einstein equation)。 相對論的愛因斯坦的方程式 $$G_{\mu \nu} =\kappa T_{\mu \nu} ,$$ 是說 Einstein tensor $G_{\mu \nu}$ 等於 $\kappa$ 乘上 energy momentum tensor $T_{\mu \nu}$。 這個 Einstein tensor $G_{\mu \nu}$ 和空間的曲率有關係, 所以你看到: 這整個 Einstein equation, 基本上是微分幾何的一個方程式, 所以我在這邊強調說, 基本科學的發展跟數學是息息相關的。 下一個例子講到 1910 年代; 當時科學除了相對論以外, 最重要的就是所謂的量子力學。 量子力學方程式 (Schrödinger equation) 寫下來是這個樣子 $$i\hbar \frac{\partial\psi}{\partial t}=H\psi ,\qquad \hbox{其中}\ \hbar =1.054\times 10^{-27}\ \hbox{erg sec},$$ 這是量子力學的方程式; $\psi$ 叫做波函數, $H$ 同樣是能量, 和 Boltzmann 方程的 $H$ 一樣是個能量算子。 你看到說, 整個量子力學寫出來, 其實也是一個數學的方程式。 它影響到數學的算子代數與泛函分析, 還有偏微分方程, 很多都和這有關係。 當然它還與近代物理和代數幾何, 或是量子場論相關。 現代科技: 國際象棋、圍棋、MRI Image、Blockchain、量子計算談到這些東西的時候, 我想要講一些故事。對我來說, 在我整個學術研究過程裡面, 看到第一個滿 shocking 的是國際象棋; 當年 IBM 的 Deep Blue, 打贏了當時的世界冠軍 Kasparov。 我們當時在看國際象棋的演變的時候, 大家一直在等, 等著看哪一年的電腦會贏國際象棋。 在 1996 年之前的 1990 或 1980 年代, 大家就覺得說, 電腦每一年都在進步, 覺得總有一年電腦會超過人類下象棋。 可是電腦還是一直沒有辦法贏, 一直到了最後, 在 1997 年才贏了第一局。 雖然這在當時是一個 historical event, 但是其實並不是一個 surprise, 大家並沒有很驚訝電腦下贏了人類, 因為覺得這事情遲早要發生。 因為國際象棋的棋盤很小, 它的子也滿有限, 所以一直並不覺得這是一件很奇怪的事情。 但是下一件事情, 在 2016 年。 我覺得這個是所有學科學和學數學的人都要記得的日子。 我不知道大家有沒有看整個那個比賽? 2016 年, DeepMind 的 AlphaGo, 四比一打敗韓國 Lee Sedol。 韓國那位是$\cdots$, 我不知道在圍棋界他算不算是世界冠軍, 但是就算不是真正的第一名, 也差不多是了。 你知道圍棋這個事情。 你如果在 2010 年的時候去問所有的人: 什麼時候電腦會下贏人類的圍棋? 很多人會跟你說我們這輩子看不到。 所以這是這麼樣的一個非常非常的驚訝的事情, 竟然 computer 會下贏人類。 非常奇怪。 我等一下稍微解釋一下, 因為我自己, 我也不是寫這程式的人, 我和這個差得滿遠, 但是我自己在旁邊的觀察, 看到一些現象, 然後等一下可以跟大家分享一下。 另外我們來談 MRI 的 image。 以前照 MRI, 你要進去裡面躺一個小時, 甚至更長時間, 在那裡不能動的。 現在 MRI 很快, 十幾分鐘、二十分鐘就結束了。 這主要是, 才差不多在十幾年前, compressed sensing 方面有很大的進展, 才會現在 MRI image 進步這麼多。 大家可能覺得 MRI image 好像真的是把你身體照得很清楚, 可是你如果真的看過 MRI image 就知道, 看起來東西全部是黑的和白的, 你根本看不出什麼東西。 其實真的要做到所謂的 MRI image, 真的看得很清楚, 我想這還是非常地遙遠。 但是和以前比起來, 這個進步已經是非常不可思議。 這 compressed sensing, 大概在數學裡面和 electrical engineering 電機系裡面, 將近有 20 年, 有非常非常多人都在做這個工作。


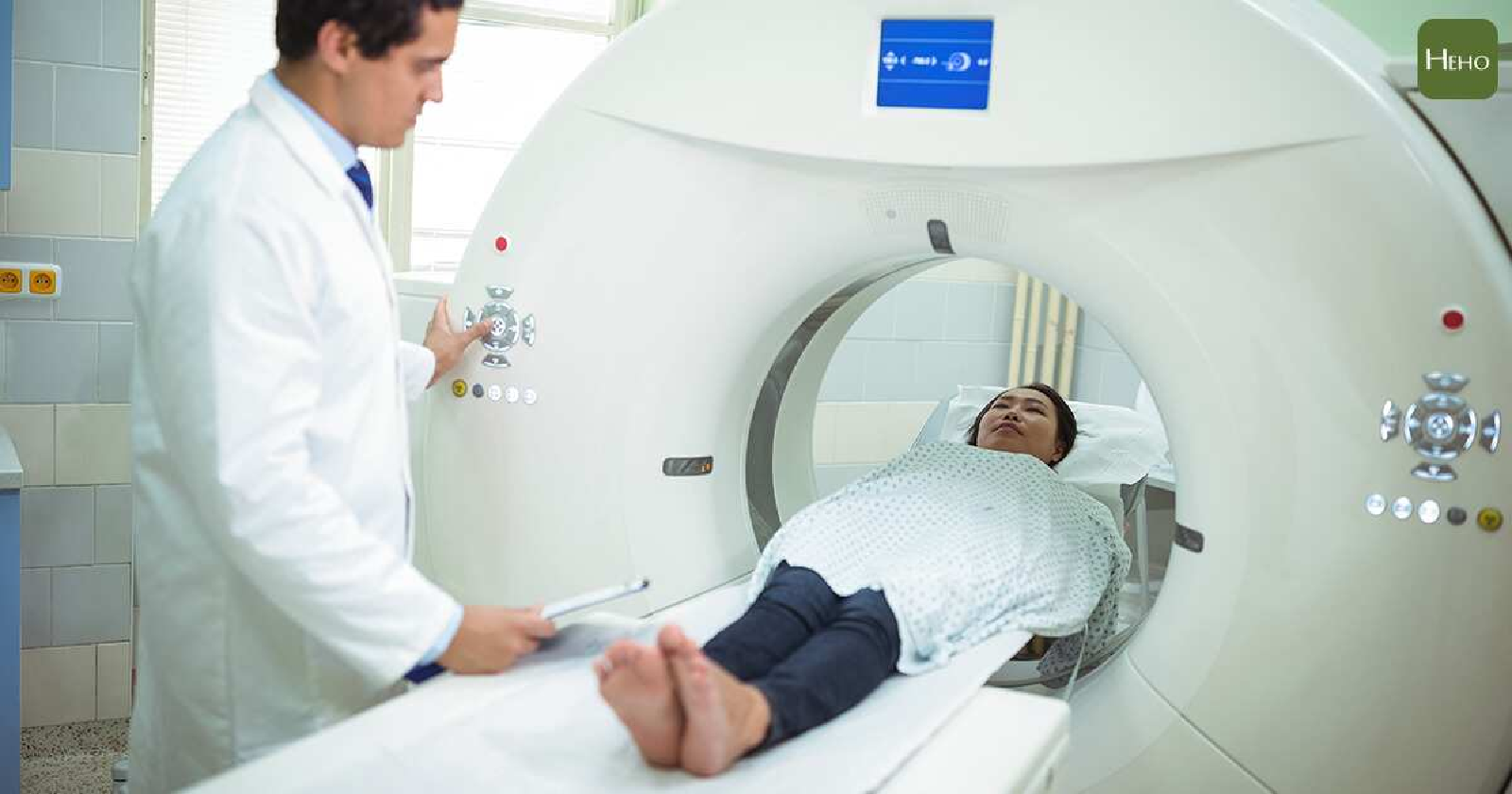
另外我再提幾個例子。 第一個是所謂的 blockchain, 就是cryptocurrency。 它和數學的代數和數論有關係。 如果你問我 blockchain, 其實我不太清楚它真的 exactly 怎麼 work 的, 我只提到說現在很多這樣的東西。 另外一個我想要提的例子, 是所謂的量子計算 quantum computing。 Google 大概是兩年前吧? 我記得是 2019。 兩年前還三年前, 大概兩年前, Google 的 Sycamore, 它有 54 個量子位元 qubits。 Qubit 就是和古典的 bit, 1、 0 的 bit, 相對應的量子的東西。 它做出一個計算, 號稱這個計算超級電腦要算一萬年, 可是大家不要聽到一萬年, 好像覺得差別很多。 Google 這個東西, 它的成就其實 IBM 有意見。 IBM 說兩天就算得出來。 但是我也不知道是真的還是假的。 那麼 Google 到底是算什麼東西? 其實我也不是很清楚。 我也問過一些人, 他們也沒辦法跟我解釋 Google 到底算了什麼東西。 所以現在量子電腦當然還有很大的限制, 它到底能不能真的去 run 這些量子演算法 quantum algorithm? 其實也不是很清楚。 我只是想跟大家提到說, 你看這樣的東西, 其實和數學有什麼樣的關係。 除了這 Google 的 Sycamore 之外, IBM 還有一個 Eagle, 它有 127 個 qubits。 除了這個以外還有其他的, 現在 Google 聽說在做一個有 1,000 個 qubits 的 quantum computer。 它後面的數學, 這個 quantum algorithm 要怎麼去寫? 這 quantum algorithm 的限制是什麼? 什麼是這所謂的量子糾錯碼 quantum error correcting code? 是要怎麼樣? 這個 quantum error correcting code 和 quantum algorithm, 還有它最後所謂的這個 quantum information, 到底它的基礎是什麼? 很多很多數學家, 很多電腦學家也在做, 但是它其實和數學非常相關。 我等一下有可能的話就稍微解釋一下。 另外還有其他例子, 就像大家常聽到的圖像辨識 (image recognition), 甚至是自動駕駛 (autopilot)、 數學金融 (mathematical finance), 還有一些市場設計 (market designing) 和賽局理論 (game theory) 等等。



你會看到現在數學在各個地方的應用。不是像大家想說, 數學家一定要去做代數幾何。 並沒有這種事情。 沒有說數學家一定要做數論。 其實有非常多的事情可以做。 你可以從數學進去, 然後往其他的方向走。 當然你也可以留在數學裡面做純數學, 如果你自己真的那麼有興趣。 當我在講這個東西的時候, 我想跟同學講, 我並不是說因為我是數學家, 所以就建議你們學數學。 我兒子大學也是念數學的, 不是說$\cdots$, 我是真的這麼想。 他是數學和 Computer Science 的 double major。 線性回歸、Loss Function我稍微解釋一下。 剛才講這些都是 technology, 現在我先講幾行的數學。 我稍微介紹一下, 這個可能稍微困難一點, 譬如說, 我們常看到 Lasso 這個字, 就是說在統計上面看到 Lasso (Least Absolute Shrinkage and Selection Operation) 這個字。 Lasso 這個字是什麼意思呢? 這個英文名字其實現在已經沒有人知道、沒有人記得了。 最重要的是, 它是一種線性的回歸分析的方法。 那麼什麼叫線性回歸分析呢? 就是說你現在先看到一個圖像, 看到一個 image, 不管是貓還是狗的 image, 你把這個圖像的每一個 pixel 寫出來之後, 寫成一個向量 $$x_J=\left(\begin{array}{c} x_{j1}\\ \vdots\\ x_{jd}\end{array}\right);$$ 你把它寫出來這樣子。 一張圖就是這麼一個向量。 這是一個很高維數的空間的向量; 因為譬如說 1000 多個乘 1000 多個等等, 它是一個非常高維數的一個向量。 那麼你要做的是什麼? 現在假設給一個 $y_j\in\{0,1\}$, 它是 0 或是 1, 譬如說 1 就是一隻貓, 0 就是一隻狗。 你現在要做的事情是, 你要找到一個函數 $$f(x)=y;$$ 這樣來看, 你就覺得有點可笑, 我們弄半天其實只要找一個函數 $f(x)=y$, 就這樣子而已。 這個 $x$ 是貓, $y$ 就是 1; 如果 $x$ 是其他東西, $y$ 就要是 0, 就這麼簡單。 你就是要找這麽一個函數。 那麼這個函數 $f$ 到底是什麼? 你真的可以說這函數存在? 它是 discrete 的, 當然是存在。 但是你要怎麼樣把這函數表達出來? 一個方法是這樣, 就是說: 你現在給我一組 image $\{x_i\}$; $x_i$ 就是一個 copy 的 image。 現在你有很多組 image。 這些 image 有的 $y_i$ 是 1, 這時候就是貓, 它是 0 的時候就不是貓。 那麼你現在從這一組, 我給你的這一組, 所謂的訓練的 training data, 你要怎麼去找這個函數 $f$? 現在問題是: 怎麼找到一個函數呢? 當 $x_i$ 是貓的時候就要是 1, 當 $x_i$ 不是貓的時候就要是 0, 就這樣子。 所謂的 loss function 通常數學寫做 $$L=\frac 1{2n}\sum_{i=1}^n(f(x_i)-y_i)^2.$$ Loss function 這個名字其實也沒什麼意義, 因為英文有各式各樣不同的名字, 中文更不用講, 也有很多的翻譯。 你現在考慮這個量, 這個量是什麼? 就是說, 當你的 assignment 是對的話, 也就是 $f(x_i )=y_i$ 的時候, 它就是 0; 它錯的話, 就不是 0。 你希望說這個量越小越好; 就是這樣, 你就是要找出這個 $f$。 你要找出這個 $f$, 你要怎麼找呢? 第一要找出線性的。 所謂的線性回歸分析就是說你找個 $x$ 的線性函數, 就是像 $$f=x^t\theta=\sum_{k=1}^d x_k\theta_k,$$ 的多項式, degree 剛好是一的多項式。 你在 degree 是一的函數裡面去找, 找最好的 $f$。 你要找 degree 是一的函數, 你就去找這個 $\theta $, 找最好的 $\theta $, 就這樣子。 所以你把這所有整個問題寫出來, 它就是變成說你要去做考慮, 找這個 $\theta $, 讓它取得 $\inf_{\theta \in \mathbb{R}^d}\|y-x^t \theta\|^2 $; 你要找最好的 $\theta $, 就是找讓 $\|y-x^t \theta \|^2=\sum_{i=1}^n(f(x_i )-y_i )^2$ 最小的 $\theta $。 然後它後面有時候要加上一個 penalty $\|\theta\|_p^p$, $$\inf_{\theta \in\mathbb{R}^d}\|y-x^t \|^2+\lambda\|\theta\|_p^p,\qquad (\|\theta\|_p^p=\sum_k|\theta_k|^p);$$ $\theta$ 的某一種 norm 的 penalty; 在 technique 來說, $p$ 通常是取 0 或是 1。 這個 $p$-norm 寫做剛好是 $p$ 次方。 這個當然有點專業。 $\lambda$ 要看你的 penalty 要調得多強。 通常 $p=1$; compress sensing 通常 $p$ 取 0 或是 1; $p=2$ 大概就是 Lasso 的。 我給你一組圖像, 然後你就去找這個 $\theta$; 我再給你另外一組, 你可能又找出另外一組 $\theta$; 並且真正最好的 $\theta$ 你也不見得找得到。 你現在找到這個 $\theta$, 就得到這個函數的 approximation $f=x^t\theta$。 你接下來給我一個新的 image, 我就把它帶到這個函數; 這個函數如果給我的值是 0, 我就說它是貓; 從新的 image 把它帶到這個函數 $f$, 出來看是 1 或是 0; 你看它是 1 還是 0, 決定它是貓或不是貓, 就這樣子。 古典的統計與現在的這種高維度的、 high dimensional 的 data 到底有什麼差別? 在古典的統計, image 的 dimension $d$ 通常是小的。 你的一個圖像在 $d$ 維空間裡面; 通常以前的 $d$ 很小, 是 10、 20 等等, 現在 $d$ 都是 1000、 都上萬的, 或是一百萬之類的, 非常高維度。 所以整個的差別就是說, 當 $d$ 在變的時候, 從這個小的 $d$ 到很大的 $d$, 到底有什麼大的差別? 它的差別就是說, 原先的古典統計, 通常關心的是這個概率裡面的大數法則, 或中央極限定理。 但是當你這個 $d$ 變得很大的時候, 這些大數法則、中央極限定理, 雖然還是有用, 可是你已經不能完全用這樣的東西, 其實整個數學的基礎都已完全改變了。 它改變之後, 你需要的是其它各種東西, 譬如說你需要隨機矩陣, 需要高維度的分析, 需要一些 concentration 的一些不等式, 然後數學的統計力學等等都會進來。 Neural Network那麼, 下一個我想再說幾分鐘, 就是現在很熱門的這個 neural network; 每次都看到這個圖, 你到哪裡去大家都給你看這個圖, 那這圖是什麼意思?

這張圖的意思就說, 我剛才要去找函數 $f$, 是用一個線性函數。 可是線性函數是非常特別的函數, 它其實不太可能會對。 那就是為什麼以前數學人一講到統計, 就覺得說統計人都在用線性回歸分析, 都覺得這些東西一點都沒有希望、沒有未來。 那麼 neural network 的 idea 是這個樣子。 (另外說一個題外話, 真的人腦、這個生物的腦袋是不是這個樣子, 現在已經沒有人關心了, 反正現在最重要是這個 idea 能 work)。 然後它怎麼做呢? 現在這函數, 你想用 neural network, 像上圖的東西表達出來。 這樣的東西是什麼意思呢? 這個東西是說, 我還是給你一組像剛才講的 $\{x_i,y_i \}_{i=1}^n$, image 是 $x_i=\left(\begin{array}{c} x_{i1}\\ \vdots\\ x_{id}\end{array}\right)$, $y_i$ 是 1 或是 0, 表示是貓或不是貓。 可是 loss 函數改變了, 變成這個樣子 $$\min_{\theta}L(\theta)=\frac 1{2n}\sum_{k=1}^n(f(x_i,\theta)-y_i)^2,$$ 其中 $$f(x,\theta)=\sum_{i=1}^ma_i\sigma\Big[\sum_{j=1}^m W_{ij}^{(2)}\sigma\Big(\sum_{k=1}^{d} W_{jk}^{(1)}x_k\Big)\Big],\quad \theta=(W^{(1)},W^{(2)},a).$$ 我再把這函數解釋一下。 你從這個 $x$ 開始, 就是 image 那個 $x$, 用一個 parameter, 就是用一個矩陣 $W$, 把 $x$ 對到這個新的矩陣上去, 得到 $\sum_{k=1}^dW_{jk}^{(1)}x_k$, 接著 summation over $k$。 之後你給它作用一個非線性的函數 $\sigma$。 這非線性函數 $\sigma$ 作用完了之後, 你把它再做一層。 所以前面 layer 1 的 $x$ 跑到 hidden layer 1 的 $\sum_{k=1}^dW_{jk}^{(1)}x_k$, 然後你就 apply $\sigma$。 之後你到下一層, 再乘上下一層的 $W_{ij}^{(2)}$, 它就跑到下一層 hidden layer 2。 跑到下一層來之後, 你最後還要歸結到一個東西。 你再乘上一個 $a$; 因為最後這不是一個矩陣, 就乘上一個 $a$, 再把它加起來。 它就是你這個函數。 現在要調參數。 你要調的參數就是這個 $\theta=(W^{(1)}$, $W^{(2)},a)$; 我們剛才線性回歸要找 $\theta$, 現在變成有兩層的矩陣, 加上最後這個 $a$。 這是兩層, 但是你也可以做更多層。 所以它的意思是什麼?意思是說, 我現在要怎麼去 approximate 這個函數? 我現在有更多的選擇。 這個選擇就是這個參數 $W$ 和 $a$。 我現在寫的就是一個兩層的 neural network, 就是要做這個事情。 從你的 data 裡面, 你從你的 data 看到這 $\{x_i,y_i\}_{i=1}^n$, 你去選 $W$ 和 $a$, 讓剛才這個函數 $\sum_{i=1}^n (f(x_i,\theta)-y_i )^2$ 最小。 這是兩層。 這個函數 $\sigma$ 通常叫做 activation function, 例如常看到的 ReLU function: $$\sigma(x)=\left\{\begin{array}{lcl} x,&&\hbox{if}\ x\ge 0,\\[5pt] 0,&&\hbox{if}\ x\lt 0. \end{array}\right.$$ 基本上 $\sigma$ 有很多選擇, 現在大家不是很確定哪一個 $\sigma$ 最好; 有各式各樣不同的 $\sigma$, 但是它一定要是 nonlinear。 因為它如果是線性的話就不行;它是線性的話, $W^{(1)}$ 和 $W^{(2)}$ 和起來也是線性, 那就只是古典線性函數, 並沒有新的改變。 AlphaGo、圍棋、Reinforcement LearningIBM 當年的 Deep Blue 是一個搜尋 search 的演算法; 也就是說, 下國際象棋其實是滿容易的。 它就是你從每一步再往底下一直做, 所以像是一個 tree, 像一個 tree 的 searching。 你分配分數給每個棋子, 譬如說兵你就給 1 分, 馬或象就給 3 分, 然後皇后給 9 分。 這樣就可以 assign 一些分數。 它子比較少, 它的選擇也比較少, 你比較容易評估說到底這個東西是好還是不好。 可是到 AlphaGo 的時候, 就有很大的問題。 因為你如果下過圍棋就知道, 圍棋是 19 乘 19, 你可以做的選擇是多的不得了。 你每一次是有將近 400 個選擇; 你只要走個 5 步 6 步的話, 根本就沒有辦法、完全沒有辦法、不可能計算了。 並且圍棋也不像國際象棋, 沒有說哪一個子值多少分, 那你怎麼辦呢? 你可以說, 你就看它圍多少地、還是什麼的。 可是你看, 通常圍棋這個棋盤一擺出來, 你怎麼知道, 你要怎麼告訴它到底圍多少地? 其實也完全看不清楚。 所以這是為什麼我們 (我圍棋是很差, 但是稍微以前小時候玩了一陣子) 覺得這幾乎是一個不可能的任務, 因為最後你不知道到底什麼樣子是好, 什麼樣子是不好, 你搞不太清楚。 所以當時 AlphaGo 做了這個事情; 它用一個 12 層的 neural network, 就是剛剛給你看的那個東西, 有 12 層。 並且它做了 reinforcement learning。 Reinforcement learning 就是說, 你每次給新的 data, 它就再一次 update新的 $\theta$。 所謂的 reinforcement learning 是每次給你一組 data, 你就找出最好的 $\theta$ 來。 我現在再給你新的 image, 你再去把它調; based on 前面的選擇, 你再去調出新的東西, 一直往上、一直往上調。 Reinforcement learning 這樣做下來之後, 最後真正解決了圍棋這個事情, 是非常的 surprising。
以前我們一直覺得說, 圍棋是電腦不可能贏的。 因為你如果下過圍棋就知道, 老師在教你圍棋時, 常常跟你講說, 你這樣下的話看起來比較厚。 我不知道大家有沒有下過圍棋?這樣下棋的話你的形式比較厚, 那樣下起來太薄了。 電腦怎麼知道什麼叫「厚」? 根本是搞不清楚的事情。 可是圍棋, 什麼樣看起來情勢是比較好、情勢比較不好? 最後在某種程度是一種 pattern recognition。 它去看圍棋下起來之後的這些 pattern; 從一再地重複學習 pattern 之後, 它慢慢從這 pattern recognition 感覺出來: 什麼樣是一個比較好的? 什麼樣是對它比較有利? 什麼樣比較對它沒有利? 當時對我們來說, 這是一個 shocking 的、非常驚訝的發展。 量子計算Quantum computing 到底是什麼? 以前電腦的 classical bits, 每一個都是 1 或是 0: $$\eta=(\eta_1,\eta_2,\ldots,\eta_n ),\qquad \eta_i\in\{0,1\}.$$ 但到 quantum bit 的時候, 譬如說 3 個 quantum bits 的話, 寫出來就是一個八維空間 $\{\psi\}$ 的一個 state, $$\psi=c_{000} e_0\otimes e_0\otimes e_0+c_{100} e_1\otimes e_0\otimes e_0+\cdots+c_{111} e_1\otimes e_1\otimes e_1,$$ 其中 $$e_1=\left(\begin{array}{c} 1\\ 0\end{array}\right),\quad e_0=\left(\begin{array}{c} 0\\ 1\end{array}\right), e_1\otimes e_0\otimes e_0=\mid 100\gt.$$ 光是 3 個 qubits, 它就組成一個 8 dimensions 的 space。 它的 dimensions 增加很快, 和 3 個 classical bit 的 1 或 0 的選擇完全不一樣, 因為它的每個 coefficient 都是一個 complex number。 這些 quantum bits 的所謂的 quantum algorithm, 每個 step 就是一個 $\mathbb{C}^8$ 的 unitary matrix。 所以 quantum algorithm 跟 classical algorithm 是完全不一樣的東西。 結論我現在沒有太多時間, 我就把結論說一下好了。 我們以前發明古典數學, 來瞭解自然現象跟物理定律; 很多物理定律也是與數學的發展是同步的。 以前很多科技的發展, 常是工程的發展、工程的進步, 大部分是各式各樣的硬體發展, 數學的角色比較不明顯。 可是現在看看新的科技。在新的科技, 我自己覺得數學扮演了一個非常核心的角色。 你看整個人工神經網絡 artificial neural network, 它是一個 nonlinear 的多層概括 (multilayer generalizations of linear regression)。 Compressed sensing 很多是稀疏約束 (sparsity constraints) 的優化問題 optimization problem。 另外說到量子計算, 很重要的是你要能設計; 除了物理上要怎麼樣去做量子電腦以外, 很重要的是你要怎麼設計 quantum algorithm? 你要怎麼做這 quantum error correcting code? 所以你就發現, 數學在新科技裡面有非常重要的核心的角色, 包括高維的分析和高維的機率, 還有離散數學, 還有很多的 optimization, 就是優化問題, 還有很多和時間相關的數學現象, 其實都是現在非常重要的課題。 那麼最後我講一下 artificial neural network。 當時有三個人: Bengio 在 Montreal, Hinton 在 Toronto, 及 NYU 的 Yann LeCun; 他們在 2018 年得到了 Turing Award, 這是電腦科學最大的一個獎。 Hinton 在 1986 年做了應該是第一篇 multi-layer neural network 的主要工作。 你看到, 這其實是相當久之前, 1986 到現在已經 30 幾年了。 這個文章寫完之後, 很長一陣子這個方向沒有什麼發展; 因為它沒有辦法發展; 因為當時你要去 train 這個 neural network, 做這些 optimization、這些 $W$ 和 $\theta$, 當時根本沒有辦法做, 因為當時電腦的計算能力太差了。 可是後來到了 1990 年代、2000 年初期的時候, 就發現其實好像是有機會做的。 這是為什麼後來 DeepMind 很快就把這個方法真正一直往前推動了, 用真正大型電腦在做這些計算。 所以我們看到有兩個關鍵。 一個關鍵是現在的尖端的軟體。 現在所有的東西一定都會有一個非常重要的軟體的設備。 你現在看不到一個東西, 底下沒有一個很好的軟體。 這個軟體。 雖然你寫下來, 大家說在寫 code, 可是其實它最重要是後面的數學問題, 如果沒有解決的話, 是沒有辦法寫 code 的。 這是第一個 trend。 第二個, 我們現在看到的數學其實跟我們以前的數學比較不一樣。 以前我們很多的傳統數學, 需要重新在這個 high dimension、 discrete 和 sparsity 的情況中間, 重新探討、重新研究。 我覺得這是兩個主要的訊息。 那麼, 我再跟同學說一遍。 我自己小孩大學是 2017 年畢業的。 2017 年畢業之後, 他們的同學非常多人就往數學、 computer science, 或解決這些問題的方向走, 因為他們當時在$\cdots$。 你們可能沒有感覺到, 當時 2016 年, 當 AlphaGo 贏了人類圍棋之後, 那種 shock 你們可能沒有感覺到。 我當時在看到這個事情之後, 我自己在學校裡面 run 了兩三年的 seminar, 看看說到底是怎麼回事。 傳統上大家覺得數學只是在黑板上教了一些東西, 好像沒有實際的用途, 其實現在的世界已經不是這個樣子了。 所以我是覺得同學不用擔心說, 學數學就要當補習班老師, 那個時代已經過去了, 不用擔心這個事情。 你還是應該要找你自己想做的方向、想做的東西, 我覺得這才是重點。 好, 謝謝大家。 問答龍津高中數學老師: 教授你好, 我是台中市龍津高中的數學老師。我自己當初學習的時候會有這樣的問題: 數學課教的是模型, 資訊課教的是語法, 這裡有很大的問題是, 學生沒有資料。 因為我自己在學習過程中, 發現的很大問題是, 其實這裡面很大部分在處理大數據, 就是資料量很大的情況下產生模型及處理。 但其實我們在教學的時候, 無論是資訊也好、還是數學也好, 都有個問題是: 我們沒有數據。 我們當然可以人工產生大量的數據, 讓學生去體驗, 可是我們上課的時候都會有個問題, 就是真實世界的數據其實學生沒有感覺。 他們只知道我們今天統計需要處理很多量的數據, 可是那數量多少?如果是手算的, 好, 我們考試頂多 10 筆, 大概算是極限。 資訊科技老師上課著重在語法, 所以他們根本不會有數據處理的部分, 甚至於處理之後他們也不知道該怎麼辦。 所以我想知道, 對於要怎麼提供學生真的看到大量數據去處理, 教授有沒有什麼建議或是想法? 姚鴻澤: 好。 因為我自己也不是做電腦的, 但是我知道現在很多 deposit, 譬如說, 你說圖像對不對? 圖像它有一些標準的 website, 有非常非常多的圖, 非常非常多的標準的圖。 現在很多東西、很多文章都要求去 run 那些標準的 data, 然後看那些標準 data 所 run 出來結果是什麼。 我不是很清楚它們 exactly 叫什麼名字, 但是很多那樣的東西。 譬如說, 最簡單的, 手寫的 1 到 9 那些, 你怎麼去 recognize 這些? 他們也有標準圖在那裡。 到底那是 exactly 哪個網站我不知道, 但是那種 deposit 是有的。 另外, 現在很多都是在 Internet 上面, 很多人在 maintain 那些標準的 data, 很多現在的文章都是在 run 那些標準的 data。 可是當然對高中生來說, 這個我想是太困難了。 除非老師把那些 download 之後, 挑一部分讓學生練習, 不然的話, 直接要取那些 data 直接 run, 我想是非常困難。 並且也不知道說現在學生手上的電腦有沒有辦法真的 run 這麼大的 data。 這些都是問題。 但是 website 上面是真的有這些標準的 data。 我是覺得高中的學生, 基本上要知道, 現在很多人都說他們在做大數據。 現在所謂做大數據的, 他們就拿這圖的 model; 當然那是我現在這麼寫, 實際上不見得是那樣子, 因為實際上有所謂 neural network design, 看這東西要把它設計成什麼樣子。 有些時候這種一排一排直直往前走不見得是最好, 中間還有一些各式各樣的 trick, 我們這裡沒有畫出來。

很多人說, 因為這個是 minimization, 這是一個優化問題, 那麼最重要就是這些參數 $W$ 你要挑出來。 可是現在很多人就說, 我現在如果給你一組 data, 我給你這些 $x$, 給你這些 $y$, 就從那 data 進來給你 $x$, 你放進 package; 你丟進去的話, 答案就出來了。 你用這個 package 在 run 的時候, 你根本其實已經都不太知道到底背後在做什麼。 但是我想, 一個很重要的事情是說, 將來的東西、將來的世界不是都是 deep neural network就結束了。 我不相信這個事情。 等到現在的學生到我這個年紀的時候, 你會發現這世界完全已經沒有人在管 deep neural network, 說不定它們不知道跑哪裡去了, 或者說 deep neural network 不知道會變成什麼樣子。 我覺得一個很重要事情是說, 大家還是要對它背後的科學要有相當的理解, 就是說你在數學上有一些訓練, 譬如說像微積分, 像optimization、 minimization 這個問題要怎麼處理, 然後這上面的一些不管是數學的工作, 或者是 computer science 怎麼 implement, 這些東西都要了解。 因為如果你沒有了解的話, 最後人類的文化不可能在 deep neural network 就停止了。 現在很多人反而有一個想法說, 我現在什麼都不用學, 什麼東西就把它丟進 deep neural network 就結束了, 好像說人類文化到了 deep neural network 就已經是 the end, 這是不可能的事情的。 我舉圍棋這個例子, 並不是要幫 deep neural network 吹牛, 說這個東西多偉大。 這個東西做出一些很不可思議的結果是真的, 但是我想科學會一直往前走; 科學一直往前走, 數學一直往前走, 最好的方法是什麼? 最好的方法其實是說你還是要把一些基本的東西先學會, 學會之後你再看它怎麼應用。 我覺得, 在數學系, 很多人強調要最純的數學, 這也不是一個不對的方式。 但是另外一個想法是說, 我們只要應用, 不用學基礎的東西, 其實這也是不對的。 我是覺得這兩者都需要。 我自己覺得我是純數學, 我一直覺得我自己是純數學, 但是我自己也對應用非常有興趣。 對高中學生最重要的, 我覺得是其實你們不用擔心選科系等等, 其實沒什麼好怕的, 你想選什麼就選什麼。 崔茂培: 線上其實有滿多人提問, 我先代問一個問題。他想請教一下, 學習數學用什麼樣的態度與方法是正確呢? 姚鴻澤: 這個問題太大了, 也太嚴肅了。 當年老師都不讓我們學。 我當時在學校裡面自己讀數學, 被老師踢出去。 所以我覺得其實也不用把事情想得這麼嚴肅。 第一個還是你要覺得東西有趣。 你如果覺得你讀了那些數學, 你看的那些東西沒有趣的話, 其實你很難做下去, 即使你告訴自己這東西真的很重要。 很多時候, 像數學這種東西, 你必須要花一點時間, 就像學下棋一樣, 剛開始的時候, 可能要有一段很長的時間, 你才會覺得它有趣。 那麼, 我是建議大家可以多花點時間, 先讓自己試試看, 給自己長一點時間去學習一些基本的東西, 看看自己會不會覺得很有意思。 我們以前高中時候, 根本微積分都沒有教, 微積分都要自己去學。我記得我在高中的時候, 一直到晚上 12 點才開始念我自己的數學。 我到高中第三年, 每天晚上都很高興說, 現在可以自己做我自己的東西, 學我的東西, 不用去準備聯考。 你如果有那樣的心情, 你就會覺得數學滿有趣的。 崔茂培: 有人問說, 數學系的程式訓練實作能力偏弱, 但也不可能有餘裕到電資學院修課惡補, 選課是一個問題。他說想做深度學習或量子電腦的專題, 您有什麼見解? 姚鴻澤: 這我不知道怎麼講。 現在舉個例子好了。 現在 Harvard 的數學系學生的 requirement, 其實已經非常少了。 很多學生有辦法 double major。 現在 double major 的學生非常多。 你說你正在數學系, 想要去修 algorithm, 我覺得是不太可能的, 不切實際。 數學系不可能教你那麼多 algorithm 的。 你和另外的系可以 double 的話, 會是一個好的方向, 是必走的方向。 至於說實際上學校會不會這麼做, 這我也沒辦法。 我可以去跟學校談談, 但是這種東西我不知道談了之後會怎麼樣? 現在我們最大的 double major 就是數學和統計, 還有數學和電腦。 這兩個 double major 非常多。 因為現在很多電腦系的學生, 其實也想學數學; 因為以前的電腦可能需要的數學比較少, 現在相當多。 所以在 Harvard 數學 major 的學生現在是越來越多, 尤其是在 AlphaGo 之後, 現在是真的越來越多。 你說去電腦系、電機系修課好像不切實際, 可是好像我也看不出有什麼辦法, 因為數學系其實是真的沒有辦法教這麼多 algorithm。 崔茂培: 有好幾個是數學系, 不過我先跳過。有小學的家長問:有沒有什麼給家長的建議, 如何讓小學的孩子喜歡數學?有推薦的方法或書籍嗎? 姚鴻澤: 這個我沒有辦法。 我兒子小時候通通在玩, 他小學的時候都在玩, 我也沒有管他。 另外說到寫程式, 其實一個好辦法是, summer 的時候去找一些 summer project, 真的去處理一兩個問題。 你試過了之後, 真的做一兩個 project, 其實比你修一大堆課有用很多。 能找到一些 summer project, 然後讓小孩子真正可以去處理真正的問題, 那其實是最有用的, 那樣學出來的東西最 solid。 在上課裡面教的、學的 algorithm, 通常碰到真的問題是沒有辦法的。 但是你只要做會一個 summer project, 那就差非常多。 崔茂培: 問題太多, 有點麻煩。我可能稍微選一下。有人說因為今天你提到的比較偏數學和軟體的部分, 硬體的比較少, 你覺得說數學和硬體方面的關聯, 可以稍作$\cdots$。 姚鴻澤: 和硬體的關聯我根本沒有資格講, 因為這完全是另外一件事情。 譬如說像 quantum computing, quantum computer, 他們現在要怎麼 build quantum computer, 這個東西我差了非常遠。 我真的覺得我是沒有辦法comment, 我們只是聽其他人的一些意見, 我覺得我不應該在這裡轉達, 因為我自己沒有什麼把握; 不是說沒什麼把握, 其實是不懂。 像 artificial neural network 這個東西, 因為它基本上對我來說完全是數學, 所以我可以解釋得比較清楚。 崔茂培: 好, 這裡還提一個問題。 他說: 現在的國、高中生最重要的還是把基礎學科打好嗎? 然後說: 但是課綱好像把學科的數學時段縮減了, 把時間拿過去給學生發展一些其他的興趣。 在大學部分, 大學分發考試是比過去困難些。 他說學生這樣該怎麼選擇? 姚鴻澤: 課綱數學的基礎東西變少了, 我們已經向教育部等等或各個單位反應過, 其實是吵架吵過很多次了。 現在是要保留這些時數, 因為本來還是更少的。 這個沒有辦法, 我沒有選票, 所以我只能跟他們建議; 實際上他們怎麼做, 我比較沒有辦法。 我想唯一的方法就是說, 除了課堂之外, 我剛才講到 summer, 找讓小孩子做的 summer project, 真的可以處理一兩個問題, 是滿重要的。 另外在高中這個階段, 還是讓小孩子較自由發展, 就算比較 focus 在一些比較基礎的東西, 其實也沒有什麼關係。 我覺得, 也是因為畢竟未來時間還滿長的, 大學還是有很多機會做 project。 在高中的時候, 因為知識上的限制, 真要去做 project, 很多實驗室是不會讓高中小孩去參加這些 project, 所以比較困難。 崔茂培: 這邊有個也是數學系的同學在問說, 他未來想要走 machine learning 的領域的話, 數學系有什麼優勢嗎? 另外, machine learning 比較注重實作, 好像做 computer science 的人比較有優勢; 實作沒有很重視數學理論。 所以他想問, 到底學數學的做這方面有沒有什麼優勢? 姚鴻澤: 就看你將來想做什麼。 你如果說你要去 implement 這樣的東西, 你要去 optimize 這些 $W$ 然後在 computer 上面 run 的話, 那麼知道理論其實是沒有什麼優勢, 這我也同意。 可是你碰到很多問題的時候, 其實你並不知道說, 什麼樣的方法最合適。 像很多各式各樣的這些 reinforcement learning 等等新的方式, 你其實對理論沒有瞭解的話, 其實很難處理。 譬如說我現在給你 10,000 個圖, 你 optimize 出來這些 $W$ 和 $a$ 之後, 我再給你 10 張圖, 那麼你要怎麼辦呢? 你不能把這個 10,000 張加上這 10 張, 然後重新再 run, 這樣時間就不得了。 所以你要想個辦法, 這 10 張新進來的圖, 你要怎麼樣把這 information 加進去? 覺得其實不是一個那麼容易的問題。 很多東西看起來好像很簡單, 可是你真的實際上操作的時候就不是了, 因為電腦速度不是無限大。 我給你 10,000 張之後, 再給你 100 張, 這 100 張對你這 10,000 張, 得到的 training 的結果, 要怎麼樣 adjust, 讓這最後的 100 張的 information 也進來, 其實不是那麼容易的。 你不能把這 10,000 張加 100 張重新再 run。 所以我覺得對基礎理論有相當的了解, 其實是會有好處的。 不需要覺得說, 好像我們懂這些, 比較知道原因、基礎, 在做這些 mechanical 的事情, 好像沒有 advantage。 它還是有 advantage 的。 主要就是說, 只要你面對的問題, 是有變化的問題, 你就會有好處。 但是這世界上當然很多人專門在做 mechanical 的事情, 那當然就沒有好處了。 所以主要看你要選什麼樣的問題。 高中生: 教授您好。 我想請問, 您在國內外待了那麼多年, 請問您覺得國內外的數學系的優勢和劣勢分別在哪裡? 你會覺得他們的差異性在哪裡? 姚鴻澤: 要我比較台大和 Harvard 數學系。 我想一個最重要的一件事情是, 美國的大學, 尤其美國的私立大學, 其實很現實的, 學生交學費, 學校就必須讓學生畢業的時候能找到工作, 然後能高高興興地畢業; 這非常重要。 在台灣就比較沒有這個壓力。 所以我們對學生的 major 的要求一直在降低, 降低的原因就是, 希望學生可以 double major, 可以和其他的系合併等等, 然後可以去選擇一個和數學相關, 但是不一定絕對要是數學的方向。 這個壓力是相當大的。 所以其實有一陣子, 1980 末期、1990 初期, 很多數學系幾乎是收不到學生。 我記得那個時候, Princeton 最差的時候, 一個學校數學系不到 10 個 major。 當時大家都不知道怎麼辦; 世界末日了, 沒人要學數學。 可是現在很多學校數學系 major 的人, 每一年接近 100 個, 是沒有問題的。 這個主要就是說, 數學和其他系 double major 這個事情越來越廣泛, 在要求上面也越來越少。 我是覺得, 台灣也應該往這方向走, 想辦法試圖降低一下數學系的 requirement。 但這個東西也不能只有數學系做。 你要降低很多系的 requirement, 讓學生可以在不同的科系之間選擇他要的東西。 你看我們畢業學生裡面那麼多是 double major 的; 在台灣, 相對來講就少很多。 Double major 的好處就是說, 學生可以比較有彈性, 可以隨著時代科技的變化來調整, 我覺得這對我來說, 是一個最重要的事情。 學生如果自己真的很喜歡數學, 也可以只選數學, 不選其他的 double 也沒有關係。 我相信以學生的 flexibility 為導向, 是一個很重要的方向, 我也希望說大家可以朝這個方向走。 這也不只是數學系, 因為如果只有數學系降低標準也沒有用, 因為電機系如果不讓你進去你也是沒有辦法。 我是覺得, 學生其實也不用覺得說一定要去很困難的科系, 很困難的 major; 其實沒有關係的;因為你自己學會一些東西, 畢業以後有很多的方向可以選擇的, 其實沒有什麼關係的。 就這樣子。 我不知道我有沒有回答你的問題? 那就是一些我自己個人的感想, 謝謝你。 非常謝謝大家。 本文演講者姚鴻澤任教美國哈佛大學 |
2022年12月 46卷4期
數學與現代科技

