| 發刊日期 |
2024年9月
|
|---|---|
| 標題 | 直三棱柱截面與底面夾角公式的相對性推廣 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
摘要: 本文對世界數學名著《近代歐氏幾何學》中的一個重要定理進行了相對性推廣, 得到了一個簡明深刻的直三棱柱截面與底面夾角公式及其有趣推論。 關鍵詞: 直三棱柱、 二面夾角公式、 相對性推廣。 世界通俗數學名著 定理0: 底面三角形的 (特徵) Brocard 角為 $\omega_0$ 的直三棱柱, 被某平面所截的截面為正三角形, 該截面與三棱柱底面所成的角為 $\phi_0$, 則 $$\cos\phi_0=\frac{\sqrt 3}{3}(\cot\omega_0-\sqrt{\cot^2\omega_0-3}).$$ 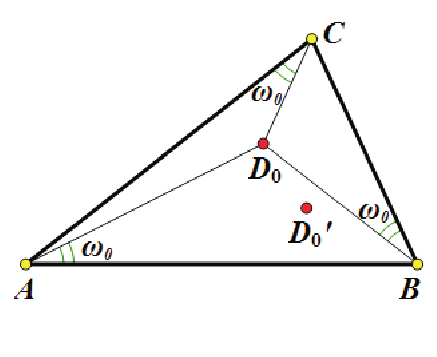 稱上列公式為特徵二面夾角公式。 三角形的 (特徵) Brocard 角 $\omega_0$ 是與三角形的兩個 (特徵) Brocard點有關的一個特殊角。 如圖1, 在非等邊 $\triangle ABC$ 中, 存在兩點 $D_0$、 $D'_0$, 滿足 $\angle D_0AB =\angle D_0BC=\angle D_0CA=\angle D'_0BA=\angle D'_0AC=\angle D'_0CB$, 這一對特殊點 $D_0$、 $D'_0$ 稱為 $\triangle ABC$ 的特徵正、 負 Brocard 點, 這六個相等的角, 稱為特徵 Brocard 角, 記為 $\omega_0$. 特徵 Brocard 點和特徵 Brocard 角具有許多奇異的性質, 如: (1) 設 $\triangle ABC$ 的三邊長分別為 $a$、 $b$、 $c$, 面積為 $\triangle$, 特徵 Brocard 角為 $\omega_0$, 則 $$\cot \omega_0=\frac{a^2+b^2+c^2}{4\triangle}.$$ (2) 設 $\triangle ABC$ 的三內角分別為 $\angle A$、 $\angle B$、 $\angle C$, 特徵 Brocard 角為 $\omega_0$, 則 \begin{align*} \cot \omega_0=\,&\cot A+\cot B+\cot C;\\ 1/\sin^2\omega_0=\,& 1/\sin^2 A+1/\sin^2 B+1/\sin^2 C. \end{align*} (3) $\triangle ABC$ 的特徵 Brocard 角 $\omega_0\in (0,\pi/6]$, 當且僅當 $\triangle ABC$ 為正三角形時, $\omega_0=\pi/6$. (4) 特徵正、 負 Brocard 點 $D_0$、 $D'_0$ 是 $\triangle ABC$ 的一對等角共軛點。 (5) 設 $\triangle ABC$ 的邊長分別為 $a$、 $b$、 $c$, 特徵 Brocard 角為 $\omega_0$, 則特徵正、 負 Brocard 點 $D_0$、 $D'_0$ 到 $\triangle ABC$ 的頂點 $A$、 $B$、 $C$ 之距依次為 \begin{align*} D_0A=&\frac ba \cdot 2R\sin \omega_0,\quad D_0B=\frac cb \cdot 2R\sin \omega_0,\quad D_0C=\frac ac \cdot 2R\sin \omega_0; \\ D'_0A=&\frac ca \cdot 2R\sin \omega_0,\quad D'_0B=\frac ab \cdot 2R\sin \omega_0,\quad D'_0C=\frac bc \cdot 2R\sin \omega_0. \end{align*} (6) 設 $\triangle ABC$ 的外接圓為 $\odot O(R)$, 特徵正、 負 Brocard 點為 $D_0$、 $D'_0$, 特徵 Brocard 角為 $\omega_0$, 則 \begin{align*} OD_0=&OD'_0=R\sqrt{1-4\sin^2\omega_0}\ , \\ D_0D'_0=&2R\sin\omega_0\sqrt{1-4\sin^2\omega_0}\ . \end{align*} 特徵 Brocard 點和特徵 Brocard 角的其他性質詳見名著 現在, 我們給出三角形的特徵正、負等角線長的概念: 如圖 2, 以 $\triangle ABC$ 的三邊為邊, 向外作正三角形 $A_0CB$、 $B_0AC$、 $C_0BA$, 則線段 $AA_0=BB_0=CC_0$, 其長度記為 $e_0$, 稱 $e_0$ 為 $\triangle ABC$ 的特徵正等角線長; 如圖 3, 以 $\triangle ABC$ 的三邊為邊, 向內作正三角形 $A_1BC$、 $B_1CA$、 $C_1AB$, 則線段 $AA_1=BB_1=CC_1$, 其長度記為 $f_0$, 稱 $f_0$ 為 $\triangle ABC$ 的特徵負等角線長。 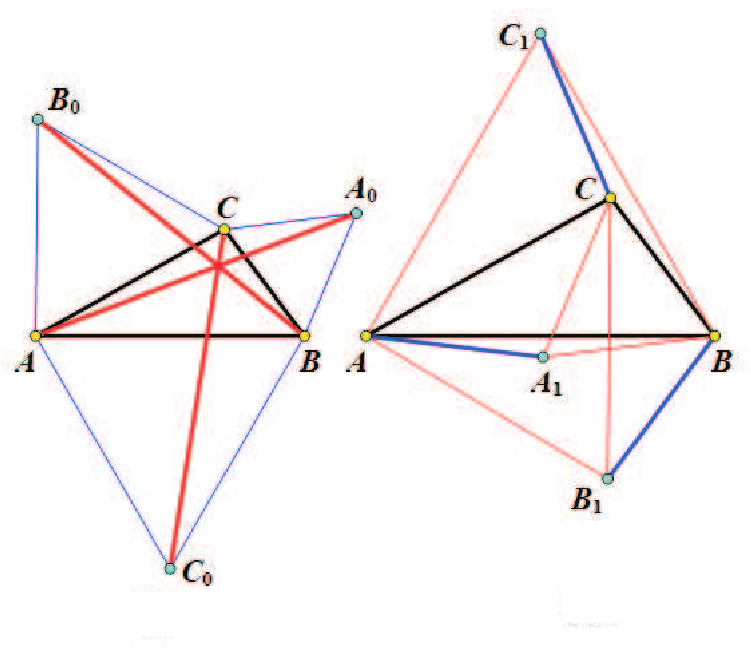 由文獻 結論: 設 $\triangle ABC$ 的三邊長、 面積分別為 $a$、 $b$、 $c$、 $\triangle$, 它的特徵正、 負等角線長為 $e_0$、 $f_0$, 特徵 Brocard 角為 $\omega_0$, 則有 \begin{align*} &e_0=\, \frac 12(a^2+b^2+c^2+4\sqrt 3\triangle),\quad \ f_0^2=\frac 12(a^2+b^2+c^2-4\sqrt 3\triangle),\\ &\cot\omega_0=\,\sqrt 3\cdot\frac{e_0^2+f_0^2}{e_0^2-f_0^2}. \end{align*} 下面, 我們從全新的視角, 將上述定理0進行相對性推廣, 證明了一個簡潔優美的相對二面夾角公式, 並以定理 0 中的特徵二面夾角公式作為它的特例。 需要如下: 引理1: 設角 $\alpha$ 的兩邊與某平面所成的角分別為 $\beta $、 $\gamma $, 它在該平面上的射影角為 $\alpha'$, 則 $$\cos\alpha'=\frac{\cos\alpha-\sin\beta\sin\gamma}{\cos\beta\cos\gamma}.$$ (*) 上式是三面角的二面角餘弦公式 (文 現在, 我們給出三個新幾何量(相對正、負等角線長和相對 Brocard 角) 的定義: 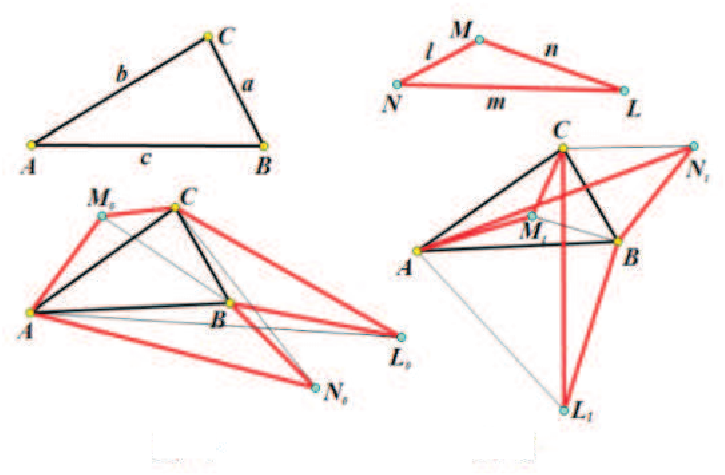 如圖 4、5, 已知 $\triangle ABC$ 和 $\triangle LMN$, 在 $\triangle ABC$ 的外側, 分別作三角形 $L_0CB$、 $M_0AC$、 $N_0BA$, 使 $\triangle L_0BC$、 $\triangle AM_0C$、 $\triangle ABN_0$ 逆相似 $\triangle LMN$; 對偶地, 在 $\triangle ABC$ 的內側, 分別作三角形 $L_1BC$、 $M_1CA$、 $N_1AB$, 使 $\triangle L_1BC$、 $\triangle AM_1C$、 $\triangle ABN_1$ 順相似 $\triangle LMN$. 文 引理2: 設 $\triangle ABC$, $\triangle LMN$ 的三邊長、 面積分別為 $a$、 $b$、 $c$、 $\triangle$, $l$、 $m$、 $n$、$\bigtriangledown$, 記 \begin{align*} h^4=&a^2(-l^2+m^2+n^2)+b^2(l^2-m^2+n^2)+c^2(l^2+m^2-n^2)\\ =&l^2(-a^2+b^2+c^2)+m^2(a^2-b^2+c^2)+n^2(a^2+b^2-c^2)\\ =&(a^2+b^2+c^2)(l^2+m^2+n^2)-2(a^2l^2+b^2m^2+c^2n^2), \end{align*} $e^4=(h^4+16\triangle\bigtriangledown)/2\gt0,\quad f^4=(h^4-16\triangle\bigtriangledown)/2\ge 0$, 則 $l\cdot AL_0=m\cdot BM_0=n\cdot CN_0=e^2$; $l\cdot AL_1=m\cdot BM_1=n\cdot CN_1=f^2$. 稱 $e$ 是 $\triangle ABC$ 相對 $\triangle LMN$ 的正等角線長 (或稱 $\triangle ABC$ 與 $\triangle LMN$ 的相對正等角線長); 稱 $f$ 是 $\triangle ABC$ 相對 $\triangle LMN$ 的負等角線長(或稱 $\triangle ABC$ 與 $\triangle LMN$ 的相對負等角線長)。 據此, 可以給出相對 Brocard 角 $\omega$ 的定義: 設 $\triangle ABC$ 相對 $\triangle LMN$ 的正、 負等角線長分別為 $e$、$f$, 令 $\cot\omega=\sqrt 3\cdot\dfrac{e^4+f^4}{e^4-f^4}$, 則稱 $\omega$ 是 $\triangle ABC$ 相對 $\triangle LMN$ 的 Brocard 角 (或稱 $\triangle ABC$ 與 $\triangle LMN$ 的相對 Brocard 角) 。 上述關於相對 Brocard 角的定義是合理而自洽的, 因為該定義不僅與相對正、 負等角線長 $e$、 $f$ 的定義協調, 而且當 $\triangle LMN$ 為正三角形時, 相對 Brocard 角公式就退化為特徵 Brocard 角公式。 具體說, 若 $l\!=\!m\!=\!n$, 則 $\triangle LMN$ 的面積 $\bigtriangledown =\sqrt 3 l^2/4$, 有 $16\triangle \bigtriangledown =4\sqrt 3\triangle l^2$, $h^4=(a^2+b^2+c^2)l^2$, 從而 \begin{align*} e^4=\,&\frac 12(a^2+b^2+c^2+4\sqrt 3\triangle )l^2=e^2_0l^2,\\ f^4=\,&\frac 12(a^2+b^2+c^2-4\sqrt 3\triangle )l^2=f_0^2l^2, \end{align*} 將以上二式代入相對 Brocard 角公式: $$\cot\omega=\sqrt 3\cdot\dfrac{e^4+f^4}{e^4-f^4},$$ 就可得到特徵 Brocard 角公式 $\cot\omega_0=\sqrt 3\cdot\dfrac{e_0^2+f_0^2}{e_0^2-f_0^2}=\dfrac{a^2+b^2+c^2}{4\triangle}.$ 現在, 我們對直三棱柱截面與底面的(特徵)夾角公式進行相對性推廣: 定理: 設 $\triangle ABC$ 與 $\triangle LMN$ 的相對正、 負等角線長分別為 $e$、 $f$, 相對 Brocard 角為 $\omega$, 以 $\triangle ABC$ 為底面的直三棱柱, 被某平面所截的截面 $\triangle L_1M_1N_1\sim \triangle LMN$, 該截面與三棱柱底面所成的角為 $\phi$, 則 $$\cos\phi=\dfrac{e^2-f^2}{e^2+f^2}=\dfrac{\sqrt 3}{3}(\cot\omega-\sqrt{\cot^2\omega-3}).$$ 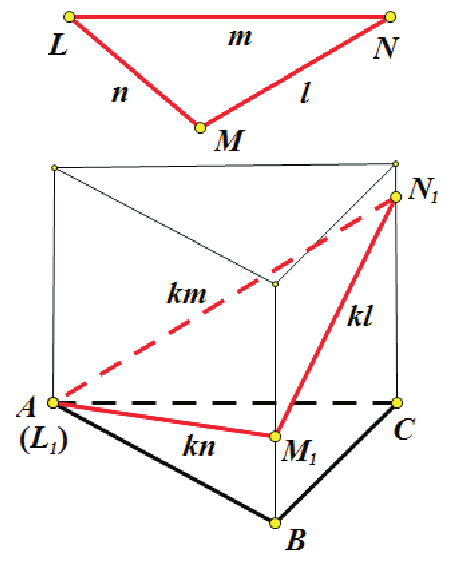 證明: 如圖 6, 設截面 $\triangle L_1M_1N_1\sim \triangle LMN$, 相似比為 $k$, 則 $L_1M_1=k\cdot LM =kn$, $L_1N_1=k\cdot LN=km$, 不妨使頂點 $L_1$ 與 $A$ 重合, 在公式 $(*)$ 中, 令 $\alpha=\angle N_1AM_1=\angle L$, $\alpha' = \angle CAB= \angle A$, $\beta =\angle M_1AB$, $\gamma = \angle N_1AC$, 則 $\cos\beta = AB/AM_1=c/kn$, $\cos \gamma = AC/AN_1=b/km$, $$\sin\beta=\sqrt{1-\dfrac{c^2}{k^2n^2}},\quad \sin\gamma=\sqrt{1-\dfrac{b^2}{k^2m^2}},$$ 代入公式 $(*)$, 得 \begin{align*} \frac{bc}{k^2mn}\cos A=&\cos L-\sqrt{\Big(1-\frac{c^2}{k^2n^2}\Big)\Big(1-\frac{b^2}{k^2m^2}\Big)}\qquad\qquad~\\ =&\cos L-\frac{\sqrt{(k^2m^2-b^2)(k^2n^2-c^2)}}{k^2mn}, \end{align*} 即 $bc\cos A=k^2mn\cos L-\sqrt{(k^2m^2-b^2)(k^2n^2-c^2)}$, 移項, 兩邊平方, 得 $$(k^2mn\cos L-bc\cos A)^2=(k^2m^2-b^2)(k^2n^2-c^2),$$ 展開, 並整理, 得 $$m^2n^2(1-\cos^2L)k^4-(b^2n^2+c^2m^2-2bcmn\cos A\cos L)k^2+b^2c^2(1-\cos^2A)=0.$$ 上式中, $m^2n^2(1-\cos^2L)=m^2n^2\sin^2L=4\bigtriangledown^2$, $b^2c^2(1-\cos^2A)=b^2c^2\sin^2A=4\triangle ^2$, \begin{align*} &\hskip -20pt b^2n^2+c^2m^2-2bcmn\cos A\cos L\\ =& \frac 12(2b^2n^2+2c^2m^2-2bc\cos A\cdot 2mn\cos L)\\ =&\frac 12[2b^2n^2+2c^2m^2-(-a^2+b^2+c^2)(-l^2+m^2+n^2)]\\ =&\frac 12[a^2(-l^2+m^2+n^2)+b^2(l^2-m^2+n^2)+c^2(l^2+m^2-n^2)]\\ =&\frac 12h^4, \end{align*} 於是, $4\bigtriangledown^2k^4-\dfrac 12h^4k^2+4\triangle ^2=0$. 這是一個關於 $k^2$ 的一元二次方程, 其判別式 \begin{align*} \delta=&\Big(-\frac 12 h^4\Big)^2-4\cdot 4\triangle^2\cdot 4\bigtriangledown^2=\frac 14(h^8-16^2\triangle^2\bigtriangledown^2)\\ =&\frac 12(h^4+16\triangle\bigtriangledown)\cdot \frac 12(h^4-16\triangle\bigtriangledown)=e^4f^4,\\ \therefore\ k^2=&\Big(\frac 12h^4\pm e^2f^2\Big)/8\bigtriangledown^2=(h^4\pm 2e^2f^2)/16\bigtriangledown^2\\ =&(e^4+f^4\pm 2e^2f^2)/16\bigtriangledown^2=(e^2\pm f^2)^2/16\bigtriangledown^2, \end{align*} 設 $\triangle L_1M_1N_1$ 的面積為 $\bigtriangledown_1$, 則 $\bigtriangledown_1=k^2\bigtriangledown$, 由射影面積公式, 得 \begin{align*} \cos\phi=&\triangle/\bigtriangledown_1=\triangle/k^2\bigtriangledown=\frac{\triangle}\bigtriangledown \div\frac{(e^2\pm f^2)^2}{16\bigtriangledown^2}\\ =&\frac{16\triangle\bigtriangledown}{(e^2\pm f^2)^2}=\frac{e^4-f^4}{(e^2\pm f^2)^2}\\ =&\frac{e^2-f^2}{e^2+f^2}\quad \Big(\hbox{捨去}\ \frac{e^2+f^2}{e^2-f^2}\Big);\hskip 4cm~\\ \hbox{又}\quad \cot\omega=&\sqrt{3}\cdot\frac{e^4+f^4}{e^4-f^4},\\ \hbox{解得}\quad \frac{f^2}{e^2}=&\sqrt{\dfrac{\cot\omega-\sqrt 3}{\cot\omega+\sqrt 3}},\\ \therefore\quad \cos\phi=&\frac{e^2-f^2}{e^2+f^2}=\bigg(1-\frac{f^2}{e^2}\Big)\div \Big(1+\frac{f^2}{e^2}\bigg)\\ =&\Bigg(1-\sqrt{\dfrac{\cot\omega-\sqrt 3}{\cot\omega+\sqrt 3}}\Bigg)\div \Bigg(1+\sqrt{\dfrac{\cot\omega-\sqrt 3}{\cot\omega+\sqrt 3}}\Bigg)\\ =&\Bigg(1-\sqrt{\dfrac{\cot\omega-\sqrt 3}{\cot\omega+\sqrt 3}}\Bigg)^2\div \Bigg(1-{\dfrac{\cot\omega-\sqrt 3}{\cot\omega+\sqrt 3}}\Bigg)\\ =&2\cdot \frac{\cot\omega-\sqrt{\cot^2\omega-3}}{\cot\omega+\sqrt 3}\div \frac{2\sqrt 3}{\cot\omega+\sqrt 3}\\ =&\dfrac{\sqrt 3}{3}(\cot\omega-\sqrt{\cot^2\omega-3}). \end{align*} 綜上, $\cos\phi=\dfrac{e^2-f^2}{e^2+f^2}=\dfrac{\sqrt 3}{3}(\cot\omega-\sqrt{\cot^2\omega-3})$. 證畢。 推論1: $\sin\phi=\dfrac{2ef}{e^2+f^2}$. 推論2: $\tan\dfrac \phi 2=\dfrac{f}{e}$. 推論3: 設 $\triangle ABC$ 的三邊長、 面積分別為 $a$、 $b$、 $c$、 $\triangle$, 它的特徵正、 負等角線長為 $e_0$、$f_0$, 特徵 Brocard 角為 $\omega_0$, 若 $\triangle LMN$ 為正三角形, 以 $\triangle ABC$ 為底的三棱柱的正三角形截面與底面所成角為 $\phi_0$, 則 $$\cos\phi_0=\frac{e_0-f_0}{e_0+f_0}=\frac{\sqrt 3}{3}\Big(\cot\omega_0-\sqrt{\cot^2\omega_0-3}\Big).$$ 證明: 因為 $\triangle LMN$ 為正三角形, 記其邊長為 $l$, 有面積 $\bigtriangledown=\sqrt 3l^2/4$, 從而 $16\triangle\bigtriangledown=4\sqrt 3\triangle l^2$, $h^4=(a^2+b^2+c^2)l^2$, 則 \begin{align*} e^4=&\frac 12(a^2+b^2+c^2+4\sqrt 3 \triangle)l^2=e_0^2l^2,\hskip 3cm~\\ f^4=&\frac 12(a^2+b^2+c^2-4\sqrt 3 \triangle)l^2=f_0^2l^2,\\ \therefore\quad \cos\phi_0=&\frac{e^2-f^2}{e^2+f^2}=\frac{e_0-f_0}{e_0+f_0}. \end{align*} 又由名著 $e^4=2l^2\triangle (\cot\omega_0+\sqrt 3),\quad f^4=2l^2\triangle (\cot\omega_0-\sqrt 3),$ \begin{align*} \therefore\ \cos\phi_0=\frac{e^2-f^2}{e^2+f^2}=&\frac{\sqrt{\cot\omega_0+\sqrt 3}-\sqrt{\cot\omega_0-\sqrt 3}} {\sqrt{\cot\omega_0+\sqrt 3}+\sqrt{\cot\omega_0-\sqrt 3}}\hskip 3cm~\\ =&\frac{(\sqrt{\cot\omega_0+\sqrt 3}-\sqrt{\cot\omega_0-\sqrt 3})^2}{(\cot\omega_0+\sqrt 3)-(\cot\omega_0-\sqrt 3)}\\ =&\frac{2(\cot\omega_0-\sqrt{\cot^2\omega_0-3})}{2\sqrt 3}\\ =&\frac{\sqrt 3}{3}(\cot\omega_0-\sqrt{\cot^2\omega_0-3}). \end{align*} 綜上, 推論 3 獲證。 顯然, 推論 3 中的後一式, 即為文首定理 0 中的公式。 參考資料本文作者任教中國湖南省祁東縣文武學校普高部 |
2024年9月 48卷3期
直三棱柱截面與底面夾角公式的相對性推廣

