| 發刊日期 |
2024年12月
|
|---|---|
| 標題 | 哈那克兄弟們(Harnacks)-數學與神學的雙生子- |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
謹將此文獻給李志豪教授並祝他 70 歲生日快樂 1. 前言『人們總是抱怨我們這一代沒有哲學家。 他們錯了, 哲學家如今在另一個學院。 他們的名字是馬克斯$\cdot$普朗克和阿爾伯特$\cdot$愛因斯坦。』 --- Adolf von Harnack (1851$\sim$1930) --- 數學史與科學史上有不少的兄弟檔與父子檔, 例如瑞士的 Bernoulli 家族、 美國哈佛大學 (Harvard University) 的 George David Birkhoff 父子, 匈牙利的 Riesz 兩兄弟、 另外美國的 Felix E. Browder 三兄弟都是數學家。 而雙胞胎則絕無僅有的是哈那克 (Harnack) 兄弟, 他們是出生在 Dorpat (現在名為 Tartu 屬於愛沙尼亞) 波羅的海德國人 (Baltic German)。 其父是研究馬丁路德的神學教授, 除了 Dorpat 之外也曾經在 Erlangen 大學任教過。 基本上我們可以說他們是書香門第。 先介紹數學家 Carl Gustav Axel Harnack (1851$\sim$1888), 他就是在偏微分方程與複變函數論出現的 Harnack 不等式的真身。 由於舉家搬遷到 Erlangen, 而數學史著名的 Erlangen 綱領 (1872) 發表者 Felix Klein (1849$\sim$1925) 此時正是 Erlangen 大學數學系的台柱, 自然 Axel Harnack 就成為大數學家 F. Klein 的學生。 他在數學的主要貢獻是位勢理論 (potential theory), 其中調和函數 (harmonic function) 的 Harnack 不等式與 Harnack 定理就是最典型代表。 自 1882 年起由於健康的緣故, Axel 大部分的時間都待在療養院直到離世, 他去世時是一位著名的數學家。 我相信 Axel Harnack 如果夠長壽他對於數學的貢獻還會更大。  Axel Harnack 的雙胞胎哥哥 Adolf von Harnack (1851$\sim$1930) 的名氣比 Axel Harnack 更響亮也遠比他長壽, 跟他們的神學教授父親一樣, Adolf von Harnack 也成為神學家。他繼承了馬丁路得 (M. Luther; 1483$\sim$1546) 士來馬赫 (Friedrich Schlereimacher; 1768$\sim$1834) 與立敕爾 (Albrecht Ritschl; 1822$\sim$1889) 的神學傳統並加以普遍推廣。 他有自己的一套神學思想, 不願去拾人牙慧, 是著名基督教 (路得會) 神學家, 屬於自由派教會史學者。 他所寫的《何謂基督教》(What is Christianity?) 於 1901 年出版, 馬上成為空前的暢銷書。 這本書是 Adolf von Harnack 於 1899$\sim$1900 年冬季在柏林大學的演講, 當時現場聽眾就擠得水洩不通。 Adolf Harnack的演講沒有講稿是現場即席演說, 那時候也沒有錄音設備, 唯聽眾裡面有一學生以速記法將演講筆錄, 之後再稍加整理而刊行成書。 此書一出版馬上成為當時最暢銷的神學書。 除了神學活動之外, Adolf von Harnack 還是一位傑出的科學組織者。 1911年德意志帝國成立了威廉皇帝學會(是一個科學研究機構, 是後來馬克斯--普朗克 (Max--Planck) 學會的前身), 而 Adolf von Harnack 是首任的學會會長。 Adolf von Harnack 為這個學會爭取了政府和工業界的支持, 並建立了自然科學和醫學科學研究所。 普朗克學會的最高榮譽哈納克獎章 (Harnack medel) 是根據神學家 Adolf von Harnack 而命名的, 並不是數學家 Axel Harnack。  2. Poisson 積分公式Axel Harnack 主要的研究是位勢理論 (potential theory) 也就是調和函數(harmonic function), 所以最好是從單位圓的 Dirichlet 問題談起。 所謂 Dirichlet 問題 (Dirichlet problem) 意思是: 給定一平滑區域 $\Omega$ 其邊界為 $\partial \Omega$, 與已知定義在 $\partial \Omega$ 的連續函數 $f:\partial \Omega \mapsto \mathbb{R}$。 試求一函數 $u(x,y)$ 在 $\Omega$ 內部滿足 Laplace 方程, 且該函數在區域邊界 $\partial \Omega$ 上取指定值 $f(x,y)$。 問題 2.1: (單位圓盤的 Dirichlet 問題) $$ \left\{ \begin{aligned} \hbox{ (D.E.)}\quad & \Delta u = u_{xx} +u_{yy}=0,\qquad 0\le x^2+y^2\lt1, \\[2mm] \hbox{ (B.C.)}\quad & u(x,y) = f(x,y),\hskip1.9cm x^2+y^2=1. \end{aligned} \right. \qquad(2.1) $$ Dirichlet 問題可追溯自格林 (George Green; 1793$\sim$1841) 關於電磁學的研究 《An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism, $1828$》。 他將問題簡化為構造我們現在所說的格林函數 (Green function) 的問題, 並認為格林函數對於任何區域都存在。 格林論述的方式並不嚴格, 但他的想法對於後世卻有深遠的影響。 在格林之後, 高斯 (Karl Friedrich Gauss; 1777$\sim$1855), William Thomson (Lord Kelvin; 1824$\sim$1907) 以及高斯的學生 Peter Gustav Lejeune Dirichlet (1805$\sim$1859) 對此問題都有重要貢獻, 尤其 Dirichlet 已經知道利用 Poisson 核 (Poisson kernel) 來表示 Dirichlet 問題的解。 Dirichlet 問題最重要的突破是黎曼 (B. Riemann; 1826$\sim$1866) 的貢獻, 雖然如此, 但謙遜的黎曼由於在 Dirichlet 的課堂上首次學到這問題, 所以稱之為 《Dirichlet問題》 以歸功於 Dirichlet。 1 1 另外還有《Dirichlet原理》 (Dirichlet principle)也是因此而命名! 2.1. Daniel Bernoulli 的分離變數法我們回到 Dirichlet 問題 (2.1), 座標只是權宜之計過渡而已, 並不是一成不變。 數學的常識 (common sense) 告訴我們看到圓除了聯想到 $\pi$ 之外就是極座標 (polar coordinate)。 由於區域的特殊性必須將 (2.1) 改寫為極座標 $$ \left\{ \begin{aligned} \hbox{ (D.E.)}\quad & \Delta u = u_{rr} + {1\over r}u_r +{1\over r^2}u_{\theta\theta}=0,\qquad 0\le r \lt1\,, \\[2mm] \hbox{ (B.C.)}\quad & u(1,\theta) = f(\theta)\,,\qquad 0\le \theta \le 2\pi, \end{aligned} \right. \qquad(2.2) $$ 並要求 $$ u(r,\theta+2\pi)= u(r,\theta),\qquad f(\theta+2\pi)= f(\theta)\,. \qquad(2.3) $$ 研究(2.2)--(2.3) 的第一招就是分離變數法 (separation of variables), 這是偏微分方程必學的方法, 是任何一個接受過理工高等教育的人該知道的。 通常我們將這個方法歸功於瑞士數學家 Daniel Bernoulli (1700$\sim$1782), 他是 John Bernoulli (1667$\sim$1748) 的兒子, 同時是偏微分方程的拓荒者之一也是流體力學的開創者。 假設 $u(r,\theta)$ 可以分解為(視為因式分解!) $$ u(r,\theta) = R(r)\Theta(\theta). \qquad(2.4) $$ 由於 $u(r,\theta)$ 是 $\theta$ 的週期函數我們必須先考慮函數 $\Theta(\theta)$, 將 (2.4) 代入 (2.2) 則 $\Theta$ 滿足二階常微分方程的邊界值問題 $$ \Theta^{\prime\prime}+{\lambda}\Theta=0, \qquad \Theta(0)=\Theta(2\pi), \qquad 0\le \theta \le 2\pi. \qquad(2.5) $$ 這是一個 Sturm-Liuoville 問題, 對應於(有限維)聯立代數方程組這是(無窮維)微分方程的固有值問題。 其固有值、 固有函數為(經計算) $$ \left\{ \begin{aligned} \lambda_{n}&=n^2, \qquad n=0,1,2,3, \ldots, \\[2mm] \Theta_{0}(\theta)&={1\over 2} a_0, \\[2mm] \Theta_{n}(\theta)&=a_n\cos n\theta+b_n\sin n\theta,\qquad n=1,2,\ldots, \end{aligned} \right. \qquad(2.6) $$ 其中 $a_0, a_n, b_n \in \mathbb{R}$。 這裡要特別強調固有值是由邊界產生的, 換句話說: 固有值問題本質上是一個邊界值問題 ! 固有值 $\lambda_n=n^2$ 對應的 $R(r)$ 標記為 $R_n(r)$ 則滿足 Cauchy-Euler 常微分方程 $$ r(rR_n^{\prime})^{\prime} - n^2 R_n=0, \qquad 0\le r\lt1, \qquad(2.7) $$ 其解分別是 $$ R_{n}(r)=\alpha_nr^n+\beta_n r^{-n}, \qquad R_{0}(r)=\alpha_0+\beta_0\log{r}. \qquad(2.8) $$ 有界的解才會列入考慮, 因此 $\beta_n=0, n=0, 1, 2,\ldots $。 根據線性或重疊原理 (principle of superposition), Dirichlet 問題 (2.2) 的一般解可以表示為 (將 $\alpha_0, \alpha_n$ 都視為 $1$!) $$ u(r,\theta)={1 \over 2}a_0 +\sum_{n=1}^{\infty}\big(a_{n}\cos n\theta +b_{n}\sin n\theta\big)r^n,\qquad 0\le r\lt1. \qquad(2.9) $$ 這裡我們是刻意將常數項表示為 ${1 \over 2}a_0$, 因為這形式的 Fourier 級數才是對稱的。 一個真正懂 Fourier 分析或調和分析的學者一定是堅持這個形式。 Fourier 係數 $a_{0}$、 $a_{n}$、 $b_{n}$是由調和函數 $u(r,\theta)$ 的邊界值來決定: $$ u(1,\theta)=f(\theta)={1 \over 2}a_0 +\sum_{n=1}^{\infty}\big(a_{n}\cos n\theta +b_{n}\sin n\theta\big). \qquad(2.10) $$ (2.10) 兩邊分別乘 $\cos n\theta $、 $\sin n\theta$ 後從 $-\pi$ 積分到 $\pi$ 得 $$ \begin{pmatrix} a_n \\[2mm] b_n \end{pmatrix} ={1\over 2\pi}\int_{-\pi}^{\pi} f(\theta) \begin{pmatrix} \cos n\theta \\[2mm] \sin n\theta \end{pmatrix} d\theta. \qquad(2.11) $$ 把 $\theta$ 換為 $\varphi$ 之後將 (2.11) 代入 (2.9), 假設積分與級數順序可以交換得 $$ \begin{aligned} u(r,\theta) &={1\over 2\pi} \int_{-\pi}^{\pi} f(\varphi) d\varphi \\ &\qquad +\sum_{n=1}^\infty {r^n\over \pi} \int_{-\pi}^{\pi} f(\varphi) \big(\cos n \varphi \cos n \theta +\sin n \varphi \sin n \theta\big) d\varphi \\ &={1\over 2\pi} \int_{-\pi}^{\pi} f(\varphi) \bigg[1+2\sum_{n=1}^\infty r^n \cos n( \theta-\varphi)\bigg] d\varphi. \end{aligned} \qquad(2.12) $$ 藉由等比級數可以將 (2.12) 積分符號內的無窮級數表示為 Poisson 核 (Poisson kernel)。 定義 2.2: 給定 $0\le r\lt1$, Poisson 核定義為 $$ P(r,\theta) \overset{\rm def}{=} 1+2 \sum_{n=1}^\infty r^n \cos n\theta = {1-r^2 \over 1-2r\cos \theta +r^2}. \qquad(2.13) $$ (2.13) 對 $\theta$ 積分並利用 $$ \int_{-\pi}^\pi \cos n\theta d\theta=0,\qquad n=1,2,\ldots, $$ 然後根據一致收斂可以變換積分與無窮級數的順序得 Poisson 核的歸一化性質 $$ {1\over 2\pi}\int_{-\pi}^{\pi} P(r,\theta) d\theta ={1\over 2\pi}\int_{-\pi}^{\pi} {1-r^2 \over 1-2r\cos \theta +r^2} d\theta =1. \qquad(2.14) $$ 定理 2.3: (Poisson 積分公式) Dirichlet 問題 (2.1) 的解可以表示為: $$ \begin{aligned} u(r,\theta) &={1\over 2\pi} \int_{-\pi}^{\pi} f(\varphi) P(r, \theta-\varphi) d\varphi \\[2mm] &={1\over 2\pi} \int_{-\pi}^{\pi} f(\varphi) {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi. \end{aligned} \qquad(2.15) $$ 證明: 嚴格的證明沒有需要, 首先由 (2.13) 無窮級數形式的 Poisson 核, 我們需要變換微分與無窮級數的順序以證明 $P(r,\theta)$ 滿足 Laplace 方程 $$ \Delta P(r,\theta) = P_{rr} +{1\over r}P_r +{1\over r^2}P_{\theta\theta}=0. $$ 其次由積分公式 (2.15) 變換微分與積分的順序與上式證明 $u(r,\theta)$ 是一個調和函數。 $\Box$ 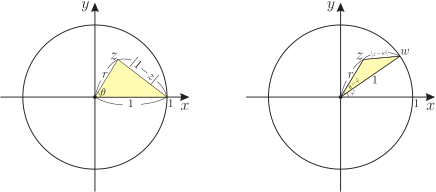 註解: 1. Poisson 積分公式 (2.15) 的幾何意義可以這麼看: 將 Poisson 核 $P(r,\theta-\varphi)$ 視為權重函數 (weight function), 則 Dirichlet 問題 (2.1) 的解 $u(r,\theta)$ 是邊界值 $f(\varphi)$ 的加權平均, 而且這個加權平均隨著位置的改變而變化。 假設邊界點 $(\cos \varphi, \sin \varphi)$ 固定, 則當 $(x,y)=(r\cos\theta, r\sin \theta)$ 越接近 $(\cos \varphi, \sin \varphi)$ 時, $P(r,\theta-\varphi)$ 的值變大, 所以邊界值會得到越多的權重, 同理 $(x,y)=(r\cos\theta, r\sin \theta)$ 離邊界點 $(\cos \varphi, \sin \varphi)$ 越遠, $P(r,\theta-\varphi)$ 的值變小, 則邊界值就會得到越少的權重, 在 (4.1)--(4.3) 還會詳細討論。 2. Poisson 核的歸一化性質 (2.14) 是透過無窮級數 (Fourier級數) 而得, 這讓人覺得不踏實。 實際上也可以直接積分而得, 但我們需要積分公式 $$ \int_0^{2\pi} {dx \over 1-a\cos x} = {2\pi \over \sqrt{1-a^2}},\qquad a^2\lt1. $$ 有興趣的讀者可以利用複變函數論的留數定理得此公式, 然後簡單的變數變換可推得(2.14)。 3. 利用變數變換可推得極座標 Laplace 算子 (2.2) $$ \Delta u = u_{xx} + u_{yy}= u_{rr} + {1\over r}u_r +{1\over r^2}u_{\theta\theta} ={1\over r}{\partial \over \partial r}\bigg(r {\partial u\over \partial r}\bigg) +{1\over r^2}u_{\theta\theta}. \qquad(2.16) $$ 這是一個很好的題目, 我都要求學生當場就可以推出這個結果。 因為角度不具量綱(dimensionless), $[\theta]=1$, 而 $x,y,r$ 是長度, $[x]=[y]=[r]$, 簡單的量綱分析或因次分析容易判斷 (2.16) 是量綱平衡 (dimensional balance): \begin{align*} [u_{xx}]&=[u_{yy}]= [u_{rr}] ={[u]\over [x]^2}={[u]\over [y]^2}={[u]\over [r]^2},\\ \bigg[{1\over r}u_r\bigg]&={1\over [r]}{[u]\over [r]} ={[u]\over [x]^2}, \qquad \bigg[{1\over r^2}u_{\theta\theta}\bigg]={1\over [r]^2}{[u]\over [\theta]^2}={[u]\over [r]^2}={[u]\over [x]^2}, \end{align*} 所以 Laplace 算子 $\Delta u$ 中的 $u_r$ 與 $u_{\theta\theta}$ 前面的係數分別是 ${1\over r}$ 與 ${1\over r^2}$ 完全是合理也不需要背。 事實上歐拉 (L. Euler) 比 Laplace 更早之前就已經發現這個算子, 但 Laplace 在他的名著天體力學中, 因為研究重力位能而有系統地研究了這個算子, 所以後人將此歸功於他並稱之為 Laplace 算子。 順便一提的是歷史上第一次出現的 Laplace 算子是極座標 (2.16) 而不是垂直座標 (2.1), 因為當初他們研究的天體力學是圓周運動。 4. 比較 (2.9)--(2.10) 兩式是有趣且有意義的。 (2.10) 可視為函數 $f(\theta)$ 在單位圓上的 Fourier 級數, (2.9) 則是把半徑 $r$ 也考慮進來, 也就是說考慮 $f$ 之 Fourier 級數的 Abel 和, 換句話說 : $u(r,\theta)$ 是 $f(\theta)$ 之 Fourier 級數的 Abel 平均 (Abel mean)。 一旦邊界條件確定了 (表示為 Fourier 級數), 則只需將對應的角度 $n\theta$ 的 $\cos n\theta, \sin n\theta$ 乘上 $r^n$, 就可以得到單位圓內的調和函數: \begin{align*} f(\theta)&={1 \over 2}a_0 +\sum_{n=1}^{\infty}\big(a_{n}\cos n\theta +b_{n}\sin n\theta\big)\\ \Longrightarrow\quad u(r,\theta)&={1 \over 2}a_0 +\sum_{n=1}^{\infty}\big(a_{n}\cos n\theta +b_{n}\sin n\theta\big)r^n. \end{align*} 這裡自然要問: Poisson 積分公式 (2.15) 這個調和函數解是否滿足邊界條件? 同時也引進分析中最重要的問題: Fourier 級數的收斂性問題: $$ \lim_{r\to 1^-} u(r,\theta) \overset{??}{=} f(\theta). \qquad(2.17) $$ 這裡以 $r$ 為參數, 也暗示了這是一個邊界值問題 (boundary value problem)! 5. 在 (2.12) 的推導過程中我們真正體會到三角函數的積化和差公式的意義是: 『將非線性轉化為線性。』 因此使得非線性(乘積)三角函數的積分與微分成為可能。 而且透過積化和差這個動作, Dirichlet 問題的解 $u(r,\theta)$ 最終是以卷積 (convolution) 的形式表達出來, 積化和差其中的 和差本質上就是卷積, 這裡面是有非常深刻的物理內涵。 主要原因是 Laplace 算子 $\Delta$ 具有很好的對稱性 (symmetry), 其中之一是經過正交變換 (orthogonal transformation) 之後是不變的, 而旋轉 (rotation) 是最典型的正交變換, 所以 Laplace 算子是旋轉不變的, 也就是與角度無關。 由於 Laplace 算子是角度平移不變, 所以 Poisson 積分公式 (2.15) 是以角度的卷積表示出來 $$ u(r,\theta)= {1\over 2\pi} P(r,\theta)*_\theta f(\theta) \qquad(2.18) $$ 一個物理系統如果是平移不變的, 最終它的解會以卷積的形式顯現出來! 6. 根據卷積的特質由 (2.18) 可知 Fourier 級數的收斂性問題 (2.17) 可以改寫為: $$ \lim_{r\to 1^-}{1\over 2\pi} P(r,\theta)\overset{??}{=}\delta(\theta). \qquad(2.19) $$ 因此 Fourier 級數收斂的問題就等價於 ${1\over 2\pi} P(r,\theta)$ 以 $r$ 為參數是否形成一 Dirac 序列? 這是數學分析最核心的主題。 學了一年的高等微積分 (數學分析), 如果學生只會像鸚鵡說著 $\epsilon - \delta$, 這表示已經走火入魔了 (學錯了)! $\Box$ 我們回答(2.17)--(2.19)這個數學分析的收斂問題。 定理 2.4: 假設 $f:[0,2\pi]\to \mathbb{R}$ 是一分段連續的周期函數則 $$ \lim_{r\to 1^-}u(r,\theta) = f(\theta). \qquad(2.20) $$ 也就是說: 由 Poisson 積分公式 (2.15) 得出的解 $u(r,\theta)$, 真的是單位圓盤上 Dirichlet 問題 (2.1) 的解。 證明: 好的分析是從不等式出發, 也就是比較一下, 先看 (2.20) 左右兩邊減一減 $$ u(r,\theta) -f(\theta)={1\over 2\pi} \int_{-\pi}^{\pi} f(\varphi) {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi -f(\theta). $$ 這裡我們遇見第一個困難: 一個函數乘上積分核 (Poisson 核) 的積分與該函數在某一點值的相減! 此時將不在積分符號內的函數 $f(\theta)$ 刻意寫為 $f(\theta)\cdot 1$ 再利用 Poisson 核的歸一性質 (2.14), 將 $f(\theta)$ 表示為積分 $$ f(\theta)= f(\theta)\cdot 1= {1\over 2\pi} \int_{-\pi}^{\pi} f(\theta) {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi. $$ 其次利用三角不等式可得 $u(r,\theta)$ 與 $f(\theta)$ 之間的估計 $$ \begin{aligned} |u(r,\theta) -f(\theta)|&=\bigg|{1\over 2\pi} \int_{-\pi}^{\pi} (f(\varphi)-f(\theta)) {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi\bigg|\\ &\le {1\over 2\pi} \int_{-\pi}^{\pi} \Big|f(\varphi)-f(\theta)\Big| {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi. \end{aligned} \qquad(2.21) $$ 這裡我們用到 Poisson 核是非負性的條件。 到這一步我們遇見分析的根本問題: 函數分解與定義域分解。 由函數 $f$ 的連續性將積分區域拆解為兩部分 $$ {1\over 2\pi} \int_{-\pi}^{\pi} \Big|f(\varphi)-f(\theta)\Big| {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi= I_1 +I_2, \qquad(2.22) $$ 其中 $$ \left\{ \begin{aligned} I_1&={1\over 2\pi} \int\limits_{|\varphi-\theta|\lt\delta} \Big|f(\varphi)-f(\theta)\Big| {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi, \\[2mm] I_2&={1\over 2\pi} \int\limits_{|\varphi-\theta|\ge \delta} \Big|f(\varphi)-f(\theta)\Big| {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi. \end{aligned} \right. \qquad(2.23) $$ 我們先看 $I_1$, 根據 $f$ 的連續性與 Poisson 核是非負與歸一性得 $$ I_1\le \epsilon {1\over 2\pi} \int\limits_{|\varphi-\theta|\lt\delta} {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi \le \epsilon {1\over 2\pi} \int_{-\pi}^{\pi}P(r, \theta -\varphi) d\varphi=\epsilon. \qquad(2.24) $$ 其次看 $I_2$, 通常這部分沒有那麼直觀也就比較困難。 由於積分區域已拆解, 現在只能從函數的性質出發。 基本上被積分函數是 $f(\theta)$ 與 Poisson 核 $P(r,\theta)$ 的相乘, 而兩個函數相乘的積分這件事情是困難的! 也是非線性分析 (nonlinear analysis) 最關心的問題。 一個定義在緊緻區間的連續函數必定是一致有界, \begin{align*} f\in C[-\pi,\pi] \quad\Longrightarrow&\quad |f(t)|\lt M,\quad \forall t\in [-\pi,\pi].\\ {\hbox{因此}} |f(\varphi)-f(\theta)|\le 2M \quad\Longrightarrow&\quad I_2\le {M\over \pi} \int\limits_{|\varphi-\theta|\ge \delta} {1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2} d\varphi. \end{align*} 直觀而言當 $\theta\gt0$ 時 $\cos \theta$ 基本上是一遞減函數 $$ |\varphi-\theta|\ge \delta \quad\Longrightarrow\quad {1\over 1-2r \cos (\theta-\varphi)+r^2} \le {1\over 1-2r \cos \delta+r^2}. $$ 簡單的微分容易驗證分母 $1-2r \cos \delta+r^2$ 的最小值等於 $1-(\cos\delta)^2$ 並產生在 $r=\cos \delta$ $$ {1 \over 1-2r \cos (\theta-\varphi)+r^2}\le {1\over 1-(\cos\delta)^2}. $$ Poisson 核是一致有界, 所以 $$ \lim_{r\to 1^-}{1-r^2 \over 1-2r \cos (\theta-\varphi)+r^2}=0 \quad\Longrightarrow\quad \lim_{r\to 1^-}I_2 =0. \qquad(2.25) $$ 將 (2.21)--(2.25) 合併就證明了 Poisson 收斂定理 (2.20)。 $\Box$ 註解: 1. Dirac--$\delta$ 函數: 證明過程中我們得出了 Poisson 核的三個重要性質, (a) 非負性: 對所有的 $r$ 滿足 $0\le r\lt1$, 總是有 $P(r,\theta)\ge 0$。 $$ 0\lt 1-r^2\le 1-2r\cos\theta+r^2 \quad\Longrightarrow\quad P(r,\theta)\ge 0. $$ (b) 歸一化: 同 1 之條件 $P(r,\theta)$ 滿足 $$ {1\over 2\pi}\int_{-\pi}^{\pi} P(r,\theta) d\theta =1. $$ (c) 邊界行為: 存在 $r_0$ 使得 $r_0\le r \lt1$ 總是有 $$ \int\limits_{\delta \le |\theta|\le \pi} P(r,\theta) d\theta \lt\epsilon. $$ 也因為如此我們稱 Poisson 核是好核, 實際上它就是逼近單位元素 (approximate identity), 這相當於說它差不多就是 Dirac-$\delta$ 函數。 2. 處理積分 $I_2$ 的時候, 我們已經面對非線性分析 (nonlinear analysis) 的核心問題。 如果 $f$ 不是連續而只是可積函數, 則 (2.25) 的論述必須更改為用 Cauchy-Schwarz 或 Hölder 不等式, 如此 Poisson 收斂定理 (2.2) 就可以推廣為一般的 $L^p$ 空間 $$ \lim_{r\to 1^-}\Vert u(r,\theta) - f(\theta)\Vert_p =0,\qquad 1\le p\le \infty. $$ 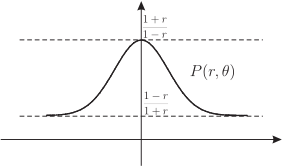 2.2. Cauchy 積分公式透過 Euler 公式可以將 (2.13) 的 Poisson 核 $P(r,\theta)$ 寫得更精簡 $$ P(r,\theta) =\sum_{n=-\infty}^\infty r^{|n|} e^{in\theta} =\sum_{n=0}^\infty r^n e^{in\theta} +\sum_{n=1}^\infty r^n e^{-in\theta}. \qquad(2.26) $$ 我們必須要求 $r\lt1$, 此時 (2.26) 之右式才是兩個收斂的等比級數。 令 $z=r e^{i\theta}$ 則 $$ \begin{aligned} S(z)&={1+z\over 1-z} = (1+z)(1+z+z^2+\cdots) \\[2mm] &= 1+ 2\sum_{n=1}^\infty z^n =1+2\sum_{n=1}^\infty r^n e^{in\theta}. \end{aligned} \qquad(2.27) $$ 然後利用 ${\rm Re}(z)={1\over 2}(z+\bar z)$ 將 Poisson 核 (2.26) 重新表示為 $$ \begin{aligned} P(r,\theta) &={\rm Re} ( 1+2z+2z^2 + 2z^3 +\cdots\cdots)={\rm Re} \bigg({1+z\over 1-z}\bigg) \\[2mm] &= {1\over 2}\bigg({1+z\over 1-z}+ {1+\bar{z}\over 1-\bar{z}}\bigg) ={1-z\bar{z}\over (1-z)(1-\bar{z})} ={1\over 1-z} +{\bar{z}\over 1-\bar{z}} \\[2mm] & ={1\over 1-z}-{1\over 1-(1/\bar{z})}={1\over 1-z} -{1\over 1-z^*} ={1\over 1-r e^{i\theta}}+{re^{-i\theta}\over 1-r e^{-i\theta}} \\[2mm] &= {1-r^2 \over (1-r e^{i\theta})(1-r e^{-i\theta})} ={1-r^2 \over 1-2r\cos \theta +r^2}. \end{aligned} \qquad(2.28) $$ 順便一提做個旋轉將 1 換為 $w=e^{i\varphi}$, 則 (2.28) 可以推廣為 $$ \begin{aligned} P(r,\theta-\varphi)&={\rm Re} \bigg({w+z\over w-z}\bigg)={1\over 2}\bigg[{w+z\over w-z} +{\overline{w}-\bar{z}\over \overline{w}-\bar{z}} \bigg] \\[2mm] &={1-z\bar{z}\over (w-z)(\overline{w}-\bar{z})} ={w\over w-z} +{\bar{z}\over \overline{w}-\bar{z}} \\[2mm] &={1\over 1-(z/w)}-{1\over 1-(\overline{w}/\bar{z})} ={1\over 1-(z/w)}-{1\over 1-(z/w)^*} \\[2mm] &={1\over 1-r e^{i(\theta-\varphi)}}+{re^{-i(\theta-\varphi)}\over 1-r e^{-i(\theta-\varphi)}} = {1-r^2 \over (1-r e^{i(\theta-\varphi)})(1-r e^{-i(\theta-\varphi)})} \\[2mm] &={1-r^2 \over 1-2r\cos (\theta-\varphi) +r^2}. \end{aligned} \qquad(2.29) $$ 這裡 $(z/w)^*=(\overline{w}/\bar{z})$ 是 $(z/w)$ 的對稱點。 由 (2.27) 定義的 $S(z)={1+z\over 1-z}$ 這個分式是 Cayley 變換的變形, 而實際上是一個 Möbius 變換, 因此上面的推導也暗示了 Poisson 核與 Möbius 變換有密切關係。 在複變函數中有兩個重要的變換: $$ \left\{ \begin{aligned} w_1(z) & = {z-a\over 1-\bar az}, \qquad |a|\lt1, \quad a,z \in \mathbb{C}, \\[2mm] w_2(z) & = e^{i \theta} z. \end{aligned} \right. \qquad(2.30) $$ 第二個變換 $(2.30)_2$ 基本上是旋轉, 它將單位圓映至單位圓, 單位圓內部映至單位圓內部。 $(2.30)_1$ 也是如此, 而且它將 $z=a$ 變換為 $w_1=0$, 將對稱點 $z^*={1/\bar{z}}$ 帶到 $\infty$, 第一個變換 $(2.30)_1$ 就是鼎鼎大名的 Möbius 變換, 在保角映射 (comformal mapping) 中是很重要的。 利用 Möbius 變換可得 Poisson 核。 定理 2.4: Poisson 核是單位圓映至單位圓之 Möbius 變換的 Jacobian。 證明: 對 $(2.30)_1$ 取全微分得 $$ dw_1 = {dz\over 1-{\bar a}z}+ {(z-a)\bar a dz\over (1-\bar az)^2} = {1-a\bar a \over (1-\bar az)^2}dz. \qquad(2.31) $$ 由於 $(2.30)_1$ 是將單位圓 $|z|=1$ 映至單位圓 $|w_1|=1$, 可以假設 $z = e^{i\varphi}$、$w_1=e^{i\psi}$、 $\varphi,\psi \in [0,2\pi]$, 因此 $(2.31)$、 $(2.30)_1$ 成為 $$ \left\{ \begin{aligned} dw_1&= e^{i\psi}d\psi ={1-a\bar a\over (1-\bar a e^{i\varphi} )^2}e^{i\varphi } d\varphi, \\[2mm] w_1&=e^{i\psi} ={{e^{i\varphi} -a}\over{1-\bar a e^{i\varphi}}} ={1-a e^{ -i\varphi} \over 1-\bar a e^{i\varphi}}e^{i\varphi}. \end{aligned} \right. \qquad(2.32) $$ 將 (2.32) 的兩式相除得 $$ d\psi ={1-a\bar a\over {|1-\bar a e^{i\varphi}|}^2}d\varphi. \qquad(2.33) $$ 因為 $|a|\lt1$, 可設 $a=re^{i\theta}$、 $0\leq r\lt1$, 故 $$ d\psi= {1-r^2\over 1-2r\cos(\theta -\varphi )+r^2}d\varphi = P(r,\theta -\varphi)d\varphi, \qquad(2.34) $$ 其中 $P(r,\theta -\varphi)$ 就是 Poisson 核 (Poisson kernel)。 由 $(2.34)$ 明顯可知 Poisson 核就是將單位圓映至單位圓之 Möbius 變換的 Jacobian。 $\Box$ 利用 Cauchy 積分公式與對稱點 (symmetric point) 可以推得 Poisson 積分公式。 首先 $|z|\lt1$, 所以 Cauchy 積分公式為 $$ f(z)={1\over 2\pi i}{\oint\limits_{|w|=1}}{f(w)\over w-z}dw. \qquad(2.35) $$ 另外 $z$ 針對單位圓的對稱點為 $$ z^*= {1\over |z|}{z\over |z|}= {z\over |z|^2}={z\over z\bar{z}}= {1\over \bar z}. \qquad(2.36) $$ 此時 $z^*$ 在單位圓外部由 Cauchy 積分公式知 $$ \begin{aligned} {1\over 2\pi i}{\oint\limits_{|w|=1}}{1\over w-z^*}f(w)dw &={1\over 2\pi i}{\oint\limits_{|w|=1}}{1\over w-{1\over \bar z}}f(w)dw \\[2mm] &={1\over 2\pi i}{\oint\limits_{|w|=1}}{\bar z\over \bar z w-1}f(w)dw=0. \end{aligned} \qquad(2.37) $$ 因為考慮的是 Dirichlet 問題, 所以 (2.35)、 (2.37) 兩式相減並由 (2.29) 得 $$ \begin{aligned} f(z)&={1\over 2\pi i}{\oint\limits_{|w|=1}}\bigg({1\over w-z}+ {\bar z\over 1-w\bar z}\bigg)f(w)dw \\[2mm] &={1\over 2\pi }\int_{-\pi}^{\pi}{1-|z|^2\over (w-z)(\overline{w}-\bar z) }f(e^{i\varphi} )d\varphi, \qquad ( w=e^{i\varphi} ) \\[2mm] &={1\over 2\pi }\int_{-\pi}^{\pi}\hbox{Re}\bigg({w+z\over w-z}\bigg) f(e^{i\varphi} )d\varphi, \qquad (z=re^{i\theta}) \\[2mm] &={1\over 2\pi }\int_{-\pi}^{\pi}f(e^{i\varphi}) {1-r^2\over 1-2r\cos(\theta -\varphi )+r^2}d\varphi \\[2mm] &={1\over 2\pi }\int_{-\pi}^{\pi}f(e^{i\varphi})P(r,\theta-\varphi)d\varphi. \end{aligned} \qquad(2.38) $$ 註解: $\ $ 1. Poisson 核是 Möbius 變換的 Jacobian, 因此從量綱平衡的角度而言, Poisson 核必定是不帶量綱即無量綱 (dimensionless)、 $[P(r,\theta)]=1$, 另外 $\theta$、 $\varphi$ 是角度, 而角度是無量綱: $[\theta]=[\varphi]=1$, 或進一步將 $\theta$、 $\varphi$ 視為參數 (parameter) 而非角度則 $[d\varphi]= [2\pi]=[\theta]$, 則 Poisson積分公式 $(2.14)$ 是量綱平衡: $$ [u]={1\over [\pi]}[f][P][d\varphi]=[f]. $$ 而 $u$ 的邊界值等於 $f$, 因此 $u$ 與 $f$ 有相同的量綱。 2. 關於 Cauchy 積分公式 (2.35) 或更廣義的 Cauchy 積分公式 (將單位圓換為一般的單純封閉曲線 $C$!) $$ f(z)={1\over 2\pi i}\oint_C {f(w)\over w-z}dw, \qquad f^{(n)}(z)={n!\over 2\pi i}\oint_C {f(w)\over (w-z)^{n+1}}dw. \qquad(2.39) $$ 我個人有一些心得分享並確信在書本是看不到的。 首先圓周率是圓的周長除以直徑, 所以是無量綱, 因此 (2.39) 是量綱平衡 \begin{align*} [\pi]=[i]=1,\quad [w]=[z]=[dw] \quad\Longrightarrow\quad [f]={1\over [2\pi i]}{[f]\over [w-z]}[dw],\\[2mm] \big[f^{(n)}(z)\big]=\bigg[{d^n f \over dz^n}\bigg]={[f]\over [z]^n},\hskip 4cm~\\[2mm] \bigg[{n!\over 2\pi i}\oint_C {f(w)\over (w-z)^{n+1}}dw\bigg] ={1\over [2\pi i]}{[f]\over [w-z]^{n+1}}[dw]={[f]\over [z]^n}.\hskip .8cm~ \end{align*} 所有的公式都會講話, 如果沒有這種感覺就表示你還不了解這個公式。 Cauchy 積分公式中的另外兩項可以這麼看 $$ \begin{aligned} 2\pi i &\quad\Longleftrightarrow\quad \hbox{線積分沿著封閉單純曲線 $C$ 繞一圈。}\\ n!&\quad\Longleftrightarrow\quad f^{(n)}(z)\quad \hbox{Taylor 級數第 $n$ 項係數 $\dfrac{f^{(n)}}{n!}$。} \end{aligned} $$ 3. Cauchy 積分公式 (2.35) 或 (2.39) 等號左邊的 $f(z)$ 與線積分 (圍道積分) 內被積分函數 $f(w)$ 乍看之下是一樣的, 但這是表象! 假設 $C=\partial \Omega$ 是平面區域 $\Omega$ 的邊界, 則 $z\in \Omega$ 是封閉單純曲線 $C$ 所圍區域 $\Omega$ 的任意點, 因此等號左邊的 $f(z)$ 是解析函數 $f$ 在 $C$ 內部 $\Omega$ 任意點 $z$ 的值。 而 $w\in C$, 所以被積分函數 $f(w)$ 是解析函數 $f$ 的邊界值。 Cauchy 積分公式告訴我們: 解析函數在 $\Omega$ 任意點的值 $f(z)$ 完完全全由它的邊界值 $f(w)$ 所決定, 甚至它的任意階微分也是 $f(w)$ 就足夠決定, 並沒有要求邊界值 $f(w)$ 有更高階的微分, 因為 Cauchy 積分公式是一種卷積, 微分是微到積分核 ${1\over w-z}$ 上。 這件事與 Laplace 方程或更一般的橢圓偏微分方程的正則性問題 (regularity problem) 有關, 要對複變函數論有深刻的認知, 我們需要有偏微分方程的知識, 這正是當初黎曼 (B. Riemann, 1826$\sim$1866) 發展複變函數論的初心! 4. 根據解析函數的定義: $\Omega \subset \mathbb{C}$ 是複數平面上的開集(open set), 如果 $f:\Omega \to \mathbb{C}$ 是連續可微則稱 $f$ 為一解析函數。 然後利用 Cauchy 積分公式可推得 $f$ 是無窮多次可微 $$ f\in C^1(\Omega) \quad\Longrightarrow\quad f\in C^\infty(\Omega). $$ 對初學者而言這簡直難以想像! 倒過來無窮多次可微當然是連續可微, 但現在是反其道而行。 之所以會有此困惑那是因為我們被一維的思考 (one dimensional thinking) 所綁架。 複數平面的微分的逼近路線除了 $x$-軸、 四面八方直線之外, 各種的迂迴路徑都是有可能的。 例如, 複數平面的兩點是以拋物線逼近, 這就蘊含連續可微是二次可微。 同理, 高次曲線逼近就是高次可微。 這是解析函數內在的結構, 跟前一個註解一樣, 可以透過橢圓偏微分方程尤其是 bootstrap process 2 2 我把 bootstrap 翻譯為自力更生! 來理解。 5. 對稱點 (2.36) 我是刻意如此表達的。 首先將 $z$ 與 $z^*$ 視為向量, 因為兩者在同一直線上所以 $z^*$ 的方向與 $z$ 相同為 ${z\over |z|}$。 其次 $z^*$ 是 $z$ 的反轉 (inversion) 所以 $z^*$ 的大小為 $|z^*|={1\over |z|}$ $$ {z\over |z|}\hbox{(方向)}, \quad {1\over |z|}\hbox{(大小)} \quad\Longrightarrow\quad z^*= {1\over |z|}{z\over |z|}={1\over |z|^2}z={1\over \bar z}. $$ 利用極座標可以容易想像這個事實 $$ z=r e^{i\theta}\quad\Longrightarrow\quad z^* = {1\over r}e^{i\theta}, \qquad |z||z^*|=1. $$ 如果半徑是 $R$, 做個縮放 (dilation) 令 $\hat{z}={z\over R}$ 則 $$ \hat{z}^*={1\over \bar{\hat z}}={R\over \bar z}, \quad \hat{z}^*={z^*\over R} \quad\Longrightarrow\quad z^*={R^2\over \bar z}={R^2\over |z|^2}z. \qquad(2.40) $$ 如果圓心是 $a\in \mathbb{C}$ 則簡單的平移即可: $$ z\to z-a, \quad z^*\to z^*-a \quad\Longrightarrow\quad z^*-a = {R^2\over \bar{z}- \bar{a}}. \qquad(2.41) $$  6. 雖然 (2.36) 給出單位圓內任意點 $z$ 的對稱點之表現式, 但是幾何意義並不清楚, 我們在此給一個精確的定義。 考慮半徑等於 $R$ 的圓盤 $B_2(R)$, 令 $z\in B_2(R)$ 是圓盤內的任意點, 而 $z^*$ 是 $z$ 的對稱點, 則存在 $\kappa\in \mathbb{R}$, 使得 $$ {|w-z|\over |w-z^*|}=\kappa, \qquad \forall w\in \partial B_2(R). \qquad(2.42) $$ 現在決定常數 $\kappa$, 將 $w$ 旋轉到 $x$-軸, 也就是 $z, w, z^*$ 三點共線代入 (2.42) 得 $$ \kappa={R-|z|\over |z^*|-R}={|z|\over R}{R-|z|\over R-|z|} = {|z|\over R},\qquad z^* = {R^2\over |z|^2} z. \qquad(2.43) $$ 因此對稱關係 (2.42) 為 $$ |w-z|={|z|\over R} |w-z^*|, \qquad \forall w\in \partial B_2(R). \qquad(2.44) $$ 這個關係式也可以藉由內積這麼看 $$ \begin{aligned} |w-z|^2&= (w-z)\cdot(w-z)=|w|^2 -2 w\cdot z + |z|^2 \\[2mm] &= R^2 - 2 w\cdot z + |z|^2\hskip2cm (|w|=R) \\[2mm] &={|z|^2\over R^2}\bigg({R^4\over |z|^2} - 2w\cdot {R^2 \over |z|^2}z+R^2\bigg) \\[2mm] &={|z|^2\over R^2}\bigg(|w|^2 - 2w\cdot {R^2 \over |z|^2}z+{R^4\over |z|^4}|z|^2\bigg) \\[2mm] &={|z|^2\over R^2}\bigg|w - {R^2 \over |z|^2}z\bigg|^2 ={|z|^2\over R^2}|w - z^*|^2. \end{aligned} \qquad(2.45) $$ 最後這個式子直接可得對稱點還有 $w-z$ 與 $w-z^*$ 兩者距離之關係式 (2.44) $$ z^*= {R^2 \over |z|^2}z,\qquad |w-z|= {|z|\over R}|w - z^*|. $$ 更且 (2.44) 也提供實際造對稱點的方法。 給定 $B_2(R)$ 內任意點 $z$ 將之標示為 $A$, 然後與原點 $O$ 連接並把這條線視為 $x$-軸, 接著在 $A$ 劃一條垂線與圓周 $\partial B_2(R)$ 相交於 $w$(標示為 $B$)。 在 $B$ 這點劃一切線與 $x$-軸 $OA$ 相交於 $z^*$ (標示為 $A^*$), 這點 $z^*$ 就是 $z$ 的對稱點。 證明是利用相似三角形, 由圖形容易看到 $$ \triangle OAB\sim \triangle BAA^* \quad\Longrightarrow\quad {R\over |z|}={|w-z^*|\over |w-z|}. $$ $\Box$ 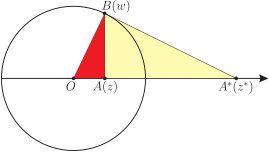 3. 格林等式與格林函數(2.28) 或 (2.29) 的 Poisson 核中有個特別形式 $$ \left\{ \begin{aligned} P(r,\theta)&= {1\over 1-z} - {1\over 1-z^*},\qquad z=e^{i\theta}, \\[2mm] P(r,\theta-\varphi)&= {w\over w-z} - {w^*\over w^*-z^*},\qquad w= e^{i\varphi}. \end{aligned} \right. $$ 這是為了格林函數鋪路的。在討論格林函數之前最好是先談格林定理(Green Theorem): $$ \int\!\!\!\int_\Omega \bigg({\partial P\over \partial x} +{\partial Q\over \partial y}\bigg) dA =\oint\limits_C P(x,y) dy - Q(x,y) dx,\qquad C=\partial \Omega. \qquad(3.1) $$ 細心的讀者會發現 $(3.1)$ 這個形式與一般的格林定理略有不同, 這裡我們將切向量 $(dx, dy)$ 換為朝外法向量 $(dy, -dx)$, 因為我們關心的是散度 (divergence) 或通量 (flux)。 給定函數 $u(x,y), v(x,y)$ 並令 $$ P(x,y)=u(x,y){\partial \over \partial x}v(x,y), \qquad Q(x,y)=u(x,y){\partial \over \partial y}v(x,y), $$ 代入 $(3.1)$ 可以得格林第一等式 $$ \int\!\!\!\int_\Omega (u\Delta v + \nabla u\cdot \nabla v) dA =\oint\limits_C u \bigg({\partial v \over \partial x} dy \!-\! {\partial v \over \partial y} dx\bigg) =\oint\limits_C u (\nabla v\cdot \boldsymbol{n}) ds =\oint\limits_C u {\partial v\over \partial \boldsymbol{n}} ds, \qquad(3.2)_1 $$ 其中 $ \boldsymbol{n} = ({dy\over ds}, - {dx\over ds}) $ 是單位朝外法向量而 $ds = \sqrt{dx^2 +dy^2}$ 則是弧長元素。 將 $u, v$ 對調得 $$ \int\!\!\!\int_\Omega (v\Delta u + \nabla u\cdot \nabla v) dA =\oint\limits_C v {\partial u\over \partial \boldsymbol{n}} ds. \qquad(3.2)_2 $$ (3.2) 兩式相減 $(3.2)_1 -(3.2)_2$ 得格林第二等式 $$ \int\!\!\!\int_\Omega (u\Delta v - v\Delta u) dA =\oint\limits_C \bigg(u {\partial v\over \partial \boldsymbol{n}}- v {\partial u\over \partial \boldsymbol{n}}\bigg) ds. \qquad(3.3) $$ 透過格林第二等式 $(3.3)$ 與 Dirichlet 問題 (2.1) 比較, 考慮 $\Omega=B_2(1)$ 是二維單位圓盤 $C=\partial B_2(1)$ 是單位圓周, 如果選取 $v(x,y)$ 滿足 $$ \left\{ \begin{aligned} \hbox{ (D.E.)}\quad & \Delta v = v_{xx} +v_{yy}=\delta(x,y),\qquad (x,y)\in B_2(1), \\[2mm] \hbox{ (B.C.)}\quad & v(x,y) = 0,\hskip2.9cm (x,y)\in \partial B_2(1). \end{aligned} \right. \qquad(3.4) $$ 滿足 (3.4) 的 $v(x,y)$ 就稱為 Dirichlet 問題 (2.1) 的格林函數(Green's function), 利用$\delta$-函數的性質由格林第二等式 $(3.3)$ 可得 Dirichlet 問題 (2.1) 的表現式 $$ u(x,y)={\oint\limits_{\partial B_2(1)}} f{\partial v\over \partial \boldsymbol{n}}ds,\qquad (x,y)\in B_2(1). \qquad(3.5) $$ 它的意義是: 藉由格林函數, 可以將單位圓內的調和函數在圓內部任意點的值, 表示為其邊界值與格林函數在邊界的法向導數相乘的線積分。 所謂格林函數是滿足邊界條件的基本解 (fundamental solution), 我們有必要介紹一下 $n$ 維 Laplace 方程的基本解 $$ \Delta E_n(\boldsymbol{x}) =\delta(\boldsymbol{x}),\qquad \boldsymbol{x}=(x_1,x_2,\ldots , x_n)\in \mathbb{R}^n. \qquad(3.6) $$ 我將以直觀非典型的方式來推導 (3.6) 的基本解 3 3 這是我教授休假 (sabbatical leave) 訪問 University of Alberta (Edmonton, Alberta, Canada), 有一天講完課在研究室望著窗外滿天的雪花體會出來的。 我記得那年冬天是歷史低溫 ($-46^\circ$ C)。 。我們拆成四部分討論: 1. 量綱分析(dimensional analysis): 先討論 $n\ge 3$。 根據 $\delta$-函數的定義其積分等於 1, 所以可以視為無量綱 (dimensionless), 並由此得 $\delta$-函數的量綱 $$ \bigg[\int_{\mathbb{R}^n} \delta(\boldsymbol{x}) d\boldsymbol{x}\bigg]=[\delta(\boldsymbol{x})][x]^n =1 \quad\Longrightarrow\quad [\delta(\boldsymbol{x})]=[x]^{-n}. $$ 其次藉由量綱平衡的原則 (3.6) 等式兩邊有相同的量綱得 $E_n$-函數的量綱 $$ {[E_n]\over [x]^2}=[\Delta E_n(\boldsymbol{x})] =[\delta(\boldsymbol{x})]=[x]^{-n} \quad\Longrightarrow\quad [E_n]=[x]^{2-n},\qquad n\ge 3. \qquad(3.7) $$ 2. 正交不變性: 由 $\delta$-函數的定義 $$ \delta(\boldsymbol{x})= \left\{ \begin{aligned} 0,&\qquad \boldsymbol{x}\not=\boldsymbol{0}, \\ \infty,&\qquad \boldsymbol{x}=\boldsymbol{0}, \end{aligned} \right. \qquad(3.8) $$ 可以將它視為半徑函數 (radial function), $\delta(\boldsymbol{x})=\delta(|\boldsymbol{x}|)=\delta(r)$, 也就是與角度無關。 Laplace 算子 $\Delta$ 是正交不變, 所以由方程式 (3.6) 可推論 $E_n(\boldsymbol{x})$ 必定是一個半徑函數 $$ E_n(\boldsymbol{x})=E_n(|\boldsymbol{x}|)=E_n(r),\qquad r=|\boldsymbol{x}|=\sqrt{x_1^2+x_2^2+\cdots+x_n^2}. \qquad(3.9) $$ 3. 散度定理 (divergence theorem): 由 (3.7) (3.9) 可以猜測 Laplace 方程的基本解為 $$ E_n(\boldsymbol{x})= k_n{r^{2-n}\over 2-n}; \qquad(3.10) $$ 分母 $2-n$ 雖然是刻意表示的, 但其背後的, 理由是微積分基本定理 $$ \int x^n dx = {x^{n+1}\over n+1}+C,\qquad n\not=-1; \qquad(3.11) $$ 看到多項式 $x^{n+1}$ 自然要聯想分母有個 ${n+1}$, $x^{n+1} \to {x^{n+1}\over n+1}$。 這是學分析的好習慣。 現在決定常數 $k_n$, (3.6) 兩邊對 $\mathbb{R}^n$ 積分並以半徑為 $r$ 的實心球 $\mathbb{B}_n(r)$ 來逼近全空間 $\mathbb{R}^n$ 則由散度定理得 \begin{align*} 1&=\int_{\mathbb{R}^n} \delta(\boldsymbol{x}) d\boldsymbol{x}= \int_{\mathbb{R}^n} \Delta E_n(\boldsymbol{x}) d\boldsymbol{x}=\lim_{r\to \infty}{\int\limits_{\mathbb{B}_n(r)}} \hbox{div}(\nabla E_n(\boldsymbol{x})) d\boldsymbol{x} \\ &=\lim_{r\to \infty}{\int\limits_{\partial \mathbb{B}_n(r)}} \nabla E_n(\boldsymbol{x})\cdot \boldsymbol{n} dS =\lim_{r\to \infty}{\int\limits_{\partial \mathbb{B}_n(r)}} {\partial E_n(\boldsymbol{x})\over \partial \boldsymbol{n}} dS \\ &=\lim_{r\to \infty}{\int\limits_{\partial \mathbb{B}_n(r)}} {\partial E_n(r)\over \partial r} dS =\lim_{r\to \infty}{\int\limits_{\partial \mathbb{B}_n(r)}} k_n r^{1-n} dS \\ &=\lim_{r\to \infty}k_n r^{1-n}{\int\limits_{\partial \mathbb{B}_n(r)}} dS =\lim_{r\to \infty}k_n r^{1-n} r^{n-1} \omega_n=k_n\omega_n. \end{align*} 因此 $$ k_n={1\over \omega_n} \quad\Longrightarrow\quad E_n(\boldsymbol{x}) = {r^{2-n}\over (2-n)\omega_n}. \qquad(3.12) $$ 這裡 $$ \omega_n =|\partial \mathbb{B}_n(1)|=\S^{n-1}(1)= {2\pi^{n/2}\over \Gamma(n/2)} $$ 是 $n$ 維單位球表面積。 在此就清楚為何 $E_n(\boldsymbol{x})$ 的分母要有 $2-n$ 這項, 因為 $$ {\partial E_n\over \partial r} = {1\over r^{n-1} \omega_n} = {1\over r^{n-1} \S^{n-1}(1)}={1\over \S^{n-1}(r)} ={1\over |\partial \mathbb{B}_n(r)|}, $$ 基本解 $E_n(\boldsymbol{x})$ 對半徑的微分等於半徑為 $r$ 之 $n$ 維球表面積的倒數, 這裡透露了 $\delta$-函數的訊息。 4. 對數與無量綱: 由 (3.2) 可知 $E_2$ 是無量綱 (dimensionless), 所以前面的討論無法直接派上用場。 因為無量綱的緣故, 當 $r\to \infty$ 時 $E_2\not\to 0$, 我們需要動點手腳將 $r^{2-n}$ 換為 $r^{2-n}-1$ 然後取極限得 $$ E_2=\lim_{n\to 2} {r^{2-n}-1\over (2-n)\omega_n} = {1\over 2\pi} \log r. \qquad(3.13) $$ 坦白而言這一步非常的事後孔明, 為了答案不擇手段!但是結果是對的, 顯然這裡面有學問, 實際上根據 Taylor 展開式 $$ r^{2-n}= e^{\log r^{2-n}}= e^{(2-n) \log r}= 1+ (2-n)\log r +\cdots. \qquad(3.14) $$ 由此容易看出 $$ {r^{2-n}-1\over 2-n} \to \log r,\qquad n\to 2. $$ 因此 (3.13) 的論述是正確的, 並不是靈光乍現。 後來我在 V.I. Arnold的書 ( 定理 3.1: Laplace 方程的基本解 $(3.6)$ 為 $$ E_n(\boldsymbol{x})= \left\{ \begin{aligned} {|\boldsymbol{x}|^{2-n}\over (2-n)\omega_n},&\qquad n\ge 3, \\[2mm] {1\over 2\pi}\log|\boldsymbol{x}|,&\qquad n=2. \end{aligned} \right. \qquad(3.15) $$ 註解: $\ $ 1. 大部分的物理方程的基本解都是半徑函數, 那是對應到 Laplace 算子, 也因此半徑函數在數學與物理扮演了至關重要的角色。 但我們不應該一廂情願就認定所有的方程都是如此! 更深入理解一般的偏微分方程的基本解(特別是橢圓方程)需要幾何的知識, 因為我們必須重新定義距離(distance)而距離是與 Riemann metric 有關。 2. 學微積分時對數函數是定義為函數 ${1\over x}$ 的積分: $$ \int_1^x {1\over s} ds \overset{\rm def}{=} \log x. $$ 這對於積分公式 (3.11) 而言是極大的落差, 也造成學習上的困惑。 但是這個不連續性可以透過量綱分析來填補, 由於這個積分是無量綱 (dimensionless) 仿 (3.13) 的討論將 (3.11) 變更為 $$ \int_1^x {1\over s} ds =\lim_{n\to -1} {x^{n+1}-1\over n+1} = \log x. \qquad(3.16) $$ 利用量綱分析處理問題時, 無量綱的情形是最有趣的。 而這個例子告訴我們: 冪指數的臨界指數 critical exponent 必定是對數! 這個事實再次說明 『對數的發明就像是一個晴天霹靂來到世界上。 前人的任何工作都未能導致這項發明, 也沒有任何東西預見到它或預示它的到來。 這項發明是孤立的, 它沒有藉助於其他的智力工作, 也沒有遵循原有的數學思想路線, 就突然闖進人類思想中。』 ---《Napier 300年紀念文集之序言》 ---} 3. 第一次讀 Conway 的複變時, 裡面有一段話: 整個複變函數論最重要是對數函數 $\log z$! 對於一個沒有偏微分方程特別是基本解知識的學生而言, 這是極其困難理解的。 如今我會明確告訴學生複變函數論研究的對象是解析函數, 本質上是二維的調和函數, 而對數函數是二維的 Laplace 方程的基本解 4 4 基本 (fundamental) 的本意是根基 (foundation), 根本重要的意思, 並不是簡單、 容易。 例如微積分基本定理、 代數基本定理。 數學中只要看到基本定理就應該花心思弄懂並熟記。 。 $\Box$ 我們回到 Dirichlet 問題 (2.1)。 先決定格林函數, 令 $z$ 是單位圓內的點而 $z^*$ 是其對稱點則由 (2.44) 知 $$ |w-z|=|z||w-z^*|. \qquad(3.17) $$ 所謂格林函數是滿足邊界條件的基本解, 因為是 Dirichlet 問題, 直接聯想就是奇延拓 (odd extension) 或想像成奇函數。 根據 (3.17), 我們考慮以 $z$ 與 $z^*$ 為奇點 (singularity) 的兩個基本解的相減 $$ \begin{aligned} G(w,z)&= {1\over 2\pi}\log |w-z|-{1\over 2\pi}\log|z| |w-z^*| \\[2mm] &= {1\over 2\pi}\log |w-z|-{1\over 2\pi}\log|z||z^*|\bigg|{w\over z^*}-1\bigg| \\[2mm] &= {1\over 2\pi}\log |w-z|-{1\over 2\pi}\log\bigg|1-{\bar z}w\bigg|\qquad (|zz^*|=1) \\[2mm] &= {1\over 2\pi}\log \bigg|{w-z\over 1-\bar z w}\bigg| = {1\over 2\pi}\log |S_z(w)|. \end{aligned} \qquad(3.18) $$ 此時著名的 Möbius 變換自然而然就出現 $$ S_z(w)\overset{\rm def}{=}{w-z\over 1-\bar z w}. \qquad(3.19) $$ 碰見 Dirichlet 問題直接聯想就是奇函數 (odd function), 因為當 $z$ 趨近邊界時 $z^*$ 也逼近該點而格林函數滿足邊界值等於 0, 以 $z$ 與 $z^*$ 為奇點的兩個基本解必須相減才有可能滿足這個邊界條件。 另外不像上半平面, 單位圓內外區域大小不一樣, 距離 $|w-z^*|$ 前面需要參數 $|z|$ 來調整。 因為 Möbius 變換將單位圓帶到單位圓 \begin{align*} |S_z(w)|^2 &= \bigg({w-z\over 1-\bar z w}\bigg)\bigg({\overline{w}-\bar{z}\over 1-z \overline{w}}\bigg) ={|w|^2 -z\overline{w}-\bar{z} w+|z|^2\over 1-z\overline{w}-\bar{z} w +|z|^2|w|^2}\\ &={1 -z\overline{w}-\bar{z} w+|z|^2\over 1-z\overline{w}-\bar{z} w +|z|^2} =1,\qquad |w|=1, \end{align*} 格林函數 (3.18) 藉由 Möbius 變換 (3.19) 可以重新表示為 $$ \begin{aligned} G(w,z) &={1\over 2\pi}\log |S_z(w)| ={1\over 2\pi}\log \bigg|{w-z\over 1-\bar z w}\bigg| ={1\over 2\pi}\hbox{Re}\bigg(\log {w-z\over 1-\bar z w}\bigg) \\[2mm] &= {1\over 2\pi}\hbox{Re}\bigg[\log \Big(\rho e^{i\varphi}- r e^{i\theta}\Big) -\log \Big(1-r\rho e^{i(\varphi-\theta)}\Big)\bigg], \end{aligned} \qquad(3.20) $$ 其中 $z=r e^{i\theta}$, $w=\rho e^{i\varphi}$。 我們想求格林函數 (3.20) 在單位圓周的 (朝外法向量) 方向導數, 由於半徑永遠與圓周垂直, 所以該方向導數就是對 $\rho$ 的偏導數。 $$ \begin{aligned} \lim_{\rho\to 1} &{\partial \over \partial \rho}G(w,z) ={1\over 2\pi}\lim_{\rho\to 1} \hbox{Re}\bigg[{e^{i\varphi}\over \rho e^{i\varphi}- r e^{i\theta}} +{r e^{i(\varphi-\theta)}\over 1-r\rho e^{i(\varphi-\theta)}}\bigg] \\[2mm] =&{1\over 2\pi}\hbox{Re}\bigg[{e^{i\varphi}\over e^{i\varphi}- r e^{i\theta}} +{r e^{i(\varphi-\theta)}\over 1-re^{i(\varphi-\theta)}}\bigg] ={1\over 2\pi}\hbox{Re}\bigg[{1\over 1- r e^{i(\theta-\varphi)}} -{r \over r-e^{i(\theta-\varphi)}}\bigg] \\[2mm] =&{1\over 4\pi}\bigg[{1\over 1- r e^{i(\theta-\varphi)}}+{1\over 1- r e^{-i(\theta-\varphi)}}\bigg] -{1\over 4\pi}\bigg[{r \over r-e^{i(\theta-\varphi)}} + {r \over r-e^{-i(\theta-\varphi)}} \bigg] \\[2mm] =& {1\over 2\pi}{1-r^2\over 1-2r\cos(\theta-\varphi) +r^2} = {1\over 2\pi}P(r, \theta-\varphi). \end{aligned} \qquad(3.21) $$ 定理 3.2: Poisson 核是單位圓盤 Laplace 方程之格林函數在圓周的朝外法向導數 (normal derivative)! 由 (3.5) 取 $v=G$ 與 (3.21) 我們可以再次得到 Poisson 積分公式 $$ u(x,y) ={\oint\limits_{\partial B_2(1)}} f {\partial G \over \partial \boldsymbol{n}}ds ={\oint\limits_{\partial B_2(1)}} f {\partial G \over \partial r} ds ={1\over 2\pi}\int_{-\pi}^{\pi} f(\varphi) P(r, \theta -\varphi) d\varphi. \qquad(3.22) $$ 4. Harnack 不等式與 Harnack 定理Poisson 積分公式的直接推論就是 Harnack 不等式, 是由 Axel Harnack 於 1887 所提出, 主要是關於一個正的調和函數在相異兩點函數值的不等式。 Harnack 不等式主要是用來證明關於調和函數序列收斂的 Harnack 定理。 除了調和函數之外 Harnack 不等式也可以推廣到其它橢圓偏微分方程與拋物偏微分方程還有隨機偏微分方程, 它在偏微分方程有很多重要的應用, 有興趣的讀者可以參閱相關的著作 (  實際上 Poisson 核的分母並不是那麼陌生, 它是餘弦定律 (cosine law)! 平面上三個點 $(0,0)$、 $z=re^{i\theta}$、 $w=e^{i\varphi}$ 則 $$ |z-w|^2=|z|^2-2z\cdot w+|w|^2 = 1 -2r\cos (\theta -\varphi)+r^2. $$ 由於 $-1\le \cos (\theta -\varphi)\le 1$ 所以 $$ (1-r)^2\le 1 -2r\cos (\theta -\varphi)+r^2\le (1+r)^2. \qquad(4.1) $$ 其幾何意義是: $w=e^{i\varphi}$ 是單位圓周變動的點而 $z=re^{i\theta}$ 則是單位圓內部任意但固定的點, 則 $w$ 到 $z$ 的最長與最短距離正好是這兩點還有原點三點共線, 也就是連接原點與 $z$ 的直徑與圓周相交的兩點就是最長與最短距離的所在地。 由 (4.1) 得 Poisson 核之上下界 $$ {1\over 2\pi}{1-r\over 1+r}\le {1\over 2\pi}{1-r^2\over 1 -2r\cos (\theta -\varphi)+r^2}\le {1\over 2\pi}{1+r\over 1-r}. \qquad(4.2) $$ 這相當於 $$ \inf_{\theta, \varphi} P(r, \theta-\varphi) = {1-r\over 1+r}, \qquad \sup_{\theta, \varphi} P(r, \theta-\varphi) = {1+r\over 1-r}. $$ 如果 $u\ge 0$ 是一個非負的調和函數則 (4.2) 乘以邊界值 $$ u(w)=u(\cos\varphi,\sin\varphi)=u(1, \varphi) $$ 後積分, 再藉由 Poisson 積分公式得 $$ {1-r\over 1+r}{1\over 2\pi}\int_{0}^{2\pi} u(1, \varphi)d\varphi \le u(r, \theta) \le{1+r\over 1-r}{1\over 2\pi}\int_{0}^{2\pi} u(1, \varphi)d\varphi. \qquad(4.3) $$ Poisson 積分公式還可以走得更遠。 由 (2.14) 令 $r=0$ 得平均值定理 (mean value theorem) $$ u(0,0)={1\over 2\pi}\int_{0}^{2\pi} u(1, \varphi) d\varphi. \qquad(4.4) $$ (4.3)--(4.4) 合併就是 Harnack 不等式。 定理 4.1: (Harnack 不等式) 已知 $u$ 是單位圓盤內的一個正的調和函數, 則 $$ {1-r\over 1+r}u(0,0)\le u(r\cos\theta, r\sin\theta)\le{1+r\over 1-r}u(0,0),\qquad 0\le r\lt1. \qquad(4.5) $$ 半徑等於 $R$ 之圓盤的 Harnack 不等式則是 $$ {R-r\over R+r}u(0,0)\le u(r\cos\theta, r\sin\theta)\le{R+r\over R-r}u(0,0), \qquad 0\le r\lt R. \qquad(4.6) $$ 如果圓心是 $(x_0,y_0)$ 由於調和函數是平移不變, 此時 Harnack 不等式 $(4.6)$ 改寫為 $$ {R-r\over R+r}u(x_0,y_0)\le u(x_0+r\cos\theta, y_0+r\sin\theta)\le{R+r\over R-r}u(x_0,y_0). \qquad(4.7) $$ 這個不等式描述了一個非負的調和函數, 在任意半徑等於 $R$ 之圓盤的生長 (growth) 情形, 同時也凸顯了調和函數的正則性 (regularity), 表明它們在小範圍內不可能劇烈振盪。 對於非負調和函數, 在兩個不同點的值總是具有可比性, 所以由 Harnack 不等式直接導致 Hölder 空間 $C^\alpha(\Omega)$ 的引進, 這是橢圓偏微分研究最重要的空間。 有興趣的讀者可以詳細研讀 Gilbarg-Trudinger 定理 4.2: (Harnack 不等式) $u$ 是 $\Omega$ 內的一個非負的調和函數, 則 對於 $\Omega$ 內的有界區域 $\Omega'\subset \Omega$, 存在與 $\Omega'$, $\Omega$ 有關的常數 $C$ 使得 $$ \sup_{\Omega'} u \le C \inf_{\Omega'} u. $$ $\Box$ 證明 Harnack 不等式的關鍵步驟是 (4.4) 這個平均值定理 (mean value theorem), 這是調和函數特有的性質。 但 (4.4) 是直接由 Poisson 積分公式而得, 任何數學定理若需依賴精確的公式就有其侷限性。 為了擺脫 Poisson 積分公式的限制, 我們必須對 Laplace 算子有更深入的認知。 定理 4.2: (平均值定理) 已知 $\Omega\subset \mathbb{C}$ 是複數平面上的有界連通的開集, 如果 $u\in C^2(\Omega)$ 是定義在 $\Omega$ 上的調和函數, 則 $u$ 滿足 $$ \begin{aligned} u(x_0,y_0) &={1\over |\partial B(z_0, r)|}\oint\limits_{\partial B(z_0, r)} u ds ={1\over 2\pi r}\oint\limits_{\partial B(z_0, r)} u ds \\[2mm] &={1\over |B(z_0, r)|}\int\!\!\!\int_{ B(z_0, r)} u dxdy ={1\over \pi r^2}\int\!\!\!\int_{ B(z_0, r)} u dxdy, \end{aligned} \qquad(4.8) $$ 其中 $B(z_0, r)\subset \Omega$ 是 $\Omega$ 內以 $z_0=x_0+iy_0$ 為圓心半徑等於 $r$ 的圓盤。 證明: 我們將以偏微分方程的方法來證明。 1. 考慮函數 $u$ 在 $\partial B(z_0, r)$ 的平均值 $$ f(r)\overset{\rm def}{=}{1\over 2\pi r}\oint\limits_{\partial B(z_0, r)} u ds ={1\over 2\pi}\int_{-\pi}^\pi u(x_0+r\cos \theta, y_0+r\sin\theta)d\theta. \qquad(4.9) $$ 直接微分並利用 $x=x_0+r\cos \theta, y=y_0+r\sin\theta$ 得 $$ \begin{aligned} f'(r)&={1\over 2\pi}\int_{-\pi}^\pi \big(u_x \cos \theta \!+\! u_y \sin \theta \big)d\theta \!=\!{1\over 2\pi}\!\int_{-\pi}^\pi \bigg(u_x {x\!-\!x_0\over r} \!+\! u_y {y\!-\!y_0\over r} \bigg)d\theta \\[2mm] &={1\over 2\pi r}\oint\limits_{\partial B(z_0, r)} \bigg(u_x {x-x_0\over r} + u_y {y-y_0\over r} \bigg)ds ={1\over 2\pi r}\oint\limits_{\partial B(z_0, r)} \nabla u \cdot \boldsymbol{n} ds \\[2mm] &={1\over 2\pi r}\oint\limits_{\partial B(z_0, r)} {\partial u \over \partial \boldsymbol{n}} ds ={1\over 2\pi r}\int\!\!\!\int_{B(z_0, r)} \Delta u \, dxdy=0\qquad\hbox{(散度定理),} \end{aligned} \qquad(4.10) $$ 這裡 ${\boldsymbol{n}}$ 是圓盤 $B(z_0, r)$ 的單位朝外法向量 $$ {\boldsymbol{n}}= \bigg({x-x_0\over r}, {y-y_0\over r} \bigg)=(\cos\theta, \sin\theta). $$ 所以 $f(r)$ 是一個常數, 另外由連續性與平均值的特性 (4.9) 得 $$ f(0)=\lim_{r\to 0} f(r) = u(x_0, y_0)=f(r)={1\over 2\pi}\int_{-\pi}^\pi u(x_0+r\cos \theta, y_0+r\sin\theta)d\theta. $$ 這就證明了平均值定理 (4.8)。 2. (4.10) 的論述也可以藉由極座標的 Laplace 算子 (2.16) 而來: $$ \begin{aligned} r{\partial \over \partial r}\bigg( r {\partial \over \partial r} f(r)\bigg) &= -{1\over 2\pi} \int_{-\pi}^\pi {\partial^2 \over \partial\theta^2} u(x_0+r\cos\theta, y_0+r\sin\theta)d\theta \\[2mm] &=-{1\over 2\pi}{\partial \over \partial\theta} u(x_0+r\cos\theta, y_0+r\sin\theta)\bigg|_{-\pi}^\pi=0. \end{aligned} \qquad(4.11) $$ (4.11) 積分 $$ r {\partial \over \partial r} f(r)= C_1\in \mathbb{R}, \qquad \forall\ 0\lt r\le 1. $$ 令 $r\to 0$ 得 $$ C_1=\lim_{r\to 0} r {\partial \over \partial r} f(r)=0. $$ 所以 $f(r)=C_2\in \mathbb{R}$ 是一個常數, 再一次令 $r\to 0$ 得 $$ C_2=\lim_{r\to 0}f(r)=u(x_0, y_0)=f(r). $$ 3. 關於 (4.8) 中線積分與雙重積分的關係可以這麼看, 首先由 (4.8)--(4.9) 得 (將 $r$ 換為 $\rho$) $$ u(x_0, y_0)={1\over 2\pi}\int_{-\pi}^\pi u(x_0+\rho\cos \theta, y_0+\rho\sin\theta)d\theta. $$ 兩邊同時乘周長 $2\pi \rho$ 後沿半徑積分之後變換積分順序得 \begin{align*} \int_0^r u(x_0, y_0)2\pi \rho d\rho =\,&\int_0^r\int_{-\pi}^\pi u(x_0+\rho\cos \theta, y_0+\rho\sin\theta)\rho d\theta d\rho\\ =\,&\int_{-\pi}^\pi \int_0^r u(x_0+\rho\cos \theta, y_0+\rho\sin\theta)\rho d\rho d\theta.\\ {\hbox{因此}} u(x_0,y_0)=\,&{1\over \pi r^2} \int\!\!\!\int_{B(z_0, r)} u(x,y) dxdy. \end{align*} $\Box$ 註解: $\ $ 1. 這個證明並沒有用到 Poisson 積分公式, 而且可以直接推廣到 $n$ 維空間, 有興趣的讀者可以參考 2. 典型的證明是將調和函數 $u(x,y)$ 視為解析函數的實部, 然後利用複變的 Cauchy 積分公式容易得此結論。 但我們不能因此武斷地說這個證明的價值不高! 回到 Cauchy 積分公式的證明, 其中最關鍵的想法是沿著任意的單純曲線 $C$ 的線積分等於沿著半徑等於 $\rho$ 之圓周的線積分, 裡面的拓樸結構是同倫理論 (homotopy), 而這正是 (4.9)--(4.10) 想法之由來。 3. 平均值定理 (4.8) 的內在本質是質量中心 (center of mass), 因此 (4.8) 的積分區域必須是均勻的圓盤或圓周, 此時 $z_0$ 是 $B(z_0,r)$ 或 $\partial B(z_0,r)$ 的質量中心, 而 $u(z_0)=u(x_0,y_0)$ 才會是 $u(z)=u(x,y)$ 在 $B(z_0,r)$ 或 $\partial B(z_0,r)$ 的平均值。 這個事實可以透過一維空間來想像, 一維的調和函數基本就是一條直線 $$ y''(x)=0\quad\Longrightarrow\quad y(x) = ax+b. $$ 給定 $x$-軸上任意點 $x_0$, 則必須是以 $x_0$ 為中心兩邊是相等的長度 $r$ 之區間 $(x_0-r, x_0+r)$ 平均值定理才會成立 \begin{align*} y(x_0)&=a x_0+b = {1\over 2}[a(x_0+r)+b] +{1\over 2}[a(x_0-r)+b]\\ &= {1\over 2} \big(y(x_0+r) +y(x_0-r)\big). \end{align*} 4. 由於證明方法主要是散度定理, 因此平均值定理可以直接推廣為 $n$ 維空間, 這是偏微分方程方法優越之處, 因為可以看出調和函數的結構。 (4.10) 告訴我們 $$ 2\pi r f'(r)=\oint\limits_{\partial B(z_0, r)} \nabla u \cdot {\boldsymbol{n}} ds. $$ 這是梯度 $\nabla u$ 通過邊界 $\partial B(z_0, r)$ 的通量 (flux), 但是一個調和函數的通量為 0, 因此 $f'(r)=0$ 所以 $f(r)$ 是一個常數。 如果從流體力學的角度來看的話, 調和函數是對應於不可壓縮流體 (incompressible fluid)。 $\Box$ Harnack不等式的主要應用出現在 Harnack 定理的證明, 這是關於調和函數序列的一致收斂性問題, 也就是研究調和函數空間的完備性。 定理 4.3: (Harnack 定理) 已知 $\Omega\subset \mathbb{C}$ 是複數平面上的有界連通的開集, 如果 $\{u_n\}_n$ 是定義在 $\Omega$ 上的遞增調和函數序列 $$ u_1\le u_2\le \cdots \le u_n \le \cdots, $$ 則 $u_n$ 在緊緻集上一致收斂到 $\infty$, 或存在定義在 $\Omega$ 上的調和函數 $u$ 使得 $u_n$ 在緊緻集上一致收斂到 $u$。 用更簡練的語言: 單調遞增的調和函數序列在區域内要麼處處不收斂, 要麼處處收斂; 而一旦收斂, 這個收斂就是「好的」, 即在 $\Omega$ 内的緊緻集一致收斂, 且極限函數也是調和函數。 證明: 由於 $\{u_n\}$ 是一遞增函數序列, $u_{n+1}-u_n$ 是非負的。 此時可以應用 Harnack 不等式得 $$ 0\le u_{n+1}(r\cos\theta, r\sin\theta) -u_{n}(r\cos\theta, r\sin\theta) \le {R+r\over R-r}\big[u_{n+1}(0,0)- u_n(0,0)\big]. $$ 由於 $\{u_n(0,0)\}_n$ 是 $\mathbb{R}$ 的 Cauchy 數列, 由此不等式推論 $\{u_{n}(r\cos\theta, r\sin\theta)\}_n$ 也會是 $\mathbb{R}$ 的 Cauchy 數列, 再根據實數的完備性其極限存在 $$ u(r\cos\theta, r\sin\theta)\overset{\rm def}{=}\lim_{n\to\infty} u_n(r\cos\theta, r\sin\theta). \qquad(4.12) $$ 上式對任意 $(x,y)=(r\cos\theta, r\sin\theta)\in \Omega$ 都成立, 而且由極限的唯一性可知, 由 (4.11) 所定義的 $u$ 確實是一個函數, 而且 $u_n$ 會一致收斂到 $u$。 由 Poisson 積分公式 $$ u_n(r\cos\theta, r\sin\theta)={1\over 2\pi}\int_{-\pi}^\pi {R^2-r^2\over R^2 -2Rr\cos (\theta-\varphi) +r^2} u_n(\cos\varphi, \sin \varphi) d\varphi. $$ 藉由一致收斂, 兩邊同時取極限得 $$ u(r\cos\theta, r\sin\theta)={1\over 2\pi}\int_{-\pi}^\pi {R^2-r^2\over R^2 -2Rr\cos (\theta-\varphi) +r^2} u(\cos\varphi, \sin \varphi) d\varphi. $$ 再根據定理 2.3 得證 $u$ 是一個調和函數。 $\Box$ 註解: $\ $ 1. 根據極大值原理 (maximum principle), 滿足一般好條件的調和函數序列如果在邊界上一致收斂, 就在整個區域一致收斂, 而且極限函數也是調和的。 $\Box$ 誌謝: 自從研究所認識李志豪教授並參加他與陳宜良教授的 Fritz John 的 PDE 討論班之後, 就與他結下了不解之緣。 後來去美國留學回來參加的第一個研討班就是他舉辦的, 因此在學術研究的路上就不會覺得孤單。 除了數學之外我們都是喜歡閱讀雜書特別是哲學思想的人, 所以我們也是無話不談的朋友。 每一篇科普的文章在還沒有發表之前他幾乎都是我的第一個讀者, 這樣的情誼讓人備感溫暖。 在此謹將此文獻給李志豪教授並祝他 70 歲生日快樂。 參考文獻只要是 Arnold 的書都值得看但前提是啃得下。 1989 年蘇東波之後一大批蘇聯優秀的數學家紛紛移居歐美等國, Arnold 自然也是其中一員。 雖然如此, 他仍會藉由各種機會回莫斯科舉辦研討會或授課。 這本書就是他在 1994/1995 秋季大三偏微分方程的講義。 這本書的第九章單獨談基本解, 第十章探討 double layer potential (雙層位) 是我個人最感興趣的主題。 另外最有意思的是書的最後面還提供了 seminar 的題目、 homework、 期末考題目, 基本上已經是一本完整的教材。 我只能說這本書寫得非常的俄羅斯(或蘇聯)。 Arnold 的書始終有一些亮點是其它相同性質著作所沒有的。 一個真正會讀書的人一定是從前言(preface)開始, 從中不僅可以看出作者寫書的目的還可以明白他 (她) 的數學觀。 Arnold 對於 Hardy 與 Bourbaki 的公設學派有極嚴厲的批判。 所以整本書的思想 (philosophy) 是以對一些具體例子 (特別是波動方程或弦振盪方程) 有透徹的理解為前提, 而不是定義、 定理、 證明這種三段式論證。 對於他的數學觀我是完全贊同的。 這是我大三修複變函數論時黃永裕教授用的教科書, 後來去美國留學修複變函數論(第一學期)也是用這本書。 有別於 Ahlfors的書著重幾何的觀點, 這本書是比較偏重分析的角度探討複變函數論, 但是在很前面就詳細介紹了 Möbius 變換, 也因此我個人對於這主題有特別的偏愛。 本書作者與台灣有很深的淵源, 其實 John B. Conway 就是交大應數系退休教授吳培元老師之博士論文的指導教授。 華羅庚的這本書是我看過關於 Poisson 核(特別是幾何觀點) 最精彩的一本, 我是在這裡學到 Poisson 核是 Möbius 變換的 Jacobian。 另外這本書的第七章是混合型偏微分方程 (PDE of Mixed type), 正是我碩士論文的主題, 所以我也花了不少心血專研這一章。 該書1997就出版了, 但是按作者的建議如果你想買的話就應該選這個版本。 這本書幾乎以從未見過的方式向您展示複變函數論。 透過幾何 (而不是計算) 將複變這個美麗而強大的主題帶入生活。 作者借鏡歷史從頭發展每個主題, 並在每一步繪製出吸引人的圖畫來解釋抽象的數學概念, 這是讓人愛不釋手之處。 作為一個學期的複變函數論, 這本書的設計是相當合適的教材。 如果有機會教複變我鐵定會用這本書。 書中最後三章是物理與幾何的應用, 也是我個人最喜歡的主題。 對於複變函數論的應用有興趣的同學, 不妨找幾個好友組織讀書會研讀這三章, 相信會有大收穫的。 本文作者為國立交通大學應用數學系退休教授 |
| 頁碼 | 73-101 |
2024年12月 48卷4期
哈那克兄弟們(Harnacks)-數學與神學的雙生子-

