| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | 量子糾纏背後的計算難題 : 新型複雜度理論的探索 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
本文於 2025 年 3 月 4 日刊載於中研院訊漫步科研專欄, 作者及中研院訊同意本刊轉載。  鐘楷閔畢業於國立臺灣大學資訊工程學系, 並於 2011 年獲得哈佛大學資訊工程博士學位。 2013 年加入中央研究院資訊科學研究所, 擔任助理研究員, 現為特聘研究員。 研究領域聚焦於理論資訊科學, 特別關注量子密碼學與量子複雜度理論之研究。 量子糾纏的謎題:如何判斷兩個粒子具有量子糾纏?在 20 世紀初, 愛因斯坦曾對量子力學的奇異現象提出質疑, 特別是「幽靈般的遠距作用」, 即量子糾纏 (Quantum Entanglement)。 當兩個粒子處於糾纏態時, 無論它們相隔多遠, 測量其中一個粒子的狀態, 另一個粒子的狀態也會瞬間確定。 這個奇異的現象至今仍是量子力學最重要的特徵之一。 現在, 請想像自己是一名量子科學家, 手中擁有一組粒子, 你的任務是判斷它們是否處於糾纏態, 還是非糾纏態 (可分離態)。 乍看之下, 這個問題似乎屬於量子實驗科學的範疇, 然而本質上, 它也是一個「計算問題」。 具體而言, 該計算問題的輸入是一組相同的粒子 (量子態), 而輸出則是一個位元的答案: 若輸入的量子態為糾纏態, 輸出為 1; 反之, 輸出為 0。 實際上, 這是一個計算上極具挑戰性的問題。 在今天的「漫步科研」, 我們將與大家分享我們最新的理論研究成果: 針對輸入為量子態的計算問題的新型複雜度理論。 上述的計算問題便是其中一例。 接下來, 我們將依序探討以下內容: 首先, 了解何謂計算問題; 其次, 介紹傳統的複雜度理論; 最後, 討論為何需要發展新型複雜度理論及其重要性。 傳統的計算問題與它們的難易度計算問題無處不在, 從國小到大學, 我們學習過許多不同的計算問題與對應的演算法。 以乘法為例, 它本身就是一個計算問題: 輸入為兩個數字 $A$ 和 $B$, 輸出則是它們的乘積。 國小老師教授的直式乘法 (見圖 1) 便是一種求解乘法問題的演算法。 即使 $A$ 和 $B$ 是 1000 位數的龐大數字, 直式乘法依然能在合理時間內計算出 $A\times B$, 因此可稱之為「有效率」的演算法。 與乘法相關的另一個經典計算問題是「因數分解」。 因數分解問題的輸入是一個數字 $A$, 輸出則是滿足 $A = B\times C$ 的兩個數 $B$ 和 $C$。 然而, 若輸入是一個 1000 位數, 這種方法的嘗試次數將極為龐大, 甚至遠超宇宙中的粒子數量, 顯然無法在合理時間內完成, 因此並非有效率的演算法。 至今, 我們仍未找到適用於古典電腦的有效率因數分解演算法, 因此因數分解對古典電腦而言極為困難。 然而, 若使用量子電腦, 著名的 Shor's 演算法便是一種有效率的量子演算法, 即使輸入為 1000 位數, 也能在合理時間內求得對應的 $B$ 和 $C$。 除了數論相關的計算問題, 圖論中也存在許多重要的計算問題。 例如 $s$-$t$ 連通性問題 ($s$-$t$ connectivity): 給定一張圖 $G$ 及其中的兩個頂點 $s$ 和 $t$, 若 $s$ 到 $t$ 之間存在路徑, 則輸出 1; 否則輸出 0 (見圖 1)。 若熟悉隨機演算法, 便會知道此問題在古典電腦上不僅有高效的演算法, 還有一種可用極少記憶體完成計算的隨機演算法。 另一個經典的圖論問題是 3-著色 (3-coloring)。 其輸入仍為一張圖 $G$, 若能僅用三種顏色著色, 使所有相鄰頂點顏色不同, 則輸出 1; 否則輸出 0。 此問題在古典電腦上極為困難, 即使使用量子電腦, 也尚未找到有效率的量子演算法。 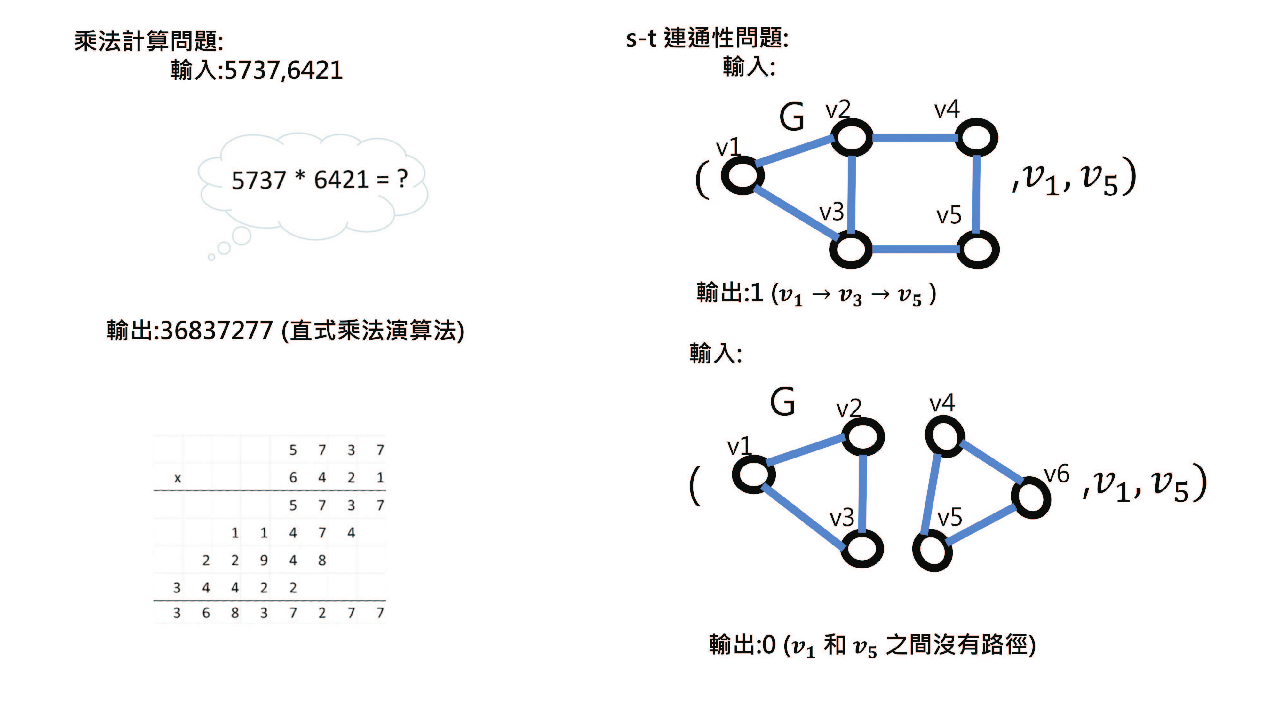 傳統複雜度理論:探索計算問題的本質前述內容中, 我們討論了多種計算問題, 例如乘法與質因數分解。 在資訊科學中, 研究這些計算問題本質的核心理論稱為複雜度理論 (Computational Complexity Theory)。 該理論提供了一種方法, 依據解決這些問題所需的計算資源進行分類, 例如古典電腦的運算時間與記憶體, 或量子電腦的計算時間與資源需求。 在此理論框架下, 所有能透過有效率的演算法 (即可在多項式時間內執行) 於古典電腦上解決的計算問題, 皆歸類為 $P$ 類問題 (Polynomial Time)。 例如, 乘法與 $s$-$t$ 連通性問題皆屬於此類。 即使輸入長度增加, 例如乘法的輸入為兩個 1000 位數, 仍可在合理時間內完成計算。 然而, 因數分解在古典電腦上難以高效求解, 故不屬於 $P$ 類問題。 同樣地, 在量子電腦上能透過有效率的演算法求解的計算問題, 歸類為 $BQP$ 類問題 (Bounded-error Quantum Polynomial Time)。 例如, 因數分解即屬於此類。 此外, 能透過使用極少記憶體的演算法解決的計算問題, 歸類為 $L$ 類問題 (Logarithmic Space)。 例如, $s$-$t$ 連通性問題即屬於 $L$ 類, 因其可在極低的記憶體需求下求解。 除了運算時間與記憶體, 複雜度理論亦關注另一類計算資源 --- 驗證解答的計算成本。 某些問題雖難以高效求解, 但若給定一個可能的解答, 則可迅速驗證其正確性。 此類問題歸類為 $NP$ 類問題 (Non-deterministic Polynomial Time)。 換言之, $NP$ 類問題的特點在於, 尋找解答可能需耗費大量計算資源, 但驗證已知解答則相對高效。 以因數分解為例, 目前尚無已知的高效古典演算法。 然而, 若有人提供某數 $A$ 的因數 $B$ 和 $C$, 僅需計算 $B \times C$ 是否等於 $A$, 即可快速驗證答案是否正確。 同樣地, 對於 3-著色問題, 若有人提供一組可能的 3-著色, 只需檢查相鄰頂點是否具有相同顏色。 因此, 因數分解與 3-著色問題皆屬於 $NP$ 類問題。 此外, 複雜度理論提供了一種方法, 以識別各類別中「最困難」的問題。 在 $NP$ 類問題中, 這些最具挑戰性的問題稱為 $NP$ 完備 ($NP$-complete) 問題。 這些問題之所以稱為 $NP$ 完備, 是因為若能找到高效的演算法來解決其中任何一個問題, 則所有 $NP$ 類問題皆可透過該演算法有效求解。 3-著色問題是 $NP$ 完備問題的經典範例, 這表示它不僅屬於 $NP$ 類問題, 亦是其中最具代表性的難題之一。 上述內容彙整於圖 2。 接下來, 我們簡要探討傳統複雜度理論為何被視為資訊科學的核心理論。 提供系統化的方式比較不同計算資源的能力: 例如「量子電腦是否真的比古典電腦強大」這個問題, 可以形式化為對 $BQP$ 類與 $P$ 類關係的研究。 而著名的千禧年大獎問題之一 : "$P$ vs $NP$ 問題", 則試圖解答一個關鍵問題: 是否所有能有效率驗證解答的問題 ($NP$ 類), 也都能有效率的求解 ($P$ 類)。 這些問題的解答不僅影響演算法與理論計算機科學, 也對密碼學與最佳化等領域產生深遠影響。 引導演算法設計目標: 當一個計算問題屬於 $NP$ 完備類時, 現有理論顯示我們無法期待找到一個能在所有情況下高效求解的演算法。 因此, 資訊科學家會根據問題的特性與需求來設計演算法。 通常有以下兩種目標: (1) 啟發式演算法 (Heuristic Algorithm): 雖無法保證在所有情況下都成功求解, 但能在實務應用中取得良好結果。 (2) 近似演算法 (Approximation Algorithm): 能在所有情況下高效求解, 但允許輸出近似解, 而非最佳解。 提供標準化的語言來描述計算問題的難度: 複雜度理論提供了一種標準語言來描述計算問題的難度, 奠定現代密碼學的理論基礎。 密碼學的本質在於利用計算問題 (如因數分解與離散對數問題) 的困難性, 來構建安全的密碼學系統。 如果我們無法精確描述何謂「計算問題的困難性」, 就無法嚴格論證所構建的密碼學系統的安全性。  我們的最新研究:量子世界中的新型複雜度理論讓我們回到最初提及的計算問題: 判斷給定粒子 (量子態) 是否具有量子糾纏。 其輸入為一系列相同的量子態, 輸出則為一個位元 (0 或 1)。 為何無法直接將此計算問題納入傳統複雜度理論的框架呢? 關鍵原因在於, 傳統複雜度理論中的計算問題, 其輸入皆以古典字串描述。 例如, 乘法問題的輸入為兩個數字 $A$ 和 $B$, $s$-$t$ 連通性問題的輸入則為一張圖, 這些輸入皆可透過古典字串加以描述。 然而, 量子態無法以 (合理長度的) 古典字串描述, 因此傳統複雜度理論無法探討輸入為量子態的計算問題。 我們的最新研究成果旨在發展新型複雜度理論, 以探討輸入為量子態的計算問題。 類似於傳統複雜度理論, 我們定義了對應於 $P$、 $BQP$、 $L$、 $NP$ 的計算類別, 並探討這些類別之間的關係, 以及該理論在量子計算與量子密碼學中的應用。 儘管我們的理論仍處於發展初期, 我們期待它能如同傳統複雜度理論一般, 成為未來量子資訊科學的重要理論。 相關研究成果:Complexity Theory for Quantum Promise Problems 本文作者鐘楷閔、 施志偉任職中央研究院資訊科學研究所 |
| 頁碼 | 3-7 |
2025年6月 49卷2期
量子糾纏背後的計算難題 : 新型複雜度理論的探索

