前言： 本文是參考資料 固定值固定值固定值 的後續; 討論量子重力 (Quantum Gravity) 和機率論以及量子力學的關連。 文章的格調, 和前者一致, 除了前言和結語外, 分成一些小節, 講述相關議題。 又, 學術名詞以及人名的呈現方式, 和"註:" 的使用, 作者仍大致依循前文。

2021年, 著名的科普雜誌 Quanta Mazagine 刊出了一篇報導, 見網站參考資料 [a], 幾位機率學者 (論文預稿發表於 arXiv, 論文至少有三篇 固定值固定值固定值), 對二維量子重力作了嚴格的討論; 手法則是機率式的量子場論 (Probabilistic Quantum Field Theory); 這源於 Barry Simon (1946$\sim$) 在其經典名著 固定值中所倡議。 介紹此工作, 是本文論述的主要原由和內容。 本文取材主要是來自 固定值; 兩位作者在報導 [a] 中皆出現。 雖然, 就理論物理學而言, 他們的工作只是所謂的 toy model; 然而, 這些工作有很大的部分, 可以應用於機率論的近年備受關注的研究方向, 特別是隨機曲面 (random surface)。 如眾皆知, 量子化就是一種離散化, 而萬有引力論和廣義相對論是連續型理論; 量子重力一詞, 即是意含先考慮一個離散模式, 再將它取適當的尺度極限 (scaling limit); 而這也是隨機曲面理論之核心工作。

(一) 回顧: 由 UFT 至 TOE

若是被問到什麼是物理學的聖杯 (Holy Grail, 註： 參考前文 固定值)？ 我想, 很多理論物理學者會回答是統一場理論 (Unified Field Theory, UFT) 吧。 這是愛因斯坦晚年致力的工作, 但是未能完成, 此名也是他賦予的; 目標是電磁場論和廣義相對論的合一。 現今, 此工作是在一個更大的目標下, 稱為萬事理論 (Theory of Everything, TOE)。 而量子重力是一個關鍵角色 (註: TOE 這名詞, 作者向兩位學者提到, 一位是最近到我系訪問的美國數學者, 一位是頗知名的台大理論物理學者, 他們的反應皆持保留態度, 或許命名太聳動吧)。

愛因斯坦在 1905年發表狹義相對論 , 1915年發表廣義相對論; 前者在兩個基本假設下, 建立時空連續體內勞倫茲變換的物理意義。 後者利用黎曼幾何學, 建立愛因斯坦場方程式 (Einstein Field Equation)。 此方程一個有意義解, 靜態黑洞, 在幾個月後被 Karl Schwarzschild (1873$\sim$1916) 解出。 有關 Schwarzschild 的非虛構小說, 可看 固定值 第二章, 此書是紐約時報 2021年十大好書。 1919 年愛丁頓爵士 (Sir Arthur Stanley Eddington, 1882$\sim$1944) 率領的探索隊, 證實了廣義相對論所預測的星光屈撓。

麥斯威爾在 1865 年發表的論文 固定值 和 1873 年發表的巨著 固定值, 將原本的磁力和電力合一為電磁力; 電磁場論成為現今科技的發展基礎。 Maxwell equations 由四個方程構成 (依 Oliver Heaviside (1850$\sim$1925) 改寫後形式) 如下附圖 (引用自: Wikipedia, Maxwell Equations); 附圖中, 分別是高斯磁場方程 (左上)、 高斯電場方 程 (右上)、法拉第磁場方程 (第二列)、 安培 - 麥斯威爾方程(第三列); 於是重力場理論和電磁場理論成為古典力學的極致。 愛因斯坦 1933年到達美國後, 除了 1935 年的 EPR 悖論 (見前文 固定值), 以及自研哲學和神學外, 就致力於的重力場和電磁場合一, 且有友人 P. G. Bergmann (1915$\sim$2002) 的合作, 但是沒能完成。 Bergman 的名書 固定值 有愛因斯坦寫的前言。　　

1950 年代以降, 高能物理和粒子物理的快速發展, 理論與實驗並行, 加上電腦的輔助, 一般稱為標準模型 (Standard Model) 的物理理論, 被普遍接受。 在標準模型之下, 宇宙有四種交互作用力 : 強力、 弱力, 電磁力, 和重力(引力)。 強力是原子核內部的作用力, 例如, 把質子和中子綁在一起的力; 弱力是原子核和電子之間, 以及電子與電子之間, 的作用力; 電磁力是磁場中帶電粒子之間的作用力。 這三種力可以利用量子力學和量子場論予以合一, 被稱為大一統理論 (Grand Unified Theory)。 自然地, 理論物理學者會追尋, 如何將重力和另三種已經合一的力揉合在一起？ 但是, 適用的尺寸差異如此大： 一端是有波粒二象性的微小質點, 另一端是巨大的星體。 再者, 進行論述的架構, 量子力學和量子場, 主要是在平直的歐氏時空中, 而廣義相對論則是在彎曲的時空中; 雖然, 已經有一些彎曲架構下的量子力學研究, 但遠遠不足用。 以下的 $cGh$ 立體圖和文氏圖 (引用自: Wikipedia, Theory of Everything), 說明了理論物理各主題的關連。 圖中, $c$, $G$, $h$, 分別代表光速、 萬有引力常數、 和普朗克常數; 在國際標凖 (SI) 制下：

\begin{align*} c=\,&3.00\times 10^8\ \hbox{$m$/sec,}\\ G=\,&6.67\times 10^{-11}\ \hbox{($m$/sec$^2$)(kg/$m^2$)},\\ h=\,&6.63\times 10^{-34}\ \hbox{Joule/Herz.} \end{align*}

我們只取至小數點第二位。 萬有引力常數和自由落體的重力加速度 $g=9.08$ 事實上無矛盾。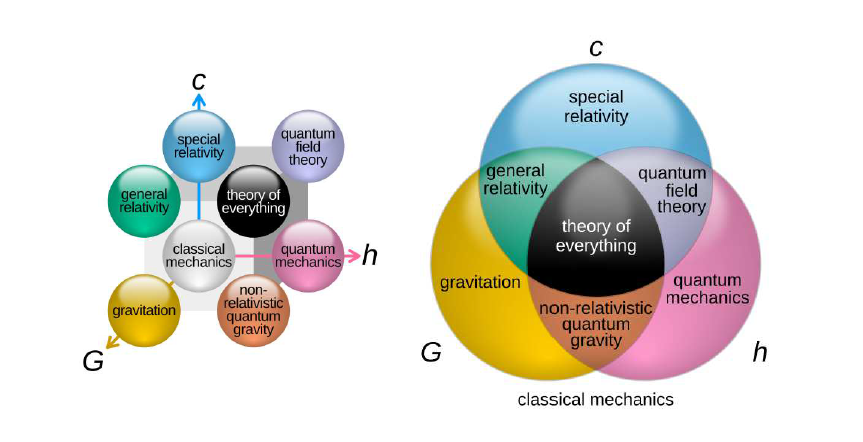

(二) 量子場和共形場

在 1920 年代, 物理學者開始把量子力學和狹義相對論用在電磁場上。 1927 年, 狄拉克將此研究命名為量子電動力學 (quantum electrodynamics, QED)。 1928 年, 他發表狄拉克方程 固定值, 這是相對論量子力學 (relativistic quantum mechanics) 的基本方程, 討論以光速運動的高能粒子之薛丁格方程:

$$\frac{\partial \psi(t,x)}{\partial t}=-i\frac 1{\hbar}(\beta mc^2+c\sum_{i=1}^3 \alpha_i\frac{\partial}{\partial x_i})\psi(t,x);\ t\ge 0,\ x\in {\Bbb R}^3.$$

上式中, $\beta ,\alpha _i$ 代表狄拉克方陣 (4 階方陣); $m$ 為粒子質量, $c$ 為光速。 此方程式 (四個聯立方程), 可以告訴我們反物質的存在, 質點的自旋; 1950 年代, 理查費曼、 朝永振一郎 (Shinichiro Tomonaga, 1906$\sim$1979)、 和 Julian Seymour Schwinger (1918$\sim$1994), 由於對 QED 有突破性進展, 三人同獲 1965 年諾貝爾物理學獎。 QED 是第一個量子場論的具體案例; 之後, 1954 年的 Yang-Mills 理論建構了第一個非交換規範場論 (non-Abelian Gauge Theory)。 近年, 有兩位數學者分別寫了為數學出身的讀者的量子場論 固定值固定值; 其中, Michael Talagrand 是 2024 年阿貝爾獎得主。

1984 年, 三位物理學者 A.A. Belavin, A.M. Polyakov, A.B. Zamolodchikov 發表共形場論的基礎論文 固定值, 討論二維量子場的共形 (保角) 對稱性。 二維量子場源於弦論中的世界單 (Worldsheet); 對應於時空連續體 (歐氏度量或 Minkovski 度量) 中的世界線 (Worldline)。 通常, 古典場或量子場, 都設定物質是由質點構成, 而弦論則設定物質是由弦構成 ; 質點在空時體 (注意：不是時空）所展成的是世界線, 而弦在空時體所展成的是世界單, 在弦論中, 也有由 brane 所展成的世界體; 如下圖所示 (引用自: Wikipedia, Brane):

(三) 黎曼球上的共形場

先作一些符號及預備工作： 以 ${\Bbb S}$ 表黎曼球, 即, 廣義複平面 ${\Bbb C}\cup\{\infty\}$ 的緊緻化, 兩者之關連, 以下圖表之 (引用自: Wikipedia, Riemann Sphere)：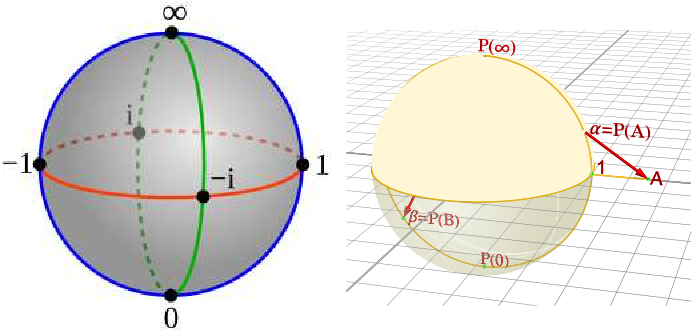

在 ${\Bbb S}$ 上, 引入標準圓度量：

$$g(z)|dz|^2,g(z):=\frac 4{(1+|z|^2 )^2},\quad z\in {\Bbb S}.$$

在此度量下, 任一 (平滑) 曲線 $\sigma :t\in [0,1]\to \sigma (t)\in {\Bbb S}$, 其長度為

$${\cal L} (\sigma )=\int_0^1 g((\sigma (t))^{1/2} |\sigma' (t)|dt.$$

任兩點 $z_1,z_2 \in {\Bbb S}$, 其距離為

$$d(z_1,z_2):=\inf\limits_{\{\forall \sigma\}} \{{\cal L}(\sigma) : \sigma (0)=z_1,\sigma (1)=z_2\},\quad z_1,z_2\in {\Bbb S}.$$

對標準度量, ${\Bbb S}$ 的曲率爲 2。

令 $\psi$ 為 ${\Bbb S}$ 上的 Möbius 函數 :

$$\psi (z)=\frac{az+b}{cz+d},\quad a,b,c,d\in {\Bbb C},\quad ad-bc=1.$$

令 $\phi_\alpha(z)$, $z\in {\Bbb C}$, $\alpha \in {\cal A}$, 為一族指標集為 ${\cal A}$ 的場。 協變函數 (correlation functions) 有如下的共形性：

$$\langle \phi_{\alpha_1}(\psi (z_1)) \cdots \phi_{\alpha_n}(\psi (z_n))\rangle =\prod_{i=1}^n |\psi' (z_i)|^{-2\Delta _{\alpha_i}} \langle \phi_{\alpha_1}(z_1) \cdots \phi_{\alpha_n}(z_n)\rangle.$$

上式中, 實數 $\{\Delta _\alpha\}$ 為場 $\{\phi_\alpha\}$ 的共形權重 (conformal weight)。

說明： 某些讀者或許會問, 協變函數應該是對某個機率測度的期望値, 此機率測度是否存在？ 在以下, 我們可以用隨機荷布 (random distributions) (即 Laurant Schwartz (1915$\sim$ 2002, 1950 年費爾茲奬得主) 廣義函數的隨機面向) 作嚴格定義。

(四) 黎曼球上的量子重力: 架構

我們考慮 ${\Bbb S}$ 上的 Liouville 量子重力 (Liouville Quantum Gravity, LQG; 命名源於 Joseph Liouville (1809$\sim$1882)), 架構如下： 指標集 $\alpha \in {\cal A}$ 的場為

$$\phi_\alpha (z):=e^{\alpha \mu (z)},\quad z\in {\Bbb S}.$$

協變函數為

$$\langle \phi_{\alpha_1}(z_1) \cdots \phi_{\alpha_n}(z_n)\rangle:=\int \{e^{\alpha _1 \mu (z_1)} \cdots e^{\alpha _n \mu (z_n)}\}e^{-S_L (\mu )} D\mu ,$$

上式中, $D\mu$ 表路徑積分 (path integral): $\mu$ 為定義於 ${\Bbb S}$ 上的函數 (看成一個路徑), 積分為 "路徑全體上的 Lebesgue 積分" (源於費曼的重要構思和工作)。 $S_L (\mu )$ 是 Lagrange 作用量：

$$S_L (\mu ):=\frac 1{4\pi} \int_{\Bbb S} (|\nabla_g \mu |^2+2Q\mu (z)+4\pi \Lambda e^{\gamma \mu (z)})g(z)dz ;$$

上式中, $\Lambda$ 是對應的 "宇宙學常數" (註：愛因斯坦場方程式所出現的宇宙學常數 $\Lambda =1.466\times 10^{-52} (m^{-2})$); $Q := \gamma /2+2/\gamma $, $0\lt\gamma \lt\sqrt{2\cdot d}=2$, $d=2$ (${\Bbb S}$ 的維度); $g (z)$ 為標準度量之密度函數。 上式右項第一式表

$$\nabla_g \mu (z):=\frac 1{g(z)} \nabla _z \mu (z),$$

是以, LQG 為一個有交互作用的量子場, 交互作用項為

$$\int_{\Bbb S} e^{\gamma \mu (z)} g(z)dz .$$

$S_L (\mu )$ 的定義式中, 右項第二式的 2, 來自 ${\Bbb S}$ 的曲率, 若是標準度量密度函數, 改成一般的密度函數 $g$, 則 2 變更成里奇曲率 (Ricci curvature)

$$R_g (z):=-\frac 1{g(z)} \Delta _z \ln g(z).$$

我們的機率角色現在上場, 如下：

所謂 "路徑全體上的 Lebesgue 積分" $D\mu$, 可以搭配 $S_L (\mu )$ 定義式之右邊第一項, 成為有數學定義的量子場, 高斯自由場 (Gaussian Free Field, GFF); 這源於 Barry Simon (1946$\sim$) 之經典名著 固定值。 首先, 我們說明, 何以有高斯這詞 ; 這是因為我們作分部積分, 可以有以下的 (註：可用一維的分部積分作比較)：

$$e^{(-1/4\pi)\int_{{\Bbb R}^2} |\nabla_g \mu |^2 (z)g(z)dz} D\mu =e^{(1/4\pi)\int_{{\Bbb R}^2}\mu (z)\Delta _g \mu (z)g(z)dz}D\mu ,$$

而上式右項, 形式上為一個變異數為 $2\pi (-\Delta _g )^{-1}$ 的均值零高斯變量。

定義： $\mathbb{S}$ 上的 GFF, 指一個以下列共變期望値所定義出的均值零高斯場 (mean zero Gaussian field) $X_g (z)$ : 對任何 $f,h\in {C}^\infty (\mathbb{S})$,

\begin{align*} &\hskip -20pt E\bigg[\Big(\int_\mathbb{S} f(z)X_g (z)g(z)dz\Big)\Big(\int_\mathbb{S} h(z')X_g (z')g(z')dz'\Big)\bigg]\\ =\,&\int_\mathbb{S} \int_\mathbb{S} G_g (z,z')f(z)h(z')g(z)g(z')dzdz'; \end{align*}

$G_g (z,z')$ 為拉普拉斯算子 $\Delta_g := \nabla_g\cdot \nabla _g$ 的 Green 函數:

$$-\Delta_g G(z,\cdot)=2\pi \big(\delta_z (\cdot)-(1/4\pi)\big),\quad \int_\mathbb{S} G_g (z,z')g(z,z')dz'=0;\quad \forall\, z\in {\mathbb{S}}.$$

$G_g (z,z')$ 的明確式則是 ：

$$G_g (z,z')=\ln \frac{(1+|z|^2)^{1/2} (1+|z'|^2 )^{1/2}}{|z-z'|}.$$

說明：

1. 自由場, 意指各成員沒有交互作用, 這通常作為建構一個場的基石; 由此, 加上一個交互作用作用項, 再堆疊上另一個交互作用項, 等等, 若是有涉及無窮, 則施以重正化手術; 這是典型的物理建構。 但是, 其數學的嚴格呈現, 則是數學者的興趣和工作。
2. 一個高斯系統, 由均值和協變決定, 在 GFF 定義中, 將 $f$ 取為常值 1, 可以得到均值零。 又, 上述的 GFF, 就是一個隨機荷布 $(C^\infty (\mathbb{S})$ 上的隨機泛函); 讀者可以參考 固定值固定值 作進階的研讀。

(五) 黎曼球上的量子重力: 建構

為了打字方便, 我們在此節中設: 上節中所出現的宇宙學常數 $\Lambda =1$。

利用前節中定義的 $\mathbb{S}$ 上的 GFF, 我們把前節出現的路徑積分定成：

$$\int F(\mu )e^{-S_L (\mu )} D\mu :=\mathbb{E}_\mu \Big[F(\mu)\big(e^{-(1/4\pi)(\int_\mathbb{S} 2Q\mu(z)g(z)dz)}\times e^{\int_\mathbb{S} e^{\gamma \mu (z)g(z)dz}}\big)\Big];$$

上式中, 期望值 $\mathbb{E}_\mu$ 表示對應於 GFF 的機率測度所作。 但是, 此定義有問題： 雙指數 (double exponential) 隨機變量的期望値會爆掉, 即無窮大。 是以, 我們作一重正化：

$$\int F(\mu )e^{-S_L (\mu )} D\mu :=\lim_{\mathbb{E} \to 0} \mathbb{E}_\mu \Big[F(\mu )(e^{-(1/4\pi )(\int_\mathbb{S} 2Q\mu (z)g(z)dz)}\times e^{(-\epsilon)^{\gamma^2/2}\int_\mathbb{S} e^{\gamma \bar\mu (z)(\epsilon)g(z)dz}})\Big];$$

上式中, $\bar\mu (z)(\epsilon)$ 表示: 對應於 "黎曼球 $\mathbb{S}$ 在標準度量 $g(z)|dz|^2$ 下, 半徑為 $\epsilon$ 之球面" (此對應於 $\mathbb{R}^2$ 中的圓盤 $D(z,\epsilon /\sqrt{g(z)})$ 的 GFF 平均值。

說明： 上述的重正化, 源於高斯變量的級距生成函數 (moment generating function): $X$ 為均值零變異數 $\sigma^2$ 高斯變量, $E[e^{tX}]=e^{(\sigma^2 t^2)/2}$, $t\in \mathbb{R}$。 但是, 若是希望有共形不變, 須把以下積分考慮進來, $\psi$ 為 $\mathbb{S}$ 上的任一 Möbius 函數及其積分

$$\int_\mathbb{S} X_g (\psi (z))g(z)dz .$$

場必須是對這些值是平移不變。 是以, 正確的重正化是：

\begin{align*} &\hskip -20pt \int F(\mu )e^{-S_L (\mu )} D\mu\\ :=\,&\lim_{\epsilon\to 0} \int_{\Bbb R} \mathbb{E}_\mu \Big[F(\mu +c)\big(e^{-(1/4\pi )(\int_S 2Q(\mu (z)+c)g(z)dz)}\times e^{(-\mathbb{E})^{\gamma ^2/2}e^{(\gamma c)}\int_\mathbb{S} e^{\gamma \bar\mu (z)(\epsilon)g(z)dz}}\big)\Big]dc. \end{align*}

最後, 我們說明： 當 $\epsilon\to 0$ 時, 上式右邊第二項對應的測度, 有個非無聊極限,

$$(-\epsilon)^{\gamma ^2/2}e^{\gamma \bar\mu (z)(\epsilon)} g(z)dz\ \Rightarrow\ M_\gamma (dz),\quad \epsilon\to 0;$$

符號 "$ \Rightarrow$" 代表測度意味的收斂, 見 固定值;上式右邊的測度

$$M_\gamma (dz):=e^{(\frac {\gamma^2}2) C}e^{\gamma \mu (z)} g(z)dz,\quad \hbox{$C$ 為某個常數；}$$

被稱為高斯乘性混沌 (Gaussian multiplicative chaos ,GMC), 是源於 Jean-Pierre Kahane (1926$\sim$2017, 生前為法國科學院院士) 的開創性論文 固定值固定值, 原先用來討論 Benoit B. Mandelbrot (1924$\sim$2010, 1993 年沃爾夫獎得主) 的碎形紊流理論。 上式的收斂, 是基於對高斯隨機變量 $\bar\mu (z)(\epsilon)$ 的二級距計算。

(六) 黎曼球上的量子重力: LQG

量子重力, 有超過十五種的論點, 參考 固定值, 例如 , 正典的 (canonical), 歐氏的 (Euclidean), 弦和超弦 (string and superstring) 的, 重正化群 (renormalization group) 的 , 量子位相 (quantum topology) 的, 以及迴圈量子重力 (loop quantum gravity, LQG), 等。 所以有兩個 LQG, 此處討論的 Liouville QG 和 loop quantum gravity, 讀者勿混淆！ 黎曼球 $\mathbb{S}$ 上的 Liouville 量子重力; 意指一個 $\mathbb{S}$ 上的共形場, 場族和協變函數 (註：時間參數巳經含在$z$中) 定義如下

\begin{align*} \phi(z):=\,&\mu (z)+c+(Q/2)\ln g(z),\\ \phi_\epsilon (z):=\,&\bar\mu (z)(\epsilon)+c+(Q/2)\ln g(z),\\ V_\alpha(z):=\,&e^{\alpha\phi(z)},\quad 0\lt\alpha,\ z\in {\Bbb S}. \end{align*}

令 $V_\alpha (z,\epsilon):=\epsilon^{\alpha^2/2} e^{\alpha\phi_\epsilon (z)}$,

\begin{align*} &\langle V_{\alpha_1} (z_1)\cdots V_{\alpha _n}(z_n)\rangle :=\\ &\frac 1{Z_g} \lim_{\epsilon\to 0} \int_\mathbb{R} \mathbb{E}_\mu \Big[\Big(\sum_{i=1}^n V_{\alpha _i}(z_i,\epsilon)\Big) \Big(e^{-(Q/4\pi)(\int_\mathbb{S} 2(\mu (z)+c)g(z)dz)}\times e^{(-\epsilon)^{\gamma^2/2} \int_\mathbb{S} e^{\gamma \phi_\epsilon (z)dz}}\Big)\Big]dc. \end{align*}

$Z_g$ 為 GFF 的分割函數 (partition function, 代表 GFF 的全質量, 名詞源於統計力學); $\mathbb{E}_\mu$ 為對 GFF 的積分 (期望值)。

定理 1： $Q := \gamma /2+2/\gamma$, $0\lt\gamma \lt\sqrt{2\cdot d}=2$, $d=2$ ($d=2$, 表示黎曼球的維度, 在 GMC 理論, 所在空間的維度可以是 $d = 1,2,3\ldots$)。 上述定義的協變函數存在之充要條件是

$$0\lt\alpha_i\lt Q,\quad i=1,\ldots,n;\quad \sum_{i=1}^n \alpha _i\gt2Q.$$

是以, 必須為 $n\ge 3$。 在此充要條件下, 協變函數為

\begin{align*} &\frac 1{Z_g} e^{(1/2)\sum_{i\not=j} \alpha _i \alpha _j G_g (z_i,z_j)} \prod_{i=1}^n g(z_i )^{\frac{\alpha_i (2Q-\alpha_i)}4} \Gamma\Big(\frac{\sum_{i=1}^n \alpha _i\!-\!Q}{\gamma} ,1\Big)\mathbb{E}_\mu \Big[Z_{(z_i,\alpha _i)}(\mathbb{S})^{-\frac{\sum_{i=1}^n \alpha _i-2Q}{\gamma}}\Big];\\ &\Gamma (\nu ,\mu )=\int_0^\infty e^{-\mu x} x^{\nu -1} dx,\quad \hbox{ (雙 Gamma 函數);}\\ &Z_{(z_i,\alpha _i)} (dz)=e^{\gamma \sum_{j=1}^n \alpha _j G_g (z_j,z)} M_\gamma (dz). \end{align*}

定理 2： LQG 的共形權重為

$$\Delta _{\alpha _i}=\frac {\alpha_i}2 (Q-\frac{\alpha_i}2),\ i=1,\ldots,n;$$

是以, 對任一 $\mathbb{S}$ 上的 Möbius 函數 $\psi$,

$$\langle V_{\alpha_1} (\psi (z_1))\cdots V_{\alpha _n}(\psi (z_n))\rangle =\prod_{i=1}^n |\psi' (z_i)|^{-2\Delta_{\alpha _i}} \langle V_{\alpha _1}(z_1)\cdots V_{\alpha _n}(z_n)\rangle .$$

結語： 在本文中, 我們所討論的, 僅是量子重力的一個機率面向, 在 Quanta Magazine 有量子重力眾多的報導, 讀者可自行選擇其它的面向來了解此主題。 在文中, 我們以費曼路徑積分作為量子場建構的切入點, 這也只是量子場論的一個面向, 參考 固定值[Recommended Books and Resources]。 本文以泛函分析和機率論作為立論基礎, 且儘可能避開一些引起困擾的名詞。 Michael Talagrand 在 固定值 之序言 (Introduction) 中寫道： The well-known obstacle of the difference of language and culture between mathematics and physics is all too real. To a mathematician's eye, some physics textbooks are chock-full of somewhat imprecise statements made about rather ill-defined quantities. It is not rare that these statements are simply untrue if taken at face value. Moreover arguments full of implicit assumptions are presented in the most authoritative manner (數學和物理之間言語和文化的差異, 所造成的障礙, 真的是確切的真實。 以一個數學者的眼光, 一些物理教科書, 充塞了由品質頗有問題的不精確敘述; 這些敍述就其字面上言, 根本就不乏不正確者。 再者, 他們是以一種極威權的方式, 來作充滿不明確假設下的論證。) 是耶, 非耶, 請讀者自行判斷。

我們以兩個說明作為本文的結束。 1. 在前言中, 我們提到量子重力理論是先離散化, 再取某個極限來得到連續形態的結果, 但是上文中卻看不到 ? 事實上是, 我們採用的費曼路徑積分面向, 本質上, 就已經把離散化含括在其內。 2. 著名的科普播客 Lex Fridman 最近訪談陶哲軒(Terence Tao, 2006年費爾茲奬得主), 見網站參考資料 [b], 也談及 TOE 的前景。 陶非常樂觀; 他認為物理學之進程, 就是一串 unification 的過程。 量子重力是否確是 TOE 的最後一塊拼圖, 且它是否確能完成 ? 我們拭目以待之外, 也不妨試著參一腳。

參考文獻

本文作者為國立台灣大學數學系退休教授